1.
Introduction
In this paper, we study the categorification of VB-Lie algebroids and VB-Courant algebroids, and establish the relations between these higher structures and super representations of Lie 2-algebroids, tangent prolongations of Lie 2-algebroids, N-manifolds of degree 3, tangent prolongations of CLWX 2-algebroids and higher analogues of the string Lie 2-algebra.
1.1. Lie n-algebroids, Courant algebroids and CLWX 2-algebroids
An NQ-manifold is an N-manifold M together with a degree 1 vector field Q satisfying [Q,Q]=0. It is well known that a degree 1 NQ manifold corresponds to a Lie algebroid. Thus, people usually think that
Some work in this direction appeared in [54]. Strictly speaking, a Lie n-algebroid gives arise to an NQ-manifold only after a degree 1 shift, just as a Lie algebroid A corresponds to a degree 1 NQ manifold A[1]. To make the shifting manifest, and to present a Lie n-algebroid in a way more used to differential geometers, that is, to use the language of vector bundles, the authors introduced the notion of a split Lie n-algebroid in [52] to study the integration of a Courant algebroid. The equivalence between the category of split NQ manifolds and the category of split Lie n-Lie algebroids was proved in [5]. The language of split Lie n-algebroids has slowly become a useful tool for differential geometers to study problems related to NQ-manifolds ([14,24,25]). Since Lie 2-algebras are the categorification of Lie algebras ([4]), we will view Lie 2-algebroids as the categorification of Lie algebroids.
To study the double of a Lie bialgebroid ([42]), Liu, Weinstein and Xu introduced the notion of a Courant algebroid in [35]. See [44] for an alternative definition. There are many important applications of Courant algebroids, e.g. in generalized complex geometry ([8,17,22]), Poisson geometry ([33]), moment maps ([9]), Poisson-Lie T-duality ([47,48]) and topological field theory ([46]). In [34], the authors introduced the notion of a CLWX 2-algebroid (named after Courant-Liu-Weinstein-Xu), which can be viewed as the categorification of a Courant algebroid. Furthermore, CLWX 2-algebroids are in one-to-one correspondence with QP-manifolds (symplectic NQ-manifolds) of degree 3, and have applications in the fields theory. See [23] for more details. The underlying algebraic structure of a CLWX 2-algebroid is a Leibniz 2-algebra, or a Lie 3-algebra. There is also a close relationship between CLWX 2-algebroids and the first Pontryagin classes of quadratic Lie 2-algebroids, which are represented by closed 5-forms. More precisely, as the higher analogue of the results given in [6,13], it was proved in [49] that the first Pontryagin class of a quadratic Lie algebroid is the obstruction of the existence of a CLWX-extension.
1.2. VB-Lie algebroids and VB-Courant algebroids
Double structures in geometry can be traced back to the work of Ehresmann on connection theory, and have been found many applications in Poisson geometry. See [40] for more details. We use the word "doublization" to indicate putting geometric structures on double vector bundles in the sequel. In [19], Gracia-Saz and Mehta introduced the notion of a VB-Lie algebroid, which is equivalent to Mackenzie's LA-vector bundle ([38]). A VB-Lie algebroid is a Lie algebroid object in the category of vector bundles and one important property is that it is closely related to superconnection (also called representation up to homotopy [1,2]) of a Lie algebroid on a 2-term complex of vector bundles. Recently, the relation between VB-algebroid morphisms and representations up to homotopy were studied in [15].
In his PhD thesis [32], Li-Bland introduced the notion of a VB-Courant algebroid which is the doublization of a Courant algebroid [35], and established abstract correspondence between NQ-manifolds of degree 2 and VB-Courant algebroids. Then in [24], Jotz Lean provided a more concrete description of the equivalence between the category of split Lie 2-algebroids and the category of decomposed VB-Courant algebroids.
Double structures, such as double principle (vector) bundles ([12,16,26,30]), double Lie algebroids ([18,37,38,39,41,55]), double Lie groupoids ([43]), VB-Lie algebroids ([7,19]) and VB-Lie groupoids ([7,20]) became more and more important recently and are widely studied. In particular, the Lie theory relating VB-Lie algebroids and VB-Lie groupoids, i.e. their relation via differentiation and integration, is established in [7].
1.3. Summary of the results and outline of the paper
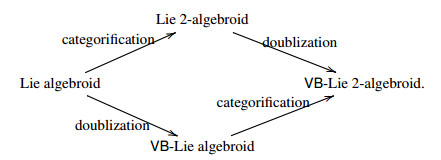
In this paper, we combine the aforementioned higher structures and double structures. First we introduce the notion of a VB-Lie 2-algebroid, which can be viewed as the categorification of a VB-Lie algebroid, or doublization of a Lie 2-algebroid:
We show that the tangent prolongation of a Lie 2-algebroid is a VB-Lie 2-algebroid and the graded fat bundle associated to a VB-Lie 2-algebroid is Lie 2-algebroid. Consequently, the graded jet bundle of a Lie 2-algebroid is also a Lie 2-algebroid. In [19], the authors showed that a VB-Lie algebroid is equivalent to a flat superconnection (representation up to homotopy ([1])) of a Lie algebroid on a 2-term complex of vector bundles after choosing a splitting. Now for a VB-Lie 2-algebroid, we establish a higher analogous result, namely, we show that after choosing a splitting, it is equivalent to a flat superconnection of a Lie 2-algebroid on a 3-term complex of vector bundles.
Then we introduce the notion of a VB-CLWX 2-algebroid, which can be viewed as both the doublization of a CLWX 2-algebroid and the categorification of a VB-Courant algebroid. More importantly, we show that after choosing a splitting, there is a one-to-one correspondence between VB-CLWX 2-algebroids and split Lie 3-algebroids (NQ-manifolds of degree 3). The tangent prolongation of a CLWX 2-algebroid is a VB-CLWX 2-algebroid naturally. We go on defining E-CLWX 2-algebroid, which can be viewed as the categorification of an E-Courant algebroid introduced in [11]. As a higher analogue of the result that associated to a VB-Courant algebroid, there is an E-Courant algebroid [24,31], we show that on the graded fat bundle associated to a VB-CLWX 2-algebroid, there is an E-CLWX 2-algebroid structure naturally. Similar to the case of a CLWX 2-algebroid, an E-CLWX 2-algebroid also gives rise to a Lie 3-algebra naturally. Thus through the following procedure:
we can construct a Lie 3-algebra from a Lie 3-algebra. We obtain new interesting examples, including the higher analogue of the string Lie 2-algebra.
The paper is organized as follows. In Section 2, we recall double vector bundles, VB-Lie algebroids and VB-Courant algebroids. In Section 3, we introduce the notion of a VB-Lie 2-algebroid, and show that both the graded side bundle and the graded fat bundle are Lie 2-algebroids. The tangent prolongation of a Lie 2-algebroid is a VB-Lie 2-algebroid naturally. In Section 4, first we construct a strict Lie 3-algebroid End(E)=(End−2(E),End−1(E),D(E),p,d,[⋅,⋅]C) from a 3-term complex of vector bundles E:E−2π⟶E−1π⟶E0 and then we define a flat superconnection of a Lie 2-algebroid A=(A−1,A0,a,l1,l2,l3) on this 3-term complex of vector bundles to be a morphism from A to End(E). We show that after choosing a splitting, VB-Lie 2-algebroids one-to-one correspond to flat superconnections of a Lie 2-algebroid on a 3-term complex of vector bundles. In Section 5, we introduce the notion of a VB-CLWX 2-algebroid and show that after choosing a splitting, there is a one-to-one correspondence between VB-CLWX 2-algebroids and Lie 3-algebroids. In Section 6, we introduce the notion of an E-CLWX 2-algebroid and show that the graded fat bundle associated to a VB-CLWX 2-algebroid is an E-CLWX 2-algebroid naturally. In particular, the graded jet bundle of a CLWX 2-algebroid, which is the graded fat bundle of the tangent prolongation of this CLWX 2-algebroid, is a T∗M-CLWX 2-algebroid. We can also obtain a Lie 3-algebra from an E-CLWX 2-algebroid. In Section 7, we construct a Lie 3-algebra from a given Lie 3-algebra using the theories established in Section 5 and Section 6, and give interesting examples. In particular, we show that associated to a quadratic Lie 2-algebra, we can obtain a Lie 3-algebra, which can be viewed as the higher analogue of the string Lie 2-algebra.
2.
Preliminaries
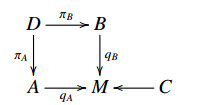
See [40,Definition 9.1.1] for the precise definition of a double vector bundle. We denote a double vector bundle
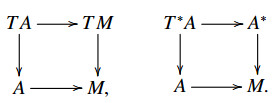
with core C by (D;A,B;M). We use DB and DA to denote vector bundles D⟶B and D⟶A respectively. For a vector bundle A, both the tangent bundle TA and the cotangent bundle T∗A are double vector bundles:
A morphism of double vector bundles
consists of maps φ: D→D′, fA:A→A′, fB:B→B′, fM:M→M′, such that each of (φ,fB), (φ,fA), (fA,fM) and (fB,fM) is a morphism of the relevant vector bundles.
The space of sections ΓB(D) of the vector bundle DB is generated as a C∞(B)-module by core sections ΓcB(D) and linear sections ΓlB(D). See [41] for more details. For a section c:M→C, the corresponding core section c†:B→D is defined as
where ˉ⋅ means the inclusion C↪D. A section ξ:B→D is called linear if it is a bundle morphism from B→M to D→A over a section X∈Γ(A). We will view B∗⊗C both as Hom(B,C) and Hom(C∗,B∗) depending on what it acts. Given ψ∈Γ(B∗⊗C), there is a linear section ˜ψ:B→D over the zero section 0A:M→A given by
Note that ΓlB(D) is locally free as a C∞(M)-module. Therefore, ΓlB(D) is equal to Γ(ˆA) for some vector bundle ˆA→M. The vector bundle ˆA is called the fat bundle of the double vector bundle (D;A,B;M). Moreover, we have the following short exact sequence of vector bundles over M
Definition 2.1. ([19,Definition 3.4]) A VB-Lie algebroid is a double vector bundle (D;A,B;M) equipped with a Lie algebroid structure (DB,a,[⋅,⋅]D) such that the anchor a:D⟶TB is linear, i.e. a:(D;A,B;M)⟶(TB;TM,B;M) is a morphism of double vector bundles, and the Lie bracket [⋅,⋅]D is linear:
The vector bundle A⟶M is then also a Lie algebroid, with the anchor a and the bracket [⋅,⋅]A defined as follows: if ξ1,ξ2 are linear over X1,X2∈Γ(A), then the bracket [ξ1,ξ2]D is linear over [X1,X2]A.
Definition 2.2. ([32,Definition 3.1.1]) A VB-Courant algebroid is a metric double vector bundle (D;A,B;M) such that (DB,S, [[⋅,⋅]],ρ) is a Courant algebroid and the following conditions are satisfied:
(i) The anchor map ρ:D→TB is linear;
(ii) The Courant bracket is linear. That is
Theorem 2.3. ([32,Proposition 3.2.1]) There is a one-to-one correspondence between Lie 2-algebroids and VB-Courant algebroids.
3.
VB-Lie 2-algebroids
In this section, we introduce the notion of a VB-Lie 2-algebroid, which can be viewed as the categorification of a VB-Lie algebroid introduced in [19]. First we recall the notion of a Lie n-algebroid. See [28,29] for more information of L∞-algebras.
Definition 3.1. ([52,Definition 2.1]) A split Lie n-algebroid is a non-positively graded vector bundle A=A0⊕A−1⊕⋯⊕A−n+1 over a manifold M equipped with a bundle map a:A0⟶TM (called the anchor), and n+1 many brackets li:Γ(∧iA)⟶Γ(A) with degree 2−i for 1≤i≤n+1, such that
1. Γ(A) is an n-term L∞-algebra:
where the summation is taken over all (i,k−i)-unshuffles Sh−1i,k−i with i≥1 and "Ksgn(σ)" is the Koszul sign for a permutation σ∈Sk, i.e.
2. l2 satisfies the Leibniz rule with respect to the anchor a:
3. For i≠2, li's are C∞(M)-linear.
Denote a split Lie n-algebroid by (A−n+1,⋯,A0,a,l1,⋯,ln+1), or simply by A. We will only use a split Lie 2-algebroid (A−1,A0,a,l1,l2,l3) and a split Lie 3-algebroid (A−2,A−1,A0,a,l1,l2,l3,l4). For a split Lie n-algebroid, we have a generalized Chevalley-Eilenberg complex (Γ(Symm(A[1])∗),δ). See [5,52] for more details. Then A[1] is an NQ-manifold of degree n. A split Lie n-algebroid morphism A→A′ can be defined to be a graded vector bundle morphism f:Symm(A[1])→Symm(A′[1]) such that the induced pull-back map f∗:C(A′[1])→C(A[1]) between functions is a morphism of NQ manifolds. However it is rather complicated to write down a morphism between split Lie n-algebroids in terms of vector bundles, anchors and brackets, please see [5,Section 4.1] for such details. We only give explicit formulas of a morphism from a split Lie 2-algebroid to a strict split Lie 3-algebroid (l3=0,l4=0) and this is what we will use in this paper to define flat superconnections.
Definition 3.2. Let A=(A−1,A0,a,l1,l2,l3) be a split Lie 2-algebroid and A′=(A′−2,A′−1,A′0,a′,l′1,l′2) a strict split Lie 3-algebroid. A morphism F from A to A′ consists of:
∙ a bundle map F0:A0⟶A′0,
∙ a bundle map F1:A−1⟶A′−1,
∙ a bundle map F20:∧2A0⟶A′−1,
∙ a bundle map F21:A0∧A−1⟶A′−2,
∙ a bundle map F3:∧3A0⟶A′−2,
such that for all X0,Y0,Z0,X0i∈Γ(A0), i=1,2,3,4, X1,Y1∈Γ(A−1), we have
and
where k<l and {k,l}∩{i,j}=∅.
Let (A−1,A0,a,l1,l2,l3) be a split Lie 2-algebroid. Then for all X0,Y0∈Γ(A0) and X1∈Γ(A−1), Lie derivatives L0X0:Γ(A∗−i)⟶Γ(A∗−i), i=0,1, L1X1:Γ(A∗−1)⟶Γ(A∗0) and L3X0,Y0:Γ(A∗−1)⟶Γ(A∗0) are defined by
for all α0∈Γ(A∗0),α1∈Γ(A∗−1),Y1∈Γ(A−1),Z0∈Γ(A0). If (A∗[1],a,l1,l2,l3) is also a split Lie 2-algebroid, we denote by L0,L1,L3,δ∗ the corresponding operations.
A graded double vector bundle consists of a double vector bundle of degree −1 and a double vector bundle of degree 0:
We denote a graded double vector bundle by (D−1;A−1,B−1;M−1D0;A0,B0;M0). Morphisms between graded double vector bundles can be defined in an obvious way. We will denote by D and A the graded vector bundles DB0⊕DB−1 and A0⊕A−1 respectively. Now we are ready to introduce the main object in this section.
Definition 3.3. A VB-Lie 2-algebroid is a graded double vector bundle
equipped with a Lie 2-algebroid structure (DB−1,DB0,a,l1,l2,l3) on D such that
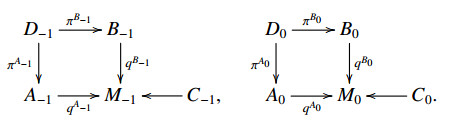
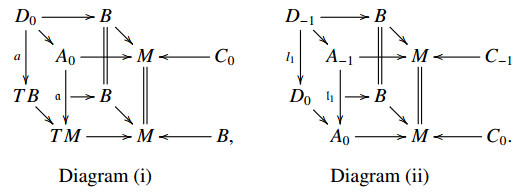
(i) The anchor a:D0⟶TB is linear, i.e. we have a bundle map a:A0⟶TM such that (a;a,idB;idM) is a double vector bundle morphism (see Diagram (i));
(ii) l1 is linear, i.e. we have a bundle map l1:A−1⟶A0 such that (l1;l1,idB;idM) is a double vector bundle morphism (see Diagram (ii));
(iii) l2 is linear, i.e.
(iv) l3 is linear, i.e.
Since Lie 2-algebroids are the categorification of Lie algebroids, VB-Lie 2-algebroids can be viewed as the categorification of VB-Lie algebroids.
Recall that if (D;A,B;M) is a VB-Lie algebroid, then A is a Lie algebroid. The following result is its higher analogue.
Theorem 3.4. Let (D−1;A−1,B;MD0;A0,B;M) be a VB-Lie 2-algebroid. Then
is a split Lie 2-algebroid, where l2 is defined by the property that if ξ01,ξ02,ξ0∈ΓlB(D0) are linear sections over X01,X02,X0∈Γ(A0), and ξ1∈ΓlB(D−1) is a linear section over X1∈Γ(A−1), then l2(ξ01,ξ02)∈ΓlB(D0) is a linear section over l2(X01,X02)∈Γ(A0) and l2(ξ0,ξ1)∈ΓlB(D−1) is a linear section over l2(X0,X1)∈Γ(A−1). Similarly, l3 is defined by the property that if ξ01,ξ02,ξ03∈ΓlB(D0) are linear sections over X01,X02,X03∈Γ(A0), then l3(ξ01,ξ02,ξ03)∈ΓlB(D−1) is a linear section over l3(X01,X02,X03)∈Γ(A−1).
Proof. Since l2 is linear, for any ξi∈ΓlB(D−i) satisfying πA−i(ξi)=0, we have
This implies that l2 is well-defined. Similarly, l3 is also well-defined.
By the fact that l1:D−1⟶D0 is a double vector bundle morphism over l1:A−1⟶A0, we can deduce that (Γ(A−1),Γ(A0),l1,l2,l3) is a Lie 2-algebra. We only give a proof of the property
The other conditions in the definition of a Lie 2-algebra can be proved similarly. In fact, let ξ0∈ΓlB(D0),ξ1∈ΓlB(D−1) be linear sections over X0,X1 respectively, then by the equality l1(l2(ξ0,ξ1))=l2(ξ0,l1(ξ1)), we have
Since l1:D−1⟶D0 is a double vector bundle morphism over l1:A−1⟶A0, the left hand side is equal to
and the right hand side is equal to
Thus, we deduce that (3.2) holds.
Finally, for all X0∈Γ(A0), Yi∈Γ(A−i) and f∈C∞(M), let ξ0∈ΓlB(D0) and ηi∈ΓlB(D−i),i=0,1 be linear sections over X0 and Yi. Then q∗B(f)ηi is a linear section over fYi. By the fact that a is a double vector bundle morphism over a, we have
Therefore, (A−1,A0,a,l1,l2,l3) is a Lie 2-algebroid.
Remark 1. By the above theorem, we can view a VB-Lie 2-algebroid as a Lie 2-algebroid object in the category of double vector bundles.
Consider the associated graded fat bundle ˆA−1⊕ˆA0, obviously we have
Proposition 1. Let (D−1;A−1,B;MD0;A0,B;M) be a VB-Lie 2-algebroid. Then (ˆA−1,ˆA0,ˆa,ˆl1,ˆl2,ˆl3) is a split Lie 2-algebroid, where ˆa=a∘pr and ˆl1,ˆl2,ˆl3 are the restriction of l1,l2,l3 on linear sections respectively.
Consequently, we have the following exact sequences of split Lie 2-algebroids:
It is helpful to give the split Lie 2-algebroid structure on B∗⊗C−1⊕B∗⊗C0. Since l1 is linear, it induces a bundle map lC1:C−1⟶C0. The restriction of ˆl1 on B∗⊗C−1 is given by
Since the anchor a:D0⟶TB is a double vector bundle morphism, it induces a bundle map ϱ:C0⟶B via
Then by the Leibniz rule, we deduce that the restriction of ˆl2 on Γ(B∗⊗C−1⊕B∗⊗C0) is given by
for all ϕ0,ψ0∈Γ(B∗⊗C0)=Γ(Hom(B,C0)), ψ1∈Γ(B∗⊗C−1)=Γ(Hom(B,C−1)). Since l3 is linear, the restriction of l3 on B∗⊗C−1⊕B∗⊗C0 vanishes. Obviously, the anchor is trivial. Thus, the split Lie 2-algebroid structure on B∗⊗C−1⊕B∗⊗C0 is exactly given by (3.4), (3.6) and (3.7). Therefore, B∗⊗C−1⊕B∗⊗C0 is a graded bundle of strict Lie 2-algebras.
An important example of VB-Lie algebroids is the tangent prolongation of a Lie algebroid. Now we explore the tangent prolongation of a Lie 2-algebroid. Recall that for a Lie algebroid A⟶M, TA is a Lie algebroid over TM. A section σ:M⟶A gives rise to a linear section σT≜dσ:TM⟶TA and a core section σC:TM⟶TA by contraction. Any section of TA over TM is generated by such sections. A function f∈C∞(M) induces two types of functions on TM by
where q:TM⟶M is the projection. We have the following relations about the module structure:
In particular, for A=TM, we have
for all X∈X(M). See [32,Example 2.5.4] and [40] for more details.
Now for split Lie 2-algebroids, we have
Proposition 2. Let A=(A−1,A0,a,l1,l2,l3) be a split Lie 2-algebroid. Then
is a split Lie 2-algebroid over TM, where a:TA0⟶TTM is given by
l1:ΓTM(TA−1)⟶ΓTM(TA0) is given by
l2:ΓTM(TA−i)×ΓTM(TA−j)⟶ΓTM(TA−(i+j)) is given by
and l3:∧3ΓTM(TA0)⟶ΓTM(TA−1) is given by
and l3(σ0T,τ0C,ς0C)=0, for all σ0,τ0,ς0∈Γ(A0) and σ1,τ1∈Γ(A−1). Moreover, we have the following VB-Lie 2-algebroid:
Proof. By the fact that A=(A−1,A0,a,l1,l2,l3) is a split Lie 2-algebroid, it is straightforward to deduce that (TA−1,TA0,a,l1,l2,l3) is a split Lie 2-algebroid over TM. Moreover, a,l1,l2,l3 are all linear, which implies that it is a VB-Lie 2-algebroid.
The associated fat bundles of double vector bundles (TA−1;A−1,TM;M) and (TA0;A0,TM;M) are the jet bundles JA−1 and JA0 respectively. By Proposition 2 and Proposition 1, we obtain the following result, which is the higher analogue of the fact that the jet bundle of a Lie algebroid is a Lie algebroid.
Corollary 1. Let (A−1,A0,a,l1,l2,l3) be a split Lie 2-algebroid. Then we obtain that (JA−1,JA0,ˆa,ˆl1,ˆl2,ˆl3) is a split Lie 2-algebroid, where ˆa,ˆl1,ˆl2,ˆl3 is given by
for all σ0,τ0,ζ0∈Γ(A0) and τ1∈Γ(A−1).
4.
Superconnections of a split Lie 2-algebroid on a 3-term complex of vector bundles
In the section, we introduce the notion of a superconnection of a split Lie 2-algebroid on a 3-term complex of vector bundles, which generalizes the notion of a superconnection of a Lie algebroid on a 2-term complex of vector bundles studied in [19]. We show that a VB-Lie 2-algebroid structure on a split graded double vector bundle is equivalent to a flat superconnection of a split Lie 2-algebroid on a 3-term complex of vector bundles.
Denote a 3-term complex of vector bundles E−2π⟶E−1π⟶E0 by E. Sections of the covariant differential operator bundle D(E) are of the form d=(d0,d1,d2), where di:Γ(E−i)⟶Γ(E−i) are R-linear maps such that there exists X∈X(M) satisfying
Equivalently, D(E)=D(E0)×TMD(E−1)×TMD(E−2). Define p:D(E)⟶TM by
Then the covariant differential operator bundle D(E) fits the following exact sequence:
Denote by End−1(E)=Hom(E0,E−1)⊕Hom(E−1,E−2). Denote by End−2(E)=Hom(E0,E−2). Define d:End−2(E)⟶End−1(E) by
and define d:End−1(E)⟶D(E) by
Then we define a degree 0 graded symmetric bracket operation [⋅,⋅]C on the section space of the graded bundle End−2(E)⊕End−1(E)⊕D(E) by
Denote by Dπ(E)⊂D(E) the subbundle of D(E) whose section d∈Γ(Dπ(E)) satisfying π∘d=d∘π, or in term of components,
It is obvious that Γ(Dπ(E)) is closed under the bracket operation [⋅,⋅]C and
Then it is straightforward to verify that
Theorem 4.1. Let E−2π⟶E−1π⟶E0 be a 3-term complex of vector bundles over M. Then (End−2(E),End−1(E),Dπ(E),p,d,[⋅,⋅]C) is a strict split Lie 3-algebroid.
With above preparations, we give the definition of a superconnection of a split Lie 2-algebroid on a 3-term complex of vector bundles as follows.
Definition 4.2 A superconnection of a split Lie 2-algebroid (A−1,A0,a,l1,l2,l3) on a 3-term complex of vector bundles E−2π⟶E−1π⟶E0 consists of:
∙ a bundle morphism F0:A0⟶Dπ(E),
∙ a bundle morphism F1:A−1⟶End−1(E),
∙ a bundle morphism F20:∧2A0⟶End−1(E),
∙ a bundle morphism F21:A0∧A−1⟶End−2(E),
∙ a bundle morphism F3:∧3A0⟶End−2(E).
A superconnection is called flat if (F0,F1,F20,F21,F3) is a Lie n-algebroid morphism from the split Lie 2-algebroid (A−1,A0,a,l1,l2,l3) to the strict split Lie 3-algebroid (End−2(E),End−1(E),Dπ(E),p,d,[⋅,⋅]C).
Remark 2. If the split Lie 2-algebroid reduces to a Lie algebroid A and the 3-term complex reduces to a 2-term complex E−1π⟶E0, a superconnection will only consists of
∙ a bundle morphism F0=(F00,F01):A⟶Dπ(E),
∙ a bundle morphism F20:∧2A0⟶Hom(E0,E−1).
Thus, we recover the notion of a superconnection (also called representation up to homotopy if it is flat) of a Lie algebroid on a 2-term complex of vector bundles. See [1,19] for more details.
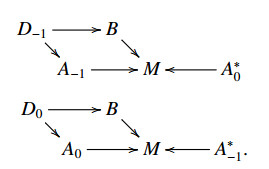
Now we come back to VB-Lie 2-algebroids. Let (DB−1,DB0,a,l1,l2,l3) be a VB-Lie 2-algebroid structure on the graded double vector bundle (D−1;A−1,B;MD0;A0,B;M). Recall from Theorem 3.4 and Proposition 1 that both (A−1,A0,a,l1,l2,l3) and (ˆA−1,ˆA0,ˆa,ˆl1,ˆl2,ˆl3) are split Lie 2-algebroids.
Choose a horizontal lift s=(s0,s1):A0⊕A−1⟶ˆA0⊕ˆA−1 of the short exact sequence of split Lie 2-algebroids (3.3). Define ∇B:A0⟶D(B) by
Since for all ϕ0∈Γ(B∗⊗C0), we have ˆa(ϕ0)=0, it follows that ∇B is well-defined.
We define ∇0:A0⟶D(C0) and ∇1:A0⟶D(C−1) by
for all X0∈Γ(A0),c0∈Γ(C0),c1∈Γ(C−1). Define Υ1:A−1⟶Hom(B,C0) and Υ2:A−1⟶Hom(C0,C−1) by
for all X1∈Γ(A−1),c0∈Γ(C0). Since l2 is linear, ∇0, ∇1 and Υ are well-defined.
Define R0:∧2Γ(A0)⟶Γ(Hom(B,C0)), Λ:∧2Γ(A0)⟶Γ(Hom(C0,C−1)) and R1:Γ(A0)∧Γ(A−1)⟶Γ(Hom(B,C−1)) by
for all X0,Y0∈Γ(A0) and Y1∈Γ(A−1) Finally, define Ξ:∧3Γ(A0)⟶Hom(B,C−1) by
By the equality l1l2(s0(X0),c1)=l2(s0(X0),lC1(c1)), we obtain
By the fact that a:D0⟶TB preserves the bracket operation, we obtain
which implies that
By (4.14) and (4.15), we deduce that (∇BX0,∇0X0,∇1X0)∈D(E), where E is the 3-term complex of vector bundles C−1lC1⟶C0ϱ⟶B. Then we obtain a superconnection (F0,F1,F20,F21,F3) of the Lie 2-algebroid (A−1,A0,a,l1,l2,l3) on the 3-term complex of vector bundles C−1lC1⟶C0ϱ⟶B, where
Theorem 4.3. There is a one-to-one correspondence between VB-Lie 2-algebroids (D−1;A−1,B;MD0;A0,B;M) and flat superconnections (F0,F1,F20,F21,F3) of the split Lie 2-algebroid (A−1,A0,a,l1,l2,l3) on the 3-term complex of vector bundles C−1lC1⟶C0ϱ⟶B by choosing a horizontal lift s=(s0,s1):A0⊕A−1⟶ˆA0⊕ˆA−1.
Proof. First it is obvious that
Using equalities a∘l1=0 and a∘l1=0, we have
which implies that
For ∇0, we can obtain
For ∇1, we have
By (4.17), (4.18) and (4.19), we deduce that
By straightforward computation, we have
which implies that
Similarly, we have
which implies that
and
which implies that
By (4.21), (4.22) and (4.23), we obtain
By the equality
we obtain
Furthermore, we have
By (4.25) and (4.26), we deduce that
By straightforward computation, we have
By the equality
we deduce that
By the equality
we deduce that
By (4.29) and (4.30), we obtain
Then by the equality
we deduce that
Finally, by the equality
we deduce that
By (4.16), (4.20), (4.24), (4.27), (4.28), (4.31)-(4.33), we deduce that (F0,F1,F20,F21,F3) is a morphism from the split Lie 2-algebroid (A−1,A0,a,l1,l2,l3) to the strict split Lie 3-algebroid
Conversely, let (A−1,A0,a,l1,l2,l3) be a split Lie 2-algebroid and (F0,F1,F20,F21,F3) a flat superconnection on the 3-term complex C−1lC1⟶C0ϱ⟶B. Then we can obtain a VB-Lie 2-algebroid structure on the split graded double vector bundle (A−1⊕B⊕C−1;A−1,B;MA0⊕B⊕C0;A0,B;M). We leave the details to readers. The proof is finished.
5.
VB-CLWX 2-algebroids
In this section, first we recall the notion of a CLWX 2-algebroid. Then we explore what is a metric graded double vector bundle, and introduce the notion of a VB-CLWX 2-algebroid, which can be viewed as the categorification of a VB-Courant algebroid introduced in [32].
As a model for "Leibniz algebras that satisfy Jacobi identity up to all higher homotopies", the notion of a strongly homotopy Leibniz algebra, or a Lod∞-algebra was given in [36] by Livernet, which was further studied by Ammar and Poncin in [3]. In [50], the authors introduced the notion of a Leibniz 2-algebra, which is the categorification of a Leibniz algebra, and proved that the category of Leibniz 2-algebras and the category of 2-term Lod∞-algebras are equivalent. Due to this reason, a 2-term Lod∞-algebra will be called a Leibniz 2-algebra directly in the sequel.
Definition 5.1. ([34]) A CLWX 2-algebroid is a graded vector bundle E=E−1⊕E0 over M equipped with a non-degenerate graded symmetric bilinear form S on E, a bilinear operation ⋄:Γ(E−i)×Γ(E−j)⟶Γ(E−(i+j)), 0≤i+j≤1, which is skewsymmetric on Γ(E0)×Γ(E0), an E−1-valued 3-form Ω on E0, two bundle maps ∂:E−1⟶E0 and ρ:E0⟶TM, such that E−1 and E0 are isotropic and the following axioms are satisfied:
(i) (Γ(E−1),Γ(E0),∂,⋄,Ω) is a Leibniz 2-algebra;
(ii) for all e∈Γ(E), e⋄e=12DS(e,e), where D:C∞(M)⟶Γ(E−1) is defined by
(iii) for all e11,e12∈Γ(E−1), S(∂(e11),e12)=S(e11,∂(e12));
(iv) for all e1,e2,e3∈Γ(E), ρ(e1)S(e2,e3)=S(e1⋄e2,e3)+S(e2,e1⋄e3);
(v) for all e01,e02,e03,e04∈Γ(E0), S(Ω(e01,e02,e03),e04)=−S(e03,Ω(e01,e02,e04)).
Denote a CLWX 2-algebroid by (E−1,E0,∂,ρ,S,⋄,Ω), or simply by E. Since the section space of a CLWX 2-algebroid is a Leibniz 2-algebra, the section space of a Courant algebroid is a Leibniz algebra and Leibniz 2-algebras are the categorification of Leibniz algebras, we can view CLWX 2-algebroids as the categorification of Courant algebroids.
As a higher analogue of Roytenberg's result about symplectic NQ manifolds of degree 2 and Courant algebroids ([45]), we have
Theorem 5.2. ([34]) Let (T∗[3]A∗[2],Θ) be a symplectic NQ manifold of degree 3, where A is an ordinary vector bundle and Θ is a degree 4 function on T∗[3]A∗[2] satisfying {Θ,Θ}=0. Here {⋅,⋅} is the canonical Poisson bracket on T∗[3]A∗[2]. Then (A∗[1],A,∂,ρ,S,⋄,Ω) is a CLWX 2-algebroid, where the bilinear form S is given by
and ∂, ρ, ⋄ and Ω are given by derived brackets. More precisely, we have
See [27,53] for more information of derived brackets. Note that various kinds of geometric structures were obtained in the study of QP manifolds of degree 3, e.g. Grutzmann's H-twisted Lie algebroids [21] and Ikeda-Uchino's Lie algebroids up to homotopy [23].
Definition 5.3. A metric graded double vector bundle is a graded double vector bundle (D−1;A−1,B;MD0;A0,B;M) equipped with a degree 1 nondegenerate graded symmetric bilinear form S on the graded bundle DB−1⊕DB0 such that it induces an isomorphism between graded double vector bundles
where ⋆B means dual over B.
Given a metric graded double vector bundle, we have
In the sequel, we will always identify C0 with A∗−1, C−1 with A∗0. Thus, a metric graded double vector bundle is of the following form:
Now we are ready to put a CLWX 2-algebroid structure on a graded double vector bundle.
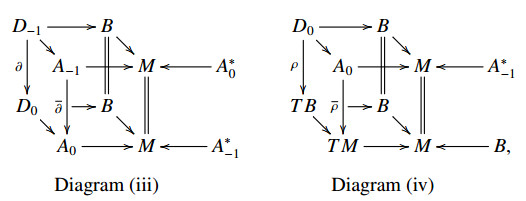
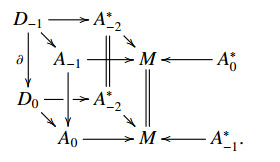
Definition 5.4. A VB-CLWX 2-algebroid is a metric graded double vector bundle
equipped with a CLWX 2-algebroid structure (DB−1,DB0,∂,ρ,S,⋄,Ω) such that
(i) ∂ is linear, i.e. there exists a unique bundle map ¯∂:A−1⟶A0 such that ∂:D−1⟶D0 is a double vector bundle morphism over ¯∂:A−1⟶A0 (see Diagram (iii));
(ii) the anchor ρ is a linear, i.e. there exists a unique bundle map ¯ρ:A0⟶TM such that ρ:D0⟶TB is a double vector bundle morphism over ¯ρ:A0⟶TM (see Diagram (iv));
(iii) the operation ⋄ is linear;
(iv) Ω is linear.
Since a CLWX 2-algebroid can be viewed as the categorification of a Courant algebroid, we can view a VB-CLWX 2-algebroid as the categorification of a VB-Courant algebroid.
Example 1. Let (A−1,A0,a,l1,l2,l3) be a Lie 2-algebroid. Let E0=A0⊕A∗−1, E−1=A−1⊕A∗0 and E=E0⊕E−1. Then (E−1,E0,∂,ρ,S,⋄,Ω) is a CLWX 2-algebroid, where ∂:E−1⟶E0 is given by
ρ:E0⟶TM is given by
the symmetric bilinear form S=(⋅,⋅)+ is given by
the operation ⋄ is given by
and the E−1-valued 3-form Ω is defined by
where L0,L1,L3 are given by (3.1). It is straightforward to see that this CLWX 2-algebroid gives rise to a VB-CLWX 2-algebroid:
Example 2. For any manifold M, (T∗[1]M,TM,∂=0,ρ=id,S,⋄,Ω=0) is a CLWX 2-algebroid, where S is the natural symmetric pairing between TM and T∗M, and ⋄ is the standard Dorfman bracket given by
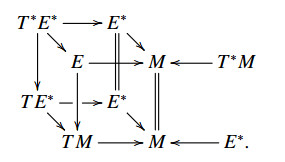
See [34,Remark 3.4] for more details. In particular, for any vector bundle E, (T∗E∗,TE∗,∂=0,ρ=id,S,⋄,Ω=0) is a CLWX 2-algebroid, which gives rise to a VB-CLWX 2-algebroid:
We have a higher analogue of Theorem 2.3:
Theorem 5.5. There is a one-to-one correspondence between split Lie 3-algebroids and split VB-CLWX 2-algebroids.
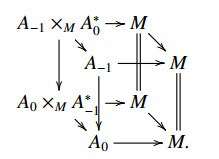
Proof. Let A=(A−2,A−1,A0,a,l1,l2,l3,l4) be a split Lie 3-algebroid. Then T∗[3]A[1] is a symplectic NQ manifold of degree 3. Note that
where A0×MA∗−1×MA∗−2 is viewed as a vector bundle over the base A∗−2 and A−1×MA∗0×MA∗−2 is its dual bundle. Denote by (xi,μj,ξk,θl,pi,μj,ξk,θl) a canonical (Darboux) coordinate on T∗[3](A0×MA∗−1×MA∗−2)[1], where xi is a smooth coordinate on M, μj∈Γ(A−2) is a fibre coordinate on A∗−2, ξk∈Γ(A∗0) is a fibre coordinate on A0, θl∈Γ(A−1) is a fibre coordinate on A∗−1 and (pi,μj,ξk,θl) are the momentum coordinates for (xi,μj,ξk,θl). About their degrees, we have
The symplectic structure is given by
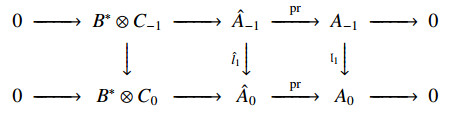
which is degree 3. The Lie 3-algebroid structure gives rise to a degree 4 function Θ satisfying {Θ,Θ}=0. By Theorem 5.2, we obtain a CLWX 2-algebroid (D−1,D0,∂,ρ,S,⋄,Ω), where D−1=A−1×MA∗0×MA∗−2 and D0=A0×MA∗−1×MA∗−2 are vector bundles over A∗−2. Obviously, they give the graded double vector bundle
The section space ΓA∗−2(D0) are generated by Γ(A∗−1) (the space of core sections) and Γ(A−2⊗A∗−1)⊕Γ(A0) (the space of linear sections) as C∞(A∗−2)-module. Similarly, The section space ΓA∗−2(D−1) are generated by Γ(A∗0) and Γ(A−2⊗A∗0)⊕Γ(A−1) as C∞(A∗−2)-module. Thus, in the sequel we only consider core sections and linear sections.
The graded symmetric bilinear form S is given by
for all e0=X0+ψ1+α1∈ΓA∗−2(D0) and e1=X1+ψ0+α0∈ΓA∗−2(D−1), where Xi∈Γ(A−i), ψi∈Γ(A−2⊗A∗−i) and αi∈Γ(A∗−i). Then it is obvious that
is a metric graded double vector bundle.
The bundle map ∂:D−1⟶D0 is given by
Thus, ∂:D−1⟶D0 is a double vector bundle morphism over l1:A−1⟶A0.
Note that functions on A∗−2 are generated by fibrewise constant functions C∞(M) and fibrewise linear functions Γ(A−2). For all f∈C∞(M) and X2∈Γ(A−2), the anchor ρ:D0⟶TA∗−2 is given by
Therefore, for a linear section X0+ψ1∈ΓlA∗−2(D0), the image ρ(X0+ψ1) is a linear vector field and for a core section α1∈Γ(A∗−1), the image ρ(α1) is a constant vector field. Thus, ρ is linear.
The bracket operation ⋄ is given by
Then it is straightforward to see that the operation ⋄ is linear.
Finally, Ω is given by
which implies that Ω is also linear.
Thus, a split Lie 3-algebroid gives rise to a split VB-CLWX 2-algebroid:
Conversely, given a split VB-CLWX 2-algebroid:
where D−1=A−1×MA∗0×MB and D0=A0×MA∗−1×MB, then we can deduce that the corresponding symplectic NQ-manifold of degree 3 is T∗[3]A[1], where A=A0⊕A−1⊕B is a graded vector bundle in which B is of degree −2, and the Q-structure gives rise to a Lie 3-algebroid structure on A. We omit details.
Remark 3. Since every double vector bundle is splitable, every VB-CLWX 2-algebroid is isomorphic to a split one. Meanwhile, by choosing a splitting, we obtain a split Lie 3-algebroid from an NQ-manifold of degree 3 (Lie 3-algebroid). Thus, we can enhance the above result to be a one-to-one correspondence between Lie 3-algebroids and VB-CLWX 2-algebroids. We omit such details.
Recall that the tangent prolongation of a Courant algebroid is a VB-Courant algebroid ([32,Proposition 3.4.1]). Now we show that the tangent prolongation of a CLWX 2-algebroid is a VB-CLWX 2-algebroid. The notations used below is the same as the ones used in Section 3.
Proposition 3. Let (E−1,E0,∂,ρ,S,⋄,Ω) be a CLWX 2-algebroid. Then we obtain that (TE−1,TE0,˜∂,˜ρ,˜S,˜⋄,˜Ω) is a CLWX 2-algebroid over TM, where the bundle map ˜∂:TE−1⟶TE0 is given by
the bundle map ˜ρ:TE0⟶TTM is given by
the degree 1 bilinear form ˜S is given by
the bilinear operation ˜⋄ is given by
and ˜Ω:∧3TE0⟶TE−1 is given by
for all σ0,τ0,ς0∈Γ(E0) and σ1,τ1∈Γ(E−1).
Moreover, we have the following VB-CLWX 2-algebroid:
Proof. Since (E−1,E0,∂,ρ,S,⋄,Ω) is a CLWX 2-algebroid, it is straightforward to deduce that (TE−1,TE0,˜∂,˜ρ,˜S,˜⋄,˜Ω) is a CLWX 2-algebroid over TM. Moveover, it is obvious that ˜∂,˜ρ,˜S,˜⋄,˜Ω are all linear, which implies that we have a VB-CLWX 2-algebroid.
6.
E-CLWX 2-algebroid
In this section, we introduce the notion of an E-CLWX 2-algebroid as the categorification of an E-Courant algebroid introduced in [11]. We show that associated to a VB-CLWX 2-algebroid, there is an E-CLWX 2-algebroid structure on the corresponding graded fat bundle.
There is an E-valued pairing ⟨⋅,⋅⟩E between the jet bundle JE and the first order covariant differential operator bundle DE defined by
Definition 6.1. Let E be a vector bundle. An E-CLWX 2-algebroid is a 6-tuple (K,∂,ρ,S,⋄,Ω), where K=K−1⊕K0 is a graded vector bundle over M and
∙ ∂:K−1⟶K0 is a bundle map;
∙ S:K⊗K⟶E is a surjective graded symmetric nondegenerate E-valued pairing of degree 1, which induces an embedding: K↪Hom(K,E);
∙ ρ:K0→DE is a bundle map, called the anchor, such that ρ⋆(JE)⊂K−1, i.e.
∙ ⋄:Γ(K−i)×Γ(K−j)⟶Γ(K−(i+j)),0≤i+j≤1 is an R-bilinear operation;
∙ Ω:∧3K0⟶K−1 is a bundle map,
such that the following properties hold:
(E1) (Γ(K),∂,⋄,Ω) is a Leibniz 2-algebra;
(E2) for all e∈Γ(K), e⋄e=12DS(e,e), where D:Γ(E)⟶Γ(K−1) is defined by
(E3) for all e11,e12∈Γ(K−1), S(∂(e11),e12)=S(e11,∂(e12));
(E4) for all e1,e2,e3∈Γ(K), ρ(e1)S(e2,e3)=S(e1⋄e2,e3)+S(e2,e1⋄e3);
(E5) for all e01,e02,e03,e04∈Γ(K0), S(Ω(e01,e02,e03),e04)=−S(e03,Ω(e01,e02,e04));
(E6) for all e01,e02∈Γ(K0), ρ(e01⋄e02)=[ρ(e01),ρ(e02)]D, where [⋅,⋅]D is the commutator bracket on Γ(DE).
A CLWX 2-algebroid can give rise to a Lie 3-algebra ([34,Theorem 3.11]). Similarly, an E-CLWX 2-algebroid can also give rise to a Lie 3-algebra. Consider the graded vector space e=e−2⊕e−1⊕e0, where e−2=Γ(E), e−1=Γ(K−1) and e0=Γ(K0). We introduce a skew-symmetric bracket on Γ(K),
which is the skew-symmetrization of ⋄.
Theorem 6.2. An E-CLWX 2-algebroid (K,∂,ρ,S,⋄,Ω) gives rise to a Lie 3-algebra (e,l1,l2,l3,l4), where li are given by
where the totally skew-symmetric T:Γ(K0)×Γ(K0)×Γ(K−1)⟶Γ(E) is given by
and ¯Ω:∧4Γ(K0)⟶Γ(E) is given by
Proof. The proof is totally parallel to the proof of [34,Theorem 3.11], we omit the details.
Let (DB−1,DB0,∂,ρ,S,⋄,Ω) be a VB-CLWX 2-algebroid on the graded double vector bundle (D−1;A−1,B;MD0;A0,B;M). Then we have the associated graded fat bundles ˆA−1⊕ˆA0, which fit the exact sequences:
Since the bundle map ∂ is linear, it induces a bundle map ˆ∂:ˆA−1⟶ˆA0. Since the anchor ρ is linear, it induces a bundle map ˆρ:ˆA0⟶DB∗, where sections of DB∗ are viewed as linear vector fields on B. Furthermore, the restriction of S on linear sections will give rise to linear functions on B. Thus, we obtain a B∗-valued degree 1 graded symmetric bilinear form ˆS on the graded fat bundle ˆA−1⊕ˆA0. Since the operation ⋄ is linear, it induces an operation ˆ⋄:ˆA−i׈A−j⟶ˆA−(i+j), 0≤i+j≤1. Finally, since Ω is linear, it induces an ˆΩ:Γ(∧3^A0)⟶ˆA−1. Then we obtain:
Theorem 6.3. A VB-CLWX 2-algebroid gives rise to a B∗-CLWX 2-algebroid structure on the corresponding graded fat bundle. More precisely, let (DB−1,DB0,∂,ρ,S,⋄,Ω) be a VB-CLWX 2-algebroid on the graded double vector bundle (D−1;A−1,B;MD0;A0,B;M) with the associated graded fat bundle ˆA−1⊕ˆA0. Then (ˆA−1,ˆA0,ˆ∂,ˆρ,ˆS,ˆ⋄,ˆΩ) is a B∗-CLWX 2-algebroid.
Proof. Since all the structures defined on the graded fat bundle ˆA−1⊕ˆA0 are the restriction of the structures in the VB-CLWX 2-algebroid, it is straightforward to see that all the axioms in Definition 6.1 hold.
Example 3. Consider the VB-CLWX 2-algebroid given in Example 2, the corresponding E-CLWX 2-algebroid is ((JE)[1],DE,∂=0,ρ=id,S=(⋅,⋅)E,⋄,Ω=0), where the graded symmetric nondegenerate E-valued pairing (⋅,⋅)E is given by
and ⋄ is given by
See [10] for more details.
Example 4. Consider the VB-CLWX 2-algebroid given in Proposition 3. The graded fat bundle is JE−1⊕JE0. It follows that the graded jet bundle associated to a CLWX 2-algebroid is a T∗M-CLWX 2-algebroid. This is the higher analogue of the result that the jet bundle of a Courant algebroid is T∗M-Courant algebroid given in [11]. See also [24] for more details. $
7.
Constructions of Lie 3-algebras
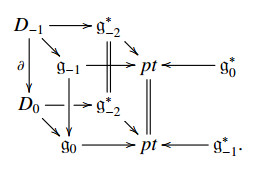
As applications of E-CLWX 2-algebroids introduced in the last section, we construct Lie 3-algebras from Lie 3-algebras in this section. Let (g−2,g−1,g0,l1,l2,l3,l4) be a Lie 3-algebra. By Theorem 5.5, the corresponding VB-CLWX 2-algebroid is given by
where D−1=g−1⊕g∗0⊕g∗−2 and D0=g0⊕g∗−1⊕g∗−2.
By Theorem 6.3, we obtain:
Proposition 4. Let (g−2,g−1,g0,l1,l2,l3,l4) be a Lie 3-algebra. Then there is an E-CLWX 2-algebroid (Hom(g0,g−2)⊕g−1,Hom(g−1,g−2)⊕g0,∂,ρ,S,⋄,Ω), where for all xi,yi,zi∈g−i, ϕi,ψi,φi∈Hom(g−i,g−2), ∂:Hom(g0,g−2)⊕g−1⟶Hom(g−1,g−2)⊕g0 is given by
ρ:Hom(g−1,g−2)⊕g0⟶gl(g−2) is given by
the g−2-valued pairing S is given by
the operation ⋄ is given by
and Ω is given by
By (7.2), it is straightforward to deduce that the corresponding D:g−2⟶Hom(g0,g−2)⊕g−1 is given by
Then by Theorem 6.2, we obtain:
Proposition 5. Let (g−2,g−1,g0,l1,l2,l3,l4) be a Lie 3-algebra. Then there is a Lie 3-algebra (¯g−2,¯g−1,¯g0,l1,l2,l3,l4), where ¯g−2=g−2, ¯g−1=Hom(g0,g−2)⊕g−1, ¯g0=Hom(g−1,g−2)⊕g0, and li are given by
where the operation D, ⋄, Ω are given by (7.6), (7.4), (7.5) respectively, T:¯g0ׯg0ׯg−1⟶g−2 is given by
and ¯Ω:∧4¯g0⟶g−2 is given by
By Proposition 5, we can give interesting examples of Lie 3-algebras.
Example 5. We view a 3-term complex of vector spaces V−2l1⟶V−1l1⟶V0 as an abelian Lie 3-algebra. By Proposition 5, we obtain the Lie 3-algebra
where li,i=1,2,3 are given by
for all x2∈V−2,ψ0+x1,ϕ0+y1,φ0+z1∈Hom(V0,V−2)⊕V−1,ψ1+x0,ϕ1+y0,φ1+z0∈Hom(V−1,V−2)⊕V0.
Example 6. (Higher analogue of the Lie 2-algebra of string type)
A Lie 2-algebra (g−1,g0,~l1,~l2,~l3) gives rise to a Lie 3-algebra (R,g−1,g0,l1,l2,l3,l4=0) naturally, where li, i=1,2,3 is given by
for all x0,y0,z0∈g0, x1,y1,z1∈g−1, and r,s∈R. By Proposition 5, we obtain the Lie 3-algebra (R,g−1⊕g∗0,g0⊕g∗−1,l1,l2,l3,l4), where li, i=1,2,3,4 are given by
for all x0,y0,z0,u0∈g0, x1,y1,z1∈g−1, α1,β1,ζ1,γ1∈g∗−1, α0,β0∈g∗0, where ad0∗x0:g∗−i⟶g∗−i, ad1∗x1:g∗−1⟶g∗0 and ad3∗x0,y0:g∗−1⟶g∗0 are defined respectively by
Remark 4. For any Lie algebra (h,[⋅,⋅]h), we have the semidirect product Lie algebra (h⋉ad∗h∗,[⋅,⋅]ad∗), which is a quadratic Lie algebra naturally. Consequently, one can construct the corresponding Lie 2-algebra (R,h⋉ad∗h∗,l1=0,l2=[⋅,⋅]ad∗,l3), where l3 is given by
This Lie 2-algebra is called the Lie 2-algebra of string type in [51]. On the other hand, associated to a Lie 2-algebra (g−1,g0,~l1,~l2,~l3), there is a naturally a quadratic Lie 2-algebra structure on (g−1⊕g∗0)⊕(g0⊕g∗−1) ([34,Example 4.8]). Thus, the Lie 3-algebra given in the above example can be viewed as the higher analogue of the Lie 2-algebra of string type.
Motivated by the above example, we show that one can obtain a Lie 3-algebra associated to a quadratic Lie 2-algebra in the sequel. This result is the higher analogue of the fact that there is a Lie 2-algebra, called the string Lie 2-algebra, associated to a quadratic Lie algebra.
A quadratic Lie 2-algebra is a Lie 2-algebra (g−1,g0,l1,l2,l3) equipped with a degree 1 graded symmetric nondegenerate bilinear form S which induces an isomorphism between g−1 and g∗0, such that the following invariant conditions hold:
for all x0,y0,z0,u0∈g0, x1,y1∈g−1.
Let (g−1,g0,l1,l2,l3,S) be a quadratic Lie 2-algebra. On the 3-term complex of vector spaces R⊕g−1⊕g0, where R is of degree −2, we define li, i=1,2,3,4, by
for all x0,y0,z0,u0∈g0, x1,y1,z1∈g−1 and r∈R.
Theorem 7.1. With above notations, (R,g−1,g0,l1,l2,l3,l4) is a Lie 3-algebra, called the higher analogue of the string Lie 2-algebra.
Proof. It follows from direct verification of the coherence conditions for l3 and l4 using the invariant conditions (7.7)-(7.9). We omit details.









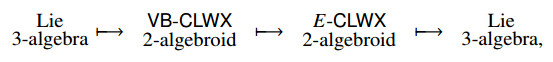
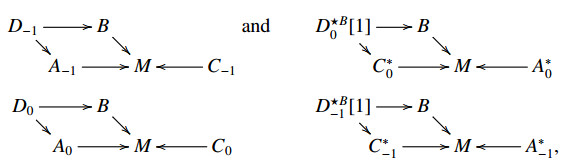


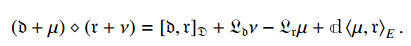



 DownLoad:
DownLoad: