1.
Introduction
Research on the link between digital transformation and corporate resilience has focused on two main areas. On the one hand, most research suggests that digitalization can contribute to corporate resilience during crises (Huang and Zhang, 2023; Jin et al., 2023; Wu et al., 2022; Yang and Deng, 2023). It can simplify administrative processes, facilitate internal communication and thus improve internal efficiency (Wernerfelt, 1984; Sriyabhand and Phoorithewet, 2020). Digitalization enhances real-time communication between firms and their suppliers and customers, which can lead to increased external cooperation and profitability (Lu et al., 2023; Zhuo and Chen, 2023). Digitalization also improves access to information, which helps to improve information asymmetries. Digital technology also facilitates innovation and increases productivity (Martín-Rojas et al., 2023). In summary, digitalization can improve the competitiveness and flexibility of companies in all areas and optimize the allocation of their resources (Li et al., 2018). These are important mechanisms for digital empowerment of corporate resilience in times of crisis.
In addition, some scholars believe that the realization of digital transformation does not necessarily help to enhance corporate resilience to respond to the crisis. Digital transformation as a long-term process requires a multifaceted approach (Blanka et al., 2022; Shen et al., 2022). The application of digital technology relies on the simultaneous reengineering of organizational processes and changes in management systems (Makarchenko et al., 2020; Jafari-Sadeghi et al., 2023). If digitalization builds on the original foundation, digital technology will not be compatible with the enterprise system when the digital transformation process becomes increasingly complex (Badasjane et al., 2022). According to the resource-based theory, resources are the core of sustainable development of a firm (Bhandari et al., 2022; Karim et al., 2022). Digital transformation takes up specific resources of the firm and undermines the ability to maintain the resilience of the firm (Zuo et al., 2022). When the firm's capacity is not sufficient to cope with digital transformation, the application of digital technology instead fails to enhance corporate resilience. On the contrary, it is likely to bring losses to the firm, causing the firm to fall into the "digital paradox" (Danneels and Viaene, 2022).
Researchers examining the contextual factors between digitalization on corporate resilience have less often considered the effects of the internal and external environment simultaneously (Zhang et al., 2023). Most researchers explore the boundary conditions of digitalization on corporate resilience out of the external environment. Factors such as the market environment and environmental uncertainty (Feliciano-Cestero et al., 2023; Wang et al., 2023). Some studies have also shown that the impact of digitalization on corporate resilience can be influenced by the internal governance of the firm, such as the nature of the firm, the size of the firm and the shareholding structure (Khattak et al., 2023; Li and Wang, 2023). This paper argues that performance feedback is an important driver of strategic change and resource allocation in firms, whether based on theories of corporate behavior or dynamical transmission mechanisms. It is therefore necessary to further integrate the influence of important internal and external factors in digitalization and corporate resilience.
Reviewing the research shows that most studies on digitalization have encompassed on the linear impact of digitalization on corporate efficiency, corporate competitiveness, corporate investment, and corporate cost (Ren et al., 2022; Xu et al., 2022). The impact of digitalization on resilience has both positive and negative aspects. The effect of digitalization on corporate resilience is not a straight line. From the point of view of complexity, the effect of digital technology on corporate resilience should be a non-linear process (Levitt and March, 1988). In order to accurately identify the process of digitalization's impact on corporate resilience, this paper verifies an inverted U-shaped relationship between the two. The paper explores the role of internal and external boundary conditions in the context of also considering the true drivers of business behavior.
In order to validate the role of digital transformation on business resilience in a crisis, we use COVID-19 as a research context. The sudden crisis at the end of 2019 with the outbreak of the COVID-19 epidemic has left companies facing a high uncertainty environment (He et al., 2021; Hu et al., 2023). The COVID-19 epidemic had a significant degree of negative impact on manufacturing companies (Chrpa et al., 2022; Mahto et al., 2022). The epidemic crisis affected firms' revenue expectations and caused a shift in consumer demand. The epidemic control has caused a blockage in the supply system for companies, which has led to the dilemma of inventory. In the face of the crisis, competition in the industry has become more intense. Differentiation strategy has become an inevitable trend. Firms urgently need to target demand and seize opportunities for change amidst environmental fluctuations (Abou-Foul et al., 2023; Muneeb et al., 2023). How to grasp the ever-changing business opportunities and reorganize internal and external resources to maintain competitive advantage under the epidemic crisis is the key to achieve enterprise counter-trend development (Aarstad and Kvitastein, 2021; Wong et al., 2022).
At present, digitalization has become an irresistible trend. The application of the firm's digital technology contributes to the intelligent and accurate production of the manufacturing industry (Matthess et al., 2023). In the face of the impact of the COVID-19 epidemic, digitalization has shown an important role in improving business efficiency and resource allocation thanks to its powerful role in intelligent analysis (Antonopoulou et al., 2023; Mithani, 2023). According to the theory of dynamic capabilities of firms, the competitive advantage accumulated by the strength of resources will be quickly eroded by the technological innovation of other firms (Dai et al., 2022). Therefore, firms must quickly respond to external environmental changes and customer needs, and reconfigure internal resources. Research shows that corporate resilience is an indispensable characteristic for firms to cope with crises (Bistrova et al., 2021; Cao and Chou, 2022). Corporate resilience is the ability of an enterprise to recover quickly and create opportunities for sustained growth in the face of risks and crises. Specifically, corporate resilience encompasses two aspects: recovering from adversity and creating new opportunities. In the face of external shocks, the resource reserve capacity and self-adjustment resilience of corporate resilience are important conditions to resolve the crisis (Del Giudice et al., 2021; Denkena et al., 2018). Macroscopically, the global economic policy uncertainty index in 2021 is 77% higher than during the financial crisis in 2008. Therefore, how to improve corporate resilience in the "VUCA" (Volatility, Uncertainty, Complexity, Ambiguity) scenario is an important issue for all firms (Troise et al., 2022; Zhang et al., 2022).
To summarize, our purpose of this paper is to address the following two questions: First, let us take a look at the link between digital technology and corporate resilience in this crisis. Second, we study the action mechanism of internal and external situational factors on digital transformation and corporate resilience. Therefore, we conduct an empirical test based on the perspective of digital empowerment and capability dysfunction using data from listed manufacturing firms in China from 2017 to 2020. We also examine important boundary conditions from the perspectives of internal performance feedback and external competitive pressure. This paper provides new evidence for the non-linear impact between digitalization and corporate resilience and provides theoretical support for the future economic stability and high-quality development of firms. This paper also has strong practical implications for countries and firms to improve resource leaning and accelerate digital transformation in the post-epidemic era.
The possible contributions of this paper are as follows: (1) Based on a nonlinear perspective, this project intends to establish a theoretical analysis framework of digital transformation and resilience from the perspective of "digital empowerment" and "capacity failure". By linking digital transformation and corporate resilience, this paper enriches the research on digital transformation affecting the behavior of microeconomic agents and expands the literature on the economic consequences of digital transformation. The results of this paper break through the research paradigm by theoretically explaining the impact of digitalization on the non-linearity of corporate resilience. Furthermore, it also provides a new perspective for us to better understand the positive and negative effects of digital strategies. (2) This paper explains the differential moderating effect of digital transformation on corporate resilience in terms of internal corporate performance feedback and external market competition. This theoretically provides new insights into the boundary conditions of digitalization and corporate resilience through an internal and external perspective. Compared with previous studies that have considered the internal and external perspectives of firms in a single way. This paper, however, is more comprehensively grounded in internal and external contexts. In practice it can guide firms to create a positive environment from performance feedback and external competition levels, which in turn can effectively drive corporate resilience.
The subsequent sections of this paper are organized as follows: In Section 2, we present the theoretical background and research hypotheses. Section 3 contains the data and methodology. Section 4 contains the empirical results and discussion. Section 5 contains the conclusion and some suggestions for future study.
2.
Theoretical background and research hypothesis
2.1. Digital transformation and corporate resilience
Firms are faced with more and more sudden external environmental turbulence and unforeseen events in their daily operations, and they need continuous self-renewal to achieve resilient development. Corporate resilience is not inherent, it is the result of a combination of factors (Conz and Magnani, 2020). In a dynamic environment, firms experience the disruptive nature of market instability, and in an unstable market, firms create new value through technological innovation, thus affecting their resilience (Iftikhar et al., 2021). Today, in the age of digital intelligence, technology-enabled businesses and services to create an environment of sustained innovation is the key to strengthening resilience and economic recovery. The resource base view assumes that firms have different tangible and intangible resources that can be transformed into unique capabilities. Resources are immobile and difficult to replicate across firms, and these unique resources and capabilities are the source of a firm's enduring competitive advantage. Resource base theory suggests that resources that are valuable, scarce, irreplaceable, and difficult to imitate are the ones that can lead to the establishment of a firm's unique competitive advantage. Firms can enhance their flexibility and sensitivity to market competition through digital management changes in key businesses, key segments, and key parts of the business (Papadopoulos et al., 2017). Digital transformation is essentially a deep-seated reshaping and reengineering of the enterprise, not a single-point breakthrough of "a set of equipment, a system", but an all-round cooperation and reconstruction of the industrial chain, value chain, and innovation chain, which means that the firm has to synergize its strategic resources.
Fundamentally speaking, digitalization is essentially a process of combining digital technology with the real economy (Chatterjee et al., 2022). The characteristics of digital technology used across time and space can help firms make up for the shortcomings in the operation of the entity (Tian et al., 2022). The process of digital transformation is also the process of firms using ICT to improve the efficiency and quality of their operations (Zhang and Luo, 2022). Digitalization also creates liquidity risk and uncertainty for businesses. Digitalization is the extraction of information from structured and unstructured data using a range of technologies (Jyoti and Efpraxia, 2023). To avoid falling into the so-called "IT paradox", firms need to send better quality signals to the market (Varadarajan, 2023).
Digital transformation is a long-term strategy for firms (Hien and Nhu, 2022). How to improve corporate resilience with the help of digital technology places higher demands on the long-term resource reserves and long-term management capabilities of firms (Seles et al., 2022). In the initial stage of digital transformation, the use of digital technology can broaden the information and information obtained by enterprises. In the initial stage, digital technology handles less information to be mined and requires a lower level of corporate capability (Lateef and Omotayo, 2019). Therefore, at the beginning of the digital strategy, the firm's capabilities and resources are sufficient to match the application of digitalization and eventually improve the resilience. However, when the digital strategy reaches a certain stage, it requires huge resources and capital investment (Frank et al., 2019). Furthermore, the long-term use of digital strategy exposes firms to a huge amount of information (Wei, 2022). The continuous investment, the difficulty of organizational change and the slow returns make corporate capabilities often lag behind the digital improvement (Sirmon et al., 2007). The enterprise capability theory shifts the attention from focusing on the enterprise's external industrial opportunities and market attractiveness to the enterprise's internal own resources and capabilities, and the theory emphasizes the impact of the enterprise's core capabilities on the enterprise's ability to obtain excess profits. According to the logic of enterprise capability theory, the key to making a firm organizationally resilient is to build capabilities that can adapt to environmental changes through continuous learning (Teece, 2019). Therefore, the dysfunctional alignment between corporate capabilities and strategic initiatives can instead be detrimental to the improvement of corporate resilience.
Therefore, we propose the first hypothesis of this paper from the perspective of digital empowerment and capability dysfunctions.
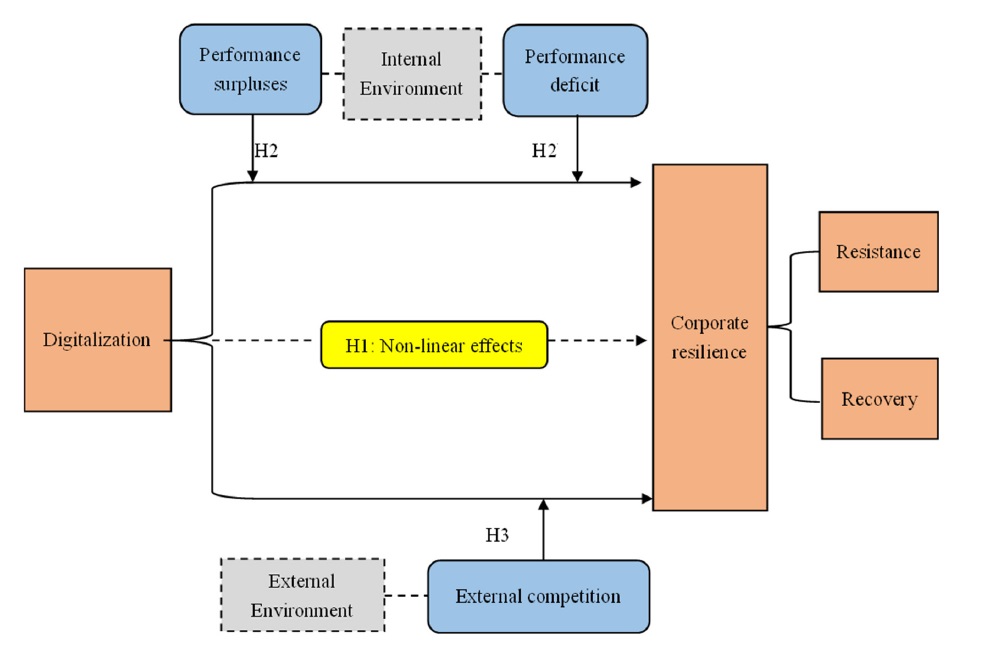
H1: There is a significant inverted U-shaped relationship between digital transformation and corporate resilience.
2.2. The moderating role of performance feedback
The view of corporate behavior is that decision makers use their inner satisfaction as a reference point when making decisions (Shinkle et al., 2021). The reference point for business strategy at the organizational level is the desired level of business performance. Performance feedback is the gap between the actual and desired performance of the firm (Jirásek, 2023). The size of the gap reflects the amount of resources and the position of the firm in the industry. According to resource base theory, differences in a firm's resource base are important conditions that lead to heterogeneous strategies. Thus, performance feedback constitutes an important boundary condition for digital transformation to drive increased corporate resilience.
In a state of performance surplus means that the firm is performing above the desired level. A performance surplus can be transformed to some extent into a firm's redundant resources (Baum et al., 2005). A firm with abundant redundant resources can be more responsive and risk-taking when facing external shocks. Second, based on higher-order theory, executive confidence is enhanced when a firm is in an expected performance surplus (Hambrick and Mason, 1984). As a result, firms can withstand a greater degree of trial-and-error behavior in the face of adverse shocks and thus become more resilient (Cameron and James, 1987). In the early stages of digital development, the requirements for various resource inputs and data processing capabilities are not high (Gomez-Mejia et al., 2018). Therefore, the role of digitalization in driving corporate resilience is more evident in the early stages. In the later stages of digitalization, the difficulty of processing massive amounts of information and the continuous investment of various resources make it difficult for enterprises to take advantage of digitalization and instead fall into the "IT paradox" (Madadian and Van den Broeke, 2023). Therefore, the inhibitory effect of digitalization on corporate resilience is more significant in the late stage of digitalization. Based on the social pressure theory, in the late stage of digitalization, firms will have more development pressure in the next stage due to good performance (Aneshensel, 1992). Due to the excessive investment of resources in the late stage of digitalization, firms avoid other risk-taking behaviors to avoid performance damage. As a result, firms are less risk-taking and lack the foundation to adapt to market changes, which leads to a reduction in corporate resilience. In the later stages of digitalization, firms with a performance surplus may lack the ability to dynamically adjust due to strategic dysfunctions and declining investment in innovation. As a result, the firm's resilience will be reduced as a result.
A performance deficit indicates that a firm is performing below expectations. A corporate in a deficit position often sends a signal that it is not doing well and is at a market disadvantage (Caves and Christensen, 1980). During the pre-digitalization phase, a performance deficit results in lower revenues and lower stakeholder confidence. Firms thus face resource constraints. Due to the lack of resources, firms are constrained in their flexibility and risk tolerance. That is, the firm lacks the basis for increasing the corporate resilience. According to the theory of threat rigidity, the firm will regard the loss of performance as a disaster that threatens the survival of the firm (Hu et al., 2011). In this situation, the firm will focus more on survival issues and less on risk-taking and innovation (Gavetti et al., 2012). So, firms will temporarily ignore the external environment changes and customer needs, but also lack the ability to reallocate resources. This hinders further improvement of corporate resilience. In the later stages of digitalization, the continued decline in resource reserves and the higher demands on management capabilities make the hindering effect of digitalization on corporate resilience more pronounced. In the later stages, the declining resilience of firms makes them face strategic choices (Shinkle, 2012). The digitalization strategy is characterized by long-term nature and high investment. In order to maintain a digital strategy, firms tend to break the inertia and seek solutions to problems (Tang and Hull, 2012). Continuous innovation is an important way to improve the resilience of a company (Harris and Bromiley, 2007). A continuous increase in the gap between performance expectations can threaten the position of management. Managers are more tolerant of risk in order to regain desired performance to strengthen their position (Chen and Miller, 2007). Thus, in the later stages of digitalization, performance deficits mitigate the negative effects of digitalization on corporate resilience.
Based on the above analysis, this paper proposes a second hypothesis.
H2: Performance surplus (performance deficit) positively (negatively) moderates the inverted U-shaped relationship between digitalization and corporate resilience. That is, the impact of digitalization on corporate resilience is stronger when performance surplus is low (performance deficit is high) and weaker when performance surplus is high (performance deficit is low).
2.3. The moderating role of external competition
Under specific economic conditions, if a company wants to survive and develop, its resource allocation and integration activities will inevitably be affected by its competitors (Bansal and Singh, 2023). In the pre-digital period, the positive effect of digitalization on the corporate resilience is more obvious. In order to maintain this positive trend, firms will pay more attention to the renewal of external product markets when the industry is highly competitive (Hasan et al., 2022). Fierce industry competition also stimulates firms to renew their strategies (Cumming et al., 2022). In order to create competitive barriers, firms will actively choose differentiation strategies. Therefore, firms will continue to develop and innovate, brand marketing and provide personalized products and services to customers. This continuous advantage of differentiation is also an important aspect of corporate resilience (Forgione and Migliardo, 2022). Thus, market competitiveness reinforces the positive effect of digitalization on corporate resilience. In the late stage of digital development, the impact on resilience is more significant. Market competitiveness, in turn, reinforces this inhibiting effect. Because of the non-recoverability of large investments, firms in the late stages of digitalization are exposed to more risk of potential losses (Martins, 2022). Today, with the increasingly fierce industrial competition, in order to obtain more market share, enterprises need to invest in resources accordingly. In order to ensure the survival of the firm, and given the existing digital strategy, the firm will focus on the stability of the strategy and give up the high risk of differentiated innovation strategy (Liu et al., 2021). Therefore, in the process of digital transformation in the future, the competition between industries will further strengthen the negative effect of digital transformation on the resilience of firms.
Based on the above research results, the third theoretical hypotheses are given at the end of the paper.
H3: External competition positively moderates the inverted U-shaped relationship between digitalization and corporate resilience. That is, the impact of digitalization on corporate resilience is stronger when external competition is low and weaker when external competition is high.
Figure 1 illustrates the theoretical framework of this paper.
3.
Data and methods
3.1. Sample selection
The manufacturing sector was hit harder during the COVID-19 epidemic compared to other industries. Many factories experienced a significant reduction in manufacturing efficiency during the epidemic. Not only that, the upstream and downstream supply chains of the industry were broken during the epidemic. Based on the significant impact on manufacturing companies and the importance of the manufacturing sector to China's GDP growth, we focused on selecting manufacturing companies listed on China's Shanghai and Shenzhen stock exchanges from 2017–2021. As China's stock market underwent strong regulation in 2017, the capital market underwent profound changes, and A-shares showed a steady rise, so this paper takes this as the starting point of the study. The following treatments are also used in this paper: (1) Exclude financial-related firms; (2) exclude ST, *ST, and other firms; (3) exclude delisted firms; and (4) perform 1% tailoring of the data. All data in this paper are obtained from the CSMAR database.
3.2. Variables and data
Explanatory variables. Referring to the research of Wu et al. (2021), we collect and organize the annual reports of all A-share listed enterprises in Shanghai Stock Exchange and Shenzhen Stock Exchange through Python crawler function. In order to determine the feature words of enterprise digital transformation, we search, match, and count the word frequency of listed enterprises' annual reports based on Python. As this kind of data has typical "right skewed" characteristics, we perform logarithmic processing and we use the logarithm of the total digitized word frequency (Lnword) to measure the degree of digitization. The ratio of digitized word frequency to total text is also used in the robustness test.
Explained variables. In this paper, the corporate resilience is divided into recovery (Recovery) and resistance (Resistance) (Desjardine et al., 2019). According to Desjardine et al. (2019) they calculated the absolute percentage loss in share prices after the start of the crisis, i.e., they calculated the percentage loss between the pre-crisis closing price and the share price at the lowest point during the window for each company. Here, we use January 2020 as the starting point of the epidemic, so the period before January 2020 is considered the pre-shock period, and the period after January 2020 is considered as the post-shock period. Resistance is measured as the change in the post-shock low of the stock price to the pre-shock high. Recovery is measured as the change in the post-shock high of the stock price to the pre-shock high. A firm's share price reflects changes in the firm's fundamentals and its expectations and is real-time in nature. The share price of a firm reflects the expectations of investors. Therefore, if digitalization improves the resilience of a firm during a crisis, the stock price of the corresponding firm will be higher.
Mediating variables. We draw on a study by Yang et al. (2019) that measured dynamic capability in terms of three dimensions: Innovative capability (Ic), absorptive capability (Absorb), and adaptive capability (Adapt) (Yang et al., 2020). The innovative capability is evaluated using two indicators: the intensity of a firm's annual R & D investment and the proportion of technical personnel. In this paper, the data of these two indicators are standardized separately and then summed to obtain the composite value of innovation capability. Innovative capability is calculated as Ic=(XRD−minRD)(maxRD−minRD)+(XIT−minIT)(maxIT−minIT) (1). Absorptive capability is measured using R & D expenditure intensity i.e. the ratio of annual R & D expenditure to operating revenue of the sample firms (Wang et al., 2014). Adaptive capacity is measured using the coefficient of variation of the three main types of annual R & D, capital, and advertising expenditures of the sample companies. In order to keep the coefficient of variation value in the same direction as the adaptive capacity, the coefficient of variation is taken to be negative in this paper. A higher adjusted coefficient of variation value indicates a higher adaptive capacity of the firm (Nadkarni and Narayanan, 2007).
Moderating variables. In this paper, performance feedback is measured as the difference between actual and desired performance. The model is set as follows: Gapi,t= Pi,t− α1HAi,t − 1− (1 − α1)SAi,t (2), where P represents the actual performance of the firm measured using return on assets (ROA) (Chen, 2008). HA represents the historical level of performance of sample firm i in year t−1 with ROA as the measure. SA is the expected performance of firm i based on social comparison, and the value is the average value of return on assets (ROA) of firms in the industry other than itself in year t. The linear combination of historical and socially expected performance levels can be used as a proxy variable for firm i 's expected performance. α1 is a weighting coefficient between 0 and 1. Considering the fitting effect of the model, α1 is assigned a value of 0.6 in this paper. In order to test the impact of digital transformation on strategic upgrading under two states of performance surplus and performance deficit separately, we group performance surplus (Ugap) and performance deficit (Dgap) according to the formula. This paper uses the Herfindahl index to calculate the degree of external competition of a firm. The HHI−A is calculated by dividing the revenue of an individual firm by its industry market share. A smaller HHI-A index means that there are more firms of the same size and the degree of competition is greater. For ease of understanding, this value is taken as the reciprocal of this value. The larger the HHI-A index, the more competitive the firm is in the industry.
Control variables. The following control variables were selected based on previous studies in this paper (Fang et al., 2023). Firm age (Lnage) is measured as the logarithm of the firm's time of establishment. Gearing (Lev) is measured by dividing total liabilities at year-end by total assets at year-end. Return on assets (ROA) is measured by dividing net income by total assets. Independent director ratio (Indep) is measured by dividing the number of independent directors by the total number of board members. Two positions in one (Dual) is expressed as a dummy variable. If the chairman and general manager of the sample company are the same person, the variable takes the value of 1 otherwise it is 0. The nature of ownership (SOE) is represented by a dummy variable. The variable takes the value of 1 if the sample company is a state-owned enterprise and 0 otherwise. number of directors (Lnboard) is measured as the logarithm of the total number of board members. Top shareholder ownership (Top1) is measured as the number of shares held by the top shareholder divided by the total number of shares.
The representation and measurement of the main variables in this paper are briefly shown in Table 1.
The descriptive statistics of all variables in this paper are presented in Table 2. the minimum value of enterprise digitalization index is 0, the maximum value is 5.298, and the variance is 1.234. the data indicate that the degree of digitalization varies widely among the sample firms. The mean value of digitalization is 1.234, which indicates that the overall digitalization level of the sample firms needs to be improved.
3.3. Methods
In this paper, panel data are used in the empirical study. Panel data can be used to explore the potential information of the model in both time and cross-sectional dimensions. The two-way fixed effects model set in this paper is a model with both "industry effects" and "time effects" (Han et al., 2022). For the problems in this paper, there may be omitted variables that do not vary over time, i.e., there is an "industry effect" because each industry is different. Furthermore, there may also be "time effects" that do not vary with industry heterogeneity, so a two-way fixed-effects model has to be built (de Chaisemartin and D'Haultfœuille, 2020). If only industry effects are considered in the analysis without adjusting for residual correlations across firms in different periods, the conclusions are often biased. In the analysis of panel data, if only individual effects are considered in the panel data model, the estimation results will be highly biased, and this bias will increase with the increase of time effects (Halder and Malikov, 2020). Therefore, in this paper, not only industry effects but also time effects are considered when building the research model.
In order to test the impact of digitalization on corporate resilience during the crisis, this paper fixes the industry and year in the model. The model setup is as follows:
The subscript i in the equation represents the individual firm and the subscript t represents the year. Year_FE and Industry_FE represent the year and industry fixed effects, respectively. εi,t represents the random disturbance term. This study uses robust standard errors. Resistance and Recovery are the explanatory variables in this paper i.e., corporate resilience. Lnword and Lnword2 are the explanatory variables in this paper i.e., the degree of digitalization and its squared term. Controls are the control variables selected in this paper.
This paper also tests the mediating path of dynamic capabilities between digitalization and corporate resilience through the following model:
Equations (7), (8), and (9) test the mediating role of innovation capability between digitalization and corporate resilience using a causal stepwise regression two-step approach. Equations (10), (11), and (12) examine the mediating effect of absorptive capacity. Equations (13), (14) and (15) test the mediating path of adaptive capacity.
In this paper, to test the moderating effects of performance feedback and external competition, we centralize the variables and construct the following model:
Equation (16) and Equation (17) test the moderating effect of the performance surplus. Equation (18) and Equation (19) examine the moderating effect of performance deficit. Equation (20) and Equation (21) examine the moderating effect of external competition.
4.
Empirical results and discussion
4.1. Benchmark regression results
The results of the baseline regressions in this paper are shown in Table 3. The coefficients of the primary term of digitalization in Model 1 and Model 2 of Table 3 are significantly positive, and the coefficients of the squared term of digitalization are significantly negative. There is an inverted U-shaped relationship between digitalization and resistance (Li et al., 2021). The coefficients of the primary term of digitalization are significantly positive and the coefficients of the squared term of digitalization are significantly negative in Model 3 and Model 4 of Table 3. The relationship between digitalization and recovery also has an inverted U-shaped relationship. Therefore, the digitalization degree and resilience show a changing trend of inverted U-shape. When the degree of digitalization is not high, it has a positive effect on resilience. In the case of excessive digitalization, it will have a negative effect on resilience. Hypothesis 1 is demonstrated.
4.2. Robustness tests
4.2.1. Substitution of explanatory variables
In the baseline regression, we use the logarithm of digitized correlated word frequencies. In the robustness test, the ratio of digitized word frequencies is used to replace the logarithm of word frequencies (Chen and Xu, 2023). This is measured using the number of digitized word frequencies divided by the total word frequency of the firm's annual report. The regression results are shown in Table 4. The primary term coefficient of the digital word frequency is positive at the 1% level and the quadratic term coefficient is negative at the 1% level, indicating that the data shows an obvious inverted U-shaped relationship.
4.2.2. Substitution of the explained variable
The question of how to measure corporate resilience in relevant studies is very important and there is no publicly accepted measure. In a previous paper, we used a market indicator like stock price. In the robustness test, we use the fluctuation of operating income before and after the outbreak to measure it. The profitability of a firm is also crucial for the firm to safely survive the crisis. Using January 2020 as the starting point of the epidemic, we continue to consider the period before January 2020 as the pre-shock period and the period after January 2020 as the post-shock period. Resistance is measured as the change from the post-shock low in operating income to the pre-shock high. The recovery is measured as the change in the highest point of operating income after the shock for the highest point before the shock. The results of the test are shown in the Table 5, the results in this paper remain robust.
4.2.3. City fixed effects
In the baseline regression model, we control for time and industry fixed effects. Since economic and social factors in cities also affect firm development. We further control for city fixed effects to capture the effects of macro factors (Castells-Quintana et al., 2021). The results are presented in the first and second columns of Table 6.
4.2.4. Excluding the sample from Hubei Province
Hubei province in China was hit the hardest during the COVID-19 epidemic. The resumption of firms in this region has different characteristics compared with other regions. Therefore, the sample from Hubei province, which was most severely affected by the COVID-19 epidemic, was removed from this paper. After changing the data, the results remain robust. These results are listed in columns 3 and 4 of Table 6.
4.2.5. Excluding the sample of municipalities directly under the central government
Municipalities directly under the central government are more demanding and constrained in terms of economic resilience, political management and epidemic planning. In order to eliminate the influence of the municipalities directly under the Central Government, we removed the samples of the municipalities directly under the Central Government from the regression (Yang et al., 2019). Columns 5 and 6 in Table 6 list the results of regression analysis. As can be seen from the table, the degree of digitalization and resilience is an inverted U-shaped relationship.
4.2.6. Propensity Matching Score Method
To solve the endogeneity problem in this paper, the propensity matching score method is used in this paper. The 1:1 nearest neighbor matching method is used in this paper (Huang et al., 2023). After fitting, the absolute error of each fitting variable is less than 5%, which proves the correctness of the fitting. Using the propensity matching score method, this paper mitigates the bias that may arise from other features and omitted variables. As can be seen from Table 7, there is an inverted U-shaped relationship between digitalization and corporate resilience holds.
4.2.7. Random sample selection
We also use a randomly selected subsample (80% of the total sample size) for the regression (Li et al., 2009). The results of the subsample are consistent with the findings found using the results of the full sample. The first and second columns of Table 8 demonstrate the robustness of the results.
4.2.8. Variables lagged by one period
To mitigate reverse causality, we lag both explanatory and control variables by one period for the regressions (Li et al., 2023). The results of the regression are given in columns 3 and 4 of Table 8. The results of regression analysis further confirm the correctness of this conclusion.
4.2.9. Instrumental variable
The instrumental variable in this paper is an interaction term between the number of post offices per million people in 1984 and the digitalization of firms lagged by one period, constructed using 1984 historical postal and telecommunications data. Due to the continuity of development, the region with a higher number of post offices historically it has a relatively better communication IT infrastructure. Businesses in this region are more receptive to IT and more widely used. This satisfies the requirement of relevance. In terms of exogeneity, as traditional post office communication is rapidly replaced by modern mobile communication, its impact on the digital development of enterprises disappears. The use of lagged one-period time series indicators to construct interaction terms can transform the cross-sectional data into indicators that fit the panel data. The research results in Table 9 show that there is a clear inverted U-shaped link between digitalization and corporate resilience. Moreover, the instrumental variables pass the non-identification test and reject the hypothesis of weak instrumental variables. This proves the validity of the selection of instrumental variables.
4.2.10. Test for inverted U-shaped relationship
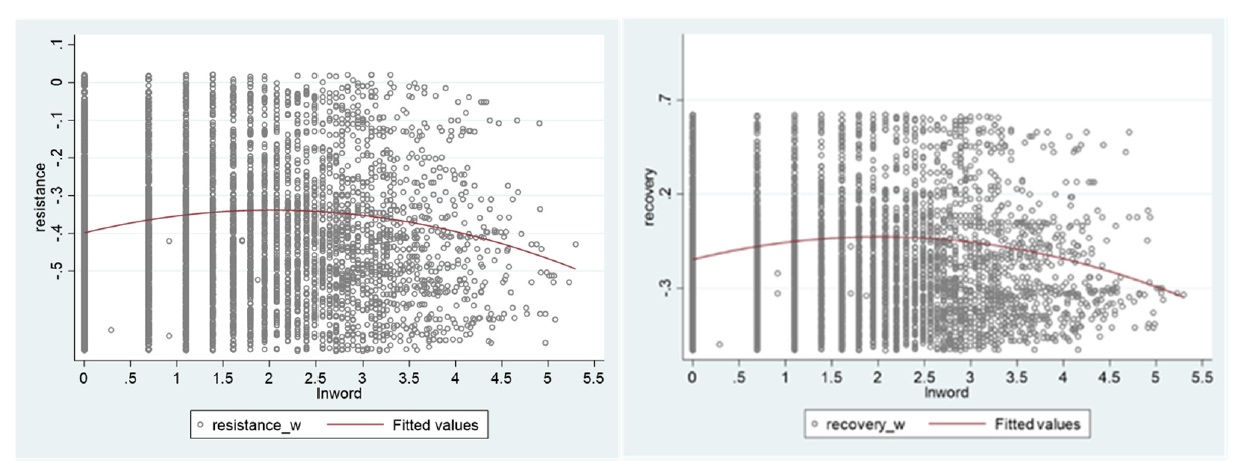
First, we plot the image based on the original data, and a clear inverted U-shaped relationship can be seen in Figure 2. The coefficients of the primary and secondary terms of digitalization have been found to be positively significant and negatively significant, respectively, by empirical tests in the previous paper. Here, we continue to test the existence of the inverted U-shaped relationship. We find the value of firm digitalization when the inverted U-shaped relationship reaches its maximum, denoted as lnwordmax. lnwordmax=−a/2b. a is the value of the primary term coefficient and b is the value of the secondary term coefficient. Next, we create new variables, which are defined as shown below: lnwordlow=lnword−lnwordmax if lnword⩽lnwordmax, 0 otherwise; lnwordhigh=lnword−lnwordmax if lnword⩾lnwordmax, 0 otherwise. We then run the regression again using the new variables. Table 10 shows that the regression coefficient of lnwordlow is significantly positive at the 1% /5% level, and the coefficient of lnwordhigh is significantly positive at the 1% level. Finally, to further check for the presence of an inverted U-shape, the Sasabuchi Lind Mehlum U (SLMU) test is performed, and the results are shown in table 11. Therefore, this paper holds that the degree of digitalization of a firm is related to its resilience in the shape of inverted U-shape.
4.3. Moderating effects
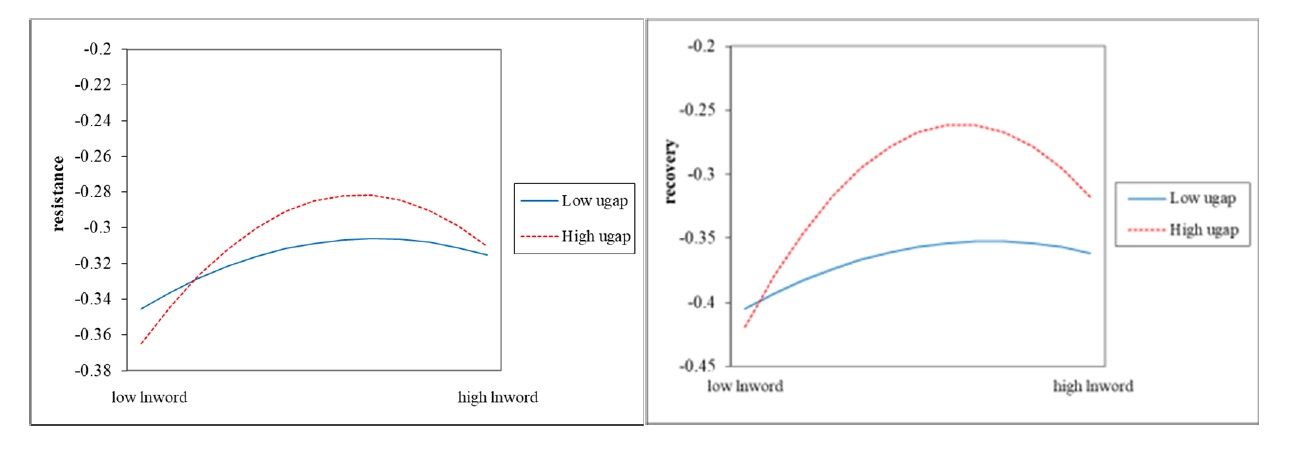
Table 12 presents the regression results for the moderating effect. The first and second columns of Table 12 show that the coefficients of the quadratic term of firm digitalization and the cross-product of performance surplus are significantly negative at the 10%/5% level. Therefore, performance surplus will positively moderate the inverted U-shaped relationship between the variables in this paper. In the pre-development stage of digitalization strategy, performance surplus makes the firm have more redundant resources (Gayed and El Ebrashi, 2023). Second, performance surplus makes management more confident, which allows the firm to focus more on risky activities. However, in the later stages of digitalization, the performance surplus exacerbates the inhibiting effect of digitalization on corporate resilience. At this point, firms with a performance surplus face both greater resource constraints and social pressures (Barney, 1991). At this point, both corporate resilience and risk appetite decline. Therefore, H2a of this paper is proven. Figure 3 illustrates the positive moderating effect of the performance surplus.
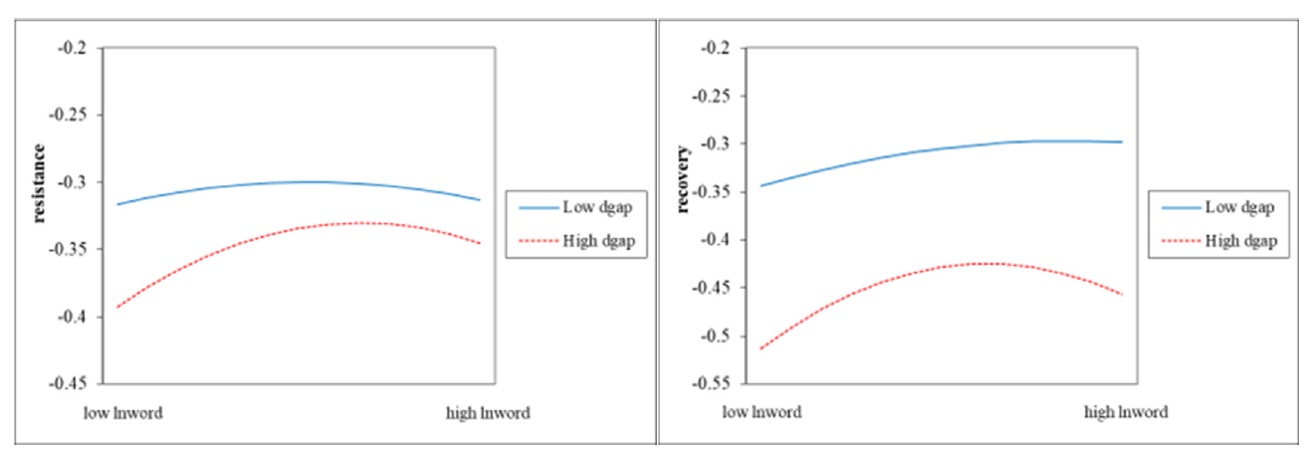
The third and fourth columns of Table 12 demonstrate that the coefficients of the quadratic term of digitalization and the cross-product of the performance deficit are significantly negative at the 10%/5% level. Since the performance deficit is negative, the performance surplus negatively moderates the inverted U-shaped relationship between digitalization and firm resilience. In the pre-digitalization phase, the performance deficit exposes firms to resource constraints (Iborra et al., 2022). This indicates that the firm's flexibility and resilience are both undermined. This hinders the further improvement of the firm's resilience. In the later stages, a large investment of resources is no longer recoverable, and companies are facing a dilemma of capacity and resources (Kim and Kung, 2017). In order to break through the dilemma of digital strategy, companies will take the initiative to continuously innovate. This is an important way to improve the resilience. At this time, the performance deficit will mitigate the negative impact of digitalization on the corporate resilience. Therefore, H2b of this paper is proved. Figure 4 illustrates the negative moderating effect of the performance deficit.
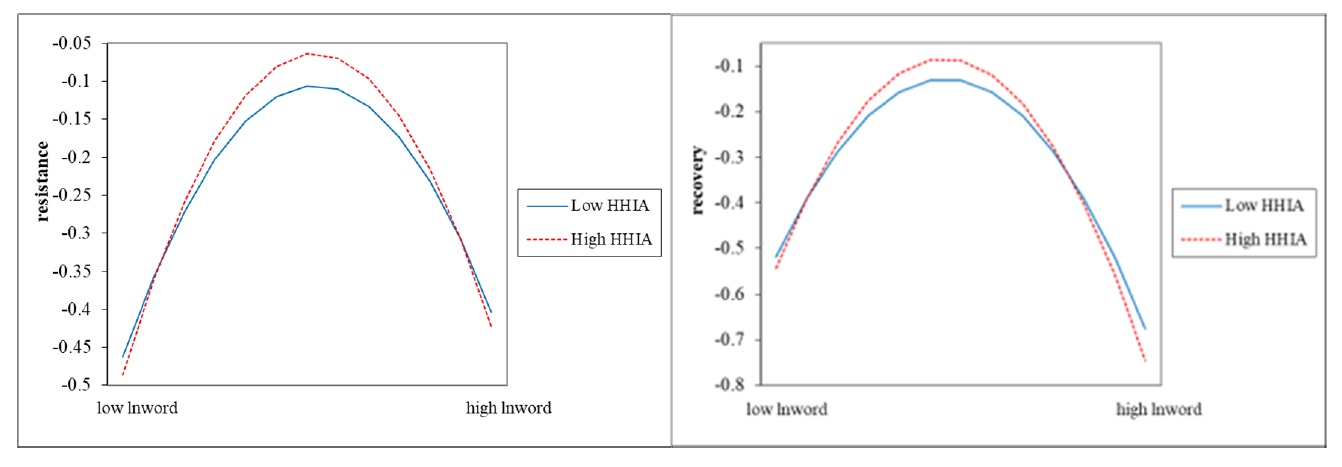
The fifth and sixth columns of Table 12 demonstrate that the coefficients of the quadratic term of digitalization and the cross-product of external competition are significantly negative at the 1% level. In the pre-digitalization period, in order to maintain the positive trend of firm resilience, firms engage in rapid differentiation of products, etc., in response to market changes (Aghion et al., 2015). This ensures that firms raise their barriers in the face of external shocks (Malesky et al., 2020). This is an important competitive strategy to improve the resilience of a firm. In the later stages of digitalization, market competitiveness reinforces the inhibiting effect of digitalization on the firm's resilience. Industry competition means that if a firm wants to stay out of the game. With the capacity and resource constraints already in place, firms will seek to be more stable (Sull, 1999). This prevents firms from reacting quickly in the face of external shocks. Thus, industry competition reinforces the positive effects and exacerbates the negative changes. Therefore, H3 of this paper is proven. Figure 5 illustrates the positive moderating effect of external competition.
4.4. Further analysis
In this paper, three dimensions of dynamic capabilities, innovative capabilities (ic), absorptive capabilities (absorb), and adaptive capabilities (adapt) were tested for the mechanism. Table 13 shows the results of the mechanism test. The first to the third columns of Table 13 show that innovative capabilities mediate between digitalization and corporate resilience. Digitalization on the one hand allows more information to be accessed at low cost through a more open platform (Gao et al., 2023). The interaction with external information facilitates the improvement of innovation capabilities. On the other hand, digitalization also enables innovation efficiency through organizational management and production changes (Ren and Li, 2023). Dynamic capabilities can help companies to perceive market information and thus react consciously and dynamically (Zhan et al., 2023). Therefore, the digitalization of a company can contribute to the resilience of the company through the improvement of innovation capabilities.
The fourth to sixth columns of Table 13 show that absorptive capabilities can play a mediating role between digitalization and corporate resilience.
Absorptive capabilities are a firm's ability to learn and use external knowledge and translate new knowledge and skills into business outcomes (Cohen and Levinthal, 1990). Digitalization can help firms use digital technology to identify and access external information that is valuable to them and optimize their knowledge accumulation (Lerman et al., 2022). The new knowledge and technology brought by digitalization can effectively help firms predict market trends and develop differentiated marketing programs (Huang et al., 2018). This ensures that firms can sense and respond quickly to changes in market demand in the face of external changes (Mikalef et al., 2020). Thus, digitalization can contribute to corporate resilience through increased absorptive capacity.
Columns seven through nine of Table 13 show that adaptive capabilities do not mediate the relationship between digitalization and corporate resilience. Adaptive capabilities are the ability to coordinate a firm's own resources to respond to environmental changes (Li et al., 2022). Adaptive capabilities help companies perceive external environmental threats and identify favorable strategic opportunities (Pongtanalert and Assarut, 2022). Adaptive capabilities place high demands on a firm's overall capabilities. Furthermore, corporate resource reserves have a fundamental role in corporate resilience (Gayed and El Ebrashi, 2023). The failure of the mechanism test here also indicates from another perspective that the resource allocation capability of firms is relatively weak.
4.5. Heterogeneity analysis
4.5.1. Redundant resources
Table 14 shows the results of the heterogeneity analysis regarding redundant resources. The results show that the inverted U-shaped relationship between digitalization and corporate resilience is more significant for firms with more redundant resources. More redundant resources mitigate the competition for resources between improving firm resilience and other business activities (Troilo et al., 2014). The redundancy scenario allows firms to flexibly allocate various types of resources to provide support for shaping corporate resilience (Bourgeois, 1981). In the later stages of digitalization, when firms are caught in a capacity dilemma and "digital paradox", more redundant resources may be unevenly distributed within the organization (Love and Nohria, 2005). This is likely to lead to intra-organizational conflict and negatively affect resilience. Therefore, the inverted U-shaped relationship between digitalization and corporate resilience is evident in firms with more redundant resources.
4.5.2. Level of marketability
Table 15 presents the results of the heterogeneity analysis regarding the level of marketization. The results show that the inverted U-shaped relationship in this paper is more significant if the region where the firms are located has a higher degree of marketisation. When the level of marketization is higher, it facilitates the alleviation of corporate financing constraints (Goldfarb and Tucker, 2019). This provides a good basis for digitalization and firm resilience. In addition, a higher level of marketization helps to help firms create a good business environment, which in turn promotes corporate resilience (Branstetter et al., 2014). However, if the digitalization has a negative effect on resilience, then a higher level of the market will further strengthen the adverse effects of resilience. This is because regions with higher levels of marketization will also have stronger competition in the industry (Tang, 2006). From this, we can see that in the case of a high degree of marketization, the digitalization and resilience show a more evident inverted U-shaped trend.
4.5.3. Corporate social responsibility
Table 16 shows the results of the heterogeneity analysis regarding CSR. The results show that the inverted U-shaped relationship is more significant if firms take on more CSR. Digital technology reduces the cost of economic engagement for all parties in society. This provides a natural facility for practicing social responsibility. When a company behaves greener and performs well socially, the company is loved and sought after by consumers (Saeed et al., 2023). This leads to a higher economic performance and market position of the company. Therefore, this strengthens the contribution of corporate digitalization to corporate resilience (DesJardine et al., 2019). Furthermore, it can reinforce the negative effect of corporate digitalization on firm resilience. CSR exhibits a tendency toward corporate long-termism (Yao, 2023). More CSR investments can crowd out more corporate resources. This can undermine the basis for maintaining corporate resilience (Chen et al., 2023). Therefore, in firms with high CSR, digital transformation and corporate resilience show an inverted U-shaped trend.
5.
Conclusion and implication
The data in this paper are obtained from firms in the manufacturing industry listed in Shanghai and Shenzhen from 2017 to 2020. We empirically analyze the relationship between digital transformation and corporate resilience using a two-way fixed-effects model.
The major findings of this paper include the following four points:
It is found that digitalization and resilience show an obvious trend of inverted U-shaped. After rich robustness tests, the major findings of this paper hold. Therefore, in the pre-digitalization period, digitalization mainly plays a positive role in promoting corporate resilience. In the late stage of digitalization, digitalization mainly plays a negative inhibitory role on corporate resilience. Therefore, when focusing on the role of digital transformation, one needs to consider multiple aspects of the digitalization process and the advantages and disadvantages of digitalization.
In the mechanism test, this paper finds that innovative capabilities and absorptive capabilities in corporate dynamic capabilities are important mechanisms between digitalization and corporate resilience. The adaptive capabilities in the dynamic capabilities of the firm have not been able to play a mediating role. Therefore, in order to take advantage of the facilitating role of digitalization, firms should enhance their own innovation capacity and strive to digest new technologies and transform them into their own competitiveness.
In the moderating effect analysis, we find that the performance surplus positively moderates the inverted U-shaped relationship between digitalization and corporate resilience. The performance deficit negatively moderates the inverted U-shaped relationship. External competition positively moderates the inverted U-shaped relationship between digitalization and corporate resilience. Firms can change their digitalization strategy in response to changes in their internal and external operations.
In the heterogeneity analysis, we find that the inverted U-shaped relationship between digitalization and corporate resilience is more significant in firms with more redundant resources, higher levels of marketization, and more corporate social responsibility. Due to the differences in the characteristics of different industries, the role of digitalization in resilience is also different. Therefore, all industries should be carefully considered when implementing digital transformation.
The policy recommendations of this paper are shown below:
First, in the face of external shocks, enterprises should gain a deeper understanding of the underlying logic of digitalization and corporate resilience and develop a reasonable digital strategy. Firms should dynamically analyze the potential impact of digital transformation on corporate resilience.
Second, managers should recognize that the elements of corporate capabilities and digital technologies are complementary to each other. Firms should not only focus on the change of digital strategy, but also on the improvement of their own management capabilities and resource reserves. The long-term nature of digital strategy makes firms pay attention to its dynamic development pattern. Firms should enhance their data penetration and information flow capabilities and should make good use of digital technology to enhance the relevance of corporate data processing in order to realize the empowering effect of digital technology on corporate resilience.
Third, managers should plan for different stages of digital business development in the early stages of the objectives, and in the early planning should be sufficiently thorough and detailed to ensure that the planning is reasonable. Finally, managers should not set too few or too many digital business indicators. Managers should make it clear that digital transformation KPIs are designed to assess the development process of the enterprise's digital transformation, which in turn leads to performance improvement, and performance changes can be reflected in the enterprise's KPIs. Only with clear measurement criteria for digital transformation can they provide guidance for digital business development.
Fourth, firms should comprehensively analyze the internal and external environment of the organization. Firms can analyze their current resource reserves and organizational capabilities and other effective information with the help of performance feedback status. Firms can analyze information such as current risk taking and corporate competitiveness by obtaining market information of external competition. This information can help firms determine the stage of development of digital strategy and whether the strategy is compatible with the development of the firm. By providing feedback on key information, companies can adjust their organizational strategies to avoid the trap of "digital paradox".
Fifth, firms with redundant resources and a good institutional environment can mitigate internal conflicts and reduce risks in the process of digital transformation, thereby enhancing corporate resilience. In the face of an increasingly competitive market environment and rigid resource constraints, firms must flexibly develop and make good use of internal and external resources to adapt to market changes. Firms have to continuously gain competitive advantages from self-improvement, thus enhancing corporate resilience.
Authors contributions
Yan Aimin: Conceptualization, Supervision, Methodology, Software, Validation, Funding acquisition.
Ma Hao: Data analysis, Methodology, Writing - original draft, Writing - review & editing.
Zhu Dandan: Conceptualization, Writing - original draft, Writing - review & editing.
Xie Julan: Conceptualization, Supervision, Validation, Writing - review & editing.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The present research was supported by the Project of the National Natural Science Foundation of China (Grant No.72172160, 71972185), Hunan Provincial Education Department Foundation for Excellent Youth Scholars (22B0012). The Project of the Social Science Foundation of Hunan Province (20YBA255). Project of the Social Science Achievement Appraisal Committee of Hunan Province (Grant No. XSP22YBZ139).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: