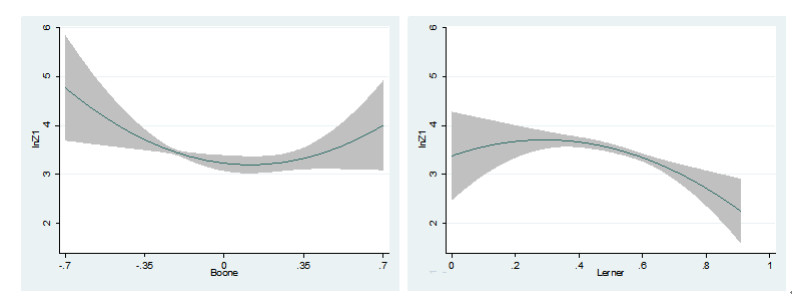
Considering the importance of the competition-stability trade-off, contradictory theoretical predictions, and empirical evidence, its re-investigation from the angle of non-linearity is needed. Therefore, this paper focuses on the association between bank stability and competition in Europe by employing a Boone indicator and alternative competition measures. Bank stability is measured with the z-score and loan loss reserves ratio. System-GMM estimations are carried out on a panel of banks from 27 European Union member countries over the period of 2004–2014. The results confirm that when a linear association between bank stability and competition is assumed, competition-stability argument prevails. However, when potential non-linearity of this association is assumed, the results appear more diverse and complex across different competition proxies. We observe signs of U-shape association between bank stability and competition for the Boone indicator and weaker signs of an inverse U-shape association with Lerner index. This indicates that before taking policy measures, it is important to consider the potentially non-linear association between bank stability and competition and to define which aspect of competition regulators want to address. The results concerning mature and emerging Europe exhibit also some differences, indicating that suitable regulatory approaches applied even within the EU could be rather different.
1.
Introduction
Synchronization in complex networks has been a focus of interest for researchers from different disciplines[1,2,4,8,15]. In this paper, we investigate synchronous phenomena in an ensemble of Kuramoto-like oscillators which is regarded as a model for power grid. In [9], a mathematical model for power grid is given by
where Pisource>0 is power source (the energy feeding rate) of the ith node, I≥0 is the moment of inertia, KD>0 is the ratio between the dissipated energy by the turbine and the square of the angular velocity, and ail>0 is the maximum transmitted power between the ith and lth nodes. The phase angle θi of ith node is given by θi(t)=Ωt+˜θi(t) with a standard frequency Ω (50 or 60 Hz) and small deviations ˜θi(t). Power plants in a big connected network should be synchronized to the same frequency. If loads are too strong and unevenly distributed or if some major fault or a lightening occurs, an oscillator (power plant) may lose synchronization. In that situation the synchronization landscape may change drastically and a blackout may occur. The transient stability of power grids can be regarded as a synchronization problem for nonstationary generator rotor angles aiming to restore synchronism subject to local excitations. Therefore, the region of attraction of synchronized states is a central problem for the transient stability.
By denoting ωi=PisourceKD and assuming ailKD=KN(∀i,l∈{1,2,…,N}) and I=0 in (1), Choi et. al derived a Kuramoto-like model for the power grid as follows [5]:
Here, the setting ˙θi>0 was made in accordance to the observation in system (1) that the grid is operating at a frequency close to the standard frequency with small deviations. In order to ensure that the right-hand side of (2) is positive, it is reasonable to assume that ωi>K,i=1,2,…,N. This model can be used to understand the emergence of synchronization in networks of oscillators. As far as the authors know, there are few analytical results. In [5], the authors considered this model with identical natural frequencies and prove that complete phase synchronization occurs if the initial phases are distributed inside an arc with geodesic length less than π/2.
If (˙θi)2 in (2) is replaced by ˙θi, the model is the famous Kuramoto model [13]; for its synchronization analysis we refer to [3,6,10], etc. Sakaguchi and Kuramoto [16] proposed a variant of the Kuramoto model to describe richer dynamical phenomena by introducing a phase shift (frustration) in the coupling function, i.e., by replacing sin(θl−θi) with sin(θl−θi+α). They inferred the need of α from the empirical fact that a pair of oscillators coupled strongly begin to oscillate with a common frequency deviating from the simple average of their natural frequencies. Some physicists also realized via many experiments that the emergence of the phase shift term requires larger coupling strength K and longer relaxation time to exhibit mutual synchronization compared to the zero phase shift case. This is why we call the phase shift a frustration. The effect of frustration has been intensively studied, for example, [11,12,14]. In power grid model using Kuramoto oscillators, people use the phase shift to depict the energy loss due to the transfer conductance [7]. In this paper, we will incorporate the phase shift term in (2) and study the Kuramoto-like model with frustration α∈(−π4,π4):
We will find a trapping region such that any nonstationary state located in this region will evolve to a synchronous state.
The contributions of this paper are twofold: First, for identical oscillators without frustration, we show that the initial phase configurations located in the half circle will converge to complete phase and frequency synchronization. This extends the analytical results in [5] in which the initial phase configuration for synchronization needs to be confined in a quarter of circle. Second, we consider the nonidentical oscillators with frustration and present a framework leading to the boundness of the phase diameter and complete frequency synchronization. To the best of our knowledge, this is the first result for the synchronization of (3) with nonidentical oscillators and frustration.
The rest of this paper is organized as follows. In Section 2, we recall the definitions for synchronization and summarize our main results. In Section 3, we give synchronization analysis and prove the main results. Finally, Section 4 is devoted to a concluding summary.
Notations. We use the following simplified notations throughout this paper:
2.
Preliminaries
In this paper, we consider the system
Next we introduce the concepts of complete synchronization and conclude this introductory section with the main result of this paper.
Definition 2.1. Let θ:=(θ1,θ2,…,θN) be a dynamical solution to the system (4). We say
1. it exhibits asymptotically complete phase synchronization if
2. it exhibits asymptotically complete frequency synchronization if
For identical oscillators without frustration, we have the following result.
Theorem 2.2. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (4) with α=0,ωi=ω0,i=1,2,…,N and ω0>K. If the initial configuration
then there exits λ1,λ2>0 and t0>0 such that
and
Next we introduce the main result for nonidentical oscillators with frustration. For ˉω<12sin2|α|, we set
For suitable parameters, we denote by D∞1 and D∞∗ the two angles as follows:
Theorem 2.3. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (4) with K>Kc and [ω_,ˉω]⊂[K+1,12sin2|α|). If
then for any small ε>0 with D∞1+ε<π2, there exists λ3>0 and T>0 such that
Remark 1. If the parametric conditions in Theorem 2.3 are fulfilled, the reference angles D∞1 and D∞∗ are well-defined. Indeed, because K>Kc and ˉω<12sin2|α|, we have
This implies
Then, by ω_≥K+1 and K≤ˉω we obtain
Remark 2. In order to make 1<K+1<12sin2|α|, it is necessary to assume α∈(−π4,π4). This is the reason for the setting α∈(−π4,π4).
3.
Synchronization analysis
3.1. Synchronization estimates: Identical oscillators without frustration
In this subsection we consider the system (4) with identical natural frequencies and zero frustration:
To obtain the complete synchronization, we need to derive a trapping region. We start with two elementary estimates for the transient frequencies.
Lemma 3.1. Suppose θ:=(θ1,θ2,…,θN) be a solution to the coupled system (8), then for any i,j∈{1,2,…,N}, we have
Proof. It is immediately obtained by (8).
Lemma 3.2. Suppose θ:=(θ1,θ2,…,θN) be a solution to the coupled system (8) and Ω>K, then we have
Proof. It follows from (8) and ˙θi>0 that we have
Next we give an estimate for trapping region and prove Theorem 2.2. For this aim, we will use the time derivative of D(θ(t)) and D(ν(t)). Note that D(θ(t)) is Lipschitz continuous and differentiable except at times of collision between the extremal phases and their neighboring phases. Therefore, for the collision time t at which D(θ(t)) is not differentiable, we can use the so-called Dini derivative to replace the classic derivative. In this manner, we can proceed the analysis with differential inequality for D(θ(t)). For D(ν(t)) we can proceed in the similar way. In the following context, we will always use the notation of classic derivative for D(θ(t)) and D(ν(t)).
Lemma 3.3. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (8) and Ω>K. If the initial configuration θ(0)∈A, then θ(t)∈A,t≥0.
Proof. For any θ0∈A, there exists D∞∈(0,π) such that D(θ0)<D∞. Let
Since D(θ0)<D∞, and D(θ(t)) is a continuous function of t, there exists η>0 such that
Therefore, the set T is not empty. Let T∗:=supT. We claim that
Suppose to the contrary that T∗<∞. Then from the continuity of D(θ(t)), we have
We use Lemma 3.1 and Lemma 3.2 to obtain
Here we used the relations
and
Therefore, we have
which implies that
This is contradictory to D(θ(T∗))=D∞. The claim (9) is proved, which yields the desired result.
Now we can give a proof for Theorem 2.2.
Proof of Theorem 2.2.. According to Lemma 3.3, we substitute T∗=∞ into (10), then (5) is proved with λ1=KcosD∞2π√ω0+K.
On the other hand, by (5) there exist t0 and δ(0<δ<π2) such that D(θ(t))≤δ for t≥t0. Now we differentiate (8) to find
Using Lemma 3.2, we now consider the temporal evolution of D(ν(t)):
This implies that
and proves (6) with λ2=Kcosδ2√ω0+K.
Remark 3. Theorem 2.2 shows, as long as the initial phases are confined inside an arc with geodesic length strictly less than π, complete phase synchronization occurs exponentially fast. This extends the main result in [5] where the initial phases for synchronization need to be confined in an arc with geodesic length less than π/2.
3.2. Synchronization estimates: Nonidentical oscillators with frustration
In this subsection, we prove the main result for nonidentical oscillators with frustration.
Lemma 3.4. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (4), then for any i,j∈{1,2,…,N}, we have
Proof. By (4) and for any i,j∈{1,2,…,N}
the result is immediately obtained.
Lemma 3.5. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (4) and ω_≥K+1, then we have
Proof. From (4), we have
and also because ˙θi>0. The following lemma gives a trapping region for nonidentical oscillators.
Lemma 3.6. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (4) with K>Kc and [ω_,ˉω]⊂[K+1,12sin2|α|). If the initial configuration θ0∈B, then θ(t)∈B for t≥0.
Proof. We define the set T and its supremum:
Since θ0∈B, and note that D(θ(t)) is a continuous function of t, we see that the set T is not empty and T∗ is well-defined. We now claim that
Suppose to the contrary that T∗<∞. Then from the continuity of D(θ(t)), we have
We use Lemma 3.4 to obtain
For I, we have
We now consider two cases according to the sign of α.
(1) α∈[0,π4). In this case, we have
(2) α∈(−π4,0). In this case, we have
Here we used the relations
and
Since D(θ(t))+|α|<D∞∗<π for t∈[0,T∗), we obtain
By (12) and Lemma 3.5 we have
Then we obtain
i.e.,
Here we used the definition of sinD∞∗. By Gronwall's inequality, we obtain
Thus
Let t→T∗− and we have
which is contradictory to D(θ(T∗))=D∞∗−|α|. Therefore, we have
That is,
Lemma 3.7. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (4) with K>Kc and [ω_,ˉω]⊂[K+1,12sin2|α|). If the initial configuration θ(0)∈B, then
Proof. It follows from (11) and Lemma 3.5, Lemma 3.6 and that we have
The proof is completed.
Lemma 3.8. Let θ:=(θ1,θ2,…,θN) be a solution to the coupled system (4) with K>Kc and [ω_,ˉω]⊂[K+1,12sin2|α|). If the initial configuration θ(0)∈B, then for any small ε>0 with D∞1+ε<π2, there exists some time T>0 such that
Proof. Consider the ordinary differential equation:
It is easy to find that y∗=D∞1 is a locally stable equilibrium of (13), while y∗∗=D∞∗ is unstable. Therefore, for any initial data y0 with 0<y0<D∞∗, the trajectory y(t) monotonically approaches y∗. Then, for any ε>0 with D∞1+ε<π2, there exists some time T>0 such that
In particular, y(t)<y∗+ε for t≥T. By Lemma 3.7 and the comparison principle, we have
which is the desired result.
Remark 4. Since
we have D∞1>|α|.
Proof of Theorem 2.3. It follows from Lemma 3.8 that for any small ε>0, there exists some time T>0 such that
We differentiate the equation (4) to find
We now consider the temporal evolution of D(ν(t)):
where we used
Thus we obtain
and proves (7) with λ3=Kcos(D∞1+ε)2√ˉω+K.
4.
Conclusions
In this paper, we presented synchronization estimates for the Kuramoto-like model. We show that for identical oscillators with zero frustration, complete phase synchronization occurs exponentially fast if the initial phases are confined inside an arc with geodesic length strictly less than π. For nonidentical oscillators with frustration, we present a framework to guarantee the emergence of frequency synchronization.
Acknowledgments
We would like to thank the anonymous referee for his/her comments which helped us to improve this paper.













 DownLoad:
DownLoad: