Chaotic perturbations of solitons in complex conformable Maccari system

1.   Introduction

Fractional partial differential equations (FPDEs) are acquiring significance in a variety of scientific and engineering fields due to their unique ability to articulate complex physical processes, which outperforms the restrictions imposed by conventional integer-order PDEs ^[1,2]. FPDEs are applied to represent system with reminiscent and inherited features, where the system's reaction is determined by its earlier states ^[3,4]. They can simulate complex phenomena in fields such as finance, physics, engineering, and biology, as they effectively capture long-range dependencies and power-law behaviour ^[5,6,7]. FPDEs also offer several advantages over traditional integer-order PDEs, including the ability to describe complex physical processes with greater precision, capture long-range dependencies and manage non-local interplays. The use of FPDEs is expected to increase in the future, as they provide a more accurate and complete understanding of complex physical phenomena.

Finding analytical solutions for FPDEs is a challenging task, and multiple numerical and analytical approaches have been established to tackle this issue. Researchers often prefer analytical solutions over numerical methods because they provide a better understanding of the fundamental physical processes and reveal the real-world behaviour of the modeled system. As a result, developing analytical solutions for FPDEs is a significant field of research, for which researchers have developed several mathematical methods. Many of these have been used to solve FPDEs analytically, including the fractional variational iteration method ^[8], Adomian decomposition method ^[9], optimal homotopy analysis method ^[10], variable separable method ^[11], integral transforms method ^[12], differential transform method ^[13], exp-function approach ^[14], elliptic expansion technique ^[15,16], Hirota bilinear method ^[17], Bäcklund transformation bilinear method ^[18,19], fractional reduced differential transform method (FRDTM) ^[20], and the Khater method (KM) ^[21,22].

Among these approaches, some researchers have employed the generalized Bernoulli equation method (gBEM) ^[23,24] to generate soliton solutions for nonlinear fractional partial differential equations (NFPDEs). In this technique, a variable transformation is used to transform NFPDE into an nonlinear ordinary differential equations (NODE). The proposed procedure then adopts a series-form solution with specific factors for the subsequent NODE, leading to an algebraic system of equations that gives soliton solutions for the proposed NFPDE. For finding a broad range of soliton solutions for NFPDEs, the gBEM presents substantial advantages over other approaches. For instance, the gBEM provides multiple families of soliton solutions. This makes it possible for researchers to forecast the behaviour of the system they are modelling with greater accuracy and to obtain a deeper knowledge of the physical processes that underlie the system. The approach, which yields novel families of soliton solutions, including chaotic perturbed soliton solutions, can a shed light on many aspects of system behaviour including decay over time, dispersion, and wave propagation.

Our current research efforts are intend to demonstrate that the suggested gBEM is effective for analyzing the soliton solutions of the conformable coupled Maccari system (CCMS), a fractional generalization of the Complex Maccari System (CMS). The CMS is a mathematical model initially developed to simulate hydraulic systems and nowadays used in a wide range of applications, namely for non-linear systems with complex structures. In particular, it is extensively applied used in fluid dynamics to model non-Newtonian behaviors emerging, for example, in viscoelastic fluids. Fluids in this category can exhibit pseudoplastic or dilatant properties. These fluids do not follow a linear relationship between pseudoplastic and dilatant that is depends of Newtonian fluids. Instead, they display more complex behaviour that depends on the applied stress or shear rate. The CMS is modelled in the following system of equations ^[25]:

in which functions $Q, S, N,$ and $R$ are complex valued functions and depend on $x, y,$ and time $t$. The CCMS is a useful tool for modeling complex nonlinear systems, particularly for characterizing the behaviour of capped waves within a small region. Several researchers have solved CCMS with the help of different methodologies. Baskonus et al. ^[25], for example, used the Sine-Gordon expansion approach to produce soliton solutions to the coupled nonlinear CCMS. Demiray et al. ^[26] solved the CCMS using the generalized Kudryashov method. In ^[27], Ahmad et al. obtained certain soliton and other numerical solutions for CCMS in integer-order. Maccari's model was used to characterize rogue waves in ^[28]. Based on the currently available literature, the chaotic soliton solutions for CCMS have not been determined and examined prior to this investigation. Thus, by applying gBEM to investigate the chaotic behavior of soiltons within the framework of CCMS, the current study closes this research gap.

The behavior of viscoelastic fluids cannot be described using traditional integer-order derivatives in CCMS. Integer-order derivatives were developed to describe the behavior of Newtonian fluids and assume that the fluids reaction is immediate and linear. These assumptions are not accurate for non-Newtonian fluids, and when applied, they contribute to inaccurate predictions and limited applicability. Fractional calculus allowing the use of fractional derivatives to better describe of time-dependent and non-linear behaviors of viscoelastic fluids. These fractional derivatives are developed with non-integer orders and can consider the deformation history of the fluid, thus yielding a more accurate description of its behavior. Thus, the CCMS has become the object of our research in this paper. The CCMS is a type of the CCMS in which NPDEs are replace with the NFPDEs to account for the behaviour of complex nonlinear systems. The CCMS helps to achieve a more detailed representation of the nonlinear systems with complex structures such as in heat transfer and fluid dynamics. The CCMS is denoted as follows:

where $0 < \alpha, \beta, \gamma \leq1$ denotes the order of the conformable fractional derivatives. By applying fractional derivatives in the CMS, it becomes possible to more accurately represent the non-Newtonian behavior of the viscoelastic fluids, resulting in more accurate predictions and a deeper understanding of their behavior. This is particularly important for example, for fluid behavior, in vats used in the industry; or in medicine. Smalls et al. noted that one of the advantages of the fractional calculus employed in the CMS is that it describes the behavior of viscoelastic fluids in a precise and realistic manner, which provides benefits when it comes to predicting and recognizing their behavior in reality. Another unique feature of the CCMS is that it may contain fractional derivatives, which enables boundary conditions to be define at an initial stage of the problem. As a result, we can model systems with anomalous diffusion or non-local transport phenomena, which standard integer-order models cannot model.

The current study aims to construct and analyze chaotic solitons in CCMS using gBEM. Solitons are stable, localized wave solutions that preserve their form and velocity while traveling through matter. These are distinctive solutions observed in some nonlinear FPDEs. They have proven to be exceptional solutions due to their ability to maintain their shape and coherence after collision with other solitons. First, by converting the CCMS into a collection of NODEs, we establish a new set of soliton options. The rational, trigonometric, hyperbolic, and exponential functions are used to express these perturbed soliton solutions. A series of 3D and counter plots are used to visually represent the chaotic perturbations of some obtained solitons in order to aid in their interpretation. This indicates that there are two types of perturbations exhibited by solitons in CCMS: axial and periodic. Moreover, the approach and findings presented here enable engineers and scientists to address increasingly intricate systems and unearth novel occurrences in the field of nonlinear dynamics.

2.   Method & materials

This section describes the conformable fractional derivative and outlines the working mechanism of the proposed gBEM.

2.1.   Conformable fractional derivative

Recently, various types of fractional derivative operators have been introduced in the literature, such as Riemann-Liouville, Caputo, Hadamard, Erdelyi-Kober, Grunwald-Letnikov, Marchaud and Riesz by means of the Fourier or Mellin integral transforms ^[29,30]. The advantages of conformable fractional derivatives over other fractional derivative operators allow them to be used to achieve explicit soliton solutions to nonlinear FPDEs. Interestingly, some alternate formulations of fractional derivatives do not yield the soliton solutions for Eq (2) because they violate the chain rule ^[25,26]. Conformable fractional derivatives were so incorporated into Eq (2). Recently, a new local, limit-based definition of the conformable derivative was formulated in ^[27,34,35] as follows:

Note that, the derivative $D_\alpha(f)(t) = t^{1-\alpha}f^{'}(t)$ exists if function $f$ is fully differentiable at $t$. Furthermore, we provide a new definition and derive several outcomes, including the sum rule, power rule, constant rule, product rule, and chain rule. Starting with a generalization of the conformable fractional derivative, we have the following definition.

Definition 2.1. If a function $f: [\Upsilon, b]\rightarrow \Re$ is given with $0\leq \Upsilon < b$, then the $\Upsilon$-conformable fractional derivative of the given function $f$ of order $\varsigma$ is defined as

If $f$ is $(\varsigma, \Upsilon)$-differentiable in some $(\Upsilon, b), \, \Upsilon > 0, \, \lim_{t \to \Upsilon^+}D^\Upsilon_{\varsigma}$ exists, then define

If the $\Upsilon$-conformable fractional derivative of a given function $f$ of order $\varsigma$ exists, then we simply say that $f$ is $(\varsigma, \Upsilon)$-differentiable.

Theorem 2.1. Let $h(t)$ and $g(t)$ be the $(\Upsilon, \varsigma)$-differentiable functions on $(\varsigma, b)$, and let $c_1, c_2 \in \Re$. Then, the function $\zeta(t) = c_1 h(t) + c_2 g(t)$ is $(\Upsilon, \varsigma)$-differentiable on $(\varsigma, b)$, and its $(\Upsilon, \varsigma)$-conformable fractional derivative is given by

Theorem 2.2. Let $\zeta(t) = t^p$ where $p \in \Re$ and $\zeta$ is defined on $(\varsigma, b)$. The $(\Upsilon, \varsigma)$-conformable fractional derivative of $\zeta$ is given by

Theorem 2.3. Let $\zeta(t) = c$ where $c$ is a constant. The $(\Upsilon, \varsigma)$-conformable fractional derivative of $\zeta$ is zero:

Theorem 2.4. Let $h(t)$ and $g(t)$ be $(\Upsilon, \varsigma)$-differentiable functions on $(\varsigma, b)$. Then the product $\zeta(t) = h(t)g(t)$ is $(\Upsilon, \varsigma)$-differentiable on $(\varsigma, b)$, and its $(\Upsilon, \varsigma)$-conformable fractional derivative is given by

With these definitions in hand, we can present the following properties for $(\varsigma, \Upsilon)$-diferentiable functions. Regarding the conformable fractional derivative, Khalil et al. ^[35] defined further properties such as the Laplace transformation, Taylor's series expansion, Gronwall's inequality, and several integration techniques. However, the main result that we use here is the chain rule, which we discuss in the following theorem.

Theorem 2.5. Let $f(t)$ and $h(t)$ be arbitrary differentiable functions; then

Proof. If the function $h$ is a constant in a neighbourhood $t_0$, then $D_\varsigma^\Upsilon(f\circ h)(t_0) = 0$. However, we make the following assumption about non-constant function $h$ in the vicinity of $t_0$. Here, we are able to find an $\varepsilon > 0$ $\ni$ $h(t_1) \neq h(t_2)$ for any $t_1, t_2 \in (t_0-\varepsilon_0, t_0+\varepsilon_0)$. Thus, since the function $h$ is continuous at $t_0$, for $t_0 > \Upsilon$, $t^\varsigma_0 \neq \Upsilon$ (where $\Upsilon\geq0$), we obtain that

Theorem 2.6. Suppose that if a function $f:[\Upsilon, b]\rightarrow \Re$ is $(\varsigma, \Upsilon)-$ differentiable with $0\leq \Upsilon < b$ and $\varsigma\in(0, 1]$ at $t_0 > \Upsilon, \, t_{0}^{\varsigma}\neq \Upsilon,$ then $f$ is continuous at $t_0$.

Proof. Since

we have

let $h = \varepsilon t^{-\varsigma}_0(t_0 -\Upsilon)$. Then, we get $\lim_{\varepsilon \to 0}f(t_0+h)-f(t_0) = D^{\Upsilon}_{\varsigma}(f)(t_0).0,$ which implies that $f$ is continuous at $t_0$.

2.2.   The working methodology of gBEM

In the following section, we present the operational procedure of gBEM, an elegant technique for solving nonlinear FPDEs. The basic structure of FPDEs is summarized as follows:

where $u$ represents an unknown function that depends upon $x, y, z$, and $t$, and $D_t^\alpha$, $D_x^\beta$, $D_y^\delta$, and $D_z^\varphi$ are conformable fractional derivative operators. To solve Eq (11), we shall do the following:

Step 1: We begin our adventure by applying a variable transformation in the following manner:

By using several definitions of the function $\xi$, we design a transformation that transforms Eq (11) into the next NODE.

Step 2: Following that, we consider a solution to Eq (13) derived using a series-based technique. This technique not only speeds our study, but also shows an orderly and visually appealing solution to the equation.

here, $B_i$ represents non-zero constants while $G(\xi)$ is the solution for the following ordinary differential equation (ODE).

Step 3: The nonlinear component and the highest-order derivative of Eq (13) are then balanced homogeneously to obtain the positive integer $N$, as shown in Eq (14). This balancing technique is crucial because it ensures that the resulting equation may be effectively handled using the analytical approaches outlined below.

Step 4: By inserting Eq (14) into Eq (13), we establish an algebraic system of equations by grouping all terms with the same power of $G(\xi)$ and putting them equal to zero.

Step 5: Following that, the established system is handled using Maple, which generates the computed values for the relevant parameters.

Step 6: The sets of soliton solutions are then produced by combining the values of parameters in Eq (14) with the suitable solution in (15). In addition, the many soliton solutions for Eq (15) applied to the various conditions are presented below:

Family1: For any non-zero real numbers $\tau$ and $\mu$ with the conditions $\tau^2 > 0$ and $\mu\neq0$, respectively, Eq (13) generates the following families of solutions:

where $N^2-M^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $M^2-N^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $\chi$ is arbitrary unknown constant.

Family2: If $\tau = 0$ and $\mu\neq0$, the solution of Eq (13) is:

3.   Execution of the gBEM

We apply the following variable transformation to derive innovative soliton solutions for the CCMS given in (2):

Where $\Omega = i(\lambda \frac{t^\alpha}{\alpha}+ K \frac{x^\beta}{\beta} +j \frac{y^\delta}{\delta}) + m$, and $\lambda$, $K$, $j$ and $m$ are arbitrary constants to be defined later. Substituting (29) by considering $\xi = \eta(\frac{x^\beta}{\beta} + \frac{y^\delta}{\delta} - 2K\frac{t^\alpha}{\alpha})$ into (2), we get:

Using the transformation $u = U(\xi)$, $v = V(\xi)$, $w = W(\xi)$, and $R = R(\xi)$, where $\xi = \eta(\frac{x^\beta}{\beta} + \frac{y^\delta}{\delta} - 2K\frac{t^\alpha}{\alpha})$ to (30) yields the following set of equations:

When we integrate the fourth part (31) with regard to $\xi$, we get:

Substituting Eq (32) into the first three sections of (31) gives the following result:

We may simplify the system of equations in (33) to a single NODE in $U$, assuming values for $V$ and $W$ with arbitrary constants $K_1$ and $K_2$, such that,

By substituting (34) with (33), we get the following NODE:

We get $N = 1$ by applying the balancing principle to the largest derivative $U^{''}(\xi)$ and the nonlinear term $U^3$ in (35).

Putting (36) in (35) and collecting all the terms with the same power of $G(\xi)$ provides an expression in $G(\xi)$. We obtain a system of algebraic equations by equating each coefficient of the expression to zero. Using Maple and solving the resulting system yields the following three scenarios of solutions for the relevant parameters:

Case 1:

Case 2:

Case 3:

Where $\frac {-2\, {\eta}^{2}{\mu}^{2}+4\, {\eta}^{2}{\mu}^{2}K+K_{{2}}{B_{{1} }}^{2}+{B_{{1}}}^{2}}{{B_{{1}}}^{2}}$

Assuming Case 1, we obtain the subsequent families of soliton solutions for CCMS given in (2):

Family 1.1. For any non-zero real numbers $\tau$ and $\mu$ with the conditions $\tau^2 > 0$ and $\mu\neq0$, respectively, Eq (35) for Case 1 generates the following families of solutions:

where $U_{1, 1}(t, x, y) = \frac {B_{{0}} \left(-\tau+\tanh \left(\frac{1}{2}\, \tau\, \xi \right) \right) }{\tau+\tanh \left(\frac{1}{2}\, \tau\, \xi \right) }$.

where $U_{1, 2}(t, x, y) = {\frac {B_{{0}} \left(\tau+\coth \left(\frac{1}{2}\, \tau\, \xi \right) \right) }{-\tau+\coth \left(\frac{1}{2}\, \tau\, \xi \right) }}$.

where $U_{1, 3}(t, x, y) = {\frac {-2\, B_{{0}}}{1+\tanh \left(\tau\, \xi \right) \pm \left(i{\it sech} \left(\tau\, \xi \right) \right) }}+B_{{0 }}$.

where $U_{1, 4}(t, x, y) = {\frac {-2\, B_{{0}}}{1+\coth \left(\tau\, \xi \right) \pm \left(i{\it csch} \left(\tau\, \xi \right) \right) }}+B_{{0 }}$.

where $U_{1, 5}(t, x, y) = B_{{0}} \left(2\, \cosh \left(\frac{1}{4}\, \tau\, \xi \right) \sinh \left(\frac{1}{4} \, \tau\, \xi \right) -2\, \left(\cosh \left(\frac{1}{4}\, \tau\, \xi \right) \right) ^{2}+1 \right) ^{2}$.

where $U_{1, 6}(t, x, y) = {\frac {B_{{0}} \left(M\sinh \left(\tau\, \xi \right) +N+\sqrt {{M}^{ 2}+{N}^{2}}-M\cosh \left(\tau\, \xi \right) \right) }{\sqrt {{M}^{2}+ {N}^{2}}-M\cosh \left(\tau\, \xi \right) -M\sinh \left(\tau\, \xi \right) -N}}$.

where $U_{1, 7}(t, x, y) = -{\frac {B_{{0}} \left(M\cosh \left(\tau\, \xi \right) +N-\sqrt {{N}^ {2}-{M}^{2}}+M\sinh \left(\tau\, \xi \right) \right) }{\sqrt {{N}^{2} -{M}^{2}}-M\sinh \left(\tau\, \xi \right) +M\cosh \left(\tau\, \xi \right) +N}}$.

Where $N^2-M^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $U_{1, 8}(t, x, y) = {\frac {B_{{0}} \left(1\mp \left({{\rm e}^{\tau\, \xi}} \right) \right) }{\pm \left({{\rm e}^{\tau\, \xi}} \right) }}+B_{{0}}$.

where $U_{1, 9}(t, x, y) = {\frac {B_{{0}} \left(i \mp \left({{\rm e}^{\tau\, \xi}} \right) \right) }{\pm \left({{\rm e}^{\tau\, \xi}} \right) }}+B_{{0}}$.

where $U_{1, 10}(t, x, y) = {\frac {B_{{0}} \left(\mp \left(M \left({{\rm e}^{ \tau\, \xi}}-{{\rm e}^{-\tau\, \xi}} \right) \right) \pm \left(2\, iR \right) \right) }{\sqrt {{M}^{2}-{N}^{2}} \pm \left(M{{\rm e}^{\tau\, \xi}}-iR \right) }}+B_{{0 }}$.

Where $M^2-N^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $U_{1, 11}(t, x, y) = -{\frac {B_{{0}} \left(1+\chi\, {{\rm e}^{\tau\, \xi}} \right) }{\chi\, {{\rm e}^{\tau\, \xi}}}}+B_{{0}}$.

where $U_{1, 12}(t, x, y) = -{\frac {B_{{0}} \left(\chi+{{\rm e}^{\tau\, \xi}} \right) }{{{\rm e}^ {\tau\, \xi}}}}+B_{{0}}$.

Where $\chi$ is an arbitrary unknown constant.

Family 1.2. If $\tau = 0$ and $\mu\neq0$, the solution of Eq (35) for Case 1 is:

Where $U_{1, 13}(t, x, y) = -{\frac {B_{{0}}\tau\, \left(\mu\, \xi+\Psi \right) }{\mu}}+B_{{0}}$.

Assuming Case 2, we get the subsequent families of soliton solutions for CCMS given in (2):

Family 2.1. For any non-zero real numbers $\tau$ and $\mu$ with the conditions $\tau^2 > 0$ and $\mu\neq0$, respectively, Eq (35) for Case 2 generates the following families of solutions:

where $U_{2, 1}(t, x, y) = {\frac {-2 \, B_{{-1}}\mu}{\, \tau+\, \tanh \left(\frac{1}{2}\, \tau\, \xi \right) }}+B_{{0}}-{\frac {\, B_{{1}}\tau+\, B_{{1}}\tanh \left(\frac{1}{2}\, \tau\, \xi \right) }{2 \, \mu}}$.

where $U_{2, 2}(t, x, y) = {\frac {2 \, B_{{-1}}\mu}{-\, \tau+\, \coth \left(\frac{1}{2}\, \tau\, \xi \right) }}+B_{{0}}+{\frac {-\, B_{{1}}\tau+\, B_{{1}}\coth \left(\frac{1}{2}\, \tau\, \xi \right) }{2 \, \mu}}$.

where $U_{2, 3}(t, x, y) = -2\, {\frac {B_{{-1}}\mu}{\tau\, \left(1+\tanh \left(\tau\, \xi \right) \pm \left(i{\it sech} \left(\tau\, \xi \right) \right) \right) }}+B_{{0}}-\, {\frac {B_{{1}}\tau\, \left(1+\tanh \left(\tau\, \xi \right) \pm \left(i{\it sech} \left(\tau\, \xi \right) \right) \right) }{2 \, \mu}}$.

where $U_{2, 4}(t, x, y) = -2\, {\frac {B_{{-1}}\mu}{\tau\, \left(1+\coth \left(\tau\, \xi \right) \pm \left(i{\it csch} \left(\tau\, \xi \right) \right) \right) }}+B_{{0}}-\, {\frac {B_{{1}}\tau\, \left(1+\coth \left(\tau\, \xi \right) \pm \left(i{\it csch} \left(\tau\, \xi \right) \right) \right) }{2 \, \mu}}$.

where $U_{2, 5}(t, x, y) = {\frac {-4 \, B_{{-1}}\mu}{ \left(2+\, \tanh \left(\frac{1}{4}\, \tau\, \xi \right) +\, \coth \left(\frac{1}{4}\, \tau\, \xi \right) \right) \tau}}+B_{ {0}}-{\frac {B_{{1}} \left(2+\, \tanh \left(\frac{1}{4}\, \tau\, \xi \right) +\, \coth \left(\frac{1}{4}\, \tau\, \xi \right) \right) \tau}{4 \, \mu}}$.

where $U_{2, 6}(t, x, y) = \frac{2\, B_{{-1}}\mu}{\tau} \left(\, {\frac {\sqrt {{M}^{2}+{N}^{2}}-M\cosh \left(\tau\, \xi \right) }{M\sinh \left(\tau\, \xi \right) +N}}-1 \right) ^ {-1}+B_{{0}}+ \frac{\, B_{{1}} \tau}{2\mu} \left(\, {\frac {\sqrt {{M}^{2}+{N}^{2}}-M\cosh \left(\tau\, \xi \right) }{M\sinh \left(\tau\, \xi \right) +N}}-1 \right) ^ {-1}$.

where $U_{2, 7}(t, x, y) = -\frac{2 B_{{-1}}\mu}{\tau} \left(\, {\frac {\sqrt {{N}^{2}-{M}^{2}}-M\sinh \left(\tau\, \xi \right) }{M\cosh \left(\tau\, \xi \right) +N}}+1 \right) ^{-1}+B_{{0}}-\frac{ B_{{1}}\tau}{2\mu} \left({\frac {\sqrt {{N}^{2}-{M}^{2}}-M\sinh \left(\tau\, \xi \right) }{M\cosh \left(\tau \, \xi \right) +N}}+1 \right)$.

Where $N^2-M^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $U_{2, 8}(t, x, y) = {\frac {B_{{-1}}\mu\, \left(1 \mp \left({{\rm e}^{ \tau\, \xi}} \right) \right) }{\tau\, \pm \left({ {\rm e}^{\tau\, \xi}} \right) }}+B_{{0}}+{\frac {B_{{1}}\tau\, \pm \left({{\rm e}^{\tau\, \xi}} \right) }{\mu\, \left(1 \mp \left({{\rm e}^{\tau\, \xi}} \right) \right) }}$.

where $U_{2, 9}(t, x, y) = {\frac {B_{{-1}}\mu\, \left(i \mp \left({{\rm e}^{ \tau\, \xi}} \right) \right) }{\tau\, \pm \left({{\rm e}^{\tau\, \xi}} \right) }}+B_{{0}}+{\frac {B_{{1}}\tau\, \pm \left({{\rm e}^{\tau\, \xi}} \right) }{\mu\, \left(i \mp \left({{\rm e}^{\tau\, \xi}} \right) \right) }}$.

where $U_{2, 10}(t, x, y) = {\frac {B_{{-1}}\mu\, \left(\mp \left(M \left({ {\rm e}^{\tau\, \xi}}-{{\rm e}^{-\tau\, \xi}} \right) \right) \pm \left(2\, iR \right) \right) }{\tau\, \left(\sqrt {{M}^ {2}-{N}^{2}} \pm \left(M{{\rm e}^{\tau\, \xi}}-iR \right) \right) }}+B_{{0}}+{\frac {B_{{1}}\tau\, \left(\sqrt {{M}^{ 2}-{N}^{2}} \pm \left(M{{\rm e}^{\tau\, \xi}}-iR \right) \right) }{\mu\, \left(\mp \left(M \left({{\rm e}^{\tau\, \xi}}-{{\rm e}^{-\tau\, \xi}} \right) \right) \pm \left(2\, iR \right) \right) }}$.

Where $M^2-N^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $U_{2, 11}(t, x, y) = -{\frac {B_{{-1}}\mu\, \left(1+\chi\, {{\rm e}^{\tau\, \xi}} \right) }{ \tau\, \chi\, {{\rm e}^{\tau\, \xi}}}}+B_{{0}}-{\frac {B_{{1}}\tau\, \chi \, {{\rm e}^{\tau\, \xi}}}{\mu\, \left(1+\chi\, {{\rm e}^{\tau\, \xi}} \right) }}$.

where $U_{2, 12}(t, x, y) = -{\frac {B_{{-1}}\mu\, \left(\chi+{{\rm e}^{\tau\, \xi}} \right) }{ \tau\, {{\rm e}^{\tau\, \xi}}}}+B_{{0}}-{\frac {B_{{1}}\tau\, {{\rm e}^{ \tau\, \xi}}}{\mu\, \left(\chi+{{\rm e}^{\tau\, \xi}} \right) }}$.

Where $\chi$ is an arbitrary unknown constant.

Family 2.2. If $\tau = 0$ and $\mu\neq0$, the solution of Eq (35) for Case 2 is:

Where $U_{2, 13}(t, x, y) = -B_{{-1}} \left(\mu\, \xi+\Psi \right) +B_{{0}}-{\frac {B_{{1}}}{\mu\, \xi+\Psi}}$.

Assuming Case 3, we get the subsequent families of soliton solutions for CCMS given in (2):

Family 3.1. For any non-zero real numbers $\tau$ and $\mu$ with the conditions $\tau^2 > 0$ and $\mu\neq0$, respectively, Eq (35) for Case 3 generates the following families of solutions:

where $U_{3, 1}(t, x, y) = -\frac{1}{2}\, {\frac {B_{{1}}\tanh \left(\frac{1}{2}\, \tau\, \xi \right) }{\mu}}$.

where $U_{3, 2}(t, x, y) = \frac{1}{2}\, {\frac {B_{{1}}\coth \left(\frac{1}{2}\, \tau\, \xi \right) }{\mu}}$.

where $U_{3, 3}(t, x, y) = \, \frac {B_{{1}}\tau}{\mu}\bigg(-\frac{1}{2}\, \tanh \left(\tau\, \xi \right) -\frac{1}{2}\, \pm \left(i{\it sech} \left(\tau\, \xi \right) \right) \bigg)$.

where $U_{3, 4}(t, x, y) = \frac {B_{{1}}\tau}{2 \, \mu}\bigg(-\, \coth \left(\tau\, \xi \right) -1\, \pm 2 \, \left(i{\it csch} \left(\tau\, \xi \right) \right)\bigg)$.

where $U_{3, 5}(t, x, y) = -\frac {B_{{1}}\tau}{4 \, \mu} \bigg(\, \tanh \left(\frac{1}{4}\, \tau\, \xi \right) +\, \coth \left(\frac{1}{4}\, \tau\, \xi \right) \bigg)$.

where $U_{3, 6}(t, x, y) = \frac{1}{2}\, {\frac { \left(\sqrt {{M}^{2}+{N}^{2}}-M\cosh \left(\tau\, \xi \right) \right) B_{{1}}\tau}{\mu\, \left(M\sinh \left(\tau\, \xi \right) +N \right) }}$.

where $U_{3, 7}(t, x, y) = -\frac{1}{2}\, {\frac { \left(\sqrt {{N}^{2}-{M}^{2}}-M\sinh \left(\tau\, \xi \right) \right) B_{{1}}\tau}{\mu\, \left(M\cosh \left(\tau\, \xi \right) +N \right) }}$.

Where $N^2-M^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $U_{3, 8}(t, x, y) = \frac{B_{{1}}\tau}{\mu} \left(\frac{1}{2}\pm {\frac { \left({{\rm e}^{\tau\, \xi}} \right) }{1 \mp \left({{\rm e}^{\tau\, \xi}} \right) }} \right)$.

where $U_{3, 9}(t, x, y) = \frac{B_{{1}}\tau}{\mu} \left(\frac{1}{2}+{\frac {\pm \left({{\rm e}^{\tau\, \xi}} \right) }{i \mp \left({{\rm e}^{\tau\, \xi}} \right) }} \right)$.

where $U_{3, 10}(t, x, y) = \frac{B_{{1}}\tau}{\mu} \left(\frac{1}{2}+{\frac {\sqrt {{M}^{2}-{N}^{2}} \pm M{{\rm e}^{\tau\, \xi}} -iR}{\mp \left(M \left({{\rm e}^{\tau\, \xi}}-{{\rm e}^{-\tau\, \xi}} \right) \right) \pm \left(2\, iR \right) }} \right)$.

Where $M^2-N^2 > 0$, for all $M$ and $N$ non-zero real constants.

where $U_{3, 11}(t, x, y) = \left(\frac{1}{2}\, {\mu}^{-1}-{\frac {\chi\, {{\rm e}^{\tau\, \xi}}}{\mu\, \left(1+\chi\, {{\rm e}^{\tau\, \xi}} \right) }} \right) B_{{1}}\tau$.

where $U_{3, 12}(t, x, y) = \frac{1}{2}\, {\frac {B_{{1}}\tau}{\mu}}-{\frac {B_{{1}}\tau\, {{\rm e}^{\tau\, \xi}}}{\mu\, \left(\chi+{{\rm e}^{\tau\, \xi}} \right) }}$.

Where $\chi$ is an arbitrary unknown constant.

Family 3.2. If $\tau = 0$ and $\mu\neq0$, the solution of Eq (35) for Case 3 is:

Where $U_{3, 13}(t, x, y) = \frac{1}{2}\, {\frac {B_{{1}}\tau}{\mu}}-{\frac {B_{{1}}}{\mu\, \xi+\Psi}}$.

4.   Discussion and graphs

The current study's primary objective was to use gBEM to solve CCMS, which offered several families of soliton solutions. Furthermore, our present method may be considered an efficient extension of simple BEM, resulting in a comprehensive tool for several nonlinear situations. The findings of our suggested fractional-order solutions are noteworthy, in contrast to those of the conventional and previously employed integer-order solutions, which are unable to accurately depict all physical phenomena. Our method eliminates the necessity to linearize the equation, which is required by certain other previously published methodologies, and allows acquiring the precise solution to nonlinear problems in the physical sciences. Additionally, the gBEM technique employed in this study is a reliable tool with demonstrated effectiveness in a range of physical phenomena, underscoring their applicability and versatility in resolving complex nonlinear problems.

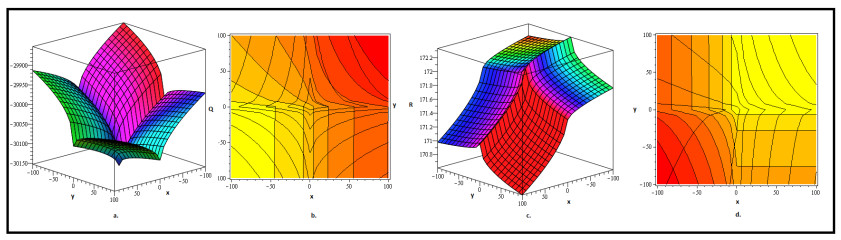
In the field of CCMS, we identified chaotic solutions with axial and periodic perturbations that may be linked to a variety of hydraulic systems. The term chaotic perturbation refers to the complex behavioral shifts that can occur in soliton frameworks as a consequence of envisaged or unanticipated shocks that resemble chaos. In our study, these perturbations manifest as structural alterations in solitons, where certain kink solitons transform into fractal-like forms, while predicted periodic solitons become breather solitons among chaotic perturbations. The behavior of fluid flow is significantly impacted by these chaotic solitons. In the context of hydraulic systems, such chaotic solitons can manifest as unpredictable and irregular flow patterns, resulting in intricate system dynamics. The axial and periodic perturbations in the chaotic solitons, which can be linked to variations or perturbations in the flow characteristics, may have an impact on the overall behavior and robustness of the hydraulic system. Axial and radial velocities are two flow variables that may be directly impacted by these obtained chaotic solitons from CCMS. These chaotic solitons with perturbations cause the flow to become irregular and nonlinear, which impacts the fluid's dynamics and velocity distribution in hydraulic systems. Such phenomena may simplify the overall behavior and effectiveness of the hydraulic system, especially with regard to energy dissipation and flow stability. The existence of disturbed chaotic solitons might indicate complicated nonlinear dynamics in the system, which can result in a number of phenomena that impact the overall behavior and performance of the hydraulic system, such as complex wave interactions, vorticity, and turbulence. It is essential to comprehend the relationships between chaotic solitons and system phenomena in order to comprehend the intricate behavior of hydraulic systems under nonlinear settings. Moreover, Figure 1 shows the perturbed chaotic fractal-like solition solutions $Q_{1, 1}$ and $R_{1, 1}$ in (40). Figure 2 shows the perturbed chaotic kink solition solutions $Q_{1, 3}$ and $R_{1, 3}$ in (42). Figure 3 shows the perturbed chaotic hump-breather solition solutions $Q_{1, 8}$ and $R_{1, 8}$ in (47). Figure 4 shows the perturbed chaotic kink solition solutions $Q_{2, 2}$ and $R_{2, 2}$ in (54). Figure 5 shows the perturbed chaotic fractal-like periodic solition solutions $Q_{2, 6}$ and $R_{2, 6}$ in (58). Figure 6 shows the perturbed chaotic parabolic solition solutions $Q_{2, 9}$ and $R_{2, 9}$ in (61). Figure 7 shows the perturbed chaotic fractal-like kink solition solutions $Q_{3, 4}$ and $R_{3, 4}$ in (69). Finally, Figure 8 shows the perturbed chaotic kink solition solutions $Q_{3, 10}$ and $R_{3, 10}$ in (75). In hydraulic models, each of these solitons reflects unique wave dynamics subject to perturbations. A moving wavefront that connects two distinct fluid states, for example, is known as a perturbed kink soliton. It is altered by external perturbations like turbulence, viscosity, or external forces, resulting in variations in wave form or velocity. A perturbed breather soliton is a confined, oscillating wave structure that experiences recurring energy exchanges as a result of minor perturbations, which frequently result from changes in the pressure or flow velocity in shallow water channels. Frequently observed in flow transitions over barriers or in stratified fluid layers, a perturbed parabolic soliton is a single wave with a parabolic pattern that undergoes external perturbations, resulting in asymmetric deformation. Lastly, a perturbed periodic soliton is a wave train that comprises repeating structures that are affected by perturbations, leading to modulations in phase, frequency, or amplitude. These are frequently seen in hydraulic leaps or tidal waves.

5.   Conclusions

In conclusion, we used the gBEM to investigate the chaotic nature of solitons in CCMS, a fractional generalization of a nonlinear CMS initially created to simulate hydraulic systems. The proposed gBEM converted the CCMS into a set of NODEs to construct a new set of soliton solutions in the form of rational, trigonometric, hyperbolic, and exponential functions. To comprehend the dynamics of acquired solitons in CCMS, a series of 3D and counter plots graphically illustrated and revealed two types of chaotic perturbations, namely axial and periodic perturbations, in the acquired solitons. The discovered chaotic soliton solutions with axial and periodic perturbations were further analyzed and linked to a variety of hydraulic systems. Furthermore, the efficiency and adaptability of our method in handling a range of nonlinear models in mathematical science and engineering were confirmed by our computational work. While the suggested approach advanced our comprehension about soliton analysis, it has some limitations. In particular, this approach fails when the nonlinear term and the highest derivative term do not balance homogeneously as this imbalance between nonlinearity and dispersion hinders the method's ability to provide soliton solutions, which depends on this exact balance. Finally, future works will aim to analyze the chaotic nature of the model with the aid of knot theory in fractional sense.

Author contributions

M. Mossa Al-Sawalha: Conceptualization, Writing-review & editing; Safyan Mukhtar: Visualization, Writing-review & editing, Data curation; Azzh Saad Alshehry: Data curation, Project administration; Mohammad Alqudah: Resources, Validation, Software; Musaad S. Aldhabani: Formal analysis, Investigation, Resources. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Funding

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU250858]. Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R183), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU250858]. Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R183), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that they have no conflict of interest.