Mathematical modeling of a Hybrid Mutated Tunicate Swarm Algorithm for Feature Selection and Global Optimization

1.   Introduction

The severe acute respiratory syndrome coronavirus 2 (SAR-CoV-2), which is responsible for COVID-19, is a type of highly contagious virus and has posed an unprecedent threat to public health worldwide. Since the first emerging in 2019, the virus has been spreading throughout the world and had a devastating impact not only on the high-income countries in Europe and North America but also in low and middle-income countries. As of 1 August 2022, there were 567,312,625 confirmed cases and 6,378,748 deaths of COVID-19 worldwide, making it the most far-reaching global health crisis since the 1918 influenza pandemic ^[1]. It has caused a ripple effect on the global economy including prolonged shutdowns and increased unemployment. Many a country or region has experienced multiple epidemic waves or outbreaks even with stringent interventions. So it is critical to explore the key reason for so many epidemic waves. In fact, there still exist quite a lot of urgent problems for those countries having experienced or experiencing multiple waves to solve including how to effectively prevent and control the spread of COVID-19 and how the impact of COVID-19 on public health and production can be reduced. So in this work, we will assess the efficiency of containments and provide insights with possible factors that aggravate the outbreak.

Since the outbreak of COVID-19, many dynamic models have been proposed to estimate the transmission risks, predict the final scale and evaluate the efficacy of non-pharmaceutical interventions on the control of the epidemic, which has important theoretical and practical significance ^{[2,3,4,5,6,7,8]}. Tang et al. ^[2] proposed a deterministic model and showed that intensive contact tracing can effectively reduce the potential and severity of the outbreak, especially in the early stage of the outbreak. Wu et al. ^[3,4] assessed the effectiveness of major prevention and control strategies, including the quarantine and isolation, by building mathematical models and applying statistical methods. $\ddot Ozk\ddot ose$ Fatma et al. ^[5] established a fractional epidemic model to test the relationship between the spread of COVID-19 and its correlation with diabetes. Huang et al. ^[6] constructed a mathematical model and used real-time data to determine peak time, peak size and final infection scale of the outbreak. Kumar et al. ^[7,8] established mathematical models to explore the dynamics of COVID-19 epidemic in multiple susceptible populations and the transmission trend of COVID-19 in India. However, to the authors' best knowledge, few modelling studies have examined the role of multiple factors, such as shortage of medical resources, mutant strain, et al., on the spread of COVID-19.

India, as one of the countries facing shortage of medical resources, has experienced its second wave of COVID-19 pandemic from early March, 2021 and the daily number of confirmed cases was still more than 20,000 at the end of September, 2021, which has caused more than four million reported confirmed cases and four thousand reported deaths during the peak infection ^[9]. So in this work, we will take India as an example to reveal the key factors affecting the outbreak and development of the epidemic. In fact, the driving factors of virus transmission in India are various, including economics, seasonality, geo-environmental and climatic factor ^[10,11,12]. And the commercial trade is also an important factor which can accelerate the diffusion of COVID-19 ^[13]. In addition, India's high population density, sever shortage of medical resources, simultaneous spread of the wild and mutant strains have caused the epidemic to be so serious. In this work, we consider the medical resource-constraints, mutant strain, environmental transmission and assess the efficiency of these factors on the containment of the outbreak. Given that about 70% of the population was already vaccinated during this outbreak of COVID-19 in India, the effect of vaccine in controlling the outbreak was also taken into account in the modelling, despite of low vaccine coverage.

India, as a populated dense country, has been struck by the second wave of COVID-19 severely with a overburdened healthcare system and significant case fatality rate, which has raised public health pressing concerns in the fight against the COVID-19 pandemic ^[14,15,16]. The high patient-to-doctor proportion 1456:1 besides the major imbalance in the size of healthcare workers and the size of people has added the difficulty in dealing with the second COVID-19 wave in India ^[17]. There are only about 8 physicians and 8.5 hospital beds for every 10,000 individuals. That, together with the overwhelming number of cases, are the maim burden borne by the healthcare workers. This phenomenon is even worse in rural India, where only 3.2 hospital beds are available for 10,000 individuals ^[18]. And for the states Uttar Pradesh, Rajasthan and Jharhand, there are only 2.5, 2.4 and 2.3 hospital beds every 10,000 individuals, respectively ^[19]. Medical-resource constraints is true in some of the developed countries ^[20]. Brendon et al. ^[21] has investigated the capacities of hospital beds, intensive care units (ICU) and acute care beds in more than 180 countries including the high-income countries, such as the United States and United Kingdom, and the middle countries, such as India. They found that the high-income countries have 12.79 ICU beds and 402.32 hospital beds every 10,000 individuals, but the rapid surge of cases has overwhelmed the available resources some time. The present studies highlight the viral role of medical resources in the outbreak of COVID-19. And there are research work that assessed the effect of medical resource in the spread of COVID-19 by developing mathematical models ^{[20,22,23,24]}. Zhu et al. ^[22,23] designed compartment models with three or two phases to explore the vital role of the hospital bed capacity in containing the outbreak of COVID-19 in Wuhan. They found that increasing hospital-bed capacity to isolate those infecteds with mild symptoms could help curb the outbreaks in regions with medical-resource constrained. Tang et al. ^[20,24] proposed piecewise-defined models to reveal the effect of hospital bed shortages in the transmission of COVID-19 in certain regions. They highlighted the critical role of timely improvement of abilities to supplement medical resources in effective controlling the COVID-19 epidemic. However, how the shortage of hospital bed, together with other containments, affected the spread of COVID-19 in India has not yet been well evaluated.

Lin et al. ^[25] emphasizes the effect of various feature factors on the spread of COVID-19 epidemic. In fact, many a factor is involved in driving the second COVID-19 wave in India, such as the complex interplay of mutant strains with higher pathogenicity and environmental transmission caused by infected individuals' respiratory droplets, in the context of the medical-resource constraints. During the second COVID-19 wave in India, Delta strain, a type of new strain of COVID-19 characterized by rapid transmission and strong infectivity, is circulating in India ^[26,27]. Because of the abundant genetic diversity and high evolution capability, SAR-CoV-2 has already exhibits dynamically evolving mutation ^{[28,29,30,31]}. Many a mutant strain of COVID-19 with high transmission rate was identified around the world, including the Beta strain in South Africa, Alpha strain in the UK and the Omicron strain in Gauteng province, South Africa ^[32]. Delta strain compromises the effectiveness of existing COVID-19 vaccines and leads to the insurgence of anti-microbial drug resistance, in addition to inducing a surge of cases and deaths in India ^[33,34]. In fact, as the supply of COVID-19 vaccines increases, a mass vaccination campaign was implemented in India on January 16, 2021 with the first dose for 30 million front-line workers, including health care workers and security forces, and the second dose for those aged over 50 or under 50 but with multiple diseases. However, the efficiency of vaccines is reduced since Delta strain, as a mutant strain, can help the virus replicate more efficiently or escape the immune system ^[33]. More than one work has studied the effect of mutant strain and vaccination strategy on the transmission of the COVID-19 epidemic by formulating mathematical models ^{[27,30,31,34,35]}. Sonabend et al. ^[27,30] proposed novel COVID-19 models to investigate how the vaccination and delta variant affect the outbreak of COVID-19 in England and Jiangsu China. They found that the increasing population immunity and lifting non-pharmaceutical interventions resulted in a decreasing of the transmission; while delta variant lead to an increasing of the peak size. Betti et al. ^[31] devised a two-strain mathematical model and used the data of COVID-19 epidemic in Ontario to parameterize the model. They found that a variant strain was unlikely to dominate in short period. Khyar et al. ^[34] investigated the global dynamics of a two-strain epidemic model, which can fit the COVID-19 clinical data well. Britto et al. ^[35] expanded and SEIR model to assess age-specific vaccine allocation strategies in India. The results supported global recommendations to prioritize COVID-19 vaccine allocation for older age groups. However, how much the vaccines help contain the outbreak by protecting the exposed individuals with Delta strain being infected, in the context of medical resource shortage, such as in countries like India, is not fully understood.

According to the updated scientific brief on COVID-19 transmission by WHO, the transmission modes of SARS-CoV-2 include contaminated environment besides close contact ^[36]. During the outbreak of second wave of COVID-19 in India, the virus, which was spread by respiratory droplets produced when infected individuals cough, sneeze, talk, et al., persists in the environment and on hard surfaces. There is study suggests that the virus can stay on plastic and stainless metal surfaces, such as door handles, desktops and tables, from two to three days ^[37]. Moreover, the transmission from improperly or not timely handled deceased cases to susceptibles is also a considerable way of transmission ^[38]. With the sudden rise in the number of deceased cases as well as shortage of medical resources in India, the deceased cases cannot be handled properly or in time ^[39], which releases virus into the environments. More than one research has revealed the indispensable role of contaminated environments in the outbreak of COVID-19 ^{[40,41,42,43]}, which provides more information on the infected risk and infectivity of contaminated surfaces. Zu et al. ^[40] proposed a nonlinear mathematical model to analyze the effects of the environmental virus on the transmission patters. By fitting the targeted model to the data in India, they highlighted the necessity of reducing the virus in the environment. He et al. ^[41] proposed a novel dynamic model to assess the effect of environmental contribution in the transmission dynamics of COVID-19. By validating the model using the COVID-19 reported data in Saudi Arabia, they revealed the crucial role of environmental transmission in the outbreak. Wang et al. ^[42] formulated a mathematical model incorporating multiple transmission pathways and fitted the model to the publicly reported data in China. The result emphasized the important role of environmental reservoirs in the transmission of COVID-19. Babington-Ashaye et al. ^[43] did a scoping review to understand the risks of infection with COVID-19 via contaminated surfaces. They have selected 565 relevant articles and found that the risk of SARS-CoV-2 infection via contaminated surfaces assessed as low in the majority of the reviewed articles. As a result, the knowledge regarding the environmental transmission and transmission mechanism of COVID-19, especially in the case of the spread of mutant strain and shortage of medical resources, remains limited.

As a result, the second wave of COVID-19 pandemic in India has resulted in mass destruction due to the shortage of medical resource, heavy load of patients, spread of delta strain and environmental transmission although a vaccination strategy has been implemented. This outbreak have raised the pressing concerns of much of the world in the fight against the current pandemic. So it is necessary to provide insights into the lessons learnt from the second wave as well as the possible strategies could be implemented to contain the viral spread. Up to this point, many mathematical models have focused on the spread and control strategies of COVID-19 from different perspectives ^{[5,20,22,23,24,27,30,31,34,35,40,41,42,43,44,45]}. These models were established based on the monitoring data of COVID-19 to capture the characteristics of the SAR-CoV-2, assess the risk of reinfection, evaluate the epidemic scale, explore the reasonable allocation of medical emergency resources, et al. However, the previous models only studied the impact of one or two factors on the tackling of the COVID-19 outbreak although. As known to all, many factors including the medical resource shortages, spread of mutant strain, environmental transmission and vaccination are reported to affect the second wave of COVID-19 outbreak in India. To the best of our knowledge, little work was done to mimic the the combined effect of multiple factors in the transmission and control of this outbreak. And it falls within the scope of this work.

To give a detailed understanding on how the simultaneous spread of the more pathogenic mutant strain and the wild strain, implementation of vaccination and indirect transmission caused by contaminated environments, in the context of shortage of medical resources, affect the outbreak of COVID-19 in the regions or countries with heavy population, it is urgent to quantitatively analyze the relationship between various factors and the outbreak of COVID-19. And the above introduction demonstrates that these problems are very prominent in India, especially the shortage of medical resources, so we chose India as an example to study. In this work, we propose a nonsmooth dynamic model for the COVID-19 pandemic incorporating the combined effects of these factors on the overall dynamics of the disease.

2.   Materials and methods

● Sample and data

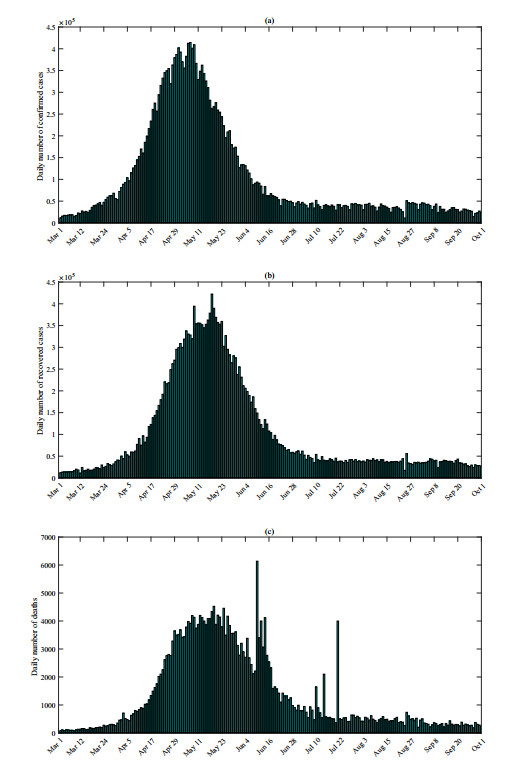
We obtained the data of COVID-19 cases in India from 1 March to 1 October 2021 from Baidu's Real Time Big Data Report on COVID-19 ^[9]. The data included the daily number of confirmed cases, recovered cases and deaths, as shown in Figure 1. Since the beginning of March, the daily number of confirmed cases has continuously climbed, which was the second major outbreak in India caused by the emergence of mutant strain and local large-scale gatherings. As of 1 October 2021, the cumulative number of confirmed cases, recovered cases and deaths climbed up to 33,789,398, 33,060,980 and 448,605, respectively. On 15 April when the huge religious gatherings held, the daily number of confirmed cases exceeded 200,000 for the first time and it took just a week to reach 315,800. On April 30, the number rose to more than 400,000, as shown in Figure 1(a).

As the outbreak in India got worse, many countries sent medical supplies to India, and then the daily number of recovered cases reached 422,394 on 17 May, which was the highest number of daily recovered cases, as shown in Figure 1(b). With the number of confirmed cases continuously rising and medical resources becoming inadequate severely, the daily number of reported deaths exceeded 1000 on 13 April and soon the daily number of reported deaths rose to 6,148 that was the highest number of new deaths in a single day in India, as shown in Figure 1(c). One of the reasons for such a big number of daily reported deaths was one of India's poorest state Bihar fixed the method of counting new deaths, following which 3951 deaths were added. However, those who died of post-COVID complications after testing negative were not included in the death toll. In this work, we assumed that only the deaths died in hospitals were included in the death toll.

In India, a mass vaccination campaign began on 16 January. The first phase was for 30 million front-line workers, such as health care workers and security forces. The second phase was for people aged over 50 and those under 50 with multiple diseases. Vaccination was available in more than 8,600 public and private hospitals since 1 March and vaccines are free for the public ^[7]. About 1 billion doses of vaccines has been completed in India. About 75 percent of the adults in India received at least one dose of the coronavirus vaccine, and about 30 percent of them have been fully vaccinated. So we consider the impact of vaccination on the spread of COVID-19 in India in this paper.

Shortage of hospital beds, oxygen, vaccines and medicines occurred in many parts of India as the outbreak aggravated dramatically. In some hospitals, there were 50 patients fighting for a bed. In Maharashtra, one of the states with severe outbreak, patients had to take shelter in ambulances, private cars and even electric three-wheelers with long queues at hospitals and patients lying in car parks taking oxygen ^[46,47]. Thus we considered the impact of the shortage of essential medical resources on the spread in India. We used the capacity of hospital beds to evaluate the amount of medical resources in this work. Because of a lack of data on the number of hospital beds, and India government has been gradually strengthening their medical resources and other control measures, in particular, more and more beds were provided in response to the outbreak, we adopted a logistic model to estimate the number of hospital beds used to treat patients infected with COVID-19 in India. In fact, the logistic model has been successfully adopted to mimic the number of hospital beds in combating the outbreak of COVID-19 in China, South Korea, Japan, Italy, Spain and Iran ^[20].

● Measures of variables

In this work, we assumed that the number of hospital beds $H_c(t)$ was a constant $H_{c0}$ before 1 March, and it was an increasing function submitted to the following logistic model

from then on. It is worth emphasizing that during the second wave of the COVID-19 outbreak in India, many a people shared a bed, so here $H_c(t)$ represented the number of people having hospital beds, not the number of hospital beds, and for simplicity, we will call $H_c(t)$ the number of hospital beds in the rest of this paper. In model (2.1), $r$ denoted the net increasing rate of hospital beds and $M$ stood for the maximum number of hospital beds in India during the COVID-19 outbreak. We embed model (2.1) into our targeted model and fitted the final model to the data on the daily number of confirmed cases, recovered cases and deaths to estimate the parameters, including $r$ and $M$. Taking into account of the pivotal role of the indirect transmission caused by the contaminated environments in COVID-19 infection as introduced in Section 1, we also mimic the effects of contaminated environments on transmission dynamics in India in this work.

Denote $T_0$ as the date 9 April, 2021 when the lockdown strategy began to implement, $T_1$ as the date 31 May, 2021 when the containment measures were gradually lifted, $T_2$ as the date 27 April, 2021 when the first batch of medical aid from the UK arrived at the airport in Indian capital New Delhi, $T_3$ as the date 10 May, 2021 when the last batch of medical aid from China arrived in India, and $T_4$ as the date 10 July, 2021, since then the daily number of confirmed cases has been basically below 40,000 and the epidemic has been in effective control. Thus we assume the public awareness as well as the prevention and control measures were improved and strengthened gradually after 9 April, so we assumed that the contact rate $c(t)$, the diagnosis rates $\delta(t)$, the recovery rate $\gamma_H(t)$ and the disease-induced death rate $\alpha_H(t)$ of hospitalized individuals are time-dependent.

The contact rate $c(t)$ is assumed to be a constant before 9 April and a decreasing function with respect to time t after 9 April due to the implementation of lockdown strategies and the raising of public awareness. After 31 May, containment measures were gradually enhanced, and the contact rate became anther constant. So, $c(t)$ took the following form:

where $c_0$ was the contact rate without control measures or awareness of the disease, $c_1 (c_1 < c_0$) was the minimum contact rate with the unprecedented intervention measures and self-isolation, $r_c$ was the corresponding decreasing rate of the contact rate. Here $T_0 = 39, T_1 = 92$, since the data we used for model fitting started at 1 March 2021.

The period from onset of symptoms to being diagnosed ($\frac{1}{\delta}$) was gradually shortened due to the increasing of public awareness and medical assistance from multiple countries. The first batch of medical supplies from Britain arrived in India on 27 April, so the diagnosis rate $\delta(t)$ was an increasing function with respect to time $t$ from 27 April to 10 May when the last batch of medical supplies from China arrived in India. From May 10 to July 10, the diagnosis rate $\delta(t)$ was assumed to be a decreasing function with respect to time $t$ as the medical resources running out. After 10 July, the daily number of confirmed individuals has changed relatively little, so the diagnosis rate $\delta(t)$ was assumed to be a constant. Thus, the diagnosis period was described by the following piecewise-defined function:

where $T_2 = 57, T_3 = 71, T_4 = 132, \delta_0$ was the initial diagnosis rate of infected individuals, $\delta_1 (\delta_0 < \delta_1)$ was the maximum diagnosis rate of individuals, $\delta_2 (\delta_0 < \delta_2 < \delta_1)$ was the final diagnosis rate of infected individuals and $r_{\delta}$ was the corresponding decreasing rate.

With the aid of medical resources from various countries, the recovery rate $\gamma_H(t)$ increased and the disease-induced death rate $\alpha_H(t)$ decreased before the end of medical assistance on 19 May. As the medical resources running out, the recovery rate $\gamma_H(t)$ was decreasing with respect to time $t$ from 19 May to 10 July and it remained a constant after 10 July. As for the disease-induced death rate $\alpha_H(t)$, as the daily number of confirmed cases decreasing gradually and Indian government increasing the capacity of hospital beds, a large number of cases entered the hospital for treatment, so $\alpha_H(t)$ remained decreasing, but at a smaller decreasing rate from 19 May to 10 July; while it took a constant after 10 July. Thus $\gamma_H(t)$ and $\alpha_H(t)$ took the following form:

where $\gamma_{H0}$ (resp. $\alpha_{H0}$) was the recovery rate (resp. disease-induced death rate) of hospitalized individuals before 27 April, $\gamma_{H1} (\gamma_{H0} < \gamma_{H1}$) (resp. $\alpha_{H1}(\alpha_{H1} < \alpha_{H0}$) was the maximum recovery rate (resp. small disease-induced death rate), $\gamma_{H2} (\gamma_{H2} < \gamma_{H0} < \gamma_{H1}$) was the final recovery rate after two months of consuming of the medical resources from the foreign countries, $\alpha_{H2} (\alpha_{H2} < \alpha_{H1} < \alpha_{H0}$) was the minimum disease-induced death rate, $r_{H}$ (resp. $r_{\alpha}$) was the corresponding exponential changing rate of the recovery rate (resp. disease-induced death rate).

● Models and data analysis procedure

Based on the disease progression and the intervention measures, we extended the basic SEIR model by considering the wild and mutant strains of SARS-CoV-2 in India, contamination of the environment, vaccination, and constraints of medical resources on the spread of the epidemic. The population is divided into ten compartments: susceptible ($S$), vaccinated ($V$), exposed ($E$), undiagnosed infecteds with the wild strain ($I_w$), undiagnosed infecteds with the mutant strain ($I_m$), confirmed with the wild strain but not hospitalized ($P_w$), confirmed with the mutant strain but not hospitalized ($P_m$), confirmed and hospitalized ($H$), recovered ($R$) and deceased ($D$). The density of pathogen in the contaminated environments is denoted by $W$, as shown in Figure 2.

The modelling framework SEIPR is used to describe the transmission dynamics, where the undiagnosed infecteds are divided into two classes according to the strain of infection: undiagnosed infecteds with the wild strain (i.e., $I_w$) and with the mutant strain (i.e., $I_m$). For simplicity, we call $I_m$ (resp. $I_w$) the infecteds with wild strain (resp. the infecteds with mutant strain) in the rest of this work. Due to the limitation of medical resources, some of the confirmed individuals enter the hospitalized class $H$ with a certain admission rate, and the other confirmed individuals progress into the class $R$ without receiving treatment. The virus in the environment can accelerate the infection of susceptibles and vaccinated individuals, as shown in Figure 2. The total population size is denoted by $N$, where $N = S+V+E+I_w+I_m+P_w+P_m+H+R$. The model is described by the following system of ordinary differential equations

where

Here the contact rate is denoted by $c(t)$ and the per-act transmission probability in contact with $I_w$ (resp. $I_m$) and $P_w$ (resp. $P_m$) is $\beta_1$ (resp. $\beta_2$). And the term $\beta_w$ describes the indirect transmission rate at which the susceptible individuals ($S$) or vaccinated individuals ($V$) gets infected with the virus in the environments ($W$). Note that health experts and government have been advising the public to minimize contacts with infectious individuals as much as possible during the outbreak. It follows that the increasing rate of the number of infected individuals caused by indirect transmission decreases as the viral load in the environments increases. Therefore in our model we propose new infections through indirect transmission occur in the form $\frac{\beta_w S W}{1+\alpha_w W}, \frac{\theta\beta_w V W}{1+\alpha_w W}$, where $\frac{1}{1+\alpha_w W}$ reflects an inhibition effect resulting from the reducing contact rate as the density of virus in the environment increases, $\alpha_w$ is called the saturation coefficient, $\theta$ denotes the ratio of the probability at which the vaccinated individuals $V$ is infected compared with the susceptible individuals $S$. A susceptible ($S$) or vaccinated individual ($V$) may be infected by a SARS-CoV-2 strain (either the wild or the mutant) through direct transmission and entered a latent infection stage ($E$), where infections occur in the form $\frac{\beta_1 c(t)S (I_m+P_m)}{N}$, $\frac{\beta_2 c(t)S(I_w+P_w)}{N}$, $\frac{\theta \beta_1 c(t)V(I_w+P_w)}{N}$, $\frac{\theta \beta_2 c(t)V(I_m + P_m)}{N}$. Undergoing a mean incubation of $\frac{1}{\sigma}$ days, $q$ proportion of infected individuals progressed into the infecteds with mutant strains ($I_m$), $1-q$ proportion of infected individuals progressed into the infecteds with wild strains ($I_w$). In model (2.6), $\delta(t)$ denotes the diagnosis rate for infected individuals, $\alpha_1$, $\alpha_2$ and $\alpha_H(t)$ denote the disease-induced death rates for $I_w, P_w, I_m, P_m$ and $H$, respectively, $\frac{H_c-H}{P_w+P_m}$ denotes the hospitalization rate, $\gamma_1$, $\gamma_2$ and $\gamma_H(t)$ are the recovery rates for $I_w, P_w, I_m, P_m$ and $H$, respectively. Note that those individuals confirmed with COVID-19 may not be hospitalized due to the shortage of hospital beds, so whether the confirmed individuals could be hospitalized or not depends on the daily number of empty hospital beds. If the hospital beds are insufficient, only a part of the confirmed individuals ($H_c(t)- H$) could be hospitalized, where $H_c(t)$ denotes the number of hospital beds at time $t$ in India, taking the form derived from the logistic model (1). See more detailed definitions and values of variables and parameters listed in Table 1.

To fit our targeted model to the data, we initially analyzed the data to set the initial values for the state variables. According to the news reports, 1,500,000 Indian health workers and frontline workers had received at least one dose of COVID-19 vaccine as of March 1, 2021, so we set $V(0) = 15,000,000$. During the initial stage of the second wave of COVID-19 outbreak in India, all the Indians, with a total population of 1,354,051,854, except the vaccinated and infected individuals (the cumulative number of infecteds was 11,123,619 as of 1 March 2021) were susceptible to the virus, so direct calculation yields $S(0) = 1,327,100,000$. We assumed that all the previously infected individuals were either recovered (the cumulative number of recovereds was 10,796,558), dead (the cumulative number of deaths was 157,275) or received treatment in the hospital till 1 March, 2021, so we derived the initial value of hospitalized individuals $H(0) = 14,786.$ On March 1, 2021, the daily number of recovered individuals was 11,990, so we set $R(0) = 11,990.$ All other parameters and variables were estimated or from the reference.

We next conducted data fitting using our targeted model to estimate the values of the parameters. There are generally three parameter estimation methods, i.e., least square method, maximum likelihood estimation method, and Bayesian estimation method. It is necessary to define the maximum likelihood function in advance when we adopt the maximum likelihood estimation method to estimate parameters. The prior probability density of the estimated parameters should be determined in advance if we will estimate the parameters using the Bayes estimation method. When the least square method is chosen to estimate parameters, we do not need prior statistical characteristics, so it is easier to solve and is widely used. Compared with other parameter estimation methods, the unknown parameters can be easily obtained by using the least square method, and the sum of squares of errors between the obtained data and the actual data is minimized ^[48]. The nonlinear least-square method is carried out in MATLAB, using the command fmincon, which is a part of the optimization toolbox in MATLAB and finds a constrained minimum of a function of several variables. So in the following, we used the nonlinear least-square method to validate our targeted model. The objective function is

where $\Theta$ is the vector of parameters to be estimated, $n$ is the length of the epidemic data period. Here $n = 215$ since we used data from 1 March to 1 October, lasting for 215 days. $T_k$ is the corresponding date of the $k-th$ day since 1 March 2021. $\tilde{C}(T_k), \tilde{R}(T_k), \tilde{D}(T_k)$ are the actual reported daily number of confirmed cases, recovered cases and deaths on the date $T_k$, respectively. $C(T_k), R(T_k), D(T_k)$ are the estimated daily number of confirmed cases, recovered cases and deaths on the date $T_k$, respectively. The dynamics of $C(t), R(t), D(t)$ are governed by

where $P_w(t), P_m(t)$ and $H(t)$ are determined by model (2), $h(t), \gamma_H(t)$ and $\alpha_H(t)$ are as defined above.

3.   Results

● Parameter estimation and model fitting

By fitting our targeted model to the data of the daily number of confirmed cases, recovered cases and deaths from 1 March to 1 October, 2021, we have obtained the estimated values of the unknown parameters. The fitting result of the targeted model (2) to the epidemic data was shown in Figure 3(a)–(c). The estimated values of unknown parameters and initial conditions of variables and parameters are reported in Table 1. In Figure 3, the red circles represent the data from 1 March to 1 October, 2021, the best-fitting results of the daily number of confirmed cases, recovered cases and deaths are plotted in black solid lines, showing that our targeted model captures the data well.

Note that the data we used to fit the model, including the daily number of confirmed cases, recovered cases and deaths, are not highly linearly correlated, and there are very few outliers in the data, so the least square method used in this paper is stable. In addition, in order to improve the stability of parameter estimation adopted in this work, we selected a relatively large amount of data, i.e., 215 days of data, for fitting. In fact, the parameter estimation in this work was difficult. On the one hand, there were many parameters needed to be estimated; on the other hand, some of the parameters were piece-wise defined or time-dependent, which increased the difficulty in parameter estimation. In addition, the magnitude of the data on the second wave of COVID-19 epidemic in India was relatively large, and the error between the reported data and the actual situation was also relatively large, which also increased the difficulty of parameter estimation. Nevertheless, we have provided a good estimate, as shown in Figure 3.

To further validate the targeted model, we compared the actual data and estimates on the cumulative number of confirmed cases, recovered cases and deaths from 1 March to 1 October, 2021, as shown in Table 2. Table 2 shows that the estimated value of the cumulative number of confirmed cases is 6% higher than the actual data, i.e., 1,445,908 more cases. The estimated values on the cumulative number of recovered cases (resp. deaths) are 0.4% (resp. 6%) lower than the actual data, i.e., 81,982 less recovered cases (resp. 18,803 less deaths). Note that in order to fit the data on the death used in this paper, the number of deaths here is only those died in the hospital. The proportion in the first row of Table 2 refers to the proportion of the cumulative number of confirmed cases in the total population; while that in the second (resp. third) row refers to the proportion of the cumulative number of recovered cases (resp. deaths) in the confirmed population. We observe that the errors between the estimated value and the actual data of these three ratios are small, i.e., 0.108, 6.228 and 0.155%, respectively. In Table 3, we compared the peak size of the data on the daily number of confirmed cases, recovered cases and deaths with the estimated ones. We found that the peak size of the data on the daily number of confirmed cases was 10,593 larger than that of the estimated value, with a relative error 2.556%. The peak size of the data on the daily number of deaths was 34 smaller than that of the estimated value, with a relative error 0.760%. In Table 4, we compared the time of the data when the daily number of confirmed cases less than 50,000 and that when the daily number of deaths less than 600. We found that the estimated time when the daily number of confirmed cases less than 50,000 is 4 days later than the that in the data; the estimated time when the daily number of deaths less than 600 is 7 days earlier than that in the data. As a result, our targeted model fitted the data well and it was reliable.

We calculated the basic reproduction number by using the next generation matrix method ^[50]. Denoting $Z\equiv(E, I_w, I_m, P_w, P_m, W)$, we had $\dot{Z} = G(Z)$. Let $G(Z) = \mathcal F+\mathcal V$, where $\mathcal F$ represent the vector of new infections and $\mathcal V$ represent the vector of all other transitions, respectively. And we get

Differentiating $\mathcal{F}$ and $\mathcal{V}$ with respect to $Z$ and computing them at the initial state give

Then the effective reproduction number can be approximately defined as

where $R_e^s(t)$ and $R_e^w(t)$ denote the effective reproduction numbers of direct transmission and indirect transmission, respectively, and

According to the reported values of the parameters and initial conditions, we get the estimated effective reproduction number, as shown in Figure 4, where the grey region indicates the lockdown period, i.e., from 9 April to 31 May, 2021. It follows from Figure 4 that the effective reproduction number $R_e(t)$ falls below the threshold of 1 since 9 April when the lockdown strategy was implemented. And the effective reproduction number is relatively small during the lockdown, i.e., from 9 April to 31 May, 2021 when the public was not allowed to go out except for essential activities such as buying daily necessities and seeking medical treatment. Note that a slight rebound occurred on 31 May, 2021 when the lockdown strategy was suspended. It follows that the outbreak becomes controllable since the implementation of lockdown.

● Uncertainty and sensitivity analysis

Considering the uncertainty of the model parameters, we conducted sensitivity analysis of the effective reproduction number $R_e(t)$ with respect to various parameters over time by computing the partial rank correlation coefficients (PRCCs) based on Latin Hyperbolic Sampling ^[51]. We chose the parameters closely related to the epidemic transmission and containments including the parameters related to the evolution of contact rate ($c_0$), proportion of infected individuals with the mutant strain ($q$), vaccination rate for susceptible individuals ($\Psi$), ratio of the probability of the vaccinated population being infected compared with the susceptible population ($\theta$), initial diagnose rate of infected individuals ($\delta_0$), the per-act transmission probability in contact with $I_m$ and $P_m$ ($\beta_2$), net increasing rate of hospital beds ($r$), maximum capacity of hospital beds($M$), with other parameters fixed, as shown in Figure 5. The monotonic relationship between the outcomes of effective reproduction number $R_e(t)$ and each parameter was assessed over the entire time interval. The values of the partial rank correlation coefficients (PRCCs) of each parameter over the time interval was calculated, which allowed us to determine whether the significance of one parameter occurred during the progression of the dynamics of our targeted model. The absolute values of PRCCs greater than 0.5 were considered as indicating significant correlations between the parameters and the effective reproduction number. Figure 5 showed that the proportion of $I_m$ (i.e., $q$), ratio of the probability of $V$ being infected compared with $S$ (i.e., $\theta$), and initial contact rate (i.e., $c_0$) were positively correlated with $R_e(t)$ almost over the entire time interval, which indicated that declining $q, \theta$ and $c_0$ led to a significant decreasing of the effective reproduction number $R_e(t)$ over the whole time interval. The initial diagnose rate of infected individuals $\delta_0$ was negatively correlated with $R_e(t)$ before 29 April; while the vaccination rate of $S$ (i.e., $\Psi$) was negatively correlated with $R_e(t)$ before the end of lockdown. It followed that increasing the diagnose rate and vaccination rate could lead to a significant decreasing of the effective reproduction number $R_e(t)$. It was worth emphasizing that the correlation between the effective reproduction number $R_e(t)$ and the contact rate $c_0$ became very weak during the implementation of lockdown, which was because very little social activities occurred during the lockdown and the effective reproduction number was mainly determined by other factors. According to Figure 5, increasing the intensity of social distancing (i.e., decreasing $c_0$), strengthening awareness of self-protection (i.e., reducing $q$), vaccinating on time to improve the efficiency of vaccine protection (i.e., decreasing $\theta$ and increasing $\Psi$ before the end of lockdown), and increasing the diagnosis rate (i.e., increasing $\delta_0$), all could assist in containing the epidemic.

It was reported that India has crossed 300,000 COVID-19 deaths till 24 May, 2021, making it the third country after the United States and Brazil ^[52]. In fact, this outbreak in India crippled the health system and many people died from a shortage of medical resources. According to the report from the Global News on 20 July, 2021, most experts believed India's official toll of more than 414,000 deaths was a vast undercount although the government has dismissed these concerns ^[53]. The count could have missed those deaths occurring in overwhelmed hospitals or while health care was delayed or disrupted. And it was estimated that the death toll from COVID-19 in India could be nearly 10 times the deaths reported by India government, which indicates the number of COVID-19 deaths in India was far higher than that was reported. In the following, we choose the number of deaths as an index and identify the key factors affected the COVID-19 outbreak in India by exploring the impact of the factors on the number of deaths. To this end, we initially use the targeted model to estimate the total deaths in reality, including deaths with the wild strain or mutant strain before hospitalization and deaths in the hospitals. For convenience, we denote the deaths with the wild (resp. mutant) strain before hospitalization and the deaths in the hospitals as $D_w$ (resp. $D_m$) and $D_h$ in the following, respectively. The sum of the deaths with wild ($D_w$) or mutant strain ($D_m$) before hospitalization or in hospitals ($D_h$) is referred as total deaths in the rest of this work. We calculate the average number of deaths with the mutant (resp. wild) strain before hospitalization for each day of the weeks from 1 March to 27 September, 2021. For instance, we calculate the average number of daily deaths from 1 March to 7 March, 2021, and recorded it as the average daily number of deaths of the first week. And the average daily number of deaths of the second week is calculated in terms of the daily deaths from 8 March to 14 March, 2021. Repeating the above process, we obtain the average daily number of deaths for any week between 1 March and 1 October, 2021. We similarly calculate the average daily number of deaths in the hospitals for each week from 1 March to 1 October, 2021, as shown in Figure 6. Note that the data we used to fit our model is from 1 March to 1 October, 2021, but there is little change in the last days, so here we ignored the data of the last four days such that the remained days are exactly 30 weeks. Figure 6 suggests that more people die from the mutant strain than from the wild strain, and more people die before hospitalization than in the hospital. It is also found that the peak time of the actual deaths is at weeks 6–7, in which days the average daily number of deaths rises up to about 12,000, about six times the reported death toll. This is consistent with a recent study of actual deaths in COVID-19, India ^[54].

In the next, we quantify how the mutant strain, contaminated environments and vaccination with the shortage of medical resources affect the spread of COVID-19 in India. To this end, we choose the per-act transmission probability in contact with the infecteds with symptoms caused by mutant strain ($\beta_2$), proportion of infected individuals with the mutant strain ($q$), indirect transmission rate ($\beta_w$), saturation coefficient ($\alpha_w$), vaccination rate ($\Psi$), ratio of the probability of the vaccinated population being infected compared with the susceptible population ($\theta$), recovery rate of the infecteds and confirmed individuals with the mutant strain before hospitalization ($\gamma_2$), and disease-induced death rate of the infecteds and confirmed individuals with the mutant strain before hospitalization ($\alpha_2$) to explore what would happen if these factors vary.

We first used contour plots to examine the dependence of the peak time and peak size of the daily number of total deaths in reality on $\beta_2$ and q, as shown in Figure 7. It follows from Figure 7 that reducing the proportion of infected individuals with the mutant strain $q$, and the per-act transmission probability in contact with the infecteds with symptoms caused by mutant strain $\beta_2$, would delay the peak time of the number of total deaths in reality (Figure 7(a)), and the peak size of the number of total deaths in reality would be lowered substantially (Figure 7(b)). We also conducted contour plotting to investigate the dependence of the peak time and peak size of the daily number of total deaths in reality on other key parameters including $\gamma_2$ and $\alpha_2$ (Figure 10), $\beta_w$ and $\alpha_w$ (Figure 11), and $\Psi$ and $\theta$ (Figure 12). Figure 10 shows that the peak time mainly depends on the recovery rate of infected and confirmed individuals with the mutant strain before hospitalization $\gamma_2$; while the peak size mainly depends on the disease-induced death rate of infected and confirmed individuals with the mutant strain before hospitalization $\alpha_2$. Increasing $\gamma_2$ could lead to an earlier peak time and decreasing $\alpha_2$ would result in a smaller peak size. Figure 11 demonstrates that reducing the indirect transmission rate $\beta_w$ while increasing the saturation coefficient $\alpha_w$ would lead to a delay in the peak time (Figure 11(a)) and a significant decreasing in the peak size (Figure 11(b)). A small increasing in the indirect transmission rate $\beta_w$ will trigger into a significant advancing of the peak time as well as a great increasing of the peak size, which indicates a more impact of the indirect transmission rate than the saturation coefficient $\alpha_w$ on the peak time and peak size of the total deaths. Figure 12 demonstrates that the ratio of the probability of the vaccinated population being infected $\theta$ has a more significant impact on the peak time compared with the vaccination rate $\Psi$; while the vaccinate rate $\Psi$ has a greater effect on the peak size compared with $\theta$. As a result, Figures 7–12 demonstrate that reducing the proportion of infected individuals with the mutant strain $q$, the transmission probability of mutant strain $\beta_2$, the disease-induced death rate caused the mutant strain $\alpha_2$, or the vaccination rate, all could alleviate the outbreak by diminishing the peak size of the daily number of total deaths in reality.

To further explore the exact impact of the mutant strain on the COVID-19 outbreak in India, we investigated how the daily deaths with the wild strain ($D_w$), the mutant strain ($D_m$) and the sum of daily deaths before hospitalization (i.e., the sum of $D_w$ and $D_m$, which we denote as $D_w+D_m$ in the rest) vary with different values of the per-act transmission probability in contact with the infecteds with symptoms caused by mutant strain ($\beta_2$) and the proportion of infected individuals with the mutant strain ($q$). We conducted a sensitivity analysis to show what would happen if $\beta_2$ was increased by 20, 50, 80%, $q$ was increased to 0.7, 0.8, 0.9, as shown in Figure 8(a)–(d). It follows that increasing the per-act transmission probability in contact with the infecteds with symptoms caused by mutant strain ($\beta_2$), or the proportion of infected individuals with the mutant strain ($q$), both could lead to an increasing of the average daily deaths with the wild or mutant strain before hospitalization ($D_w$ or $D_m$). We also explored the variation of the daily deaths with the wild strain ($D_w$), the mutant strain ($D_m$) and the sum of them ($D_w+D_m$) as the recovery rate and disease-induced death rate of the infecteds and confirmed individuals with the mutant strain before hospitalization ($\gamma_2$ and $\alpha_2$) varied. We analyzed what would happen when the recovery rate of the infecteds and the confirmed individuals with the mutant strain before hospitalization ($\gamma_2$) was increased by 20, 50, 80% while the disease-induced death rate of the infecteds and the confirmed individuals with the mutant strain before hospitalization ($\alpha_2$) was declined by 20, 40, 60%, respectively, as shown in Figure 13(a)–(b). They demonstrated that increasing $\gamma_2$ while decreasing $\alpha_2$ would lead to the decline of the daily deaths with the wild strain and mutant strain before hospitalization ($D_w$ and $D_m$). It's worth emphasizing that increasing $\gamma_2$ while decreasing $\alpha_2$ had a more significant decline on the daily deaths with mutant strain than that on the daily deaths with the wild strain. We found that the mutant strain played a vital role in the outbreak of the epidemic. A significant increasing of the daily deaths would occur if the transmission probability ($\beta_2$) or the proportion ($q$) was raised; while a great decreasing would happen on the daily deaths if the the recovery rate ($\gamma_2$) was increased with a decline of the disease-induced death rate ($\alpha_2$). We further investigated the impact of vaccination rate ($\Psi$), vaccine effectiveness ($1-\theta$) and the indirect transmission rate of the contaminated environments ($\beta_w$) on the daily deaths with the wild strain or mutant strain ($D_w$ or $D_m$) or the sum of daily deaths before hospitalization ($D_w+D_m$). We conducted a sensitivity analysis to examine the variation of $D_w, D_m$ and $D_h$ if $\Psi, \theta$ or $\beta_w$ were raised by 20 50, 80%, respectively, as shown in Figure 13. It follows from Figure 13 that increasing the vaccination rate or the rate of the probability of infection in a vaccinated individual would trigger a significantly decreasing or increasing of the daily deaths before hospitalization, as shown in Figure 13(c)–(f). If the indirect transmission rate was raised to $1.2\beta_w, 1.5\beta_w$ and $1.8\beta_w$, the daily deaths with the wild strain, mutant strain or the total deaths before hospitalization increases although it is not very obvious. We found that the vaccination strategy had a more significant effect than the environmental transmission on the spread of the epidemic. A noteworthy decreasing of the daily deaths occurred if the vaccination rate ($\Psi$) or vaccine effectiveness ($1-\theta$) was raised. In order to better understand the effect of the mutant strain on the epidemic, we further examined the variation of the total deaths in reality as the key parameters ($\beta_2, q$) vary. We calculated the average daily number of total deaths, including deaths with the wild strain ($D_w$), mutant strain ($D_m$) before hospitalization and the deaths in the hospital ($D_h$), for very two weeks between 1 March to 27 September, 2021, as shown in Figure 9. It follows from Figure 9(a) and (b) that increasing the per-act transmission probability in contact with the infecteds with symptoms caused by mutant strain ($\beta_2$) and the proportion of infected individuals with the mutant strain ($q$), both could result in a great increasing of the total number of deaths in reality. To highlight the effect of the environmental transmission and vaccination on the epidemic, we calculated the average daily number of total deaths in reality as the key parameters ($\gamma_2, \alpha_2, \Psi, \theta, \beta_w$) varied, as shown in Figure 14. We can easily obtained from Figure 14 (c) that increasing the ratio of the probability of the vaccinated individuals being infected ($\theta$) could result in a great increasing of the total number of deaths in reality. Figure 14(a) and (b) showed that increasing the recovery rate of the infecteds and the confirmed individuals with the mutant strain before hospitalization ($\gamma_2$) while decreasing the disease-induced death rate of the infecteds and the confirmed individuals with the mutant strain before hospitalization ($\alpha_2$), or raising the vaccination rate ($\Psi$), both could lead to a decreasing of the total number of deaths. It can be seen from Figure 14(d) that an increase in the indirect transmission rate ($\beta_w$) could lead to a slight increase in the total number of deaths. It is worth noting that all of these factors have a strong influence on the total number of deaths in the early stage of the outbreak, such as during the early eight weeks; while only a very weak effect on the total number of deaths in the late stage of the outbreak, such as during the period through week 11 to week 30. This was because during the later stage of the epidemic, Indian government implemented a lot of containments including lockdown and other control measures to stop the further spread, and the assistance of medical resource from other countries reduced the death toll. The mutant strain and vaccination, besides the contaminated environments, had a more significant effect on the deaths with the mutant strain before hospitalization than they on the deaths with the wild strain before hospitalization. The number of deaths in the hospitals was very little affected by these factors compared to the number of deaths before hospitalization. The findings demonstrate that the vaccination strategy and the environmental transmission have an obvious impact on the transmission of the epidemic, especially during the early stage. The vaccination strategy (resp. environmental transmission) could alleviate (resp. aggravate) the outbreak by decreasing (resp. increasing) the total deaths.

4.   Discussion and conclusions

● Discussion

Since the starting of the COVID-19 pandemic in early 2020, countries worldwide are devoted to finding effective containments to halt the number of cases and deaths. India, as one of the countries with very high population density, has experienced multiple waves of COVID-19 although they have always been struggling to curb the outbreak. The second wave of COVID-19 in India has had a heavy blow to the country, although vaccine distribution had already commenced in India. There are many a factor, including the more pathogenic mutant strain than the wild one, the contaminated environments and the serious shortage of medical resources, that triggered this outbreak. Quantification of the effect of these factors and the public health mitigation programs, including vaccination and implementation of lockdown, on the containment of the outbreak, are, thus, needed. We have done a retrospective study to quantify how these factors, together with the gradually strengthening of the nonpharmaceutical interventions (NPIs) affect the spread of COVID-19. In this work, we have proposed a nonsmooth compartment epidemic model that incorporated direct and indirect transmission as the potential transmission pathways of COVID-19. The model also mimicked the shortage of medical resources, the prevalence of mutant strains and the implementation of vaccination.

We assumed the key control parameters are time dependent and piecewise defined due to the strengthening of prevention and control measures including the implementation of lockdown strategy on 9 April, 2021, the arriving of the first batch of medical aid from UK on 27 April, the arriving of the last batch of medical aid from China on 10 May, and the gradually lifting of the containment measures on 31 May. By using the nonlinear least-square method to fit our targeted model, these time-dependent parameters and other model parameters are estimated, as reported in Table 1. The fitting results shown in Figure 3 illustrated that the targeted model captured the data, including the daily number of confirmed cases, recovered cases and deaths well. The estimated effective reproduction number is much smaller during the implementation of lockdown than that in other time, as shown in Figure 4, which highly support the policy of lockdown. The PRCCs of the effective reproduction number $R_e(t)$ with respect to the key parameters over time indicated that reducing the proportion of infecteds with mutant strain ($q$), probability of vaccinated individuals being infected ($\theta$), and initial contact rate ($c_0$), all could significantly decline $R_e(t)$, as shown in Figure 5. It follows that decreasing the proportion of mutant strain, infection probability of the vaccinateds, or the contact rate, all could aid in controlling the outbreak.

To reveal the vital role of the multiple factors including the mutant strain, contaminated environments and vaccination with the medical-resource constraints in the transmission of the COVID-19 in India, we chose the number of deaths as an index and explored what would happen as these factors varied. We gave an estimate of the deaths with wild strain or mutant strain before hospitalization as well as the deaths in the hospital. It revealed that there were more deaths before hospitalization than in the hospital and more people were dying from the mutant strain than from the wild strain among the deaths before hospitalization. Our sensitivity analysis showed that increasing the transmission probability of the mutant strain ($\beta_2$) and the proportion of the infecteds with mutant strain ($q$) could bring forward the peak time of the number of total deaths and raise the peak size, as shown in Figure 7. A slight increasing of the indirect transmission rate ($\beta_w$) could result in a significant advancing of the peak time as well as a great increasing of the peak size, shown in Figure 11. The probability of the vaccinated individuals being infected ($\theta$) has a more significant effect on the peak time compared with the vaccination rate $\Psi$; while the vaccination rate ($\Psi$) has a greater impact on the peak size than the probability of the vaccinated individuals being infected ($\theta$), as shown in Figure 12. The main findings demonstrate that the mutant strain and the contaminated environment trigger a significant increasing of the peak size; while the vaccination strategy leads to an obvious decreasing of the peak size.

To better understand how the multiple factors affect the second wave of the COVID-19 in India, we further explored the variation of the number of deaths with wild strain or mutant strain before hospitalization or deaths in the hospital as these factors varied, shown in Figures 8, 9, 13 and 14. We observed from these Figures that the number of deaths with mutant strain ($D_m$) or wild strain before hospitalization ($D_w$) or the deaths in the hospital ($D_h$) increased significantly if the transmission probability of the mutant strain ($\beta_2$), the proportion of infecteds with the mutant strain ($q$), or the infection probability of the vaccinated individuals ($\theta$) was increased. We also obtained that $D_m, D_w$ and $D_h$ declined obviously if the recovery rate of infecteds with the mutant strain ($\gamma_2$) was increased while their disease-induced death rate ($\alpha_2$) was declined, or the vaccination rate ($\Psi$) was raised. An increase in the indirect transmission rate ($\beta_w$) would trigger a small increase in the number of deaths with mutant strain or wild strain before hospitalization or the deaths in the hospital. The prevalence of the mutant strain and implementation of vaccination besides the contaminated environments have a strong effect on the total number of deaths in the early stage of the outbreak while they have only a very weak effect in the late stage of the outbreak. All these factors have a more significant influence on the deaths with the mutant strain than the influence they have on the deaths with the wild strain. And they have a very small influence on the deaths in the hospital. The main results show that reducing the prevalence of the mutant strain, strengthening vaccination, and increasing the virus clearance rate in the contaminated environment can effectively inhibit the spread of the epidemic, especially in the initial stage of the outbreak.

To present a complete demonstration of the impact of the key factors mentioned in this work on the COVID-19 epidemic in India in 2021, we used the number of deaths in reality as an indicator and examined the impact of different factors on the number of deaths in the following, as shown in Table 5, where the death referred to the cumulative number of deaths in India from March 1 to October 1, 2021, $10^3$ denoted every number should be multiplied by $10^3$. Table 5 shows that if the transmission probability of mutant strains ($\beta_2$) increased to $1.8\beta_2$, or the proportion of infecteds with the mutant strain ($q$) increased to $0.9$ (its baseline value is about 0.6), the total death would increase by 181,692 and 117,256 cases, respectively, with an increasing of 0.753 and 0.486% on the mortality rate, respectively. If the vaccination rate $\Psi$ (resp. the infection probability of the vaccinated individuals $\theta$) increased by 80%, the total deaths would decrease by 83,445 (resp. increase by 191,050) and the mortality rate would decrease by 0.346% (resp. increase by 0.792%). If the indirect transmission rate $\beta_w$ increased by 80%, there would be an increasing of 94,057 on the the total death with an increasing of 0.39% on the mortality rate. Furthermore, we investigated the effect of contact tracing on the containment of the epidemic. If 30, 50 and 70% of infected individuals were contact traced and required to implement social distancing, i.e., the infectious cases ($I_w, I_m$) decreased by 30, 50, 70%, the total number of deaths would decrease by 79,915,129,162 and 173,925 and the mortality rate would decrease by 0.331, 0.536 and 0.721%, respectively. The results indicated that the mutant strain and environmental transmission have aggravated the outbreak significantly while the vaccination have alleviated the outbreak greatly. The contact tracing measure also has a significant effect on curbing the epidemic. Countries with large population density and medical resource-constraints like India should strengthen controlling the spread of the mutated strain, accelerate the introduction of booster shots for COVID-19 vaccines, and enhance the clearance of virus from the environment to combat the possible COVID-19 outbreak in future. In the event of a future outbreak of COVID-19 in a similar country, contact tracing should also be implemented due to its imperative role in controlling the epidemic, especially during the early stage of the outbreak.

Among the mathematical modeling studies on the spread of COVID-19 ^{[5,7,8,20,22,23,24,27,30,31,34,35,40,41,42,43,44,45]}, only a few research focused on the epidemic in India ^[7,8,35,40]. Khajanchi et al. ^[7] focused on the effect of contact tracing. They revealed that combining the restrictive social distancing and contact tracing could eliminate the COVID-19 pandemic. Kumar et al. ^[8] focused on the dynamics of omicron variant virus. They investigated the transmission dynamics of the COVID-19 in India during the omicron variant virus transmission and vaccination drive. Britto et al. ^[35] concerned the vaccine allocation strategies and demonstrated a relative reduction in deaths if the older population got the priority for the COVID-19 vaccine. Zu et al. ^[40] concerned the influence of contaminated environments on the transmission of COVID-19 in India. These studies have only analyzed the transmission dynamics of the novel coronavirus when one or two factors are in effect. In fact, in many outbreaks of COVID-19 since 2021, such as the one in India investigated in this work, many a factor played an important role in the spread of the outbreak. That drove us to mimic the combined effects of these factors, including simultaneous transmission of mutant strain and wild strain, environmental transmission, vaccination, shortage of medical resource and contact tracing measures, on controlling the epidemic in India. In this work, we quantitatively assessed the efficiency of each factor in epidemic control in India if the other factors were also effective. We found that both mutant strain and contaminated environments had significant effect on worsening the outbreak even after vaccination was implemented. The vaccine mitigated the outbreak to some extent, although there was mutated strain and environmental transmission. And in cases where multiple factors were in effect at the same time, contact tracing and quarantine still played an imperative role in curbing the epidemic, especially when vaccine effectiveness and vaccine coverage were not high enough.

● Conclusions

This paper is the first to mimic the impact of the multiple factors, including mutated strain, environmental pollution, vaccination and resource constraints, on the COVID-19 outbreak in India from 1 March to 1 October, 2021. Our results demonstrated that, in the context of shortage of essential medical resource, the parameters related to the mutant strain ($\beta_2, q, \gamma_2, \alpha_2$) and vaccines ($\theta, \Psi$) are the key parameters and should be prioritized to control the epidemics. The main findings suggest a significant effect of the mutant strain, contaminated environments and vaccination on the spread of the epidemic. Although this study are based on India, the main findings are applicable to other countries with limited medical resources. We found that, to curb the possible future outbreak of COVID-19, inhibiting the prevalence of mutant strain, clearing the virus in the environments as soon as possible, enhancing the vaccination of booster shots and strengthening the contact tracing, especially in the early stage of the outbreak, are required for those countries facing shortage of medical resources.

There are some limitations of our work. The key issue is assessing the impact of mutant strain, environmental transmission and shortage of medical resources. During the outbreak of this wave in India, about 70% of individuals completed the first dose of vaccine, although the percentage completed the full dose was lower, so we modeled the vaccine's protective effect. In fact, it is not ideal to evaluate the efficacy of the vaccine using the epidemic data from India due to the relatively low vaccine coverage in India, especially the low percentage of booster shots completed. It is more reasonable to choose other countries with higher vaccine coverage, such as the United States and Italy, to evaluate the protective effect of the vaccine. In the future work, we will take these countries as examples to study the effect of vaccines in detail. Moreover, it is not very good to use a single model to mimic the transmission dynamics of COVID-19 in the whole country of India since India is a very vast country with many geographical difference. And we have not looked deeply into how the good governance, like improving the effectiveness of administering COVID-19 vaccinations and social distancing, can help mitigate the outbreak ^[55,56].

In summary, this study quantitatively assessed the impact of the key factors on the outbreak of the epidemic. The main findings in this work can help those similar countries and policy-making sectors to effectively mitigate against the future possible outbreak.

Acknowledgements

This research was funded by the National Natural Science Foundation of China (grant number: 12271431) and special scientific research project of emergency public health security of education department of Shaanxi province (grant number: 20JG002).Our data are collected from publicly published data, have no privacy implications and can be found in https://voice.baidu.com/act/newpneumonia/newpneumonia/?from=osari_aladin_banner#tab4, https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports.

Conflict of interest

The authors declare that they have no conflict of interests.

Appendix A

In this appendix, we provided some figures on the sensitivity analysis. We note that during the outbreak of COVID-19 in India from 1 March to 1 October, 2021, many a factor, including the mutant strain, environmental transmission and vaccination, in the context of medical resource-constraints, played a vital role. We have examined the effect of each factor on the spread of the epidemic, and plotted a series of figures at the same time. We inserted some of the figures in the main text and put the others in this appendix. To highlight the effect of these factors on the outbreak of the epidemic, we put the according descriptions and explanations of these figures in the text.