Solution of the SIR epidemic model of arbitrary orders containing Caputo-Fabrizio, Atangana-Baleanu and Caputo derivatives

1.   Introduction

The need to quantitatively study human-nature interactions has been evident since the work of Thomas Malthus, who believed that informed public policy could prevent the occurrence of human-made catastrophes ^[1] and inspired the Club of Rome to commission detailed futuristic scenarios for our techno-industrial civilization in the early 1970s ^[2] (see also ^[3]). Human-nature interactions have been studied using minimal population dynamics models based on a predator-prey analogy, where humans are seen as predators and resources as prey ^[4], and on the more modern concept of ecosystem engineering ^[5], where instead of (or perhaps in addition to) preying on nature, humans transform their environment into a more hospitable place for themselves ^[6,7]. Here we approach human-nature interactions from the perspective of evolutionary game theory ^[8,9] by considering the conditions under which humans can cooperate to prevent avoidable disasters. In fact, when people have to build or maintain a public good, such as a dam that could protect their community from flooding, they find themselves in a social dilemma known as the tragedy of the commons ^[10]: either they bear the cost of cooperating and advancing the collective interest, or they free-ride on the efforts of others to pursue their own interests. This is probably why understanding what promotes cooperation in human societies is considered one of the greatest challenges for science in the twenty-first century ^[11].

We consider a variant of public goods games known as the threshold public goods game (TPGG), in which individuals may choose to contribute a fixed amount to a public good, but the good itself is available only if a certain number (or more) of contributions are made ^[12]. This game models a scenario where, say, half a dam is no better than none. A particularly interesting variant of the TPGG, the collective-risk social dilemma, has been introduced to study human decisions in the face of dangerous climate change, where failure to reach the minimum cumulative contribution may result in catastrophe and the loss of all private wealth ^[13]. (The dam imagery seems even more fitting than the dangerous climate change scenario.) The catch is that the dire predictions of climate scientists or high floods may never materialize (at least in the individual's lifetime), and so the investment in the public good is lost. Thus, unlike typical public goods games ^[14,15], the collective risk social dilemma involves investing in a public good not to achieve a gain but to avoid a loss, and so the risk perception plays an important role in individuals' decisions to contribute (i.e., cooperate) or not to contribute (i.e., defect) to the public good ^[13].

In the evolutionary game-theory version of TPGG, we assume that individuals repeatedly gather in randomly formed groups of fixed size to play the game ^[16,17,18]: those who were affected by the disaster, regardless of whether they contributed to the public good or not, are not copied by anyone during the imitation phase. Not being imitated is the social learning counterpart of not producing offspring in the biological context ^[19]. Our results confirm the expectation that the higher the risk of loss, the higher the proportion of cooperators in the population. More importantly, we find that increasing group size is always detrimental to cooperation. These are interesting results in the sense that they account for the dire consequences of digital disinformation on people's willingness to contribute to public goods, as it simultaneously reduces the perception of risk and enormously increases the play group size. We find that for typical values of the model parameters in the infinite population limit, cooperators coexist with defectors at best. There is a discontinuous transition between the regime dominated by defectors and the coexistence regime when the risk loss reaches a threshold. Completely eliminating defectors requires a high-risk loss and an extreme scenario where safety can only be guaranteed if all members of the play group are cooperators. However, the difficulty with the coexistence scenario is that it is not stable against demographic noise, since the deterministic coexistence fixed point is not an absorbing state of the finite population dynamics. In fact, besides clarifying some technical details and providing analytical approximate expressions for the risk threshold in the infinite population limit analysis, our main original contribution to the study of the TPGG is the derivation of the scaling laws of the transient lifetimes or half-lives of the coexistence metastable state using finite-size scaling methods ^[20]. In particular, we find that for a risk loss above the threshold, the half-life increases exponentially with the population size, while at the threshold it increases as a power law with the universal exponent $1/3$. Somewhat surprisingly, our finite-size scaling analysis of the scenario where only groups of all cooperators are safe shows that the effect of demographic noise is stronger for large group sizes.

The rest of this paper is organized as follows. In Section 2, we introduce the payoffs of the TPGG and highlight the differences between the experimental setup of the collective-risk dilemma ^[13] and the evolutionary game approach ^[16]. In Section 3, we present the stochastic imitation dynamics for the TPGG. This dynamics governs the time evolution of the two strategies (cooperation or defection) in a population of finite size $M$, where only better-off individuals can be imitated, and reduces to the replicator equation in the deterministic limit $M \to \infty$ ^[21] (see ^[19,22] for different imitation rules that lead to the replicator equation in the large population limit.) In Section 4, we then present the analytical study of the deterministic limit to identify the regions in the parameter space where there is coexistence or dominance of one strategy. Although the study of the equilibrium solutions of the replicator equation contains some original results, in particular regarding the dependence of the risk threshold on the group size, Section 5 is where we present our main original contribution to the TPGG, viz., the computational study of the demographic noise on the equilibrium states of the imitation dynamics, in particular the analysis of the lifetimes of the metastable coexistence state. Finally, in Section 6 we present some closing remarks.

2.   TPGG

We consider a population of size $M$ consisting of individuals who may or may not contribute to a collective goal that can prevent a potential disaster (e.g., preventing the global temperature from exceeding a certain threshold, building or maintaining a dam to protect the city, or raising the minimum wage to avert social unrest). There are two different types of individuals, cooperators and defectors, depending on whether they contribute to the public good or not. These types (or strategies) are not fixed, since an individual can change her type by copying a better-off individual, as will be explained in Section 3. The game we describe next is a one-round variant of the game introduced in Milinski et al. ^[13] and played by adult human subjects.

Following the theoretical setup proposed by Wang et al. ^[16] (see also ^[17,18]), a group of $n$ individuals is randomly selected from the population without replacement, and each individual receives a fixed endowment $W$. They have the option of either contributing a fixed amount $C \leq W$ to the public goods or contributing nothing. The potential disaster is averted if the contributions reach or exceed the value $T = mC$, which requires the presence of at least $m \in \{1, 2, \ldots n \}$ cooperators in the group. In this case, the payoff of a cooperator in the group is $W-C$, while the payoff of a defector is $W$. However, if the contributions do not reach the value $T$, then the potential disaster becomes a reality with probability $p$, and the group members lose all their assets, so their payoffs are zero, regardless of their type. With probability $1-p$, the disaster does not occur, so a cooperator's payoff is $W-C$ and a defector's is $W$. The risk of loss $p$ will be the leading parameter in our study. By measuring $C$ and $T$ in units of $W$, we can introduce the dimensionless variable $c = C/W \leq 1$, so that the initial endowment can be set to $1$ without loss of generality.

This framework differs from the original experimental setup of Milinski et al. ^[13], where participants have ten rounds to contribute to the public good while having access to the amount contributed by others, before rolling the dice that determines the onset of a disaster that could wipe out their savings. The participants, who form groups of size $n = 6$, are informed of both the number of rounds (ten in this case) and the risk of loss $p$, but they are not allowed to communicate with each other (see ^[12] for the effect of communication in a risk-free scenario). The strategies used in this scenario, where players receive feedback on each other's savings in each round, are more complicated to model because the probability of contributing depends on the amount still needed to reach the threshold as well as on information about other players' savings. Receiving feedback about others' savings, especially the defector's savings, undermines cooperation ^[13,23] (but see ^[24]) probably for reasons similar to those that lead people to reject unfair offers in the ultimatum game ^[25]. All of these difficulties are avoided in the one-round variant, where players have only one opportunity to contribute to the public good once their play group is formed. In the one-round evolutionary game, a player may meet members of her previous play groups again, which will certainly happen in finite populations, as new play groups form. However, in contrast to the experimental setup of Milinski et al. ^[13], in the one-round evolutionary version there are no repeated interactions between players within their play groups.

There are variants of TPGG in which players receive different initial endowments to model the inequality of the distribution of wealth among them ^[26,27], which is a more realistic scenario especially when the players are countries negotiating quotas for greenhouse gas emissions at UN climate change conferences ^[28]. In addition, to describe the uncertainties in defining the target required to avoid the disaster, there are variants of the TPGG where $m$ is considered a random variable ^[18]. In an effort to describe even more realistic scenarios, we mention a risk-driven migration variant of the TPGG in which players can switch groups if they perceive that collective failure becomes too likely ^[29]. Finally, we note that Pacheco et al. ^[30] have considered a similar model with a cumulative threshold to be reached by cooperators, but with different payoffs and, more importantly, without the threat of catastrophe. Interestingly, their model actually describes the original risk-free version of TPGG introduced by Kragt et al. ^[12], although this fact went unnoticed at the time. Here we stick to the simpler variant described above in order to provide a thorough analysis of the replicator dynamics for both infinite and especially finite populations.

3.   Imitation dynamics

At time $t$, we randomly select an individual $i$ from the population of size $M$. This is the focal individual. To determine the focal individual's payoff $f_i$, we randomly choose $n-1$ other individuals in the population without replacement, which form the focal individual's play group. All $n$ individuals in the play group receive the same endowment which we set to $1$ without loss of generality, as discussed before. Regardless of the composition of the group, if the focal individual is a cooperator, she contributes an amount $c$ to the public goods, so her endowment becomes $1-c$, whereas if she is a defector, her endowment remains at its initial value of $1$. By introducing the indicator function $I_c(i) = 1$ when individual $i$ is a cooperator and $I_c(i) = 0$ when individual $i$ is a defector, we can write the endowment of individual $i$ as $1 - c I_c(i)$ after her decision to contribute or not to the public goods. Whether the focal individual keeps her endowment or not depends on the number $k$ of cooperators among the other members of her play group (excluding herself): if $k +I_c(i) \geq m$ then she keeps the endowment with certainty, otherwise she keeps the endowment with probability $1-p$ and loses it with probability $p$. In summary, if $k +I_c(i) < m$, then the focal individual's payoff is $f_i = 0$ with probability $p$ and $f_i = 1 - c I_c(i)$ with probability $1-p$. If $k +I_c(i) \geq m$, then the focal individual's payoff is $f_i = 1 - c I_c(i)$.

The next step is to randomly select an individual $j \neq i$ from the population. This is the model individual. We then evaluate the payoff $f_j$ using the same procedure described above for the focal individual $i$. If $f_j \leq f_i$, the focal individual maintains her strategy, otherwise she switches to the model individual's strategy with a probability $\rho$ given by the difference in payoffs, i.e.,

Note that the maximum value of the switching probability ($\rho = 1$) occurs when the model individual is a defector whose group was spared from the disaster (i.e., $f_j = 1$) and the focal individual was in a group affected by the disaster (i.e., $f_i = 0$). Following this rule, a model individual with payoff $f_j = 0$ will never persuade a focal individual to change strategy. Regardless of whether the focal individual changes her strategy or not, time $t$ is increased by $1/M$. Then new focal and model individuals are selected and the process is repeated, so that as time goes from $t$ to $t+1$, $M$ focal individuals are randomly selected. In the limit $M \to \infty$, this dynamics, where only better-off individuals can be imitated, is described by the deterministic replicator equation ^[21] (see also ^[19,22]).

A more realistic imitation scenario probably requires relaxing the condition that only more successful individuals can be imitated. In fact, human imitation behavior in problem-solving experiments is best described by introducing a factor that accounts for noise in the imitation rule ^[31]. A common switching probability $\rho$ that has a noise parameter is the Fermi update rule (see, e.g., ^[32]), where the temperature regulates the influence of payoffs on the individual's decision to change or not to change strategy. The Fermi update rule has been used to simulate finite population scenarios of the TPGG ^[17,18] but the corresponding stochastic dynamics is not described by the replicator equation in the infinite population limit. Only if the switching probability is a linear function of the payoff difference $f_{j} - f_{i}$, the resulting imitation stochastic dynamics is described by the replicator equation in the infinite population limit ^[21]. This point is fundamental to studying the effect of demographic noise, the strength of which is measured by how much the noise can deviate the stochastic trajectories from their deterministic counterparts.

4.   Deterministic limit: the replicator equation

Here we assume that the population is infinite and is completely characterized by the frequency of cooperator at a given time, $x = x(t)$. The expected payoffs of each strategy are the only information from the game that we need to write down the replicator equation that determines the time evolution of the frequency of cooperators ^[9].

Let us calculate the expected payoff $\pi_c$ of a cooperator. As explained before, her payoff depends on the composition of her play group, in particular on the number $k = 0, \ldots, n-1$ of other cooperators in the group. Clearly, our cooperator's expected payoff is $1-c$ times the probability that her group evades disaster. This happens with certainty if $k+1 \geq m$, and with probability $1-p$ otherwise. Since the members of a play group are sampled randomly from the infinite population we obtain

where $\theta(z) = 1$ if $z \geq 0$ and $0$, otherwise. A similar reasoning leads to the expected payoff $\pi_d$ of a defector,

Thus, the replicator equation for the frequency of cooperators is ^[9]

where $g(x) \equiv \pi_c(x) - \pi_d(x)$ is written explicitly as

We note that Eqs (4.3) and (4.4) are the same as in Wang et al. ^[16], but the results of the analysis of their equilibrium solutions differ slightly, as we will see next. The equilibrium solutions or fixed points are $x = 0$, $x = 1$ and the roots of the function $g(x)$. The stability of the fixed point $x = x^*$ is determined by the condition that the derivative of the function on the rhs of Eq (4.3) evaluated at $x^*$ is negative ^[33], i.e.,

where

Let us first examine the stability of the all-defectors fixed point $x^* = 0$. Clearly, for $p < 1$ this fixed point is stable since $g(0) = -c(1-p) < 0$. For $p = 1$, which means that the disaster is certain if the public good is not produced to prevent it, we need to expand $g(x)$ in powers of $x$ and keep the lower order terms. This gives

which implies that $x^* = 0$ is unstable for $p = 1$, since the rhs of Eq (4.3) is always positive.

We now consider the stability of the all-cooperators fixed point $x^* = 1$. Since $g(1) = -c + p \delta_{n, m}$, condition (4.5) implies that this fixed point is unstable if $m < n$ and is stable if $m = n$ provided that $p > c$. Note that in the latter case (i.e., $m = n$), the all-defectors fixed point is also stable if $p < 1$, so we have a bistability situation, where the domains of attraction of the two stable extreme fixed points are separated by the only real root of $g(x)$, viz., $x = [(1/p-1)/(1/c-1)]^{1/(n-1)}$. Thus, increase of the group size $n$ decreases the size of the basin of attraction of the all-cooperators fixed point.

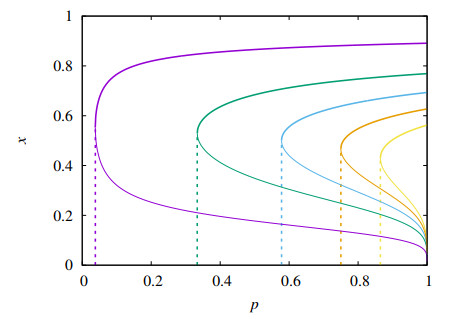
The most interesting and challenging feature of the TPGG is the possibility of stable internal fixed points $0 < x^* < 1$ of the replicator dynamics, which are the roots of the $n-1$-th order polynomial $g(x)$ and correspond to the coexistence of the two strategies (see also ^[30]). As discussed above, for $m = n$ there is only one internal fixed point, which happens to be unstable. From now on we will only consider the case $m < n$ in the analysis of the deterministic regime. Here we show that there are at most two internal fixed points, thus correcting Wang et al. ^[16] who suggested that there could be many more. In fact, we begin by noting that $g'(x) = 0$ has only one solution in the range $(0, 1)$, viz.,

which is the absolute maximum of $g(x)$, since $g''(\tilde{x}) < 0$. Recalling that $g(0) < 0$ and $g(1) < 0$, we conclude that there are no internal fixed points if $g(\tilde{x}) < 0$. In this case, the all-defectors fixed point is the only stable fixed point of the replicator dynamics. However, if $g(\tilde{x}) > 0$ then there are exactly two internal fixed points, which we denote by $x_u$ and $x_s$ with $x_u \leq \tilde{x} \leq x_s$. It is clear that $g'(x_u) > 0$, so the stability condition (4.5) implies that $x^* = x_u$ is unstable. In a similar vein, since $g'(x_s) < 0$ we have that $x^* = x_s$ is stable. Hence, we have a bistability scenario, where the replicator dynamics can be attracted to the all-defectors fixed point $x^* = 0$ if $x(0) < x_u$ or to the coexistence fixed point $x^* = x_s$ if $x(0) > x_u$. The sudden appearance of the two internal fixed points occurs when $g(\tilde{x}) = 0$, i.e., when $x_s = x_u$ is a double root of $g(x)$. This analysis agrees with Santos and Pacheco ^[17].

Figure 1 summarizes the main results of the analysis of the fixed points of the replicator equation (4.3). For the parameter set of this figure, the all-defectors fixed point $x = 0$ is always stable, except at $p = 1$, which is confirmed by the finding that $x_u \to 0$ as $p \to 1$. Recall that in this case (i.e., $m < n$ and $p = 1$) only the coexistence fixed point $x_s$ is stable. The most notable feature in this figure is the risk threshold $p_c$, where the coexistence fixed point appears discontinuously. When the risk is lower than this threshold (i.e., $p < p_c$), the all-defectors fixed point is the only attractor of the replicator dynamics. This discontinuous transition, which is located at $p = p_c$, is characterized by the jump $\Delta x = x_s$ at $p_c$, as shown in Figure 2. Note that $\Delta x$ is given by Eq (4.8) and thus does not depend on the risk $p$ and has a monotonic dependence on $c$ and $m$, as shown in the right panel of Figure 2. For fixed $c$, the threshold $p_c$ is easily obtained by finding the value of $p$ such that $g(\tilde{x}) = 0$. Although $p_c$ increases monotonically with increasing $c$, as expected, it has a nonmonotonic dependence on $m$, as shown in the left panel of Figure 2. Recall that $m$ is the minimum number of cooperators in the play group that will prevent the disaster with certainty. This non-monotonicity can be verified analytically for small $c$, where we have

so that $p_c$ is invariant to the change of $m$ for $n-m+1$. For example, in Figure 2 where $n = 10$, the risk threshold is the same for $m = 2$ and $m = 9$ in the region near $c = 0$.

Figure 1.  Frequency of cooperators $x$ as function of the risk $p$ for $c = 0.01$ (violet curves) $c = 0.1$ (green curves), $c = 0.2$ (blue curves), $c = 0.3$ (goldenrod curves), and $c = 0.4$ (yellow curves). The thick curves are the stable coexistence fixed point $x_s$, and the thin curves are the unstable fixed point $x_u$, which delimits the basins of attraction of the fixed points $x_s$ and $x = 0$. The vertical dashed lines indicate the risk threshold $p_c$ below which $x = 0$ is the only stable fixed point. The other parameters are $n = 10$ and $m = 6$.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Risk threshold $p_c$ (left panel) and jump at the threshold $\Delta x = \tilde{x}$ (right panel) as functions of the contribution to the public goods $c$ for $m = 2$ (violet curves) $m = 4$ (green curves), $m = 6$ (blue curves), and $m = 9$ (goldenrod curves). The play group size is $n = 10$.

DownLoad: Full-Size Img PowerPoint

We now consider large group sizes $n$, which is a more realistic scenario for TPGG, since successfully tackling the problems that threaten our society requires large numbers of individuals. We note, however, that in behavioral economics games the typical group size used in the experiments is $n = 6$ ^[13,27,34]. Here, we will vary $n$ and $m$ such that the ratio

is fixed. Figure 3 shows the internal fixed points for a variety of group sizes. In the limit $n \to \infty$, the jump at the threshold $p_c$ tends to

which is a good approximation for $x_s$ in this limit. The important result of Figure 3 is that $p_c$ tends to $1$ as $n$ increases: the larger the group size, the greater the risk must be for individuals to mobilize to avoid threatening disasters. The detrimental effect of large groups on cooperation is a phenomenon observed in social psychology and called the diffusion of responsibility effect, since it is thought that people in large groups often fail to contribute to a common good because they believe that others will ^[35]. Since it is a general observation in most $n$-person games (see, e.g., the snowdrift game ^{[36,37,38,39]}, the $n$-person prisoner's dilemma ^[14,40], and the volunteers' dilemma which is the TPGG with $p = 1$ ^[41]) that cooperation is harder to achieve in large groups there may be no need to invoke people's expectations to explain this result, which may be a simple consequence of playing in large groups. More specifically, for large $n$ we find

where

so $p_c$ tends exponentially fast to $1$ with increasing $n$. Note that $h(c, \zeta)$ is a monotonically increasing function of $c$, as expected: the risk must be greater to compensate for the greater per capita contribution to the public good. In addition, since $h(c, 0) = h(c, 1) = 0$ this function has a maximum at $\zeta = 1/c +1/\ln(1-c)$. Of course, this is the same nonmonotonic dependence of $p_c$ on $m$ shown in Figure 2. The key result that $p_c$ tends to $1$ as $n$ increases was already known from the original TPGG studies ^[16,17], but here we offer the analytical equation for the increase of the risk threshold with group size.

Figure 3.  Frequency of cooperators $x$ as function of the risk $p$ for $c = 0.1$, $\zeta = m/n = 0.2$, $n = 100$ (violet curves) $n = 200$ (green curves), $n = 400$ (blue curves), and $n = 800$ (goldenrod curves). The thick curves are the stable coexistence fixed point $x_s$, and the thin curves are the unstable fixed point $x_u$. The horizontal dashed line is the jump at $p_c$ for $n \to \infty$ given in Eq (4.11).

DownLoad: Full-Size Img PowerPoint

Since the above analysis is only valid if $m$ increases with $n$ so that their ratio is fixed, we now consider the alternative scenario where $n$ increases but $m$ remains fixed. In this case, the jump of cooperators frequency at the threshold given in Eq (4.8) becomes

so $n \tilde{x}$ tends to a constant value when $n \to \infty$. Since $x_u < \tilde{x}$, a very small initial fraction of cooperators can drive the dynamics to a coexistence solution that is also characterized by a small fraction of cooperators. To obtain the threshold $p_c$ in this case, we need to find the value of $p$ for which $g(\tilde{x}) = 0$, where $g(x)$ is given in Eq (4.4). This yields

By fixing $m$ and obtaining $p_c$ numerically for increasing $n$, we find that $p_c$ increases with $n$ and tends to the above result in the limit $n \to \infty$. In addition, we find that if we fix $p > p_c$ and increase $n$, then the stable coexistence fixed point vanishes as $1/n$, i.e., $x_s \sim 1/n$.

Our results imply that increasing group size $n$ is always detrimental to cooperation, which contrasts with the conclusion of Wang et al. ^[16] that for $p = 1$ and $m < n$ increasing group size can promote the emergence of cooperation. In this case, $g(x)$ has a single root, the stable coexistence fixed point $x_s$, and Figure 3 shows that $x_s$ decreases with increasing $n$ for $p = 1$.

5.   Finite population simulations

The deterministic replicator equation formalism was originally proposed to study biological evolution in models where individuals' payoffs are interpreted as fitness, i.e., roughly the number of offspring they contribute to the next generation ^[8]. An important development in the mathematical study of public goods games is the realization that this formalism also describes models of social dynamics in which individuals are more likely to imitate the behavior of their more successful peers ^[19,21], according to the stochastic imitation dynamics presented in Section 3. This dynamics allows us to study the effects of demographic noise (finite population) on the deterministic predictions of the replicator equation formalism. In the following, we present finite population simulations for two different scenarios, according to the nature of the deterministic equilibrium solutions. First, we consider the more challenging and general scenario where the coexistence solution is stable in the deterministic limit, but corresponds to a metastable state for finite populations. Second, we consider the simpler scenario that occurs for $m = n$, where both the all-defectors and all-cooperators solutions are stable in the deterministic limit and correspond to absorbing states for finite populations.

5.1.   Metastable coexistence states

Figure 4 shows the numerical solution of Eq (4.3) along with four independent runs of the stochastic simulation algorithm for three different initial conditions and populations of size $M = 1000$. The finite-size effects in the dynamics are small in the time range shown in the figure, and the results confirm the link between the imitation dynamics and the replicator equation. However, since the coexistence fixed point of the replicator equation corresponds to a metastable stable of the finite $M$ simulations, the trajectories will eventually deviate from it and fall into the all-defectors absorbing state. (We will see next that the probability of the trajectories falling into the all-cooperators absorbing state is zero.) To quantify this phenomenon we introduce the probability $\Pi_\tau$ that there is at least one cooperator in the population at time $\tau$. This probability is estimated by counting the number of trajectories that have not fallen into the all-defectors absorbing state at time $\tau$. The total number of trajectories varies from $10^4$ to $10^6$ to ensure that the estimation of small values of $\Pi_\tau$ is accurate.

Figure 4.  Frequency of cooperators as a function of time for $x(0) = 0.8$ (violet curves), $x(0) = 0.5$ (green curves), and $x(0) = 0.3$ (blue curves). The jagged thin curves are trajectories of the stochastic dynamics for $M = 1000$, and the smooth thick curves are the deterministic results. The other parameters are $c = 0.1$, $p = 0.5$, $n = 10$ and $m = 6$.

DownLoad: Full-Size Img PowerPoint

For fixed $p > p_c$, so that the coexistence solution is stable in the deterministic limit, Figure 5 shows that $\Pi_\tau$ decreases exponentially with increasing $\tau$, so we assume that the scaling relation

holds for large $\tau$. Here $\xi = \xi (p, M)$ is interpreted as the half-life of the cooperators and is obtained by fitting $\Pi_\tau$ with an exponential in the large $\tau$ range. The results indicate that $\xi$ increases exponentially with increasing $M$, i.e., $\xi \sim \exp (\alpha M)$ and that the rate of increase $\alpha$ decreases as $p$ approaches $p_c$. In fact, $\alpha$ vanishes linearly with the distance to the risk threshold, i.e., $\alpha \sim (p-p_c)$, as shown in the figure. Since $\Pi_\tau \to 0$ when $\tau \to \infty$, the probability of the trajectories falling into the all-cooperators absorbing state is zero, as mentioned before.

Figure 5.  (Left) Probability $\Pi_\tau$ that there is at least one cooperator in the population at time $\tau$ for $p = 0.5$ and $M = 50$ (violet circles), $M = 75$ (green circles), $M = 100$ (blue circles), $M = 125$ (goldenrod circles), and $M = 150$ (yellow circles). The lines are the fit $\Pi_\tau = a \exp(-\tau/\xi)$ for large $\tau$, where $a$ and $\xi$ are fit parameters. (Middle) Half-life of cooperators $\xi$ as a function of population size $M$ for $p = 0.5$ (violet triangles), $p = 0.45$ (green triangles), and $p = 0.4$ (blue triangles). The lines are the fit $\xi = a \exp(\alpha M)$, where $a$ and $\alpha$ are the fit parameters. (Right) Increase rate $\alpha$ as a function of the distance to the threshold $p-p_c$. The line is the fit $\alpha = 0.22 (p-p_c)$. The initial condition is $x(0) = 0.8$ and the risk threshold is $p_c \approx 0.3336$. The other parameters are $c = 0.1$, $n = 10$, and $m = 6$.

DownLoad: Full-Size Img PowerPoint

We now turn to the analysis of the case $p < p_c$, where there are no metastable states to slow down the convergence to the all-defectors absorbing state. Figure 6 shows that the probability of finding cooperators in a population of fixed size $M$ decreases exponentially with time $\tau$, as expected, so that Eq (5.1) holds for this case as well. What changes is the dependence of the cooperators' half-life $\xi$ on the population size $M$. Now $\xi$ decreases with increasing $M$ and tends to a finite value, as shown in the figure, since a non-zero minimum time is needed to remove the cooperators from the population. As expected, this minimum time increases with the risk $p$, since high risk tends to favor cooperation. However, it is difficult to quantify this increase, because the rate of decrease of $\xi$ (i.e., the fit parameter $\beta$ introduced in the caption of Figure 6) decreases very rapidly with increasing $p$.

Figure 6.  (Left) Probability $\Pi_\tau$ that there is at least one cooperator in the population at time $\tau$ for $p = 0.3$ and $M = 200$ (violet circles), $M = 400$ (green circles), $M = 800$ (blue circles), and $M = 1600$ (goldenrod circles). The lines are the fit $\Pi_\tau = a \exp(-\tau/\xi)$ for large $\tau$, where $a$ and $\xi$ are fit parameters. (Right) Half-life of cooperators $\xi$ as a function of population size $M$ for $p = 0.3$ (violet triangles), $p = 0.25$ (green triangles), and $p = 0.2$ (blue triangles). The lines are the fit $\xi = a + b \exp(-\beta M)$, where $a$, $b$ and $\beta$ are the fit parameters. The initial condition is $x(0) = 0.8$ and the threshold is $p_c \approx 0.3336$. The other parameters are $c = 0.1$, $n = 10$, and $m = 6$.

DownLoad: Full-Size Img PowerPoint

Finally, we now consider the case $p = p_c$. We recall that for fixed model parameters, the risk threshold $p_c$ is obtained with arbitrary precision by determining the value of $p$ at which the coexistence fixed points first appear, as shown in Figure 1. Moreover, the threshold phenomenon only occurs in the deterministic limit, i.e., for $M \to \infty$. Figure 7 shows that $\Pi_\tau$ decreases exponentially with increasing $\tau$, as expected. The remarkable result is that the cooperators' half-life increases with a fractional power of the population size, i.e., $\xi \sim M^{1/3}$. This is consistent with statistical physics findings that at the threshold the exponential functional form governing the convergence to equilibrium away from the critical region is replaced by a power law ^[42].

Figure 7.  (Left) Probability $\Pi_\tau$ that there is at least one cooperator in the population at time $\tau$ for $p = p_c$, $n = 10$, $m = 6$, and $M = 500$ (violet circles), $M = 1000$ (green circles), $M = 1500$ (blue circles), and $M = 2000$ (goldenrod circles). The lines are the fit $\Pi_\tau = a \exp(-\tau/\xi)$ for large $\tau$, where $a$ and $\xi$ are fit parameters. (Right) Half-life of cooperators $\xi$ as a function of population size $M$ at $p = p_c$ for $n = 5$ and $m = 3$ (violet triangles), $n = 10$ and $m = 6$ (green triangles), and $n = 20$ and $m = 12$ (blue triangles). The lines are the fit $\xi = a M^{1/3}$, where $a$ is a fit parameter. The initial condition is $x(0) = 0.8$ and $c = 0.1$.

DownLoad: Full-Size Img PowerPoint

In the case of $2$-person games, it is possible to study analytically the game dynamics in finite populations as a frequency-dependent Moran process ^[43]. For large populations, this approach corresponds to Kimura's diffusion approximation ^[44], which was used to prove that a variant of the stochastic imitation dynamics leads to the replicator equation in the infinite population limit ^[19]. This analytical approach is probably impractical for $n$-person games as complicated as the TPGG considered here. Remarkably, Antal and Scheuring ^[43] were able to show analytically for their $2 \times 2$ matrix games that the mean lifetime of the coexistence metastable state increases exponentially with population size and as a power law with exponent $3/2$ at the threshold. The exponent of the power law is different from the $1/3$ exponent because the games are different. Given the universal nature of the power law exponents ^[42], it would be interesting to determine what properties of the game define their values.

The fact that the threshold $p_c$ depends on the group size complicates the analysis of the effect of $n$ on the cooperators' half-life $\xi$. We recall that according to Eq (4.12), $p_c$ tends exponentially fast to $1$ with increasing $n$. For example, for a fixed risk $p$, the half-life decreases with population size $M$ for small groups (because $p_c < p$), but increases with $M$ for large groups (because $p_c > p$). For this reason, we choose to study the effect of $n$ for $p = p_c$ in the right panel of Figure 7. The results show that for fixed $M$, the half-life decreases with increasing group size at the risk threshold. More explicitly, by rescaling $\xi \sim 1/n^{0.8}$, we can make the data in this panel collapse into a single straight line. This is consistent with our conclusion that increasing group size is detrimental to cooperation. In this case, cooperation is disrupted by reducing the time the population spends in the coexistence metastable state. For fixed $n$, the dependence on $M$ follows the power law with exponent $1/3$, supporting the universality of this growth law.

In contrast to the analysis of the deterministic limit, where we could offer analytical expressions or simple numerical procedures to obtain the effect of all model parameters on the quantities of interest, the finite population simulations discussed here are necessarily limited to a small range of parameters. However, according to the universality assumption of critical phenomena our general conclusions should not depend on the choice of parameters ^[42]. In particular, we verified that the exponent $1/3$ governs the power-law growth of the cooperators' half-life at the risk threshold for several choices of the parameters $c$ and $x(0)$.

5.2.   All-defectors and all-cooperators absorbing states

We now consider a simpler scenario where the stable equilibrium solutions of the replicator equation (4.3) are absorbing states of the finite $M$ imitation dynamics. This happens only if both the all-defectors $x = 0$ and the all-cooperators $x = 1$ fixed points are stable, a situation that occurs only when $m = n$ and $p > c$. In this case, for a fixed initial condition $x_0 = x(0)$, the transition between the two equilibrium regimes takes place at

in the limit $M \to \infty$, so $p_c \to 1$ exponentially fast with increasing $n$. Figure 8 shows the fixation probability of cooperators $\Pi_\infty$ as a function of the risk for increasing population size $M$. Since for fixed $M$ we follow the dynamics until fixation of one of the strategies occurs, we first take the limit $\tau \to \infty$. The limit $M \to \infty$ is determined by inferring how $\Pi_\infty$ changes with increasing $M$ using finite-size scaling methods, in particular the data collapse technique ^[20,45]. As expected, the demographic noise smooths out the sharp transition at $p = p_c$. In particular, for large $M$ and near $p_c$ we find that the data obeys the scaling form

where $F_n(u)$ is a scaling function such that $F_n(0) = 1/2$. Since the derivative of $\Pi_\infty$ at the threshold is proportional to $M^{1/2}$ we conclude that the sharpness of the threshold increases with $M^{1/2}$ or, equivalently, the width of the transition region shrinks as $M^{-1/2}$ with increasing $M$. Note that the effect of demographic noise is only significant in the transition region, where it can nudge the trajectories into a different absorbing state than predicted by the replicator equation (4.3).

Figure 8.  (Left) Probability of fixation $\Pi_\infty$ of cooperators as a function of the risk $p$ for $M = 200$ (goldenrod curve), $M = 400$ (blue curve), $M = 800$ (green curve), and $M = 1600$ (violet curve). The vertical dashed line indicates the threshold $p_c = 0.453$ beyond which the fixed point $x = 1$ is stable for $M \to \infty$. (Right) $\Pi_\infty$ as a function of the scaled variable $(p-p_c)M^{1/2}$. The initial condition is $x(0) = 0.8$. The other parameters are $c = 0.1$ and $n = m = 10$.

DownLoad: Full-Size Img PowerPoint

Another useful quantity to characterize the stochastic dynamics in the absence of metastable states is the mean time to fixation $T_f$, i.e., the mean time for the dynamics to fall into the all-cooperators or the all-defectors absorbing state. Figure 9 shows the influence of the risk loss and the population size on the mean fixation time. Convergence to the all-cooperators absorbing state ($p > p_c$) is much faster than to the all-defectors absorbing state ($p < p_c$). More specifically, the results show that $T_f$ diverges as $\ln M$ with increasing $M$ for all $p$. The nonmonotonic behavior with $M$ observed for, e.g., $p = 0.55$ is due to the crossover between the large fixation times when the dynamics goes to the all-defectors state and the small fixation times when it goes to the all-cooperators state. For sufficiently large $M$, all trajectories go to the all-cooperators state since $0.55 > p_c$, and we recover the monotonic increase of $T_f$ with $M$, as shown in the right panel of Figure 9. For finite $M$, the maximum of $T_f$ does not occur at the risk threshold, but moves in its direction as $M$ increases. We note that a similar analysis of the mean time to fixation is computationally prohibitive for parameter settings that allow the existence of metastable states since, as shown before, the time to fixation grows exponentially fast with increasing $M$ for $p > p_c$.

Figure 9.  (Left) Mean fixation time $T_f$ as function of the risk $p$ for $M = 200$ (goldenrod curve), $M = 400$ (blue curve), $M = 800$ (green curve), and $M = 1600$ (violet curve). The vertical dashed line indicates the risk threshold $p_c = 0.453$. (Right) $T_f$ as a function of the population size $M$ for $p = 0$ (blue circles), $p = p_c$ (violet circles), $p = 0.55$ (green circles), and $p = 1$ (goldenrod circles). The lines are the fit $T_f = a +b \ln M$, where $a$ and $b$ are fit parameters. The initial condition is $x(0) = 0.8$. The other parameters are $c = 0.1$ and $n = m = 10$.

DownLoad: Full-Size Img PowerPoint

To complete the analysis of the scenario where all members of the group must cooperate to avoid the disaster with certainty (i.e., $m = n$), we now consider the effect of varying the group size $n$. Since the risk threshold $p_c$ depends on $n$, the effect of demographic noise, which is essentially the width of the transition region, is better appreciated when the probability of fixation is plotted as a function of distance to the risk threshold, as in Figure 10. The results show that the effect of demographic noise is enhanced by increasing group size. In particular, near $p_c$ and for $n \ll M$ we find that the data obeys the scaling form

where $F(u)$ is a scaling function such that $F(0) = 1/2$. Although this result may seem surprising, since we expect noise to be suppressed by large numbers, for small $n$ it is much easier to form an all-cooperators group and thus avoid the random occurrence of disaster, leading to a reduction in stochasticity that may explain our result.

Figure 10.  (Left) Probability of fixation $\Pi_\infty$ of cooperators as a function of the distance to the risk threshold $p -p_c$ for $M = 1600$, $n = m = 2$ (violet curve), $n = m = 4$ (green curve), $n = m = 6$ (blue curve), $n = m = 8$ (goldenrod curve), and $n = m = 10$ (yellow curve). (Right) $\Pi_\infty$ as a function of the scaled variable $(p-p_c) n^{-1.6}$. The initial condition is $x(0) = 0.8$ and $c = 0.1$.

DownLoad: Full-Size Img PowerPoint

6.   Discussion

Collective risk social dilemmas are timely research problems, the study of which can guide public policy on pressing issues that threaten the existence of our techno-industrial civilization. This motivates our re-examination of the evolutionary game-theoretic version of this dilemma ^[16,17,18] with emphasis on the effect of demographic noise on the stability of cooperation. The main difference of this game from the traditional public goods games, such as the $n$-person prisoner's dilemma ^[14,15] or the $n$-person snowdrift game ^{[36,37,38,39]}, is that the incentive to invest in a public good is not to realize a gain (e.g., the amplified return on the amount invested), but to avoid a loss resulting from an avoidable disaster.

The evolutionary game framework introduces an extraneous element to collective risk social dilemmas, viz., the chance for individuals to play the game repeatedly, and thus to face the threat of catastrophe and suffer its consequences if it occurs an infinite number of times. In the original experimental setup of the TPGG ^[13], like in real-world collective risk scenarios, there are typically no second chances once the disaster has occurred. The evolutionary game framework essentially assumes that the population is formed by recurrent players of these games, and that those affected by the disaster, whether they have contributed to the public good or not, do not have followers. Although the risk of loss has been considered as an alternative mechanism to promote cooperation, it can be seen simply as indiscriminate punishment, as opposed to selective punishment of defectors only, which is an effective way of promoting cooperation ^[46,47], even though it is not free of flaws ^[48,49,50].

Our results confirm the theoretical findings of previous TPGG studies, in particular, and not surprisingly, that higher risk of loss encourages cooperation. This is the same general conclusion drawn from experiments where players have several rounds to contribute to the common good, but only face the thread of disaster once ^[13,24,27]. In addition, we also confirm that increasing group size is always detrimental to cooperation, which is a general observation in most $n$-person games. Interestingly, this result was inferred by Milinski et al. ^[13] when they argued that if some small experimental groups fail to collect the target, larger groups would certainly fail with higher probability. Our analysis complements and offers some corrections to a previous theoretical study of the TPGG ^[16] by giving explicit analytical expressions for the critical risk loss below which cooperation is not possible. In fact, for most parameter values, cooperators coexist with defectors at best. The total elimination of defectors requires an extreme scenario in which disaster can only be avoided if all members of the group cooperate and the risk loss is greater than the individual contribution to the public good.

The difficulty with the coexistence scenario is that it is not stable against demographic noise, since the deterministic coexistence fixed point is not an absorbing state of the finite population dynamics. In fact, our main contribution to the TPGG was to obtain the scaling laws of the transient lifetimes or half-lives of the cooperators using finite-size scaling methods. When the population of players is not too large, as in the case of countries negotiating climate change mitigations at world summits ^[28], demographic effects are important, and our results show that cooperators who formed the coexistence state will eventually change their strategy, leading to a population composed only of defectors. For the finite population TPGG, long transients have the important role of keeping cooperators in the population for a period of time, giving the chance to evolve more robust maintenance mechanisms such as selective punishment ^[46], reputation and reciprocity ^[51], and positive assortment ^[52]. Finally, we note that the characterization of the duration of the transient of metastable states is also a topic of interest in deterministic models of population dynamics and ecology, where the density dependence of the population growth rate plays a key role on the transient lifetimes ^[53].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

J. F. F. is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico, grant number 305620/2021-5.

Conflict of interest

The author declares there is no conflict of interest.