Efficient method for solving nonlinear weakly singular kernel fractional integro-differential equations

1.   Introduction

Recently, fractional calculus (FC) has attracted much attention since it can be used to model physical and engineering problems ^[1,2,3]. There are several definitions of fractional derivatives that do not coincide in general, like, Gröunwald-Letnikov, Riemann-Liouville, Caputo, Atangana-Baleanu, and Caputo-Fabrizio (see, e.g., ^[4,5]). In our work, we intend to use the Caputo fractional derivative (CFD), which is the most commonly used derivative among physicists and scientists because it provides a physical interpretation that is consistent with the behavior of many physical and biological systems, making it a valuable tool for modeling and analyzing various natural phenomena, including biology ^[6], energy systems ^[7], physics ^[8,9], groundwater flow modeling ^[10], and geomechanics ^[11]. The performance of many life systems can be represented utilizing fractional integro-differential equations (FIDEs) ^{[12,13,14,15,16,17]} by virtue of the recent works of FC in different trends of science and technology. In fact, solving fractional weakly singular kernels integral and integro-differential equations can be challenging but there are numerical methods that can be used to approximate their solutions; for example, the finite volume method ^[18], finite difference method ^[19,20,21], finite element method ^[22], two-grid method ^[23,24], backward substitution method ^[25], and the spectral collocation method that is commonly used in literatures.

The spectral collocation method involves approximating the solution to the FIDE using certain basis functions. These basis functions can have orthogonal or nonorthogonal basis. One of the common nonorthogonal bases is the Mittag-Leffler function (MLF) ^[26,27]. Computing unknown coefficients using collocation points in the weakly singular kernel can be handled using a special quadrature technique. Generally, this approach is efficient and accurate, but can be computationally intensive for large-scale problems. There are different approaches for treating these kinds of equations such as the Sinc approximation with smoothing transformations ^[28], wavelet-based technique ^[29], and alternative operational matrix Legendre polynomials technique ^[30].

In the present article, we intend to merge the generalized fractional Mittag-Leffler function (GFMLF) with a simple step function to obtain a powerful base for approximation called the generalized fractional step-Mittag-Leffler function (GFSMLF) and use it to gain a convenient solution for the following general form of the weakly singular kernel fractional integro-differential equations (WSKFIDEs).

● Linear kernel:

● Nonlinear kernel:

where $O(t)$ is the unknown function, $G(t), H(t)$ are continuous functions on $I$, $\theta_k\; (k = 0, 1, ..., N-1)$, $\kappa$ is a real constant, $N = \lceil \digamma\rceil$ equals the smallest integer that is bigger than $\digamma$, and $\mathbb{D}^\digamma$ is CFD of order $\digamma$.

The main aim of our work is to provide an efficient method to obtain the solution of linear and nonlinear WSKFIDEs. We remove the singularity via Riemann-Liouville fractional integration (R-LFI). The original problem is transformed into a regular integro-differential problem. In order to construct a new method to approximate the solution of such a problem, we developed the GFSMLF method, which integrates GFMLF with a step function to obtain a powerful base for approximation. Also, we construct the operational integral fractional Mittag matrix (OIFMM) method, which is more efficient to approximate the fractional integral even if it has a nonlinear term in the integrand. The proposed approach combines two methods in order to get the approximate solutions of the considered problems. The first one is the GFSMLF method and the second is the OIFMM method. We implemented the proposed method by approximating the fractional integral via the OIFMM method while approximating each fractional derivative in the problem via the GFSMLF method. This implementation of the proposed method yields nonlinear algebraic equations, which we transformed into an optimization problem. Additionally, we provide a proof of the error analysis for the suggested method in approximating any function, its fractional differentiation, and integration of the WSKFIDE. We include some numerical examples to demonstrate the efficacy and accuracy of our method.

The organization of this paper is as follows: In Section 2, we present some important preliminaries of FC. In Section 3, we discuss the approximation base. The procedures of the proposed method are placed in Section 4. Error analysis of the proposed method is deduced in Section 5. Numerical simulations of some examples are shown in Section 6. Our conclusions are presented in Section 7.

2.   Preliminaries

Here, we give some preliminaries of FC, which are especially useful for the outcomes of our work.

Definition 2.1. The CFD $\mathbb{D}^\digamma$ of order $\digamma$ is given as follows ^[31]:

The CFD $\mathbb{D}^\digamma$ is satisfied in the following properties:

Definition 2.2. The R-LFI $\mathbb{I}^\digamma$ of order $\digamma > 0$ is given as follows ^[31]:

The R-LFI $\mathbb{I}^\digamma$ has these properties (see, e.g., ^[32]):

3.   Approximation base

Here, we are thinking of creating a method similar to wavelet approximations using a class of nonorthogonal functions such as the MLF ^[26]. It is noticeable that most of those who deal with wavelet approximations tend to use orthogonal functions as a basis (see, e.g., ^[33,34,35]). Therefore, it is necessary for us to start with the basics of the subject, and we have chosen to define the step function and GFMLF.

3.1.   Step function and GFMLF

For the step function, let

where $j = 1, 2, ..., 2^k = n$, then for any function $O(t) \in L^2$, there exist step functions as ^[36]

such that

Now, the MLF of two-parameter is given by the following power series ^[37]:

Furthermore, the generalized MLF is defined in ^[27] as

In our work, we shall define the GFMLF as

Seeking the fractional differentiation and integration of Eq (3.1) with the use of Eqs (2.1) and (2.3), we have

and

3.2.   Approximation via GFSMLF

We now define GFSMLF, which can be described as a new function for approximation

where $j = 1, 2, ..., 2^k = n$. Its fractional differentiation and integration are defined with the use of Eqs (3.2) and (3.3) by

and

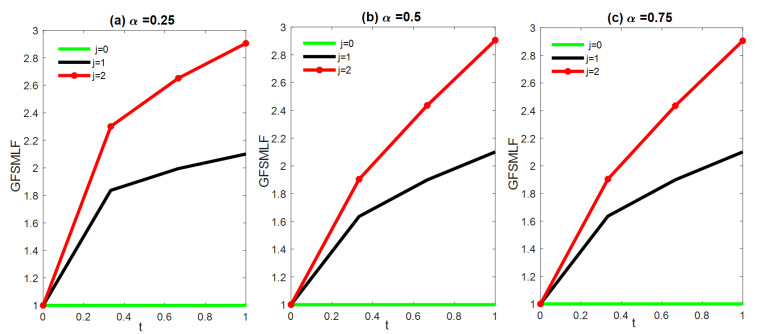
Figure 1 shows graphs of the GFSMLF for $n = 4$ with various values of MLF parameter $\alpha$.

Obviously, most authors in this field use the following approximation (see, e.g., ^[38]):

where $C = \{c_{jk}\}_{j = 1, k = 1}^{n, m}$ is $n*m$ unknown constants. However, in this work, we suggest the following approximation of $O(t)$ in terms of GSFMLF as

and its fractional derivative is defined as

where $\bar{A} = [b_1, b_2, ..., b_m](\sum_{j = 1}^{n} a_j)$; $A = [a_{1}, a_{2}, ..., a_{n}], B = [b_1, b_2, ..., b_m]$ and $\bar{Q} (t) = [Q_{j}^{\alpha, \beta, \gamma}]_{j = 1}^{n}$. Here, $A$ and $B$ represent $n+m$ unknowns and this reduces the effort to implement the present approach. This family of functions is not normalized or orthogonal, in contrast to most of the wavelet functions.

3.3.   Operational integral fractional Mittag matrix

As we may have a nonlinear term in the integrand, it may be difficult to treat this situation making use of the GSFMLF method. So, in this subsection, we shall construct the OIFMM method for this object. Let $\chi(t)$ be any function, and it can be approximated via GSFMLF as

with $\varPhi(t) = [W_1^{\alpha, \beta, \gamma}(t), W_2^{\alpha, \beta, \gamma}(t), ..., W_n^{\alpha, \beta, \gamma}(t)]^{T}$, as defined by Eq (3.1). The unknown coefficients $R = [r_{k}]_{k = 0}^{n}$ can be written as

where $\Theta = [\theta_{lk}]_{l, k = 0}^{n}$ is to be obtained. By combining Eqs (3.8) and (3.9), we conclude that

or

It is clear that $\Theta$ in Eq (3.11) can be easily calculated. For an approximation of frational integrals, we can integrate Eq (3.10) with fractional order $\digamma$ to obtain

where $I_W^\digamma(t) = \Theta^{T} \mathbb{I}^\digamma\varPhi(t)$ is the OIFMM.

4.   Implementation of the method

To begin, the singularity of the problems (1.1)–(1.3) will be removed via R-LFI (2.2). The resulting regular FIDEs for linear and nonlinear kernels are, respectively:

subject to the following initial conditions for each:

The linear problem (4.1) with (4.3) and nonlinear problem (4.2) with (4.3) in view of Eqs (3.6) and (3.7) can be written, respectively, as

and

where $\digamma > 0, \; 0 < \beta\le 1, \; t\in [0, 1]$. On the other hand, the fractional integrations of Eqs (4.4) and (4.5) shall be approximated by making use of the OIFMM to obtain

and

The obtained system of linear algebraic equations (4.6) with (4.3) and (4.7) with (4.3) can be reformulated as minimization problems, with the following objective functions, respectively:

and

By solving the above equations for the unknowns $A$ and $B$, the approximate solution (3.6) of the given problem can be determined.

5.   Error analysis

The main purpose of this section is to discuss the error of the numerical solution obtained by the proposed method in the previous section.

Theorem 5.1. Suppose that $O(t)\in C^\infty [0, T]; T\in \mathbb{R}$, is approximated by Eq (3.6), then $\forall$ $t\in[0, T]$. There exists $\tau \in[0, T]$, such that

and the uniform norm error is

where $\epsilon = \boldsymbol{sup}_{\tau \in [0, T]}||O_{nm}^{(n+1)}(\tau)||$.

Proof. Let $O(t)\in C^\infty [0, T]$ be approximated by Eq (3.6) and define the function: $T(t) = O(t)-O_{nm} (t)-\theta Q_{n+1}^{\alpha, \beta, \gamma}(t)$. We can choose the parameter $\theta$ such that the equation $T(t) = 0$ has a solution $z_0$ with the property $Q_{n+1}^{\alpha, \beta, \gamma}(t)\ne 0$. In this case, we can write $O(t_0)-O_{nm} (t_0)-\theta Q_{n+1}^{\alpha, \beta, \gamma}(z_0) = 0$, so

Since $O(t) \in C^\infty [0, 1]$, $Q_{n}^{\alpha \beta, \gamma}(t_0) \in C^n [0, \infty]$ and $Q_{n+1}^{\alpha \beta, \gamma}(z_0) \in C^{n+1} [0, \infty]$; thus, $T(t) \in C^{n+1}[0, 1]$. So, its $(n+1)$-th order derivative, namely, $T^{(n+1)} (t)$, has at least one root, that is,

where $Q_{n}^{\alpha, \beta, \gamma} (\varpi)$ is a polynomial of degree of at most $n$, the last term of Eq (5.4), $[Q_{n}^{\alpha \beta, \gamma} (\varpi)]^{(n)} = 0$. Also, we have

Substituting in Eq (5.4), we obtain

Equations (5.3)–(5.5) yield

and so

Finally, we take the maximum of $||O^{n+1} (\varpi)||$ to obtain the second result (i.e., Eq (5.2)). □

Theorem 5.2. Let $\mathbb{D}^\digamma O_{nm}(t)$, obtained by using GSFM, be the approximation of $\mathbb{D}^\digamma O(t)$, then we have

where $\epsilon = \boldsymbol{sup}_{\tau \in [0, T]}||O_{nm}^{(n+1)}(\tau)||$.

Proof. By differentiating Eq (5.1), we have

Taking the uniform norm, we get the result. □

Theorem 5.3. Suppose that $\chi(t)\in C^\infty [0, T]; \; T\in \mathbb{R}$, is approximated by Eq (3.8), then $\forall$ $t\in[0, T]$. There exists $\tau \in[0, T]$, such that

and the error in the OIFMM approximation of the fractional finite integration is

so

where $\epsilon = \boldsymbol{sup}_{\tau \in [0, T]}||\chi^{(n+1)}(\tau)||$.

Proof. Replacing $Q_{n}^{\alpha, \beta, \gamma}(t)$ by $W_{n+1}^{\alpha, \beta, \gamma} (t)$ in the proof of Theorem 5.1, we obatin

By integrating this equation and taking the uniform norm, we get the result. □

Theorem 5.4. Suppose that the above theorems holds, then the error in the approximation of the linear problem (4.1) with (4.3) is

with $t \in (0, T]$ and

Proof. Equation (4.1) with (4.3) can be rewritten as

Making use of the approximations (4.1) with (4.3), Eqs (5.12) and (5.13) can be approximated as follows:

Subtracting Eq (5.12) from Eq (5.14), the error in approximating the proposed problem is

and, similarly,

Making use of Eqs (5.1), (5.7) and (5.9), we obtain the results. □

6.   Numerical results

Linear and nonlinear WSKFIDES are used to model various physical phenomenon such as: heat conduction problem ^[39], radiative equilibrium ^[40], elasticity and fracture mechanics ^[41,42], etc. In this section, three examples are given to show the applicability and accuracy of the proposed method. All the computations were performed in a personal computer with Intel(R) Core(TM) i7-10510U CPU @2.30 GHz with 8 GB of RAM and the codes were written in MATLAB software (R2017a). The computing time is in seconds for the obtained numerical solution of the following examples.

Example 6.1. We consider the linear WSKFIDE, as follows:

The analytic solution is $O(t) = t^\rho$. This example is discussed in ^[43,44], with $\rho = 2$. We present in Figure 2 the numerical solutions for some values of the fractional order $\digamma$ and $\rho = 2$. This figure also shows the agreement of the numerical and exact solution when $\digamma = 1$. It is evident from Figure 2 that as $\digamma \rightarrow 1$, approximate solutions converge to the exact one.

Table 1 shows the maximum numerical error obtained from the GSFMLF method with a number of unknowns $n+m = 4+1$, $\digamma = 1$, and $\rho = 2$, compared to the error in ^[43] making use of the second kind Chebyshev polynomials (SKCP) method with a number of unknowns $m = 8$, as well as in ^[44] via the fractional-order Euler functions (FEFs) method with a number of unknowns $m = 8$. It is clear that the present method gives a very accurate solution compared to their solution.

Figure 3 presents the Logarithmic of absolute error with $\rho = 1.5, m = 3, n = 1$, and some values of fractional Mittag parameter $\alpha$. It is clear that $\alpha = 0.75$ gives the most accurate solution and any other values give less accuracy. The effects of the remaining Mittag parameters: $\beta$ is introduced in Figure 4(a) (where $\alpha = 0.75$ and $\gamma = 1.0$) and $\gamma$ in Figure 4(b) (here, $\alpha = 0.75$ and $\beta = 0.9$). We found that there is a small effect that tends to be negligible.

Example 6.2. We consider the nonlinear WSKFIDE, as follows:

The analytic solution is $O(t) = t^\rho$. This example is examined in ^[29,30,45] with $\rho = \frac{3}{2}$ and $\digamma = \frac{2}{3}$. Figure 5 represents the Logarithmic of absolute error for $m = 4, n = 1$, with some values of fractional Mittag parameter $\alpha$ (where $\beta = 0.9$ and $\gamma = 1$).

We report in Table 2 comparisons of the maximum numerical errors obtained by the present method with $m = 4, \; n = 1$, those in ^[29] by the wavelet-based technique (WBT) with $m = 4, \; n = 3$, the alternative Legendre polynomials operational matrix (ALPOM) method ^[30] with $m = 7$, and the modification of hat functions (MHFs) method ^[45] with $m = 64$.

Example 6.3. We consider the nonlinear WSKFIDE, as follows:

where $\Psi(t)$ is given such that the exact solution is $O(t) = t^\rho+\kappa\; t^\varrho$. This example is discussed in ^[29,30], with $\rho = 3, \kappa = 1$, and $\varrho = 4/3$. We display in Table 3 the numerical error obtained via our method with $\rho = 3/2, \; \kappa = 0, \; \digamma = 2/3, \; m = 4$, and $n = 1$. At the same data of the problem, Figure 6 includes absolute error for some values of fractional order $\digamma$.

For purpose of comparison, we present in Table 4 the maximum numerical errors obtained by the used method with $m = 4, n = 1$ and those obtained by the WBT method ^[29] with $m = 2, \; n = 3$, $\rho = 3, \; \kappa = 1, \; \digamma = 4/5$, and $\varrho = 4/3$.

We present in Figure 7 the approximate and exact solution of Example 6.3 for some values of the fractional Mittag parameter $\alpha$ at $\rho = 3, \kappa = 1$, and $\varrho = 4/3$.

7.   Conclusions

In this study, we have developed an efficient technique to obtain the appropriate solution for linear and nonlinear WSKFIDEs. The proposed approach combines two methods in order to get the approximate solution of the considered problems. Part of this technique is the GFSMLF, constructed in the same manner as wavelet approximations by a class of nonorthogonal functions. Precisely, the combination of the fractional MLF with the step function has provided more accurate solutions for WSKFIDEs. The second part is the OIFMM method. This implementation of the proposed method yields nonlinear algebraic equations, which we transformed into an optimization problem. In addition, we presented the error analysis of the proposed method in approximating any function, its fractional differentiation, and integration of the WSKFIDE. The efficiency and accuracy of our method was tested on three examples. We can summarize the following observations that resulted from the implementation of the proposed method:

● We impose R-LFI to remove the singularity of the problem.

● The proposed method obtained a very accurate solution compared to those obtained in ^[43,44,45] and ^[29,30], making use of a smaller number of unknowns (see Tables 1, 2 and 4).

● The fractional Mittag parameter $\alpha$ has a significant impact on the method's accuracy compared to the effect of $\beta$ and $\gamma$ (see Figure 3 (for $\alpha$ in Example 6.1), Figure 4 (for $\beta, \gamma$ in Example 6.1), and Figure 5 (for $\alpha$ in Example 6.2)).

● Formulating test problems to be dependent on fractional differentiation of order $\digamma$, introducing a large number of cases as in Figure 6 of Example 6.3. Indeed, each curve of this figure represents a different problem in which the proposed method is so accurate.

● The suggested method here can be used to solve other kinds of fractional differential equations and related problems such as systems of nonlinear FIDEs with weakly singular kernel.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflicts of interest in this paper.