Multi-modal feature selection with self-expression topological manifold for end-stage renal disease associated with mild cognitive impairment

1.   Introduction

In recent years, multi-modal neuroimaging techniques, such as functional magnetic resonance imaging (fMRI) ^[1], structural magnetic resonance imaging (sMRI) ^[2], arterial spin labeling (ASL) ^[3] and diffusion kurtosis imaging (DKI) ^[4], have been widely used in the diagnosis of brain diseases. Many studies have revealed that the combination of complementary information from multi-modal neuroimaging technology can improve the presentation capability and classification performance of mild cognitive impairment (MCI) ^[5,6,7]. Different brain image imaging methods can reflect the structural and functional features of the brain from different angles ^[8,9]. For example, fMRI depicts changes in deoxyhemoglobin on account of task-induced or spontaneous regulation of neural metabolism, while ASL perfusion MRI can quantitatively reflect the degree of ischemia by adopting arterial water as an endogenous tracer to measure cerebral blood flow (CBF) ^[10]. It is pointed out that ASL perfusion MRI provided a more direct quantitative correlation of neural activity than fMRI ^[11]. In contrast, ASL perfusion MRI exists shortcomings such as low temporal resolution and power deposition ^[12]. Literature ^[13] adopted the complementary features conveyed by fMRI and ASL in the MCI classification framework, in which the connectivity of the brain functional network reflected by fMRI was correlated with the CBF of the related network region reflected by ASL. In other words, combined analysis of fMRI and ASL features can more comprehensively select discriminative brain regions and improve classification performance.

End-stage renal disease (ESRD) is usually accompanied by temporary or permanent damage to the kidneys. Some studies have shown that ESRD patients suffer impairment to functions, such as attention, memory, executive function, language function and visuospatial function, after receiving hemodialysis (HD) treatment ^[14]. Cognitive impairments occur in about 30%–60% of patients undergoing HD treatment ^[15], among which roughly 8.3%–31.4% of individuals with MCI will develop dementia ^[16]. This has adverse implications for the ensuing cognitive training and rehabilitation treatment of patients with ESRD. Currently, the neuropathological mechanism of cognitive impairment in ESRD patients receiving HD is not clear, making it difficult to effectively identify ESRD patients with cognitive impairment. ASL provides a non-invasive method for measuring CBF, offering advantages in terms of accuracy and reproducibility. It is more suitable for clinical applications than other imaging technologies without requiring the use of radioactive substances ^[17]. Furthermore, ASL can visualize CBF levels, thereby facilitating a more comprehensive understanding of the changes in brain function among ESRDaMCI patients ^[18]. Combined with fMRI and ASL, quantitative and qualitative data analysis is helpful to improve the accuracy of the description of neural activity in the brain of ESRDaMCI patients, and reduce the misdiagnosis rate.

The effective selection of discriminative brain regions in multi-modal neuroimages plays a key role in the process of classifying ESRDaMCI patients ^[19,20,21]. Most of the multi-mode feature selection models simply spliced the single mode feature matrix in previous studies. Zhang et al. ^[22] utilized a multicore support vector machine (MKSVM) to classify MCI patients employing a kernel combination approach combined with three biomarkers. In contrast, multi-modal feature selection models have focused on capturing complementary information between features by constructing similarity models between multi-modal features as well as structured models in recent years. Jie et al. ^[23] proposed a streaming regularized multi-task feature learning method (M2TFS), which depends on group sparse regularizes to capture the intrinsic similarity between multiple modalities and construct a similarity matrix to fuse multi-modal features with complementary information. Shi et al. ^[24] developed a multi-modal feature selection method (ASMFS) based on adaptive similarity to classify Alzheimer's disease (AD) in patients. Compared with M2TFS, the similarity of ASMFS adaptively changes with the change of low-dimensional representation of feature vectors after feature selection. That is, the construction of similarity matrix and feature selection are alternately updated and carried out simultaneously.

The above adopt Euclidean distance to calculate the similarity of multimodal features, ignore the topological correlation between features, and do not capture the implicit data manifold. In this study, a self-expression topological manifolds based multi-modal feature selection method (SETMFS) is proposed to classify ESRDaMCI patients. First, a dynamic brain functional network is established according to fMRI, after which the betweenness centrality is extracted. The feature matrix of fMRI is constructed based on this centrality measure. Second, the feature matrix of ASL is constructed by extracting the CBF. Then, the topological relationship matrices are constructed by calculating the topological relationship between each data point in the two feature matrices to measure the intrinsic similarity between the features, respectively. Subsequently, the graph regularization method is utilized to embed the self-expression model into topological manifold learning to identify the linear self-expression of the features. Well-represented feature vectors are selected according to the proposed method and trained by a 10-fold cross validation and a multicore support vector machine to obtain classification results. Finally, the selected discriminative brain regions are obtained by ranking the brain regions according to the regression coefficient matrix.

The major contributions and novelty of this study are as follows. (a) The application status of ASL and fMRI imaging techniques is explored in the study of ESRDaMCI. Multi-modal feature matrices are constructed with ASL and fMRI to investigate the relationship between CBF and neural activity in the brain regions of patients with ESRDaMCI. (b) The study proposes a novel multi-modal feature selection method called SETMFS. Self-expression model and topological manifold learning are combined in a multi-modal feature selection model to explore the self-correlation and implied topological manifold between features. (c) The study identifies the discriminative brain regions of ESRDaMCI patients. Better scientific evidence is provided for the treatment and intervention of ESRDaMCI by analyzing and evaluating the changes and damage to these discriminative brain regions in ESRDaMCI patients.

2.   Materials and methods

2.1.   Research framework

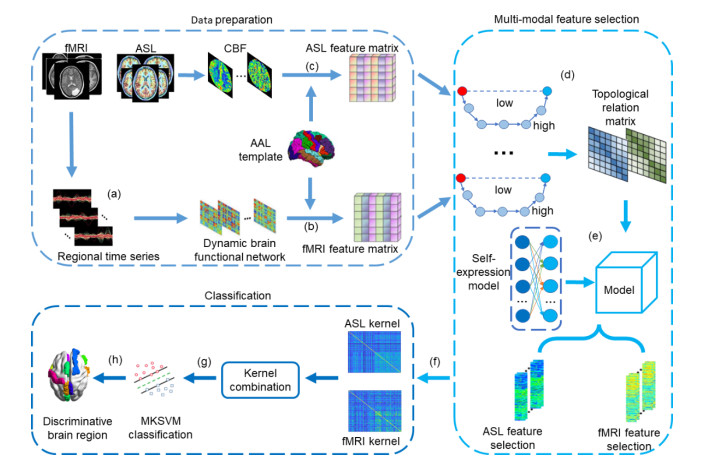
Figure 1 shows the research framework. It mainly consists of the following steps: (a) Extracting time series from fMRI data according to the automated anatomical labeling (AAL) template and constructing dynamic brain functional networks; (b) Extracting the betweenness centrality of the dynamic brain functional networks to construct feature matrices of fMRI; (c) Extracting the CBF of each brain region in ASL according to AAL template to construct the feature matrices of ASL; (d) Calculating the topological relationship between each data point within the two feature matrices and constructing a topological relationship matrix, respectively; (e) Embedding the self-expression model into the topological manifold learning, we obtain the final multi-modal feature selection model; (f) Selecting the well-represented feature vectors according to the proposed method and calculating their kernel matrices separately for linear fusion to obtain the new fused feature matrix; (g) Dividing the fused feature matrix into testing and training sets, training them by employing a 10-fold cross validation and MKSVM; (h) Visualizing discriminative brain regions based on the selected feature vectors and analyzing the discriminative brain regions of ESRDaMCI.

Figure 1.  The research framework.

DownLoad: Full-Size Img PowerPoint

2.2.   Data preparation

The participants include 44 ESRDaMCI patients diagnosed as MCI and 44 healthy volunteers from the Affiliated Changzhou No.2 People's Hospital of Nanjing Medical University. The study is approved and supervised by the Ethics Committee of the hospital. All participants voluntarily signed a written informed consent form.

The Montreal Cognitive Assessment Scale (MoCA) is a rapid screening assessment tool for MCI that measures cognitive domains including attention and concentration, executive function, language, memory and computational and orienting skills ^[25]. The total score of the scale is 30, and the normal value of the assessment result is greater than or equal to 26. The MoCA is more sensitive for screening MCI compared to other scales resulting from the factors such as patient completion and cooperation. It can well reflect the differences in cognitive function between ESRDaMCI patients and normal individuals. The mean MoCA score for the diagnosis of MCI in ESRDaMCI patients is 23.87 ± 4.51. Table 1 demonstrates the specific demographic information for ESRDaMCI patients and normal controls.

Table 1.  Demographic information.

	ESRDaMCI	Normal	P
Age ($\overline{x}\pm s$)	49.25 ± 11.15	46.25 ± 11.39	0.171a
Education years ($\overline{x}\pm s$)	9.58 ± 2.72	9.65 ± 2.59	0.916a
Gender (M/F)	24/20	13/31	0.086b
MoCA score ($\overline{x}\pm s$)	23.87 ± 4.51	26.63 ± 3.93	0.008a
Note: a: Two-sample two-tailed t test; b: Pearson chi-square test.

---

 | Show Table

DownLoad: CSV

ASL and fMRI scans are performed on all participants by means of the GE Discovery MR 750W 3.0T scanner. Participants are placed on the MRI equipment and positioning their head within the MRI coil. The head of the participants is fixed using rubber cork to avoid pseudo-images caused by head movements. T1-weighted brain structural images are acquired by adopting 3D brain volume imaging (3D-BRAVO) sequence. The machine scanning parameters are repetition time (TR) = 7.5 ms, echo time (TE) = 2.5 ms, reversal time = 450 ms, layer interval = 1 mm, flip angle (FA) = 15°, the field of view (FOV) = 240 mm × 240 mm, layer thickness = 1 mm, the number of scanning layers = 154 and the scanning time = 3 min 51 s.

ASL is scanned by employing 3D pseudo-continuous arterial spin labeling (3D-pcASL) sequence. The machine scanning parameters are TR = 5335 ms, TE = 10.7 ms, layer thickness = 4 mm, post-labeling delay (PLD) = 2525 ms, FOV = 240 mm × 240 mm, layer thickness = 4 mm, the number of scanning layers = 36 and the scanning time = 3 min 44 s. fMRI is scanned by employing gradient-echo plane echo imaging (GRE-EPI) sequence. The machine scanning parameters are TR = 2000 ms, TE = 40 ms, layer thickness = 4 mm, FA = 90°, FOV = 240 mm × 240 mm, matrix size = 64 × 64 and the scanning time = 8 min.

The ASL raw data are preprocessed by means of the Statistical Parametric Mapping (SPM12) and the Resting State Functional MRI Data Processing Toolbox (REST 1.8) within Matlab 2021a ^[26]. The main steps include the following: (a) Format conversion: Converting the disordered DICOM format files in the original ASL data into standard NIFTI format files for integrated processing in the SPM pipeline; (b) Image alignment: Aligning the CBF as the reference image and T1 as the source image by utilizing the normalized mutual information (NMI) method, to eliminate the possible image shift and rotation of structural and functional images; (c) Image segmentation: Segmenting the structured image T1 after the alignment by utilizing the Voxel-Based Morphometry (VBM) method and simultaneously generating the matrix rT1 for the transformation to the MNI standard space; (d) Normalization: Normalizing the CBF image to the spatial transformation matrix obtained from the segmentation to eliminate errors caused by direct mutual influence of local brain structures. (Bounding box: [-90, -126, -72; 90, 90,108], Voxel Size: [3 3 3]); (e) Smooth: Performing Gaussian kernel smoothing on the normalized CBF image to compensate for the spatial alignment errors in the standardization process as well as to improve the signal-to-noise ratio of the images. (FWHM: [5 5 5]); (f) CBF extraction: Performing feature extraction on the CBF images obtained from the smoothing process using the REST toolkit; Dividing the brain regions according to the AAL template and the CBF of 90 brain regions are extracted as features of ASL.

The fMRI raw data are preprocessed according to SPM12, the Resting State Data Processing Assistant (DPARSF) ^[27] and the Graph Theory Network Analysis (GreTna 2.0) toolkit within Matlab 2021a. The main steps include the following: (a) Time point removal: Removing the first 10 time points of each participant because of the high image noise in the first few time points; (b) Head motion correction: Normalizing the fMRI images to MNI space, and then standardizing them to reduce head movement changes in participants. (Bounding box: [-90, -126, -72; 90, 90,108], Voxel Size: [3 3 3]); (c) Smooth: Processing the normalized fMRI images to Gaussian kernel smoothing in order to enhance signal-to-noise ratio. (FWHM: [5 5 5]); (d) Band-pass filtering: Removing low-frequency drift and high-frequency noise from fMRI data and setting frequency range to 0.01~0.08 Hz; (e) Time series extraction: Dividing the brain regions according to the AAL template and extracting the time series of 90 brain regions; (f) Brain network construction: Constructing dynamic brain functional network by adopting Pearson correlation coefficient based on each participant's time series; (g) Betweenness centrality extraction: Calculating the topological properties of dynamic brain functional network by adopting the Gretna toolkit.

The features of different magnitudes are to be transformed into the same magnitude by the Z-Score method because the features of fMRI and ASL belong to different magnitudes. Uniformly measured using the calculated Z-Score values to ensure comparability between features. The standardized formula is ${h}_{i}^{\text{'}} = ({h}_{i}-\overline{{h}_{i}})/{\sigma }_{i}$, where $\overline{{h}_{i}}$ and ${\sigma }_{i}$ represent the mean and standard deviation of the i-th feature in the feature vector, respectively.

2.3.   Topological manifold learning

Define a similarity matrix $\boldsymbol{Z} = \left[{z}_{ij}\right]\in {\mathbb{R}}^{n\times n}$, which describes the intrinsic similarity relation of the feature matrix $\boldsymbol{X}\in {\mathbb{R}}^{d\times n}$, where n is the number of participants and d is the feature dimension. Literature ^[28] calculates the topological relationship between features by solving the following objective functions:

where i, j and k are the index of data, and I is the identity matrix; S represents the object relation topological matrix, ${s}_{ij}$ represents the topological correlation between feature i and j; ${||.||}_{F}$ represents the Frobenius norm of the matrix; $\alpha$ is the equilibrium parameter of Eq (1). In Eq (1), the first term is a smoothing constraint, which ensures that when features k and j are similar, both features k and j have a potential topological relationship with i. The second term is a reasonable constraint that prevents trivial solutions. The function of Eq (1) is to capture the topological relationship between features that are far apart if they have similar nearest neighbor connections.

Equation (1) is normalized to ensure that each feature is treated equally ^[29]:

where $\boldsymbol{D} = \left[{d}_{ij}\right]\in {\mathbb{R}}^{n\times n}$ is the degree matrix of Z.

2.4.   Multi-modal feature selection model

The new model for multi-modal feature selection is defined as follows by integrating topological manifold learning and multi-modal feature selection:

where ${y}_{i}$ is the label of the i-th participant; ${||.||}_{2}$ represents the ${l}_{2}$ norm of the matrix; M is the number of modes; $\boldsymbol{W} = [{\boldsymbol{w}}_{1}, {\boldsymbol{w}}_{2}, ..., {\boldsymbol{w}}_{M}]\in {\mathbb{R}}^{d\times M}$ is the regression coefficient matrix, ${\boldsymbol{w}}_{m}\in {\mathbb{R}}^{d}$ is the coefficient of the m-th mode; ${||.||}_{\mathrm{2, 1}}$ represents the ${l}_{\mathrm{2, 1}}$ norm of the matrix, thus realizing the sparsity of W and feature selection; $\alpha , \lambda$ is the parameter of equilibrium Eq (3).

2.5.   Multi-modal feature selection model based on self-expression topological manifold

Considering the potential autocorrelation between features, we embed the self-expression model into topological manifold learning. For a given feature matrix X, set each column to be a data point ${\boldsymbol{x}}_{j}\in {\mathbb{R}}^{d}$. In the process of finding linear self-expression of features, the self-expression model uses each data point ${\boldsymbol{x}}_{j}$ as a linear combination of other data points, namely:

where ${v}_{ij}$ is the element of the self-expression coefficient matrix $\boldsymbol{V}\in {\mathbb{R}}^{n\times n}$.

The local geometric structure of data can be examined through the implementation of graph regularization, self-expression model and topological manifold learning are also carried out simultaneously. On this basis, the multi-modal feature selection model of self-expression topological manifolds is formulated as follows:

where $\gamma$ is the self-adjusting parameter; ${\boldsymbol{L}}_{\boldsymbol{S}}$ is the Laplace matrix of S.

2.6.   Optimization algorithm

The iterative updating algorithm is adopted to solve the optimization problem of the four variables in Eq (5). The objective function of one variable is optimized while other variables are fixed. Table 2 shows the main process of solving Eq (5) by iterative updating algorithm.

Table 2.  Algorithm 1 summarizes the main process of solving Eq (5) by iterative updating algorithm.

Algorithm 1: Iterative update algorithm to solve the problem.

Input: Multi-modal feature matrix $\left\{{\boldsymbol{X}}^{1}, {\boldsymbol{X}}^{2}, ..., {\boldsymbol{X}}^{m}\right\}$; Label matrix $\left\{{y}_{1}, {y}_{2}, ..., {y}_{n}\right\}$. Initialization: $\alpha > 0$, $\lambda > 0$, $\gamma > 0$; Initialize Z of each mode with Eq (2) and initialize V of each mode with Eq (4). Repeat 20 times; 1). Update Z by Eq (6); 2). Update S by Eq (9); 3). Update W by Eq (13); 4). Update V by Eq (14); Until convergence; Output: W.

---

 | Show Table

DownLoad: CSV

Since different modes are independent, for a specific mode, the optimization problem of Z can be expressed as:

where ${h}_{ij}^{s} = {\left(\frac{{s}_{ki}}{\sqrt{{d}_{ii}^{m}}}-\frac{{s}_{kj}}{\sqrt{{d}_{jj}^{m}}}\right)}^{2}$.

The optimization problem of S can be expressed as:

where ${\boldsymbol{e}}_{i}$ is the i-th row vector of the identity matrix I; the j-th element of ${\boldsymbol{u}}_{i}$ is ${u}_{ij} = \gamma {||{\boldsymbol{v}}_{i}-{\boldsymbol{v}}_{j}||}_{2}^{2}$.

Let's define $\boldsymbol{A} = {\sum }_{m = 1}^{M}\left(\boldsymbol{I}-{\boldsymbol{D}}^{(m{)}^{-\frac{1}{2}}}{\boldsymbol{Z}}^{m}{\boldsymbol{D}}^{(m{)}^{-\frac{1}{2}}}\right)+\alpha \boldsymbol{I}$ and $\boldsymbol{B} = 2\alpha {\boldsymbol{e}}_{i}-{\boldsymbol{u}}_{i}$. Equation (7) can be expressed as:

Equation (8) is a quadratic convexity problem, which is solved by the classical augmented Lagrange multiplier method ^[30]. Specifically, Eq (8) can be solved by the following equation:

where p is the Lagrange multiplier.

The optimization problem of W can be expressed as:

Inspired by ^[31], we utilize weighted iterative method to solve Eq (10). Take the derivative with respect to ${||\boldsymbol{W}||}_{\mathrm{2, 1}}$ when the row element of W is non-zero:

where ${g}_{ii} = \frac{1}{2}{||{\boldsymbol{w}}_{i}, :||}_{2}^{-1}$.

It can be obtained from Eq (11) that:

where $\boldsymbol{G}\in {\mathbb{R}}^{d\times d}$ is a diagonal matrix whose i-th diagonal element is ${g}_{ii}$.

The derivative of W in Eq (12) is equivalent to taking the derivative in the following objectives when G is fixed:

The optimization problem of V can be expressed as:

3.   Results

3.1.   Classification performance

We employ a multicore support vector machine (MKSVM) to classify ESRDaMCI patients ^[22]. The multicore support vector machine linearly fuses kernel functions of different modalities based on the traditional support vector machine, and then trains a support vector machine classifier based on this kernel function.

We represent the classification performance of different multi-modal feature selection methods using accuracy (ACC), sensitivity (SEN), specificity (SPE), and area under the curve (AUC). A 10-fold cross validation is implemented for the lack of participants. Specifically, all participants are divided into 10 copies. Then each participant is taken in turn as the validation set, and the rest are taken as the training set to perform training and validation. The above process is repeated 10 times and averaged to reduce the multi-modal feature selection model contingency and improve the generalization ability.

The classification performance of the proposed method (SETMFS) is compared with those of 7 existing methods. Seven multi-modal classification methods using ASL-fMRI as the dataset are: (a) Linear kernel support vector machine (SVM) ^[32]; (b) Multicore support vector machine (MKSVM) ^[22]; (c) Streamwise regularized multi-task feature selection algorithm (M2TFS) ^[23]; (d) Discrete social learning particle swarm optimization algorithm (DSLPSO) ^[33]; (e) Multi-task feature selection algorithm with the introduction of hypergraphs (HMTFS) ^[34]; (f) Adaptive similarity multi-modal feature selection algorithm (ASMFS) ^[24]; (g) Hybrid deep neural networks (HDNN) ^[35]. Table 3 shows the classification performance of each method.

Table 3.  Classification performance of different methods.

Methods	ACC (%)	SEN (%)	SPE (%)	AUC
SVM	64.36 ± 0.1724	63.00 ± 0.2523	66.15 ± 0.2304	0.7039 ± 0.0018
MKSVM	72.21 ± 0.1295	63.95 ± 0.2144	80.30 ± 0.1977	0.7382 ± 0.0016
M2TFS	75.28 ± 0.1605	60.10 ± 0.2458	80.50 ± 0.2186	0.6965 ± 0.0020
DSLPSO	76.80 ± 0.1140	77.50 ± 0.1532	75.50 ± 0.2407	0.7325 ± 0.0012
HMTFS	77.74 ± 0.1429	65.75 ± 0.2402	76.10 ± 0.1935	0.7248 ± 0.0016
ASMFS	81.76 ± 0.1202	65.35 ± 0.2878	85.30 ± 0.1813	0.7242 ± 0.0020
HDNN	83.58 ± 0.0973	85.00 ± 0.1700	82.50 ± 0.1687	0.8257 ± 0.0015
SETMFS	86.10 ± 0.1068	81.70 ± 0.1908	88.60 ± 0.1414	0.8373 ± 0.0013

---

 | Show Table

DownLoad: CSV

In Table 3, the ACC, SEN, SPE and AUC of SETMFS reached 86.10 ± 0.1068%, 81.70 ± 0.1908%, 88.60 ± 0.1414% and 0.8373 ± 0.0013, respectively. Its classification performance is better than those of the other 7 methods. SVM achieved the lowest ACC among all the multi-modal classification methods. This is because it does not reduce the dimensionality of the feature matrix, but simply splices the feature matrices of the two modalities together and performs the classification directly. The noise and redundant features of the original data affect the classification performance, while MKSVM exploits the complementary information of different modalities to greatly improve the accuracy. Compared with MKSVM, M2TFS achieves an ACC of 75.28 ± 0.1605%, indicating that M2TFS fully captures the intrinsic similarity between different modalities and the geometric distribution information of the data. The ACC of DSLPSO reached 76.80 ± 0.1140%. DSLPSO can find a compact subset of high-dimensional features to improve ACC by learning the common features of sparse populations. HMTFS outperforms DSLPSO, indicating that HMTFS effectively discovers the higher-order relationships between features after the introduction of hypergraphs. ASMFS proposes adaptive similarity based on the fixed similarity adopted by M2TFS. ASMFS improves ACC by performing feature selection while constructing the similarity matrix and adaptively updating the extracted feature vectors with the similarity matrix. The ACC of HDNN based on a deep learning model reached 83.58 ± 0.0973%. It is shown that HDNN effectively combines the advantages of a convolutional neural network and LSTM (long short-term memory) to effectively process global feature structure information and the dependency between features. In addition, the classification performance of SETMFS outperforms those of the above-mentioned methods, indicating that the use of topological manifolds to calculate the similarity between data points within the feature matrix is superior to the conventional use of Euclidean distance as a similarity measure. The topological correlation between the multi-modal features is fully considered. It is also shown that the topological flow form learning with joint self-expression model can effectively discover the potential autocorrelation among features and improve the classification performance.

The classification performance of 8 methods for ESRDaMCI is shown more graphically using bar graphs as in Figure 2.

Figure 2.  Classification performance of different methods.

DownLoad: Full-Size Img PowerPoint

3.2.   Parameter sensitivity analysis

The selection of parameters will directly affect the performance of ESRDaMCI classification, so different regularization parameter settings are sensitive to the multi-mode feature selection model. As mentioned above γ is a self-adjusting parameter that can be adjusted in a heuristic way. Therefore, it is only necessary to explore the effect of different parameter combinations of the group sparse regularization parameter $\lambda$ as well as the topological manifold learning regularization parameter $\alpha$ on the classification performance. Thus, reducing the time complexity of SETMFS. The above parameters are determined based on the 10-fold cross validation results for all participants. Figure 3 shows the classification results of $\alpha$ and $\lambda$, where the values of $\alpha$ and $\lambda$ range from [0.05, 0.1, 0.5, 1, 2, 5, 10]. From the figure, the classification performance of the multi-modal feature selection model is relatively stable under different settings of the regularization parameters, which illustrates the robustness of the proposed method. However, the appropriate combination of $\alpha$ and $\lambda$ helps to improve the classification performance. The ACC reaches the highest value (86.10%) when $\alpha = 1$ and $\lambda = 1$. As above, the regularization parameters $\alpha = 1$, $\lambda = 1$ are utilized to construct a multi-modal feature selection model.

Figure 3.  Classification accuracy of different regularization parameter combinations.

DownLoad: Full-Size Img PowerPoint

3.3.   Discriminative brain regions

The brain regions corresponding to the top 15 feature nodes are further statistically obtained by ranking the discriminative ability of each brain region based on the regression coefficient matrix W. The Brain Net Viewer toolbox (https://www.nitrc.org/projects/bnv/) is employed to map to the ICBMl52 template space to visualize the selected discriminative brain regions, to better discuss the extent of the effect of ESRDaMCI on brain regions, as shown in Figure 4.

Figure 4.  Discriminative brain regions.

DownLoad: Full-Size Img PowerPoint

The top 15 most discriminative brain regions are determined by conducting a classification analysis of the ESRDaMCI patient group and normal group, with a significant portion being located in the temporal lobe, frontal lobe, occipital lobe and parietal lobe. The temporal lobe regions mainly included the left hippocampus (Hippocampus_L), left superior temporal gyrus (Temporal_Sup_L), right hippocampus (Hippocampus_R), left parahippocampal gyrus (ParaHippocampal_L) and right parahippocampal gyrus (ParaHippocampal_R). The temporal lobe is closely related to the verbal receptivity and visual memory capacity of ESRDaMCI patients ^[36]. The left hippocampus (Hippocampus_L) and right hippocampus (Hippocampus_R) are important organs of the brain involved in short-term memory and orientation, and damage to both causes a decrease in memory storage function ^[37]. Damage to the left parahippocampal gyrus (ParaHippocampal_L) and the right parahippocampal gyrus (ParaHippocampal_R), in turn, leads to impaired spatial memory storage and retrieval in patients ^[38,39]. The frontal regions mainly include the right inferior orbital frontal gyrus (Frontal_Inf_Orb_R), the right dorsolateral superior frontal gyrus (Frontal_Sup_R) and the right rolandic operculum (Rolandic_Oper_R). If these brain regions are damaged, it can lead to decreased decision-making, self-control and cognitive abilities in patients. Occipital lobe lesions and damage to the visual centers can cause visual cognitive impairment, memory impairment and motor perception impairment ^[40]. The parietal lobe contains the use center and the visual center. Parietal lobe lesions can cause problems such as quadrant blindness and inability to use power. The selected occipital and parietal discriminative brain regions mainly include the left cuneus (Cuneus_L), left postcentral gyrus (Postcentral_L), left precuneus (Precuneus_L) and right precuneus (Precuneus_R).

Notably, among the selected discriminative brain regions include the left hippocampus (Hippocampus_L), left parahippocampal gyrus (ParaHippocampal_L) and left cuneus (Cuneus_L)), all of which belong to the default network (DMN) in the core network of cognitive function pathological features. The DMN is important for understanding the early recognition markers of cognitive dysfunction. The above results indicate that the proposed method can provide discriminative brain regions for the classification of ESRDaMCI patients, which is valuable for clinical reference.

3.4.   Algorithm convergence

This section aims to investigate the convergence of SETMFS on the ESRDaMCI dataset. Figure 5 shows the change of the objective function value of Eq (5) during iterations. Through study, we find that the algorithm gradually approaches the global optimum through repeated iterations. After approximately 10 iterations, the algorithm basically converges. In addition, SETMFS has an average training time of 4.241 s on Intel(R) Core (TM) i5-7300HQ CPU @2.50 GHz MATLAB R2021a after 10 runs.

Figure 5.  Algorithm convergence of SETMFS.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

In recent years, concomitant diseases associated with MCI have received increasing attention, and the classification of such concomitant diseases remains a challenge. With the development of multiple brain image acquisition techniques, the diagnosis of ESRDaMCI has been assisted. Multi-modal machine learning is an important tool for classifying multi-modal data. Conversely, the small number of participants and high feature dimensionality of multi-modal classification methods have been limiting the improvement of classification accuracy. Many methods on multi-modal brain image feature selection have been proposed and applied to MCI classification ^{[41,42,43,44]}. These methods mostly include the measure of similarity between features and the relation between feature similarity and multi-modal feature selection models. They do not consider the data manifolds implied between features and ignore the low-dimensional manifold structures between different modes or different features of the same mode.

We develop SETMFS to select discriminative brain regions for ESRD-aMCI patients based on multi-modal ASL-fMRI raw data to this end. We extract the betweenness centrality of fMRI and the CBF of ASL as features to construct the feature matrices. The topological relationship matrices are constructed to capture the topological correlation between the features by calculating the topological relationship between each data point within the two feature matrices. Next, the self-expression model is embedded in topological manifold learning to find the linear self-expression of features, and then construct a multi-modal feature selection model. Finally, the discriminative brain regions are selected based on the proposed method and applied for identifying ESRD-aMCI patients. Compared to previous studies ^[24], SETMFS discards the traditional use of Euclidean distance to capture the similarity between features and instead uses a more suitable topological manifold learning to mine the low-dimensional manifold structure between features. Specifically, the predefined similarity in the previous similarity matrix construction method is biased towards neighboring nodes and ignores data points that are far apart within the feature matrix. Since the raw data collected in the real world are usually of nonlinear stream shape, if these data points with low spatial similarity are connected by neighbors, they may exhibit high intrinsic similarity. Therefore, SETMFS calculates the intrinsic similarity by learning the topological relationships between features. Propagating the topological manifold connections of features from near to far and mining the potential relation between different features.

It is worth noting that ASL-fMRI is utilized as the brain imaging data for the participants in this study. The combination of brain functional connectivity and quantitative indicators of CBF in related brain regions can ensure adequate temporal resolution and temporal stability, and improve classification performance. The feature matrices of both modalities are extracted progressively from the original images and each feature node represents a different brain region. The loss function essentially selects the feature node with better recognition of brain regions to complete the classification by calculating the regression coefficient for each brain region in the process of selecting discriminative features. As a result, this method improves the interpretability of the multi-modal feature selection model. However, ASL-fMRI ignores the effect of structural connectivity on brain networks. The literature ^[45,46,47] indicated that points out that if there are more stable structural connections between regions of interest in the brain, there will be stronger functional connectivity. In future work, the classification performance can be improved by introducing brain imaging data, such as DKI in combination with ASL-fMRI, to reveal the structural connectivity of brain network. In addition, the sample size of the dataset is limited in this study. Therefore, it is necessary to expand the sample size to improve the generalization ability of the multi-modal feature selection model in the follow-up work.

As for the experimental results, the proposed method demonstrates good superiority for classification of ESRDaMCI patients and has some clinical significance. Moreover, SETMFS can also identify brain regions of high clinical relevance in selected discriminative brain regions of ESRDaMCI patients. Nevertheless, the proposed method also needs some improvements. The brain functional network construction method can be optimized using some methods, such as dynamic hypergraph popular regularization ^[48,49], to construct feature matrices from extracting more accurate topological attributes. The similar graph Z constructed in SETMFS belongs to a predefined and fixed type of graph, which may have adverse effects on subsequent feature selection. In the following work, adaptive learning can be combined to explore the topological correlation between features in multiple sets of adaptive graphs. In addition, we plan to approximate the topology relationship matrix with different confidence levels by learning the consensus matrix in the next stage. Then, a hypergraph based on the consensus matrix can be constructed to explore the high-order connectivity between features. Finally, deep learning knowledge such as convolutional neural network, recurrent neural network and deep autoencoder can be combined into the multi-modal feature selection model in the following work ^[50,51,52]. Thus, efficient feature extraction and dimensionality reduction can be achieved.

5.   Conclusions

In summary, a self-expression topological manifold based multi-modal feature selection method (SETMFS) is proposed. We extract the betweenness centrality of fMRI and the CBF of ASL as features to construct the feature matrices. The topological relationship matrices are constructed to capture the underlying data manifold between the features by calculating the topological relationship between each data point within the two feature matrices. Then, the graph regularization method is employed to embed the self-expression model in topological manifold learning to find the linear self-expression of features, remove redundant features and improve classification performance. Well-represented feature vectors are selected according to the proposed method and trained by a 10-fold cross validation and a multicore support vector machine to obtain classification results. Better performance is demonstrated on the real ESRDaMCI dataset, with ACC, SEN, SPE and AUC reaching 86.10%, 81.70%, 88.60% and 0.8373, respectively. Furthermore, the discriminative brain regions identified according to the regression coefficient matrix better reflected the pathological mechanisms of ESRDaMCI patients. The superiority of SETMFS is also demonstrated in the effective recognition of discriminative features in the ASL-fMRI brain network.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by National Natural Science Foundation of China (grant No. 51877013), and Jiangsu Provincial Key Research and Development Program (grant No. BE2021636). This work was also sponsored by Qing Lan Project of Jiangsu Province.

Conflict of interest

The authors declare there is no conflict of interest.