In this study, we consider the analysis of monotonicity for the Riemann-Liouville fractional differences of sequential type. The results are defined on the subsets of (0,1)×(0,1) with a certain restriction. By analysing the difference operator in the point-wise form into a delta form, we use the standard sequential formulas as stated in Theorems 2.1 and 2.2 to establish the positivity of the delta difference operator of the proposed the discrete sequential operators. Finally, some numerical experiments are conducted which confirm our theoretical monotonicity results.
Citation: Pshtiwan Othman Mohammed, Musawa Yahya Almusawa. On analysing discrete sequential operators of fractional order and their monotonicity results[J]. AIMS Mathematics, 2023, 8(6): 12872-12888. doi: 10.3934/math.2023649
| [1] | Natalie M. Linton, Sung-mok Jung, Hiroshi Nishiura . Not all fun and games: Potential incidence of SARS-CoV-2 infections during the Tokyo 2020 Olympic Games. Mathematical Biosciences and Engineering, 2021, 18(6): 9685-9696. doi: 10.3934/mbe.2021474 |
| [2] | Andrea Guazzini, Enrico Imbimbo, Federica Stefanelli, Franco Bagnoli, Ezio Venturino . Quantifying fairness to overcome selfishness: A behavioural model to describe the evolution and stabilization of inter-group bias using the Ultimatum Game. Mathematical Biosciences and Engineering, 2019, 16(5): 3718-3733. doi: 10.3934/mbe.2019184 |
| [3] | S. J. Gutowska, K. A. Hoffman, K. F. Gurski . The effect of PrEP uptake and adherence on the spread of HIV in the presence of casual and long-term partnerships. Mathematical Biosciences and Engineering, 2022, 19(12): 11903-11934. doi: 10.3934/mbe.2022555 |
| [4] | Lin Zhao, Haifeng Huo . Spatial propagation for a reaction-diffusion SI epidemic model with vertical transmission. Mathematical Biosciences and Engineering, 2021, 18(5): 6012-6033. doi: 10.3934/mbe.2021301 |
| [5] | Yuanyuan Huang, Yiping Hao, Min Wang, Wen Zhou, Zhijun Wu . Optimality and stability of symmetric evolutionary games with applications in genetic selection. Mathematical Biosciences and Engineering, 2015, 12(3): 503-523. doi: 10.3934/mbe.2015.12.503 |
| [6] | Huan Zhao, Xi Chen . Study on knowledge cooperation of interdisciplinary research team based on evolutionary game theory. Mathematical Biosciences and Engineering, 2023, 20(5): 8782-8799. doi: 10.3934/mbe.2023386 |
| [7] | Anthony Morciglio, R. K. P. Zia, James M. Hyman, Yi Jiang . Understanding the oscillations of an epidemic due to vaccine hesitancy. Mathematical Biosciences and Engineering, 2024, 21(8): 6829-6846. doi: 10.3934/mbe.2024299 |
| [8] | Rhiannon Loster, Sarah Smook, Lia Humphrey, David Lyver, Zahra Mohammadi, Edward W. Thommes, Monica G. Cojocaru . Behaviour quantification of public health policy adoption - the case of non-pharmaceutical measures during COVID-19. Mathematical Biosciences and Engineering, 2025, 22(4): 920-942. doi: 10.3934/mbe.2025033 |
| [9] | Khalid Hattaf, Noura Yousfi . Dynamics of SARS-CoV-2 infection model with two modes of transmission and immune response. Mathematical Biosciences and Engineering, 2020, 17(5): 5326-5340. doi: 10.3934/mbe.2020288 |
| [10] | Notice Ringa, Chris T. Bauch . Spatially-implicit modelling of disease-behaviour interactions in the context of non-pharmaceutical interventions. Mathematical Biosciences and Engineering, 2018, 15(2): 461-483. doi: 10.3934/mbe.2018021 |
In this study, we consider the analysis of monotonicity for the Riemann-Liouville fractional differences of sequential type. The results are defined on the subsets of (0,1)×(0,1) with a certain restriction. By analysing the difference operator in the point-wise form into a delta form, we use the standard sequential formulas as stated in Theorems 2.1 and 2.2 to establish the positivity of the delta difference operator of the proposed the discrete sequential operators. Finally, some numerical experiments are conducted which confirm our theoretical monotonicity results.
Soil nutrients are the basic substances required for soil to play its function, which is not only the basis of soil fertility and plant growth, but also closely related to the agricultural ecosystem and sustainable development. Human activities and climate change lead to significant changes in soil function [1,2,3,4]; when the speed of change is much greater than the running speed of the soil nutrients cycling mechanism, the content of soil nutrients will begin to fluctuate. It may manifest as gains/losses in soil fertility and a decline in soil productivity, thus affecting the sustainability of agricultural production, the balance of ecosystem and the healthy development of human society and economy [5,6,7,8]. This, it can be seen that under the background of intensified human activities and climate change, the adaptability and reaction extent of soil nutrients, as well as the content gain and loss change of soil nutrients, are the contents that need to be urgently studied.
Human activities have a profound impact on the soil. The use and management of cultivated land are the most important and direct activities for human beings to utilize and transform soil and to intervene in soil ecosystem with consciousness and purpose [9,10]. The use and management of cultivated land have a bidirectional influence on the occurrence and development of soil; the reasonable cultivated use of land and the intensity can make the soil develop towards a benign direction and improve the content of soil nutrients on the original basis, while excessive and unreasonable cultivated use of land and the intensity will cause soil degradation [11,12,13,14]. However, traditional studies mostly analyzed the impact of human activities on soil nutrients from a certain aspect or a single dimension [15,16,17], and lacked the research revealing the response of soil nutrients to human cultivated land use activities from a systematic perspective.
Water and heat are often exchanged between the soil and the atmosphere. The climate directly affects the water and heat of soil, the migration and conversion process of minerals and the nutrients within soil and determines the direction and intensity of soil formation. Among the climatic factors, air temperature and precipitation have the most universal meaning for soil formation. Currently, research on the response of soil nutrients to climate change mainly focuses on a quantitative analysis of the direct or indirect relationship between climate factors and soil nutrients [18,19], and the level of soil nutrients under the background of different land use types or regional climate [20,21,22]. In the meantime, the regions involved in these studies are mainly located within semi-humid/humid regions; additionally, these regions lack continuous, long-term and large-scale attention from researchers. Some studies show that the warming trend in arid regions is significantly higher than that of humid regions; a similar rise in temperature in arid regions may have a greater impact on the natural environment and socioeconomic systems.
The existing research on the response of soil nutrients to human activities and climate factors utilizes quantitative analyses to measure the response or correlativity between them in a fixed time-space dimension and evaluate the content of soil nutrients, while the soil nutrient composition changes alongside the dynamic changes of human activities and climate factors. At the same time, the response of soil nutrients to human activities and climate change under the large-scale time-space background has regional differences, and there are some studies that quantitatively evaluated such differences, which can lead to either an increase or loss of soil nutrients.
Xinjiang is located in the arid region of northwest China within the hinterland of Asia. It is one of the most sensitive regions affected by global climate change, and the contradiction of water resources shortage is prominent. The development of modern agriculture is mainly guided by agricultural mechanization and the efficient utilization of integrated water and fertilizer. Within the climatic environment characterized by drought and the suitable agricultural cultivation mode, it is important to study the response degree of soil nutrients to human activities and climate change and either the content gain or loss of soil nutrients for the protection of agricultural system, the improvement of soil ecosystem's ability in arid regions to cope with climate change, the promotion of the sustainable development of ecological safety and social economy in arid regions, and the formation of a coping strategy for an oasis cultivated land system in the context of future climate change.
In conclusion, there are fewer studies to discuss the response degree of soil nutrients and its spatial pattern in the context of human activities and climate dynamic changes, as well as the content gain or loss of soil nutrients in differentially response regions. Therefore, two research hypotheses are proposed in this paper: soil nutrients are sensitive to LUI and climate; and LUI and climate change cause changes in soil nutrient content.
Taking Xinjiang, which is the most typical and largest arid region in China, as an example, this study establishes the LUI dataset, climate dataset and soil nutrients database based on the "Input-Output-System"; this system uses a multi-factor comprehensive evaluation method, liner regression equation and ordinary Kriging interpolation method to comprehensively reflect the cultivated land use activities by human beings, studies the changes of LUI, climate and soil nutrients in Xinjiang, China and produces thematic maps. On this basis, the sensitivity analysis method is used to quantitatively analyze the sensitivity and spatial pattern of soil nutrients in oasis cultivated land using LUI and climate change datasets. Finally, the content gain and loss change and range in differentially sensitive regions are compared and analyzed, and the process and technical methods for soil nutrients maintenance and restoration in arid regions are put forward.
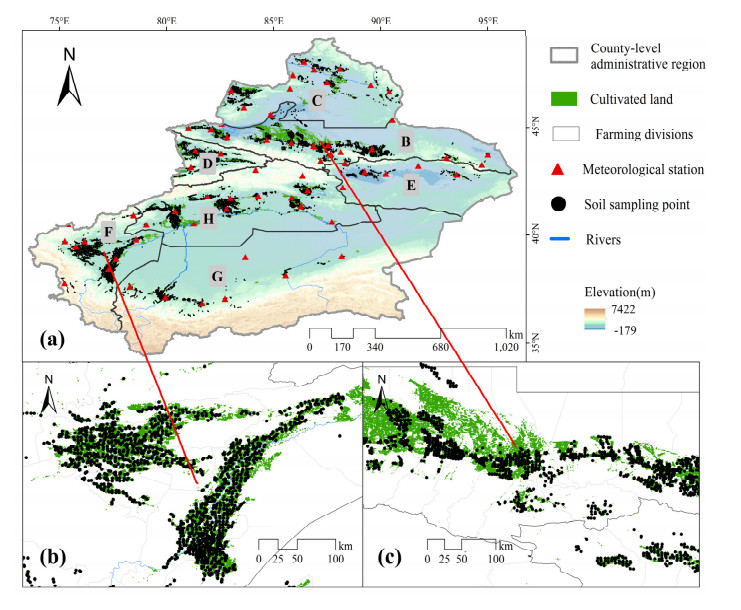
Xinjiang is located within the arid region of China and Mongolia in the hinterland of Eurasian continent, with geoFigureical coordinates from 73°40′E to 96°18′E and from 34°25′N to 48°10′N. In this region, mountains and basins are alternately arranged, thereby forming a unique topoFigurey of "Three Mountains and Two Basins" (Figure 1). This region belongs to a typical temperate continental climate, with climate features of strong continentality, dry and little rainfall, uneven distribution of temperature and precipitation and abundant light and heat resources; the area of the cultivated land is about 5,242,270 hm2, of which the area of water-saving irrigation is about 2,916,150 hm2. Wheat, maize and cotton are mainly planted, and, to date, the comprehensive mechanization of the main crops within the whole region has reached 85%; the soil types are mainly aeolian sandy soil, gray desert soil, brown desert soil and brown calcium soil. According to the second general survey of soil nutrients in China, rapidly available potassium is relatively rich in soil nutrients, with other nutrients in either a medium or deficient state.
In line with the Regulation for Gradation on Agricultural Land Quality in China and differences in the natural environment, socioeconomic conditions and crops types, structures and maturation between regions [23], this study divides the distribution space of cultivated land in Xinjiang (A) into seven farming divisions, including the southern area of Junggar Basin (B), the northern area of Junggar Basin (C), the Ili Valley area (D), the Tuha Basin (Turpan Basin and Hami Basin) (E), the western area of Tarim Basin (F), the southern area of Tarim Basin (G) and the northern area of Tarim Basin (H) (Figure 1).
The remote sensing monitoring data of land use is derived from the Resource and Environment Data Center of Chinese Academy of Sciences (https://www.resdc.cn/). In this study, data on land use, management, and agricultural production is derived from the Xinjiang Statistical Yearbook (2010–2020).
The climate data is derived from the common dataset of the National Meteorological Science Data Center at 66 meteorological stations in Xinjiang (Figure 1), which was observed day by day from 1960 to 2019; this study mainly uses the temperature and precipitation data. First, the processing of climate data is to make a statistical summary of the daily observation data to obtain yearly data; then, the Arcgis software (Version 10.2) geostatistical analysis tool is used to conduct an ordinary Kriging interpolation in combination with the elevation of meteorological stations. Second, taking the simulated climate spatial distribution map as the base map, the fishnet creation tool within Arcgis is used to establish a fishnet map with a rank of 500 × 650, and the extraction point tool of value is used to extract the climate value. Finally, the obtained climate data in the county is processed through the identification, screening and summery statistical tools within Arcgis.
The soil nutrient data are derived from two datasets: the evaluation of cultivated land fertility and monitoring the cultivated land quality. From May to October in 2008–2009 and 2017–2019, soil sampling was carried out within the plough layer (0–30cm) throughout Xinjiang, collecting 7,241 and 7,244 samples, respectively (Figure 1). The sampling points were laid out based on the county, where the ArcGIS software was used to superimpose the cultivated land resource map and soil type map to produce the sampling base map. Considering the factors such as the number of cultivated land map spots, area, crops and yield level, as well as the uniformity of the sampling points in the spatial distribution, the sampling points were evenly arranged on the cultivated land plots to ensure that each plot had sampling points, and the number of sampling points increased within the larger cultivated land plots. During the collection of soil samples, the sampling points were laid out on the sampling base map and taken as the guide to collect soil samples by use of GPS positioning; 2–10 mu of representative plots were selected from 300–500 mu of strip fields to mix a soil sample with 15–20 points, and the protection forest, road, use of agricultural film and natural environment around the cultivated land was recorded. The collected soil samples were taken back to the laboratory for air drying, impurity removal, grinding and screening, and about 20g of samples was utilized for fine grinding with a frozen mixing ball mill. The content of the soil nutrients was determined with the following methods: (1) the total soil nitrogen level by the Kjeldahl distillation method; (2) the available soil phosphorus level by the sodium bicarbonate digestion-anti colorimetry method of molybdenum antimony; (3) the rapid available soil potassium level by the ammonium acetate digestion-flame photometer method; and (4) the total soil organic matter by the oil bath heating potassium dichromate oxidation capacity method.
The comprehensive measurement of the LUI establishes a dataset based on the input-output-system while considering different aspects and levels. Therefore, this study utilizes a LUI dataset from 10 aspects of land use type, management and agricultural production, and divides the LUI measurement into three dimensions: input, output and system. Among them, the input dimension refers to the LUI of different inputs, such as chemical fertilizer and irrigation; the output dimension refers to the ratio between the agricultural production output and the cultivated area, such as per unit area yield of grain; and the system dimension refers to the relationship between the production input and the output based on the cultivated land and the whole system, such as yield gap. See S1, the Supplementary Information Table for the specific information of the LUI dataset.
The multi-factor comprehensive evaluation method can transform the indices of the three aforementioned dimensions into one index [24], which can comprehensively reflect the LUI; its calculation formula is as follows:
| LUI=n∑i=1Xi×wi | (1) |
where Xi is the standardized value of the ith index, which is calculated by the extreme value standardization method, wi is the weight of the ith index, which is determined by the entroy weight method (S2, Supplementary Information Table), and n is the index number within the dataset.
The climate tendency rate can reflect the variation trend of climate factors. A regression analysis can establish the specific quantitative relationship between regional climate factors and the time series, thus expressing the climate tendency rate. It is assumed that a certain climate factor is a dependent variable X, which is affected by the independent variable t of the time series, there are n observation values (X1, X2, ,, Xn) and time series values are (t1, t2, ,, tn). Then, their unary linear regression equation is as follows:
| Xn=atn+b | (2) |
where Xn is the fitted value of meteorological factors, tn is the time series, and the regression coefficient a and the constant term b are calculated using the least square method, where a×10 usually represents the tendency rate of climate factors.
The conspicuousness of the variation trend of climate factors is judged by the Mann Kendall test method [25] (S3, Supplementary Information Table).
The ordinary Kriging method is used to make a spatial interpolation for the climate factors and soil nutrients. The precondition of the ordinary Kriging interpolation is that the index data shows a normal distribution. In this study, the data of the temperature is in line with a normal distribution, and that of the precipitation and soil nutrients are necessary to make a logarithmic conversion to conform to the law of normal distribution. The Arcgis software was used to highlight the logarithmic conversion of the index data.
The variations of temperature and precipitation usually abide by the law of vertical zonal differentiation, which are related to the elevation of meteorological stations; therefore, it is necessary to incorporate the elevation collaborative interpolation of meteorological stations when using the ordinary Kriging method to simulate spatial distribution. The GS+ (Version 9.0) software was used to screen the spatial interpolation model of the soil nutrients; the larger the determination coefficient (R2), the smaller the quadratic sum of residuals (RSS). The available phosphorus, the rapid available potassium and organic matter conform to the index model, and the total nitrogen conformed to the spherical model, and the specific information is shown in S4, Supplementary Information Table.
A sensitivity analysis is widely used in climatological studies and economic analyses (elasticity). This is a method that can measure the sensitivity between regional environmental factors without regard to the unit of measurement, and is defined as the ratio of the change rate of one factor to that of another factor in form [26]. A sensitivity analysis was used to measure the sensitivity of the total nitrogen, available phosphorus, rapid available potassium and organic matter in cultivated soil nutrients to the regional LUI and variations of temperature and precipitation. The formula is as follows:
| Sx=limx→0Δn0/n0Δx/x=∂n0∂x×xn0 | (3) |
where n0 is the soil nutrients (total nitrogen, available phosphorus, rapid available potassium and organic matter), x is either the LUI, temperature or precipitation, and Sx is the sensitivity coefficient of the soil nutrients to the LUI, temperature and precipitation. A positive sensitivity coefficient indicates that the soil nutrients will increase with an increase of the LUI, temperature and precipitation. A negative sensitivity coefficient indicates that the soil nutrients will decrease with a decrease of the LUI, temperature and precipitation. The greater the absolute value of the sensitivity coefficient, the greater the impact of the LUI and climate change on the soil nutrients.
The classification of the sensitivity coefficient refers to the classification system established by Lenhart [27] (S5, Supplementary Information Table).
In this study, the LUI measurements were made on a county basis, while the spatial presentation of the soil nutrients and climate data was formed by spatial modeling using the ordinary kriging method. In order to improve the robustness of the calculation of the soil nutrient sensitivity to the LUI and climate change, soil nutrient and climate data were extracted on a county basis using the "Extract by Mask Tool" in ArcGIS. The results of the soil nutrient sensitivity calculations to the LUI and climate change are shown in Figures 2, 3 and 4.
From 2009 to 2019, the LUI of Xinjiang slightly increased from 0.111 to 0.158. The changes in the LUI for the seven farming sub-regions were significantly different. Excluding the Tuha Basin, which decreased slightly, the other sub-cultivation sub-regions increased in different magnitudes; the spatial variation of the LUI was heterogeneous. In essence, the growth rate presents a large spatial pattern in southern Xinjiang and a small spatial pattern in northern Xinjiang (S1a, S2a, 2b and 2c, Supplementary Information Figure).
The overall trend of temperature and precipitation in Xinjiang from 1960 to 2019 shows a more significant increase in amplitude (temperature tendency rate = 0.332 ℃/10a, precipitation tendency rate = 15.401 mm/10a). Among them, the amplitudes of temperature and precipitation from 2009 to 2019 are more significant (temperature tendency rate = 1.086℃/10a, precipitation tendency rate = −11.924 mm/10a) (S1, Supplementary Information Figure). In terms of spatial variation, the temperature shows a rising trend from southeast to northwest (S2d, 2e and 2f, Supplementary Information Figure). The precipitation is bounded by the Tianshan Mountains, which shows an increasing in the south and a decreasing trend in the north (S2g, 2h and 2i, Supplementary Information Figure).
The average values of the sensitivity coefficient of the total nitrogen, available phosphorus, rapid available potassium and organic matter are 0.319, 0.344, 0.435 and 3.322, respectively, the proportions of counties exceeding the average value are 25%, 23%, 26% and 22%, respectively, and that with a high grade of sensitivity are 41%, 40%, 39% and 78%, respectively.
Excluding the organic matter, there are prominent spatial differences in the sensitivity coefficients of the total nitrogen, available phosphorus and rapid available potassium (Figure 2). Among them, the sensitive regions above the high grade of total nitrogen, available phosphorus and rapid available potassium are mainly distributed in the northern, western and eastern parts of the Junggar Basin, and counties and cities within the Tuha Basin and southern part of Tarim Basin. The sensitive regions below medium grade are mainly distributed in the northern and southern regions of the Tianshan Mountain, Ili River Valley and Aksu River Basin (Figure 2a, 2b and 2c); the sensitivity areas with high grade of organic matter are essentially distributed throughout the entire region of Xinjiang (Figure 2d).
The results show that the organic matter of the soil was extremely sensitive to a change of the LUI, which has the greatest impact and the widest coverage. The total nitrogen, available phosphorus and rapid available potassium were more sensitive to a change of the LUI, of which the overall spatial distribution is scattered with concentrated regions.
The mean values of the sensitivity coefficients of the total nitrogen, effective phosphorus, quick-acting potassium and organic matter to temperature were 2.041, 1.517, 1.861 and 9.578, respectively, the proportion of counties and municipalities exceeding the mean values were 24%, 30%, 26% and 31%, respectively, and the proportion of counties and municipalities with a high level of sensitivity and above were 77%, 78%, 73% and 94%, respectively. In terms of spatial distribution, the areas with a soil nutrient sensitivity to high grade temperatures and above were generally distributed within Xinjiang, and the areas of medium grade temperatures and below were distributed within the northern and southern slopes of the Tianshan Mountain and the western part of the Tarim Basin (Figs. 7a, 7c, 7e, and 7g); specifically, the sensitivity coefficients of most areas within Xinjiang were more than 0.20, which indicated that the soil nutrients were extremely sensitive to the temperature changes. Among them, in most counties and cities in Xinjiang, the sensitivity coefficients of the total nitrogen and organic matter to climate were more than 1, which were basically in an extremely sensitive state. The sensitivity of the effective phosphorus and quick-acting potassium to temperature was slightly lower, which was due to the spatial heterogeneity of the temperature change, resulting in greater variability in the spatial distribution of the effective phosphorus and quick-acting potassium to temperature. The arid climatic environment of the region lead to a greater impact of temperature change on the ecosystem, and temperature is an important factor in determining the deepening or slowing down of the arid climatic environment; the conduction effect of the temperature change will lead to a change of the soil physicochemical properties, and the soil nutrients will be affected by a more significant impact.
The mean values of the sensitivity coefficients of the total nitrogen, effective phosphorus, quick-acting potassium and organic matter to precipitation were 0.261, 0.274, 0.211 and 2.503, respectively, the proportion of counties exceeding the mean values were 22%, 27%, 26% and 25%, respectively, and the proportion of counties and cities with high grade sensitivities or higher were 30%, 27%, 28% and 61%, respectively. The western valley and eastern basin of Xinjiang are high-grade sensitivity areas of total nitrogen to precipitation (≥0.2), and most of the remaining areas have either a low sensitivity or a very low sensitivity (<0.2 or < 0.05). The effective phosphorus and quick-acting potassium in the north and east of Xinjiang are highly sensitivity to precipitation (≥0.20), and the west and south of the country are less sensitive to precipitation. The sensitivity of organic matter to precipitation was not obvious in the southern part of Xinjiang, with more areas having a very low sensitivity (<0.05), while most areas in the northern regions showed a very high sensitivity (≥1) (Figs. 7b, 7d, 7f and 7h). With abundant precipitation in the river valleys in western Xinjiang and extreme drought in the eastern basin, the non-robustness of climate change in the two regions resulted in a high sensitivity of the soil nutrients to precipitation. Scarce precipitation in southern Xinjiang resulted in a generally low sensitivity of the soil nutrients to precipitation. The relatively high precipitation in northern Xinjiang was the main reason for the higher sensitivity of the soil nutrients to precipitation.
The results show that the sensitivity of the soil nutrients to temperature changes is greater than that of precipitation, and the sensitivity of the soil nutrients to the north of the Tianshan Mountain in Xinjiang is greater than that to the south of the Tianshan Mountain. The impact of climate change on organic matter is significantly greater than that of total nitrogen, available phosphorus and rapid available potassium.
To compare and analyze the impact of the LUI and climate change on the change of the soil nutrient content gain and loss, the parts of which absolute values of the sensitivity coefficient to the LUI and climate change are Grade Ⅰ and Grade Ⅱ (|S| < 0.20 = are combined into lowly sensitive regions (LSR), and the parts with Grade Ⅲ and Grade Ⅳ (|S| ≥ 0.20) are combined into highly sensitive regions (HSR) according to the classification system of the sensitivity coefficients. Lowly sensitive regions are the areas where the LUI and climate change have a weak impact on the soil nutrients. The highly sensitive regions are the overlapping areas where the LUI and climate change have a great impact on the soil nutrients, and the main types include the LUI and climate (temperature and precipitation), the LUI and precipitation, the LUI and temperature, and temperature and precipitation (Figure 4).
In general, the increase/decrease of the average values of the soil nutrients are different in highly/lowly sensitive regions, the absolute values of the changes in highly sensitive regions are larger than those in lowly sensitive regions, and there are differences among the changes of average values in the content of the soil nutrients in highly/lowly sensitive regions in the seven farming areas.
From the perspective of the changes of soil nutrient content in highly/lowly sensitive regions, the total nitrogen increased by 8.840% in highly sensitive regions, which was greater than the 2.308% of the lowly sensitive regions (Figure 5a and 5e). The available phosphorus in highly sensitive regions decreased by 12.215%, which was greater than the 8.978% of the lowly sensitive regions (Figure 5b and 5e). The rapid available potassium increased by 15.618% in highly sensitive regions and decreased by 1.191% in low sensitive regions (Figure 5c and 5e). Compared with the increase of organic matter in the lowly sensitive regions (4.997%), that of the highly sensitive regions (20.026%) was the largest among the indices of the soil nutrients, with a difference of 15.029% (Figure 5d and 5e).
As seen from the overall changes of soil nutrients in the seven farming divisions, the content of total nitrogen decreased by 5.934% only in the highly sensitive regions of the Ili River Valley, which is lower than the 8.608% increase of the lowly sensitive regions. The absolute values of the soil nutrient content changes in the remaining highly sensitive regions were larger than those of the lowly sensitive regions (Figure 6), among which, the farming areas in western part of Tarim had the largest gap of increase, reaching 22.177% (Figure 6a, 6b, and Figure 7). Among the seven farming divisions, the available phosphorus displayed a downward trend for both the highly and lowly sensitive regions, and the decrease for the highly sensitive regions was greater than that of the lowly sensitive regions. Among them, the northern part of the Junggar Basin had the largest decrease for highly sensitive regions (−30.574%) and its southern part had the smallest decrease (−7.889%), while the decrease for the lowly sensitive regions was less than 0.1% (Figure 6c, 6d, and Figure 7). The increase of rapidly available potassium in highly sensitive regions was greater than that of the lowly sensitive regions, and the largest difference was 19.036% in the northern part of the Junggar Basin (Figure 6e, 6f, and Figure 7). In the seven farming areas, the increase of organic matter in lowly sensitive regions was far less than that of the highly sensitive regions. The highly sensitive regions in the southern part of the Junggar Basin and the northern and southern parts of the Tarim Basin were the regions with the largest increase in the soil nutrients, among which the difference between the highly sensitive regions and lowly sensitive regions in the southern part of the Junggar Basin was the largest (17.160 %) (Figure 6g, 6h, and Figure 7).
The results show that the contents of the total nitrogen, rapid available potassium and organic matter in highly sensitive regions increased with a gain and the range was far more than that within the lowly sensitive regions under the combined action of the LUI and climate change, while the content of available phosphorus decreased with a loss and the range was far more than that within the lowly sensitive regions. The LUI and climate change had a great impact on the content of the soil nutrients, especially in the area where higher or high sensitivity coefficients are overlapped. This impact is the result of the combined effect of the changes in two climate factors, temperature and precipitation, as well as differences in the use and management of human cultivated land.
The use and management of cultivated land is the most important and direct activity of human beings to intervene the soil ecosystem of oasis cultivated land. It changes the structure and function of the soil ecosystem through differentiated use patterns and intensity, resulting in changes of the soil nutrients of the cultivated land. This study adopts an LUI to characterize the use and management of cultivated land. Previous studies mostly used yield as a single index to measure the LUI [28]; however, there are many methods to improve the crop yield, such as chemical fertilizer application, mechanical tillage and watering, which may cause certain environmental consequences to the soil ecosystems. Furthermore, phenological differences may limit crop yield, so the regions with similar yields should not be considered to have the same LUI [29]. Meanwhile, harvested agricultural products and crop residues can take a large amount of nutrients away from the soil [30From the aforementioned analysis, it can be seen that the LUI stretches over multiple dimensions and involves various processes that connect the relationship between humans and cultivated land. Therefore, the LUI can't be measured by use of a single index, and it is necessary to establish a systematic multi-dimensional dataset to measure the LUI. This study establishes a comprehensive dataset based on the "Input-Output-System" to measure the LUI and to uncover a more scientific measurement of the sensitivity of the soil nutrients to LUI changes.
Climate change will cause changes of the soil nutrients in arid regions [31]. Previous studies on the response of soil nutrients to factor changes were mostly in response or correlation of the soil nutrients to the changes of a certain factor or factor class and were carried out in fixed time nodes and smaller spatial scales under non-dynamic changes [32,33,34]. This study established a database based on the measured data of the soil nutrient of cultivated land in the Xinjiang oasis ecosystem in two long-term time series, and measured the sensitivity of soil nutrients in the context of human activities (LUI) and climate change, which not only produced a spatial distribution map of sensitivity of the soil nutrients, but was also more tridimensional and hierarchical than previous studies.
Soil degradation is always accompanied by the loss of soil nutrients. Soil degradation is a complex process jointly affected by human factors and natural factors, in which the change of climate and land complex is the basis to influence soil degradation, and the human land use mode and socio-economic activities are the root causes of soil degradation [35,36,37] (see Fig S5 in the Supplementary Materials). This study established two databases of cultivated land soil nutrients and an LUI comprehensive dataset based on the "Input-Output-System". Additionally, this study established a temperature and precipitation dataset which considered arid regions as being extremely sensitive to the response of climate change, and temperature and precipitation were significant factors affecting soil function [38,39,40,41]. Based on the three aforementioned datasets, the sensitivity analysis method was introduced to explore the sensitivity and spatial pattern of cultivated land soil nutrients to the LUI and climate change, thus providing a useful reference for arid regions to cope with climate change and improve soil quality.
This study found that soil nutrients in arid regions were highly sensitive to LUI and climate change, and the spatial difference of sensitivity distribution was significant. The total nitrogen, rapid available potassium and organic matter increased with an increase of the LUI, temperature and precipitation, while the available phosphorus displayed the opposite effect. Through 12 years of protective farming tests (no tillage, deep scarification and ridge farming) in the dry lands of North China, Shao et al. found that the contents of total nitrogen, available phosphorus, rapid available potassium and organic matter in the soil tillage layer increased in varying degrees [42], and Yuan et al. found that the gradient change of climate had a positive impact on the soil nutrients for a long time, while the short-term experimental climate change had a negative impact [43]. Compared with previous studies, this study combined human activities (use and management of cultivated land) and the climate change characteristics in arid regions to establish a dataset, comprehensively measured and compared the response and spatial differentiation characteristics of soil nutrients to the LUI and climate change, analyzed the change and range of the soil nutrient content in differentiation sensitive regions, and more systematically and comprehensively interpreted the impact of human activities and climate change on soil nutrients, which is conducive to the efficient utilization of the oasis cultivated land soil and the improvement of the soil quality in divisions, and is conducive to the sustainable production of oasis agriculture, the balance of ecosystem and the healthy development of human society.
The soil nutrients are the basic material for the function of arable land system, and its quality directly affects the production, life and ecological function of arable land system. The soil nutrient system is the cross link between the elements of the environmental systems in the cropland system, which is easily influenced by external factors and has a high sensitivity.
Temperature and precipitation are of a general significance for the soil nutrient changes and have a major impact on the nature and intensity of chemical and physical processes in soil nutrients. Changes in temperature and precipitation exacerbate the uncertainty in the soil nutrient system; when the rate of change is greater than the rate of functioning of the cycling mechanisms within the soil nutrient system, the soil nutrient system fluctuates, which may be manifested in the form of nutrient losses, land degradation, and other phenomena. When either the rate of change is steady or when the soil nutrient system is effectively replenished with the necessary elements (water, light and heat resources, etc.), the healthy and efficient operation of the soil nutrient system will be promoted. Due to typical arid climate characteristics, the effects of temperature and precipitation on the soil nutrients are more pronounced in arid zones than in other climate type regions, with warm drying, scarce precipitation, extreme droughts, and consequent desertification and soil erosion leading to significant soil nutrient changes [44,45].
Cropland utilization and management is a conscious and purposeful modification of the land system by human beings, which has a bidirectional effect on the development and coordination of the soil nutrient system. Reasonable cropland utilization and management can make the soil nutrient system develop in a benign direction (e.g., increased crop yields), whereas transitory and irrational cropland utilization and management may cause the coordination of the soil nutrient system to be destroyed and soil degradation to occur. Transitional land development and utilization activities in arid zones deplete the fertility of arable land and disrupt the balance of soil ecosystems, the application of chemical fertilizers, mulching, and soil salinization lead to drastic changes in the soil nutrients of arable land, and the robustness of soil nutrients is greatly affected by arable land utilization and management [46,47].
The LUI, temperature and precipitation had a large impact on the soil nutrient changes, and the superimposed effects of the three were more significant. In this study, we analyzed the changes and magnitude of soil nutrient content loss and gain in differentially sensitive areas, and the results showed that total nitrogen, quick-acting potassium, and organic matter content significantly increased in highly sensitive areas and slightly increased in low-sensitive areas under the background of an increasing LUI in arid zones and warming and humidifying climate. The effective phosphorus decreased more in the highly sensitivity region compared to the lowly sensitivity region. The percentages of counties and cities in the highly sensitivity regions for total nitrogen, effective phosphorus and quick-acting potassium were 51%, 45% and 47%, respectively, which were not high. At the same time, the climate change background of the seven cropping system sub-regions and the differences in human cropland utilization led to different sensitivities of the soil nutrients to the LUI, air temperature and precipitation in each region, and this difference was the main reason for the formation of the status quo of soil nutrient content changes [48,49].
Based on the historical dataset and soil nutrient database of the LUI and climate change, this study discussed the sensitivity and spatial pattern of soil nutrients in arid regions in the context of human activities and climate change, as well as the gain and loss change of the soil nutrient content in differentiated sensitive regions. According to study findings, under the background that that LUI increased and the climate is warm and humidified in Xinjiang, China, the soil nutrient sensitivity was significantly higher, which was most sensitive to temperature change, and organic matter of soil was most affected by the LUI and climate change. In space, the soil nutrient sensitivity had obvious differential characteristics, showing a spatial pattern of decreasing from northeast to southwest; the gain and loss change of the soil nutrient content in highly sensitive regions was significantly higher than that of lowly sensitive regions. In highly sensitive regions, the contents of the total soil nitrogen, rapid available potassium and organic matter increased with a gain, among which the increase of soil organic matter was the most and the decrease of available phosphorus was the largest. In lowly sensitive regions, the content of other soil nutrients increased slightly, except that the content of available phosphorus decreased slightly with a loss. Therefore, inspired by the above research findings, this study puts forward the process and technical system for maintenance and restoration of soil nutrients in arid regions.
A sensitivity analysis can reflect the response of soil nutrients to the LUI and climate change, but it cannot determine the actual contribution of the LUI and climate factors to the soil nutrients. In future research, the analysis can be focused on the actual contribution of the LUI and climate change to the soil nutrients to form a systematic study on the relationship between cultivated land use and management, climate change and soil nutrients.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
This research was funded by the National Natural Science Foundation of China-Key projects of Xinjiang United Fund (No. U1603235).
There is no conflict of interest.
| [1] |
J. L. G. Guirao, P. O. Mohammed, H. M. Srivastava, D. Baleanu, M. S. Abualrub, Relationships between the discrete Riemann-Liouville and Liouville-Caputo fractional differences and their associated convexity results, AIMS Math., 7 (2022), 18127–18141. https://doi.org/10.3934/math.2022997 doi: 10.3934/math.2022997
|
| [2] |
C. S. Goodrich, On discrete sequential fractional boundary value problems, J. Math. Anal. Appl., 385 (2012), 111–124. https://doi.org/10.1016/j.jmaa.2011.06.022 doi: 10.1016/j.jmaa.2011.06.022
|
| [3] |
T. Abdeljawad, Different type kernel h–fractional differences and their fractional h–sums, Chaos Soliton. Fract., 116 (2018), 146–156. https://doi.org/10.1016/j.chaos.2018.09.022 doi: 10.1016/j.chaos.2018.09.022
|
| [4] |
P. O. Mohammed, H. M. Srivastava, D. Baleanu, K. M. Abualnaja, Modified fractional difference operators defined using Mittag-Leffler kernels, Symmetry, 14 (2022), 1519. https://doi.org/10.3390/sym14081519 doi: 10.3390/sym14081519
|
| [5] |
F. M. Atıcı, M. Uyanik, Analysis of discrete fractional operators, Appl. Anal. Discrete Math., 9 (2015), 139–149. http://dx.doi.org/10.2298/AADM150218007A doi: 10.2298/AADM150218007A
|
| [6] |
F. M. Atıcı, M. Atıcı, M. Belcher, D. Marshall, A new approach for modeling with discrete fractional equations, Fund. Inf., 151 (2017), 313–324. https://doi.org/10.3233/FI-2017-1494 doi: 10.3233/FI-2017-1494
|
| [7] | F. Atıcı, S. Sengul, Modeling with discrete fractional equations, J. Math. Anal. Appl., 369 (2010), 1–9. |
| [8] |
C. S. Goodrich, On discrete sequential fractional boundary value problems, J. Math. Anal. Appl., 385 (2012), 111–124. https://doi.org/10.1016/j.jmaa.2011.06.022 doi: 10.1016/j.jmaa.2011.06.022
|
| [9] |
C. R. Chen, M. Bohner, B. G. Jia, Ulam-hyers stability of Caputo fractional difference equations, Math. Meth. Appl. Sci., 42 (2019), 7461–7470. https://doi.org/10.1002/mma.5869 doi: 10.1002/mma.5869
|
| [10] |
R. Dahal, C. S. Goodrich, Theoretical and numerical analysis of monotonicity results for fractional difference operators, Appl. Math. Lett., 117 (2021), 107104. https://doi.org/10.1016/j.aml.2021.107104 doi: 10.1016/j.aml.2021.107104
|
| [11] |
C. Lizama, The Poisson distribution, abstract fractional difference equations, and stability, Proc. Amer. Math. Soc., 145 (2017), 3809–3827. http://dx.doi.org/10.1090/proc/12895 doi: 10.1090/proc/12895
|
| [12] |
H. M. Srivastava, P. O. Mohammed, C. S. Ryoo, Y. S. Hamed, Existence and uniqueness of a class of uncertain Liouville-Caputo fractional difference equations, J. King Saud Univ.-Sci., 33 (2021), 101497. https://doi.org/10.1016/j.jksus.2021.101497 doi: 10.1016/j.jksus.2021.101497
|
| [13] |
Q. Lu, Y. Zhu, Comparison theorems and distributions of solutions to uncertain fractional difference equations, J. Cmput. Appl. Math., 376 (2020), 112884. https://doi.org/10.1016/j.cam.2020.112884 doi: 10.1016/j.cam.2020.112884
|
| [14] | F. M. Atıcı, P. W. Eloe, A transform method in discrete fractional calculus, Int. J. Differ. Equ., 2 (2007), 165–176. |
| [15] | P. O. Mohammed, T. Abdeljawad, Discrete generalized fractional operators defined using h-discrete Mittag-Leffler kernels and applications to AB fractional difference systems, Math. Meth. Appl. Sci., 2020. https://doi.org/10.1002/mma.7083 |
| [16] | F. M. Atıcı, M. Atıcı, N. Nguyen, T. Zhoroev, G. Koch, A study on discrete and discrete fractional pharmaco kinetics pharmaco dynamics models for tumor growth and anti-cancer effects, Comput. Math. Biophys., 7 (2019), 10–24. |
| [17] |
A. Silem, H. Wu, D. J. Zhang, Discrete rogue waves and blow-up from solitons of a nonisospectral semi-discrete nonlinear Schrödinger equation, Appl. Math. Lett., 116 (2021), 107049. https://doi.org/10.1016/j.aml.2021.107049 doi: 10.1016/j.aml.2021.107049
|
| [18] | R. A. C. Ferreira, D. F. M. Torres, Fractional h-difference equations arising from the calculus of variations, Appl. Anal. Discrete Math., 5 (2011), 110–121. |
| [19] |
G. C. Wu, D. Baleanu, Discrete chaos in fractional delayed logistic maps, Nonlinear Dyn., 80 (2015), 1697–1703. https://doi.org/10.1007/s11071-014-1250-3 doi: 10.1007/s11071-014-1250-3
|
| [20] |
J. W. He, L. Zhang, Y. Zhou, B. Ahmad, Existence of solutions for fractional difference equations via topological degree methods, Adv. Differ. Equ., 2018 (2018), 153. https://doi.org/10.1186/s13662-018-1610-2 doi: 10.1186/s13662-018-1610-2
|
| [21] |
C. S. Goodrich, B. Lyons, Positivity and monotonicity results for triple sequential fractional differences via convolution, Analysis, 40 (2020), 89–103. http://dx.doi.org/10.1515/anly-2019-0050 doi: 10.1515/anly-2019-0050
|
| [22] |
P. O. Mohammed, T. Abdeljawad, F. K. Hamasalh, On Riemann-Liouville and Caputo fractional forward difference monotonicity analysis, Mathematics, 9 (2021), 1303. https://doi.org/10.3390/math9111303 doi: 10.3390/math9111303
|
| [23] |
P. O. Mohammed, T. Abdeljawad, F. K. Hamasalh, On discrete delta Caputo-Fabrizio fractional operators and monotonicity analysis, Fractal Fract., 5 (2021), 116. https://doi.org/10.3390/fractalfract5030116 doi: 10.3390/fractalfract5030116
|
| [24] |
T. Abdeljawad, D. Baleanu, Monotonicity analysis of a nabla discrete fractional operator with discrete Mittag-Leffler kernel, Chaos Soliton. Fract., 116 (2017), 106–110. https://doi.org/10.1016/j.chaos.2017.04.006 doi: 10.1016/j.chaos.2017.04.006
|
| [25] |
X. Liu, F. Du, D. Anderson, B. Jia, Monotonicity results for nabla fractional h-difference operators, Math. Meth. Appl. Sci., 2020 (2020), 1207–1218. https://doi.org/10.1002/mma.6823 doi: 10.1002/mma.6823
|
| [26] |
R. Dahal, C. S. Goodrich, B. Lyons, Monotonicity results for sequential fractional differences of mixed orders with negative lower bound, J. Differ. Equ. Appl., 27 (2021), 1574–1593. https://doi.org/10.1080/10236198.2021.1999434 doi: 10.1080/10236198.2021.1999434
|
| [27] |
P. O. Mohammed, O. Almutairi, R. P. Agarwal, Y. S. Hamed, On convexity, monotonicity and positivity analysis for discrete fractional operators defined using exponential kernels, Fractal Fract., 6 (2022), 55. https://doi.org/10.3390/fractalfract6020055 doi: 10.3390/fractalfract6020055
|
| [28] | C. S. Goodrich, J. M. Jonnalagadda, Monotonicity results for CFC nabla fractional differences with negative lower bound, Analysis, 41 (2021), 221–229. |
| [29] |
C. S. Goodrich, Monotonicity and non-monotonicity results for sequential fractional delta differences of mixed order, Positivity, 22 (2018), 551–573. https://doi.org/10.1007/s11117-017-0527-4 doi: 10.1007/s11117-017-0527-4
|
| [30] |
P. O. Mohammed, C. S. Goodrich, F. K. Hamasalh, A. Kashuri, Y. S. Hamed, On positivity and monotonicity analysis for discrete fractional operators with discrete Mittag-Leffler kernel, Math. Meth. Appl. Sci., 45 (2022), 6391–6410. https://doi.org/10.1002/mma.8176 doi: 10.1002/mma.8176
|
| [31] |
M. Holm, Sum and difference compositions in discrete fractional calculus, Cubo (Temuco), 13 (2011), 153–184. http://dx.doi.org/10.4067/S0719-06462011000300009 doi: 10.4067/S0719-06462011000300009
|
| [32] |
P. O. Mohammed, D. Baleanu, T. Abdeljawad, S. K. Sahoo, K. M. Abualnaja, Positivity analysis for mixed order sequential fractional difference operators, AIMS Math., 8 (2023), 2673–2685. http://dx.doi.org/10.3934/math.2023140 doi: 10.3934/math.2023140
|
| [33] |
R. Dahal, C. S. Goodrich, An almost sharp monotonicity result for discrete sequential fractional delta differences, J. Differ. Equ. Appl., 23 (2017), 1190–1203. https://doi.org/10.1080/10236198.2017.1307351 doi: 10.1080/10236198.2017.1307351
|
| [34] |
B. Jia, L. Erbe, A. Peterson, Two monotonicity results for nabla and delta fractional differences, Arch. Math., 104 (2015), 589–597. http://dx.doi.org/10.1007/s00013-015-0765-2 doi: 10.1007/s00013-015-0765-2
|
| [35] |
B. Jia, L. Erbe, A. Peterson, Convexity for nabla and delta fractional differences, J. Differ. Equ. Appl., 21 (2015), 360–373. https://doi.org/10.1080/10236198.2015.1011630 doi: 10.1080/10236198.2015.1011630
|
| [36] | J. Baoguo, L. Erbe, C. S. Goodrich, A. Peterson, The relation between nabla fractional differences and nabla integer differences, Filomat, 31 (2017), 1741–1753. |
| [37] |
J. Baoguo, L. Erbe, C. S. Goodrich, A. Peterson, Monotonicity results for delta fractional difference revisited, Math. Slovaca, 67 (2017), 895–906. http://dx.doi.org/10.1515/ms-2017-0018 doi: 10.1515/ms-2017-0018
|
| [38] | C. S. Goodrich, A uniformly sharp monotonicity result for discrete fractional sequential differences, Arch. Math., 110 (2018), 145–154. |
Figures(5)
Pshtiwan Othman Mohammed, Musawa Yahya Almusawa. On analysing discrete sequential operators of fractional order and their monotonicity results[J]. AIMS Mathematics, 2023, 8(6): 12872-12888. doi: 10.3934/math.2023649
DownLoad:
