A mathematical model of anthrax epidemic with behavioural change

1.   Introduction

Anthrax is a zoonotic disease that remains a problem in many countries worldwide ^[1]. It is caused by the bacterium Bacillus anthracis. The disease primarily affects herbivorous animals, but outbreaks in humans are largely reported. The hosts of Bacillus anthracis include domestic and wild animals such as sheep, goats, cattle, horses, pigs, camels, antelope, deer and buffaloes ^[2]. Birds are rarely infected with anthrax, but cats and dogs that feed on anthrax-contaminated meat may become infected and often recover from the disease without treatment ^[5,6]. It is worth noting that, not all infected animals die from anthrax. The survival or otherwise of an anthrax-infected animal probably depends on the dose of pathogens and the natural immunity of the animal ^[5].

Bacillus anthracis is a gram-positive, rod-shaped non-motile bacterium, the only obligate aerobic pathogen in the genus Bacillus. The bacterium has both vegetative form and a long-lasting, highly resistant spore form ^[3,4]. The bacterium exclusively remains in the vegetative form within a low oxygen environment of the host ^[3]. The anthrax Bacillus forms spores to protect itself when conditions are unfavorable. Spores have a thick outer coating which shields the bacteria from extreme conditions ^[5]. When an anthrax spore enters into its host, it germinates and results into a vegetative cell and replicates rapidly. The replicated vegetative cells then enter the bloodstream and result in septicemia and eventually lead to the sudden death of the host ^[4]. Anthrax spores have long life span, capable of persisting in the environment for decades before infecting a new host. The spores are usually present at sites where anthrax-infected carcasses decomposed for many years. The spores have been known to re-infect animals over 70 years after burial sites of anthrax-infected animals were disturbed ^[7]. Domestic and wild animals can become infected when they breathe in or ingest spores in contaminated soil, plants, or water ^[8]. Following inhalation or ingestion, the anthrax bacteria spread rapidly throughout the entire body of the animal. Dead animals that are opened and not burned or buried provide an ideal source of new spores to contaminate the soil ^[6]. The incubation period of Bacillus anthracis in animals after exposure to spores is between $3$ to $7$ days, but it may range from less than 1 day to 14 days or more. As soon as clinical signs appear, the infected animals usually die within $2$ days ^[9]. Upon or near death, blood oozes from the body openings of the infected animal into the environment. This blood is heavily laden with anthrax organisms. The carcass has a marked bloating and decomposes rapidly ^[6].

Anthrax infection in human population results from accidental exposure ^[13], and is based on rural agricultural activities or industrial processing ^[14]. The risk of humans contracting anthrax is related to many factors including the origin of infection ^[15]. The source of anthrax infection includes cutaneous, gastrointestinal and inhalation anthrax ^[16]. The cutaneous or skin infection occurs when anthrax spores invade a cut or abrasion, this happens when a person handles infected animals or contaminated animal products like wool, hides, or hair ^[6,8]. Symptoms of cutaneous infection of anthrax include itching of the infected part, followed by swelling and discoloration ^[8]. Cutaneous anthrax has a mortality rate between $5\% - 20\%,$ if infections are not treated ^[17]. Cutaneous anthrax accounts for approximately 95% of all reported human anthrax cases ^[18].

Gastrointestinal anthrax occurs as a result of eating the meat of animals infected with the vegetative Bacillus anthracis, in addition, anthrax spores can also enter the body via mucous membranes that line the mouth and intestines ^[5,19]. The intestinal tract, mouth, or throat may be infected ^[19]. Symptoms of gastrointestinal anthrax may include nausea, vomiting, anorexia, mild diarrhoea and fever. The incubation period is commonly $3–7$ days ^[18]. The fatality rate of gastrointestinal anthrax without treatment is $\geq 50\%$, but $< 40\%$ with treatment ^[9].

Inhalation anthrax occurs as a result of breathing anthrax spores into the lungs ^[19]. The incubation period reported for inhalation anthrax in humans ranges from $1$ to $43$ days ^[9]. Symptoms include fever or chills, sweats, fatigue or malaise, non-productive cough, dyspnoea, changes in mental state including confusion, and nausea or vomiting ^[18]. The case-fatality rate of inhalation anthrax in humans is $> 85\%$ ^[9].

Anthrax is global in its geographical distribution and endemic in agricultural regions of Southern and Eastern Europe, Central and Southwestern Asia, Sub-Saharan Africa, North and South America, and Australia ^[4,8,9,10]. It is estimated that there are $2,000$ to $20,000$ human anthrax cases occurring annually worldwide ^[11]. Apart from its natural occurrence, Bacillus anthracis is currently considered one of the most serious bioterrorism threats ^[10,19]. Anthrax is still endemic in most African countries, majority of which experience at least one human outbreak per year ^[12].

The use of mathematical models to explore the spread and control of infectious diseases has proved to be an important tool for scientists and epidemiologists ^[20]. This research seeks to use mathematical models to study the transmission dynamics of anthrax in animal and human populations. There are quite some number of mathematical models proposed for the study of anthrax dynamics, these include; ^{[21,22,23,24,25,26]} among others, but not so much is known about the transmission dynamics of anthrax infection in both animal and human populations using saturation incidence. This work therefore seeks to study the infection dynamics of anthrax using non-linear saturation incidence rate.

Incidence functions form a very important integral part of research in mathematical epidemiology modeling. In ^[27], incidence rate refers to the frequency with which a disease occurs over a specified period of time, thus it is the number of new cases of a disease within a time period, as a proportion of the number of individuals who are at risk of being infected with the disease. The most widely used incidence functions in epidemic models include the bilinear incidence $\beta\, SI$ and standard incidence $\frac{\beta\, SI}{N}$ ^[28]. According to ^[29], the bilinear incidence is based on the law of mass action, which requires a well-mixed population so that each infected individual has equal probability of infecting each susceptible individual. In ^[30], the bilinear incidence assumes that the disease transmission increases whenever the susceptible population increases which is a limitation of the function because of the intervention of control measures during disease outbreak. ^[31] defines standard incidence as the number of new cases per unit time due to infectious individuals. The standard incidence is often used, due to the fact that the number of contacts per individual is approximately constant, the standard incidence may be more suitable for human beings, or animals who live in groups ^[32]. The standard incidence is more suitable than the bilinear form ^[20].

The concept of saturation incidence was established by Capasso and Serio. The saturation incidence is given by $\frac{\beta SI}{1+\alpha I}$ where $\beta I$ measures the infection force of the disease and $\frac{1}{1+\alpha I}$ measures the inhibition effect from the behavioural change of the susceptible individuals when their number increases. Thus, $\frac{\beta I}{1+\alpha I}$ tends to a saturation level when the infective $I$ gets large ^[28,33]. Saturation incidence may be mores suitable for our real world situations over bilinear and standard incidence ^[28]. If a population is crowded or saturated with infectives, then saturated incidence is a better option ^[29]. The saturation incidence rate is nonmonotone, it has the quality of first increasing and then decreasing when the number of infective individuals reaches a critical value ^[34].

2.   Model formulation

In this section, a deterministic model is formulated from the work of ^[35] for the study of anthrax transmission in animal and human populations with much emphasis on saturation and behavioural change within the animal and human populations respectively, at the peak of the disease spread. In formulating the model, it is assumed that anthrax is spread through environmental contamination. Upon infection, an infected animal shows clinical symptoms of the disease and can be cured by treatment. It is further assumed that there is no human to human route of infection.

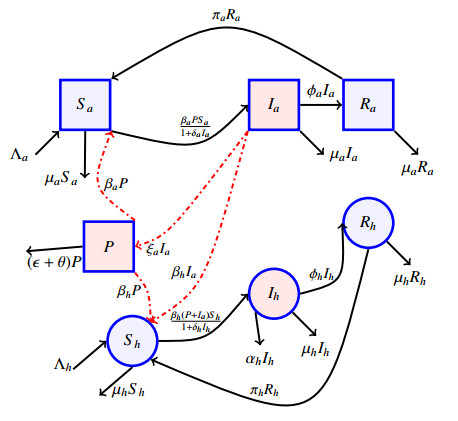
Figure 1 presents a compartmental model for the transmission of anthrax in animal and human populations. The animal population is subdivided into three compartments of susceptible animals $S_{a}$, infective animals $I_{a}$, and the class of animals who recovered from the disease $R_{a}$. The human population consists of susceptible humans $S_{h}$, the infective humans $I_{h}$ and the population of infective individuals who recovered from the disease $R_{h}$ due to treatment or natural immunity. Compartment $P$ consists of the environmental reservoir contaminated with anthrax spores or pathogens. Table 1 summarizes the definition of parameters used in the model.

The susceptible animal population is increased by an inflow rate of $\Lambda_{a}$. The susceptible animals in $S_{a}$ become infected when they ingest anthrax contaminated feed or breathe in spores in contaminated environment at a rate of $\beta_{a}PS_{a}$ which moves the newly infected population into the infected class $I_a$ with a saturation incidence of $\frac{1}{1+\delta_{a} I_a}$. The saturation incidence of the animal population measures the crowding effect of the infected animals. $\delta_{a}$ is the saturation factor that measures the inhibitory effect due to protection measures taken by farmers and the general public at large. The animals that show clinical symptoms of the disease in the infective class, $I_{a}$ are treated and undergo recovery at rate of $\phi_{a}I_a$. The treated animals then join a temporal class of $R_{a}$ for further monitory and other intensive care. Upon full recovery, the recovered population confer temporary immunity and join compartment $S_{a}$ at a rate of $\pi_{a} R_{a}$. The Susceptible, Infected and Recovered animal population reduce in population size by natural death rate of $\mu_{a}$. $\xi_{a}$ is the rate at which infective animals shed anthrax pathogens into the environment. The anthrax pathogen level in the environment $P$ decays due to the practice of environmental hygiene and by natural phenomenon at rates of $\theta P$ and $\epsilon P$ respectively.

The human population suffers a spillover transmission of anthrax from outbreaks of the disease within the animal population.

The susceptible human population $S_{h}$ increases through recruitment at a rate of $\Lambda_h$. Susceptible humans become infected with anthrax through effective contact with pathogen sources $(P, I_{a})$ at a constant rate of $\beta_{h}$.

In the infective human class $I_{h}$, infected population recover from the disease due to treatment or natural recovery at a rate of $\phi_{h}I_{h}$ and joins the recovery compartment $R_{h}$. Individuals in $R_{h}$ become susceptible at a rate of $\pi_{h}R_{h}$ due to waning of infection-acquired immunity. The Susceptible, Infected and Recovered humans die naturally at rates $\mu_{h}S_{h}$, $\mu_{h}I_{h}$ and $\mu_{h}R_{h}$ respectively. The infective human population also suffer from anthrax related deaths at rate $\alpha_{h}I_{h}$.

During an anthrax epidemic, the general public especially farmers react behaviourally, psychologically, and socially towards the disease spread. These attitudes may have an impact on the overall infection rate or number of infectious persons as well as the susceptible human population through the incidence rate. As the number of infective individuals increases, the susceptible human population may tend to reduce the number of contacts with infective animal population per unit time due to the behavioural effect. The incidence rate which describes the behavioural change towards the outbreak of the disease is given as $\frac{\beta_{h} S_{h}(P+I_{a})}{1+\delta_{h} I_{h}},$ where $\delta_{h} > 0$ is the behavioural parameter. This incidence rate describes the transmission of the anthrax pathogen from infective animals to susceptible humans taking into accounts the behavioural effect of the general public towards the spread of the disease.

The corresponding model is presented as a system of differential equations indicated in equation (2.1).

with non-negative initial conditions;

$S_{a}(0) > 0, \, I_{a}(0)\geq0, \, R_{a}(0)\geq0, \, S_{h}(0) > 0,$

$I_{h}(0) \geq0, \, R_{h}(0)\geq0, \, P(0)\geq0$.

For convenience, the following variables will be substituted where appropriate;

The total population size of the system (2.1) is given by:

where $N_{a}(t) = S_a + I_a + R_a$ and $N_{h}(t) = S_h + I_h + R_h$ represent the total population size of animals and humans respectively. The animal and human populations can be simplified as follows:

In the next section, basic properties of the model system (2.1) are discussed. These properties are useful for stability analysis.

3.   Qualitative analysis

3.1.   Invariant region

The study of the invariant region is carried-out to determine whether the solutions of the model system (2.1) make biological sense.

Recall that,

The closed set

is a feasible region to the model (2.1), where $X = \left(S_{a}, I_{a}, R_{a}, P, S_{h}, I_{h}, R_{h} \right)$.

Lemma 3.1. Let $\left(S_{a}, I_{a}, R_{a}, P, S_{h}, I_{h}, R_{h} \right)$ be the solution of the model system (2.1) with non-negative initial conditions. The closed set $\Omega$ is bounded and positively invariant.

Proof. We construct the proof by applying the theorem on the differential inequality ^[36] to equation (3.1). Solving the first equation of (3.1) gives:

Thus, the size of the animal population $N_{a}$ approaches $\frac{\Lambda_{a}}{\mu_{a}}$ as $t\rightarrow \infty$.

Similarly, as $t\rightarrow \infty$, then $N_{h}\rightarrow \frac{\Lambda_{h}}{\mu_{h}}$.

Hence, all solutions of the system (2.1) are contained in the region $\Omega$. Thus, $\Omega$ is bounded and positively invariant region for the model.

3.2.   Positivity and boundedness of model solution

This section presents a proof that all state variables of the model system (2.1) remain non-negative for all non-negative initial conditions for $t\geq 0$ and that the model equations are continuous and locally Lipschitz in $(S_{a}, \, I_{a}, \, R_{a}, \, P, \, S_{h}, \, I_{h}, \, R_{h})\in\mathbb{R}_{+}^{7}$, hence solutions of the system exist for all positive time. This is necessary since the model is a biological system representing populations of animals and humans.

The model system (2.1) can be written in the form

with $x = (S_{a}, \, I_{a}, \, R_{a}, \, P, \, S_{h}, \, I_{h}, \, R_{h})$ and $F(x) = (F_{1}(x), \, F_{2}(x), \, ..., \, F_{7}(x))$. Thus,

Proposition 3.2. For any $S_{a}(0), \, I_{a}(0), \, R_{a}(0), \, P(0), \, S_{h}(0), \, I_{h}(0), \, R_{h}(0)\, \geq0$ there exists a unique solution $S_{a0}, \, I_{a0}, \, R_{a0}, \, P_{0}, \, S_{h0}, \, I_{h0}, \, R_{h0}$ respectively, defined on $\mathbb{R}_{+}^{7} = \left[0, \infty\right)^{7}$. Also, $F_{j}(x, t)\geq0$ for every $j = 1, \, 2, \, ..., \, 7$ if $x\in \left[0, \infty \right) ^7$ and $x_{j} = 0$ for $t\geq 0$. In addition $x(0)\in \left[0, \infty \right)$.

Theorem 3.3. (^[39]). Let $\mathbb{R}_{+}^{n} = \left[0, \infty\right)^{n}$ be the cone of nonnegative vectors in $\mathbb{R}_{+}^{n}$. Let $F:\mathbb{R}_{+}^{n+1}\rightarrow \mathbb{R}^{n}$ be locally Lipschitz and

$F_{j}(x, t)\geq0$ whenever $t\geq 0$, $x\in \mathbb{R}_{+}^7$, $x_{j} = 0$ for $j = 1, \, 2, \, ..., \, 7$.

Then, for every $x_{0}\in \mathbb{R}_{+}^7$ there exist a unique solution of $x^{'} = F(x, t),$ $x(0) = x_{0}$, with values in $\mathbb{R}_{+}^7$ which is defined on some interval $\left[0, b \right)$, $b > 0$. If $b < \infty$. Then $\limsup\limits_{t\nearrow b}\sum\limits_{j = 1}^{7}x_{j} = \infty$.

Proof. From the first equation of the model system (2.1) if $S_{a} = 0$ then

It follows that $\frac{dI_{a}}{dt} \geq0$ if $I_{a} = 0$, $\frac{dR_{a}}{dt} \geq0$ if $R_{a} = 0$, $\frac{dP}{dt} \geq0$ if $P = 0$, $\frac{dS_{h}}{dt} \geq0$ if $S_{h} = 0$, $\frac{dI_{h}}{dt} \geq0$ if $I_{h} = 0$, $\frac{dR_{h}}{dt} \geq0$ if $R_{h} = 0$ where $S_{a}, \, I_{a}, \, R_{a}, \, P, \, S_{h}, \, I_{h}, \, R_{h} \in \mathbb{R}_{+}^7$.

Also,

Lemma 3.4 (Lipschitz condition). The system equations $F_{j}(x)$ for $j = 1, 2, ..., 7$ satisfy Lipschitz's conditions and are contraction mappings, if the following condition holds,

Applying the Lipschitz condition in Lemma (3.2) on the first equation of system (2.1) where $S_{a}, \, S_{a}^{'}\in \mathbb{R}_{+}^{7}$ gives

where $b_{1} = \frac{\beta_{a} P }{1+\delta_{a}I_{a}}+\mu_{a}$ thus, $F_{1}(t, S_a)$ satisfies the Lipschitz condition. Similarly, it can be shown that $F_{j}(x)$ for $j = 2, ..., 7$ also satisfy the Lipschitz condition for

Next, it is important to show that $F_{j}(x), \; \forall\, j$ are continuously differentiable and bounded in $\mathbb{R}_{+}^{7}$, by first determining the norm of the partial derivatives of the system equations in (2.1). From the first equation of system (2.1) gives

By extending the same analogy to the remaining equations in system (2.1), it can be established that $\frac{\partial F_{j}(t, x)}{\partial x_i} < \infty$ for $i, j = 2, ..., 7.$ Therefore, all the partial derivatives are continuous and bounded. Hence, there exist a unique solution for the model system (2.1) for all positive time. Thus the model system is well posed.

3.3.   Equilibrium and stability analysis

Two types of equilibrium points are studied in this section, the anthrax-free equilibrium point and the endemic equilibrium point. The equilibrium points of the model system are obtained by first setting the differential equations in (2.1) to zero as given in (3.4).

The anthrax-free equilibrium point is a steady state solution where there is no disease spreading in the populations. Thus, disease-free equilibrium point of the system is attained when all the variables and parameters related to anthrax infection are zero. Thus, $I_{a} = 0, \, P = 0$ and $I_{h} = 0$.

From the first equation of (3.4), $S_{a} = \frac{1}{\mu_{a}}(\Lambda_{a}+\pi_{a}R_{a})$, plugging in $R_{a} = 0$ gives $S_{a} = \frac{1}{\mu_{a}}\Lambda_{a}$. Also, from the fifth equation of (3.4), $S_{h} = \frac{1}{\mu_{h}}(\Lambda_{h}+\pi_{h}R_{h})$ and substituting $R_{h} = 0$ gives $S_{h} = \frac{1}{\mu_{h}}\Lambda_{h}$. Therefore, the anthrax-free equilibrium point is given as $\mathcal{E}_{0} = \left\lbrace S_{a0}, 0, 0, 0, S_{h0}, 0, 0 \right\rbrace$, where $S_{a0} = \frac{\Lambda_{a}}{\mu_{a}}$ and $S_{h0} = \frac{\Lambda_{h}}{\mu_{h}}$.

Next the basic reproduction number is determined using the method described in ^[37]. The basic reproduction number is defined as the average number of secondary anthrax infections a single infected animal causes during its infectious life, if it is introduced into an initially anthrax-free human-animal system ^[35]. The basic reproduction number $\mathcal{R}_{0}$ is the dominant eigenvalue of $\rho(\mathcal{F}\mathcal{V}^{-1})$ corresponding to the spectral radius of the next generation matrix $\mathcal{F}\mathcal{V}^{-1}$, where $\mathcal{F}$ and $\mathcal{V}^{-1}$ are the transmission and the inverse of transition matrices respectively. For this model, the $\mathcal{F}$ and $\mathcal{V}^{-1}$ matrices are defined as follows

Evaluating $\mathcal{F}\mathcal{V}^{-1}$ at the anthrax-free equilibrium point $\mathcal{E}_{0}$ and solving give

the reproduction number of the model system as

.

It is noticed that the infection force of the human population $\beta_{h}$ does not contribute to the reproduction number $\mathcal{R}_{0}$, this shows that the stability of anthrax epidemic within the animal-human system is strongly influenced by the spread of the disease within the animal population. Thus, controlling the anthrax transmission within the animal population will lead to a reduction in the spread of the disease within the human population.

The endemic equilibrium point is a non-disease free state of the model, it is the point at which the anthrax persist in the populations. It is obtained by setting the derivatives in the model system (2.1) equal to zero and solving for the state variables. The endemic equilibrium point is given by $\mathcal{E}_{\ast} = \left\lbrace S_{a}^{\ast}, I_{a}^{\ast}, R_{a}^{\ast}, P^{\ast}, S_{h}^{\ast}, I_{h}^{\ast}, R_{h}^{\ast} \right\rbrace$, where the elements of $\mathcal{E}_{\ast}$ are defined by equation (3.5).

where $I_{h}$ satisfies the function $H(I_{h}) = 0$, defined by

where $\Psi_{1} = \left[c_{ h2}\left(\beta_{h}c_{h1}\left(P^{\ast}+I_{a}^{\ast} \right)+\mu_{h}c_{h1}\right)-\pi_{h}\beta_{h} \left(P^{\ast}+I_{a}^{\ast}\right)\phi_{h}\right].$ It can be verified that $H(0) < 0$ and also that $H(I_{h})\rightarrow + \infty$ as $I_{h}\rightarrow + \infty$.

3.4.   Local stability of anthrax free equilibrium

This section presents a study that investigates the local stability of the anthrax free equilibrium point using the indirect Lyapunov method. By this method, the local asymptotically stability of a model system is proofed by showing that all eigenvalues of the Jacobian matrix $\mathcal{J}$, evaluated at anthrax-free equilibrium have negative real parts, otherwise the anthrax-free equilibrium is unstable.

Theorem 3.5 (Local stability of anthrax-free equilibrium). The anthrax-free equilibrium, $\mathcal{E}_{0}$ is locally asymptotically stable whenever $\mathcal{R}_{0} < 1$ and unstable otherwise.

Proof. The Jacobian matrix of the model system (2.1) is given as,

From the Jacobian matrix $\mathcal{J}_{\mathcal{E}_{0}}$, it is easy to show that $\mu_{h}, \, \mu_{a}, \, c_{h1}$ and $c_{h2}$ are the negative eigenvalues of the Jacobian of the model evaluated at ${\mathcal{E}_{0}}$ and the remaining two eigenvalues can be shown to be negative if $\mathcal{R}_{0} < 1$. Therefore, the anthrax-free equilibrium is locally asymptotically stable when ever $\mathcal{R}_{0} < 1$, concluding the proof.

3.5.   Local stability of endemic equilibrium points

The local stability of the endemic equilibrium is determined by linearizing the system evaluated at the endemic equilibrium points using the Jacobian matrix approach. The characteristic equation of the Jacobian matrix of the system is obtained by the equation $\left|\mathcal{J}_{\mathcal{E}_{\ast}}-\lambda I\right| = 0$.

Theorem 3.6 (Local stability of the endemic equilibrium). The endemic equilibrium, $\mathcal{E}_{\ast}$ is locally asymptotically stable whenever $\mathcal{R}_{0} > 1$ and unstable otherwise.

Proof. Using the Jacobian matrix of the system evaluated at endemic equilibrium points the characteristic equation is given in (3.6).

where,

It can be noticed that $A_{i} > 0\, \forall {i}$, if $\mathcal{R}_{0} > 1$. By Descartes' rule of signs, the characteristic equation in (3.6) has all its roots in the left half of the real plane. Thus, the eigenvalues of the Jacobian matrix of the model evaluated at the endemic equilibrium point have all it's real parts negative whenever $\mathcal{R}_{0} > 1$. Hence, theorem (3.6) is satisfied.

3.6.   Global stability of anthrax-free equilibrium points

^[48] outlined two conditions for determining the global asymptotic stability of anthrax-free equilibrium of a system which is rewritten in the form:

where $\mathcal{Q} \in \mathbb{R}^{m}$ represents the number of uninfected individuals $\mathcal{W} \in \mathbb{R}^{n}$ denotes the number of infected population and $\mathcal{E}_{0} = (\mathcal{Q}^{\ast}, 0)$ represents the anthrax-free equilibrium. The following assumptions must be satisfied for anthrax-free equilibrium of a system to be globally asymptotically stable:

$\mathcal{H}1 = \frac{d\mathcal{Q}}{dt} = F(\mathcal{Q}, 0)$, $\mathcal{Q}^{\ast}$ is globally asymptotically stable. $\mathcal{H}2 = G(\mathcal{Q}, \mathcal{W}) = \mathcal{A} \mathcal{W}- G_{\ast}(\mathcal{Q}, \mathcal{W}),$ where $G_{\ast}(\mathcal{Q}, \mathcal{W})\geq 0$ for $(\mathcal{Q}, \mathcal{W})\in \Omega$, and $\mathcal{A} = D_{\mathcal{W}} G(\mathcal{Q}^{\ast}, 0)$ is an M–matrix (the off diagonal elements are nonnegative).

Theorem 3.7. The equilibrium point $\mathcal{E}_{0}$ of the system (2.1) is globally asymptotically stable if $\mathcal{R}_{0} < 1$(locally asymptotically stable) and the assumptions $\mathcal{H}1$ and $\mathcal{H}2$ are satisfied.

Proof.

Let $\mathcal{Q}(S_{a}, R_{a}, S_{h}, R_{h}) \in \mathbb{R}^{4}$ and $\mathcal{Q}(I_{a}, P, I_{h}, )\in \mathbb{R}^{3}$

The reduced system is given as $\frac{d\mathcal{Q}}{dt} = F(\mathcal{Q}, 0)$

The reduced system $\frac{d\mathcal{Q}}{dt} = F(\mathcal{Q}, 0)$ is globally asymptotically stable at the anthrax-free equilibrium point $\mathcal{E}_{0} = \left(\frac{\Lambda_{a}}{\mu_{a}}, 0, \frac{\Lambda_{h}}{\mu_{h}}\right)$. It can be shown from the first equation of (3.8) that $S_{a}(t) = \frac{\Lambda_{a}}{\mu_{a}}+(S_{a}(0)- \frac{\Lambda_{a}}{\mu_{a}})e^{-\mu_{a}t}$, this implies that $S_{a}(t)\rightarrow \frac{\Lambda_{a}}{\mu_{a}}$ as $t \rightarrow \infty$. Similarly, from the second equation of (3.8), $S_{h}(t)\rightarrow \frac{\Lambda_{h}}{\mu_{h}}$ as $t \rightarrow \infty$. It can be observed that this particular dynamics does not depend on the initial conditions. Hence, the convergence of the solutions of the reduced system in (3.8) is global in $\Omega$.

From the second assumption $\mathcal{H}2$, $G(\mathcal{Q}, \mathcal{W})$ can be expressed as $G(\mathcal{Q}, \mathcal{W}) = D_{\mathcal{W}} G(\mathcal{Q}^{\ast}, 0)\mathcal{W} - G_{\ast}(\mathcal{Q}, \mathcal{W})$.

Clearly, since $S_{a}$ and $S_{h}$ are bounded above by $\frac{\Lambda_{a}}{\mu_{a}}$ and $\frac{\Lambda_{h}}{\mu_{h}}$ respectively, it implies that $\frac{\Lambda_{a}}{\mu_{a}} \geq S_{a}$ and $\frac{\Lambda_{h}}{\mu_{h}} \geq S_{h}$. Therefore, $G_{\ast}(\mathcal{Q}, \mathcal{W}) \geq 0, \forall\, \mathcal{Q}, \mathcal{W} \in \Omega.$ This conclude the proof that anthrax-free equilibrium is globally asymptotically stable when $\mathcal{R}_{0} < 1$.

3.7.   Sensitivity analysis

In this section, sensitivity analysis is performed to study the impact of individual parameters on the basic reproduction number ($\mathcal{R}_{0}$). Here, the Normalized Forward Sensitivity Index is used for this study. The normalized forward sensitivity index of model output $y$ relative to parameter $x$ is given by $\varUpsilon_{y}^{x} = \frac{\partial y}{\partial x}\times \frac{x}{y}$. Thus, the sensitivity indexes in Table 2 were evaluated using the base line parameter values in Table 1 with respect to the reproduction number expressed in the form $\varUpsilon_{\mathcal{R}_{0}}^{p_i} = \frac{\partial \mathcal{R}_{0}}{\partial p_i}\times \frac{p_i}{\mathcal{R}_{0}}$, where $p_i$ are the parameters in $\mathcal{R}_{0}$.

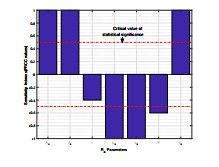
Similarly, the sensitivity indexes of $\mathcal{E}_{\ast}$ of the animal sub-population were computed and the results presented in Table 3. The impact of each parameter on both $\mathcal{E}_{\ast}$ and $\mathcal{R}_{0}$ are presented in Table 4. The partial rank correction coefficient$(PRCC)$ is presented in Figure 2 which further highlighted the contributions of each parameter value towards the overall reproduction number. The length of each bar suggests the statistical influence of each parameter on $\mathcal{R}_{0}$.

4.   Numerical simulation

The numerical simulation of the model system (2.1) was performed using the fourth order Runge-Kutta scheme. The simulation shows the impact of parameters on the entire model as well as demonstrate the influence of parameters on individual state variables. The parameter values in Table 1 were used for running the simulations.

4.1.   Findings

The following are the findings of the study:

$({\rm{i}})$ The anthrax-free equilibrium point is globally asymptotically stable anytime the basic reproduction number $\mathcal{R}_{0}$ is less than unity.

$({\rm{ii}})$ The most sensitive negative parameters on the reproduction number are the natural death rate and recovery rate of infected animals, whereas recruitment rate, pathogen shedding rate and the rate of infection of susceptible animals are the most positive sensitive parameters.

$({\rm{iii}})$ Increase in behavioural change within the human population causes an increase in the susceptible human population.

$({\rm{iv}})$ Increase in saturation effect causes an increase in the susceptible animal population.

$({\rm{v}})$ The saturation effect of the animal population and behavioural change within the human population has the tendency to reduce the number of infective population.

4.2.   Results and discussion.

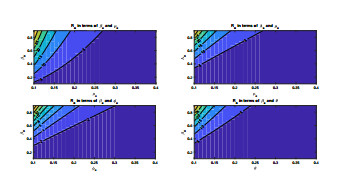
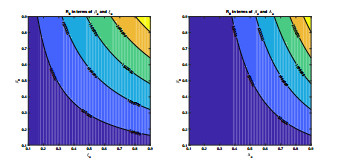
The contour plots in Figures 3 and 4 show the relationship between the reproduction number and two of its parameters $(\mu_{a}, \beta_{a})$, $(\phi_{a}, \beta_{a})$, $(\theta, \beta_{a})$, $(\mu_{a}, \Lambda_{a})$, $(\xi_a, \beta_{a})$ and $(\Lambda_a, \beta_{a})$. Figure 3 suggests that $\beta_{a}$ increases $\mathcal{R}_0$ while $\mu_{a}, \phi_{a}$ and $\theta$ reduce the $\mathcal{R}_0$. Figure 4 shows that $\beta_{a}$, $\xi_{a}$ and $\Lambda_{a}$ increase the reproduction number. These results show that it is essential to reduce the infection force while increasing both environmental hygiene and recovery of infected population in other to control the spread of anthrax.

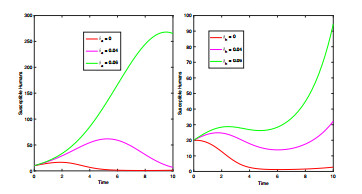
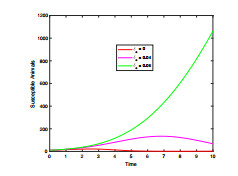
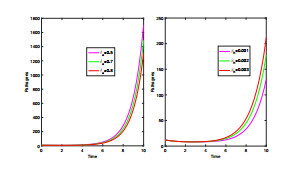
Figure 5 shows the impact of saturation effect of the animal population and behavioural change of humans towards the spread of anthrax on susceptible human population. Increase in saturation effect or behavioural change leads to an increase in the susceptible human population, in addition, increasing the saturation effect also causes an increase in the susceptible animal population as shown in Figure 6.

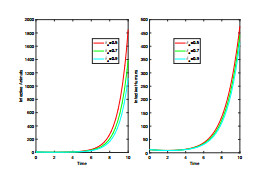
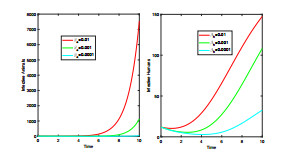
In Figure 7, increase in saturation effect of the animal population leads to a decrease in the infective populations of both animals and humans in a time period. It can be noticed in Figure 8 that behavioural change towards the spread of the disease and infected human population are inversely related. A decrease or negative behavioural change leads to an increase in the infective population whereas an increase, in other words, a positive behaviour towards the spread of the disease as infective population gets higher leads to a decrease in the infected population within a time period. Similarly, an increase in saturation factor trigger a reduction in the pathogen level within the environment in a long run as shown in Figure 10.

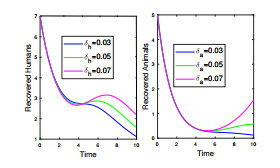
Figure 9 shows the impact of behavioural change and saturation effect on recovered humans and animals respectively. Implementing attitudinal change towards disease spread and saturation effect lead to a general decrease in recovered population, but increasing these rates further result in slightly increase in the recovered population and finally declines in a short run. The slightly increment may be as a result of many infective population recovering faster at that point in time due to stringent treatment measures resulting from the behavioural change.

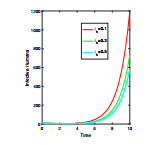
It is noticed in Figure 10 and 11 that an increase in the force of infection leads to a corresponding increase in the level of pathogens in the environment as well as an increase in the number of infective population.

5.   Conclusions

In this paper, we proposed an Ordinary differential equation (ODE) model to describe the transmission dynamics of anthrax disease in both animal and human populations taking into consideration the saturation effect in the animal population as infective population gets higher. The model also takes account of the behavioural changes of the general public as the human infective increases. The impact on the susceptible population as well as other state variables are studied.

Qualitative analyses revealed that the model system has two unique equilibrium points the anthrax-free and endemic equilibrium points. It is proofed that the anthrax-free equilibrium point is locally asymptotically stable if the reproduction number is less than unity $(\mathcal{R}_{0} < 1)$ and the endemic equilibrium point is locally asymptotically stable whenever $\mathcal{R}_{0} > 1$. A study of global stability shows that the anthrax-free equilibrium point is globally asymptotically stable anytime $\mathcal{R}_{0} < 1$.

In other to reduce the spread of anthrax, it is essential to reduce the levels of anthrax infection rate in animals and pathogen shedding rate while increasing the rate of environmental hygiene, recovery of infective animals and decay rate of pathogens.

The numerical simulations demonstrate the importance of saturation effect and behavioural change towards the outbreak of the disease. These parameters have the potential to control disease spread since an increase in their values increase the number of susceptible population, reduce the number of infective population and also reduce the pathogen level in the environment. The behavioural change of the general public influences the recovery rate of infective individuals, since health care personnel can change their attitude towards the disease and improve in quality health care in other to reduce anthrax related fatality.

The stability of anthrax epidemic within the animal-human system is strongly influenced by the spread of the disease within the animal population. It is worth noting that, controlling the spread of anthrax within the animal population will reduce the transmission of the disease in human population.

Data Availability

The numerical data used to support the findings of this research are included within the article.

Conflict of Interest

The authors declare that there are no conflicts of interest regarding the publication of this research.