Modified Marine Predators Algorithm hybridized with teaching-learning mechanism for solving optimization problems

1.   Introduction

Lots of real-life engineering optimization problems have complex characteristics, such as multi-modality, high-dimensional and non-differentiable, so that they are not easy to solve by traditional optimization methods. For instance, if we use traditional optimization methods (such as steepest decent, dynamic programming and linear programming) to address an optimization problem, we need to calculate its gradient. So the traditional method cannot solve non-differentiable problems. Luckily, as the meta-heuristic optimization algorithms are proposed and developed, many complicated optimization problems can be solved easily and efficiently.

During the last three decades, the research of meta-heuristics intelligent optimization algorithm has become a research hot-spot, so that many state-of-the-art swarm optimization algorithms were proposed and developed. For example, inspired by the foraging behavior of the birds, particle swarm optimization (PSO) was proposed ^[1]. Krill herds (KH) algorithm ^[2] was proposed based on the foraging behavior of krill herds, which shows fast convergence speed but poor convergence accuracy. Based on cuckoo parasitic brood behavior, Cuckoo Search (CS) ^[3] was proposed in 2009, which has good versatility and global searching ability. Grey wolf optimization algorithm (GWO) ^[4] was proposed based on the foraging behavior of wolves, which shows good performance and has been applied in many fields. Inspired by the teaching learning phenomenon, a kind of teaching learning based optimization algorithm (TLBO) ^{[5,38,39,40,41,42,45]} was proposed, which has good global searching ability but poor local searching ability. The whale optimization algorithm (WOA) ^[6] was proposed based on the foraging behavior of whales, which is good at solving large spatial gradient problem, but it cannot jump out of the local optima. Marine Predator algorithm (MPA) ^[7] was proposed based on the foraging behavior of ocean predators. Moreover, many researchers have proved that these swarm-inspired optimization algorithms are suitable to solve complex function problems and difficult real-life optimization problems ^{[8,9,10,11,12,13,14]}. In deep learning, the optimizer was used to find the optimal solution of the model. The improvement of the optimizer was also applied in all areas of life ^{[15,16,17,36,37]}.

In this paper, we focus on studying the Marine Predator Algorithm (MPA). The MPA is a novel simple and efficient meta-heuristic optimization algorithm inspired by the survival of the fittest theory in the ocean. MPA has many advantages, including fewer parameters, simple configureuration, ease of implementation and high calculation accuracy. Therefore, since the MPA was proposed, it has caused researchers' attentions and applied in many fields successfully. Chen et al. proposed a rolling bearing fault diagnosis method based on the MPA based-support vector machine ^[18]. The MPA was utilized to fuse base layers by optimal parameters, allowing the output image to have good quality ^[19]. The optimum design of the controller was established by using MPA ^[20]. However, the MPA still exists several drawbacks, such as falling into local optima easily, poor balance ability of exploitation and exploration, weak convergence speed and solution quality. In order to enhance the performance of MPA, researchers have proposed many variants of MPA. In ^[21], MPA was compared with high-performance optimizer and other classical algorithms that recently developed. Elaziz et al. ^[22] proposed an improved MPA based on quantum theory to handle multi-level image segmentation problems. Ramezani et al. ^[23] noted that MPA is deficient in terms of local optimization of fast escape and exploration of space and enhanced the algorithm by incorporating the characteristics of opposition learning, chaos graphs and so on. The enhanced MPA ^[24] implemented a population enhancement strategy to improve solution quality, which was applied to the parameter estimation of the photovoltaic model. In ^[25], a multi-objective MPA was proposed. Optimal vehicle-to-grid and grid-to-vehicle scheduling strategy ^[26] using improved marine predator algorithm. An improved MPA was presented ^[27] for the optimal design of hybrid renewable energy systems. An enhanced multi-objective optimization algorithm of the MPA was proposed for minimizing the operating cost and emission ^[28].

The MPA has four phases: MPA formulation, MPA optimization scenarios, eddy formation and FAD's effect, marine memory. The most core phase of the MPA is 'MPA optimization scenarios'. The MPA algorithm has been applied into many fields because of its superior performance. However, the MPA still includes some disadvantages, such as falling into local optima easily, slow convergence rate and poor solution quality. Therefore, this paper introduces teaching-learning group mechanisms in the 'MPA optimization scenarios' phase to improve the convergence accuracy and solution quality. Moreover, there are three phases in 'MPA optimization scenarios'. In the first phase, a kind of teaching group mechanism is introduced, which was proposed in MTLBO ^[29] by our team. Actually, the population individuals will be divided into two groups based on the fitness values of function. And the two group individuals have different position updating mechanism. In the third phase, another kind of learning group mechanism is introduced to update those population individuals. The proposed MTLMPA is verified by 23 benchmark numerical testing functions and several CEC-2017 functions. Experimental results reveal that the MTLMPA presents better performance on most testing functions compared with state-of-the-art heuristic optimization algorithms.

The main contributions of this paper can be summarized as follows:

1) Based on conventional MPA, a modified marine predators algorithm hybridized with teaching-learning group mechanism is proposed.

2) 23 benchmark numerical functions and several CEC 2017 testing functions are used to evaluate the performance of MTLMPA. Compared with other state-of-the-art algorithms, MTLMPA can provide competitive solutions on most testing functions.

The rest of the paper is organized as follows. Section 2 presents preliminaries of marine predator algorithm in detail. Section 3 proposes the MTLMPA algorithm. The performance of the proposed method is tested and analyzed in Section 4. Finally, Section 5 concludes the work and outlines several advises for future work.

2.   Marine Predators Algorithm

Inspired by the widespread foraging strategy of ocean predators, a nature-inspired meta-heuristic optimization algorithm, called Marine Predators Algorithm (MPA), was proposed in 2019. During foraging, the predators obey the Brownian motion and Lévy flight ^{[30,31,32,33,34,35,43,44]}. In MPA, the prey and predators update their position based on Brownian motion or Lévy flight. The MPA has four basic phases, which are described in detail as follows.

2.1.   Initialization phase

In this subsection, population individuals are generated randomly by uniform distributed method, denoted ${\mathrm{X}}_{0} = {\mathrm{X}}_{\mathrm{m}\mathrm{i}\mathrm{n}}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}({\mathrm{X}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{X}}_{\mathrm{m}\mathrm{i}\mathrm{n}})$. ${\mathrm{X}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and ${\mathrm{X}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the lower limit and upper limit of variables, respectively. rand is a random vector in the range 0–1. Then, the fitness function value of every individual is calculated. Finally, Elite matrix and Prey matrix are constructed. Based on the Elite matrix and Prey matrix, population individuals update their positions.

The Elite matrix is constructed from the optimal solution being specified as the top predator. The second matrix is defined as the Prey matrix. The predator updates its position according to the Prey matrix.

${X}_{ij}^{l}$ is the vector representing the top predator. d is the number of dimensions. n is the number of search agents. ${X}_{ij}$ is the jth dimension of the ith Prey.

2.2.   MPA optimization scenarios

The optimization scenarios of MPA can be divided into three main phases based on different velocity ratio of predator and prey. In the first phase, the prey moves faster than predator. In the second phase, both predator and prey move at almost same pace. In the third phase, the predator moves faster than prey. Based on the movement rules of predator and prey, a specific period of iteration is specified and assigned for each phase.

Phase 1: In the initial stage of MPA, in high-velocity ratio ($\mathrm{v}\ge 10$), the best strategy of the predator is not moving at all. The mathematical model of this phase can be presented as follows.

While $Iter < \frac{1}{3}Max\_Iter$,

$\stackrel{⃑}{\mathrm{R}}$ is a vector of uniform random numbers in [0, 1]. Iter is the current iteration number. $\mathrm{M}\mathrm{a}\mathrm{x}\_\mathrm{I}\mathrm{t}\mathrm{e}\mathrm{r}$ is the maximum iteration number. P = 0.5. ${\stackrel{⃑}{\mathrm{R}}}_{\mathrm{B}}$ is a random vector based on Normal distribution representing the Brownian motion. The standard Brownian motion is a random process. The step size has the characteristics of zero mean ($\mu = 0$) and unit variance (${\sigma }^{2} = 1$). The symbol $\otimes$ represents entry-wise multiplications.

Phase 2: In unit speed ratio, predators try to make the transition from exploration to exploitation. Therefore, half of the organisms are earmarked for exploration and the other half of them for exploitation.

While $\frac{1}{3}Max\_Iter < Iter < \frac{2}{3}Max\_Iter$, the first half of individuals update their positions based on the following Eq (2):

And the second half of individuals update their positions based on the following Eq (3):

${\stackrel{⃑}{\mathrm{R}}}_{\mathrm{L}}$ is a vector of random numbers based on Lévy distribution representing Lévy movement. CF is considered as an adaptive parameter to control the step size for predator movement. ${\stackrel{⃑}{\mathrm{R}}}_{\mathrm{B}}\otimes$ Elite is the Brownian motion of a predator chasing its prey. The preys also update their position according to predators in Brownian motion.

Phase 3: Low-velocity ratio or when predator moves faster than prey.

While $Iter > \frac{2}{3}Max\_Iter$, individuals update their positions based on the following Eq (4).

${\overrightarrow{R}}_{L}\otimes {\overrightarrow{Elite}}_{i}$ simulates the movement of predators in the Lévy strategy.

2.3.   Eddy formation and FADs' effect

The environmental problems can change the behavior of Marine predators, such as the eddy formation and FADs' effect. According to research ^[32], predators always move around FADs. The FADs are considered as local optima and their effect as trapping in these points. Consideration of these longer jumps during simulation avoids stagnation in local optima. Therefore, the FADs effect can be presented as a mathematical Eq (5).

where FADs = 0.2 is the probability of FADs effect on the optimization process. $\vec U$ is the binary vector. r is a uniform random number between [0, 1]. ${\overrightarrow{X}}_{max}$ and $\vec X{}_{\min }$ are upper and lower bounds of containing dimensions. r1 and r2 subscripts denote random indexes of prey matrix.

2.4.   Marine memory

Marine predators usually have good memories and remember places where they've been successful in foraging. After updating prey and performing FADs effect, this matrix is evaluated for fitness to update the Elite. Each solution in the current iteration is compared to the previous iteration to determine its fitness. If the current solution is more fitted, it will be replaced. This process also improves the solution quality with the lapse successful foraging.

3.   A modified teaching learning Marine Predators Algorithm

The MPA is a recently proposed population-based meta-heuristic algorithm that has been proven to be more competitive with other algorithms. However, the MPA still has several deficiencies to be addressed, such as falling into local optima easily, poor balance ability of exploitation and exploration, weak convergence speed and solution quality.

To solve above-mentioned problems, this paper proposes a modified teaching learning Marine Predators algorithm. In literature ^[29], we have proposed a kind of teaching learning group mechanism that were introduced in the conventional teaching-learning-based optimization algorithm (namely MTLBO) to enhance solution quality and balance exploration and exploitation. Thus, this paper combines MPA with the teaching learning group mechanism to increase its performance, called MTLMPA. Firstly, the population updating mechanism of the MTLBO in teacher phase is integrated into the first phase of MPA, which can make predators target their preys successfully. Simultaneously, the convergence speed and accuracy of MPA can be improved. Secondly, the population updating mechanism of the MTLBO in learner phase is integrated into the third phase of MPA. Marine predators can simulate students' learning method and optimize their position quickly. Thus, the exploitation and exploration ability of MPA can be enhanced. Now, the variant of MPA is described in the following subsection.

3.1.   The population updating mechanism of MTLMPA in first phase

Phase 1: In this phase, a kind of group mechanism is introduced. Firstly, calculate the fitness function values of predators. Based on the fitness values, an elite predator is selected as the most knowledgeable individual in the population. Secondly, calculate the mean value of predators' position, noted as ${\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{y}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$. Based on the mean value, predators are divided into two groups. One group contains superior predators, another group are poor predators. During the food capture period, these superior predators update their position mainly rely on their experience and elite predator. And those poor predators mainly follow the elite predator to capture prey. Finally, all predators still move in Brownian motion. Therefore, the specific model is presented as follows.

where w is the inertia weight. $w = {w}_{start}-({w}_{start}-{w}_{end})\times \frac{iter}{Max\_Iter}$ The inertia weight is linear decreasing, which is helpful to improve the local development ability of the algorithm. $\mathit{sin}(\frac{\pi }{2}\frac{iter}{Max\_Iter})$, $\mathit{cos}(\frac{\pi }{2}\frac{iter}{Max\_Iter})$ are two weight coefficients.$\mathit{sin}(\frac{\pi }{2}\frac{iter}{Max\_Iter})$ increases with increasing iteration and gradually tends towards 1. $\mathit{cos}(\frac{\pi }{2}\frac{iter}{Max\_Iter})$ decreases with increasing iteration and gradually decreases to 0.

3.2.   The population updating mechanism of MTLMPA in third phase

Phase 3: This stage is the low speed ratio or when the predators is moving faster than the prey. This procedure is frequently associated with strong exploitation capability. In this phase, the Lévy flight mode is the best strategy for predators. When the new population updating mechanism is introduced, all predators are still divided into two groups based on their fitness function values. After sorting the fitness values, the first half of predators are regarded as the superior predator. Simultaneously, the rest of the predators are considered as inferior predator. Superior predators have strong predation capability, so they update their position rely on themself information and elite predator information during the predation. Moreover, superior predators can learn to hunt by themselves. Additionally, inferior predators have relatively weak predation ability, so that they only follow the elite predator to hunt. Based on the phenomenon, the specific mathematical model is summarized as follows.

Seen from Eq (7), the superior predators randomly chose a nearby predator $P\text{re}{\text{y}}_{\text{neighbor}}$ to follow. If the $P\text{re}{\text{y}}_{i}$ is better than $P\text{re}{\text{y}}_{\text{neighbor}}$, the $P\text{re}{\text{y}}_{i}$ mainly updates its position by itself. Otherwise $P\text{re}{\text{y}}_{i}$ learns from $P\text{re}{\text{y}}_{\text{neighbor}}$. The weight coefficient $\mathit{cos}(\frac{\pi }{2}\frac{iter}{Max\_Iter})$ is introduced to improve convergence speed and local exploitation ability.

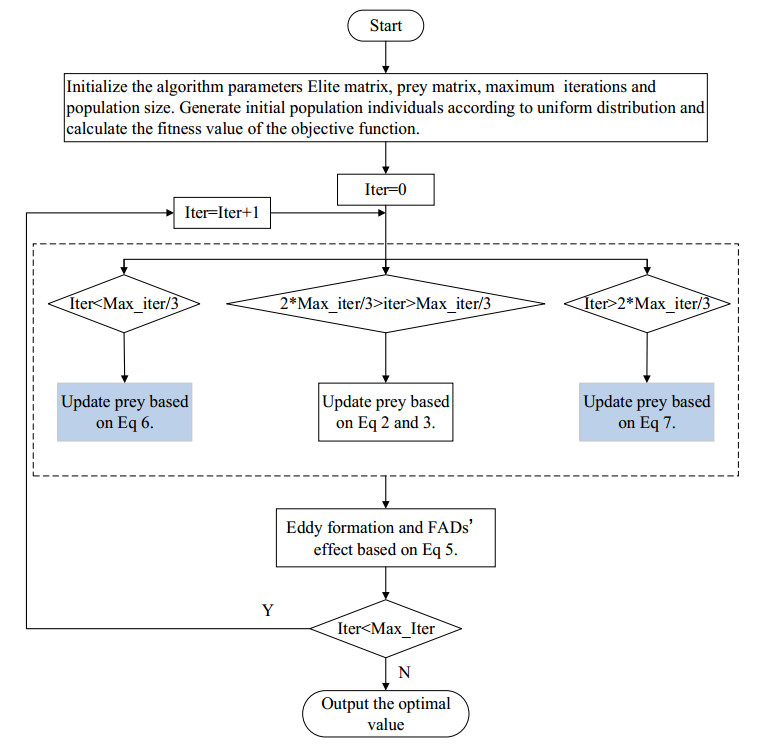
The flow chart of MTLMPA is presented as follows.

4.   Performance testing

In order to verify the effectiveness of MTLMPA, 23 benchmark testing functions are applied to evaluate MTLMPA's performance in exploration, exploitation and minimization. The detailed description of these functions are presented in Table 1. Seen from Table 1, TF1–TF7 belong to the unimodal functions which are used to evaluate the exploitation capability of MTLMPA. TF8–TF13 simulate multi-modal functions to test the exploration performance of MTLMPA. The functions TF14–TF23 with fixed dimensions are used to test the algorithm's performance in low dimensions. In addition, 29 CEC-2017 testing functions are used to verify the performance of MTLMPA as well.

All testing were conducted on a single machine. CPU: Intel (R) Core (TM) i5-6300HQ CPU @ 2.30 GHz, Windows10 operating system and MATLAB R2016a. The population number is set as 40. The maximum iteration number is set as 500. In order to reduce statistical errors, each algorithm is independently simulated 30 times.

4.1.   Comparison with MPA

In this subsection, the performance comparisons between MTLMPA and MPA are given on 23 testing benchmark functions with 50 dimensions, including exploitation capability evaluation, exploration capability evaluation and algorithm convergence ability. For every testing function, the MTLMPA and MPA independently run 30 times to find the global optima solution, separately. And then, we find the best solution in the thirty times results, which is denoted as Best. Finally, we calculate the mean and standard deviation of the thirty results, separately. The mean value is recorded as Ave and the standard deviation is abbreviated as Std. The mean value represents convergence accuracy and the standard deviation represents stability of algorithm. Noted that: the smaller the mean and standard deviation, the better the algorithm performs.

4.1.1.   Exploitation capability evaluation

Uni-modal functions are real-valued functions that have a single strictly local maximum in the interval. There is only one global optimal solution in each testing function. These functions are fitness to evaluate the exploitation ability of the optimization algorithm. Therefore, functions TF1–TF7 are used to investigate the exploitation capability of MPA and MTLPA. The experiment results are recorded in the Table 2. The best performance index is presented in bold font.

Seen from Table 2, we can find that the proposed MTLMPA shows better performance than conventional MPA on five functions, including TF1, TF2, TF3, TF4, TF7. On functions TF5 and TF6, the MPA presents relatively better performance than MTLMPA. Therefore, these experiment results reveal that the MTLMPA has stronger exploitation capability than the MPA.

4.1.2.   Exploration ability evaluation

In general, multi-modal testing functions have a large number of local optimal values, so that these functions are fitness to verify the exploration ability of optimization algorithm. Functions TF8–TF13 are the multi-modal function with high dimensions. Functions TF14–TF23 are the multi-modal function with fixed (low) dimensions. Therefore, these multi-modal functions are used to evaluate the exploration ability of MTLMPA and MPA. Experiment results of MTLMPA and MPA are recorded in Tables 3 and 4, separately.

Shown in Table 3, for high-dimensional multi-modal functions, the proposed MTLMPA presents better performance than MPA on TF8–TF11. Moreover, the two optimization algorithms obtain similar results on TF12 and TF13. Seen from Table 4, for fixed dimensional multi-modal functions, MTLMPA and MPA can find the global optima solution on all testing functions. Although they have the similar convergence accuracy, the MTLMPA owns stronger algorithm stability than conventional MPA. In conclusion, the MTLMPA has better exploration capability than MPA on most testing functions.

4.1.3.   Analysis of convergence performance

In this subsection, several simulation Figures of testing functions are given to analyse the convergence accuracy and convergence speed of two algorithms. Seen from these figures, it is easy to contrast the convergence performance of the two algorithms. The blue line is the convergence curve of MPA. The green line is the convergence curve of MTLMPA. Seen from Figures 2 to 7, we can find that the MTLMPA has better convergence accuracy and convergence speed than MPA.

4.1.4.   Test on CEC-2017 functions

The CEC-2017 contains 29 benchmark functions for evaluating optimization problems. These functions can be divided into four categories: uni-modal function, multi-modal function, mixed function and combined function. The uni-modal function and the multi-modal function would be much more complex in this section. The combined function and mixed function are considered in test. In the mixed function, the variable is randomly divided into several sub-components, and different basic functions are used for different sub-components. The composition function better integrates the properties of the sub-functions and maintains the continuity of the optimal solution. This section compared MPA with MTLMPA on CEC-2017. The specific results are listed in Table 5.

As can be seen from the Table 5, the results of MPA and MTLMPA are similar in terms of optimal values. However, there are huge differences in mean and standard deviations. The MTLMPA has a strong stability. The MTLMPA converged to the optimal value each time with 500 iterations. The MPA did not converge to the optimum in the partial tests and the standard deviations are also large.

The figures show that the convergence value of MTLMPA is significantly better than MPA. And there exist no convergence in some results of MPA. In conclusion, MTLMPA has strong stability and can accurately converge to the optimal values. Its application value is high compared with MPA.

4.2.   Performance comparison with other algorithms

In order to further evaluate the performance of MTLMPA, 23 benchmark testing functions with different dimensions (including 10, 50,100 dimensions) are used. Moreover, several state-of-the-art optimization algorithms are applied and considered as comparison algorithm, including PSO, GWO, SCA, WOA, CS, KH, MPA and TLBO etc. For the fairness of the comparison, the number of population individual is set as 40 for every algorithm, the maximum iteration number is set as 500, each algorithm is independently simulated 30 times. The unique parameters of every algorithm are set based on their requirements.

As illustrated in Table 6, MTLMPA can still converge to an accurate value in the situation of low dimension. MTLMPA has a significantly higher accuracy than MPA. MTLMPA and KH algorithms continue to have significant benefits over other algorithms in TF1, TF2, TF3, TF4, TF7, TF9, TF11, TF13. In particular, MTLMPA performs well than KH in TF5, TF6, TF10, TF12. At the same time, the MTLMPA is stable. And the standard deviation of 30 cycles is small. It can be seen that MTLMPA converges faster than other algorithms in TF2, TF3, TF4, TF6, TF7, TF9, TF10, TF11, TF12. And the algorithm is stable. It can find the optimal solution to the maximum extent within its own allowable range.

As can be observed from the Table 8, MTLMPA performs the best performance on functions TF3, TF5, TF9, TF10, TF11, TF14, TF15, TF16, TF17, TF18, TF19 and TF20. Although others functions are not optimal, it is not an order of magnitude away from optimal accuracy. In general, MTLMPA is an algorithm that can accurately converge to the optimal value.

At the same time, all the standard deviations of each algorithm are compared in Table 9. MPA has strong stability. MTLMPA also has excellent performance in standard deviation. It surpassed most of the algorithms on TF2, TF3, TF4, TF7, TF9, TF10, TF11, TF13. To better illustrate each algorithm's convergence performance, the simulating curves are produced as illustrated in the image below. Seen from these figures, the convergence speed and convergence accuracy are better than other algorithms on most functions.

The following Tables 10 and 11 summarize the mean and standard deviation of all the algorithms for 100 dimensions functions. As can be seen from the two tables, MTLMPA algorithm still performs well on TF1, TF2, TF3, TF4, TF7, TF9, TF10, TF11, TF13. And the MTLMPA algorithm is stable and performs well on TF1, TF2, TF3, TF4, TF7, TF9, TF10, TF11, TF12.

In order to clearly observe the convergence performance of MTLMPA, Figures 30–38 are given. The horizontal axis is the iteration number. And the vertical axis represents the fitness values of testing functions for all optimization algorithms. The green line presents the performance of MTLMPA. Seen from these figures, the convergence speed and convergence accuracy are better than other algorithms on most functions.

5.   Conclusions

To improve the convergence performance and balance the exploitation and exploration ability of MPA, a kind of modified marine predators algorithm hybridized with teaching-learning mechanism (MTLMPA) is proposed. Compared with the conventional MPA, two different population group mechanisms are separately introduced in the first phase and third phase of MTLMPA to update the individuals' position. The new population individual mechanisms can improve the solution quality and balance the exploration and exploitation. To verify the performance of MTLMPA, 23 benchmark testing functions and 29 CEC-2017 functions are used. Experimental results show that the proposed MTLMPA has better convergence performance and stronger stability than other state-of-the-art heuristic optimization algorithms on most functions.

In the future, we will focus on the following tasks:

Based on the MTLMPA, a novel multi-objective MTLMPA will be designed to solve multi-objective optimization problems. The MTLMPA will be further improved to address dynamic constrained optimization problems.

Acknowledgments

Funding: This work is supported by the National Natural Science Foundation of China (Grant No. 62203332) and the Natural Science Foundation of Tianjin (Grant No. 20JCQNJC00430) and The Special fund Project of Tianjin Technology Innovation Guidance (Grand No. 21YDTPJC00370) and the Technical Innovation Guide Foundation of Tianjin (Grant No. 20YDTPJC00320) and College Students' Innovative Entrepreneurial Training Plan Program (Grant Nos. 202010069066, 202110069034, 202110069003).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.