Figure 1.
XRD patterns (using CuKα radiation) of the (a) Fe3O4, rGO, RAM1 sample (Mn0.25Fe2.75O4/rGO) and (b) MnxFe3–xO4 (x = 0.25, 0.50, 0.75) (Reprinted from Ref. [21] with permission).
Physics-informed neural networks (PINN) have lately become a research hotspot in the interdisciplinary field of machine learning and computational mathematics thanks to the flexibility in tackling forward and inverse problems. In this work, we explore the generality of the PINN training algorithm for solving Hamilton-Jacobi equations, and propose physics-informed neural networks based on adaptive weighted loss functions (AW-PINN) that is trained to solve unsupervised learning tasks with fewer training data while physical information constraints are imposed during the training process. To balance the contributions from different constrains automatically, the AW-PINN training algorithm adaptively update the weight coefficients of different loss terms by using the logarithmic mean to avoid additional hyperparameter. Moreover, the proposed AW-PINN algorithm imposes the periodicity requirement on the boundary condition and its gradient. The fully connected feedforward neural networks are considered and the optimizing procedure is taken as the Adam optimizer for some steps followed by the L-BFGS-B optimizer. The series of numerical experiments illustrate that the proposed algorithm effectively achieves noticeable improvements in predictive accuracy and the convergence rate of the total training error, and can approximate the solution even when the Hamiltonian is nonconvex. A comparison between the proposed algorithm and the original PINN algorithm for Hamilton-Jacobi equations indicates that the proposed AW-PINN algorithm can train the solutions more accurately with fewer iterations.
Citation: Youqiong Liu, Li Cai, Yaping Chen, Bin Wang. Physics-informed neural networks based on adaptive weighted loss functions for Hamilton-Jacobi equations[J]. Mathematical Biosciences and Engineering, 2022, 19(12): 12866-12896. doi: 10.3934/mbe.2022601
| [1] | Khang Duy Vu Nguyen, Khoa Dang Nguyen Vo . Magnetite nanoparticles-TiO2 nanoparticles-graphene oxide nanocomposite: Synthesis, characterization and photocatalytic degradation for Rhodamine-B dye. AIMS Materials Science, 2020, 7(3): 288-301. doi: 10.3934/matersci.2020.3.288 |
| [2] | Ayu Azera Izad, Rosimah Nulit, Che Azurahanim Che Abdullah, A'fifah Abdul Razak, Teh Huey Fang, Mohd Hafiz Ibrahim . Growth, leaf gas exchange and biochemical changes of oil palm (Elaeis guineensis Jacq.) seedlings as affected by iron oxide nanoparticles. AIMS Materials Science, 2019, 6(6): 960-984. doi: 10.3934/matersci.2019.6.960 |
| [3] | Min Kang, Hai Zhou . Facile Synthesis and Structural Characterization of Co3O4 Nanocubes. AIMS Materials Science, 2015, 2(1): 16-27. doi: 10.3934/matersci.2015.1.16 |
| [4] | Leydi J. Cardenas F., Josep Ma. Chimenos, Luis C. Moreno A., Elaine C. Paris, Miryam R. Joya . Enhancing Co3O4 nanoparticles: Investigating the impact of nickel doping and high-temperature annealing on NiCo2O4/CoO heterostructures. AIMS Materials Science, 2023, 10(6): 1090-1104. doi: 10.3934/matersci.2023058 |
| [5] | Dao Viet Thang, Nguyen Manh Hung, Nguyen Cao Khang, Le Thi Mai Oanh . Structural and multiferroic properties of (Sm, Mn) co-doped BiFeO3 materials. AIMS Materials Science, 2020, 7(2): 160-169. doi: 10.3934/matersci.2020.2.160 |
| [6] | Muhammad Yakob, Hamdani Umar, Puji Wahyuningsih, Rachmad Almi Putra . Characterization of microstructural and optical CoFe2O4/SiO2 ferrite nanocomposite for photodegradation of methylene blue. AIMS Materials Science, 2019, 6(1): 45-51. doi: 10.3934/matersci.2019.1.45 |
| [7] | Mohamed Jaffer Sadiq Mohamed, Denthaje Krishna Bhat . Novel ZnWO4/RGO nanocomposite as high performance photocatalyst. AIMS Materials Science, 2017, 4(1): 158-171. doi: 10.3934/matersci.2017.1.158 |
| [8] | Narayan Poudyal, Kinjal Gandha, Kevin Elkins, J. Ping Liu . Anisotropic SmCo5/FeCo core/shell nanocomposite chips prepared via electroless coating. AIMS Materials Science, 2015, 2(3): 294-302. doi: 10.3934/matersci.2015.3.294 |
| [9] | Dao Viet Thang, Le Thi Mai Oanh, Nguyen Cao Khang, Nguyen Manh Hung, Do Danh Bich, Du Thi Xuan Thao, Nguyen Van Minh . Structural, magnetic and electric properties of Nd and Ni co-doped BiFeO3 materials. AIMS Materials Science, 2017, 4(4): 982-990. doi: 10.3934/matersci.2017.4.982 |
| [10] | Dung Nguyen Trong, Van Cao Long, Phu Nguyen Dang, Ştefan Ţălu . A molecular dynamics study concerning the effect of high-temperature and high-pressure on the structure and phase transition of Fe2O3 material. AIMS Materials Science, 2022, 9(3): 406-429. doi: 10.3934/matersci.2022024 |
Physics-informed neural networks (PINN) have lately become a research hotspot in the interdisciplinary field of machine learning and computational mathematics thanks to the flexibility in tackling forward and inverse problems. In this work, we explore the generality of the PINN training algorithm for solving Hamilton-Jacobi equations, and propose physics-informed neural networks based on adaptive weighted loss functions (AW-PINN) that is trained to solve unsupervised learning tasks with fewer training data while physical information constraints are imposed during the training process. To balance the contributions from different constrains automatically, the AW-PINN training algorithm adaptively update the weight coefficients of different loss terms by using the logarithmic mean to avoid additional hyperparameter. Moreover, the proposed AW-PINN algorithm imposes the periodicity requirement on the boundary condition and its gradient. The fully connected feedforward neural networks are considered and the optimizing procedure is taken as the Adam optimizer for some steps followed by the L-BFGS-B optimizer. The series of numerical experiments illustrate that the proposed algorithm effectively achieves noticeable improvements in predictive accuracy and the convergence rate of the total training error, and can approximate the solution even when the Hamiltonian is nonconvex. A comparison between the proposed algorithm and the original PINN algorithm for Hamilton-Jacobi equations indicates that the proposed AW-PINN algorithm can train the solutions more accurately with fewer iterations.
The development of telecommunications technology certainly cannot be separated from the use of electromagnetic waves, one of which is radar (radio detection and ranging) waves. The use of radar waves is superior in military applications [1], antenna technology [2], and radar wave processing [3]. Along with the rapid development of technology, several problems were found due to the use of radar. These problems such as electromagnetic wave pollutions [4] and human health problems [5] cause electromagnetic wave interference [6]. In the last decade, some of the above problems can be overcome by the use of radar absorbing material/RAM [7,8]. One example of the application is coating the body of military vehicles such as tanks or military aircraft [9]. Radar transmitted from the source is ensured to be absorbed and dissipated by RAM so that it can reduce the results of radar reflection of radar waves from an object [10].
Generally, RAM works on the principle of combining a dielectric material and a magnetic material, so that the incoming radar wave will be absorbed through an impedance match to a polarizing effect [11,12]. The main ingredients of RAM basically have magnetic and electrical properties that aim to produce magnetic and dielectric losses [13]. Magnetic metal powders, ferrites, and nanotubes are some of the magnetic materials that have high adhesion and density [14,15]. Ferrimagnetic materials such as Fe3O4 based on natural iron sand were chosen as magnetic materials, because they have high saturation magnetization, good flexibility [16], heat resistance [12], good chemical and thermal stability [17], high permeability, and low cost of synthesis [18,19]. However, Fe3O4 is not sufficient in RAM applications because it only produces a reflection loss (RL) of −5 dB [20]. Thus, it is necessary to have a combination of other materials that can increase the dielectric loss value. Efforts to increase the value of dielectric loss in Fe3O4 are generally carried out by doping divalent cations such as Mn2+. This is important, because it provides an opportunity to improve the dielectric and magnetic properties [18,21]. Furthermore, Mn2+ has soft magnetic properties which affect the low coercivity field, making it suitable for RAM applications [22,23,24].
Regarding the methods used in recent years, several synthesis methods were found, namely solid state reaction [25], solvothermal [26], ball milling [27], sol-gel [28], dan co-precipitation [29]. From the various synthesis methods, the co-precipitation method has advantages in the form of economic value, easy to perform, fast processing and relatively homogeneous results [30,31]. Furthermore, the co-precipitation method can be applied to various materials, including natural materials. In this research, MnxFe3–xO4 was synthesized by co-precipitation method using natural materials based on iron sand. Iron sand was selected and taken from Bajul Mati Beach because it contains a fairly high magnetite material, which is 90.4% [32,33].
To improve the absorption performance of radar waves, a material with better dielectricity is needed. Previous studies reported that MnxFe3–xO4 materials still have limitations, such as low permittivity and complex permeability [24,34]. In addition, one of the main causes of limitations in the application of MnxFe3–xO4 RAM is the high density value [18,35], low stability, and small dielectric loss making it difficult to apply as RAM [13].
Carbon-based materials are often used as dielectric materials for RAM purposes because they have advantages such as high electrical conductivity and low density [36,37]. Saeed et al. carried out the synthesis of magnetic nano composites/MWCNT and they obtained excellent wave absorption results [38]. In another study, Taufiq et al. synthesize magnetic materials combined with activated carbon to increase the value of RL [11]. According to the research of Zhao et al., reduced-graphene oxide (rGO) materials can also be combined with magnetic materials for the purpose of increasing reflection loss (RL) [39].
Regarding the selection of rGO, the advantages of rGO include materials with good dielectric properties, low density, high surface area and good electrical conductivity [40,41], so it is necessary to stabilize the density and dielectric properties of the material from RAM to obtain optimal radar wave absorption capability. Furthermore, the residual and functional group defects cause a polarizing effect that contributes to the increase in the RL value [42]. Thus, in this study, the synthesis of rGO based on coconut shell waste material as a precursor with MnxFe3–xO4 was carried out. The choice of coconut shell used as a dielectric material because it has a carbon element with a content that reaches 80 wt% [43], so it is able to absorb radar waves well [44]. Meanwhile, rGO has properties in hydroxyl and carboxyl structural defects that support the absorption of radar waves through the principle of surface polarization [36,40]. In addition, rGO has a low density and reduces the aggression of MnxFe3–xO4, making it suitable for use as an antiradar dielectric material [45]. The method used for the synthesis of rGO is solid state reaction, because the method is simple. Then, the process of combining MnxFe3–xO4 (x = 0.25, 0.50, 0.75) with rGO in the form of MnxFe3–xO4/rGO nano composites through the coprecipitation method. These results present a discussion of the structure, elemental content, morphology, and RAM potential of the MnxFe3–xO4/rGO nanocomposite.
The materials used in this study were iron sand obtained from Bajul Mati Beach, Malang as the main component for Fe and coconut shell waste obtained from Malang. Then, the powder of manganese(II) chloride hydrate (MnCl2∙4H2O, 99.99%, Sigma-Aldrich, Germany), chloride acid (HCl, 99.99%, Merck, Germany), ammonium hydroxide (NH4OH, 99.99%, Merck, Germany), ethanol (EtOH, 100%, Merck, Germany), distilled water and ultrafiltered water (MQ).
The rGO material was synthesized using the solid-state reaction method. The process began with the cleaned coconut shell which. The coconut shells were washed with distilled water and dried in the sun for 3 d. After drying, the coconut shell was burned to form charcoal. Furthermore, the charcoal was sieved using a 200 mesh sieve to obtain charcoal powder. Then, the sample was carbonated at 400 °C for 5 h.
The MnxFe3–xO4/rGO nanocomposite was synthesized using the co-precipitation method with the following steps. In general, the MnxFe3–xO4 synthesis procedure has been corresponded in previous studies [21]. At first, the iron sand was washed and dried in the sun to dry. It was then separated using permanent magnets to remove impurities. Next, 20 g of iron sand was dissolved in 58 mL of HCl with a stirring speed of 720 rpm for 30 min at room temperature. The solution was filtered and separated from the residue using filter paper to obtain a solution of FeCl2 and FeCl3. Simultaneously, the rGO powder was dispersed into 50 mL of distilled water and sonicated for 2 h at room temperature. Then, each mole fraction, namely: x = 0.25 was 1.36 g, x = 0.50 was 2.72 g, x = 0.75 was 4.09 g MnCl2∙4H2O and rGO suspension was added to a mixture of 18 mL of FeCl2 and FeCl3 solution. The mixing process was carried out with a stirring speed of 720 rpm which was then titrated with 25 mL of NH4OH at room temperature. This synthesis process was carried out for 30 min until a black precipitate was produced. The precipitate was washed repeatedly using distilled water until it was odorless with a pH value of 7. Then, each precipitate was filtered using filter paper and dried in an oven at 100 ℃ for 1 h. After drying, 1.5 g of MnxFe3–xO4/rGO material was compacted with manual pressure to become pellets with a diameter of 0.5 cm and thickness of 1 cm. It was sintered at 400 ℃ for 1 h. The synthesized material was characterized by instruments. The rGO samples were coded as rGO and the MnxFe3–xO4/rGO samples with various mole fraction x = 0.25, 0.50, 0.75 coded respectively RAM1, RAM2, RAM3 for Mn0.25Fe2.75O4, Mn0.5Fe2.5O4, and Mn0.75Fe2.25O4.
X-ray diffraction characterization (XRD; PANalytical, X'Pert Pro, Cu-Kα 1.5406 Å) was used to determine the phase, lattice parameters, and crystal size of the samples. Investigation of the lattice parameters, crystal size, and density of MnxFe3–xO4/rGO was carried out based on the data XRD with refinement rietveld method using Rietica program. Next, identification of microscopic morphology and elemental content was used for Scanning Electron Microscopy (SEM, FEINSPECT-S50) characterization. Particle Size Analyzer (PSA, Mastersizer 3000) was used to identify the particle size of the samples. Then, to study the magnetic properties and absorption ability of the radar waves of the MnxFe3–xO4/rGO nanocomposite, Vector Network Analyzer (VNA, Advantest R3770, 8–12 GHz (X-Band)) and Permagraph (Magnet Physik Streigroever GmbH) were used to study the magnetic properties and absorption capabilities of radar waves.
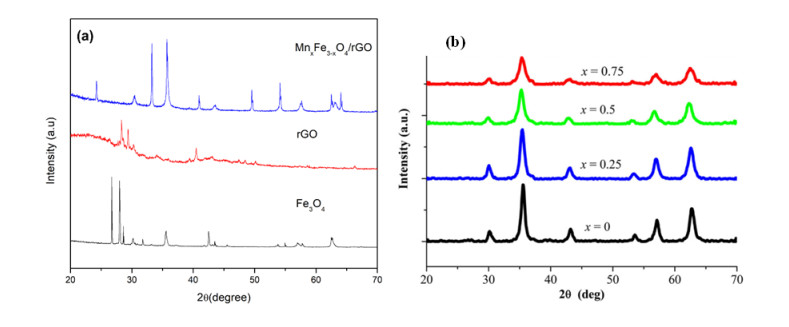
XRD patterns of all the samples are displayed in Figure 1. First, the data confirm the presence of only magnetite (PDF No. 19-0629) without any impurities for all samples from other study. In that study, the data of XRD supported by lattice parameter and crystal volume (Figure 2). The diffraction peaks shift to a lower angle as x increases, implying that the lattice parameter increases with Mn2+ incorporation [21]. Besides, the ionic radius of Mn2+ (0.89 Å) is larger than that of Fe2+ (0.77 Å) and Fe3+ (0.64 Å) [46]. Exactly, Mn2+ ions were inserted into Fe3O4 succesfully by replacing Fe2+ or Fe3+ ions to form MnxFe3−xO4 partially. Moreover, the lattice parameters of the MnxFe3–xO4 with x = 0.25 to 0.50 increased from 8.377 to 8.439 Å.
In this study, the structure of the MnxFe3–xO4/rGO nanocomposite was successfully characterized. The results of XRD characterization were carried out on samples of iron sand (MnxFe3–xO4), coconut shell (rGO), and MnxFe3–xO4/r-GO nanocomposites shown by RAM1 samples (Mn0.25Fe2.75O4/rGO). The XRD MnxFe3–xO4 diffraction pattern shows that iron sand has formed a crystalline phase consisting of 93.4% magnetite (Fe3O4) compound and 6.6% hematite (F2O3) compound with a hexagonal structure with space group P63/mmc (reference code: 98-002-9041). In the rGO, the diffraction pattern consists of the main elements of carbon and oxides detected with the chemical formula C50O12H72. Based on Figure 1, the synthesized rGO sample qualitatively shows two amorphous peaks at 2θ = 24° (002) and 43° (001) according to Acharya et al. [47] by modified Hummers method and Lavin-Lopez et al. [48] by chemical reduction, heat reduction and multiphase reduction methods. This study confirmed that coconut shell was successfully synthesized into rGO material through the solid-state reaction method.
The nanocomposite compound showed a two-phase structure consisting of MnxFe3–xO4 and rGO compounds. The diffraction pattern of the nanocomposite sample is different compared to the single-phase rGO (a) and MnxFe3–xO4 (b). Therefore, the two main phases which are MnxFe3–xO4 and rGO respectively can be identified in the diffraction pattern of the nanocomposite without the appearance of additional diffraction peaks. The MnxFe3–xO4 (a) pattern appears more than the rGO pattern (b), this is because the amount of MnxFe3–xO4 content is more than the rGO content.
For sample RAM1, the X-ray diffraction peak was identified from MnxFe3–xO4/rGO particles at 2θ = 29.9°; 35.2°; 42.9°; 53.3°; 56.6°, and 62.5° which represent Miller indices (220), (311), (400), (422), (511) and (440). The X-ray diffraction pattern of the MnxFe3–xO4/rGO nanocomposite shows a characteristic spinel ferrite structure and no other phases are formed [28,49,50]. The structural study confirms spinel structure formation with Fd3m space group for the 0 ≤ x ≤ 0.5 samples. The combination with rGO did not significantly affect the shift in the X-ray diffraction pattern of MnxFe3–xO4, which has been clarified by previous studies [21,51,52]. The RAM1 sample also shows no rGO peak was found which could be caused by the XRD characterization scan (2θ angle increment) which was too fast. In another report, the disappearance of the X-ray diffraction pattern of rGO caused by the interfacial bonding of MnxFe3–xO4 with rGO resulted in a separate structure of rGO thus preventing the repetition of rGO [18]. This was also clarified by a previous study [21]. The hierarchical size of the nanocomposites was explained in detail the particle size with Particle Size Analyzer (PSA).
The sketch of the doping of Mn into Fe3O4 can be seen in Figure 3. The composition and cationic distributions of the MnxFe3–xO4 particles for x composition between 0 and 1 can be analyzed using the following formula in Eq 1 [53]:
| [Mn2+xFe3+1−x]𝐴[Fe2+1−xFe3+1+x]𝐵O2−4 | (1) |
The MnxFe3–xO4/rGO composite fabrication process was carried out using the co-precipitation method, by first doping Mn on Fe3O4 which was reacted with HCl to produce FeCl2 and FeCl3. This was carried out to get the same phase, so that the reaction can take place [54]. MnxFe3–xO4/rGO composite preparation through stoichiometric calculations has resulted in composite compounds that have been mixed with the ultrasonic method. Variations in the composition were carried out as many as 3, namely x = 0.25, x = 0.5, and x = 0.75, resulting in 3 (three) samples named consecutively as RAM1, RAM2, and RAM3. The purpose of adding Mn to Fe3O4 is to improve the performance of Fe3O4 as a radar absorbing material (RAM). In line with the research of Taufiq et al. [54]. stated that Fe3O4 still has a low absorption ability of radar waves. The reaction that occurs is described in Eq 2.
| (2–x)FeCl3+FeCl2+xMnCl2+(8–x)NH4OH+4H2O→MnxFe3–xO4+(8–x)NH4Cl+(8–x)H2O | (2) |
The iron metal ions (Fe2+ and Fe3+) enclosed in the square bracket represent those in the octahedral positions, while the other metal ions (Mn2+ and Fe3+) in the round bracket represent those in the tetrahedral positions depending on the x value. Six oxygen atoms surround the metal ions in the octahedral sites, while four oxygen atoms surround the metal spinel structure can be classified into three types: inverse, ions in the tetrahedral sites. Generally, Fe3O4 has an inverted spinel structure [54]. In the MnxFe3–xO4 system, the spinel, which has eight Fe3+ ions located in the tetrahedral mixed, and normal spinel. The systems for x = 0.25, 0.5, and 0.75 form mixed spinel structure because Mn2+ ions partially shift the Fe3+ ions in the tetrahedral positions. Physically, the MnxFe3–xO4 crystal structure modeled using the Vesta program can be seen in Figure 4 below.
Figure 5 relates the rGO structure modeled using the ChemDraw program. Basically, graphene is composed of thin atoms of 2D sp2 carbon layers that form a honeycomb-like structure. Meanwhile GO, which is a graphene derivative, contains sp2 and sp3 carbons and binds to a fairly high hydroxyl group (–OH) [55,56]. This is very different from rGO which has few oxygen groups and sp3 carbon. Consequently, rGO is more similar to graphene and also has structural defects [57].
The curve of the measurement results with PSA can be seen in Figure 6. The particle size characterization of the iron sand sample that has been separated from the non-magnetic material that has been mashed and filtered shows that the raw material has a homogeneous particle size with a single peak with an average value of 531.8 nm (Table 1). This powder was detected to be still in micro size because it still has a size of more than 100 nm. This is because there is still a coagulation process or clumping at the time of measurement, resulting in a precipitate [58]. The particle size characterization for the detected rGO samples had an average particle size of 1359 nm. This size is larger than the iron sand sample. The deposition process that occurs in rGO powder is faster than iron sand powder, so the clumping process is faster and is detected as having a larger particle size.
| Samples | Distribution results | Z-Avg (nm) | |||
| Size (d.nm) | % Int | σ | %Pd | ||
| Fe3O4 | 369.3 | 53.3 | 93.00 | 25.2 | 531.8 |
| 194.8 | 46.7 | 41.21 | 21.2 | ||
| rGO | 835.0 | 100.0 | 134.9 | 16.2 | 1359 |
| Mn0.25Fe2.75O4 | 416.8 | 100.0 | 63.62 | 15.3 | 1049 |
| Mn0.5Fe2.5O4 | 613.9 | 100.0 | 110.5 | 18.0 | 1432 |
| Mn0.75Fe2.25O4 | 440.4 | 100.0 | 53.65 | 12.2 | 1531 |
DownLoad:
CSV
In general, the addition of the composition of Mn and rGO to Fe3O4 nanoparticles causes the crystallinity level of Fe3O4 to increase teorically [12]. This is proven in Figure 6 which shows that the distribution peaks of MnxFe3O4/rGO in nanocomposites (x = 0.25 to x = 0.75) appear sharper when compared to pure Fe3O4. The increase in Mn composition in MnxFe3–xO4/rGO nanocomposites results in an increase in the intensity of the MnxFe3–xO4/rGO peak except for x = 0.75 which is lower when compared to x = 0.5. This is because the x = 0.75 particle distribution is lower than other nanocomposites of particle sizes (440.4 nm), but the average of particle size from x = 0.25 to x = 0.75 increase. The increase in particle size is caused by the large number of Mn particles that push Fe. Theoretically, the size of Fe2+ and Fe3+ ions is larger than that of Mn2+ ions. However, when the number of Mn2+ ions is more pressing the Fe2+ ions will result in clumping, resulting in a larger particle size than before being pushed by Mn2+. This phenomenon is theoretically reinforced that in the voltaic series, Mn is to the left of Fe, so it has more reactive properties and is stronger against Fe. The more Mn metal ions push Fe from Fe3O4, the larger the particle size of the MnxFe3–xO4 nanocomposite. This is also confirmed in Table 1 which shows the particle size of the sample.
Uniquely, the Fe3O4 available in this work did not produce polymorphs. Polymorphs that are often produced in the synthesis of Fe3O4, like α-Fe2O3, γ-Fe2O3, dan α-Fe3O4 [59]. This is because the synthesized Fe3O4 comes from natural iron sand. Natural iron sand contains stable Fe2O3, so it does not cause porosity which causes Fe2O3 variations in Fe3O4 synthesis [54].
The SEM images of MnxFe3–xO4/rGO nanocomposites with Mn doping composition of x = 0.5 is shown in Figure 7. As shown in Figure 7a, the morphology of the nanocomposites consists of 3 particle shapes namely spheres, chunks, and worm-like structures. Sequentially, these shapes describe the Fe3O4 nanoparticles, Mn [60,61], and rGO [62]. Qualitatively, it is observed that the sphere of Fe3O4 tends to agglomerate. The size of Fe3O4 nanoparticles is smaller than that of Mn which has relatively irregular chunks. In addition, the Mn surface also shows some agglomeration of Fe3O4, while rGO fills the gap between Fe3O4 and Mn [63]. Illustrated in Figure 5, rGO is a carbon material that is activated with acids to form OH-functional groups, so that the rGO will bind to the positive charge of Fe3O4 which causes the Fe3O4 to fill the surface of the carbon material. Based on Figure 5a, few rGO surfaces are covered by agglomeration of Fe3O4. This is because the density of Fe3O4 is higher than that of rGO [64]. Figure 5b indicates the morphology of Mn-doped Fe3O4 nanoparticles with a magnification of 50,000 and shows that the Fe3O4 and Mn nanoparticles are evenly dispersed on the rGO surface. Furthermore, the EDX results show that the composition of heavy elements C, O, and Fe are 28.72, 36.17, and 27.78% and another is Mn, respectively, which confirms the presence of Fe3O4 nanoparticles, rGO, and Mn that form MnxFe3–xO4 composites. The presence of Fe3O4 was confirmed by the presence of Fe and O elements. Meanwhile, the rGO were confirmed by the presence of element C, and doping of Mn were confirmed by the presence of element Mn.
Magnetic properties in the form of hysteresis loops for MnxFe3–xO4/rGO nanocomposite samples can be seen in Figure 8. All curves show the characteristics of soft and tall soft magnetic hysteresis loops.
A summary of the magnetic properties that obtained in this research, can be seen in Table 2.
| Samples | Br (kG) | HcJ (kOe) | Hmax (kOe) |
| Mn0.25Fe2.75O4 | 0.12 | 0.132 | 14.370 |
| Mn0.5Fe2.5O4 | 0.11 | 0.048 | 12.275 |
| Mn0.75Fe2.25O4 | 0.10 | 0.045 | 8.880 |
DownLoad:
CSV
The sample of Mn0.25Fe2.75O4 had the highest remanent induction (Br), coercivity (HcJ), and the highest magnetic field strength (Hmax) compared to the other samples, 0.12 kg, 0.132 kOe, and 14.370 kOe, respectively. The results of this characterization indicate that the effect of composition affects the magnetic properties. The addition of Mn elements reduces the values of Br, HcJ, and Hmax. Theoretically, Fe has higher magnetic properties than Mn. Thus, when more Mn replaces Fe, the magnetic properties will decrease. However, it must be analyzed further through the results of the reflection loss of the synthesized sample.
Reflection loss is a characteristic that shows the ability of radar wave absorption from MnxFe3–xO4/rGO. Reflection loss of each sample has been characterized using VNA with the results of the reflection loss and frequency curves as shown in Figure 9. The results show that there has been absorption of electromagnetic waves in the frequency range between 7–13 GHz with the absorption frequency range at 2–14 GHz. At this frequency, it shows that the MnxFe3–xO4/r-GO nanocomposite can be applied as a RAM material in the X-Band 8–12 GHz frequency range. Figure 9 shows RL of the MnxFe3–xO4/rGO nanocomposites at a frequency of 8–12 GHz which were calculated by using Eqs 3 and 4.
| RL=20log |Zin−Z0||Zin+Z0| | (3) |
Zin value was calculated by using Eq 3 below.
| Zin=Z0√μrϵr tanh [j2πfdc√μrϵr] | (4) |
where Zin and Zin are input and output impedance values. While µr and Ɛr are the permeability and complex permittivity of the material, c represents the velocity of the radar in a vacuum, f is the frequency of radar, and d is the thickness of the material when tested [65].
In Figure 9 for the sample of Mn0.25Fe2.75O4/rGO nanocomposite, absorption of electromagnetic waves has occurred in the frequency range between 8.9–11.5 GHz with the absorption peak frequency at 11.5 GHz of −11.8 dB with a thickness of 1.5 mm adsorption field. Likewise for the Mn0.5Fe2.5O4/rGO nanocomposite sample, absorption occurs in the frequency range between 9–11.3 GHz with the absorption peak frequency at 11.3 GHz of −11.5 dB. Meanwhile, for the Mn0.75Fe2.25O4/r-GO nanocomposite sample, absorption has occurred in the frequency range between 8.8–11.5 GHz with the absorption peak frequency at 11.5 GHz of −1.95 dB.
Fe3O4 has an RL of −5.58 dB at a frequency of 10.58 GHz. The low RL value owned by Fe3O4 is due to the fact that this sample only consists of magnetic material, thus RAM only absorbs the magnetic part of the radar. In this study, the increase in radar absorption is increased by adding Fe3O4 with rGO materials. That is because rGO belongs to good dielectric material. Based on Figure 9, it is noticed that the absorption capability of radar from MnxFe3–xO4/rGO nanocomposites is stronger than that of Fe3O4 nanoparticles. This indicates that the absorption properties of radar increase if added by rGO materials. Physically, this phenomenon occurs since the absorption of radar from Fe3O4 nanoparticles only comes from natural resonance and domain wall resonance, so that with the addition of rGO, the dielectric loss properties of the rGO is introduced and the interface polarization between Fe3O4 and rGO is introduced. In detail, the RL values of nanocomposites are shown in Table 3. Based on Table 3, it can be seen that the RL values of the MnxFe3–xO4/rGO nanocomposites are higher than those of MWCNT/Fe3O4 [66] and ZnFe2O4 [67]. The addition of dielectric material also causes the absorption bandwidth of the MnxFe3–xO4/rGO nanocomposites to widen. Differences in composition affect the absorption of MnxFe3–xO4/rGO nanocomposite RAM material. At composition x = 0.75 is the highest absorption with −11.95 dB.
| Samples | RL (dB) | Ref. |
| Mn0.25Fe2.75O4/rGO | −11.8 | - |
| Mn0.5Fe2.5O4/rGO | −11.5 | - |
| Mn0.75Fe2.25O4/rGO | −11.95 | - |
| rGO | −5 | [52] |
| rGO | −3.3 | [37] |
| Fe3O4 | −3.3 | [66] |
| Fe3O4 | −5 | [68] |
| ZnFe2O4 | −10.0 | [67] |
| MWCNT/Fe3O4 | −10.0 | [66] |
DownLoad:
CSV
Generally, the MnxFe3–xO4 material in RAM applications acts as a magnetic material. Based on Table 3, the single material is not optimal in absorbing radar waves. Fe3O4 material obtained a low RL value of −5 dB [68]. The Mn0.75Fe2.25O4/rGO material was able to increase the RL value to −6.95 dB compared to pure Fe3O4 [17]. This is due to the presence of Mn2+ ions which can increase the polarization of the space charge [69]. The ability of magnetic loss in MnxFe3–xO4 material occurs when the direction of the magnetic moment which is relatively antiparallel in the tetrahedral and octahedral regions will be rectified [19]. Generally, MnxFe3–xO4 materials can produce magnetic loss consisting of eddy current loss and natural resonance loss [30]. Furthermore, the magnetic loss capability is more dominant due to the eddy current loss phenomenon, as expressed in Eq 5 [28].
| C0=μ″(μ′)−2f−1 | (5) |
With C0 as the value representing the eddy current loss. If depicted in a graph C0 with f, then the eddy current loss is indicated by a constant value of C0. In the study of Tajik et al., the MnxFe3–xO4 material showed a constant C0 value at frequencies above 8 GHz [70]. In another report, Modaresi et al. reported the same [28]. Conversely, if the value of C0 is not constant, it can be indicated that there is a natural resonance loss phenomenon from the magnetic material. The relatively small crystal size has the potential to increase the RL value, which is caused by the exchange length resonance of the magnetic energy of a material [55]. Thus, the MnxFe3–xO4 material can be used as a potential magnetic material in RAM applications.
Furthermore, rGO is a unique material, which refers to its special characteristic which is it can produce dielectric loss. In the report of Liu et al., dielectric materials depend on the phenomenon of dipole and electron polarization [37]. Inside an atom, the influence of the electric field from electromagnetic waves will cause electron polarization. If viewed at the molecular level, each molecule has a dipole moment, which when applied by an external electric field will form a charge separation or dipole polarization. In the rGO system, dipole polarization occurs in the structural defects and the presence of various functional groups [71]. For example, Qiao et al. representing the interaction of electromagnetic waves with the structural defects of rGO, will result in an asymmetric charge distribution to form a dipole formation [72]. This causes the dipole to continue to rotate in electromagnetic waves, which in turn converts electromagnetic wave energy into heat energy [73]. In fact, electrons on the surface of rGO can interact with electromagnetic wave energy [74]. Consequently, the electrons will migrate and collide with the rGO lattice, where the energy of the electromagnetic waves is converted into heat energy [73]. Debye's dipolar relaxation theory is usually used to confirm the ability of dielectric loss, as expressed in Eq 6 [28].
| εʹ–(εs+ε∞/2)2+(ε″)2=(εs–ε∞/2)2 | (6) |
Where εs and ε∞ are static permittivity and relative dielectric permittivity. If and are expressed as x and y axes, a semi-circular Cole-Cole graph is formed. According to Chai and colleagues, the presence of a semi-circle pattern indicates a relaxation process, which is caused by the absorption of the electric field from electromagnetic waves [67]. Furthermore, Shu et al. reported that the distortion of the semi-circular Cole-Cole graph in the rGO material indicates the presence of polarization [74]. Furthermore, based on the previous SEM image of the composite sample in Figure 7, rGO forms cavities and is filled with MnxFe3–xO4 particles. The presence of cavities in rGO has the potential to increase the value of reflection loss, which is caused by electromagnetic waves undergoing multiple reflections [75]. Thus, the rGO material has potential in RAM applications. Although, based on Table 3, the reflection loss value of rGO is still low at −5 dB, so it is necessary to combine it with magnetic materials.
MnxFe3–xO4 deposition strategy on the surface of rGO is one of the appropriate ways to produce microcurrent networks [76]. The mechanism, MnxFe3–xO4 acts as an electron-hopping bridge between adjacent rGO layers [55]. More deeply, electron-hopping is expressed as contact conductivity (σcontact) as a function of temperature (T) as in Eq 7 [76].
| σcontact(T)=Kh/Texp(−U/kBT) | (7) |
Where Kh is the prefactor, U is the barrier potential and kB is the Boltzmann constant. As the equation above, conductivity is caused by electron-hopping followed by an increase in temperature. The micro current network that is formed will produce a conduction loss [55]. The phenomenon of conduction loss is characterized by a decrease in the permittivity value as the frequency increases, which is useful for weakening the energy of electromagnetic waves. However, Cao and colleagues reported that the phenomenon of relaxation or an increase in temperature that is too high causes a conductivity network not to form [71]. Consequently, at high frequencies, the dielectric loss capability will decrease. One solution is to adjust the mass composition of rGO with MnxFe3–xO4. In addition, the presence of interfacial interactions between MnxFe3–xO4 and rGO has the potential to produce interfacial polarization [13]. Physically, the interface interaction accumulates the migration and diffusion of the carrier so as to form a spatial separation consisting of positive and negative charges [77]. Consequently, between the boundaries of the MnxFe3–xO4 and rGO materials, a balance formation is formed in the form of a region of spatial charges and an electric field. However, changing the direction of the electromagnetic wave field can change the charge pattern so that the electromagnetic wave energy will be dissipated [78]. Interfacial polarization can also be identified through Debye's dipolar relaxation theory as studied above.
According to Table 3, the MnxFe3–xO4/rGO composite of the three variations showed fantastic results, namely higher reflection loss values than the single material. The combination of magnetic and dielectric materials provides a synergy effect with good impedance match results (Z ~ 1) [79]. Furthermore, this composite system contains a magnetic material, this is in accordance with the results of the reflection loss value obtained from the tests that have been carried out.
Based on the results of the previous research, it was shown that, if the RL value obtained < −15 dB, it indicates that if 96.9% of the radar waves are absorbed by the nanocomposite. Meanwhile, if the RL value obtained < −20 dB, then the absorbed wave is almost 99.0% [80]. In this research, the RL value of nanocomposites has a range between −2 to −14 dB or < −20 dB. Thus, it can be concluded that the waves absorbed by nanocomposites in this study are around 96.9–99.0%. Two main aspects affecting the increase of radar absorption by MnxFe3–xO4/rGO nanocomposites in this study are first, the efficient complementarity between dielectric loss and magnetic loss which is indicated by the relative permittivity and permeability values must be fulfilled [68,81]. If Fe3O4 nanoparticles stand alone as a compiler of RAM, it can be construed that the resulting RL value is still low. This is due to the large disparity between permeability and permittivity which interferes with impedance matching. Thus, in the MnxFe3–xO4/rGO system, the Fe3O4 nanoparticles act as absorbents of the magnetic parts, and rGO, is as dielectric absorbers of incoming radar. Besides, the rGO also acts as a nucleation site for Fe3O4 which prevents or reduces the aggregation of these nanoparticles. Second, there is interfacial polarization between Fe3O4-rGO, where multi-interfaces on nanocomposites will produce significant polarization interfaces that will increase the value of dielectric loss at high frequencies [65]. This is indicated when the addition of rGO absorption material occurs at a frequency of around 11 GHz. Thus, the development of MnxFe3–xO4/rGO nanocomposites in this research provides new opportunities for large-scale development for the application of high-performance microwave absorbing materials based on local natural materials through environmentally friendly synthesis.
Uniquely, in this study, reduced-graphene oxide (rGO) synthesized from coconut shell waste has the potential to be developed as a dielectric material from RAM. This is relevant to the data presented in Table 3 that rGO can absorb electromagnetic waves of −5 dB [52] added with the findings from this study which combines natural materials of natural iron sand and coconut shell waste, it produces an RL value of −11.95 dB. In general, coconut shell waste is very easy to obtain from the community, especially in Indonesia. Theorically, coconut shell has a high cellulose content, so it contains a high carbon content as well [82,83]. Carbon has the ability to absorb electromagnetic waves, so it has the potential to be developed as a dielectric material. Further research on the use of natural materials can be developed towards extracting the potential of the material itself. Natural iron sand can be extracted as a source of Fe2O3 which can be synthesized into Fe3O4 with benefits as an environmentally friendly magnetic material [84], antimicrobial [69], and anti-cancer agent [79]. Meanwhile, coconut shell waste can be synthesized into rGO with the benefit of being a dielectric material for Radar Absorbing Material (RAM) [56], corrosion protection [85], and electrochemical sensor [70].
The MnxFe3–xO4/rGO nanocomposites were successfully synthesized by using an environmental precipitation method. Meanwhile, with the addition of rGO in the MnxFe3–xO4/rGO nanocomposites, their RL increases significantly because the nanocomposites consist of magnetic loss and dielectric loss which increases the radar absorption. Interestingly, the RL value of the MnxFe3–xO4/rGO nanocomposites ranges from −2.0 to −14.0 dB which shows their radar absorption capability is in the range of 96.9%–99.0%.
This work was supported by Faculty of Mathematics and Natural Sciences, Universitas Negeri Malang. The writer was inspired by the special people, like KH. Muhammad Zaini Abdul Ghani, Prof. Effendy, Ph.D, and Prof. Hadi Nur, Ph.D. Special thanks to my best close friend, Muhammad Roy Asrori, S.Pd.
The authors stated that there is no conflict of interest.
| [1] |
K. Guo, Z. Yang, C. H. Yu, M. J. Buehler, Artificial intelligence and machine learning in design of mechanical materials, Mater. Horiz., 8 (2021), 1153–1172. https://doi.org/10.1039/D0MH01451F doi: 10.1039/D0MH01451F
|
| [2] |
R. Pestourie, Y. Mroueh, T. V. Nguyen, P. Das, S. G. Johnson, Active learning of deep surrogates for PDEs: Application to metasurface design, npj Comput. Mater., 6 (2020), 1–7. https://doi.org/10.1038/s41524-020-00431-2 doi: 10.1038/s41524-020-00431-2
|
| [3] |
H. Sasaki, H. Igarashi, Topology optimization accelerated by deep learning, IEEE Trans. Magn., 55 (2019), 1–5. https://doi.org/10.1109/TMAG.2019.2901906 doi: 10.1109/TMAG.2019.2901906
|
| [4] |
D. A. White, W. J. Arrighi, J. Kudo, S. E. Watts, Multiscale topology optimization using neural network surrogate models, Comput. Method. Appl. Mech. Eng., 346 (2019), 1118–1135. https://doi.org/10.1016/j.cma.2018.09.007 doi: 10.1016/j.cma.2018.09.007
|
| [5] |
M. Raissi, G. E. Karniadakis, Hidden physics models: Machine learning of nonlinear partial differential equations, J. Comput. Phys., 357 (2018), 125–141. https://doi.org/10.1016/j.jcp.2017.11.039 doi: 10.1016/j.jcp.2017.11.039
|
| [6] |
M. Raissi, P. Perdikaris, G. E. Karniadakis, Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, J. Comput. Phys., 378 (2019), 686–707. https://doi.org/10.1016/j.jcp.2018.10.045 doi: 10.1016/j.jcp.2018.10.045
|
| [7] |
L. Lu, X. Meng, Z. Mao, G. E. Karniadakis, DeepXDE: A deep learning library for solving differential equations, SIAM Rev., 63 (2021), 208–228. https://doi.org/10.1137/19M1274067 doi: 10.1137/19M1274067
|
| [8] |
S. Wang, Y. Teng, P. Perdikaris, Understanding and mitigating gradient flow pathologies in physics-informed neural networks, SIAM J. Sci. Comput., 43 (2021), A3055–A3081. https://doi.org/10.1137/20M1318043 doi: 10.1137/20M1318043
|
| [9] |
S. Wang, X. Yu, P. Perdikaris, When and why PINNs fail to train: A neural tangent kernel perspective, J. Comput. Phys., 449 (2022), 110768. https://doi.org/10.1016/j.jcp.2021.110768 doi: 10.1016/j.jcp.2021.110768
|
| [10] |
W. Ji, W. Qiu, Z. Shi, S. Pan, S. Deng, Stiff-PINN: Physics-informed neural network for stiff chemical kinetics, J. Phys. Chem. A, 125 (2021), 8098–8106. https://doi.org/10.1021/acs.jpca.1c05102 doi: 10.1021/acs.jpca.1c05102
|
| [11] | C. Yu, Y. Tang, B. Liu, An adaptive activation function for multilayer feedforward neural networks, in 2002 IEEE Region 10 Conference on Computers, Communications, Control and Power Engineering. TENCOM'02. Proceedings, (2002), 645–650. https://doi.org/10.1109/TENCON.2002.1181357 |
| [12] |
S. Qian, H. Liu, C. Liu, S. Wu, H. S. Wong, Adaptive activation functions in convolutional neural networks, Neurocomputing, 272 (2018), 204–212. https://doi.org/10.1016/j.neucom.2017.06.070 doi: 10.1016/j.neucom.2017.06.070
|
| [13] |
A. D. Jagtap, K. Kawaguchi, G. E. Karniadakis, Adaptive activation functions accelerate convergence in deep and physics-informed neural networks, J. Comput. Phys., 404 (2020), 109136. https://doi.org/10.1016/j.jcp.2019.109136 doi: 10.1016/j.jcp.2019.109136
|
| [14] |
A. D. Jagtap, K. Kawaguchi, G. E. Karniadakis, Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks, Proceed. R. Soc. A, 476 (2020), 20200334. https://doi.org/10.1098/rspa.2020.0334 doi: 10.1098/rspa.2020.0334
|
| [15] |
M. Raissi, A. Yazdani, G. E. Karniadakis, Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations, Science, 367 (2020), 1026–1030. https://doi.org/10.1126/science.aaw4741 doi: 10.1126/science.aaw4741
|
| [16] |
F. S. Costabal, Y. Yang, P. Perdikaris, D. E. Hurtado, E. Kuhl, Physics-informed neural networks for cardiac activation mapping, Front. Phys., 8 (2020), 42. https://doi.org/10.3389/fphy.2020.00042 doi: 10.3389/fphy.2020.00042
|
| [17] |
G. Kissas, Y. Yang, E. Hwuang, W. R. Witschey, J. A. Detre, P. Perdikaris, Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks, Comput. Method. Appl. Mech. Eng., 358 (2020), 112623. https://doi.org/10.1016/j.cma.2019.112623 doi: 10.1016/j.cma.2019.112623
|
| [18] |
G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, L. Yang, Physics-informed machine learning, Nat. Rev. Phys., 3 (2021), 422–440. https://doi.org/10.1038/s42254-021-00314-5 doi: 10.1038/s42254-021-00314-5
|
| [19] |
S. Lin, Y. Chen, A two-stage physics-informed neural network method based on conserved quantities and applications in localized wave solutions, J. Comput. Phys., 457 (2022), 111053. https://doi.org/10.1016/j.jcp.2022.111053 doi: 10.1016/j.jcp.2022.111053
|
| [20] |
J. C. Pu, Y. Chen Data-driven vector localized waves and parameters discovery for Manakov system using deep learning approach, Chaos Solitons Fractals, 160 (2022), 112182. https://doi.org/10.1016/j.chaos.2022.112182 doi: 10.1016/j.chaos.2022.112182
|
| [21] |
Z. W. Miao, Y. Chen, Physics-informed neural networks method in high-dimensional integrable systems, Mod. Phys. Lett. B, 36 (2022), 2150531. https://doi.org/10.1142/S021798492150531X doi: 10.1142/S021798492150531X
|
| [22] |
L. Shen, D. Li, W. Zha, X. Li, X. Liu Surrogate modeling for porous flow using deep neural networks, J. Pet. Sci. Eng., 213 (2022), 110460. https://doi.org/10.1016/j.petrol.2022.110460 doi: 10.1016/j.petrol.2022.110460
|
| [23] |
D. Li, L. Shen, W. Zha, X. Liu, J. Tan Physics-constrained deep learning for solving seepage equation, J. Pet. Sci. Eng., 206 (2021), 109046. https://doi.org/10.1016/j.petrol.2021.109046 doi: 10.1016/j.petrol.2021.109046
|
| [24] |
M. Zhu, Y. Xu, J. Cao, The asymptotic profile of a dengue fever model on a periodically evolving domain, Appl. Math. Comput., 362 (2019), 124531. https://doi.org/10.1016/j.amc.2019.06.045 doi: 10.1016/j.amc.2019.06.045
|
| [25] |
G. J. Pettet, H. M. Byrne, D. L. S. Mcelwain, J. Norbury, A model of wound-healing angiogenesis in soft tissue, Math. Biosci., 136 (1996), 35–63. https://doi.org/10.1016/0025-5564(96)00044-2 doi: 10.1016/0025-5564(96)00044-2
|
| [26] |
T. Höfer, J. A. Sherratt, P. K. Maini, Cellular pattern formation during dictyostelium aggregation, Phys. D, 85 (1995), 425–444. https://doi.org/10.1016/0167-2789(95)00075-F doi: 10.1016/0167-2789(95)00075-F
|
| [27] |
J. King, R. Ahmadian, R. A. Falconer, Hydro-epidemiological modelling of bacterial transport and decay in nearshore coastal waters, Water Res., 196 (2021), 117049. https://doi.org/10.1016/j.watres.2021.117049 doi: 10.1016/j.watres.2021.117049
|
| [28] |
X. Wang, F. B. Wang, Impact of bacterial hyperinfectivity on cholera epidemics in a spatially heterogeneous environment, J. Math. Anal. Appl., 480 (2019), 123407. https://doi.org/10.1016/j.jmaa.2019.123407 doi: 10.1016/j.jmaa.2019.123407
|
| [29] |
Y. Wang, L. Cai, X. Luo, W. Ying, H. Gao, Simulation of action potential propagation based on the ghost structure method, Sci. Rep., 9 (2019), 10927. https://doi.org/10.1038/s41598-019-47321-2 doi: 10.1038/s41598-019-47321-2
|
| [30] |
Y. Wang, L. Cai, X. Feng, X. Luo, H. Gao, A ghost structure finite difference method for a fractional FitzHugh-Nagumo monodomain model on moving irregular domain, J. Comput. Phys., 428 (2021), 110081. https://doi.org/10.1016/j.jcp.2020.110081 doi: 10.1016/j.jcp.2020.110081
|
| [31] |
S. Bryson, D. Levy, High-order central WENO schemes for multidimensional Hamilton-Jacobi equations, SIAM J. Num. Anal., 41 (2003), 1339–1369. https://doi.org/10.1137/S0036142902408404 doi: 10.1137/S0036142902408404
|
| [32] |
C. L. Lin, E. Tadmor, High-resolution nonoscillatory central schemes for Hamilton-Jacobi equations, SIAM J. Sci. Comput., 21 (2000), 2163–2186. https://doi.org/10.1137/S1064827598344856 doi: 10.1137/S1064827598344856
|
| [33] |
S. Bryson, D. Levy, High-order semi-discrete central-upwind schemes for multi-dimensional Hamilton-Jacobi equations, J. Comput. Phys., 189 (2003), 63–87. https://doi.org/10.1016/S0021-9991(03)00201-8 doi: 10.1016/S0021-9991(03)00201-8
|
| [34] |
A. Kurganov, E. Tadmor, New high-resolution semi-discrete central schemes for Hamilton-Jacobi equations, J. Comput. Phys., 160 (2000), 720–742. https://doi.org/10.1006/jcph.2000.6485 doi: 10.1006/jcph.2000.6485
|
| [35] |
L. Cai, W. Xie, Y. Nie, J. Feng, High-resolution semi-discrete Hermite central-upwind scheme for multidimensional Hamilton-Jacobi equations, Appl. Num. Math., 80 (2014), 22–45. https://doi.org/10.1016/j.apnum.2014.02.002 doi: 10.1016/j.apnum.2014.02.002
|
| [36] |
S. Bryson, D. Levy, Mapped WENO and weighted power ENO reconstructions in semi-discrete central schemes for Hamilton-Jacobi equations, Appl. Num. Math., 56 (2006), 1211–1224. https://doi.org/10.1016/j.apnum.2006.03.005 doi: 10.1016/j.apnum.2006.03.005
|
| [37] |
F. Zheng, J. Qiu, Directly solving the Hamilton-Jacobi equations by Hermite WENO Schemes, J. Comput. Phys., 307 (2021), 423–445. https://doi.org/10.1016/j.jcp.2015.12.011 doi: 10.1016/j.jcp.2015.12.011
|
| [38] |
C. H. Kim, Y. Ha, H. Yang, J. Yoon, A third-order WENO scheme based on exponential polynomials for Hamilton-Jacobi equations, Appl. Num. Math., 165 (2021), 167–183. https://doi.org/10.1016/j.apnum.2021.01.020 doi: 10.1016/j.apnum.2021.01.020
|
| [39] |
P. J. Graber, C. Hermosilla, H. Zidani, Discontinuous solutions of Hamilton-Jacobi equations on networks, J. Differ. Equations, 263 (2017), 8418–8466. https://doi.org/10.1016/j.jde.2017.08.040 doi: 10.1016/j.jde.2017.08.040
|
| [40] |
J. Sirignano, K. Spiliopoulos, DGM: A deep learning algorithm for solving partial differential equations, J. Comput. Phys., 375 (2018), 1339-1364. https://doi.org/10.1016/j.jcp.2018.08.029 doi: 10.1016/j.jcp.2018.08.029
|
| [41] |
T. Nakamura-Zimmerer, Q. Gong, W. Kang, Adaptive deep learning for high-dimensional Hamilton-Jacobi-Bellman equations, SIAM J. Sci. Comput., 43 (2021), A1221-A1247. https://doi.org/10.1137/19M1288802 doi: 10.1137/19M1288802
|
| [42] |
J. Darbon, G. P. Langlois, T. Meng, Overcoming the curse of dimensionality for some Hamilton-Jacobi partial differential equations via neural network architectures, Res. Math. Sci., 7 (2020), 1–50. https://doi.org/10.1007/s40687-020-00215-6 doi: 10.1007/s40687-020-00215-6
|
| [43] |
J. Darbon, T. Meng, On some neural network architectures that can represent viscosity solutions of certain high dimensional Hamilton-Jacobi partial differential equations, J. Comput. Phys., 425 (2021), 109907. https://doi.org/10.1016/j.jcp.2020.109907 doi: 10.1016/j.jcp.2020.109907
|
| [44] | A. G. Baydin, B. A. Pearlmutter, A. A. Radul, J. M. Siskind, Automatic differentiation in machine learning: A survey, J. March. Learn. Res., 18 (2018), 1–43. http://jmlr.org/papers/v18/17-468.html |
| [45] | D. Kingma, J. Ba, Adam: A method for stochastic optimization, preprint, arXiv: 1412.6980. |
| [46] | J. Duchi, E. Hazan, Y. Singer, Adaptive subgradient methods for online learning and stochastic optimization, J. Mach. Learn. Res., 12 (2011), 2121–2159. http://jmlr.org/papers/v12/duchi11a.html |
| [47] |
D. C. Liu, J. Nocedal, On the limited memory BFGS method for large scale optimization, Math. Program., 45 (1989), 503–528. https://doi.org/10.1007/BF01589116 doi: 10.1007/BF01589116
|
| [48] |
R. van der Meer, C. W. Oosterlee, A. Borovykh, Optimally weighted loss functions for solving PDEs with neural networks, J. Comput. Appl. Math., 405 (2022), 113887. https://doi.org/10.1016/j.cam.2021.113887 doi: 10.1016/j.cam.2021.113887
|
| [49] |
F. Ismail, P. L. Roe, Affordable, entropy-consistent Euler flux functions II: Entropy production at shocks, J. Comput. Phys., 228 (2009), 5410–5436. https://doi.org/10.1016/j.jcp.2009.04.021 doi: 10.1016/j.jcp.2009.04.021
|
| [50] | X. Glorot, Y. Bengio, Understanding the difficulty of training deep feedforward neural networks, J. Mach. Learn. Res., 9 (2010), 249–256. http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf |
| [51] |
S. Osher, C. W. Shu, High-order essentially nonoscillatory schemes for Hamilton-Jacobi equations, SIAM J. Numer. Anal., 28 (1991), 907–922. https://doi.org/10.1137/0728049 doi: 10.1137/0728049
|
| [52] |
A. A. Loya, D. Appelö, A Hermite method with a discontinuity sensor for Hamilton-Jacobi equations, J. Sci. Comput., 90 (2022), 1–31. https://doi.org/10.1007/s10915-022-01766-2 doi: 10.1007/s10915-022-01766-2
|
| [53] |
E. Rouy, A. Tourin, A viscosity solutions approach to Shape-From-Shading, SIAM J. Numer. Anal., 29 (1992), 867–884. https://doi.org/10.1137/0729053 doi: 10.1137/0729053
|
| [54] |
P. L. Lions, E. Rouy, A. Tourin, Shape-From-Shading, viscosity solutions and edges, Numer. Math., 64 (1993), 323–353. https://doi.org/10.1007/BF01388692 doi: 10.1007/BF01388692
|
| [55] |
G. Jiang, D. Peng, Weighted ENO schemes for Hamilton-Jacobi equations, SIAM J. Sci. Comput., 21 (2000), 2126–2143. https://doi.org/10.1137/S106482759732455X doi: 10.1137/S106482759732455X
|
| 1. | W.Q. Guo, B. Hong, J.C. Xu, Y.B. Han, X.L. Peng, H.L. Ge, J. Li, H.W. Chen, X.Q. Wang, CNTs-improved electromagnetic wave absorption performance of Sr-doped Fe3O4/CNTs nanocomposites and physical mechanism, 2024, 141, 09259635, 110699, 10.1016/j.diamond.2023.110699 |
Figures(17) / Tables(6)
Youqiong Liu, Li Cai, Yaping Chen, Bin Wang. Physics-informed neural networks based on adaptive weighted loss functions for Hamilton-Jacobi equations[J]. Mathematical Biosciences and Engineering, 2022, 19(12): 12866-12896. doi: 10.3934/mbe.2022601
| Samples | Distribution results | Z-Avg (nm) | |||
| Size (d.nm) | % Int | σ | %Pd | ||
| Fe3O4 | 369.3 | 53.3 | 93.00 | 25.2 | 531.8 |
| 194.8 | 46.7 | 41.21 | 21.2 | ||
| rGO | 835.0 | 100.0 | 134.9 | 16.2 | 1359 |
| Mn0.25Fe2.75O4 | 416.8 | 100.0 | 63.62 | 15.3 | 1049 |
| Mn0.5Fe2.5O4 | 613.9 | 100.0 | 110.5 | 18.0 | 1432 |
| Mn0.75Fe2.25O4 | 440.4 | 100.0 | 53.65 | 12.2 | 1531 |
DownLoad:
CSV
| Samples | Br (kG) | HcJ (kOe) | Hmax (kOe) |
| Mn0.25Fe2.75O4 | 0.12 | 0.132 | 14.370 |
| Mn0.5Fe2.5O4 | 0.11 | 0.048 | 12.275 |
| Mn0.75Fe2.25O4 | 0.10 | 0.045 | 8.880 |
DownLoad:
CSV
| Samples | Distribution results | Z-Avg (nm) | |||
| Size (d.nm) | % Int | σ | %Pd | ||
| Fe3O4 | 369.3 | 53.3 | 93.00 | 25.2 | 531.8 |
| 194.8 | 46.7 | 41.21 | 21.2 | ||
| rGO | 835.0 | 100.0 | 134.9 | 16.2 | 1359 |
| Mn0.25Fe2.75O4 | 416.8 | 100.0 | 63.62 | 15.3 | 1049 |
| Mn0.5Fe2.5O4 | 613.9 | 100.0 | 110.5 | 18.0 | 1432 |
| Mn0.75Fe2.25O4 | 440.4 | 100.0 | 53.65 | 12.2 | 1531 |
| Samples | Br (kG) | HcJ (kOe) | Hmax (kOe) |
| Mn0.25Fe2.75O4 | 0.12 | 0.132 | 14.370 |
| Mn0.5Fe2.5O4 | 0.11 | 0.048 | 12.275 |
| Mn0.75Fe2.25O4 | 0.10 | 0.045 | 8.880 |
| Samples | RL (dB) | Ref. |
| Mn0.25Fe2.75O4/rGO | −11.8 | - |
| Mn0.5Fe2.5O4/rGO | −11.5 | - |
| Mn0.75Fe2.25O4/rGO | −11.95 | - |
| rGO | −5 | [52] |
| rGO | −3.3 | [37] |
| Fe3O4 | −3.3 | [66] |
| Fe3O4 | −5 | [68] |
| ZnFe2O4 | −10.0 | [67] |
| MWCNT/Fe3O4 | −10.0 | [66] |
