1.
Introduction
The notion of convexity and its related entities are very fundamental concepts in the area of mathematics and other scientific fields due to their dynamic and extensive applications [9,24,33]. The fundamental characteristics and properties of the concept of convexity have been developed into essential tools that are vital to the progress of theoretical understanding, computational methodologies, and practical implementations across various domains [15,18,20]. Convex functions are extremely useful at addressing and solving problems that are complex or assumed unsolvable in previous years [2,6,32]. Thus, the broad significance of convex functions is highlighted by their rich properties and extensive applicability [3,4]. We now provide a formal definition of a convex function.
A function Θ:[γ1,γ2]→R is convex, if for all ϱ1,ϱ2∈[γ1,γ2] and 0≤Υ≤1,
If the aforementioned inequality is true in the reverse sense, then Θ is concave on [γ1,γ2].
Over the past few years, convex functions have been refined, extended, and generalized in various angles through their properties and behaviors [16,30]. Some well-known examples of convex functions, with regard to their extensions, generalizations, and refinements, include P-convex [25], η-convex [8], s-convex [10], h-convex [28], and coordinate convex functions [17]. In many domains, convex functions and their generalizations have been essential however, their most significant impact is observed in the area of inequalities [14,31]. Several inequalities, such as Ostrowski's [12], the majorization [20], the Hermite-Hadamard [9], and the Jensen-Mercer inequalities, cannot be proven without the use of convex functions; however, the introduction of convex functions has made it possible to establish and prove these inequalities. One of the most notable contributions of convex functions to the study of inequality in mathematics is the establishment of Jensen's inequality. This inequality holds significant interest as it generalizes ordinary convexity, the triangular inequality and serves as the origin for various other classical inequalities. Researchers have applied Jensen's inequality to explore and solve complex problems across diverse domains, ranging from pure mathematics to applied mathematics [5,18,29], engineering [24], economics [1], information theory [27], and epidemiology [26].
The Jensen inequality for the continuous version was developed by taking integrable functions in place of tuples, which is stated below:
Let 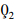 :[α1,α2]→[0,∞],
:[α1,α2]→[0,∞], 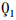 :[α1,α2]→[β1,β2] be integrable functions such that
:[α1,α2]→[β1,β2] be integrable functions such that 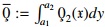 . In addition, the function F:[β1,β2]→R is a convex and the function
. In addition, the function F:[β1,β2]→R is a convex and the function 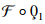 is an integrable. Then,
is an integrable. Then,
For the concave function F, the inequality (1.2) flips.
Recently, Jensen's inequality has been generalized in various directions through the use of convex functions and their generalizations. In 2018, Lu [19] introduced refined versions of discrete Jensen's inequality, yielding improved results compared to earlier results of the similar nature. Additional uses of these obtained modifications are stronger upper bounds for the Shannon entropy. In 2010, Dragomir [7] examined a refinement of Jensen's inequality for convex functions over linear spaces and subsequently demonstrated applications of the acquired refinement in the context of norms, mean f-deviation, and f-divergences. Mikić et al. [21] derived Jensen-type inequalities for positive linear functionals through the utilization of the concept of 3-convex functions. The applications of the obtained results are then examined in the domains of generalized means, power means, and the generalized f-divergence functional. Ivelić and Pečarić [11] introduced generalizations of the reverse of the Jensen inequality for convex functions defined on convex hulls. Additionally, for convex functions, they deduced expansions of the Hermite-Hadamard inequality defined on k-simplices in Rk as direct consequences of their main findings. Rasheed et al. [23] expanded the Jensen integral inequality for real Stieltjes integrals by applying the Montgomery identity in the context of n-convex functions. Furthermore, they provided various formulations of the discrete Jensen inequality and its converses for weights real.
This manuscript is organized as follows: In Section 2, we present the major results. In Section 3, we discuss the significance of these results, focusing on conditions imposed on the function and the derived bounds. Section 4 contains applications of the major results to the Hölder and Hermite-Hadamard inequalities, while Section 5 contains applications to means, including graphical verification of the results. In Section 6, we explore applications in information theory. Finally, the conclusion of the manuscript is provided in the last section.
2.
Main findings
To begin this section, let us consider the following theorem, which offers an enhancement of Jensen's inequality.
Theorem 2.1. Assume that the function F:[ℏ1,ℏ2]→R is thrice differentiable with |F‴| is a convex function and ℘:[ρ1,ρ2]→(−∞,∞), Γ:[ρ1,ρ2]→[ℏ1,ℏ2] be any integrable functions. Further, presume that ¯℘:=∫ρ2ρ1℘(σ)dσ≠0 and ¯⅁:=1¯℘∫ρ2ρ1℘(σ)Γ(σ)dσ∈[ℏ1,ℏ2]. Then,
Proof. Without loss of generality, assume that ¯⅁≠Γ(σ). Now, by applying the rule of integration, we get
This implies that
Taking absolute value of identity (2.2), and subsequently using triangular inequality, we arrive at
Since, the function |F‴| is convex. Therefore, utilize the convexity of |F‴| in (2.3), we get
By simplifying the inequality (2.4), we obtain (2.1). □
The theorem stated below presents another improvement of the Jensen inequality using concave functions.
Theorem 2.2. Let F:[ℏ1,ℏ2]→R be any function such that F‴ exists. Also, assume that ℘:[ρ1,ρ2]→R and Γ:[ρ1,ρ2]→[ℏ1,ℏ2] are integrable functions with ¯℘:=∫ρ2ρ1℘(σ)dσ≠0, ¯⅁:=1¯℘∫ρ2ρ1℘(σ)Γ(σ)dσ∈[ℏ1,ℏ2]. If |F‴| is a concave function, then,
Proof. We can infer from inequality (2.3) that
Using integral Jensen's inequality for the concave function, we obtain (2.7):
We determine (2.5), after computing the integral in the inequality (2.7). □
3.
Importance of the main results
In this section, we analyze the relevance of the observed improvements in bitterness compared to previously established findings.
3.1. Functions fit the criteria
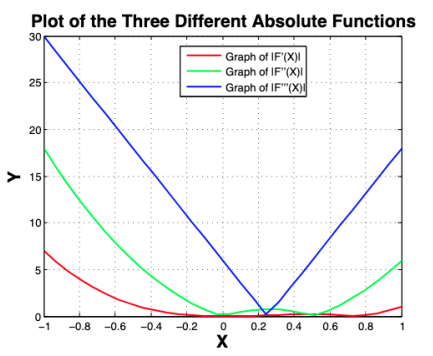
To demonstrate the importance of our main finding across various applications in different fields, we outline the process that led us to this conclusion, specifically deriving bounds for the third-order derivative absolute function is being a convex. During our literature review, we identified functions for which the first and second-order derivatives absolute functions are not convex. An example of such a function is presented below:
First-order absolute function lacks convexity.
Second-order absolute function lacks convexity.
Third-order absolute function is convex.
This is illustrated with the help of the following graph (see Figure 1), which shows that the first- and second-order absolute functions lack convexity, while the third-order absolute function is convex. This highlights the unique contribution of our article.
3.2. Numerical estimation for the Jensen difference
We perform numerical experiments in this part to illustrate how bitter the performance of our major findings over some other results is.
Example 3.1. Let F(σ)=expσ,σ∈[0,1], then |F‴(σ)|=expσ, which indicates that |F‴(σ)| is convex function. Therefore, using the inequality (2.1) for ℘(σ)=1,Γ(σ)=σ, where σ∈[0,1], we have
Using the aforementioned information and the particular function in the inequality (2.24) provided in the article [13], we obtain
The estimates for Jensen's difference given in this study are better than the estimate archived from [13], as demonstrated by (3.1) and (3.2).
Example 3.2. Let F(σ)=σ4,σ∈[0,1], then |F‴(σ)|=24σ, which indicates that |F‴(σ)| is convex function. So, using the inequality (2.1) for Γ(σ)=σ, ℘(σ)=1, where σ∈[0,1], we get
Using the inequality (2.24) provided in the article [13] along with the previously mentioned values, we can now obtain
This paper's estimates of Jensen's difference surpass those in [13], as evidenced by (3.3) and (3.4).
4.
Applications to Hölder and Hermite-Hadamard inequalities
Hölder's inequality is a powerful mathematical tool widely employed in various fields, including functional analysis, probability theory, and optimization. Named after the mathematician Otto Hölder, this inequality provides a fundamental relationship between different norms and their inner products. Its application extends to problems involving integrals, series, and vector spaces, allowing for the establishment of bounds and inequalities that are crucial in mathematical modeling and analysis. Hölder's Inequality has proven particularly useful in the study of inequalities arising in probability and statistics, functional analysis, and harmonic analysis. The versatility of this inequality makes it an indispensable tool for researchers and practitioners in diverse mathematical disciplines [22]. In this section, we focus on the applicability of major results for the Hölder and Hermite-Hadamard inequalities. Theorem 2.1 leads to an improvement of the Hölder inequality, as presented in this proposition.
Proposition 4.1. Let γ and η be two positive functions such that ηm1,γn1 and ηγ are integrable. Also, assume that m1,n1>1 with 1m1+1n1=1. If m1∈(1,3]∪[4,∞), then,
Proof. Consider the function F(σ)=σm1,σ>0, then by the successive differentiation of the given function F, we obtain F″(σ)=m1(m1−1)σm1−2 and |F‴(σ)|″=|m1(m1−1)(m1−2)|(m1−3)(m1−4)σm1−5. Clearly, both F″ and |F‴(σ)|″ are nonnegative on (0,∞) for m1∈(1,3]∪[4,∞), which substantiate the convexity as well as |F‴(σ)| convexity of F(σ)=σm1. Therefore, utilizing (2.1) for F(σ)=σm1 and p(σ)=γn1,Γ(σ)=ηγ−n1m1 and then taking power 1m1, we get
Since, the inequality kl1−kl2≤(k1−k2)l holds for l∈[0,1] and 0≤k1≤k2. Therefore, using this inequality for k1=(∫ρ2ρ1ηm1dσ)(∫ρ2ρ1γn1dσ)m1−1,k2=(∫ρ2ρ1ηγdσ)m1 and l=1m1, we get
By comparing the inequalities (4.2) and (4.3), we arrive to the inequality (4.1). □
The next proposition from Theorem 2.1 improves the Hölder inequality.
Proposition 4.2. Let γ and η be two positive functions such that ηm1,γn1 and ηγ are integrable functions and m1∈(0,1), with n1=m1m1−1. If 1m1∈(1,3]∪[4,∞), then,
Proof. Let us take the function F(σ)=σ1m1, defined on (0,∞). Then, F″(σ)=1m1(1m1−1)σ1m1−2 and |F‴(σ)|″=|1m1(1m1−1)(1m1−2)|(1m1−3)(1m1−4)σ1m1−5. Surely, F″ and |F‴(σ)|″ ≥0. This validates the functions F(σ)=σ1m1 and |F‴(σ)| both are convex on (0,∞), for 1m1∈(1,3]∪[4,∞). Therefore, utilizing (2.1) for F(σ)=σ1m1 and ℘(σ)=γn1,Γ(σ)=ηm1γ−n1, we get
Now, multiplying both sides of the inequality (4.5) by ∫ρ2ρ1γn1dσ, we get inequality (4.4). □
The next corollary provides an improvement for the Hölder inequality as a consequence of Theorem 2.2.
Proposition 4.3. Let γ,η:[β1,β2]→(0,∞) be any functions and m1,n1>1 with 1m1+1n1=1. Further, let γn1, ηm1, γη and ηγ−n1m1 be integrable over the interval [β1,β2]. If m1∈(3,4), then,
Proof. Consider the function F(σ)=σm1,σ>0, then by differentiating the function F, we obtain F″(σ)=m1(m1−1)σm1−2 and |F‴(σ)|″=|m1(m1−1)(m1−2)|(m1−3)(m1−4)σm1−5. So, the function F″ is positive on (0,∞) and |F‴(σ)|″ <0 for m1∈(3,4), which substantiate the convexity of F(σ)=σm1 and |F‴(σ)| concavity. Therefore, utilizing (2.5) for F(σ)=σm1 and ℘(σ)=γn1,Γ(σ)=ηγ−n1m1 and then taking power 1m1, we get
Note that, the inequality kl1−kl2≤(k1−k2)l holds for l∈[0,1] and 0≤k1≤k2. Therefore, by putting k1=(∫ρ2ρ1ηm1dσ)(∫ρ2ρ1γn1dσ)m1−1,k2=(∫ρ2ρ1ηγdσ)m1 and l=1m1, in (4.7), we receive
By comparing the inequalities (4.7) and (4.8), we arrive to the inequality (4.6). □
The following corollary improves the Hölder inequality due to Theorem 2.2.
Proposition 4.4. Assume that γ and η are positive functions such that ηm1,γn1, and ηγ are integrable functions and m1∈(0,1), with n1=m1m1−1. If 1m1∈(3,4), then,
Proof. (i) Consider the function F(σ)=σ1m1, defined on (0,∞). Then, F″(σ)=1m1(1m1−1)σ1m1−2 and |F‴(σ)|″=|1m1(1m1−1)(1m1−2)|(1m1−3)(1m1−4)σ1m1−5. Obviously, F″(σ)>0 and |F‴(σ)|″ <0 for 1m1∈(3,4), which shows the convexity of F(σ)=σ1m1 and concavity of |F‴(σ)|. Therefore, utilizing (2.5) for F(σ)=σ1m1 and ℘(σ)=γn1, Γ(σ)=ηm1γ−n1, we get
Now, multiplying both sides of the inequality (4.10) by ∫ρ2ρ1γn1dσ, we get inequality (4.9). □
The following corollary gives improvement for the Hermite-Hadamard inequality.
Corollary 4.5. Let F:[ℏ1,ℏ2]→R be a thrice differentiable function such that the function |F‴| is an integrable and |F‴| is a convex. Then,
Proof. Since the function |F‴| is convex on the interval [ℏ1,ℏ2]. Therefore, using (2.1) for Γ(σ)=σ and ℘(σ)=1, we get (4.11). □
Corollary 4.6. Consider the function F:[ℏ1,ℏ2]→R is thrice differentiable such that |F‴| is an integrable. If |F‴| is a concave, then,
Proof. Inequality (4.12) can be obtained by substituting Γ(σ)=σ and ℘(σ)=1 in (2.5). □
5.
Applications for quasi-arithmetic and power means
Definition 5.1. If the two positive integrable functions γ and η in the interval [ρ1,ρ2] with ¯γ=∫ρ2ρ1γ(σ)dσ, then,
is the power mean of order κ∈R.
Theorem 2.1 enables us to give an inequality for the power mean as follows:
Corollary 5.2. Let γ and η be any two positive functions with ¯γ=∫ρ2ρ1γdσ. In addition, let κ,τ∈R−{0}.
(i) If κ≤3τ or κ≥4τ or κ<0 such that τ>0, then,
(ii) If κ≥3τ or κ≤4τ or κ>0 such that τ<0, then (5.1) holds.
Proof. (i) Let the function F(σ)=σκτ, σ>0. Then, F″(σ)=κτ(κτ−1)σκτ−2 and |F‴(σ)|″=|κτ(κτ−1)(κτ−2)|(κτ−3)(κτ−4)σκτ−5. Clearly, both F″ and |F‴(σ)|″ are positive with the given conditions and consequently this confirms the convexity of the function F(σ)=σκτ on (0,∞). Therefore, take F(σ)=σκτ, ℘(σ)=γ and Γ(σ)=ητ in (2.1), we obtain (5.1).
(ii) For the stated circumstances of κ and τ, the function Γ(σ)=σκτ and |F‴(σ)| are convex on (0,∞). Thus, by following the process of (i), we will get (5.1). □
Theorem 2.2 allows us to provide an additional inequality for the power mean as follows:
Corollary 5.3. Let γ and η be any two positive functions such that κ,τ∈R−{0} and ¯γ=∫ρ2ρ1γdσ.
(i) If τ>0 with 3τ<κ<4τ, then,
(ii) If 4τ<κ<3τ such that τ<0, then (5.2) holds.
Proof. (i) Let F(σ)=σκτ for σ>0. Then, given the values of κ,τ the function F is convex and |F‴|″<0, which shows concave. Thus using (2.5) for F(σ)=σκτ, ℘(σ)=γ and Γ(σ)=ητ, we get (5.2).
(ii) Under the specified parameters for τ and κ, the function Γ(σ)=σκτ is convex and |F‴(σ)| is concave on (0,∞). Therefore, by following the procedure of (i), we receive (5.2). □
Theorem 2.1 can be used to create a relation as shown below:
Corollary 5.4. Let γ and η be any two positive functions with ¯γ=∫ρ2ρ1γdσ. Then,
Proof. Let Γ(σ)=−lnσ be defined on the interval (0,∞). Then, F″(σ)=σ−2 and |F‴(σ)|″=24σ−5. The above expressions clearly indicate that F″>0 and |F‴(σ)|″>0, Which is evidence of convexity. Therefore, using (2.1) by substituting Γ(σ)=−lnσ, ℘(σ)=γ and Γ(σ)=η, we get (5.3). □
As a result of Theorem 2.1, the following corollary provides an additional relation for the power means.
Corollary 5.5. Assume Corollary 5.4 meets its criteria. Then,
Proof. Consider the function F(σ)=exp(σ),σ∈R, then F″(σ)=exp(σ) and the function |F‴(σ)|″=exp(σ). Clearly, both F(σ)=exp(σ) and |F‴(σ)| are convex functions. Consequently, by using (2.1) for Γ(σ)=lnη, ℘(σ)=γ and F(σ)=exp(σ), we get (5.4). □
The quasi-arithmetic mean can be defined in the following manner:
Definition 5.6. If γ(σ) and (g∘η)(σ) are any integrable functions defined on [ρ1,ρ2] with ¯γ=∫ρ2ρ1γ(σ)dσ and γ(σ)>0. Additionally, let g(σ) be continuous and strictly monotonic function on [ρ1,ρ2]. Then,
Theorem 2.1 allows us to state an inequality for the quasi-arithmetic mean as follows:
Corollary 5.7. Consider the two positive functions γ, η and (g∘η)(σ) with ∫ρ2ρ1γdσ=¯γ>0. Moreover, suppose that a function F∘g−1 with |(F∘g−1)‴| is convex and g be a continuous and strictly monotone function. Then the following inequality holds:
Proof. Since, the function |(F∘g−1)‴| is convex. So, inequality (5.5) can get from (2.1) by setting F→F∘g−1, Γ(σ)→g(η) and ℘(σ)→γ. □
Theorem 2.2 provides an inequality for the quasi-arithmetic mean as shown below:
Corollary 5.8. Let us assume that γ,η and (g∘η)(σ) be the following two positive functions with ¯γ=∫ρ2ρ1γdσ>0. Also, assume that g be strictly monotonic and continuous function and the function F∘g−1 such that |(F∘g−1)‴| is concave. Then,
Proof. Since, the function |(F∘g−1)‴| is concave. Therefore, to deduce inequality (5.6), assume F→F∘g−1, Γ(σ)→g(η) and ℘(σ)→γ in (2.5). □
Graphical interpretation for the comparison of left and right hand sides of the inequalities
This part of the section is introduced for the comparison of the left- and right-sides of the inequalities obtained above. For this, first of all the relation (4.1) is considered. In this integral inequality, there are functions, and constants, specify these functions by substituting γ(x)=x12, η(x)=x, m1=2, n1=2, a=ρ1∈[0,4], b=ρ2∈(4,10], such that ρ2>ρ1. Using the above values for an inequality (4.1), we get
and
For the examination of the graphical representation, see Figure 2.
Consider inequality (4.11), by substituting F(σ)=σ3, a=ℏ1∈[0,10], and b=ℏ2∈(0,10], we get
and
For the comparison, see Figure 3.
Now, consider inequality (4.12). By making the same above substitution in (4.12), we get
and
The graphical representation is shown in Figure 4.
6.
Applications in information theory
Information theory has found a multitude of applications across various domains, revolutionizing the way we transmit, store, and process data. In telecommunications, it underpins the efficient compression of data for transmission, ensuring minimal bandwidth usage while preserving information integrity. In cryptography, information theory provides the foundation for secure communication and encryption methods that safeguard sensitive information. In machine learning, it guides the design of algorithms for pattern recognition, classification, and clustering. Furthermore, information theory has influenced genetics, aiding in the understanding of DNA sequences and genetic diversity. From the realms of engineering to biology, information theory's applications continue to shape the modern world's technological landscape, enhancing our ability to handle and extract meaning from vast volumes of information. There are few bounds associated with the Bhattacharyya coefficient, Renyi divergence, Csizar divergence, Kullback-Leibler divergence, Zipf-Mandelbrot entropy, and Shannon entropy. Csisár divergence is defined at the beginning of this section.
Definition 6.1. Let g:[ℏ1,ℏ2]→R be a convex function and also assume that the function γ and is an integrable on [ρ1,ρ2] such that η(σ)γ(σ)∈[ℏ1,ℏ2] and γ(σ)>0 for all σ∈[ρ1,ρ2]. Then,
The following corollary estimates the Csiszár divergence using Theorem 2.1.
Theorem 6.2. Let g:[ℏ1,ℏ2]→R be a function such that the function |g‴| is convex as well as integrable. Also, suppose that γ:[ρ1,ρ2]→(0,∞) and η:[ρ1,ρ2]→[ℏ1,ℏ2] are integrable functions such that ∫ρ2ρ1ηdσ∫ρ2ρ1γdσ,ηγ∈[ℏ1,ℏ2]. Then,
Proof. Since the given function |g‴| is convex. Therefore, using Theorem 2.1 for F=g, Γ(σ)=ηγ and ℘(σ)=γ, we obtain (6.1). □
Now, we will discuss several related concepts to the Csiszár divergence.
Definition 6.3. Let γ and η be positive probability density functions. Then:
● The Rënyi divergence can be described as
● As defined by the Shannon entropy:
● According to the Kullback-Leibler divergence:
● The Bhattacharyya coefficient is stated below:
With the help of Theorem 2.1, a bound for the Rényi divergence is deduced, which is stated in the following corollary.
Corollary 6.4. Let γ and η be probability density function and for any c∈(0,∞),c≠1. Then,
Proof. Let us take the function F(σ)=−1c−1lnσ, σ>0, then, F″(σ)=1(c−1)σ2 and |F‴(σ)|″=24(c−1)σ5. This ensures that the function F(σ)=−1c−1lnσ is convex as well as |F‴(σ)| is convex. Therefore, by substituting F(σ)=−1c−1lnσ, ℘(σ)=γ and Γ(σ)=(γη)c−1 in (2.1), we obtain (6.2). □
Shannon entropy estimates as an application of Theorem 2.1 is provided in the next corollary.
Corollary 6.5. Let γ be positive probability density function. Then,
Proof. Let g(σ)=−logx,σ∈(0,∞), then clearly g(σ) is convex as well as |g‴(σ)| is convex on (0,∞). By taking g(σ)=−logx, in (6.1), we get (6.3). □
The following corollary explains the impact of Theorem 2.1 on the Kullback-Leibler divergence.
Corollary 6.6. Let γ and η be two positive probability density functions. Then,
Proof. Let g(σ)=σlnσ,x>0, then by differentiating the given function with respect to σ, we acquire g″(x)=1x and |g‴(σ)|″=6σ−4, which admits that both the functions g(x)=xlnσ and |g‴| are convex. So, by putting g(σ)=σlnσ in (6.1), we get (6.4). □
The following corollary applies Theorem 2.1 to yield an estimate for the Bhattacharyya coefficient.
Corollary 6.7. If γ and η are probability density functions such that γ,η>0, then,
Proof. Let g(σ)=−√σ,σ∈(0,∞), then, g″(σ)=14σ−32>0, and |g‴|″=10532σ−112>0. It is confirmed that g and |g‴| are convex functions. Therefore, using (6.1) for g(σ)=−√σ, we get (6.5).
7.
Conclusions
In the literature on inequalities for convex functions, the Jensen inequality stands out as the most interesting and dynamic inequality. There are many fascinating characteristics to this inequality. Therefore, it has been applied as a fundamental tool in science, engineering, and other technologies. The purpose of this study is to present new improvements to the Jensen inequality along with its applications. Improvements for the Jensen difference are provided by applying convexity of the thrice differentiable function in absolute sense. Through numerical experiments, the sharpness of the proposed results is discussed. Some consequences of our primary results are highlighted for the Hermite-Hadamard, quasi-arithmetic, power means and Hölder, inequalities. Graphical verification of the derived results is also provided (see Figures 2–4). In addition, we gave some applications of the derived improvements in information theory. These applications provided some bounds for Kullback-Leibler Divergence, Zipf-Mandelbrot entropy, Shannon entropy, Bhattacharyya coefficient, and Rényi divergence.
Author contributions
Asadullah Sohail and Muhammad Adil Khan: Methodology, Writing-original draft; Xiaoye Ding and Mohamed Sharaf: Conceptualization, Writing–review and editing; Muhammad Adil Khan and Mohammed A. El-Meligy: Supervision, Writing–review and editing, Validation. All authors have read and approved the final version of the manuscript for publication.
Acknowledgments
The authors extend their appreciation to King Saud University, Saudi Arabia, for funding this work through Researchers Supporting Project number (RSPD2024R704), King Saud University, Riyadh, Saudi Arabia. The work was supported by the key Scientific Research Projects of Hunan Provincial Department of Education in 2021 (grant number: 21A0526).
Conflict of interest
The authors declare that there are no conflicts of interest in this paper.









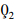
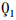
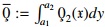 . In addition, the function
. In addition, the function 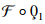 is an integrable. Then,
is an integrable. Then,
 DownLoad:
DownLoad:






