1.
Introduction
In [31], Schein investigated systems of the form (∅,∘,∖), which is a collection of closed functions under the composition ∘ of functions (and thus (∅,∘) is a function semigroup) and the set theoretic subtraction ∖ (and thus (∅,∖) is a subtraction algebra), and he demonstrated that every subtraction semigroup is isomorphic to an invertible function of a difference semigroup. Zelinka [34] discussed Schein's proposal for the structure of multiplication in a subtraction semigroup. He figured out how to solve a problem involving atomic subtraction algebras, a type of subtraction algebra. Jun et al.[7] studied the characterization of ideals in subtraction algebras and established the concept of ideals. Jun and Kim established the ideals generated by a set and their related outcomes in their paper [8].
Near-rings are one of the generalized structures of rings. In 1930, Zassenhaus and Wielandt studied near-rings in relation to group theory and ring theory. However, Wielandt, Frohlich and Blackett redeveloped near-ring research in 1950. Since then, this field has expanded its applications to include automata theory, formal language theory, non-linear interpolation theory and optimization theory, among others (see [2,12,14]). Near-subtraction semigroups and strongly regular near-subtraction semigroups were introduced by Dheena et al.[3], and it was demonstrated that a near subtraction semigroup is strongly regular if and only if it is regular and contains no non-zero nilpotent elements.
Zadeh[33] introduced the notion of a fuzzy subset ν of a set T as a mapping from T into [0,1], which has since been successfully applied in a variety of applications such as control systems engineering, image processing, industrial automation, robotics and optimization. Rosenfeld[30] first proposed the concept of a fuzzy subgroup of a group in 1971. Jun et al.[9] proposed the definition of fuzzy ideals in a gamma near-ring and investigated the related properties. Lee and Park[11] introduced the concept of a fuzzy ideal in subtraction algebras and outlined several conditions for a fuzzy set to be a fuzzy ideal. In near-subtraction semigroups, Prince Williams [32] proposed the concept of fuzzy ideals and fuzzy intersection, as well as the fuzzy image and preimage of the near-subtraction semigroup under homomorphism.
Molodtsov[15] established the concept of a soft set (F,Z) for an initial universe set Y and the set of parameters Z as a mapping from Z into the power set of Y in 1999, and he successfully applied it to a wide range of fields. Maji et al.[13] were the first to apply soft sets to decision-making problems. Jun et al. [10] pioneered the concept of hybrid structures, which is similar to fuzzy set theory and soft set theory, and investigated several properties of hybrid structures in a set of parameters over an initial universe set. Based on this concept, they created the notions of a hybrid linear space, a hybrid subalgebra and a hybrid field.
Anis et al. [1] proposed the ideas of hybrid subsemigroups and hybrid left (resp., right) ideals in semigroups and described the notions of hybrid products, which were used to examine the characterizations of hybrid subsemigroups and hybrid left (resp., right) ideals. In [4], Elavarasan and Jun obtained some equivalent characterizations of regular and intra-regular semigroups in terms of their hybrid ideals and hybrid bi-ideals, and they derived major results of semigroup characterization through the properties of their hybrid ideals and hybrid bi-ideals. In [6], Elavarasan et al. discussed the properties of a hybrid generalised bi-ideal, an extension of a hybrid bi-ideal, and characterised the regularity of semigroups in terms of hybrid generalised bi-ideals.
In [5], Elavarasan et al. defined the concept of hybrid ideals in near-rings and investigated their properties, as well as the relation between hybrid intersections and hybrid products of hybrid left (resp., right) ideals in zero-symmetric near-rings. G. Muhiuddin et al. introduced the concept of hybrid subsemimodules and examined the hybrid ideals over semirings in [16]. They also obtained equivalent conditions for a semiring to be completely idempotent. Hybrid structures have been applied to a wide range of algebraic systems, yielding a variety of results (see [17,18,19,20,21]). More concepts related to this study have been studied in [22,23,24,25,26,27,28,29].
We introduce the concept of hybrid ideals in near-subtraction semigroups and their associated properties in this paper. In addition, we build an example of a hybrid left ideal that is not a hybrid right ideal and vice versa. We also define the hybrid intersection, as well as the hybrid image and preimage of the near-subtraction semigroup under homomorphism.
2.
Preliminaries
We collect a few fundamental definitions in this section that are related to near-subtraction semigroups, which we will use in this paper.
Definition 2.1. [31] A subtraction algebra is defined as a set Z(≠∅) with a binary operation "−" that meets the below criteria: ∀q0,l0,i0∈Z,
(i) q0−(l0−q0)=q0.
(ii) q0−(q0−l0)=l0−(l0−q0).
(iii) (q0−l0)−i0=(q0−i0)−l0.
The properties of a subtraction algebra are as follows:
(i) q0−0=q0 and 0−q0=0.
(ii) (q0−l0)−q0=0.
(iii) (q0−l0)−l0=q0−l0.
(iv) (q0−l0)−(l0−q0)=q0−l0, where 0=q0−q0 is a value independent of the choice of q0∈Z.
Definition 2.2. [34] A subtraction semigroup is defined as a set Z(≠∅) with the binary operations "−" and "." that meets the below criteria:
(i) (Z,−) is a subtraction algebra.
(ii) (Z,.) is a semigroup.
(iii) l0(l1−l2)=l0l1−l0l2 and (l0−l1)l2=l0l2−l1l2,∀l0,l1,l2∈Z.
Definition 2.3. [3] A near-subtraction semigroup (briefly, NSS) is defined as a set Z(≠∅) with the binary operations "−" and "." that meets the below criteria:
(i) (Z,−) is a subtraction algebra.
(ii) (Z,.) is a semigroup.
(iii) (l0−l1)l2=l0l2−l1l2,∀l0,l1,l2∈Z.
It is obvious that 0l0=0,∀l0∈Z.
Definition 2.4. A subset L(≠∅) of Z is described as a subalgebra of Z if l0−l1∈L whenever l0,l1∈L.
Definition 2.5. Let (Z,−,.) be an NSS. A subset C(≠∅) of Z is described as follows:
(i) A left ideal if C is a subalgebra of (Z,−) and nc1−n(v−c1)∈C,∀n,v∈Z,c1∈C;
(ii) A right ideal if C is a subalgebra of (Z,−) and CZ⊆C;
(iii) An ideal if C is both a left and right ideal.
Throughout the paper, Z denotes a near-subtraction semigroup, and P(Q) represents the power set of a set Q.
3.
Hybrid structures in near-subtraction semigroups
We collect some basic definitions of hybrid structure provided by Jun et al.[10] and define the notion of hybrid ideals in near-subtraction semigroup. We also construct an example of a hybrid left ideal that is not a hybrid right ideal and vice versa.
Definition 3.1. [10] Let Y be a universal set. A hybrid structure in Z over Y is defined to be a mapping
where ˜d:Z→P(Y) and ρ:Z→[0,1] are mappings.
Define a relation ≪ on the gathering of all hybrid structures, denoted by H(Z), in Z over Y as below:
where ˜d˜⊆˜b means that ˜d(u)⊆˜b(u) and ρ⪰γ means that ρ(u)≥γ(u),∀u∈Z. Then, the set (H(Z),≪) is partially ordered.
Definition 3.2. ˜dρ∈H(Z) is described as a hybrid ideal if it meets the below criteria:
(i) (∀l,g∈Z)(˜d(g−l)⊇˜d(g)∩˜d(l)ρ(g−l)≤ρ(g)∨ρ(l)).
(ii) (∀s,j,l∈Z)(˜d(sl−s(j−l))⊇˜d(l)ρ(sl−s(j−l))≤ρ(l)).
(iii) (∀l,q∈Z)(˜d(lq)⊇˜d(l)ρ(lq)≤ρ(l)).
Note that ˜dρ is a left hybrid ideal of Z if it satisfies (i) and (ii), and ˜dρ is a right hybrid ideal of Z if it satisfies (i) and (iii).
Below are some examples of hybrid ideals.
Example 3.1. Let Z={0,i,p} be a set in which "−" and "." are defined as below.
Then, (Z,−,.) is an NSS. For V,K,L∈P(Y) and with w,r,y∈[0,1], define a hybrid structure ˜dρ in Z by ˜d(0)=L, ˜d(i)=K, ˜d(p)=V and ρ(0)=w, ρ(i)=r, ρ(p)=y.
(i) If V⊂K=L, and y>r=w, then ˜dρ is a hybrid ideal of Z.
(ii) If K=V⊂L, and y=r>w, then ˜dρ is a hybrid right ideal, but it is not a hybrid left ideal, as ˜d(p.0−p.(p−0))=˜d(i)=K⊉L=˜d(0), and ρ(p.0−p.(p−0))=ρ(i)=r≰w=ρ(0).
(iii) If K⊂V⊂L, and r>y>w, then ˜dρ is neither a hybrid right ideal nor a hybrid left ideal, as ˜d(p.0−p.(i−0))=˜d(i)=K⊉L=˜d(0), ρ(p.0−p.(i−0))=ρ(i)=r≰w=ρ(0), and ˜d(p.0)=˜d(i)=K⊉V=˜d(p), ρ(p.0)=ρ(i)=r≰y=ρ(p). However, it satisfies condition (i) of Definition 3.2.
Example 3.2. Let Z={0,r,a,k} be a set in which "−" and "." are defined as below.
Then, (Z,−,.) is an NSS. For P,W,N∈P(Y) and m,y,s∈[0,1], define a hybrid structure ˜dρ in Z by ˜d(0)=P, ˜d(r)=W, ˜d(a)=N=˜d(k) and ρ(0)=m, ρ(r)=y, ρ(a)=s=ρ(k).
If N⊂W⊂P, and s>y>m, then ˜dρ is a hybrid left ideal, but it is not a hybrid right ideal, as ˜d(r.a)=˜d(a)=N⊉W=˜d(r), and ρ(r.a)=ρ(a)=s≰y=ρ(r).
Definition 3.3. For ˜dτ∈H(Z) and G∈P(Z)∖{∅}, the characteristic hybrid structure in Z over Y is denoted by χG(˜dτ), and it is described as
where
for any u∈Z.
Definition 3.4. Let ˜dρ∈H(Z). For any (Γ,ω)∈P(Y)×[0,1], we define
Definition 3.5. For ˜dρ∈H(Z), the set
is known as the [T,t]-hybrid cut of ˜dρ, where T∈P(Y), and t∈[0,1].
Note that ZΓ˜d∩Zωρ={l∈Z:˜d(l)⊇Γandρ(l)≤ω}=˜dρ[Γ,ω].
Definition 3.6. Let {˜diρi} be the family of hybrid structures in Z. Then, the hybrid intersection {˜⋒˜diρi} of (˜diρi) over Y is defined by {˜⋒˜diρi}:=(˜∩˜di,˜∨ρi), where (˜∩i˜di)(l)=⋂(˜di(l)), and (˜∨iρi)(l)=⋁(ρi(l)).
4.
Hybrid ideals in near-subtraction semigroups
Theorem 4.1. If ˜dρ is a hybrid left (resp., right) ideal of Z, then the sets
are left (resp., right) ideals of Z.
Proof. For l,w∈Z˜dρ, ˜d(l−w)⊇˜d(l)∩˜d(w)=˜d(0), and ρ(l−w)≤ρ(l)∨ρ(w)=ρ(0). Thus, l−w∈Z˜dρ. For s∈Z, we have ˜d(sl−s(w−l))⊇˜d(l)=˜d(0), and ρ(sl−s(w−l))≤ρ(l)=ρ(0). Thus, sl−s(w−l)∈Z˜dρ. So, Z˜dρ is a left ideal of Z.
Theorem 4.2. Let ˜dρ,˜yν∈H(Z). If they are hybrid ideals of Z, then ˜dρ⋒˜yν is a hybrid ideal of Z.
Proof. Let w,g∈Z. Then,
For s∈Z, we have
Also,
So, ˜dρ⋒˜yν is a hybrid ideal of Z.
Note that for a family of hybrid ideals {˜diρi} of Z, ˜⋒˜diρi of Z is a hybrid ideal.
Theorem 4.3. For G∈P(Z)∖{∅}, define a hybrid structure ˜dρ in Z by
where Q0,Q1∈P(Y) with Q0⊃Q1 and q0,q1∈[0,1] with q0<q1. The conditions mentioned below are equivalent.
(i) ˜dρ is a hybrid ideal of Z.
(ii) G of Z is an ideal.Moreover, Z˜dρ=G.
Proof. (i)⇒(ii) Let l,b∈G. Then, ˜d(l−b)⊇˜d(l)∩˜d(b)=Q0, and ρ(l−b)≤ρ(l)∨ρ(b)=q0. So, l−b∈G. For s∈Z, we have ˜d(sl−s(b−l))⊇˜d(l)=Q0, and ρ(sl−s(b−l))≤ρ(l)=q0, implying that sl−s(b−l)∈G. Also, ˜d(lb)⊇˜d(l)=Q0, and ρ(lb)≤ρ(l)=q0. We get lb∈G. Therefore, G of Z is an ideal.
(ii)⇒(i) Let l,b,s∈Z. If l∉G or b∉G, then ˜d(l−b)⊇Q1=˜d(l)∩˜d(b), and ρ(l−b)≤q1=ρ(l)∨ρ(b). Otherwise, l,b∈G, and then l−b∈G, which implies ˜d(l−b)⊇Q0=˜d(l)∩˜d(b), and ρ(l−b)≤q0=ρ(l)∨ρ(g).
If l∈G, then sl−s(b−l)∈G, which implies ˜d(sl−s(b−l))⊇Q0=˜d(l), and ρ(sl−s(b−l))≤q0=ρ(l). Otherwise, l∉G, and then ˜d(sl−s(b−l))⊇Q1=˜d(l), and ρ(sl−s(b−l))≤q1=ρ(l).
If l∈G, then lb∈G, which implies ˜d(lb)⊇Q0=˜d(l), and ρ(lb)≤q0=ρ(l). Otherwise, l∉G, and then ˜d(lb)⊇Q1=˜d(l), and ρ(lb)≤q1=ρ(l).
Therefore, ˜dρ is a hybrid ideal of Z.
Moreover,
Hence, Z˜dρ=G.
Corollary 4.1. For G∈P(Z)∖{∅} and ˜dρ∈H(Z), the below conditions are equivalent:
(i) χG(˜dρ) of Z is a hybrid left (resp., right) ideal.
(ii) G of Z is a left (resp., right) ideal.
Theorem 4.4. Let ˜dρ∈H(Z). Then, the assertions mentioned below are equivalent:
(i) ˜dρ is a hybrid ideal in Z.
(ii) ∀(Γ,ω)∈P(Y)×[0,1],the sets ZΓ˜d≠∅ and Zωρ≠∅ are ideals of Z.
Proof. (i)⇒(ii) Let Γ∈P(Y) and ω∈[0,1] be such that ZΓ˜d≠∅, and Zωρ≠∅. Let l,g,s∈Z.
If l,g∈ZΓ˜d∩Zωρ, then ˜d(l−g)⊇˜d(l)∩˜d(g)⊇Γ, ρ(l−g)≤ρ(l)∨ρ(g)≤ω, and so l−g∈ZΓ˜d∩Zωρ.
Also, if l∈ZΓ˜d∩Zωρ, then ˜d(sl−s(g−l))⊇˜d(l)⊇Γ,ρ(sl−s(g−l))≤ρ(l)≤ω, and ˜d(lg)⊇˜d(l)⊇Γ,ρ(lg)≤ρ(l)≤ω. Thus, sl−s(g−l),lg∈ZΓ˜d∩Zωρ, and hence ZΓ˜d and Zωρ are ideals in Z.
(ii)⇒(i) Let l,g∈Z be such that ˜d(l)=Γl, and ˜d(g)=Γg for some Γl,Γg∈P(Y). If we put Γ:=Γl∩Γg, then l,g∈ZΓ˜d, and l−g∈ZΓ˜d, so ˜d(l−g)⊇Γ=Γl∩Γg=˜d(l)∩˜d(g). Let s∈Z. Then, sl−s(g−l)∈ZΓ˜d, and ls∈ZΓ˜d, implying that ˜d(sl−s(g−l))⊇Γl=˜d(l), and ˜d(ls)⊇Γl=˜d(l).
Also, let ρ(l)=ωl and ρ(g)=ωg for some ωl,ωg∈[0,1]. Then, by taking ω:=ωl∨ωg, we get l,g∈Zωρ and l−g∈Zωρ, so ρ(l−g)≤ω=ωl∨ωg=ρ(l)∨ρ(g). Let s∈Z. Then, sl−s(g−l), and ls∈Zωρ imply ρ(sl−s(g−l))≤ωl=ρ(l), and ρ(ls)≤ωl=ρ(l).
So, ˜dρ in Z over Y is a hybrid ideal.
Theorem 4.5. For ˜dρ∈H(Z), let {ZΓ˜d|Γ∈P(Y)} and {Zσρ:σ∈[0,1]} be the gathering of ideals of Z such that
(i) Z=⋃Γ∈P(Y)ZΓ˜d=⋃σ∈[0,1]Zσρ,
(ii) Z⊃H if and only if ZZ˜d⊂ZH˜d, ∀Z,H∈P(Y),
(iii) z<h if and only if Zzρ⊂Zhρ, ∀z,h∈[0,1].
Construct a hybrid structure ˜bδ in Z over Y by ˜b(c)=⋃{Γ|Γ∈P(Y) and c∈ZΓ˜d}, and δ(c)=⋀{σ|σ∈[0,1] and c∈Zσρ},∀c∈Z. Then, ˜bδ is a hybrid ideal in Z over Y.
Proof. By Theorem 4.4, it is enough to show that ZΓ˜b and Zσδ are ideals of Z for all (Γ,σ)∈P(Y)×[0,1].
Now, we prove that ZΓ˜b is an ideal of Z for Γ∈P(Y).
Consider the below two cases:
(i)Γ=⋃{Γ0|Γ0∈P(Y) and c∈ZΓ0˜d}.
(ii)Γ≠⋃{Γ0|Γ0∈P(Y) and c∈ZΓ0˜d}.
Case (i) gives that c∈ZΓ˜b if and only if c∈ZΓ1˜d,∀Γ1⊂Γ if and only if c∈⋂Γ1⊂ΓZΓ1˜d. Thus, ZΓ˜b=⋂Γ1⊂ΓZΓ1˜d, and hence ZΓ˜b is an ideal of Z.
For case (ii), we claim that ZΓ˜b=⋃Γ1⊇ΓZΓ1˜d. If c1∈⋃Γ1⊇ΓZΓ1˜d, then c1∈ZΓ1˜d for some Γ1⊇Γ. By assumption, we have c1∈ZΓ˜d, so ⋃Γ1⊇ΓZΓ1˜d⊆ZΓ˜b. For the converse, if c1∉⋃Γ1⊇ΓZΓ1˜d, then c1∉ZΓ1˜d,∀Γ1⊇Γ. In particular, c1∉ZΓ˜b, so ZΓ˜b=⋃Γ1⊇ΓZΓ1˜d, and ZΓ˜b is an ideal of Z.
Next, we prove that Zσ0ρ is an ideal of Z for σ0∈[0,1].
Consider the two cases:
(i) σ0=⋀{σ|σ∈[0,1] and σ>σ0}.
(ii)σ0≠⋀{σ|σ∈[0,1] and σ>σ0}.
Case (i) gives that c∈Zσ0δ if and only if c∈Zσρ,∀σ>σ0 if and only if c∈⋂σ>σ0Zσρ. Thus, Zσ0δ=⋂σ>σ0Zσρ, and Zσ0δ is an ideal of Z.
For case (ii), we claim that Zσ0δ=⋃σ≥σ0Zσρ. If c∈⋃σ≥σ0Zσρ, then c∈Zσρ for some σ≤σ0. By assumption, we have c∈Zσδ, so ⋃σ≥σ0Zσρ⊆Zσ0δ. For the converse, if c1∉⋃σ≥σ0Zσρ, then c1∉Zσρ,∀σ≥σ0. In particular, c1∉Zσ0δ. So, Zσ0δ=⋃σ≥σ0Zσρ, and Zσ0δ is an ideal of Z.
Theorem 4.6. For a family of ideals {Gm:m is a positive integer and Z=G1⊃G2⊃...} in Z, define a hybrid structure ˜dρ in Z over Y=[0,1] by
∀l∈Z. Then, ˜dρ in Z is a hybrid ideal over Y=[0,1].
Proof. Let l,g∈Z.
(i) Consider that l∈Gp∖Gp+1 and g∈Ga∖Ga+1 for some p,a∈{1,2,...}. Without loss of generality, consider that p≤a. Then, l−g∈Gp implies ˜d(l−g)⊇[0,pp+1]=˜d(l)∩˜d(g), and ρ(l−g)≤1p+1=ρ(l)∨ρ(g).
If l,g∈∞⋂m=1Gm, then l−g∈∞⋂m=1Gm, and thus ˜d(l−g)=[0,1]=˜d(l)∩˜d(g), and ρ(l−g)=0=ρ(l)∨ρ(g).
If l∈∞⋂m=1Gm, and g∉∞⋂m=1Gm, then ∃q∈N:g∈Gq∖Gq+1. It follows that l−g∈Gq, ˜d(l−g)⊇[0,qq+1]=˜d(l)∩˜d(g), and ρ(l−g)≤1q+1=ρ(l)∨ρ(g).
Similarly, ˜d(l−g)⊇˜d(l)∩˜d(g), and ρ(l−g)≤ρ(l)∨ρ(g) whenever l∉∞⋂m=1Gm and g∈∞⋂m=1Gm.
(ii) If s,g∈Z and l∈Gp∖Gp+1 for some p=1,2,..., then sl−s(g−l)∈Gp. Thus, ˜d(sl−s(g−l))⊇[0,pp+1]=˜d(l), and ρ(sl−s(g−l))≤1p+1=ρ(l).
If l∈∞⋂m=1Gm, then sl−s(g−l)∈∞⋂m=1Gm,∀s,g∈Z. Thus, ˜d(sl−s(g−l))=[0,1]=˜d(l), and ρ(sl−s(g−l))=0=ρ(l).
If s∈Ga∖Ga+1 for some a=1,2,..., and g∈∞⋂m=1Gm (or, s∈∞⋂m=1Gm, and g∈Ga∖Ga+1 for some a=1,2,...), then l∈Ga. Thus,
(iii) Now, if l,g∈Gp∖Gp+1 for some p=1,2,..., then lg∈Ga, as Ga is an ideal of Z. Thus,
If l,g∈∞⋂m=1Gm, then g∈∞⋂m=1Gm. Thus, ˜d(lg)=[0,1]=˜d(l), and ρ(lg)=0=ρ(l).
Therefore, ˜dρ of Z is a hybrid ideal over Y=[0,1].
5.
Homomorphism of a hybrid structure
In this section, we present some characteristics related to homomorphism of hybrid structures in a near-subtraction semigroup. Throughout this section, Z and Z′ denote the near-subtraction semigroups.
Definition 5.1. A homomorphism of Z into Z′ such that ϑ(w−a)=ϑ(w)−ϑ(a) and ϑ(wa)=ϑ(w)ϑ(a), ∀w,a∈Z is defined.
Definition 5.2. Let ϑ:Z→Z′ be a mapping, where Z,Z′≠{∅} and ˜dρ∈H(Z′). The preimage of ˜dρ under ϑ, denoted as ϑ−1(˜dρ), is a hybrid structure of Z defined by ϑ−1(˜dρ):=(ϑ−1(˜d),ϑ−1(ρ)), where ϑ−1(˜d)=˜d(ϑ(l))andϑ−1(ρ)=ρ(ϑ(l)),∀l∈Z.
Theorem 5.1. Let ϑ:Z→Z′ be a homomorphism of an NSS. If ˜dρ of Z′ is a hybrid ideal, then ϑ−1(˜dρ) of Z is a hybrid ideal.
Proof. Assume that ˜dρ of Z′ is a hybrid ideal. Let a,g∈Z. Then,
Let q∈Z. Then,
Also,
So, ϑ−1(˜dρ) of Z is a hybrid ideal.
Theorem 5.2. Let ϑ:Z→Z′ be an onto homomorphism of an NSS, and ˜dρ∈H(Z′). If ϑ−1(˜dρ) of Z is a hybrid ideal, then ˜dρ of Z′ is a hybrid ideal.
Proof. Let ϑ−1(˜dρ) in Z be a hybrid ideal, and l′,r′∈Z′. Then, ∃l,r∈Z such that ϑ(l)=l′ and ϑ(r)=r′. Now,
Let s′∈Z′. Then, ∃s∈Z such that ϑ(s)=s′. Now,
Also,
So, ˜dρ in Z′ is a hybrid ideal.
Definition 5.3. Let ˜dρ∈H(Z) and Λ:Z→Z′ be a mapping. Then, the hybrid structure Λ(˜dρ):=(Λ(˜d),Λ(ρ)) in Λ(Z) defined by
∀v∈Z′, is said to be the image of ˜dρ under Λ.
A hybrid structure ˜dρ in Z is said to satisfy the sup property if for every subset G⊆Z, ∃k0∈G such that
Proposition 5.1. A homomorphic image of a hybrid ideal with the sup property is a hybrid ideal.
Proof. Consider a homomorphism of an NSS ς:Z→Z′, and let ˜dρ of Z be a hybrid ideal with the sup property.
Given ς(p),ς(w)∈Z′, let p0∈ς−1(ς(p)) and w0∈ς−1(ς(w)) be such that
Then,
Given ς(s)∈Z′, let s0∈ς−1(ς(s)).
Also,
Hence, ς(˜dρ) is a hybrid ideal in ς(Z).
6.
Conclusions
In this paper, we have defined and investigated hybrid ideals in near-subtraction semigroups. In a near-subtraction semigroup, we formed ideals for a hybrid ideal, and various properties of the hybrid image and hybrid preimage of a near-subtraction semigroup's hybrid ideal under homomorphism mapping were also discussed. Using the ideas and results presented in this paper, it is intended to demonstrate the concept of a hybrid prime (resp., semi) ideal and its related properties for a hybrid ideal to be a hybrid prime (resp., semi) ideal in near-subtraction semigroups.
Acknowledgments
This work was supported by the Taif University Researchers Supporting Project (TURSP-2020/246), Taif University, Taif, Saudi Arabia.
Conflict of interest
The authors declare no conflicts of interest.









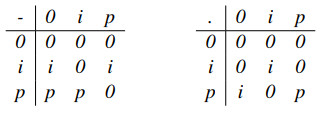
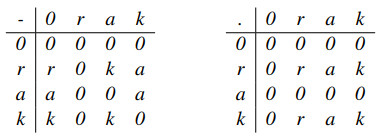




 DownLoad:
DownLoad: