Recent analytic development of the dynamic $Q$-tensor theory for nematic liquid crystals

1.   Introduction

Influenza A is a highly contagious respiratory viral disease caused by influenza viruses. It is sometimes called "the flu". It can easily spread from person to another by direct contact, where an infected individual can spread it to others up to about 6 feet away. The virus spreads by droplets made by infected individuals when they cough, sneeze or talk. Such droplets may land in the mouth or the nose of nearby susceptible people or they could even be inhaled by them to enter their lungs, which finally lead them to catch the flu ^[1,2]. Among the three types of influenza (namely, influenza A, influenza B and influenza C), influenza A is the most common one that is known to cause widespread outbreaks. It has many subtypes of which the two subtypes H1N1 and H3N2 are mostly circulating among humans ^[1,3].

Due to its ability to rapidly evolve and mutate, seasonal flu epidemics and (rarely) pandemics do occur. Such epidemics and pandemics impact significantly on the public health as well as on the economy over the globe. For example, in the united states, seasonal influenza infections are responsible for thousands of deaths and for hundreds of thousands of hospitalisations every year ^[4]. It is also responsible for the loss of billions of dollars yearly, as a cost of treatment or due to lost days of work and/or education. Consequently, public health communities are always interested in finding not only strategies to mitigate the impact of seasonal influenza but also strategies aiming at reducing morbidity and mortality in the case of pandemics ^[3,5].

Numerous studies have been done to understand more about the epidemiology of influenza. In particular, mathematical models have been extensively used to extend our understanding about the transmission dynamics of influenza and to help find public health strategies aiming at preventing/containing it ^[6]. Some models are used to study the epidemic situation of influenza A, where its severity is explored by estimating the (basic) reproduction number (a threshold quantity that is defined to determine the average number of secondary infected individuals who get infected due to successful contacts occurring between susceptible individuals and an infected one, during the infectious period) based on data collected during outbreaks ^[7,8,9]. Other models study the endemic situation, where the demographic parameters (births and natural deaths) are taken into account ^[4,10,11].

The general motivation behind these studies is to help find strategies to contain influenza A. Some strategies are individually-based (in the sense that individuals are aware of the way influenza is transmitted and they avoid catching it) and others are based on intervention programmes (e.g., isolation/quarantine or vaccination) directed by the governments and public health decision makers. For example, some control strategies are based on treating infected individuals by either resting in bed, drinking plenty of liquids or taking mild pain killers to relieve the pain. Other strategies may be educational, based on reducing the successful contacts through staying at home while being sick, covering the face when sneezing or coughing, and regularly washing the hands. Isolating or quarantining infected individuals is another strategy ^[4,12]. Also, applying mass vaccination programmes could be helpful ^[13]. Influenza vaccine is particularly helpful for those suffering from influenza complications or those being at high risk of getting infected with the flu.

A review paper on influenza epidemics and pandemics ^[6] discussed the usefulness of mathematical models in understanding the spatial-temporal transmission dynamics of influenza and in helping evaluate the potential effectiveness of public health interventions in controlling pandemics of varying severity. The review deduced that "the current models may not be useful in identifying interventions for epidemics generated by strains" (e.g., influenza A H1N1) and recommends that further studies taking into account more biological complexities are needed. One of such complexities is the sex and gender disparity.

The terms sex and gender are often used interchangeably ^[14]. However, the literature shows that they refer to different meanings. The term sex refers to the human biology, while the term gender refers to the human behaviour and activities that are determined by the societies or the cultures ^[15]. The biology literature shows that the gender can affect the health seeking behaviours, while the biological sex affects the exposure to pathogens, vulnerability and immune response to influenza and consequently to vaccination ^{[15,16,17,18,19]}. All these effects together result in differences between males and females in response to influenza-vaccination-campaigns as well as the susceptibility, severity and duration of influenza. Moreover, biological studies show that females are less susceptible to influenza than males (as they develop higher innate, humoral and cellular immune responses than males), while the influenza-vaccine efficacy is higher in females than in males ^{[20,21,22,23]}. On the other hand, the influenza-vaccine uptake is influenced by the gender, where there is evidence that males are more likely to take the vaccine than females ^[20]. More details about sex and gender differences and their relation to influenza are shown in the July 2010 WHO report ^[14]. It is noteworthy that the report strikingly highlights that the role of sex and gender in acute infectious diseases, including influenza, has not been explored extensively and further work that takes these factors in consideration is lacked so that a more effective public health influenza control programme is produced.

To the best of our knowledge, neither the sex nor the gender has been considered while formulating a mathematical model for studying the transmission dynamics of respiratory infections (e.g., influenza) and this is the first work that takes these factors into consideration. Here, the impact of sex and gender on the transmission dynamics and possibility to contain influenza A infection is explored. To this end, we constructed a deterministic SIR influenza model in which it is differentiated between both females and males through two sex-difference factors (namely, the susceptibility and recovery rates), see section 2. In addition to carrying out equilibrium and stability analysis, the impact of disparities in these parameters on the influenza infection outcome has been explored, section 3. Moreover, the possibility to contain/eliminate influenza with a public health strategy based on the application of influenza-mass-vaccination programme solely has been investigated. Therefore, the model has been generalised to take into account disparity in the influenza-vaccine efficacy (that is sex-difference factor) and in the response to influenza-mass vaccination campaigns (i.e, the vaccination rate, which is a gender behavioural difference factor), section 4. The paper closes with a summary and conclusion of our results in section 5.

2.   Model building

Consider a closed homogeneously mixing heterosexual population of constant size $N$, for which both the female and male subpopulations are splitted, according to their epidemiological status, into susceptible $S$, infected $I$ and recovered with full immunity $R$. State variables for the female population are denoted by the subscript "1", while those of the male population have the subscript "2". If $B(t)$ is the total number of births at time $t$, $q$ is the probability that a newborn is female, while $\mu$ is the per-capita death rate, then the demographic dynamics of the populations could be described by

where $N_1(t)$ and $N_2(t)$ denote the total number of females and males, respectively, at time $t$ and $N_1(t) + N_2(t) = N(t)$. Since the total population size is assumed constant, then $B(t) = \mu N$. If we further assume that the male-to-female newborns ratio is 1- to - 1, then $q = 1/2$. This assumption implies that the equilibrium proportion of females as well as males is $1/2$.

As influenza is not vertically transmitted, it is assumed that all newbirths are susceptible. Female newborns (whose number at time $t$ is $\mu N/2$) enter the class of susceptible females $S_1(t)$. They either die naturally (at per-capita rate $\mu$) or acquire influenza infection due to successful contacts with infected males and females at rate $\lambda_1(t)$ and transit to the infected females class. Infected females either die at per-capita rate $\mu$ or recover and acquire full immunity against the attacking influenza strain at a per-capita rate $\gamma_1$. Once they recover, females acquire full immunity against the strain and die naturally at rate $\mu$. Therefore, the dynamics of the female population is governed by the system

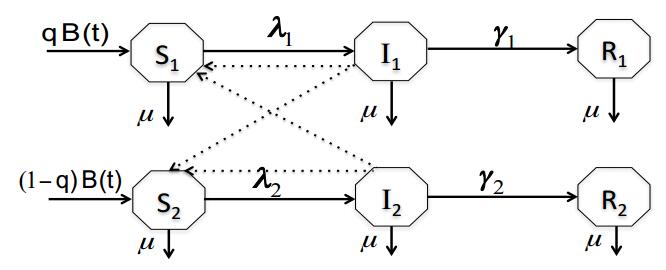
Similarly, susceptible males increase due to male newbirths (of size $\mu N / 2$) and decrease due to either natural death (at rate $\mu$) or acquiring influenza infection at rate $\lambda_2$. Infected males either die at rate $\mu$ or they recover from the attacking strain at rate $\gamma_2$. Recovered males acquire full immunity against the attacking strain and die naturally at rate $\mu$. A flowchart for the transition between the model states is shown in Figure 1, while model states and parameters' physical meaning are shown in Tables 1 and 2, respectively. Hence, the male population's dynamics is described through

Assume now that $\tilde\beta$ denotes the average number of contacts that an individual has with other individuals in the total population. Also, $r_1$ is the susceptibility of females (which is proportional to the probability of success that a susceptible female gets infected due to contacts with infected males and females ^[25]), while $r_2$ is the susceptibility of males (which is proportional to the probability that a susceptible male gets successfully infected as a result of contacts with infected individuals ^[25]). Assume also that $r_{ij}$ accounts for the transmissibility of influenza from infected individuals in the population $i$ to susceptible individuals in the population $j$, for all $i, j \in \{1, 2\}$. Hence, the rate at which susceptible females acquire infection $\lambda_1(t)$ and that at which susceptible males acquire infection read

Assume further that infected males and females are equally likely to transmit influenza, in the sense that the effective rate at which infected females infect susceptible males/females equals that at which infected males infect susceptible males/females (i.e., $r_{11} = r_{12} = r_{21} = r_{22}: = r$). Hence, $\beta = r_2 r \tilde\beta : = r_2 \bar\beta$ accounts for the effective contact rate at which susceptible males acquire influenza and $r_1 r \tilde\beta = (r_1/r_2) r_2 \bar\beta : = g \beta$ is the effective contact rate at which susceptible females acquire influenza virus. Here, $g = r_1/r_2$ accounts for the relative susceptibility ^[26,27] of females with respect to males. Hence, (2.4) reads

The recovery rates could also be rescaled by assuming that $\gamma_2 = \gamma$ and $\gamma_1 = a\gamma$. Hence, $a$ is a dimensionless parameter accounting for the relative recoverability of females with respect to males. Thus, the populations' overall dynamics is described by the following system of ordinary differential equations

It is noteworthy that this modelling approach could be applied to several other infectious diseases, including but not limited to tuberculosis (TB), pertussis (whooping cough) and human immunodeficiency virus (HIV) infection, where the literature shows evidence that sex and gender have significant impact on their spread. For example, in most countries, TB notification is twice as high in men as in women (with a male/female ratio of $1.96 \pm 0.6$ for the worldwide case notification rate) ^[28,29]. However, in case of pertussis, females have been shown to be more affected than males with male-to-female ratio of $0.8 : 1$ ^[30]. On the other hand, although the proportion of females living with HIV is about $51%$ of the global total, it varies from region to another. For example, in the United States, one in four people having HIV is a woman. However, women account for a proportion of $56%$ of those having HIV in Western and Central Africa. Moreover, in Eastern and Southern Africa, females account for more than $59%$ of the total number of people having HIV in that region ^[31,32,33].

3.   Rescaled model and equilibria

Let

Hence,

where the rescaled force of infection $\lambda$ is a function of both variables $y_1$ and $y_2$ with

and $x_1 + y_1 + z_1 + x_2 + y_2 + z_2 = 1$.

If we assume that $p_1 = N_1/N = x_1 + y_1 + z_1$ and $p_2 = N_2/N = x_2 + y_2 + z_2$, then the rate of change in the proportion of females and males at time $t$ is given by

Its solution is given by

where $p_1(0)$ and $p_2(0)$ are the initial proportions of females and males, respectively, and $p_1(0) + p_2(0) = 1$. It is easy to check that the fact that $p_1(t) + p_2(t) = 1$ implies that $p_1(0) = p_2(0) = 1/2$. Thus, $p_1(t) = p_2(t) = 1/2$. I.e., the female-to-male ratio at any time $t$ is $1 : 1$. Hence, $x_1(t) + y_1(t) + z_1(t) = x_2(t) + y_2(t) + z_2(t) = 1/2$.

3.1.   Influenza-free equilibrium and the basic reproduction number $R_0$

Simple computations show that model (3.1) has the influenza-free equilibrium $E_0 = (x_{1, 0}, y_{1, 0}, z_{1, 0}, x_{2, 0}, y_{2, 0}, z_{2, 0})^{T} = (1/2, 0, 0, 1/2, 0, 0)^{T}$, where the prime ${}^{T}$ here means vector transpose.

The basic reproduction number is computed by following the approach shown in Diekmann et al ^[34]. The linearised infection subsystem, at the influenza-free equilibrium, is

which is two-dimensional. Hence, the corresponding non-negative matrix for the new-infection terms ${\bf T}$ and the non-singular matrix for the remaining transfer terms ${\bf \Sigma}$ are two-dimensional too, with

Therefore, the next-generation matrix with large domain ${\bf K}_L = - {\bf T} {\bf \Sigma^{-1}}$ reads

Thus, the basic reproduction number $R_0$ is the dominant eigenvalue of ${\bf K}_L$ and is given by

The local stability analysis of the influenza-free equilibrium $E_0$ is investigated by considering the eigenvalues of the corresponding Jacobian matrix $J_0$ evaluated at $E_0$. The computations show that $J_0$ has four multiple eigenvalues $-\mu$, $-\mu$, $- \mu$, $- \mu$ in addition to those of the matrix

Hence, the local stability of $E_0$ depends on the determinant and trace of the matrix $J_{sub}$. Now,

Hence, $\det(J_{sub}) > 0$ if and only if $R_0 < 1$. Moreover, if $R_0 < 1$, then $\beta/2 < \gamma + \mu$ and $g \beta/ 2 < a \gamma + \mu$. Hence, $\text{tr}(J_{sub}) = [\beta/2 - (\gamma + \mu)] + [g \beta/2 - (a\gamma + \mu)] < 0$. Thus, $E_0$ is locally asymptotically stable for $R_0 < 1$ and we show the following proposition.

Proposition 1. Model (3.1) has an influenza-free equilibrium $E_0 = (1/2, 0, 0, 1/2, 0, 0)^{T}$ that is locally asymptotically stable if and only if the basic reproduction number $R_0$ is less than unity.

3.2.   Existence of a unique endemic equilibrium

To find the endemic equilibrium of system (3.1), we put the derivatives in the left hand side of its equations equal zero and solve to get

where $\bar\lambda\in [0, \infty)$ is the equilibrium force of infection and is the unique feasible solution of the equation

It is clear that the equilibrium proportion of the subpopulations depend on the equilibrium force of infection $\bar\lambda$ which is determined by the solution of equation (3.8). Once a solution of equation (3.8) is obtained, we get the endemic equilibrium of the model (3.1). The uniqueness of the feasible solution of equation (3.8) could be proven by rewriting it as

It is easy to check the following

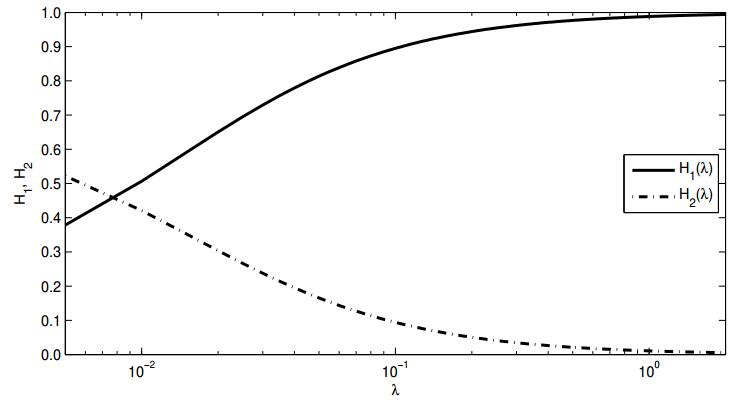
and

Hence, equation (3.9) has a unique nonnegative solution if and only if $H_1(0) \le H_2(0)$, while otherwise it has no feasible solution, see Figure 2. The condition $H_1(0) \le H_2(0)$ is equivalent to $R_0 \ge 1$ and we show the following proposition.

Proposition 2. Model (3.1) has a unique endemic equilibrium if and only if the basic reproduction number $R_0 > 1$, while otherwise it has no endemic steady state.

To find the unique feasible solution of equation (3.8), we rewrite it in the quadratic form

where

Hence,

3.3.   Local stability of the endemic equilibrium

Since $x_1 + y_1 + z_1 = x_2 + y_2 + z_2 = 1/2$ and both $z_1$ and $z_2$ do not appear in the other equations, we consider the four equations of $x_1, y_1, x_2$ and $y_2$ only. Hence, the Jacobian matrix evaluated at the endemic equilibrium, for these four equations, reads

If $\rho$ is the eigenvalue of $J$, then the characteristic polynomial of $J$ is of degree four and reads

where

● the coefficient of $\rho^3$ is

Using (3.9), we get

● the coefficient of $\rho^2$ is

Using (3.9), we obtain

● the coefficient of $\rho$ is

Using (3.9), it simplifies to

● the term-free of $\rho$ reads

which, using (3.9), simplifies to

Since, all model parameters are non-negative and since $\bar\lambda$ is positive for $R_0 > 1$, then the relations (3.13), (3.14), (3.15), and (3.16) imply that the coefficients $C_1, C_2, C_3$ and $C_4$ are all positive, for $R_0 > 1$. Hence, based on the Routh-Hurwitz criterion (see appendix A.5 of ^[35]), the roots of the characteristic polynomial (3.12) have strictly negative real parts if and only if the determinant $\Delta = C_1 C_2 C_3 - C_3^2 - C_1^2 C_4$ is strictly positive. To this end, we compute $\Delta$. On performing some tedious calculations and with the use of the relation (3.9), it is shown in appendix A that $\Delta > 0$. We show the following proposition.

Proposition 3. The unique endemic equilibrium of model (3.1) is locally asymptotically stable whenever it exists.

3.4.   Global stability of the influenza-free equilibrium

Global stability analysis of the disease-free equilibrium (for $R_0 < 1$) is established by following the approach shown in section 3 of Castillo-Chavez et al ^[36]. Model (3.1) can be rewritten as

where

and

The components of $x \in {\mathbb{R}}^4$ denote the uninfected (susceptible) subpopulations, while those of ${\bf y} \in \mathbb{R}^2$ denote the infected subpopulations. The disease-free equilibrium (DFE) of model (3.17) is $U_0 = (x^*, 0)^{T}$ which corresponds to the DFE of the original model (3.1). Thus, the global stability of $U_0$ is equivalent to that of $E_0$ and vice-versa. Castillo-Chavez et al ^[36] showed that the global stability of $U_0$ (provided that $R_0 < 1$) is guaranteed if the following two conditions are held

(H1) For $\frac{dx}{dt} = F(x, 0)$, $x^*$ is globally asymptotically stable (g. a. s.),

(H2) $G(x, {\bf y}) = B{\bf y} - \hat{G}(x, {\bf y}), \hat{G}(x, {\bf y}) \ge 0$ for $(x, \bar{y}) \in \Omega$,

where $B = D_{{\bf y}} G(x^*, 0)$ is an M-matrix and $\Omega = \{(x_1, z_1, x_2, z_2, y_1, y_2): x_1 + z_1 + x_2 + z_2 + y_1 + y_2 = 1, x_1 > 0, x_2 > 0, z_1 \ge 0, z_2 \ge 0, y_1 \ge 0, y_2 \ge 0 \}$ is the region where model (3.17) makes biological sense. To this end, we prove each condition separately. Condition (H1) is proven by considering the following Lyapunov function

Clearly, $V(x_1, z_1, x_2, z_2) \ge 0$ along the solution of the system

and is zero if and only if

The time derivative of the Lyapunov function $V(x_1, z_1, x_2, z_2)$, computed along the solutions of system (3.19), is

Thus, $\dot{V} < 0$ so that $x^*$ is globally asymptotically stable for the system (3.19).

Condition (H2) is proven by rewriting the vector matrix $G(x, {\bf y})$ in the form $B{\bf y} - \hat{G}(x, {\bf y})$, where

is an M-matrix (as the off-diagonal elements are non-negative) and

Thus, the disease-free equilibrium $U_0 = (x^*, 0)^{T}$ for model (3.17) is globally asymptotically stable for $R_0 < 1$ and we have shown the following proposition.

Proposition 4. The influenza-free equilibrium $E_0$ is globally asymptotically stable if and only if the basic reproduction number $R_0 < 1$.

3.5.   Impact of sex disparity on the overall outcome of the disease

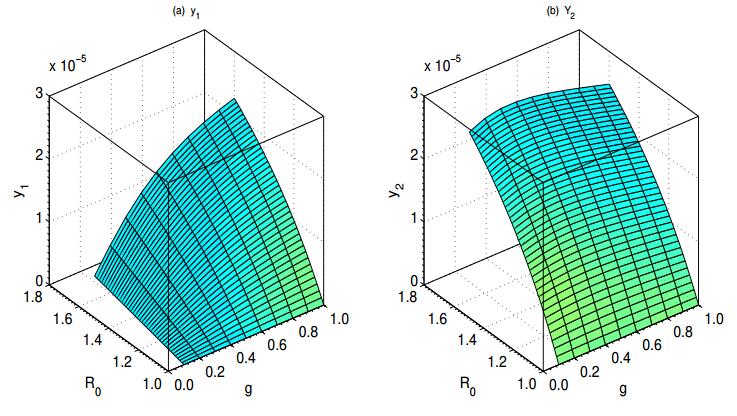
In this subsection we study the impact of sex disparity on the overall outcome of influenza. More specifically, we study how the basic reproduction number $R_0$ and the equilibrium force of infection $\bar\lambda$ depend on the variance in susceptibilities $r_1, r_2$ (of females and males, respectively) and in recovery rates if their means are kept constant. Before going into details, we study the qualitative behaviour of $R_0, \bar\lambda, \bar{y_1}$ and $\bar{y_2}$ on the relative susceptibility $g$. Formula (3.5) shows clearly that the basic reproduction number $R_0$ increases monotonically with the increase of the relative susceptibility $g$, if all other parameters are kept constant. However, numerical simulations have been done to show the dependence of $\bar{y_1}$ and $\bar{y_2}$ on $g$ and $R_0$. Figure 3 shows the qualitative behaviour of the endemic prevalence of both infected females $\bar{y_1}$ (see part(a)) and infected males $\bar{y_2}$ (see part (b)). For fixed $g$, both the endemic prevalence of infected females and males increase monotonically with the increase of $R_0$. The behaviour of $\bar{y_2}$ looks similar to that of $\bar\lambda$, while that of $\bar{y_1}$ looks different. There is a slow increase in the prevalence of infected males followed by a slow decrease in it, if $g$ is allowed to change from $0$ to $1$. A different behaviour is noticed for the case of females, especially for high values of $R_0$, where the endemic prevalence of infected females increases quickly, with the increase of the relative susceptibility $g$, till reaching a maximum at $g = 1$.

3.5.1.   Analysis in terms of the mean and variance of susceptibilities

Motivated by the work shown in ^[37], we assume that $\mu_r$ and $\nu_r$ are, respectively, the weighted mean and variance in susceptibilities of females and males. Since the proportion of females likewise that of males is $1/2$, then

where $0 < r_1 \le r_2$. Hence,

where $0 \le \nu_r \le \mu_r^2: = \nu_r^{\max}$. It is clear that $g = 1$ when $\nu_r = 0$. Moreover, $g$ decreases with the increase of $\nu_r$. On substituting from (3.22) into (3.5), we get

It is clear that

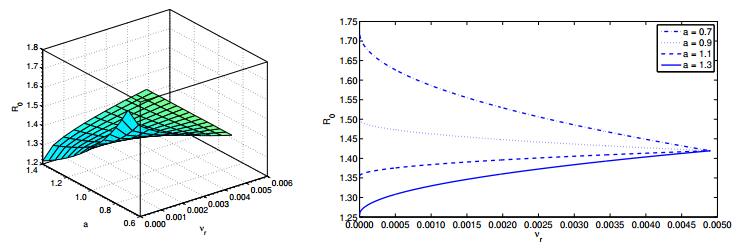
If $a < 1$, then $1/(a\gamma + \mu) > 1/(\gamma + \mu)$. Therefore, $R_0(\nu_r = 0) > R_0(\nu_r = \nu_r^{\max})$ and we get monotonically decreasing curves, see Figure 4. However, if $a > 1$, we get the opposite behaviour. Hence, if the mean of females and males susceptibilities is kept fixed, then the basic reproduction number $R_0$ increases with the increase of the variance in susceptibilities between females and males if infected females recover faster than infected males (i.e., if the duration of influenza in females is less than it in males). Conversely, if infected males recover quicker than infected females (i.e., $a < 1$), then any increase in the variance of susceptibility of females and males increases the value of the basic reproduction number $R_0$. Therefore, we show the following proposition.

Proposition 5. If influenza duration in females is shorter than its duration in males, then (for constant mean of females and males susceptibilities) the basic reproduction number $R_0$ increases with the increase of the variance in females and males susceptibilities and vice versa.

Similarly, we substitute from (3.22) into (3.11) to get

where $R_0$ in (3.24) is given by (3.23). It is easy to check that

Moreover, if $a < 1$, then $\bar\lambda\vert_{\nu_r = 0} > \bar\lambda\vert_{\nu_r = \mu_r^2}$ and vice versa.

Simulations have been done to study the impact of disparity in females and males susceptibilities on the equilibrium force of infection $\bar\lambda$ (Figure 5(a)) as well as on the endemic prevalence of infected females and males, Figure 5(b). The simulations show (for different values of the recovery rescaling parameter $a$) that $\bar\lambda$ increases initially with the increase of the variance in susceptibilities $\nu_r$ till reaching a maximum and then it decreases again to reach its final value. It is clear that the value of $\bar\lambda, \bar{y_1}$ and $\bar{y_2}$ at the maximum possible variance $\nu_r^{\max}$ does not depend on the value of $a$. Part (b) of the figure shows that the infected male population $\bar{y_2}$ has a similar behaviour to the equilibrium force of infection $\bar\lambda$, while the endemic prevalence of infected females is always decreasing with the increase of the variance $\nu_r$.

3.5.2.   Analysis in terms of the mean and variance of recovery rates

To study the impact of disparity in the recovery rates on the disease outcome, we assume that $\mu_\gamma, \nu_\gamma$ are, respectively, the weighted mean and variance ^[37] of recovery rates $a \gamma$ and $\gamma$ of infected females and males. Thus,

Hence,

Thus, there are two cases: either $a < 1$ or $a > 1$.

● Let $a < 1$. Then

where $0 \le \nu_\gamma < \mu_\gamma^2$.

● If $a > 1$, then

where $0 \le \nu_\gamma < \mu_\gamma^2$.

It is clear that $a = 1$ when $\nu_\gamma = 0$. On using (3.26) and (3.27) in (3.5), we get

Hence,

It is easy to check that

while

Moreover, $\frac{\partial R_0}{\partial \nu_\gamma} \vert_{a < 1, \: \nu_\gamma = 0} < 0$. It is noteworthy that $\nu_\gamma^{\star} < \nu_\gamma^{\max} = \mu_\gamma^2$ if and only if

It is worth noting that formula (3.28) could be rewritten as

where

The first expression $R_{01}$ represents the basic reproduction number for female population, while the second expression $R_{02}$ denotes the basic reproduction number for male population, if males recover faster than females (i.e., $a < 1$). As it is assumed that females are less susceptible than males (i.e., $g < 1$), it holds that $R_{01} < R_{02}$ for small enough disparity in recovery rates between both sexes, precisely, for

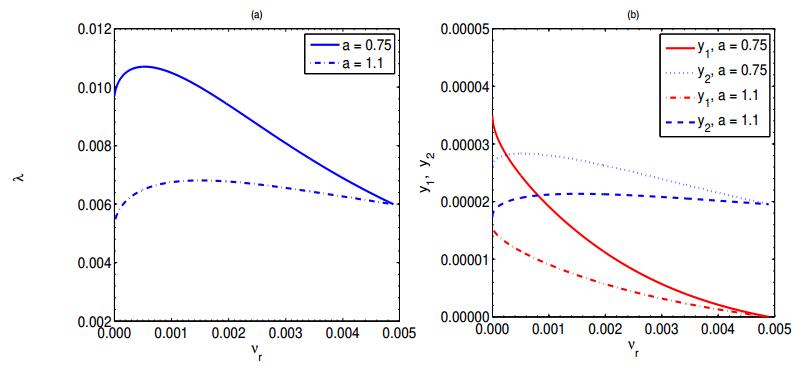
If $\nu_{\gamma}$ increases, then $R_{01}$ increases, while $R_{02}$ decreases. It is easy to check that $\vert\frac{dR_{01}}{d\nu_{\gamma}}\vert > \vert\frac{dR_{02}}{d\nu_{\gamma}}\vert$, which means that the rate of increase in $R_{01}$ is higher than the rate of decrease of $R_{02}$ with respect to $\nu_{\gamma}$. This interprets the initial reduction in the value of $R_0\vert_{a < 1}$, see the dashed-dotted curve in Figure 6. In epidemiological terms, and motivated by formulae (3.31), any increase in the recovery rates disparity enlarges (shrinks) the infectious period of infected females (males) and therefore extends (shortens) the time window during which infected individuals are capable of transmitting the infection, which in turn increases (decreases) the female (male) reproduction number.

On the other hand, formula (3.29) could be rewritten as

where

At $\nu_{\gamma} = 0$, we have ${\tilde{R}}_{01} < {\tilde{R}_{02}}$. Moreover, ${\tilde{R}}_{01}$ decreases while ${\tilde{R}_{02}}$ increases, with the increase of $\nu_\gamma$. Also, the rate of increase in ${\tilde{R}_{02}}$ is higher than the rate of decrease in ${\tilde{R}_{01}}$, with respect to $\nu_\gamma$. In other words, it holds that $\vert\frac{d {\tilde{R}_{01}}}{d\nu_{\gamma}}\vert < \vert\frac{d{\tilde{R}_{02}}}{d\nu_{\gamma}}\vert$. This clarifies the monotone increase in the basic reproduction number $R_0\vert_{a > 1}$, see the solid curve in Figure 6. Epidemiologically, formulae (3.32) say that increasing the disparity in recovery rates between both sexes enlarges (shrinks) the infectious period of infected males (females) and therefore extends (shortens) the time window during which infected individuals are capable of transmitting the infection, which in turn increases (decreases) the male (female) reproduction number. Hence, the above result is summarised in the following proposition.

Proposition 6. In analysing the impact of recovery rate disparity, two cases arise.

1. If the duration of influenza in females is shorter than in males (i.e., $a > 1$), then the basic reproduction number increases with the increase of the variance in recovery rate between infected females and males, see the solid curve in Figure 6.

2. If the duration of influenza in females is longer than in males (i.e., $a < 1$), then we have the following:

● if $\mu_\gamma < \mu_\gamma^\star$, then the basic reproduction number decreases with the increase of the variance in recovery rates between infected females and males.

● if $\mu_\gamma > \mu_\gamma^\star$, then the basic reproduction number decreases initially till reaching a minimum at $\nu_\gamma = \nu_\gamma^\star$ and then it increases again, with the increase of the variance in recovery rates between infected females and males, see the dashed-dotted curve in Figure 6.

On substituting from (3.26) and (3.27) into (3.11) we get

and

The impact of increasing the variance $\nu_\gamma$ in recovery rates of infected females and males, while keeping their mean constant, on the equilibrium force of infection $\bar\lambda$ as well as on the endemic prevalence of infected females $\bar{y_1}$ and infected males $\bar{y_2}$ is numerically investigated in Figure 7. Part(a) shows that $\bar\lambda$ and therefore the total proportion of infected individuals in the whole population at the endemic situation $(\bar{y_1} + \bar{y_2})$ behave similar to the basic reproduction number $R_0$ if the variance $\nu_\gamma$ is allowed to increase, while the mean of recovery rates $\mu_\gamma$ is kept fixed. However, the proportion of infected females and males at the endemic situation behave differently, see Figure 7(b). If females recover faster than males ($a > 1$), then the endemic prevalence of infected females $\bar{y_1}$ decreases with the increase of the variance $\nu_\gamma$, while the endemic prevalence of infected males increases $\bar{y_2}$. Such behaviour could be because the increase in disparity in recovery rates $\nu_{\gamma}$ reduces (extends) the infected female (male) infectious period and, consequently, speeds up (slows down) the process of infected females (males) recovery, which in turn lowers (raises) the endemic prevalence of infected females (males) in the total population, see Figure 7(b).

Conversely, if males recover faster than females (i.e., $a < 1$), then the prevalence of infected females increases while that of males decreases, with the increase of the variance $\nu_\gamma$ in recovery rates, while keeping their mean $\mu_\gamma$ constant. This dynamical behaviour is due to the fact that the increase in recovery rates' disparity extends (reduces) the length of infectious period in females (males) and in consequence decelerates (accelerates) the recovery process of females (males), which in turn increases (reduces) the endemic prevalence of infected females (males), see Figure 7(b).

The implication of the above results is summarised in the following items, giving that the mean recovery rate in males and females is constant.

● The faster the recovery of females than males is, the higher the value of the basic reproduction number is and the higher the prevalence of infection in the total population is, see figures 6, 7(a).

● If the duration of infection is shorter in females than in males, then the greater the disparity in recovery rates between females and males is, the higher the prevalence of infection in males is, the lower the endemic prevalence of infection in females is, but the higher the overall prevalence of infection in the total population is, see Figure 7. The converse is also true.

● If males recover quicker than females, then, as the disparity in recovery rates between both sexes is allowed to increase, an initial decrease followed by a rapid increase in the levels of the basic reproduction number as well as the total endemic prevalence of infection is remarkable, see figures 6, 7(a).

● In both male and female subpopulations, the higher the recovery rate in either subpopulations, compared to that of the other, is (i.e., the shorter the infectious period is), the lower the endemic prevalence of infection in that subpopulation is, see Figure 7(b).

4.   Effect of mass influenza vaccination

Vaccines can prevent or ameliorate morbidity from infections. They are the most effective and cost-saving tools for disease prevention, preventing untold suffering and saving tens of thousands of lives and billions of dollars in healthcare costs each year ^[38]. There are two ways to vaccinate people. Either through the application of routine immunisation programmes or through the use of mass vaccination where susceptible people receive the vaccine to protect them from a potential infectious disease outbreak.

As influenza viruses mutate regularly, influenza vaccines are modified every year based on the prevalent influenza virus strains. The modified vaccines are always ready before the beginning of the seasons during which influenza display. However, due to the high mutation rates and frequent genetic reassortments of influenza viruses that contribute to the appearance of new subtypes, influenza vaccines are not included in routine immunisation programmes. Therefore, mass vaccination against influenza is applied, where populations at risk are rapidly vaccinated before the epidemic season for influenza begins. However, the efficacy of influenza vaccines depends on the degree of antigenic match to circulating viruses ^[39].

The WHO report ^[14] shows differences between the rate of vaccination against seasonal influenza between females and males in some countries. For example, males are more likely to receive the seasonal influenza vaccine in some european countries like the Czech Republic, France, Italy, Spain, the Netherlands, Poland and Portugal. However, the report shows that males and females are equally likely to get vaccinated against seasonal influenza in other countries like Austria, Finland, Germany and Ireland. According to the report, the situation in the United States is different. The analysis of vaccination data revealed that receiving seasonal influenza vaccine is age-dependent, where in some age groups females are more likely to receive the vaccine than males, while the converse happens in other age groups. A compartmental model for the transition between population states is shown in Figure 8, where these disparities are taken into account. The mathematical model with population proportions reads

where $w_1$ and $w_2$ represent the proportion of vaccinated females and males, respectively, and

Similarly and as argued above, it holds that $x_1(t) + y_1(t) + w_1(t) + z_1(t) = x_2(t) + y_2(t) + w_2(t) + z_2(t) = 1/2$.

4.1.   Trivial equilibrium and the effective reproduction number

It is easy to check that model (4.1) has the influenza-free (trivial) equilibrium

Again, following the approach of Diekmann et al. ^[34], we compute the transmission matrix ${\bf T_v}$ and the transition matrix ${\bf \Sigma_v}$ as

and

Thus, the effective reproduction number $R_{\psi}$ is the dominant eigenvalue of the next generation matrix with large domain ${{\bf K}_L}^v = - {\bf T_v} {\bf \Sigma_v^{-1}}$, where

4.2.   Stability analysis of the trivial equilibrium $E_{0v}$

Local stability:

The stability analysis of the influenza-free equilibrium in the presence of vaccination $E_{0v}$ shows that $E_{0v}$ is locally asymptotically stable if and only if the effective reproduction number $R_{\psi} < 1$. Therefore, we state the following proposition, whose proof is shown in appendix B.

Proposition 7. Model (4.1) has an influenza-free equilibrium $E_{0v}$ that is locally asymptotically stable if and only if the effective reproduction number $R_{\psi} < 1$.

Global stability:

The global stability of the influenza-free equilibrium in the presence of vaccination $E_{0v}$ is established using the fluctuation lemma ^[40], which we state below. To this end, we introduce some notations and state the a proposition about the positivity of the solutions, whose proof is deferred to appendix C. Assume that $f$ is a real-valued function defined on the interval $[0, \infty)$. Then, we define

Proposition 8. Model (4.1) has a unique solution with components $x_1(t)$, $w_1(t)$, $y_1(t)$, $z_1(t)$, $x_2(t)$, $w_2(t)$, $y_2(t)$ and $z_2(t)$ that are non-negative for all forward times $t \ge 0$, if the initial values of the components are non-negative.

The proof of this proposition is deferred to appendix C.

Remark 1. Since all solutions $x_1(t)$, $w_1(t)$, $y_1(t)$, $z_1(t)$, $x_2(t)$, $w_2(t)$, $y_2(t)$ and $z_2(t)$ are non-negative and their sum equals $1$, then they are all bounded from above.

Now, we state (without proof) the fluctuation lemma ^[40] that is needed in the global stability analysis of $E_{0v}$.

Lemma 1. Let $f: [0, \infty) \rightarrow \mathbb{R}$ be bounded and differentiable and have no limit as $t \rightarrow \infty$. Then, there exist sequences ${\{s_n\}}_{n = 1}^{\infty}$ and ${\{t_n\}}_{n = 1}^{\infty}$, such that, for all $n$

and

It is noteworthy that $f^\infty = \lim_{n\rightarrow\infty} f(s_n) = \lim_{t\rightarrow\infty} \sup f(t)$, $f_\infty = \lim_{n\rightarrow\infty} f(t_n) = \lim_{t\rightarrow\infty} \inf f(t)$ and that $f_\infty \le f^\infty$. In the following, we introduce a proposition showing our result on the global stability of the influenza-free equilibrium in the presence of vaccination $E_{0v}$.

Proposition 9. The influenza-free equilibrium in the presence of vaccination $E_{0v}$ is globally stable if and only if the effective reproduction number $R_{\psi} < 1$.

Proof. Before going into details, we recall that all state variables are non-negative and bounded from above. From the $x_1$ equation in (4.1), it is clear that $x_1$ satisfies the differential inequality

On applying the above fluctuation lemma, there exists a sequence ${\{s_n\}}_{n = 1}^{\infty}$ such that $s_n \rightarrow \infty, x_1(s_n) \rightarrow x_1^\infty, \dot{x_1}(s_n) \rightarrow 0$, as $n \rightarrow \infty$. Hence, from the differential inequality (4.4) we get

Similarly, we apply the fluctuation lemma to the differential equations of $x_2, w_1, w_2, y_1$ and $y_2$ in (4.1). Accordingly,

● we can find a sequence ${\{s_n\}}_{n = 1}^{\infty}$ such that $s_n \rightarrow \infty$, $x_2(s_n) \rightarrow x_2^\infty, \: \dot{x_2}(s_n) \rightarrow 0$, as $n \rightarrow \infty$. Hence,

● we can find another sequence ${\{s_n\}}_{n = 1}^{\infty}$ such that $s_n \rightarrow \infty$, $w_1(s_n) \rightarrow w_1^\infty$, $\dot{w_1}(s_n) \rightarrow 0$, as $n \rightarrow \infty$. Hence,

● there can exist a different sequence ${\{s_n\}}_{n = 1}^{\infty}$ such that $s_n \rightarrow \infty$, $w_2(s_n) \rightarrow w_2^\infty$, $\dot{w_2}(s_n) \rightarrow 0$, as $n \rightarrow \infty$. Hence,

● there can also exist another sequence ${\{s_n\}}_{n = 1}^{\infty}$ such that $s_n \rightarrow \infty$, $y_1(s_n) \rightarrow y_1^\infty$, $\dot{y_1}(s_n) \rightarrow 0$, as $n \rightarrow \infty$. Hence,

Hence,

● there exists also another different sequence ${\{s_n\}}_{n = 1}^{\infty}$ such that $s_n \rightarrow \infty$, $y_2(s_n) \rightarrow y_2^\infty$, $\dot{y_2}(s_n) \rightarrow 0$, as $n \rightarrow \infty$. Hence,

Hence,

Now,

Hence,

I.e.,

Since $R_\psi < 1$, it should be held that $\lambda_v^\infty \le 0$. On the other hand, it is shown in proposition 8 that $y_1(t) \ge 0$ and $y_2(t) \ge 0$ for all forward times $t \ge 0$, which implies that ${y_1}_\infty \ge 0$ and ${y_2}_\infty \ge 0$. Therefore, ${\lambda_v}_\infty \ge 0$. Since ${\lambda_v}_ \infty \le \lambda_v^\infty$, then it should hold that ${\lambda_v}_\infty = \lambda_v^\infty = 0$. Hence, $y_1^\infty = y_2^\infty = 0$. Thus, the proof is complete.

4.3.   Existence and uniqueness of an endemic equilibrium $E_{1v}$ for model (4.1)

As the rate of change in model states vanishes at equilibrium, we put the left hand side of (4.1) equal zero and solve the resulting system with respect to the model's state variables, we get (if $\bar\lambda_v \ne 0$) the endemic equilibrium

where

and $\bar\lambda_v \in (0, \infty)$ is the equilibrium force of infection for model (4.1) and is the unique positive solution of

The analysis shows that (4.7) has a unique positive solution if and only if $R_\psi > 1$. It is clear that there is a one-to-one correspondence between the solution of (4.7) and the states in (4.6). Once the feasible solution of (4.7) is found, we substitute in (4.6) to get the unique endemic equilibrium of model (4.1).

To prove the existence of a unique positive solution for (4.7), we rewrite it as

where

It is clear that

and

Hence, $G_1$ is monotonically increasing, while $G_2$ is monotonically decreasing in $\bar\lambda_v$. Thus, equation (4.7) has a unique positive solution if and only if $G_1(0) < G_2(0)$, while otherwise it has no positive solution. Simple computations show that the existence condition $G_1(0) < G_2(0)$ is equivalent to $R_\psi > 1$.Hence, we show the following proposition.

Proposition 10. Model (4.1) has a unique endemic equilibrium that exists if and only if the effective reproduction number $R_{\psi} > 1$.

4.4.   Direct and indirect effect of influenza mass vaccination

The direct effect of vaccination is the number of vaccinated individuals who caught the infection due to imperfection of the vaccine, but would have been completely protected if the vaccine was totally perfect (i.e., it is the infection incidences in vaccinees). However, the indirect effect of vaccination is the difference between its total effect and its direct effect ^[41]. The total effect of vaccination is the reduction in the number of incidences due to vaccination. To quantify the total effect of influenza mass vaccination in our models, we assume that $I_a$ is the influenza incidences in the absence of vaccination and $I_p$ is the influenza incidences in the presence of vaccination. Hence, models (2.6) and (3.1) imply that

Similarly, model (4.1) implies that

Thus, the total effect of vaccination (i.e., the reduction in the total number of incidences due to vaccination) is

The infection incidences in vaccinee (due to the imperfection of vaccination) is denoted by $I_D$ and is given by

which accounts also for the direct effect. Thus, the indirect effect of vaccination is

If we look at the equilibrium state, then

where $\bar\lambda$ is given by (3.11), while $\bar\lambda_v$ is the solution of (4.7).

Figure 9(a) shows the total effect $I_T$, direct effect $I_D$ and indirect effect $I_{IND}$ of vaccination as functions of the effective reproduction number $R_\psi$. Both the indirect effect and total effect are monotonically decreasing in $R_\psi$, while the direct effect is monotonically increasing in $R_\psi$. Part (b) of Figure 9 shows the ratio of the indirect to direct protection $I_{IND}/I_D$ as a function of $R_\psi$. Since $R_\psi$ decreases with the increase of the vaccination rate $\psi$, we then deduce that the higher the vaccination rate is, the higher the total effect $I_T$, the indirect effect $I_{IND}$ and the protection ratio $I_{IND} / I_D$ are, the lower the direct effect $I_D$ is.

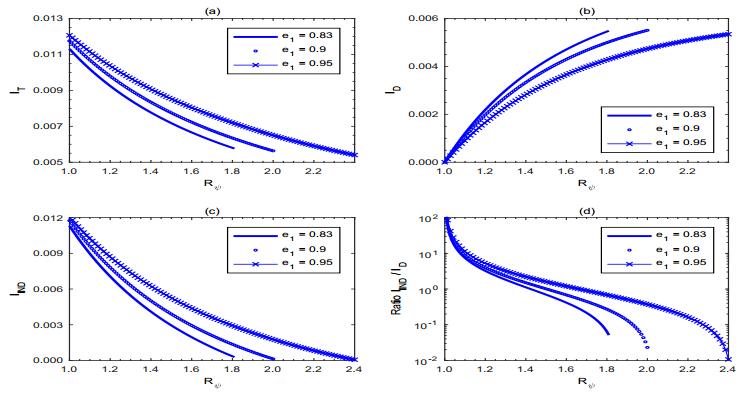
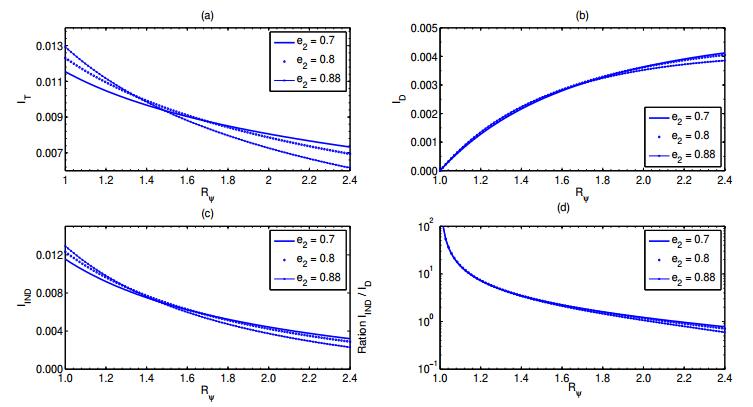
Simulations have also been done for various levels of vaccination efficacies $e_1$ and $e_2$. Figure 10 shows that (for fixed $e_2$ and other model parameters) increasing the vaccine efficacy in females $e_1$ increases the total effect, the indirect effect and the ratio of indirect to direct effects, but decreases the direct effect $I_D$ of vaccination. Hence, the higher the efficacy of females vaccine is, the more reduction in the total number of new incidences is. However, if the vaccine efficacy in females $e_1$ is kept fixed with the other parameters, while the vaccine efficacy in males $e_2$ is allowed to change, simulations in Figure 11 show that the behaviour of these effects depends on the value of the effective reproduction number $R_\psi$. For low levels of $R_\psi$ (slightly above one, but less than certain level), increasing the efficacy $e_2$ increases the protection ratio of indirect to direct effect as well as the direct, indirect, and total effect. Conversely, for high enough values of $R_\psi$, these effects as well as that ratio decrease with the increase of the vaccine efficacy in males $e_2$.

5.   Summary and conclusions

Mathematical models have been extensively used to explore the evolutionary dynamics of influenza viruses. However, to the best of our knowledge, the role of sex and/or gender in respiratory infections (e.g., influenza) transmission dynamics has not been explored mathematically and a greater understanding of the influence of sex and gender disparity on the overall outcome of influenza is lacking. Therefore, a mathematical model to describe the transmission dynamics of influenza A viruses, taking into account sex and gender disparity, has been formulated and thoroughly analysed. The model we considered is of type SIR (Susceptible - Infected - Recovered) in which it is differentiated between females and males through their susceptibility, duration of infection (based on different recovery rates), response to vaccination campaigns and their immune response to the vaccine.

In the absence of vaccination, the model has the influenza-free equilibrium $E_0$ that is shown to be globally asymptotically stable if and only if the basic reproduction number $R_0$ is less than one. However, it has a unique endemic equilibrium that exists if and only if $R_0 > 1$. This endemic equilibrium is proved to be locally asymptotically stable whenever it exists. Moreover, the impact of sex disparity (represented by differential susceptibility and differential recovery rates of infected females and males) on the influenza virus disease outcome has been studied. The analysis shows that, irrespective of the value of the rescaling recovery rate parameter $a$ which represents the ratio of the recovery rate of infected females to that of infected males, the basic reproduction number $R_0$ increases with the increase of the relative susceptibility $g$ of females with respect to males. Moreover, simulations show that the endemic prevalence of infected males $\bar{y_2}$ as well as the total proportion of infected individuals $(\bar{y_1} + \bar{y_2})$ in the whole population increase initially with the increase of $g$ till reaching a maximum (approximately at around $g = 0.5$) and then they decrease again. However, for slightly high values of $R_0$, the endemic prevalence of infected females $\bar{y_1}$ grows monotonically as $g$ increases.

On the other hand, the disease outcomes have been analysed in terms of the mean and variance of susceptibilities as well as of recovery rates of females and males. The analysis shows that if the duration of influenza A in females is shorter than in males $a > 1$, then the basic reproduction number $R_0$ increases as the variance $\nu_r$ in susceptibilities of both sexes increases, given that their mean $\mu_r$ is kept constant. However, if males recover faster than females (i.e., $a < 1$), then $R_0$ decreases with the increase of $\nu_r$. The analysis shows further that the endemic prevalence of infected males increases initially with the increase of the variance $\nu_r$ and then it decreases again to reach its final value (at $\nu_r = \mu_r^2 = \nu_r^{\max}$) that does not depend on $a$, while the endemic prevalence of infected females decreases monotonically to vanish at $\nu_r = \mu_r^2$.

In analysing the disease outcomes in terms of mean and variance of recovery rates of females and males, it is shown that if females recover faster than males, then $R_0$ increases with the increase of the variance $\nu_\gamma$ in recovery rates of females and males (given that their mean $\mu_\gamma$ is kept constant). However, if males recover faster than females, then $R_0$ decreases initially till reaching a minimum and then it increases again with the increase of the variance $\nu_\gamma$. The equilibrium force of infection $\bar\lambda$ and therefore the total proportion of infected population at equilibrium $\bar{y_1} + \bar{y_2}$ behave similar to $R_0$, although $\bar{y_1}$ and $\bar{y_2}$ have opposite behaviours.

The possibility to apply mass vaccination as a prevention strategy to contain influenza A has been studied, where it is differentiated between vaccine efficacy in both sexes. Also, the gender disparity (represented by disparity in individuals' response to vaccination campaigns) has been taken into account. A thorough equilibrium analysis of the model has been performed and the local and global stability analysis of the influenza-free equilibrium (in the presence of vaccination) have been established, when the effective reproduction number $R_\psi$ is less than one.

The direct effect (i.e., the reduction in the incidences of vaccinated individuals if the vaccine was totally perfect) and indirect effect (i.e., the rest of the total incidences) of influenza mass vaccination have been studied. The analysis revealed that the efficacy of the vaccine for both sexes ($e_1 \& e_2$) and the response of the gender to mass-vaccination campaigns $\psi$ play a crucial role in influenza A containment and elimination process. High response to vaccination campaigns and high efficacy of the vaccine in females imply to high effect of vaccination on the burden of the infection, which implies to a more reduction in the total number of new incidences. However, high efficacy of the vaccine in males would cause much reduction in the number of new incidences if the effective reproduction number $R_\psi$ is small (slightly above one, but less than certain level), while it reduces the effect of vaccination (i.e., it increases the occurrence of new incidences) for high enough values of $R_\psi$.

Limitation of the work

It is worth noting that influenza could pose a significant mortality burden to vulnerable populations and lead to changes in the demographic makeup of the population. In other words, influenza dynamics and the severity of epidemics is not only affected by the underlying population characteristics, but yearly epidemics also induce changes in population demographics. One more important component for studying epidemic effects on demographic characteristics of populations is the inclusion of age-structure factor, as the transmission rates, susceptibility, risk of death, and vaccination coverage rates vary across age groups. These factors could probably be taken into account in a future work.

Acknowledgment

The authors would like to thank the Associate editor as well as the anonymous referees very much for their invaluable and comprehensive comments which helped in improving the paper.

Conflict of interest

The author declares no conflict of interest.

Appendix A.   The Hurwitz determinant $\Delta$ for the stability of the unique endemic equilibrium for model (3.1)

Before going into details, we assume that

where, according to (3.9), $X + Y = 1$. Using the formulae of $C_1, C_2$ and $C_3$, we have

Thus, after some tedious calculations, we get

where

Here, we have two cases, either $g\le 1$ or $g > 1$, and in each case we have two sub-cases: $a\le 1$ and $a > 1$. Therefore, we study the sign of $\Delta_{\text{sub}}$ in the following four cases.

● Case (1): $g \le 1$ and $a\le 1$. Since we assume that $a \le 1$, then $-g\bar\lambda^2 X Y^2 (\gamma + \mu)(a\gamma + \mu) \ge - g\bar\lambda^2 XY^2(\gamma + \mu)^2$. Hence,

● Case (2): $g \le 1$ and $a > 1$. If we assume that $a \ge 1$, then $(\gamma + \mu)(\bar\lambda + \mu) \le (a\gamma + \mu)(\bar\lambda + \mu/g)$. Hence, $X \ge Y$. Also, $a\ge 1$ implies that $(\gamma + \mu)(a\gamma + \mu) \le (a\gamma + \mu)^2$. Hence,

Thus,

● Case (3): $g > 1$ and $a \le 1$. In this case, we have $(\gamma + \mu)(\bar\lambda + \mu) \ge (a\gamma + \mu)(\bar\lambda + \mu/g)$. Hence, $X \le Y$. Also, $a\le 1$ implies that $(\gamma + \mu)(a\gamma + \mu) \le (\gamma + \mu)^2$. Hence,

Thus,

● Case (4): $g > 1$ and $a > 1$. In this case, we have $-g\bar\lambda^2 X^2 Y (\gamma + \mu)(a\gamma + \mu) \ge - g\bar\lambda^2 X^2 Y (a \gamma + \mu)^2$. Hence,

Hence, $\Delta_{\text{sub}} > 0$. Thus, $\Delta > 0$.

Appendix B.   Proof of proposition 7 on the local stability of the influenza-free equilibrium $E_{0v}$ of model (4.1)

Proof. The local stability of the influenza-free equilibrium $E_{0v}$ of model (4.1) is investigated by considering the eigenvalues of the Jacobian matrix $J_{0v}$ of the model evaluated at the influenza-free equilibrium $E_{0v}$, where

where $D_{x_1} = e_0\psi + \mu$, $J_{1, 3} = g \beta x_{1, 0v}$, $J_{1, 7} = g \beta x_{1, 0v}$, $J_{2, 3} = g (1 - e_1)\beta w_{1, 0v}$, $J_{2, 7} = g (1 - e_1)\beta w_{1, 0v}$, $J_{3, 3} = g \beta [x_{1, 0v} + (1-e_1) w_{1, 0v}] - (a\gamma + \mu)$, $J_{3, 7} = g \beta (x_{1, 0v} + (1-e_1) w_{1, 0v})$, $J_{5, 3} = \beta x_{2, 0v}$, $J_{5, 7} = \beta x_{2, 0v}$, $D_{x_2} = \mu + \psi$, $J_{6, 3} = (1-e_2)\beta w_{2, 0v}$, $J_{6, 7} = (1-e_2) \beta w_{2, 0v}$, $J_{7, 3} = \beta[x_{2, 0v} + (1-e_2) w_{2, 0v}]$, $J_{7, 7} = \beta [x_{2, 0v} + (1-e_2) w_{2, 0v}] - (\gamma + \mu)$. Its eigenvalues are $-\mu$, $-\mu$, $-\mu$, $-\mu$, $-(\psi + \mu)$, $-(e_0\psi+\mu)$ and those of the matrix

Hence, the local stability of $E_{0v}$ depends on the determinant and trace of the matrix $J_{sub}^v$. Now,

Hence, $\det(J_{sub}^v) > 0$ if and only if $R_{\psi} < 1$. Thus, to complete proving the local stability of $E_{0v}$ for $R_{\psi} < 1$, it remains to show that $\text{tr}(J_{sub}^v) < 0$. The inequality $R_{\psi} < 1$ is equivalent to

which implies that

Therefore,

I.e.,

Thus,

Appendix C.   Proof of proposition 8 on the existence of unique positive solution for model (4.1)

Proof. As the right hand side of (4.1) is continuously differentiable functions, it is locally Lipschitz. Therefore, model (4.1) has a unique local solution with components $x_1(t)$, $w_1(t)$, $y_1(t)$, $z_1(t)$, $x_2(t)$, $w_2(t)$, $y_2(t)$ and $z_2(t)$ and with initial values $x_1(0)$, $w_1(0)$, $y_1(0)$, $z_1(0)$, $x_2(0)$, $w_2(0)$, $y_2(0)$, $z_2(0) \geq 0$, where $x_1(t) + w_1(t) + y_1(t) + z_1(t) + x_2(t) + w_2(t) + y_2(t) + z_2(t) = 1$ for all $t \ge 0$. This solution is defined on the forward invariant set

To show that the state variables are non-negative for all $t \ge 0$, we assume the converse. I.e., we assume that $x_1(0) > 0$, $w_1(0) > 0$, $y_1(0) > 0$, $z_1(0) > 0$, $x_2(0) > 0$, $w_2(0) > 0$, $y_2(0) > 0$, $z_2(0) > 0$ and that at least one of the state variables $x_1(t)$, $w_1(t)$, $y_1(t)$, $z_1(t)$, $x_2(t)$, $w_2(t)$, $y_2(t)$ and $z_2(t)$ become(s) negative for some $t > 0$. Assume further that $t = t_1^x$ is the first time at which $x_1(t) = 0$. Then

Since $x_1$ is continuous in time, it implies that $x_1(t) < 0$ for $t < t_1^x$, which contradicts our assumption that $t_1^x$ is the first time at which $x_1$ vanishes. Thus, $x_1(t)$ is non-negative for all $t \ge 0$. Similarly, if we assume that $t_1^w, t_1^y, t_1^z, t_2^x, t_2^w, t_2^y$ and $t_2^z$ represent the first times at which $w_1(t)$, $y_1(t)$, $z_1(t)$, $x_2(t)$, $w_2(t)$, $y_2(t)$ and $z_2(t)$, respectively, become zero, then we compute

which are all positive. Thus, by continuity of these state variables, it implies that $w_1(t) < 0$ for $t < t_1^w$, $y_1(t) < 0$ for $t < t_1^y$, $z_1(t) < 0$ for $t < t_1^z$, $x_2(t) < 0$ for $t < t_2^x$, $w_2(t) < 0$ for $t < t_2^w$, $y_2(t) < 0$ for $t < t_2^y$ and $z_2(t) < 0$ for $t < t_2^z$ which contradict the above assumptions. Thus, all state variables are non-negative for all forward times $t \ge 0$.