Some computable quasiconvex multiwell models in linear subspaces without rank-one matrices

On the occasion of the 75th birthday of Professor E. N. Dancer

1.   Introduction

In this paper we use the formula for the smooth approximations of the maximum function in $\mathbb{R}^n$ based on compensated convex transforms ^[1] (see Definition 2 below) to construct computable quasiconvex lower bounds with multiwell structure in the calculus of variations. By 'computable' we mean that the evaluation of the quasiconvex lower bounds only involves projection onto a linear subspace $E$ without rank-one matrices in $M^{m\times n}$, and a projection onto the simplex $\Delta^k$ where $k\geq 2$ is the number of 'wells'. The complexity of the former is $\mathcal{O}(mn)$, while the complexity of the latter is theoretically $\mathcal{O}(k\log k)$ for the algorithm proposed in ^[2,3] or observed $\mathcal{O}(k)$ in the algorithm proposed in ^[4].

The maximum function

plays an important role in many optimization problems, in the sense that many problems can be proposed as minimization of the maximum function composed with other functions ^[5]. In ^[1] a smooth approximation for the maximum function was introduced by the upper compensated convex transform $C^u_\lambda(f_m)$ for $\lambda > 0$, where the formula for the transform is given by

where ${\rm{co}}(\Delta_m/(2\lambda))$ is the convex hull of the set of the scaled basis vectors $\Delta_m/(2\lambda) = \{e_1/(2\lambda), \, e_2/(2\lambda), \dots, e_m/(2\lambda)\}$ with $e_j = (\delta_{j, 1}, \delta_{j, 1}, \dots, \delta_{j, m})\in \mathbb{R}^m$ where $\delta_{j, k} = 1$ if $j = k$ and $\delta_{j, k} = 0$ if $j\neq k$ for $j = 1, 2, \dots, m$ are Kronecker delta. Let $P_{{\rm{co}}(\Delta_m/(2\lambda))}x$ be the projection of $x\in \mathbb{R}^m$ to the simplex ${\rm{co}}(\Delta_m/(2\lambda))$, we can write

and the complexity for evaluatiing $C^u_\lambda(f_m)(x)$ is the same as finding the convex projection $P_{{\rm{co}}\left(\frac{\Delta_m}{2\lambda}\right)}x$. There are numerical schemes with complexity $\mathcal{O}(m\log m)$ to compute the convex projection above ^[2]. Our computable quasiconvex functions rely on this fact. Some generalisations of approximations by compensated convex transforms to maximum-like functions can be found in ^[6].

It is known ^[1] that $C^u_\lambda(f_m)(x)$ is a $C^{1, 1}$ approximation of $f_m(x)$ from above, that is, $f_m(x)\leq C^u_\lambda(f_m)(x)$ and $\lim_{\lambda\to +\infty} C^u_\lambda(f_m)(x) = f_m(x)$ ^[1], and in general compensated convex trnasforms are 'tight' approximations. For the special case of the maximum function, we will show in Proposition 2 below that $C^u_\lambda(f_m)(x)$ is a tight approximation in the sense that if the vector $x = (x_1, x_2, \dots, x_m)$ is sorted with the order $x_1\geq x_2\geq \cdots \geq x_m$, then $C^u_\lambda(f_m)(x) = f_m(x)$ if $x_1-x_2\geq 1/(2\lambda)$.

For the minimum function $g_m(x) = \min\{x_1, \dots, x_m\} = -\max\{-x_1, \dots, -x_m\}$ for $x\in \mathbb{R}^m$, it is easy to verify that the lower compensated convex transform of $g_m$ is given by

In this paper we apply the lower compensated convex transforms to two multiwell models in the calculus of variations. Compensated convex transforms have been applied to problems involving geometric singular extraction, shape analysis and approximation and interpolations of sampled data ^{[7,8,9,10,11]}.

The first type of multiwell functions is defined as follows. Let $\alpha > 0$ be a control parameter. Let $E\subseteq M^{m\times n}$ be a linear subspace without rank-one matrices and let $f:K\subseteq E\to E^\perp$ be an $L$-Lipschitz mapping with $0\leq L\leq 1/\alpha$, where $E^\perp$ is the orthogonal complement of $E$ in $M^{m\times n}$ and $K = \{A_i:\, i = 1, 2, \dots, k\}\subseteq E$ is a finite set. We define the multiwell function $H_2(X)$ with quadratic growth by

for $k\geq 2$. If we define the quadratic function $q_i(X) = |P_EX-A_i|^2+\alpha|P_{E^\perp}X-f(A_i)|^2+\beta_i$ for $i = 1, 2, \dots, k$, then we may write

We see that the point $X_i = A_i+f(A_i)$ is a local minimum point of $H_2(\cdot)$ if for $j\neq i$,

A sufficient condition for every $X_i = A_i+f(A_i)$ to be a local minimum point is $|A_i-A_j|^2 > |\beta_i-\beta_j|$ for $1\leq i\neq j\leq k$. So, under this additional restriction, $H_2(X)$ has a multiwell structure with each $X_i = A_i+f(A_i)$ a local minimum point.

The second type of multiwell functions is in the form

where $A_i\in E$ and $\mathcal{U}_i:E\to E$ are invertible linear transforms and $\gamma_i\geq 0$ for $i = 1, 2, \dots, k$. Again we can show that every $A_i\in E$ is a local minimum point of $H_1$ if $|\mathcal{U}_j(A_i-A_j)|^2 > |\gamma_i-\gamma_j|$.

Our aim is to use the lower compensated convex transform $C^u_\lambda(f_k)$ to construct composite functions that are quasiconvex lower bounds of $H_1$ and $H_2$. We will also consider simple generalisations of these constructions.

Next we discuss backgrounds and motivations. The Quasiconvex function in the sense of Morrey ^[12] is an important tool in the vectorial calculus of variations ^[13], with applications in nonlinear elasticity ^[14] and material microstructure. For example, under the growth condition $0\leq F(X)\leq C|X|^p+C_1$ for $X\in M^{m\times n}$, the variational integral $I(u): = \int_\Omega F(Du)\, dx$ is weakly lower-semicontinuous in the Sobolev space $W^{1, p}(\Omega, \, \mathbb{R}^m)$ if and only if $F$ is quasiconvex ^[15], where $M^{m\times n}$ is the linear space of real $m\times n$ matrices.

A continuous function $F:M^{m\times n}\to \mathbb{R}$ is quasiconvex ^[12] if for every $X\in M^{m\times n}$, for every open set $\Omega\subseteq \mathbb{R}^n$ and for every $\phi\in C_0^\infty(\Omega, \, R^m)$, we have

Convex functions are quasiconvex but the converse is not true. A large class of functions, called polyconvex functions ^[14] are quasiconvex. Quasiconvex functions satisfying certain geometric conditions have been constructed by studying the quasiconvex envelope ^[13] of a given function with the multiwell property which describes the macroscopic properties of material microstructure for non-quasiconvex multiwell models ^[16,17]. A simplified multiwell model is in the form of an (Euclidean) $p$-distance function to a compact set $K$ in $M^{m\times n}$ ^[18,19,20]. A typical example is the $p$-distance function ${\mathrm{dist}}^p(X, \, \{-I, \, I\})$ to the set $\{-I, \, I\}$ for $X\in M^{2\times 2}, 1\leq p < 2$, whose quasiconvex envelope $Q {\mathrm{dist}}^p(X, \, \{-I, \, I\})$ vanishes exactly at $-I$ and $I\in M^{2\times 2}$. So far a more explicit geometric lower bound of $Q {\mathrm{dist}}^p(X, \, \{-I, \, I\})$ above is still not known. Some more explicit quasiconvex functions can be obtained by establishing lower bounds for the quasiconvex envelope via the so-called 'translation method' (see e.g., ^[21]). In particular, the explicit formula of the quasiconvex envelope for a double-well model ^[20] and the systematic study of restrictions of microstructure ^[22] lead to the study of linear subspaces of matrices without rank-one matrices, which are simple linear 'elliptic' objects in $M^{m\times n}$. Here a linear subspace $E$ is called simple linear elliptic if $\mathrm{div}P_{E^\perp}(\mathrm{grad}\cdot)$ is a linear elliptic operator satisfying the strong Legendre-Hadamard ellipticity condition for some constant coefficient.

The following is a motivating example for our construction of computable quasiconvex lower bounds for a class of multiwell functions ^[1].

Let $E\subseteq M^{m\times n}$ be a linear subspace without rank-one matrices, where $m, \, n\geq 2$. It is known ^[22] that there exists $\varepsilon > 0$ such that

where $P_{E^\perp}: M^{m\times n}\to E^\perp$ is the Euclidean orthogonal projection of $M^{m\times n}$ to the orthogonal complement $E^\perp$ of $E$, $a\in \mathbb{R}^m$ and $b\in \mathbb{R}^n$ are treated as column vectors and $a\otimes b = ab^T\in M^{m\times n}$ with $b^T$ the transpose of $b$.

Now we optimise the above construction ^[1] by defining

where $|a|$ and $|b|$ are the Euclidean norms of $a$ and $b$ in $\mathbb{R}^m$ and $\mathbb{R}^n$ respectively, so that we have $0 < \lambda_0 < 1$ and

hence if we define $\lambda_E = \lambda_0/(1-\lambda_0)$, we have

for all $a\in \mathbb{R}^m$ and $b\in \mathbb{R}^n$. Thus the quadratic form $q_E(X) = |P_{E^\perp}X|^2- \lambda_E|P_E X|^2$ is a rank-one convex quadratic form as $q_E(a\otimes b)\geq 0$ for all $a\in \mathbb{R}^m$ and $b\in \mathbb{R}^n$, hence is a quasiconvex function (see, e.g., ^[23]).

Now we consider a simple multiwell model. Let $E\subseteq M^{m\times n}$ be a linear subspace without rank-one matrices and let $K\subseteq E$ be a closed set. Consider the (Euclidean) squared-distance function ${\mathrm{dist}}^2(X, \, K) = {\mathrm{dist}}^2(P_E(X), \, K)+|P_{E^\perp}X|^2$, then (see ^[1])

is a quasiconvex lower bound of the squared-distance function as ${\rm{co}}({\mathrm{dist}}^2(P_E(\cdot), \, K)+\lambda_E|P_E(\cdot)|^2)(X)$ is a convex function and $q_E(X) = |P_{E^\perp}X|^2- \lambda_E|P_E X|^2$ is a rank-one convex quadratic form.

However, in the above construction, even when $K\subseteq E$ is a finite set, in general, the computation of the convex envelope ${\rm{co}}({\mathrm{dist}}^2(P_E(\cdot), \, K)+\lambda_E|P_E(\cdot)|^2)(X)$ is not a simple task whose complexity is generally not known. As a general reference, it is known that to determine the convexity of a quartic polynomial is an NP-hard question ^[24]. The computation of the values of quasiconvex functions whose existence are known is one of the motivations for us to find computable quasiconvex functions with multiwell structure. For numerical computation of the rank-one convex envelope for general functions, we refer to ^[25]. On the other hand, for numerical computation of compensated convex transforms in the discrete setting, there are efficient methods ^[26].

Before we state our main results, let us first introduce some preliminary notions and results.

Definition 1. (Quasiconvex functions ^[12,13,14]) Suppose $f:M^{m\times n}\to \mathbb{R}$ is continuous. Then $f$ is quasiconvex if

$\forall X\in M^{m\times n}$, $\forall G\subseteq \mathbb{R}^n$ open and $\forall \phi\in C^{\infty}_0(G, \mathbb{R}^m)$.

For a continuous function $f:M^{m\times n}\to \mathbb{R}$ bounded below, the quasiconvex envelope $Qf:M^{ m\times n}\to \mathbb{R}$ is the largest quesiconvex function satisfying $Q(f)\leq f$. For the precise definition, we refer to ^[13]. In this paper we only consider quasiconvex lower bound $g$ of a given function $f$.

The translation method (see, e.g., ^[21]) is a simple and effective method for finding quasiconvex lower bounds. Suppose $f:M^{m\times n}\to \mathbb{R}$ is continuous and bounded below and assume that $g:M^{m\times n}\to \mathbb{R}$ is quasiconvex, then the function $h$ defined by

is quasiconvex and satisfies $h(X)\leq f(X)$ for all $X\in M^{m\times n}$. We call $h$ a translation lower bound which is quasiconvex as the sum of a convex function and a quasiconvex function remains quasiconvex.

The following example, which is a generalisation of a double-well function in ^[20] using a different method, can be used to show how the translation method applies to multiwell models when the wells are contained in subspaces without rank-one matrices ^[1]. This example is one of the motivations for the definition of compensated convex transforms ^[1].

Example 1. Let $E\subseteq M^{m\times n}$ be a linear subspace without rank-one matrices where $m,\,n\geq 2$. Let $K\subseteq E$ be a non-empty closed set. $

Consider the squared Euclidean distance function to the set $K$

which is not quasiconvex. We see that

Let $\lambda_E > 0$ be defined by

Then the translation bound by the rank-one convex quadratic form $q_E(X): = |P_{E^\perp}X|^2-\lambda_E|P_{E}X|^2$ given by

is the quasiconvex envelope of ${\mathrm{dist}}^2(X, \, K)$. Note that rank-one convex quadratic functions are quasiconvex ^[23]. For detailed calculations, we refer to ^[1].

Next we briefly describe the main tool used in this paper: the compensated convex transforms.

Motivated from the translation method, in particular, formula (1.9), compensated convex transforms were introduced in ^[1].

Definition 2. Let $f: \mathbb{R}^n \to \mathbb{R}$ be a continuous function with at most quadratic growth and let $\lambda > 0$ be large if needed, we define $\lambda$-parametrised convexity-based transforms.

The Lower compensated convex transform is defined by

The Upper compensated convex transform is defined by

where ${\rm{co}}[g] =$ convex envelope of $g$, and $|\cdot|$ denotes the Euclidean norm.

We also have $C^u_{\lambda}(f)(x) = -C^l_{\lambda}(-f)(x)$, and both $C^l_{\lambda}(f)$ and $C^u_{\lambda}(f)$ are 'tight' approximations of $f$ from below and above respectively as $\lambda\to+\infty$ in the sense that if $f$ is of $C^{1, 1}$ in a neiighbourhood of $x_0\in \mathbb{R}^n$, then when $\lambda > 0$ is sufficiently large, we have $f(x_0) = C^l_{\lambda}(f)(x_0) = C^u_{\lambda}(f)(x)$.

Next we briefly describe the properties of the smooth approximation of the finite maximum function $f_m(x) = \max\{x_1, x_2, \dots, x_m\}$ for $x = (x_1, x_2, \dots, x_m)\in \mathbb{R}^m$ by the upper compensated convex transform given by ^[1]

If we consider the minimum function $g_m(x) = \min\{x_i:\, 1\leq i\} = -f_m(-x)$, then the lower compensated convex transform $C^l_\lambda(g_m)(x)$ satisfies

It is known that there are numerical schemes to compute the convex projection $P_{\Delta_m/(2\lambda)}$ with complexity $O(m\log m)$, e.g., ^[2].

The following are some properties of $C^u_\lambda(f_m)$ and $C^l_\lambda(g_m)$. We will discuss their proofs in Section 5.

Proposition 2. i) The function $C^u_\lambda(f_m)$ is a $C^{1, 1}$ approximation of $f_m$ with linear growth and

ii) Tight approximation: Assume $x = (x_1, x_2, \dots, x_m)$ is 'sorted' in the increasing order: $x_1\geq x_2\geq \cdots\geq x_m$, then $f_m(x) = C^u_\lambda(f_m)(x)$ if and only if$x_1-x_2\geq \frac{1}{2\lambda}$.

iii) Similar to ii), if $x = (x_1, x_2, \dots, x_m)$ is 'sorted' in the decreasing order: $x_1\leq x_2\leq \cdots\leq x_m$, Then $g_m(x) = C^l_\lambda(g_m)(x)$ iff $x_2-x_1\geq \frac{1}{2\lambda}$.

iv) Error estimate:

vi) $C^u_\lambda(f_m)$ is a 'monotone' convex function ^[1]:

if $x\geq y$ in the sense that $x_i\geq y_i$ for $i = 1, 2, \dots, m$, then $C^u_\lambda(f_m)(x)\geq C^u_\lambda(f_m)(y)$.

The plan for the rest of the paper is as follows. In Section 2 we consider the multiwell function $H_2$ with quadratic growth. We give conditions on parameters involved to construct quasiconvex lower bounds $H_2$ by $C^l_\lambda(g_m)$ so that the resulting quasiconvex functions are computable. In Section 3 we consider the multiwell function $H_1$ with mixed linear-quadratic growth and take a slightly different approach from the method used for $H_2$. We present a generalisation of $H_1$ in Section 4 and conclude the paper with the proof of tight approximation of $C^u_{\lambda}(f_m)$.

2.   A construction of quasiconvex lower bounds for $H_2$

In this section we construct quasiconvex lower bounds for the multiwell function $H_2$ by the lower compensated convex transform $C^l_\lambda(g_k)(\cdot)$ where $g_k(x) = \min\{x_1, x_2, \dots, x_k\}$ is the minimum function defined on $\mathbb{R}^k$.

Let $E\subseteq M^{m\times n}$ be a linear subspace without rank-one matrices. Let $K = \{A_1, \, A_2, \, \cdots, A_k\}\subseteq E$ and let $f:K\to E^\perp$ be a Liptschitz function with a small Lipschitz constant $L\geq 0$.

Recall the definition of $H_2:M^{m\times n}\to \mathbb{R}$:

In this section we give conditions on $K$, $\alpha > 0$, $\beta_i$ and $L > 0$ so that the quasiconvex lower bound $G_2$ defined below preserves the shape of $H_2$ near the graph of $f$ defined by $\Gamma_f = \{(A_i+f(A_i):\; i = 1, 2, \dots, k\}$, i.e., $H_2(X) = G_2(X)$ if $X$ is near $\Gamma_f$.

We define

so that

where

with $c_i = |A_i|^2+\alpha|f(A_i))|^2+\beta_i$. Note that $\ell_1(X) = c_1$ is a constant.

We also define

The following is the main result of this section.

Theorem 3. Suppose $E\subseteq M^{m\times n}$ is a linear subspace without rank-one matrices with the ellipticity constant $\lambda_E > 0$ defined by (1.10). Let

Suppose $f:K\to E^\perp$ is a Lipschitz mapping with Lipschitz constant $0\leq L\leq 1/\alpha$. If $d^2 > 2\beta$, $\alpha > 1$,

Then

is a quasiconvex lower bound of $H_2(X)$, where $f_k$ is the maximum function in $\mathbb{R}^k$.

Also$G_2(X) = H_2(X)$ if

Remark 4. The assumption $d^2 > 2\beta$ implies that every 'energy well' $X_i: = A_i+f(A_i)$ for $i = 1, 2, \dots, k$ is a local minimum point of $H_2$.

Also if $X$ is close to the 'well' $X_i$, the quasiconvex lower bound $G_2(X)$ agrees with $H_2(X)$.

The computation of $G_2(X)$ requires the computation of $C^u_\lambda(f_k(-L_k(X))$ which has the complexity of $\mathcal{O}(k\log k).$

Proof of Theorem 3 By the the formula for the upper transform in the definition of $G_2(X)$, we have

Since the function ${\lambda {\mathrm{dist}}^2\left(-L_k(X), \, {\rm{co}}\left(\frac{\Delta_k}{2\lambda}\right)\right)-\frac{1}{4\lambda}}$ is convex as $-L_k(X)$ is an affine mapping, hence this function is convex. So, we need to show:

i) the quadratic function $q(X)-\lambda|L_k(X)|^2$ is a rank one convex quadratic function, which implies that $G_2(X)$ is quasiconvex.

ii) near $A_i+f(A_i)$ we have $\ell_j(X)\geq \ell_i(X) +1/(2\lambda)$ so that $-C^u_\lambda(f_k)(-L_k(X)) = \ell_i(X)$ for all $j\neq i$ hence $G_2(X) = H_2(X)$.

Proof of i) Let $\tau_k = 8(k-1)D^2$. We may write

We observe that

and

Now let $X\in M^{m\times n}$ be a rank-one matrix, we have

Thus $q(X)-\lambda|L_k(X)|^2$ is a rank-one convex quadratic function, hence is quasiconvex. Therefore $G_2(X)$ is quasiconvex on $M^{m\times n}$.

Proof of ii) We need to show that for each $i$, if (2.8) holds, i.e.,

then for each $j\neq i$, we have ${\ell_j(X)\geq \ell_i(X)+\frac{1}{2\lambda}}$. Equivalently we need to prove that

We have

Next we show that

if (2.6) and (2.8) hold.

Let $x_1 < 0 < x_2$ be the two roots of the quadratic polynomial $x^2-\frac{\sqrt{2}}{\sqrt{\lambda}}x-\beta-\frac{1}{2\lambda}$. It remains to show that $|A_j - A_i| > x_2$. From (2.6) we see that

so

Note that by our assumption on $f$, we have $|f(A_j)-f(A_i)|\leq |A_i-A_j|/\alpha$. Thus by Property iii) in Proposition 2, we have $-C^u_\lambda(f_k(-L_k(X)) = C^l_\lambda(g_k(L_k(X)) = g_k(L_k(X)) = \ell_i(X)$ as ${\ell_j(X)\geq \ell_i(X)+\frac{1}{2\lambda}}$, hence $H_2(X) = G_2(X).$

Remark 5. Due to Property iv) of the upper compensated convex transform in Propostion 2, we have the error estimate

Therefore if $\alpha > 0$ is large, then $G_2(X)$ is a very good quasiconvex lapproximation of $H_2(X)$.

The structure of the quasiconvex lower bound $G_2(\cdot)$ of the multiwell function $H_2(\cdot)$ suggests that $G_2(\cdot)$ is of $C^{1, 1}(M^{m\times n})$ and is of quadratic growth for $X\in M^{m\times n}.$ Therefore when we consider the variational integral

for minimisers or more general stationary points ^[27] the natural space would be $W^{1, 2}(\Omega, \, \mathbb{R}^m)$. This is in contrast with quasiconvex lower bounds $G_1$ for $H_1$ which will be discussed in the next section, where we will see that $G_1$ has a mixed growth which might lead to some more challenges for us to choose a proper function space to accommodate such energy density (integrands).

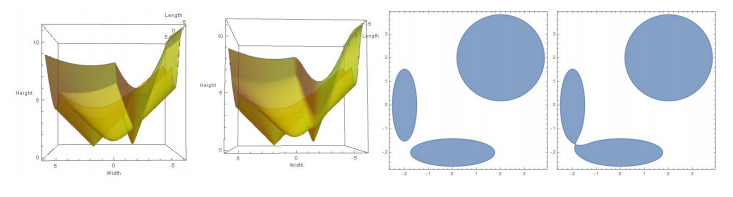
The following figure (Figure 1) gives an illustration of an example of a three well model $H_2$ restricted to $E\simeq \mathbb{R}^2$, where $f\equiv 0$ :

with the three wells at $(-2, 0), \, (0, \, -2), \, (2, \, 2)$, with different heights and a quasiconvex lower bound ($\lambda = 0.25$) restricted on $E$.

3.   A construction of quasiconvex lower bounds for $H_1$

In this section we construct quasiconvex lower bounds for the multiwell function $H_1$ defined in (1.6) by taking the lower compensated convex transform $C^l_\lambda(g_k)(\cdot) = -C^u_\lambda(-f_k)(\cdot)$, where $g_k(x)$ and $f_k(x)$ are the minimum and maximum functions defined on $\mathbb{R}^k$ respectively.

Similar to what we have defined in Section 2, let $E\subseteq M^{m\times n}$ be a linear subspace without rank-one matrices and let $K = \{A_1, \, A_2, \, \cdots, A_k\}\subseteq E$ be a finite set with $k$ distinct elements.

We recall the definition of $H_1:M^{m\times n}\to \mathbb{R}$:

where

with $U_i:E\to E$ an invertible linear transform and $\gamma_i\geq 0$ for $i = 1, 2, \dots, k$. We also define

for $i = 1, 2, \dots, k$.

Let $F_k(Y) = (h_1(Y), \, h_2(Y), \, \dots, \, h_k(Y))$ for $Y\in E.$ We define for $\lambda > 0$.

Note that $\alpha|P_{E^\perp}X|^2 -\lambda|F_k(P_EX)|^2$ is a quadratic function.

Let $d = \min_{1\leq i\neq j\leq k}| A_i-A_j|$, $\gamma = \max_{1\leq i\leq k}\gamma_i$, and $u_{\max} = \max_{1\leq i\leq k}\Vert \mathcal{U}_i\Vert_{op}$, where $\Vert \mathcal{U}_i\Vert_{op}$ is the operator norm of $\mathcal{U}_i$. Let $u_j = \inf\{| U_j Y|: \, Y\in E, \, |Y| = 1\}$ for $j = 1, 2, \dots, k$. Since $U_j:E\to E$ is an invertible linear transform for $j = 1, 2, \dots, k$, we see that $u_j > 0$ for all $j = 1, 2, \dots, k$. We define $u_{\min} = \min\{u_j:\, j = 1, 2, \dots, k\}$. Clearly, $u_{\min} > 0$. If $\gamma$ is small enough and $\alpha > 0$ is sufficiently large, we can establish a similar result for $H_1$ as we have done for $H_2$.

Theorem 6. Suppose $u_{\min} d > \sqrt{2\gamma}$. Let $\lambda_E > 0$ be defined by (1.10). If

then

is a quasiconvex lower bound of $H_1(X)$ for $X\in M^{m\times n}$ and $G_1(X) = H_1(X)$ if $|P_EX-A_i|\leq 1/\lambda$ for $i = 1, 2, \dots, k$.

The condition for $\alpha$ is a rough sufficient condition as we have just used the fact

in our estimates for $g_j(P_EX)\geq g_i(P_EX)+1/(2\lambda)$ for $j\neq i$.

The condition $u_{\min} d > \sqrt{2\gamma}$ is essentially a sufficient geometric assumption which means the minimum distance among the wells $|A_j-A_i|$ is larger that the maximum height $\sqrt{\gamma}$ so that any given well $A_i$ is a genuine 'well' with $A_i$ a local minimum point of the energy density $G_1(X)$ not swallowed by other wells.

Proof of Theorem 6 Observe that by the formula for the upper transform of the maximum function we have

We need to show that $\alpha|P_{E^\perp}X|^2-\lambda|F_k(P_EX)|^2$ is a rank-one convex quadratic function and

is convex, that is, for $Y\in E$,

is convex.

Note that $h_j(Y) = \sqrt{|\mathcal{U}_j(Y-A_j)|^2+\gamma_j^2}$ is a non-negative convex function for $Y\in E$ and for $j = 1, 2, \dots, k$. We define, for $u\in \mathbb{R}^k$, the function

Clearly $f(u)$ is convex. The key observation is that $f(u)$ is also positively increasing in the sense that if $u\geq v\geq 0$, i.e., $u_i\geq v_i\geq 0$ for all of the corresponding components, then $f(u)\geq f(v)$. This requires some more detailed structural properties of the convex projection $P_{\Delta_k/(2\lambda)}$. We have

Lemma 7. Let

If $u = (u_1, \dots, u_m), \, h = (h_1, \dots, h_m)\in \mathbb{R}^m$ satisfy that $u\geq 0$ and $h\geq 0$ componentwise in the sense that $u_i\geq 0$ and $h_i\geq 0$ for $i = 1, 2, \dots, m$, then $D f(u)\cdot h\geq 0$. Consequently, $f(u)\geq f(v)$ if $u\geq v\geq 0$ componentwise.

Proof We have

where the convex projection is in the form

with $\lambda_j\geq 0$ for $j = 1, 2, \dots, m$ and $\sum^m_{j = 1}\lambda_j = 1$. If $u\geq 0$ and $h\geq 0$ componentwise, then

as $u_ih_i\geq 0$, $\lambda_i\geq 0$ and $e_i\cdot h = h_i\geq 0$ for $i = 1, 2, \dots, m$ with $e_1, \, e_2, \, \dots, \, e_m$ the standard Euclidean basis vectors.

The last claim follows from the fundamental theorem of calculus that if $u\geq v\geq 0$, i.e., $u_i\geq v_i\geq 0$ for $i = 1, 2, \dots, m$, then $f(u)-f(v) = \int^1_0Df(tu+(1-t)v)\cdot (u-v)\, dt\geq 0$ as $tu+(1-t)v\geq 0$ and $u-v\geq 0$ componentwise.

Proof of Theorem 6 (continued) Now we can show that

is convex, where $f: \mathbb{R}^k\to R$ is defined as in Lemma 7 with $m = k$. Let $0 < t < 1$ and $X, \, Y\in M^{m\times n}$, since $F_k(P_EX) = (h_1(P_E(X)), \, h_2(P_E(X)), \, \dots, h_k(P_E(X)))$ and every component function $h_j(P_E(X))\geq 0$ is convex, we first have

hence $F_k(P_E(tX+(1-t)Y))\leq tF_k(P_EX)+(1-t)F_k(P_EY)$ componentwise.

Since $f$ is positively increasing, we have

Also $f$ is convex, which implies

Therefore $V_1(X)$ is a convex function in $M^{m\times n}$.

Next we show that the quadratic function $Q_1(X) = \alpha|P_{E^\perp}X|^2-\lambda|F_k(P_EX)|^2$ is a rank-one convex quadratic function in $M^{m\times n}$. We have for every $X\in M^{m\times n}$, we have

where

is an affine function of $P_EX$ hence is a convex function. So, we only need to show that the quadratic form

is rank-one convex. We have, for every rank-one matrix $X\in M^{m\times n}$,

as $\alpha\lambda_E = \lambda u^2k$.

Next we prove that $G_1(X) = H_1(X)$ if $|P_EX-A_i|\leq 1/\lambda$ for each $i = 1, 2, \dots, k$. By definition of the upper transform, $G_1(X) = H_1(X)$ if and only if $-C^u_\lambda(f_k)(-F_k(P_EX)) = \min\{h_1(P_EX), \, h_2(P_EX), \, \dots, \, h_k(P_EX)\}$. By Property iii) in Proposition 2, if $|P_EX-A_i|\leq 1/\lambda$, we show that $h_j(P_EX)\geq h_i(P_EX)+1/(2\lambda)$ for all $j = 1, 2, \dots, k$ with $j\neq i$ so that $-C^u_\lambda(f_k)(-F_k(P_EX)) = h_i(P_EX)$ hence $G_1(X) = H_1(X)$. If we write $P_EX = A_i+Y\in E$, the assumption $|P_EX-A_i|\leq 1/\lambda$ implies $|Y|\leq 1/\lambda$. We have

The last inequality holds as we have assumed that $u_{\min} d > \sqrt{2\gamma}$ and ${\lambda = \frac{\lambda_E\alpha}{ku^2_{\max}} }$ is large if $\alpha > 0$ is large.

Remark 8. In Theorem 6, if we consider the special case that $\mathcal{U}_i = I$ - the identity transform, then we have $u_{\max} = u_{\min} = 1$ and in this special case the assumptions will be much simpler as we can assume that

Remark 9. We may generalise Theorem 6 to deal with more complicated multiwell models. Even for a single non-elliptic well model in the form

where $U_i:E\to E$ is an invertible linear transform, we see that under the assumption that

we can show that the corresponding lower bound $G_1(X)$ is still a quasiconvex lower bound. However, at $X = 0$ we have $H_1(0) = 0$ but $G_1(0) < 0$. This is due to the fact that

Here we have used the fact that the distance between $0$ and the simplex $\Delta_k/(2\lambda)$ is attained at the center of the simplex ${\sum\limits^k_{j = 1}\frac{e_j}{2k\lambda}}$.

At any point where $|\mathcal{U}_jP_EX|\geq |\mathcal{U}_iP_EX|+1/(2\lambda)$ for all $j\neq i$, we still have $H_1(X) = G_1(X).$ Thus if we just wish to construct a quasiconvex function with the 'desired' geometric feature which is differentiable except at $0$, then we can make a simple lift by considering $G_1(X)+(k-1)/(4k\lambda)$.

Remark 10. From Theorem 6 we see that both the multiwell function $H_1$ and its quasiconvex lower bound $G_1$ are of mixed growth. In the subspace $E^\perp\subseteq M^{m\times n}$ both $H_1$ and $G_1$ are of quadratic growth. In the subspace $E$, both $H_1$ and $G_1$ are of linear growth.

If the height $\gamma_j > 0$ for all $j = 1, 2, \dots, k$, then we see that $G_1$ is at least of $C^{1, 1}_{loc}(M^{m\times n})$. However, if for some $j$, $\gamma_j = 0$, then $G_1$ is not differentiable at $A_j$.

For the variational integral $I(u) = \int_\Omega G_1(Du)\, dx$, if we consider the Dirichlet problem, say $u = 0$ on $\partial\Omega$, the natural space is $W_0^{1, 2}(\Omega, \, \mathbb{R}^m)$ where $\Omega\subseteq \mathbb{R}^n$ is, say, a bounded Lipchitz domain. The main reason is that $I(u)$ is coercive in $W_0^{1, 2}(\Omega, \, \mathbb{R}^m)$ because we have

for $\phi\in W^{1, 2}_0(\Omega, \, R^m)$. As $G_1(P_EX)\geq c_0$ for some $c_0\in \mathbb{R}$ we have both $\int_\Omega G_1(Du)\, dx\geq \alpha |P_{E^\perp}Du|^2\, dx+c_0 \mathrm{meas}(\Omega)$ and $\int_\Omega G_1(Du)\, dx\geq \alpha\lambda_E |P_{E}Du|^2\, dx+c_0 \mathrm{meas}(\Omega)$.

If we consider the natural boundary value problem for $I(u) = \int_\Omega G_1(Du)\, dx$ under the constraint, say $\int_\Omega u(x)\, dx = 0$, then $W^{1, 2}(\Omega, \, \mathbb{R}^m)$ does not seem to be the right space to study such a variational integral as $I(u)$ is not coercive in this space. We have $\alpha|P_{E^\perp}X|^2-C^u_\lambda(f_k)(-F_k(P_EX))$ and it can be verified that there are $c_0 > 0$, $c_1 > 0$, $C_0 > 0$ and $C_1 > 0$ such that $c_0|P_EX|-c_1\leq -C^u_\lambda(f_k)(-F_k(P_EX))\leq C_0|P_EX|+C_1$. However, the integral $\int_{\Omega}|P_{E^\perp}Du|^2\, dx$ does not contribute to the coercivity of $I(u)$ in the subspace $E$. An example is in ^[28] that if we consider the two dimensional conformal subspace $E_\partial\subseteq M^{2\times 2}$ which does not have rank-one matrices, then $E_\partial^\perp = E_{\bar\partial}$ is the two-dimensional anti-conformal subspace. If $u = u_1+iu_2$ is a holomophic function in $\Omega$ and we define $v: = (u_1, u_2):\Omega\to \mathbb{R}^2$, then we have $|P_{E_{\bar\partial}}Dv|^2 = |\bar\partial u|^2 = 0$ by the Cauchy-Riemann equations. Therefore $\int_\Omega |P_{E_{\bar\partial}}Dv|^2\, dx$ does not contribute to the coercivity of $I(v)$ under the condition $\int_\Omega v\, dx = 0$.

It seems that some spaces with mixed growth condition might be the correct spaces to accommodate such variational integrals. Furthermore the study of (partial) regularity of minimisers and more general critical points for $I(u)$ under the natural boundary condition seems to be a challenging question.

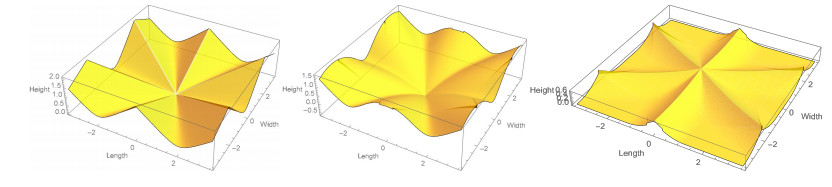
The following figure (Figure 2) gives and illustration of an example of a three well model $H_1$ restricted to $E\simeq \mathbb{R}^2$ in the form

with the three 'anisotropic' wells and with different heights at $(-2, 0), \, (0, \, -2), \, (2, \, 2)$ ($\lambda = 1/2$).

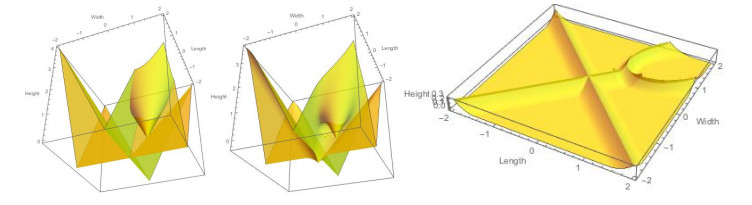
The following figure (Figure 3) gives and illustration of an example of a single non-elliptic well model $H_1$ restricted to $E\simeq \mathbb{R}^2$ in the form

with the three 'anisotropic' wells and with different heights at $(-2, 0), \, (0, \, -2), \, (2, \, 2)$ ($\lambda = 1/2$).

4.   A generalised $H_1$ with affine wells

Suppose $\dim(E) = s$. Using an orthonormal basis of $E$ given by $B_1, \, B_2, \dots, B_s$ and let $x_i = P_EX\cdot B_i$ and $x = (x_1, x_2, \dots, x_s)\in \mathbb{R}^s$, we define $L_i(x) = A_ix-b_i$ for $y\in \mathbb{R}^s$ with $A_i\in M^{m_i\times s}$ and $b_i\in \mathbb{R}^{m_i}$ with $1\leq m_i < s$ and $i = 1, 2\dots, k$.

We may consider the following more general model

where

or more generally,

where $|A_ix-b_i|$ is the Euclidean norm in $\mathbb{R}^{m_i}$ and $\gamma_i\geq 0$. For the function $V_0$, the zero set of can be the union of finitely many planes.

Let $F_k(x) = (|A_1x-b_1|, \, \dots, \, |A_kx-b_k|)$. We can approximate $H_1(x)$ from below by $G_1(x) = \alpha|P_{E^\perp}X|^2-C^u_\lambda(f_k)(-F_k(x))$, with $x = (P_EX\cdot B_1, . (P_EX\cdot B_1, \dots, (P_EX\cdot B_k)$.

We can use $G_1$ to define quasiconvex functions as before. However due to the special feature of $-C^u_\lambda(f_k)(-x)$, at intersections of the planes defined by the zero set of $V_0(x)$, we see that $-C^u_\lambda(f_k)(-F_k(x)) < 0$ at points of intersections. As we commented earlier, this is due to the fact that if $x_1 = x_2\leq x_3\leq \cdots\leq x_m$, then by Lemma 12 in Section 5 and the fact that $C^l_\lambda(g_2(x_1, x_2)) = -C^u_\lambda(f_2(-x_1, -x_2))$ in $\mathbb{R}^2$, we have

If $x_1 = x_2 = 0$, we see that

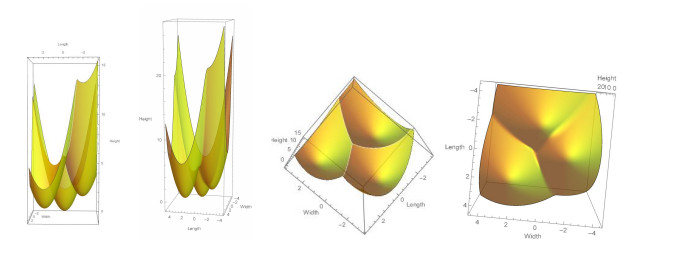
Example 11. Let $H_1(x,y) = 2\min\{|x|,\,|y|, \, \sqrt{(x-1)^2+(y-1)^2}\}$ and let $G_1(x,y) = -C^u_\lambda(f_3)(-F_3(x,y))$ $

with $F_3(x,y) = (|x|,\,|y|, \, \sqrt{(x-1)^2+(y-1)^2})\in \mathbb{R}^3$. The graphs of $H_1(x,y)$ and $G_1(x,y)$ with $\lambda = 1/2$ are shown in Figure 4.

4.1.   Proof of the tight approximation of the upper trasnform of the maximum function

In this section we prove the tight approximation of the upper compensated convex transform of the maximum function (Proposition 2 (ii)) . Recall from ^[1] that

for $x\in \mathbb{R}^m$ and $\lambda > 0$. Items i) and iv) of Proposition 2 were established in ^[1] with the maximum function as a special case. The fact that The function $C^u_\lambda(f_m)$ is a $C^{1, 1}$ approximation of $f_m$ and satisfies

for $x, \, y\in \mathbb{R}^m$ is a consequence of a general result in ^[1] (Theorem 4.1). The error estimate in iv) that

for $x\in \mathbb{R}^m$ was established in ^[1] (Theorem 5.1) which also contains the estimate $|DC^u_\lambda(f_m)(x)|\leq 1$ for $x\in \mathbb{R}^m$. Thus the statement in i) that $C^u_\lambda(f_m)$ is of linear growth is a direct consequence of this gradient estimate.

Before we prove Proposition 2 (ii) we state the following simple lemma which can be verified through a direct calculation using the definition of the upper compensated convex transform.

Lemma 12. Let $f_2(x) = \max\{x_1, x_2\}$ for $x = (x_1, x_2)\in \mathbb{R}^2$. We have

Next we prove ii), the 'Tight approximation' property: Assume $x = (x_1, x_2, \dots, x_m)$ is 'sorted' in the increasing order: $x_1\geq x_2\geq \cdots\geq x_m$, then $f_m(x) = C^u_\lambda(f_m)(x) = x_1$ if and only if $x_1-x_2\geq \frac{1}{2\lambda}$. Note that Item iii) for the lower transform of the minimum function can be proved by using the identity $C^l_{\lambda}(g_m)(x) = -C^u_\lambda(f_m(-x))$.

Proof of Proposition 2 Item ii) If $x^{(0)}_1-x^{(0)}_2\geq 1/(2\lambda)$, we see that $f_m$ is differentiable at $x^{(0)}$. By the translation invariance property of compensated convex transforms ^[7], we have,

The conclusion in this case follows if we can show that ${\rm{co}}(\lambda|\cdot-x^{(0)}|^2-f_m(\cdot))(x^{(0)}) = -f_m(x^{(0)})$. To prove this we only need to show that the tangent plane for $-f_m$ defined by $\ell(x) = -f_m(x^{(0)})-\nabla f_m(x^{(0)})\cdot(x-x^{(0)})$ lies below the graph of the function $\lambda|x-x^{(0)}|^2-f_m(x)$ for all $x\in \mathbb{R}^m$, that is,

Since $f_m(x) = x_1$ for $x$ near $x^{(0)}$, we have $f_m(x^{(0)}) = x^{(0)}_1$ and $\nabla f_m(x^{(0)}) = e_1$, hence (4.2) is equivalent to

where $x_k = f_m(x)$ for some $k\in\{1, 2, \dots, m\}$ by definition. If $k = 1$, then inequality (4.3) clearly holds. If $k\neq 1$, we have, as (4.3) is equivalent to

If we complete squares in $A$ defined in (4.4) above, we obtain

Therefore $A\geq 0$ if and only if

Since $k\neq 1$ we have

The conclusion follows.

Acknowledgments

The work of the first author is partially supported by NSFC grants 11801200 and 12141107. We wish to thank the anonymous referees for their helpful comments and suggestions which have greatly improved the presentation of this paper.

Conflict of interest

The authors declare there is no conflicts of interest.