Figure 1.
Optical micrographs of a tungsten sample: (a) before etching, (b) after etching for 5 s, (c) after etching for 20 s, (d) SEM image after etching.
We face a rigidity problem for the fractional p-Laplace operator to extend to this new framework some tools useful for the linear case. It is known that (−Δ)s(1−|x|2)s+ and −Δp(1−|x|pp−1) are constant functions in (−1,1) for fixed p and s. We evaluated (−Δp)s(1−|x|pp−1)s+ proving that it is not constant in (−1,1) for some p∈(1,+∞) and s∈(0,1). This conclusion is obtained numerically thanks to the use of very accurate Gaussian numerical quadrature formulas.
Citation: Francesca Colasuonno, Fausto Ferrari, Paola Gervasio, Alfio Quarteroni. Some evaluations of the fractional p-Laplace operator on radial functions[J]. Mathematics in Engineering, 2023, 5(1): 1-23. doi: 10.3934/mine.2023015
| [1] | Zhengtao Xi, Tongqiang Liu, Haifeng Shi, Zhuqing Jiao . Hypergraph representation of multimodal brain networks for patients with end-stage renal disease associated with mild cognitive impairment. Mathematical Biosciences and Engineering, 2023, 20(2): 1882-1902. doi: 10.3934/mbe.2023086 |
| [2] | Yu Lu, Tongqiang Liu, Quan Sheng, Yutao Zhang, Haifeng Shi, Zhuqing Jiao . Predicting the cognitive function status in end-stage renal disease patients at a functional subnetwork scale. Mathematical Biosciences and Engineering, 2024, 21(3): 3838-3859. doi: 10.3934/mbe.2024171 |
| [3] | Wei Kong, Feifan Xu, Shuaiqun Wang, Kai Wei, Gen Wen, Yaling Yu . Application of orthogonal sparse joint non-negative matrix factorization based on connectivity in Alzheimer's disease research. Mathematical Biosciences and Engineering, 2023, 20(6): 9923-9947. doi: 10.3934/mbe.2023435 |
| [4] | Wei Yin, Tao Yang, GuangYu Wan, Xiong Zhou . Identification of image genetic biomarkers of Alzheimer's disease by orthogonal structured sparse canonical correlation analysis based on a diagnostic information fusion. Mathematical Biosciences and Engineering, 2023, 20(9): 16648-16662. doi: 10.3934/mbe.2023741 |
| [5] | Ning Huang, Zhengtao Xi, Yingying Jiao, Yudong Zhang, Zhuqing Jiao, Xiaona Li . Multi-modal feature fusion with multi-head self-attention for epileptic EEG signals. Mathematical Biosciences and Engineering, 2024, 21(8): 6918-6935. doi: 10.3934/mbe.2024304 |
| [6] | Yingjian Yang, Wei Li, Yingwei Guo, Nanrong Zeng, Shicong Wang, Ziran Chen, Yang Liu, Huai Chen, Wenxin Duan, Xian Li, Wei Zhao, Rongchang Chen, Yan Kang . Lung radiomics features for characterizing and classifying COPD stage based on feature combination strategy and multi-layer perceptron classifier. Mathematical Biosciences and Engineering, 2022, 19(8): 7826-7855. doi: 10.3934/mbe.2022366 |
| [7] | Jingren Niu, Qing Tan, Xiufen Zou, Suoqin Jin . Accurate prediction of glioma grades from radiomics using a multi-filter and multi-objective-based method. Mathematical Biosciences and Engineering, 2023, 20(2): 2890-2907. doi: 10.3934/mbe.2023136 |
| [8] | Tinghua Wang, Huiying Zhou, Hanming Liu . Multi-label feature selection based on HSIC and sparrow search algorithm. Mathematical Biosciences and Engineering, 2023, 20(8): 14201-14221. doi: 10.3934/mbe.2023635 |
| [9] | Huiqing Wang, Xiao Han, Jianxue Ren, Hao Cheng, Haolin Li, Ying Li, Xue Li . A prognostic prediction model for ovarian cancer using a cross-modal view correlation discovery network. Mathematical Biosciences and Engineering, 2024, 21(1): 736-764. doi: 10.3934/mbe.2024031 |
| [10] | Jiale Lu, Jianjun Chen, Taihua Xu, Jingjing Song, Xibei Yang . Element detection and segmentation of mathematical function graphs based on improved Mask R-CNN. Mathematical Biosciences and Engineering, 2023, 20(7): 12772-12801. doi: 10.3934/mbe.2023570 |
We face a rigidity problem for the fractional p-Laplace operator to extend to this new framework some tools useful for the linear case. It is known that (−Δ)s(1−|x|2)s+ and −Δp(1−|x|pp−1) are constant functions in (−1,1) for fixed p and s. We evaluated (−Δp)s(1−|x|pp−1)s+ proving that it is not constant in (−1,1) for some p∈(1,+∞) and s∈(0,1). This conclusion is obtained numerically thanks to the use of very accurate Gaussian numerical quadrature formulas.
The main advantage of choosing tungsten as a plasma-facing material is due to its properties when interacting with plasma, namely, low sputtering ratio and low hydrogen retention. These properties make tungsten a particularly suitable material for the ITER divertor, where the effect of a high particle flux with energies below the sputtering energy of tungsten is expected [1,2]. However, high operating temperatures in the divertor (stationary up to 1200 ℃, and during breakdowns or transients at about 2000 ℃ [3,4]) can significantly change the microstructure of tungsten due to abnormal grain growth and affect the strength of tungsten [5,6]. It should also be noted that the use of an all-tungsten divertor in future fusion reactors will be complicated due to design constraints and high cost [4,7]. Such tokamaks as WEST [8], EAST [9], and JET [10] have already switched to an all-tungsten divertor. Nevertheless, to date, most fusion engineering research reactors use either tungsten coatings deposited on graphite and carbon-graphite materials, or uncoated graphite materials, including the KTM Kazakhstan materials science tokamak [11]. The presence of various materials in the chamber will lead to the formation of mixed W-C layers as a result of tungsten irradiation with eroded carbon atoms, as well as mutual diffusion at high temperatures [12,13,14,15,16].
The research carried out in the works [3,4,5,6] shows that during plasma and tungsten surface interaction, an important role is played by the orientation of surface grains, which can cause serious changes in the surface morphology (blistering, bubble formation, radiation damage). Recrystallization annealing is used to improve the mechanical properties and radiation resistance of pure tungsten, which changes the grain size and can modify their crystallographic orientation (texture). This allows for the choice of tungsten for fusion reactors with a suitable preferred orientation to reduce changes in surface morphology during plasma exposure [17,18,19,20,21]. Budayev and co-authors in the work [17] note that the brittle fracture of the recrystallized layer can lead to the formation of submicron size dust particles, which will lead to plasma contamination and its cooling. Changes in the microstructure due to recrystallization annealing should also be expected to affect the formation of mixed W-C layers.
In this regard, the purpose of this research is to study the effect of preliminary recrystallization annealing on the tungsten surface carbidization.
The studies of the effect of preliminary recrystallization annealing on the tungsten surface carbidization were conducted on a plasma-beam installation (PBI). The PBI is a linear simulator with electron-beam plasma generation, which allows combining plasma exposure with electron-beam with a high heat flux, and is also oriented on versatility and the ability for quick changeover to solve various specialized tasks. Depending on the task, it is possible to apply the regime of direct heating of materials by an electron beam and the regime of plasma irradiation in BPD [22,23,24,25,26,27,28]. Carbidization of the tungsten surface was also carried out in PBI according to the previously developed method [29,30,31,32]. This method makes it possible to study the formation of a mixed W-C layer on the tungsten surface under conditions of carbon atoms' local transfer along plasma-wetted surfaces due to hydrocarbons.
To study the effect of recrystallization annealing on the formation of a carbidized layer, tungsten of high purity was chosen in the form of a rod ∅10 mm, from which samples were cut in the form of 2.0 ± 0.1 mm thick disks. The prepared samples were subjected to mechanical grinding and polishing to roughness Ra = 0.02 µm from the irradiated side.
The microstructure of the materials was evaluated by optical microscopy (OM). To observe the samples microstructure by the OM method, chemical etching with a mixed solution of hydrofluoric acid and nitric acid in a volume ratio of 1:1 was carried out [33]. Figure 1 shows images of a tungsten sample microstructure in the initial state and after etching. Presented in Figure 1d is an image of the sample surface obtained on a scanning electron microscope, according to which it can be said that tungsten has a fine-grained structure [34].
For preliminary recrystallization annealing, the mode of direct heating of tungsten samples by an electron beam was used. Isochoric annealing [33] of samples was carried out at three temperatures (1200 ℃, 1300 ℃, 1400 ℃) for 3600 s. Isothermal annealing [33] was also conducted at a temperature of 1400 ℃ with a duration of 1800 s and 3600 s. The choice of these modes is determined by the expected operating conditions in ITER and reference data [35,36].
The pressure in the interaction chamber during annealing was (1.60 ± 0.03) × 10−3 Pa. After the recrystallization annealing, the Vickers microhardness was measured using a Q60M+ hardness tester (Qness) with an indenter load of 0.2 kgf and a holding time of 10 s. The grain sizes analysis after annealing was carried out using special Axalit software in accordance with ASTM E112-13 [34].
Tungsten surface carbidization after annealing was performed at a temperature of 1000 ℃ with irradiation duration of 3600 s. Two factors were taken into account when selecting the conditions for carbidization experiments. First, in order to reduce the effect of further heat exposure on the microstructure, the temperature of the tungsten surface during carbidization should be lower than the annealing temperature. Second, it was determined in the works [29,30,31,32] that the interaction between W and C begins at 1000 ℃ and leads to the formation of tungsten carbides. The pressure of the working gas (CH4) was (1.01 ± 0.04) × 10−1 Pa. The ion energy was set by a negative potential on the target node and amounted to 0.5 keV. In this case, the ion current on the target node was 21–23 mA.
| Sample | Recrystallization annealing temperature, ℃ | Annealing time, s | Surface temperature during carbidization, ℃ | Irradiation duration in methane environment, s |
| DC-1 | - | - | 1000 ± 10 | 3600 |
| DC-2 | 1200 ± 10 | 3600 | ||
| DC-3 | 1300 ± 10 | 3600 | ||
| DC-4 | 1400 ± 10 | 3600 | ||
| DC-5 | 1400 ± 10 | 1800 |
DownLoad:
CSV
Registration and control of temperature on the front and back sides of the sample's surface was carried out by using pyrometers of the METIS M318 and IMPAC ISR 6 Advanced brands and the VR-5/20 tungsten-rhenium thermocouple, respectively.
The X-ray diffraction patterns of the samples after carbidization for the phase composition determination of the surface were recorded on a diffractometer in Cu-Kα radiation with a PIXcel1D scanning linear detector. The surface phase composition of tungsten samples was identified using the Crystallography Open Database and the PDF-2 ICDD Release 2004 database [37,38]. Diffractometric data cards W2C No. 03-065-3896, No. 03-065-8829, No. 01-089-2371, WC No. 00-051-0939 as well as card of a metal W No. 00-004-0806 were applied. Quantitative content estimation of phases is determined by the semi-quantitative method of intensity ratio (RIR).
Micrographs presented in Figure 2 shows micrographs were obtained by the OM method of the central region of tungsten samples before and after annealing under different conditions. The microphotographs show the evolution of the tungsten microstructure upon annealing. After reaching the annealing temperature of 1200 ℃, as can be seen from Figure 2b, weakly pronounced low-angle grain boundaries (with the misorientation angle not exceeding 20º) and new high-angle grain boundaries (the misorientation angle > 20º) are observed on the surface, which are characterized by presenting inhomogeneous distribution [39]. Nevertheless, it can be seen that recrystallization nuclei appearance can be noticed mainly along the grain boundaries. According to [40], the size of recrystallized grains is an important characteristic of the annealed material, which can be used to judge the stage of recrystallization: primary, collective, and secondary. The surface microstructure of the DC-3 sample after annealing at 1300 ℃, represented in Figure 2c, corresponds to the grain structure of the primary recrystallization completion stage according to [40]. However, there are recrystallized grains of different sizes, some of them have an approximately equiaxed isometric shape. With an increase in the annealing temperature, microstructures with characteristics of the processes of the collecting and secondary stages of recrystallization are observed (Figure 2d, e). On the surface of the DC-4 and DC-5 samples (Figure 2d, e), which were annealed at a temperature of 1400 ℃, grains of considerable size were found, which was also established by the results of the grain size analysis (see below), and only a small amount of the deformed structure remained. As a result of the rapid migration of high-angle boundaries, recrystallized grains intensively consumed the deformed matrix [39,41].
Edge microstructures of tungsten samples after isochoric annealing are shown in Figure 3. In Figure 3a, obtained from the edge region of DC-4 sample, a migration of high-angle grain boundaries over the entire surface is shown. In the case of the DC-5 sample, which was annealed for 1800 s, high-angle grain boundaries are observed only in the central region of the sample (Figure 2e), while the edge region of the sample retains a fine-grained structure (Figure 3b), which may also indicate different stages of recrystallization.
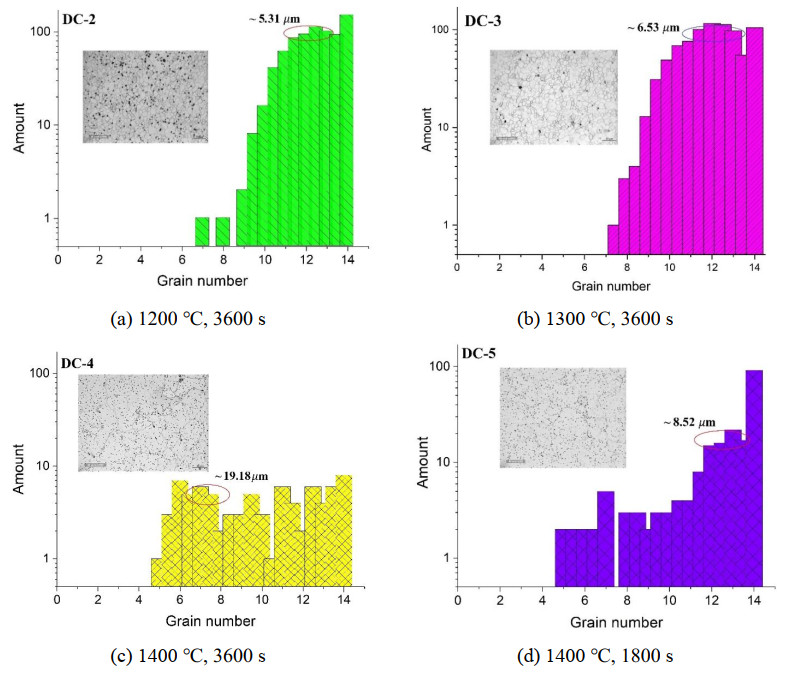
The results of the grain sizes analysis after annealing conducted using the Axalit software, are presented in the form of histograms of the conditional grain sizes distribution in points and their number in Figure 4. According to ASTM E112-13 [34], a smaller value of the grain number corresponds to a larger grain size, and a greater value to a smaller grain size (Table 2).
| Grain size No. | Average diameter |
| 0 | 359.2 |
| … | … |
| 4.5 | 75.5 |
| 5.0 | 63.5 |
| 5.5 | 53.4 |
| 6.0 | 44.9 |
| 6.5 | 37.8 |
| 7.0 | 31.8 |
| 7.5 | 26.7 |
| 8.0 | 22.5 |
| 8.5 | 18.9 |
| 9.0 | 15.9 |
| 9.5 | 13.3 |
| 10.0 | 11.2 |
| 10.5 | 9.4 |
| 11.0 | 7.9 |
| 11.5 | 6.7 |
| 12.0 | 5.6 |
| 12.5 | 4.7 |
| 13.0 | 4.0 |
| 13.5 | 3.3 |
| 14.0 | 2.8 |
DownLoad:
CSV
As seen in Figure 4, the grain size distribution tends to shift to the left with rise of annealing temperature, which indicates an increase in grain size. The minimum grain size, according to the Axalit software report, after annealing at a temperature of 1200 ℃ comprises 0.29 µm (Figure 4a). The share of these grains is 19.71% of the total number of grains. The proportion of average grain sizes corresponding to 11–13.5 points with an average grain size of ~5.31 µm reaches 63.29%. Primary recrystallization is assumed to happen at this temperature, which is characterized by irregular shape and different grain sizes. The results of the grain sizes analysis confirm that the completion of the stages of primary and the beginning of collective recrystallization occurs with an increase in the annealing temperature to 1300 ℃. Since there is a homogeneous grain growth, as evidenced by the rise in the average grain size to ~6.53 μm, the share of which is equal to 67.02% (Figure 4b). Collective recrystallization is also characterized by the growth of some recrystallized grains by means of neighboring recrystallized grains due to migration of high-angle boundaries [39,40]. A further increase in the annealing temperature to 1400 ℃ results in a uniform increase in the size of recrystallized grains (Figure 4c), which may also indicate collective recrystallization. The proportion of average size grains of ~19.18 μm, corresponding to 8–12.5 points, amounts to 57.5%, while the proportion of large grains was 33.75%. From the histogram in Figure 4d, it can be seen that after annealing for 1800 s, the structure consists of many small grains, the share of which is 44.02% of the total number of grains, and a small number of very large grains. Such a structure, according to [39,40], resulting from uneven grain growth, is called secondary recrystallization.
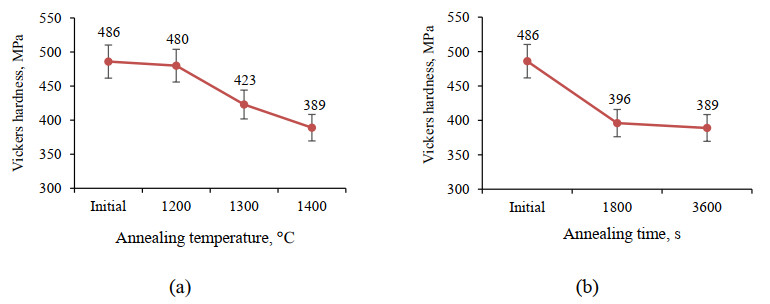
Vickers hardness changes during isochoric annealing for 3600 s and isothermal annealing at 1400 ℃ are presented in Figures 5a, b, respectively. As can be seen from Figure 5a, the hardness decreases with the growth of annealing temperature from 486 HV0.2 in the initial state to 389 HV0.2 after annealing at 1400 ℃. Figure 5b shows that the hardness was decreasing with the increase in annealing time. During the annealing process, grain growth occurs due to continuous static recrystallization, which leads to a decrease in hardness according to [42,43].
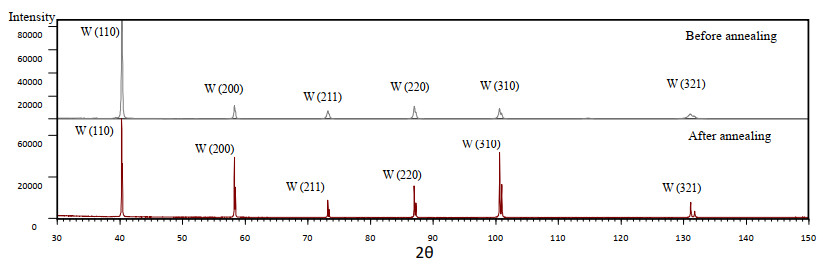
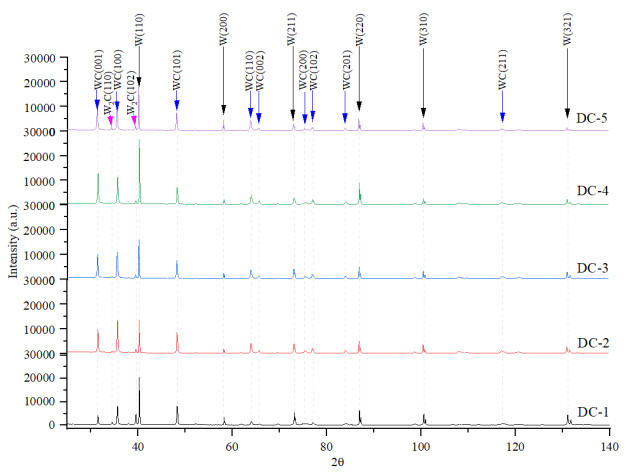
In the process of analyzing the phase composition of the samples surface, when diffractometric data corresponding to the tungsten phase are superimposed on the diffraction pattern of the cards, the experimental peak intensities were noticed to completely coincide with the bar diagram of the used card, despite the complete correspondence of the angular positions. In this regard, to identify the phase composition, diffraction data cards for metallic tungsten No. 00-004-0806, W2C No. 03-065-3896 and WC No. 00-051-0939 with the most suitable angular positions and having the highest conformity score were applied. The overlay of diffraction patterns before and after the annealing of the tungsten sample is shown in Figure 6.
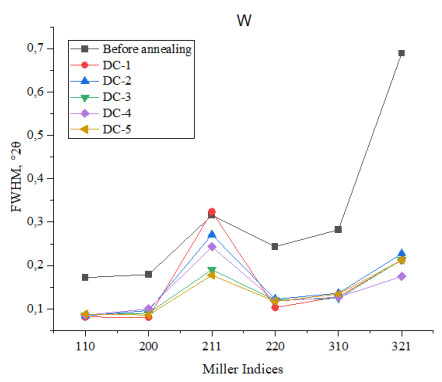
The state of the crystal structure of tungsten in the initial state is characterized by low intensity and a significant width of the peaks, indicating the distortion of the crystal lattice. Recrystallization annealing leads to an increase in the intensity of the peaks with a shift towards smaller angles and a decrease in their half-width, which points to the formation of a more perfect and homogeneous structure and the decrease in the interplanar spacing [43]. The results of the half-width (FWHM) analysis of the tungsten diffraction line are shown in a diagram in Figure 7.
After annealing under different conditions, a noticeable decrease in the half-width of the tungsten diffraction line is observed. However, the half-width of the line corresponding to the tungsten peak with Miller indices (211) after annealing at temperatures of 1200 ℃ and 1400 ℃ remains on par with the initial value, which indicates possible microstresses. As the annealing temperature increases, the microstresses disappear and the lowering of half-width takes place.
The overlay of diffraction patterns from the samples after carbidization is presenred in Figure 8. On the obtained diffractograms of the samples, diffraction peaks of WC and W2C are observed. Taking into account the similarity of the conditions of the diffraction experiment, the visual distinictions in the diffraction patterns indicate differences in the phase composition and structure.
In the phase composition of the DC-1 sample, the basis of the phase composition is the crystalline tungsten phase. The second phase in terms of intensity is the WC phase of the hexagonal syngony. The peaks of this phase are characterized by a redistribution of intensities: in accordance with the diffraction data card, the maximum peak of this phase should be dislocated in the region of angles of 35.6°2θ (Miller indices (100)). On the diffraction pattern, the maximum intensity of this phase belongs to the peak at 48.3°2θ (Miller indices (101)). Peaks of low intensity are identified as peaks belonging to the W2C phase of the hexagonal syngony. In the phase composition of DC-2 sample, the content of the carbide phase and the tungsten phase is almost the same. Peaks of low intensity are also identified as peaks belonging to the W2C phase of the hexagonal syngony. In the phase composition of DC-3–DC-5 samples, the basis of the phase composition is the phase of crystalline tungsten. The second phase in terms of intensity is the WC phase of the hexagonal syngony. Peaks of low intensity are identified as belonging to the W2C phase of the hexagonal syngony.
The results of the line widths analysis of tungsten carbides are shown in the form of diagrams in Figure 9. In Figure 9a an increase in the half-width of the WC lines depending on the conditions of preliminary recrystallization annealing is illustrated. The most noticeable broadening of the diffraction lines is noticed for the DC-5 sample annealed at a temperature of 1400 ℃ for 1800 s rather than for the unannealed DC-1 sample. An increase in the half-width of the W2C lines is also observed depending on the conditions of preliminary recrystallization annealing (Figure 9b). This fact may indicate the distortion of the lattice associated with the processes of structural rearrangement.
The results of the quantitative content assessment are presented in Table 3. Data is given with an accuracy of 0.1% to record the appearance of peaks when the experiment mode is changed.
| Sample | Results of a quantitative assessment of the phases content | ||
| W (cub.) | WC (hex., P-6m2) | W2C (hex., P-31m) | |
| DC-1 | 61.5 | 22.4 | 16.1 |
| DC-2 | 46.1 | 47.6 | 6.4 |
| DC-3 | 54.9 | 37.4 | 7.6 |
| DC-4 | 65.9 | 29.3 | 4.8 |
| DC-5 | 59.6 | 33.1 | 7.3 |
DownLoad:
CSV
According to the results of X-ray diffraction analysis, it can be found that, under the same conditions of tungsten carbidization, the phase composition of the surface has a noticeable difference. The tungsten phase remains the dominant phase both in the sample irradiated without preliminary recrystallization annealing (DC-1) and in the samples pre-annealed (DC-2–DC-5). However, the samples with preliminary recrystallization annealing show a decrease in the tungsten content, with the exception of the DC-4 sample annealed at a temperature of 1400 ℃. All samples present a noticeable increase in the WC phase and a decrease in the W2C phase relative to the initial tungsten.
As part of this research, experiments were conducted to study the effect of recrystallization annealing on the carbidization of the tungsten surface in BPD. The microstructure analysis of the surface of tungsten samples showed that recrystallization nuclei appear mainly along the grain boundaries. With an increase in the annealing temperature to 1400 ℃, high-angle grain boundaries migrate over the entire surface, which indicates normal grain growth and the transition of the whole structure to a recrystallized state. According to the results of the grain sizes analysis after annealing, primary recrystallization is established to take place at a temperature of 1200 ℃, which is characterized by irregular shape and varying sizes of grain. The completion of the stages of primary and the beginning of collective recrystallization is observed with the annealing temperature rise to 1300 ℃. The uniform growth of grains takes place evidenced by an increase in the average grain size to ~6.53 μm, the share of which reaches 67.02%. A further increase in the annealing temperature to 1400 ℃ leads to a homogenous increase in the size of recrystallized grains (Figure 4c), which may also indicate collective recrystallization. However, after being annealed for 1800 s, the structure consists of many small grains, the share of which is 44.02% of the total number of grains, and a small number of very large grains.
According to the results of the Vickers hardness measuring, the decrease in the tungsten surface hardness was established with increasing the annealing temperature from a value of 486 HV0.2 in the initial state to a value of 389 HV0.2 at an annealing temperature of 1400 ℃. The hardness had similar decreasing tendency in relation to the growing annealing time. According to literature data, a drop in hardness is an indicator for the beginning of recrystallization.
The results of the X-ray diffraction phase analysis showed WC and W2C peaks in the diffraction patterns of samples after carbidization in addition to tungsten peaks. However, after carbidization of the preliminarily annealed samples, a noticeable increase in the content of the WC phase and a decrease in the content of the W2C phase relative to the initial tungsten can be seen. A comparative analysis of the diffraction line widths of tungsten carbides implied that the most noticeable broadening of the diffraction lines is found in a sample annealed at a temperature of 1400 ℃ for 1800 s, thus indicating a distortion of the lattice related to the processes of structural rearrangement.
It follows that the differences in the structure arising during recrystallization annealing affect the transfer of carbon atoms in the near-surface area of tungsten and the formation of one or another phase of tungsten carbide. However, for a more accurate assessment of the effect of recrystallization annealing of the tungsten sample surface on carbidization, further development of experimental data is necessary.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
This research was conducted within the framework of Program No. BR09158585 "Scientific and technical support of experimental studies at the Kazakhstani Material Testing Tokamak KTM".
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
| [1] |
X. Cabré, Y. Sire, Nonlinear equations for fractional Laplacians, Ⅰ: Regularity, maximum principles, and Hamiltonian estimates, Ann. Inst. H. Poincaré Anal. Non Linéaire, 31 (2014), 23–53. http://dx.doi.org/10.1016/j.anihpc.2013.02.001 doi: 10.1016/j.anihpc.2013.02.001
|
| [2] | C. Canuto, M. Y. Hussaini, A. Quarteroni, T. A. Zang, Spectral methods: Evolution to complex geometries and applications to fluid dynamics, Berlin, Heidelberg: Springer, 2007. http://dx.doi.org/10.1007/978-3-540-30728-0 |
| [3] |
C. Canuto, A. Quarteroni, Approximation results for orthogonal polynomials in Sobolev spaces, Math. Comput., 38 (1982), 67–86. http://dx.doi.org/10.1090/S0025-5718-1982-0637287-3 doi: 10.1090/S0025-5718-1982-0637287-3
|
| [4] |
W. Chen, C. Li, Maximum principles for the fractional p-Laplacian and symmetry of solutions, Adv. Math., 335 (2018), 735–758. http://dx.doi.org/10.1016/j.aim.2018.07.016 doi: 10.1016/j.aim.2018.07.016
|
| [5] |
E. Cinti, F. Colasuonno, A nonlocal supercritical Neumann problem, J. Differ. Equations, 268 (2020), 2246–2279. http://dx.doi.org/10.1016/j.jde.2019.09.014 doi: 10.1016/j.jde.2019.09.014
|
| [6] |
F. Colasuonno, F. Ferrari, The soap bubble-theorem and a p-Laplacian overdetermined problem, Commun. Pure Appl. Anal., 19 (2020), 983–1000. http://dx.doi.org/10.3934/cpaa.2020045 doi: 10.3934/cpaa.2020045
|
| [7] |
L. M. Del Pezzo, A. Quaas, A Hopf's lemma and a strong minimum principle for the fractional p-Laplacian, J. Differ. Equations, 263 (2017), 765–778. http://dx.doi.org/10.1016/j.jde.2017.02.051 doi: 10.1016/j.jde.2017.02.051
|
| [8] |
F. del Teso, D. Gómez-Castro, J. L. Vázquez, Three representations of the fractional p-Laplacian: semigroup, extension and Balakrishnan formulas, Fract. Calc. Appl. Anal., 24 (2021), 966–1002. http://dx.doi.org/10.1515/fca-2021-0042 doi: 10.1515/fca-2021-0042
|
| [9] |
B. Dyda, Fractional calculus for power functions and eigenvalues of the fractional Laplacian, Fract. Calc. Appl. Anal., 15 (2012), 536–555. http://dx.doi.org/10.2478/s13540-012-0038-8 doi: 10.2478/s13540-012-0038-8
|
| [10] |
M. M. Fall, S. Jarohs, Overdetermined problems with fractional Laplacian, ESAIM Control Optim. Calc. Var., 21 (2015), 924–938. http://dx.doi.org/10.1051/cocv/2014048 doi: 10.1051/cocv/2014048
|
| [11] | P. Gervasio, A MATLAB tool for evaluating the fractional p-Laplace operator in 1D domains. Available from: https://github.com/pgerva/fractional-p-laplace.git. |
| [12] | A. Iannizzotto, S. Mosconi, N. Papageorgiou, On the logistic equation for the fractional p-laplacian, 2021, arXiv: 2101.05535. |
| [13] | A. Iannizzotto, S. Mosconi, M. Squassina, Global Hölder regularity for the fractional p-Laplacian, Rev. Mat. Iberoam., 32 (2016), 1353–1392. |
| [14] |
H. Ishii, G. Nakamura, A class of integral equations and approximation of p-Laplace equations, Calc. Var., 37 (2010), 485–522. http://dx.doi.org/10.1007/s00526-009-0274-x doi: 10.1007/s00526-009-0274-x
|
| [15] |
S. Jarohs, Strong comparison principle for the fractional p-Laplacian and applications to starshaped rings, Adv. Nonlinear Stud., 18 (2018), 691–704. http://dx.doi.org/10.1515/ans-2017-6039 doi: 10.1515/ans-2017-6039
|
| [16] |
S. Jarohs, T. Weth, On the strong maximum principle for nonlocal operators, Math. Z., 293 (2019), 81–111. http://dx.doi.org/10.1007/s00209-018-2193-z doi: 10.1007/s00209-018-2193-z
|
| [17] |
E. Lindgren, P. Lindqvist, Fractional eigenvalues, Calc. Var., 49 (2014), 795–826. http://dx.doi.org/10.1007/s00526-013-0600-1 doi: 10.1007/s00526-013-0600-1
|
| [18] |
J. J. Manfredi, p-harmonic functions in the plane, Proc. Amer. Math. Soc., 103 (1988), 473–479. http://dx.doi.org/10.1090/S0002-9939-1988-0943069-2 doi: 10.1090/S0002-9939-1988-0943069-2
|
| [19] |
R. Musina, A. I. Nazarov, Strong maximum principles for fractional Laplacians, Proc. Roy. Soc. Edinb. A, 149 (2019), 1223–1240. http://dx.doi.org/10.1017/prm.2018.81 doi: 10.1017/prm.2018.81
|
| [20] | S. G. Samko, A. A. Kilbas, O. I. Marichev, Fractional integrals and derivatives: theory and applications, Yverdon: Gordon and Breach Science Publishers, 1993. |
| [21] |
L. F. Shampine, Vectorized adaptive quadrature in Matlab, J. Comput. Appl. Math., 211 (2008), 131–140. http://dx.doi.org/10.1016/j.cam.2006.11.021 doi: 10.1016/j.cam.2006.11.021
|
| [22] | Wolfram Research Inc., Mathematica, Version 12.3.1, Champaign, IL, 2021. Availabe from: https://www.wolfram.com/mathematica. |
| 1. | Chaofan Song, Tongqiang Liu, Haifeng Shi, Zhuqing Jiao, HCTMFS: A multi-modal feature selection framework with higher-order correlated topological manifold for ESRDaMCI, 2024, 243, 01692607, 107905, 10.1016/j.cmpb.2023.107905 | |
| 2. | Xidong Fu, Chaofan Song, Rupu Zhang, Haifeng Shi, Zhuqing Jiao, Multimodal Classification Framework Based on Hypergraph Latent Relation for End-Stage Renal Disease Associated with Mild Cognitive Impairment, 2023, 10, 2306-5354, 958, 10.3390/bioengineering10080958 |
Figures(4) / Tables(1)
Francesca Colasuonno, Fausto Ferrari, Paola Gervasio, Alfio Quarteroni. Some evaluations of the fractional p-Laplace operator on radial functions[J]. Mathematics in Engineering, 2023, 5(1): 1-23. doi: 10.3934/mine.2023015
| Sample | Recrystallization annealing temperature, ℃ | Annealing time, s | Surface temperature during carbidization, ℃ | Irradiation duration in methane environment, s |
| DC-1 | - | - | 1000 ± 10 | 3600 |
| DC-2 | 1200 ± 10 | 3600 | ||
| DC-3 | 1300 ± 10 | 3600 | ||
| DC-4 | 1400 ± 10 | 3600 | ||
| DC-5 | 1400 ± 10 | 1800 |
DownLoad:
CSV
| Grain size No. | Average diameter |
| 0 | 359.2 |
| … | … |
| 4.5 | 75.5 |
| 5.0 | 63.5 |
| 5.5 | 53.4 |
| 6.0 | 44.9 |
| 6.5 | 37.8 |
| 7.0 | 31.8 |
| 7.5 | 26.7 |
| 8.0 | 22.5 |
| 8.5 | 18.9 |
| 9.0 | 15.9 |
| 9.5 | 13.3 |
| 10.0 | 11.2 |
| 10.5 | 9.4 |
| 11.0 | 7.9 |
| 11.5 | 6.7 |
| 12.0 | 5.6 |
| 12.5 | 4.7 |
| 13.0 | 4.0 |
| 13.5 | 3.3 |
| 14.0 | 2.8 |
DownLoad:
CSV
| Sample | Results of a quantitative assessment of the phases content | ||
| W (cub.) | WC (hex., P-6m2) | W2C (hex., P-31m) | |
| DC-1 | 61.5 | 22.4 | 16.1 |
| DC-2 | 46.1 | 47.6 | 6.4 |
| DC-3 | 54.9 | 37.4 | 7.6 |
| DC-4 | 65.9 | 29.3 | 4.8 |
| DC-5 | 59.6 | 33.1 | 7.3 |
DownLoad:
CSV
| Sample | Recrystallization annealing temperature, ℃ | Annealing time, s | Surface temperature during carbidization, ℃ | Irradiation duration in methane environment, s |
| DC-1 | - | - | 1000 ± 10 | 3600 |
| DC-2 | 1200 ± 10 | 3600 | ||
| DC-3 | 1300 ± 10 | 3600 | ||
| DC-4 | 1400 ± 10 | 3600 | ||
| DC-5 | 1400 ± 10 | 1800 |
| Grain size No. | Average diameter |
| 0 | 359.2 |
| … | … |
| 4.5 | 75.5 |
| 5.0 | 63.5 |
| 5.5 | 53.4 |
| 6.0 | 44.9 |
| 6.5 | 37.8 |
| 7.0 | 31.8 |
| 7.5 | 26.7 |
| 8.0 | 22.5 |
| 8.5 | 18.9 |
| 9.0 | 15.9 |
| 9.5 | 13.3 |
| 10.0 | 11.2 |
| 10.5 | 9.4 |
| 11.0 | 7.9 |
| 11.5 | 6.7 |
| 12.0 | 5.6 |
| 12.5 | 4.7 |
| 13.0 | 4.0 |
| 13.5 | 3.3 |
| 14.0 | 2.8 |
| Sample | Results of a quantitative assessment of the phases content | ||
| W (cub.) | WC (hex., P-6m2) | W2C (hex., P-31m) | |
| DC-1 | 61.5 | 22.4 | 16.1 |
| DC-2 | 46.1 | 47.6 | 6.4 |
| DC-3 | 54.9 | 37.4 | 7.6 |
| DC-4 | 65.9 | 29.3 | 4.8 |
| DC-5 | 59.6 | 33.1 | 7.3 |
