On three dimensional fractal dynamics with fractional inputs and applications

1.   Introduction

Cyber physical system (CPS) is commonly utilized to observe and secure a physical environment using a set of components namely control units, physical objects, actuators, and sensors ^[1]. As the result of dreadful consequences of a CPS failure, it is more important than anything else to protect a CPS from dangerous attacks. In this paper, we speak about the reliability problem of a CPS aimed at enduring hazardous attacks over a long time without energy replacement ^[2]. CPS often works in a rough environment where energy renewal is not possible, and nodes may be captured or compromised at periods. As a result, the intrusion detection system (IDS) is needed to detect harmful nodes without unnecessarily wasting energy to extend the network lifetime. IDS designed for CPSs has attracted significant interest ^[3]. IDS were used to identify security attacks and to monitor computer systems. Usually, IDS were of two major types: Signature-based and Behavior-based. Signature-based IDS deals with the comparison of the real-time performance of the computer system in contradiction of identified security attacks ^[4]. They cannot detect unknown attacks (signatures) as they depend on known attack models. This is notably important for CPS as they are operating independently for a longer time, and therefore it is difficult to interrupt the common upgrading or patching in the field ^[5].

Contrastingly, Behavior-based systems identify intrusions by observing a system's active implementation to identify suspect behavior and can identify both known and unknown attacks ^[6]. IDS, an initial layer is needed to fast assess, identify, and reply to dangerous cyber traffic. Network intrusion detection is vital for identifying and monitoring possible risks. Besides, there are key extreme data in public datasets for intrusion finding. In complex network infrastructure, managing a huge amount of data is another problem that these methods usually fail to solve ^[7]. For such reasons, classical IDSs based on predictable machine learning (ML) methods commonly have a few limitations, like poor real-time presentation and low regularization capability. In the past years, many researchers have been developed variations of IDS using deep learning (DL), ML, and other arithmetical approaches ^[8]. Over the years, DL methods have quickly been designed and it is largely used across various industries due to the continuous growth of computational capacity and much information. Both traditional and DL models were examined using familiar classification metrics. In multiple areas, involving image recognition and natural language processing (NLP), DL has created excellent outcomes ^[9]. Many researcher workers have used convolutional neural networks (CNN) effectively to find cyberattacks to raise the intelligence and correctness of network intrusion detection. The major cause of the failure is that network traffic is not in an image data format ^[10].

We introduce an Equilibrium Optimizer with Deep Recurrent Neural Networks Enabled Intrusion Detection (EODRNN-ID) technique in a Secure CPS environment. In the presented EODRNN-ID technique, a min-max normalization algorithm takes place to scale the input dataset. Besides, the EODRNN-ID technique involves an EO-based feature selection approach to choose the feature and diminish high dimensionality problem. For intrusion detection, the EODRNN-ID technique exploits the DRNN model. Finally, the hyperparameter related to the DRNN model can be tuned by the Chimp optimization algorithm (COA). The simulation study of the EODRNN-ID model is verified on a benchmark ID dataset.

2.   Related works

Almuqren et al. ^[11] proposed an Explainable AI Enabled Intrusion Detection Approach for Secured CPSs (XAIID-SCPS). This developed method especially focuses on the classification and intrusion detection in the CPS. In this study, a Hybrid Enhanced GSO (HEGSO) method was employed for the FS. In the IDS, the Improved ENN (IENN) algorithm has been applied with the Enhanced Fruitfly Optimizer (EFFO) method for parameter optimization. Hilal et al. ^[12] presented an imbalanced GAN (IGAN) with optimum kernel ELM (OKELM), named the IGAN-OKELM method for IDS in the CPS platform. Furthermore, the OKELM framework was implemented as a classification and an optimum parameter tuning of KELM architecture was executed through the applications of the sandpiper optimization (SPO) method and thus, devises the effectiveness of IDS.

The authors ^[13] implemented FID-GAN, an innovative fog-based, unsupervised ID for CPSs employing GANs. The IDS was introduced for the fog model that makes computation efficiency nearer to the terminal nodes and aids in gathering low-latency necessities. Almutairi et al. ^[14] employed a Quantum Dwarf Mongoose Optimizer with an Ensemble DL Intrusion Detection (QDMO-EDLID) method in CPS. This algorithm is targeted for identifying the survival of intrusions by employing ensemble learning and FS methods. Furthermore, a Deep Autoencoder (DAE), ensemble of Convolution Residual Network (CRN), and Deep Belief Networks (DBNs) techniques have been implemented for classifying intrusion methods.

The authors ^[15] presented an Optimum DBN-based distributed IDS (ODBN-IDS) for secured CPS platforms. The Binary Flower Pollination Algorithm (BFPA) was utilized for the FS algorithm. The achieved features have been employed for optimally DBNs for detecting the occurrence of intrusion in cloud information and generating alarms if there is an existence of intrusions. In DBN architecture, the Equilibrium Optimizer Algorithm (EOA) could be employed for finetuning the hyperparameter. Xiao et al. ^[16] implemented the software-defined network (SDN) model into the CPS framework for easily managing CPS and providing a solution against network security issues. The authors also developed an identification method that depends on ELM to secure CPS.

Duhayyim et al. ^[17] designed an original Stochastic Fractal Search Algorithm with DL Driven IDS (SFSA-DLIDS) for cloud-based CPS platform. This introduced method mainly implements a min-max data normalization algorithm for converting an input dataset into well-suited formats. For decreasing a process of dimensionality, the SFSA method was implemented for choosing a feature subset. Moreover, a chicken swarm optimizer (CSO) with deep stacked-AE (DSAE) technique is exploited for discovering and organizing intrusion. Dutta et al. ^[18] developed a robust anomaly detection mechanism according to semi-supervised ML techniques authorizing the nearby real-time location. A deep neural network (DNN) framework could be employed for identifying anomalies – relying on regeneration errors.

3.   The proposed model

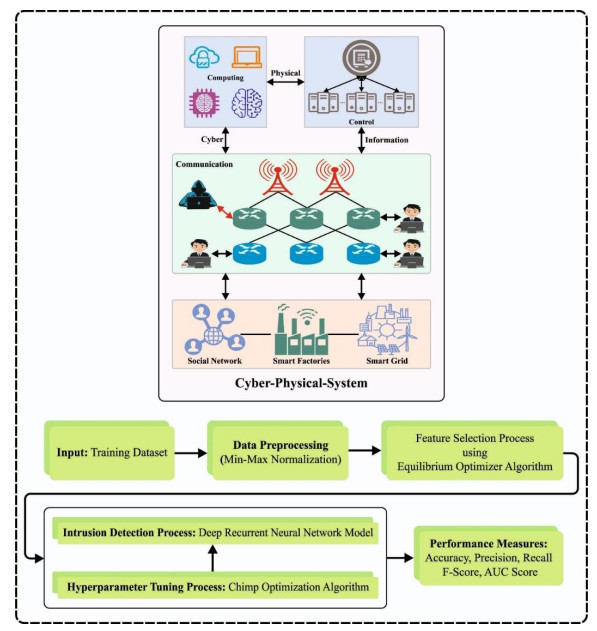
In this work, a new EODRNN-ID method has been developed for cyberattack recognition in the CPS platform. The foremost goal of the EODRNN-ID model is to classify as well as identify of intrusive actions in the CPS platform. During the proposed EODRNN-ID method, four sets of operations are involved, namely data normalization, COA-based parameter tuning, DRNN-based classification, and EO-based feature subset selection. Figure 1 portrays the workflow of the EODRNN-ID procedure.

3.1.   Data normalization

Normalization can be done by processing the variably extended data into a reliable range, thereby removing the dimension variation among logging data while preserving relationships amongst the datasets ^[19]. This method maps the dataset between 0 and 1:

where ${x}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ denotes the minimum value, ${x}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ signifies the maximum value of a certain feature in the dataset, ${x}^{\mathrm{*}}$ refers to the normalized data, and $x$ denotes an original data.

3.2.   Feature selection using EO algorithm

For electing the feature subsets, the EO model is used. The EO method is a new optimizer that draws on approximating equilibrium and dynamic states that establish control volume mass balance ^[20]. The particle with respective concentration plays the role of the searching agent. After generating a random population, the initial concentration of ${j}^{th}$ particles can be formulated as:

In Eq (2), $ran{d}_{j}$ is an arbitrarily produced value that lies in [0, 1], $s$ refers to the number of particles, and ${D}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${D}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ indicate the maximal and minimal values of the dimension.

The EO creates an equilibrium pool. Initially, the equilibrium candidate is defined (without their knowledge concerning the equilibrium state) to obtain a search pattern for the agent. This can be performed by the four better candidates (viz., large fitness value), along with other particles where the fitness equals the average of four different particles.

An exponential term ($F$) is used for the concentration updating:

In Eq (5), $\beta$ indicates the random integer ranges between [$\mathrm{0, 1}$], $\mu$ shows the constant number to control the exploitation potential. As well, $\alpha$ is a constant number to control the exploration potential, ${T}_{0}$ is evaluated using Eq (6) to ensure the convergence:

In the equation, sign $(rand-O.5)$ is used to control the exploitation and exploration direction. Thus, Eq (4), is formulated by:

A parameter used to enhance the exploitation is named generation rate ($Gr$) and is shown as follows:

Let $GrP$ and ${P}_{G}$ be the generation rate parameter and the likelihood generation, correspondingly.

Eq (11) is used as an updating rule ($W$ is defined as a unit).

In the EO, the FF is used to balance the classifier outcome (higher) attained and the amount of features elected in the solution (lower), The fitness function to evaluate solutions is given in Eq (12).

Now, $\alpha$ and $\beta$ are parameters respective to the significance of classification quality and subset length. ∈ [1, 0] and $\beta = 1-\alpha.\left|R\right|$implies the cardinality of the nominated sub-set. ${\gamma }_{R}\left(D\right)$ implies an error rate of classification. $\left|C\right|$ shows the overall feature count in the database.

3.3.   Optimal DRNN based intrusion detection

The DRNN model is used for the intrusion detection process. RNN is a special type of dense connection NN which is diametrically opposed to the typical FFNN for the introduction of "time" ^[21]. Especially, the output of the latent layer in the RNN is fed into the input, since the input is a composite of the recent and the present past. RNN exploits the peculiar structure to determine the relationship between events divided by the temporal instant. This means a kind of long‐term dependency since a specific event is often a function of a past event. Figure 2 illustrates the framework of RNN.

The RNN has a problem that degrades the performance. During the learning, the gradient tends to vanish similar to other NN models. In this network, the gradient expresses the changes in each weight regarding the change in error. Moreover, the computation gradient passes over several phases of multiplication, and when the quantity multiplied is lesser than one, then the gradient becomes smaller (vanishing), if the quantity multiplied is slightly greater than one, then the gradient becomes larger (exploding). We could not adjust the weight and train the network without accurate knowledge of the gradient. A variant of the RNN is the optimum solution for the gradient vanishing problems that exploit the LSTM unit. LSTM unit helps to retain the error information that can be backpropagated by the time and layers. LSTM unit can able to learn long‐term dependency problems on the gradient. LSTM presents a new structure named a memory cell that encompasses of four major components of gate such as a forget, an input, an output and a neuron with a self‐recurrent link. The LSTM one has three gating models as new elements in relation to the typical RNN.

The proposed architecture encompassed two recurrent layers with LSTM cells along with the softmax activation function and dense layer for the last classification. The entire network was trained by reducing the categorical cross‐entropy as a loss function:

In Eq (13), $y$ and $\widehat{y}$ denote the target and the predicted classes correspondingly.

The Adam algorithm is the chosen optimizer, a gradient‐based optimization technique that uses first and second-order moments to attain a fast and smooth convergence.

The COA is used for the optimal parameters tuning of the DRNN. Unlike the other social predators, COA is based on the sexual motivation and intelligence of chimps during group hunting ^[22]. The four dissimilar stages of hunting in COA are pushing, chasing, blocking, and assaulting. Initially, Chimpanzees are generated randomly to start the COA. The mathematical model of COA's hunting is given below:

where $t$ indicates the iteration number, $\kappa, J$, and $\zeta$ represent the coefficient vector, ${p}_{prey}$ shows the optimum solution attained r, and ${p}_{chimp}$ denotes the optimum location of the chimp. $\zeta$ refers to the chaotic mapping vector. Furthermore, $\beta$ is a nonlinearly dropped constant value that ranges from 2.5 to $0,$ ${r}_{1}$ and r2 are randomly generated values within [0, 1]. Note that the reference gives a comprehensive analysis of these mappings and coefficients.

The most effective and primary strategy for statistically duplicating the chimpanzee behavior is using prey assumed as the initial position of the target. The COA is accountable for housing four of the topmost chimpanzees. Consequently, based on the selected position of best chimpanzees, other individuals would be compelled to relocate as follows:

where

Moreover, chaotic value mimics social motivation activity in classical COA, as follows:

Where, ${\eta }_{m}$ refers to a stochastic value within [0, 1]; however, this may result in a moderate or premature convergence.

The COA method derives an FF in order to get high efficacy of classification. It defines an optimistic integer to signify the optimal outcome of the solution candidate. The decay of classification error rate is expected as FF.

4.   Results and discussion

The intrusion detection outcomes of EODRNN-ID technique are verified on 2 benchmark databases: NSLKDD2015 and CICIDS2017 datasets as defined in Table 1.

The confusion matrices achieved by the EODRNN-ID approach on the NSLKDD2015 dataset is shown in Figure 3. The results show an effective recognition of the normal as well as anomaly samples under all classes.

The recognition outcome of the EODRNN-ID methodology can be inspected on the NSLKDD2015 dataset is given in Table 2 and Figure 4. The outcome implies the effectual recognition of the normal as well as anomaly samples by the EODRNN-ID technique. With 80% of the TRAP, the EODRNN-ID method obtains average $acc{u}_{y}$, $pre{c}_{n}$, $rec{a}_{l}$, ${F}_{score}$, and $AU{C}_{score}$ values of 97.44%, 97.45%, 97.44%, 97.45%, and 97.44%, respectively. Moreover, with 20% of the TESP, the EODRNN-ID method obtains average $acc{u}_{y}$, $pre{c}_{n}$, $rec{a}_{l}$, ${F}_{score}$, and $AU{C}_{score}$ values of 97.39%, 97.41%, 97.39%, 97.40%, and 97.39%, respectively.

To evaluate the performance of EODRNN-ID method on the NSLKDD2015 dataset, TRA and TES $acc{u}_{y}$ curves are defined, as presented in Figure 5. The TRA and TES $acc{u}_{y}$ curves display the performance of EODRNN-ID method over some epochs. The outcome shows significant facts about learning task and generalization capacities of EODRNN-ID model. It is practical that the TRA and TES $acc{u}_{y}$ curves get improved with an increased epoch count. It is well-known that the EODRNN-ID technique attains superior testing results, which has high ability in detecting the pattern in TRA and TES data.

Figure 6 demonstrates the complete TRA and TES loss performances of the EODRNN-ID model on the NSLKDD2015 dataset over epochs. The TRA loss shows the model loss acquires reduced over epochs. Primarily, the loss value gets minimized as the model adapts the load to reduce the prediction error on TRA and TES datasets. The loss curves illustrate the level to which the model fit the TRA dataset. The TRA and TES loss is gradually reduced and showed that the EODRNN-ID technique efficiently learns the pattern revealed in the TRA and TES data. Also, the EODRNN-ID method adjusts the parameters to reduce the divergence among the forecast as well as original TRA labels.

The detection performance of the EODRNN-ID method can be inspected on the CICIDS2017 dataset as delivered in Table 3 and Figure 7. The outcomes indicate the effective detection of the normal and anomaly samples by the EODRNN-ID methodology. With 80% of the TRAP, the EODRNN-ID method accomplished average $acc{u}_{y}$, $pre{c}_{n}$, $rec{a}_{l}$, ${F}_{score}$, and $AU{C}_{score}$ values of 99.20%, 99.20%, 99.20%, 99.20%, and 99.20%, respectively. Besides, with 20% of the TESP, the EODRNN-ID model obtains average $acc{u}_{y}$, $pre{c}_{n}$, $rec{a}_{l}$, ${F}_{score}$, and $AU{C}_{score}$ values of 99.28%, 99.27%, 99.28%, 99.27%, and 99.28%, correspondingly.

To estimate the performance of the EODRNN-ID methodology on the dataset of CICIDS2017, TRA and TS $acc{u}_{y}$ curves are well-defined, as given in Figure 8. The TRA and TES $acc{u}_{y}$ curves illustrate the performance of EODRNN-ID model over numerous epochs. The figure delivers significant details concerning the learning task and generalization capabilities of EODRNN-ID technique. It is perceived that the TRA and TES $acc{u}_{y}$ curves get improved with an increased epoch count. The EODRNN-ID methodology attains improved testing accurateness which has the skill to detect the pattern in TRA and TES datasets.

Figure 9 shows the complete TRA and TES loss performances of the EODRNN-ID model on the CICIDS2017 dataset over epochs. The TRA loss demonstrates the model loss gets reduced over epochs. Primarily, the loss value gets minimized as the model adapts the weight to diminish the predictive error on the TRA and TES datasets. The loss curves illustrate the range to which the model fits the TRA dataset. It is perceived that the TRA and TES loss is steadily reduced and depicted that the EODRNN-ID technique learns the pattern presented in the TRA and TES datasets. Also, the EODRNN-ID technique adjusts the parameter to minimize the dissimilarity among the prediction and original TRA label.

The PR curve of the EODRNN-ID method on the CICIDS2017 dataset is established by plotting precision against recall as defined in Figure 10. The outcomes confirm that the EODRNN-ID technique achieves enlarged precision-recall values below all classes. The figure shows that the method learns to identify many classes. The EODRNN-ID method reaches upgraded outcomes in the detection of positive samples through a least false positives.

The ROC curves delivered by the EODRNN-ID methodology on the CICIDS2017 dataset are demonstrated in Figure 11, which has the ability to distinguish the classes. The figure shows valuable insights into the tradeoff amongst the TPR and FPR rates over different detection thresholds and variable numbers of epochs. It projects an accurate predictive performance of the EODRNN-ID model on the detection of different classes.

The intrusion detection results of the EODRNN-ID system are compared with the present methods in Table 4 and Figure 12 ^[11]. The outcomes established that the EODRNN-ID technique reaches improved performance over other models. It is stated that the LIB-SVM, WISARD, and Forest-PA models have resulted in worse results whereas the XAIID-SCPS, FURIA, AE-RF, and GSAE models have tried to accomplish manageable performance. However, the EODRNN-ID technique resulted in better performance with maximum $acc{u}_{y}$, $pre{c}_{n}$, $rec{a}_{l}$, and $F{1}_{score}$ of 99.28%, 99.27%, 99.28%, and 99.27% respectively. Thus, the EODRNN-ID technique can be applied to achieve security from the CPS platform.

5.   Conclusions

In this manuscript, we have established the EODRNN-ID methodology for cyberattack recognition in the CPS platform. The major intention of the EODRNN-ID algorithm is to classify and detect the intrusive actions from the CPS platforms. In the proposed EODRNN-ID method, four sets of operations are included such as data normalization, COA-based parameter tuning, DRNN-based classification, and EO-based feature subset selection. The simulation study of EODRNN-ID method can be verified on a benchmark data. Extensive outcomes illustrate the significant performance of the EODRNN-ID method over existing techniques

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare no conflicts of interest in this paper.