1.
Introduction
In real life, in the face of emerging and re-emerging infectious diseases, human behavior and environmental noise interference will produce many uncertain factors, which may accelerate the spread of the disease or make the disease exist for a long time, or even make the local epidemic situation beyond control. For example, currently popular novel coronavirus pneumonia (NCP), long-term existence of AIDS (AIDS), hepatitis B virus (HBV) and seasonal influenza virus (influenza virus). For these diseases, although there is no specific drug cure, standard treatment and appropriate prevention and control measures can control the trend of viral infection. In the long term treatment, drug tolerance and human activity with uncertain interference will affect the control of the transmission of the virus.
Many scholars find that the resistance of hepatitis B virus is affected by many factors when they study the mechanism of hepatitis B resistance. Zhang Jing et al. studied the changes of drug-resistant mutants in 268 cases of chronic hepatitis B patients and found that with the extension of drug treatment time, the increase probability of drug-resistant strains in different patients was different, but all of them would increase, even up to 100% [1]. Deng Jun et al. studied the mechanism of drug resistance of hepatitis B and found that multiple factors could lead to drug resistance, such as the reliability of viral polymerase, the pressure of drug selection, the patient's past drug use history and the patient's genetic factors (such as congenital metabolic defects), and the sensitive virus strains in the patient could mutate at one or more sites [2,3].
In order to be more practical, many scholars have combined the influence of environmental fluctuation factors to study the development trend of infectious diseases with stochastic models. Pang Haiyan et al. considered that variables oscillated around the equilibrium point caused by white noise, and the disturbance value was proportional to the amplitude of oscillation, thus establishing the virus dynamics model under immune response damage, and obtained the conclusion that the positive equilibrium point of the model was stable under random disturbance [4,5]. Xie Falan et al. took into account that the regeneration ability of liver cells was interfered by environmental factors, so that the infection rate would fluctuate around a certain average value. They established a random hepatitis B virus infection model with Logistic liver cell growth, and proved that the solution of this model had a unique stable distribution [6,7]. Hui Hongwen et al. established an HBV model with nonlinear incidence and random interference, obtained sufficient conditions for the exponential stability of the free virus in infected cells, estimated the oscillating behavior of the model near its deterministic model, and verified it by numerical simulation [8]. Bao Kangbo et al. analyzed the influence of environmental noise on stochastic hepatitis B virus dynamics model, and observed that high environmental noise intensity can inhibit the outbreak of hepatitis B, indicating the important role of intervention strategies in the control of hepatitis B [9,10]. Taking into account the variables directly proportional to the ambient noise, Liu et al. constructed a three-dimensional stochastic virus infection model, and obtained sufficient conditions for the ergonomically stationary distribution of the model solution and conditions for the extinction of the disease [11,12,13].
Xia Peiyan established a random HTLV-I model with CTL immune response by considering the random perturbation of exposure rate, and proved the existence of a unique global positive solution to the model, and found the random threshold values of virus extinction, latent and epidemic [14,15,16]. By considering the random interference of the environment on the exposure rate, Cui Xiaowei established the dynamic model of virus infection with random immune effect, proved that the unique global positive solution existed in the model solution, obtained the threshold conditions of virus extinction and persistence, and gave the upper and lower bounds of the persistence, and verified the theory through numerical simulation [17]. The research with stochastic model changes the law of the original determined model [18,19,20], and it is a meaningful work to pay attention to the problems of environment and personal noise. For patients with hepatitis B virus infection, white noise will interfere with the original infection rate in the presence of external environmental interference or drug resistance during long-term treatment. Therefore, the dynamic model of hepatitis B virus with random infection rate can be used to predict the effect of virus control under treatment more accurately. This is worthwhile work.
In the second part of this paper, according to the statistical data rules of drug treatment of hepatitis B virus, it is found that drug-resistant HBV is uncertain due to viral mutation, which resulted in the randomness of the infection rate of healthy cells, and a stochastic hepatitis B virus dynamics model is established. In the third part, Lyapunov function and Ito's formula are used to prove the existence and uniqueness of the global positive solution of the model and the asymptotic property of the model solution. In the fourth part, several cases of the influence of noise intensity on HBV treatment are simulated numerically, and the rationality of the theorem is also verified. By comparing the results of no noise interference model, it is found that strong noise can affect the variation law of hepatitis B virus.
2.
Model establishment
According to the principle of action of anti-hepatitis B virus drugs and the rule of therapeutic test data, it was found that the drug resistance of the virus was the main reason for the decrease of drug efficacy [21]. Therefore, the virus can be divided into drug sensitive virus and drug resistant virus. It is assumed that the inhibition rate of drugs to the resistant virus is related to the mutation rate of the virus, and the following kinetic model of hepatitis B virus with drug resistance is established.
here T, Ts, Vs, Tr and Vr respectively represent the number of uninfected hepatocytes at time t, the number of hepatocytes infected with drug-sensitive HBV, the number of drug-sensitive HBV, the number of hepatocytes infected with drug-resistant HBV, and the number of drug-resistant HBV; λ is the growth rate of uninfected hepatocytes; α and δ are the death rates of hepatocytes and viruses; Ks and Kr respectively denote the infection rate of drug-sensitive HBV and drug-resistant HBV on uninfected hepatocytes; Ns and Nr respectively denote the total number of viruses produced by drug-sensitive infected hepatocytes and drug-resistant infected hepatocytes during their life cycle; the mutation rate between drug-sensitive hepatocytes and drug-resistant hepatocytes is given by u; f(CN) is the rate at which drug therapy causes the decrease of HBV; CN denotes the average steady-state plasma concentration in a patient; β(u) denotes the inhibition rate of drug therapy on drug-resistant HBV; all parameters are positive. Suppose that f(CN) is a bounded function, and β=1−u. The basic regeneration number is as follows
The model has four equilibrium points, namely, the disease-free equilibrium point E0, the sensitive virus equilibrium point Es, the drug-resistant virus equilibrium point Er and the double virus equilibrium point E*. When the basic regeneration number meets different conditions, the equilibrium point is globally asymptotically stable.
In drug therapy, because the mechanism of its action on the virus is different from the body's tolerance, the blood drug concentration is inversely proportional to the rate of decline of HBV DNA, which can be used to determine the occurrence of HBV mutation. Taking lamivudine as an example, Su Ying et al. studied its drug-resistant mutation site in the catalytic region of HBV polymerase or YMDD sequence in the C region, which was due to the mutation of rtM204V /I (methionine M at position 204 was replaced by isoleucine I or valine V), and the drug-resistant strains formed by the mutation of this sequence were called YMDD variants [2]. It was also found that there were some variations in the B region. The susceptibility of the virus to the drug is slightly reduced when only the B region variation is present, and is greatly reduced when they are accompanied by the RTM204V/I variation. Due to the differences in the variation types of HBV in patients, some patients only have YMDD variant strains in the body, some patients only have mutations in the B region, and some have these two variants. So the more mutated sites on HBV DNA, the more likely the virus is to infect liver cells, which leads to different rates of infection of the mutant strains on healthy liver cells.
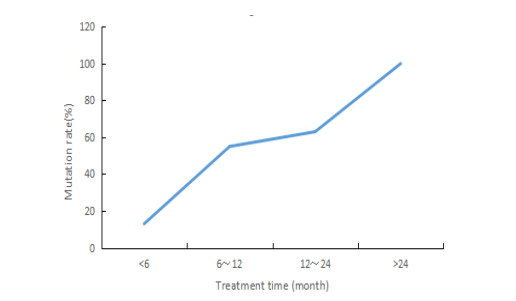
According to the statistical analysis of the duration of medication and the number of virus strains [1], the length of treatment would also lead to different probabilities of YMDD variant strains appearing in patients, as shown in Figure 1. Even for the same treatment duration, the percentage of patients with the YMDD variant varies, as shown in Figure 2. Due to the influence of individual genetic factors or variation characteristics in B region in vivo, the replication rate of HBV in patients is different, and the infection rate of the virus on liver cells is uncertain.
In [22], the hepatitis B virus genome is double-stranded relaxed circular DNA (rcDNA). When HBV DNA enters the cell, the rcDNA becomes covalently closed circular DNA (cccDNA), which is used as a template to start the replication process of the virus. Therefore, cccDNA is stable in infected liver cells, and there are about 5-50 cccDNA copies in each liver cell. When liver cells are damaged, cccDNA in the liver nucleus is released into the blood, so the amount of cccDNA detected in liver tissue and serum can be used to predict the number of infected cells. Therefore, the total amount of cccDNA and HBV DNA can be measured to determine the relationship between infected liver cells and the virus. In [23], changes in liver tissue cccDNA, serum cccDNA, and HBV DNA in 88 patients with chronic hepatitis B were recorded before and at 24, 48, and 96 weeks after treatment. The data are shown in Table 1.
The total amount of cccDNA can be considered to be composed of cccDNA in liver tissue and cccDNA in serum, represented by variable x; The amount of serum HBV DNA was denoted by variable y. Statistical analysis shows that the two are linearly correlated and satisfy the relationship y=0.6302x−0.6822, and the degree of correlation is r=0.9906. The drawing graph is shown in Figure 3.
According to the image and fitting results, it can be approximately believed that there is a linear proportional relationship between infected liver cells and virus, as shown in the following expression
To control the infection of healthy liver cells, that means to reduce the infection rate. According to the above data analysis, it is found that multiple factors during treatment will interfere with the infection rate, which may lead to some changes in the results given by Model (1). If the influence of random factors on the infection rate is considered, the infection rate Kr is rewritten into the following form
Let (Ω,Φ,P) be a complete probability space and Φ is the σ -algebra. In this probability space, a σ -algebraic stream {Ft}t⩾0 is defined, which satisfies the usual conditions.
1) For all 0⩽s<t<∞, Φs⊂Φt⊂Φ,
2) Right continuity: for all t⩾0, Φt=∩s>tΦs.
Moreover, the B(t) belongs to the independent Brownian movement in this probability space, and B(0)=0. σ2>0 is noise intensity.
In summary, the following hepatitis B virus model with random interference infection rate is established based on Model (1):
The variables and other parameters in Model (3) are the same as those in Model (1).
3.
Main research results
3.1. Existence and uniqueness of global positive solutions
Theorem 1. For any given initial value (T(0),Ts(0),Vs(0),Tr(0),Vr(0))∈R5+ , Model (3) has a unique global positive solution (T(t),Ts(t),Vs(t),Tr(t),Vr(t))(t⩾0) . That is, (T(t),Ts(t),Vs(t),Tr(t),Vr(t))∈R5+ a.s..
Proof. The function at the right end of Model (3) satisfies the local Lipschitz condition, so any given initial value (T(0),Ts(0),Vs(0),Tr(0),Vr(0))∈R5+, there is a unique local solution y(t)=(T(t),Ts(t),Vs(t),Tr(t),Vr(t)) on [0,τe), where τe is the blasting time, the solution is proved to be global, only need to prove τe=∞ a.s..
Take a sufficiently large positive number k0⩾0, so that every component of the initial y(0) is a member of the interval [1k0,k0]. For any k⩾k0, k∈N+, define the stopping time
here inf∅=∞ (∅ stands for the empty set).
From the definition of the stop time, we know that when k→∞, τk monotonically increases. Let τ∞=limk→∞τk, then τ∞⩽τe a. s..
If τ∞=∞ can be proved for all t⩾0 and (T(t),Ts(t),Vs(t),Tr(t),Vr(t))∈R5+, then τe=∞. Use contradiction. If not, there are constants ˜t>0 and δ∈(0,1), such that P{ τk⩽˜t} >δ, so there is an integer k1⩾k0, and for any k⩾k1, there is
when t⩽τk, for each k
Thus, it is obtained from Eq (5)
where
Define the function V : R5+→R+
where a is the positive number to be determined.
It is easy to prove that inequality u+1−lnu>0(u>0) is true, so there is V(T,Ts,Vs,Tr,Vr)>0. From Itˆo formula, we get
where
Let
Based on Eq (6), Eq (7) can be reduced to
where
Therefore
Integrate Eq (8) from 0 to τk∧˜t and take the expectation
Let Ωk={τk⩽˜t}, then for any k⩾k1, as shown in Eq (4), there is P(Ωk)⩾δ, and for any ω∈Ωk, as can be seen from the definition of stop time, at least one of them is equal to k or 1k, so there is
It can be obtained from Eq (9) and the above equation
where IΩk represents an indicator function of Ωk.
When k→∞, the above equation is in contradiction with the boundedness of function V, so there must be τ∞=∞ a.s., that is, the solution is positive and globally unique.
The result of Theorem 1 and Eq (3) can be obtained
For any given initial value (T(0),Ts(0),Vs(0),Tr(0),Vr(0)), the solution of Model (1) is ultimately bounded, thus the region
is the positive invariant set of Model (3). Let's assume (T(0),Ts(0),Vs(0),Tr(0),Vr(0))∈Γ*, so all the questions that follow will be discussed in Γ*.
3.2. The asymptotic behavior of the solution of Model (3)
Theorem 2. If Rs<1−u and Rr<1 , the solution (T(t),Ts(t),Vs(t),Tr(t),Vr(t)) of Model (3) has
where m=min{α,12N2s(δ+f(CN)),12N2r(δ+f(CN)),αNs(δ+f(CN))2(1−u)λcKs,12C2α},
Proof. Define the C2 -function Vi(i=1,2,3,4,5)
Applying Itˆo formula to Vi(i=1,2,3,4,5), we get
From Rs<1−u and Rr<1, Eq (10) can be reduced to the following form
We can define the function V From Vi(i=1,2,3,4,5)
where C1,C2 is the normal number to be determined.
Substitute Eqs (11)–(15) into Eq (10) to obtain
where
Inequality 2ab⩽a2+b2 and the expressions in the second, third and fourth lines of Eq (17) can be obtained
Choose
meet
Therefore, when Eqs (19) and (20) are substituted into Eq (17), there is
Then substitute Eq (21) into Eq (16), and take the expectation of both ends after the integration from 0 to t, we get
Therefore
where m=min{α,12N2s(δ+f(CN)),12N2r(δ+f(CN)),αNs(δ+f(CN))2(1−u)λcKs,12C2α}
According to Theorem 2, the solution of Model (3) will oscillate around the equilibrium point of Model (1). The amplitude of oscillation is positively correlated with the noise intensity.
In the special case, when σ=0, there is
This indicates that its equilibrium point E0 with respect to Model (1) is globally asymptotically stable.
Theorem 3. If Rs>Rr and Rs>1 , and satisfy:
where
where
where
Then, the solution (T(t),Ts(t),Vs(t),Tr(t),Vr(t)) of Model (3) has
where
Proof. Define the C2 -function Vi(i=1,2,3,4,5)
where b1, b2 is the normal number to be determined.
Applying Itˆo formula to Vi(i=1,2,3,4,5), we get
From the inequality 2ab⩽a2+b2, LVi(i=1,2,3,4,5,6) in Eq (21) can be reduced to the following form
We can define the function V From Vi(i=1,2,3,4,5)
Substituting Eqs (23)–(28) into Eq (22), we get
Then, LV in Eq (26) can be obtained from inequality 2ab⩽a2+b2 and condition (H)
where
There are positive numbers b1 and b2 such that m2(b1)>0 and m3(b1,b2)>0 are true.
In fact, it's just a matter of choosing b1 and b2 so that f(b1)>0 and g(b1,b2)>0 are true. Because f(b1) is a downward opening quadratic function of b1, the discriminant is
We know from (H1) that f(b1)=0 has two positive roots, and the expression is as follows
So, for any b1∈(b11,b12), there is a f(b1)>0. Therefore, m2(b1)>0.
We know from condition (H2) that we choose b∗1∈(b11,b12) such that A(b∗1)>0, B(b∗1)>0.
From m1(b∗1,b2)>0, we can get
Substituting b∗1 into g(b1,b2) we get that g(b∗1,b2) is a downward opening quadratic function of b2, the discriminant is
We know from (H3) that g(b∗1,b2)=0 has two positive roots, and the expression is as follows
So, for any b2∈(b21,b22), there is a g(b2)>0. Therefore, m3(b∗1,b2)>0.
We know from (H4) that there is b*2∈(max{b21,3K2r2A(b∗1)(δ+β(u)f(CN))},b22), such that m1(b∗1,b∗2)>0 and m3(b∗1,b*2)>0 are true.
Equation (30) is simplified as
Integrate Eq (29) from 0 to t and take the expectation of both ends, and we get
Therefore
where
According to Theorem 3, the solution of Model (3) will oscillate around the equilibrium point of Model (1).The amplitude of oscillation is positively correlated with the noise intensity.
In the special case, when σ=0, there is
This indicates that its equilibrium point E* with respect to Model (1) is globally asymptotically stable.
Theorem 4. If Rs>1 and Rr<1 , and satisfy:
where
where
where A(b*1)=α+c(α+KsVs1)λ−5K2s2b*1(δ+f(CN)),
Then, the solution (T(t),Ts(t),Vs(t),Tr(t),Vr(t)) of Model (3) has
where
Proof. Define the C2 -function Vi(i=1,2,3,4,5)
where b1, b2 is the normal number to be determined.
Applying Itˆo formula to Vi(i=1,2,3,4,5), we get
Same as the proof method of Eqs (23)–(28) in Theorem 3, LVi(i=1,2,3,4,5,6) in Eq (32) is simplified as
We can define the function V From Vi(i=1,2,3,4,5)
Substituting Equations (33)–(38) into Eq (32), we get
Then, LV in Eq (39) can be obtained from inequality 2ab⩽a2+b2 and condition (H)
where
Same as the proof of Theorem 3, under the conditions (H1)–(H4), we can find positive values b*1 and b*2 such that m2(b*1)>0 and m3(b∗1,b∗2)>0. Here, the discriminants are respectively
b*1 and b*2 satisfy the following conditions
The selected parameters b∗1 and b∗2 are substituted into Eq (40), and LV is simplified as
Integrate Eq (39) from 0 to t and take the expectation of both ends, and we get
Therefore
where m=min{m1(b∗1,b∗2),m2(b∗2),m3(b∗1,b∗2),b∗1(δ+f(CN))2,b∗2(δ+f(CN))2},
According to Theorem 4, the solution of Model (3) will oscillate around the equilibrium point E∗ of Model (1). The amplitude of oscillation is positively correlated with the value of noise intensity.
In the special case, when σ=0, there is
This indicates that its equilibrium point Es with respect to Model (1) is globally asymptotically stable.
Theorem 5. If Rs<1 and Rr>1 , and satisfy:
where
where
where A(b*1)=α+c(α+KrVr2)λ−5K2s2b*1(δ+f(CN)).
Then, the solution (T(t),Ts(t),Vs(t),Tr(t),Vr(t)) of Model (3) has
where m=min{m1(b∗1,b∗2),m2(b∗2),m3(b∗1,b∗2),b∗1(δ+f(CN))2,b∗2(δ+f(CN))2},
Proof. Define the C2 -function Vi(i=1,2,3,4,5)
where b1, b2 is the normal number to be determined.
Applying Itˆo formula to Vi(i=1,2,3,4,5), we get
Same as the proof method of Equations (23)–(28) in Theorem 3, LVi(i=1,2,3,4,5,6) in Eq (42) is simplified as
We can define the function V From Vi(i=1,2,3,4,5)
Substituting Eqs (43)–(48) into Eq (42), we get
Then, LV in Eq (46) can be obtained from inequality 2ab⩽a2+b2
where
Same as the proof of Theorem 3, under the conditions (H1)–(H4), we can find positive values b*1 and b*2 such that m2(b*1)>0 and m3(b*1,b*2)>0. Here, the discriminants are respectively
b*1 and b*2 satisfy the following conditions
Therefore, defined by Eq (41), the selected parameters b*1 and b*2 are substituted into Eq (50) to be simplified as
Integrate Eq (49) from 0 to t and take the expectation of both ends, and we get
Therefore
where
According to Theorem 5, the solution of Model (3) will oscillate around the equilibrium point Er of Model (1). The amplitude of oscillation is positively correlated with the noise intensity σ.
In the special case, when σ=0, there is
This indicates that its equilibrium point Er with respect to Model (1) is globally asymptotically stable.
4.
Numerical simulation
The resistance of hepatitis B virus due to individual differences or the interference of factors such as environmental changes may cause the virus to mutate and change the original infection rate. The drug cannot accurately act on the mutant virus, and the infection rate is uncertain, so it will be affected by the clinic. Treatment brings many unknown results. By studying the asymptotic behavior of the mathematical model solution with random noise, understanding the influence of the interference of uncertain factors on the model solution can provide a theoretical basis for determining the treatment plan. The following is numerical simulation of the influence of random noise intensity on the model solution.
4.1. Parameter selection
Some of the parameters in Model (1), such as the growth rate λ of healthy liver cells, the mortality rate α of liver cells, the mortality rate δ of viruses, the number of viruses Ns and Nr produced in the life cycle of sensitive and drug-resistant infected liver cells, are shown in Table 2 [24], and the average steady-state plasma concentration is CN=0.8 ng/ml.
Choose four situations to simulate the difference caused by noise. Related parameters such as virus mutation rate u, drug inhibition rate β of virus, sensitive HBV infection rate Ks, drug-resistant HBV infection rate Kr and noise intensity σ are shown in Table 3.
4.2. Influence of noise intensity on the solution of Model (1)
In order to better understand the interference of noise on virus changes, Models (1) and (3) are simulated and compared. Divide Models (1) and (3) into sensitive sub-models and drug-resistant sub-models. The initial values of the model are taken as follows
Case 1: Substituting the parameters in Tables 2 and 3 into Eq (2) can calculate Rs=0.5778 and Rr=0.1825. It can be seen from paper [14] that Model (1) has a disease-free equilibrium point E0, which is a global asymptotically stable point. From Theorem 2, we can see that the solution trajectory of Model (1) is asymptotically oscillating around E0. The simulation results are shown in Figures 3 and 4.
Comparing Figures 3 and 4, it can be found that when the noise intensity increases, the vibration amplitude of the solution of the Model (3) around E0 will also increase.
Case 2: Substituting the parameters in Tables 2 and 3 into Eq (2) can calculate Rs=1.1920 and Rr=1.1853. It can be seen from paper [14] that Model (1) has a drug-sensitive type virus equilibrium point Es, which is a global asymptotically stable point. From Theorem 4, we can see that the solution trajectory of Model (1) is asymptotically oscillating around Es. The simulation results are shown in Figures 5 and 6.
Comparing Figures 5 and 6, it can be found that when the noise intensity increases, the vibration amplitude of the solution of the Model (3) around Es will also increase.
Case 3: Substituting the parameters in Tables 2 and 3 into Eq (2) can calculate Rs=2.1286 and Rr=1.2733. It can be seen from paper [14] that Model (1) has double virus equilibrium point E∗, which is a global asymptotically stable point. From Theorem 3, we can see that the solution trajectory of Model (1) is asymptotically oscillating around E∗. The simulation results are shown in Figures 7 and 8.
Comparing Figures 7 and 8, it can be found that when the noise intensity increases, the vibration amplitude of the solution of the Model (3) around E∗ will also increase.
Case 4: Substituting the parameters in Tables 2 and 3 into Eq (2) can calculate Rs=0.0578 and Rr=1.7230. It can be seen from paper [14] that Model (1) has a drug-resistance type virus equilibrium point Er, which is a global asymptotically stable point. From Theorem 5, we can see that the solution trajectory of Model (1) is asymptotically oscillating around Er. The simulation results are shown in Figures 9 and 10.
Numerical simulation results show that:
Case 4 is different from Cases 1–3. Comparing Figures 9 and 10, when the noise intensity is σ=0.00000008, the solution of Model (3) will eventually oscillate around the drug-resistance equilibrium point Er; When the noise intensity increases to σ=0.0000002, it can be seen from H2) and H4 in Figure 10 that, with the increase of noise intensity, the number of drug-resistant infected cells and drug-resistant HBV will gradually decrease and eventually reach a disease-free equilibrium point. In the other three cases, the oscillations only increased. Therefore, it can be inferred that the increase of noise intensity, which affects the infection rate of drug-resistant HBV, can inhibit the increase of drug-resistant infected cells and drug-resistant HBV when the degree of drug resistance of the virus in patients is high. All Cases 1–4 indicate that with the increase of noise intensity, the oscillation amplitude of the solution of Model (3) will increase, which verifies the conclusion of Theorems 2–5. Case 4 also shows that when drug resistance is high, the increase of noise intensity will inhibit the replication of the virus, that is to say, the interference of human factors can be increased in real life, so that the number of viruses in the patient's body is decrease.
4.3. Influence of noise intensity on antiviral therapy
If drug-resistant virus has been produced in the treatment process, the interference of noise will produce uncertainty phenomenon, so the change trend of virus cannot be accurately judged, and the subsequent treatment cannot achieve the expected goal. Taking the drug-resistance equilibrium point as an example, the initial value in 4.2 and the parameter value in Table 2 are still selected. The average steady state plasma concentration CN is still 0.8 ng/ml. The infection rate Ks of sensitive HBV and the infection rate Kr drug-resistant HBV is 9×10−8 and 5.2×10−8, the mutation rate u is 0.4, and the drug inhibition rate β is 0.6. At this time, the Model (1) has a globally asymptotically stable equilibrium point Er. The changing law of the solution of Model (3) is numerically simulated, and the simulation result is shown in Figure 11.
It can be seen from Figure 11 that due to the influence of noise factors, the number of viruses may fluctuate around the lower limit of detection (103 copies/mL, the critical value for clinical treatment). For example, in Figure11 i1), during the period of 1070 to 1324 days of antiviral treatment, the number of virus will be below the lower limit of detection many times. From i1) to i3) in Figure 11, it can be seen that as the noise intensity increases, the fluctuations near the lower detection limit (103 copies/mL) become more frequent. When it is clinically detected that the HBV DNA of a patient is below the lower limit of detection for many times, the drug will be stopped, but the actual patient is still at the equilibrium point of drug resistance. Stopping the drug will lead to a rapid increase in the number of viruses. The intensity of noise provides an illusion for clinical detection of HBV DNA.
The simulation results found that when the drug-resistant HBV in the patient is the main group of viruses, the increase in noise intensity that affects the infection rate of drug-resistant HBV can effectively inhibit virus replication and reduce drug-resistant infected cells and HBV. But it will also interfere with the correct detection of HBV DNA. Therefore, it is recommended that in the process of clinical treatment, when the patient has strong drug resistance, measures should be taken to suppress the infection rate of the mutant strain, such as dressing change or combined drug therapy, so as to achieve the purpose of treating resistant infection cells and eliminating HBV. When the noise intensity is large, the number of detections should be strengthened during the treatment process, and the time of two detections should be lengthened to improve the accuracy of detection. Even when the number of viruses in the patient's body reaches the lower limit of detection, reasonable consolidation treatment should be carried out to make the patient's treatment more thorough. Avoid noise interference to make the detection inaccurate and affect the patient's antiviral treatment.
5.
Conclusions
This paper established a hepatitis B virus dynamic model with random interference infection rate, proved the existence and uniqueness of the global positive solution, and obtained the asymptotic behavior of the model solution near the equilibrium point of the deterministic model. Through numerical simulation, the conclusion of the theorem is verified, and when the random interference is small enough, the solution of the random model vibrates around the equilibrium point of the determined model. It is found that the amplitude of the oscillation is proportional to the noise intensity.
Acknowledgments
This work was supported by the project of Nature Scientific Foundation of Heilongjiang Province (A2016004).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:














