Application of supervised machine learning as a method for identifying DEM contact law parameters

1.   Introduction

Do et al. ^[1] concluded that a major barrier to the effective use of DEM for industrial applications is selecting appropriate input parameters so that simulations can accurately reproduce the behaviour of real systems. This problem was also raised by, for example, Bevenuti et al. ^[2]. There is a lack of a close relationship in DEM between parameters describing particles interactions and those representing the sample as a whole. The only solution to this problem is the iterative approach, called inverse modelling, in which the selection of microparameters takes place based on macroscopic parameters ^[3]. A commonly used approach is tuning microscopic parameters of bonds until compatibility between laboratory and numerical characteristics is achieved, what is a very arduous and tedious process. Moreover, DEM simulations are very time-consuming, so working on improving calibration procedure to minimize the number of required simulations is crucial to increase the efficiency of the method.

For all the reasons mentioned above, the problem of calibrating DEM models has been undertaken by many research teams using a variety of techniques and approaches, although none of these attempts has become widely used among DEM users. Out of the many interesting works in this area, an application of theoretical formulas is worth mentioning ^[4], or trying to apply dimensional analysis ^[5], stable noisy optimization ^[6], genetic algorithms ^[7] or simulated annealing algorithms ^[8]. The application of artificial neural networks ^[9,10,11] has also been a raised approach. However, the increasing popularity of machine learning algorithms seems to offer completely new possibilities. One of the newest works in this field is ^[12], where the relationship between the macro- and microparameters of rockfill was created by Relevance Vector Machine and a memetic algorithm was used for the calibration of the microparameters. Due to inspiring machine learning capabilities, this article attempts to use supervised machine learning to make further progress towards finding a universal method for calibrating DEM models.

2.   Discrete Element Method

Among the numerous particle-based numerical methods, the Discrete Element Method is one of the most popular. In DEM, the material is represented as an assembly of particles. Elements of simulation can move, rotate and interact with each other ^[3]. The elements can partially overlap each other. When two particles overlap, they start to interact. The magnitude of this interaction depends on the contact forces by the force-displacement relation. The algorithm of the DEM can be divided into two main parts: the first one is related to the creation of a contact model and the calculation of forces acting on the elements and in the second part, the second Newton's law of dynamics is applied to each component to calculate changes of position and velocity as a result of unbalanced action forces. Motion equations are solved separately for each particle ^[13]. The heavy computational burden of the DEM relative to other numerical methods is often one of the most important factors determining the quality and utility of simulation results.

2.1.   Model description

ESyS-Particle is an open-source DEM implementation applied in this work. This software was designed to provide a basis to study the physics of rocks and the nonlinear dynamics of earthquakes and to address the computational limits of existing DEM software ^[14,15]. ESyS-Particle provides different types of interactions (bonds) between particles. One of them - called BrittleBeamPrms in software notation - was designed especially for simulating brittle fracturing and therefore is commonly used in recreating laboratory tests, like uniaxial compression. The BrittleBeamPrms involves all six degrees of freedom of each interacting particle. Three parameters are used to represent the position of the center of the mass of the particle and three other parameters (such as Euler angles) to represent rotations around the center of the mass. Particle motion can be decomposed into two completely independent parts, translational motion of the center of the mass and rotation about the center of the mass. The translational motion of the center of the mass is governed by the Newtonian equations and integrated using a conventional Molecular Dynamic scheme. The particle rotation is controlled by Euler's equations. The algorithm for calculating particle motion can be found in Wang et al. ^[16].

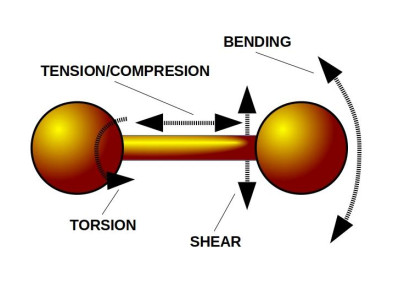
Two bonded particles may undergo normal and shear forces, as well as bending and twisting moments (Figure 1). Rotational frictional interactions impart torque to both particles, causing the particles to rotate relative to each other when they are in a frictional contact ^[15]. The physical interpretation of rotational bonds is that two particles are connected with a cylindrical elastic beam whose radius is the mean of the radii of the bonded particles and whose equilibrium length is the sum of the radii of those particles. Macroscopic elastic properties of an assembly of bonded particles do not necessarily match the microscopic elastic properties of the bonds themselves, so, consequently, model calibration is usually required.

The relationship between forces or torques and relative displacements between two bonded particles (Equation 1) could be written in the following form (assuming small deformations):

where: F - represents forces, M - torques, K - rigidity constant, $∆r$ and $∆s$ - relative translational displacement, $∆\alpha$ - relative angular displacement. The meaning of the symbols r, s, t and b is as follows: r – radial component, s – shearing component, t – twisting component, b - bending component. In the isotropic case, ${K}_{s} = {K}_{s1} = {K}_{s2}$ and ${K}_{b} = {K}_{b1} = {K}_{b2}$. Therefore only four rigidity parameters are required. The elasticity of bonds (under above assumptions and according to linear elastic beam theory) can be defined as functions of two parameters - the bond Young's modulus and the bond Poisson's ratio ^[15]. Bond between particles breaks according to a Mohr-Coulomb failure criterion. It happens when the shear stress inside the bond is bigger than its shear strength (τ), according to the formula: $\tau = c+{\sigma }_{N}tan\left({\varphi }_{f}\right)$ where c_b is the cohesion of the bond for zero normal stress (${\sigma }_{N}$) and ${\varphi }_{f}$ is the internal angle of friction of the bond. Therefore there are four bonds parameters in the model to calibrate: Young's modulus E_b, Poisson's ratio v_b, cohesion c_b, internal friction angle φ_b. Further explanations can be found in ^{[17,18,19,20]} and details of DEM implementation in ESyS-Particle are widely described in ^[16,21,22] or in ^[14,15].

2.2.   Typical approach to calibration

Calibration of the DEM model is usually done by comparing macroscopic parameters coming from laboratory tests and numerical simulations. Application of uniaxial compression test is very common for these purposes. Uniaxial compression is a laboratory test in which a cylindrical sample is compressed from the top and the bottom. A sample is subjected to a controlled compressive displacement along a vertical axis and the change in dimensions and resulting load is recorded to calculate the stress-strain curve ^[23,24]. From the obtained curve, elastic and plastic material properties can be determined. Strain is calculated as relation between the measured vertical displacement and an initial sample height. Stress is defined as a relation between the applied load and the initial cross-sectional area of the sample normal to the loading direction. The slope of the strain-stress curve within the linear elastic regime is equal to Young's modulus, which is the ratio of the stress to axial strain, and the peak of the curve is equal to the uniaxial compressive strength (UCS), maximum axial compressive stress that a right-cylindrical sample of material can withstand before failing ^[23,24]. Young's modulus and UCS are often part of the calibration procedure because they allow to compare laboratory and numerical stress-strain curves. Those two macroscopic parameters are the subject of further consideration.

3.   Supervised machine learning and Discrete Element Method

3.1.   Generating dataset for machine learning algorithms

The idea of that article was to employ supervised machine learning to find relationships between microscopic and macroscopic parameters. It seems that a DEM dataset containing an appropriate amount of data (and collected once) can facilitate any further calibration procedures. Macroscopic parameters of the sample depend, first of all, on parameters: E_b, v_b, c_b, φ_b r_min and r = r_max/r_min. Instead of calibrating those parameters for each new task anew, it could be possible to generate a dependency network between microscopic and macroscopic parameters once and then use supervised machine learning models to predict which set of microparameters will correspond to the desired set of macro-parameters. Such a supervised machine learning model would work appropriately for every task within a given DEM implementation. Presented work is an attempt to generate such a DEM dataset. Further, the collected data were used to train Multiple Linear Regression (MLR) and Random Forest (RF) algorithms.

A dataset for the needs of machine learning algorithms was created during the series of 6480 DEM simulations of uniaxial compression with applied different range of microscopic parameters of bonds. The reference sample was a cylinder with a radius of 3 mm and a height of 12 mm. The range of bonds input parameters was as follows: the minimum particle radius r_min was equal to 0.1, 0.2, 0.3, 0.4, 0.5 mm, the maximum particle radius r_max was equal to 1.0 mm, the microscopic Young's modulus E_b was equal to 1000, 3000, 5000, 7000, 9000, 11000 MPa, the microscopic Poisson ratio v_b was equal to 0.15, 0.17, 0.19, 0.21, 0.23, 0.25, cohesion c_b was equal to 10, 20, 30, 40, 50, 60 MPa, and tangent of internal friction angle φ_b was equal to 0.5, 0.7, 0.9, 1.1, 1.3, 1.5. All possible combinations of the parameters give total number of simulations 6480. Particle density was a fixed parameter equal to 2500 kg/m³. These parameters were selected to include the possibly wide range of values, but with preserve reasonable calculation time. The entire series of 6480 simulations lasted 504 h (three weeks) of continous computations on a personal computer. Particles inside the samples were connected by BrittleBeamPrms bonds, and for a given set of microparameters two macroscopic parameters were defined: the slope of numerical stress-strain curve (Young's modulus) and peak of this curve (Uniaxial Compressive Strength UCS). Model samples were compressed by two walls up to failure.

For the needs of machine learning algorithms, parameters like E_b, v_b, c_b, φ_b r_min and r = r_max/r_min were treated as independent, macroscopic Young's modulus and UCS were treated as dependent. The dataset for the needs of machine learning algorithms, in accordance with the standard approach, was divided (randomly) into the training part and the test part in the ratio of 80% to 20%.

3.2.   Selected algorithms

Supervised learning is the machine learning task of learning a function that maps an input to an output based on example input-output pairs ^[16]. It figures out a function from labelled training data consisting of a set of training examples. In supervised learning, each example is a pair consisting of an input object (typically a vector) and the desired output value. In this attempt, two algorithms have been selected: Multiple Linear Regression (MLR) and Random Forest (RF).

3.3.   Performance of Multiple Linear Regression

Multiple Linear Regression is a statistical technique that uses independent variables to predict the outcome of a dependent variable ^[26]. The goal of MLR is to model the linear relationship between the explanatory (independent) variables and response (dependent) variable. MLR fits a linear model with coefficients β = (β₁, ..., β_n) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation. Between the other algorithms, this one is distinguished due to explicit form of its equation (mapping function):$y = {\beta }_{0}+{\beta }_{1}{x}_{1}+{\beta }_{2}{x}_{2}+...+{\beta }_{n}{p}_{n}+ϵ$, where y is dependent variable, x_i are independent variables, β_i are weights for for each independent variable, ε is the model's error term also known as the residuals.

Applying the MLR algorithm to the DEM dataset gave the following results. Coefficients for macroscopic Young's modulus were as follows: E_b was 0.0019, v_b was -2.6, c_b was 0.016, φ_b was 0.25, r was 1.9, r_min was -1.1e+01 and intercept was -5.22. In case of UCS results were as follows: E_b was 0.0017, v_b was -6.1, c_b was 2.7, φ_b was -4e+01, r was 2.3e+01, r_min was -7.1e+01 and intercept was -49.53. Complete equations are presented below (Equation 2):

Such equations attempt to find out the universal relationship between microscopic and macroscopic parameters in DEM modelling. However, in further steps, it was necessary to assess the quality of predictions. Visual comparison between MLR predictions and DEM results is presented in Figure 2. MLR does not predict the outcome very precisely. Results are significantly biased from the dotted line representing ideal predictions with 100% accuracy.

3.4.   Assessment of multiple linear regression results

Assessment of the performance of the regression algorithm includes application of several essential metrics ^[25,26], namely: 1) coefficient of determination R², also called accuracy, which is the proportion of the variance in the dependent variable that is predictable from the independent variable (the best possible score is 1.0, what is an equivalent of 100% accuracy); 2) Mean Squared Error MSE, which measures the average of the squares of the errors, the average squared difference between the estimated values and the actual value; 3) Mean Absolute Error MAE, which finds all absolute errors (x_i – x), adds them all and divide by the number of errors 4) Root Mean Squared Error RMSE, the square root of the mean of the square of all of the error. Those metrics calculated in this particular case were as follows: for Young's modulus the R² was 0.84, MSE was 15.69, MAE was 2.92, RMSE was 3.96; for UCS: the R² was 0.83, MSE was 1564.10, MAE was 28.25, RMSE was 39.55.

3.5.   Algorithm assumptions

MLR is quite straightforward but it has demanding assumptions ^[26]. The most important are as follows: a linear relationship (correlation) between independent and dependent variables; a multivariate normality - residuals (errors) normally distributed; no multicollinearity - no correlations between independent variables; homoscedasticity – this assumption states that the variance of error terms are similar across the values of the independent variables.

That assumptions were verified in the following way. Linear relationship between independent and dependent variables and multicollinearity were checked with correlation matrix (Table 1). In such a matrix the standard Pearson correlation was calculated between every parameter. Pearson coefficient varied between -1 and 1, where 0 stands for total lack of linear correlations and -1 or 1 means ideal linear correlation ^[25]. From Table 1 it can be concluded that linear correlation between dependent and independent parameters was not very strong and that was probably the main reason of not very good MLR algorithm performance. It is visible that macroscopic Young's modulus was affected mostly by E_b (correlation 0.62), r (correlation 0.67) and r_min (correlation -0.63). The significance of other parameters in negligible. The most influential parameters for UCS were c_b (correlation 0.47), and again r (correlation 0.77), as well as r_min (correlation -0.71).

Deeper assessment of the multicollinearity can give the variance inflation factor (VIF), which is the ratio of the variance of estimating some parameter in a model that includes multiple other terms (parameters) by the variance of a model constructed using only one term ^[26]. VIF calculated for DEM dataset returned following results: E_b was 4.01, v_b was 25.09, c_b was 5.00, φ_b was 8.88, r_min was 12.87, r was 8.56. Basically, VIF should be smaller than 10, but fulfilling this assumption would require removal of precious parameters like v_b.

The third assumption is multivariate normality, which means that residuals (errors) are normally distributed. Graphical representation of residuals distribution is presented in the Figure 3. That assumption was satisfied quite well for both parameters, Young's modulus and UCS.

The last assumption- homoscedasticity states that the variance of error terms is similar across the values of the independent variables. Customary verification tool is a plot of standardized residuals versus predicted values (Figure 4). Ideally, residuals are randomly scattered around 0 (the horizontal line) providing a relatively even distribution. Heteroscedasticity is indicated when the residuals are not evenly scattered around the line ^[26]. There are two big reasons why homoscedasticity is desired. While heteroscedasticity does not cause bias in the coefficient estimates, it does make them less precise. Lower precision increases the likelihood that the coefficient estimates are further from the correct population value. Figures (Figure 4) below suggest that homoscedasticity assumption was not very well satisfied for both parameters.

To summarize, the MLR algorithm presented a mediocre performance on the generated DEM dataset. Probably the amount of data in the dataset was not sufficient for the algorithm, as well as the range of the parameters. Another problem is that MLR works perfectly when linear dependence between dependent and independent variables occurs, which was not the case here. Therefore, the more flexible algorithm was applied further, called Random Forest.

3.6.   Random Forest performance

Random Forest is an algorithm from ensemble family that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting ^[27]. RF is well suitable to produce a predictive model, and its defaults hyperparameters already return satisfactory results and the system is very good at avoiding overfitting. The number of trees in the forest in this particular case was 10. Random Forest was applied to the generated DEM dataset and achieved results are presented in the set of figures below (Figure 5).

Predictions of Random Forest were exceptionally well, especially in case of UCS where correspondence was almost ideal. In case of Young's modulus, some discrepancies appear for the lower values, but most of the results are also ideally suited to the dotted line representing 100% accuracy.

3.7.   Assessment of Random Forest results

Metrics of the Random Forest algorithm for the DEM dataset were as follows: Young's modulus R² metric was 0.98, Mean Squared Error MSE was 1.57, Mean Absolute Error MAE was 0.26, Root Mean Squared Error RMSE was 1.25; for UCS R² metric was 0.999, MSE was 9.08, MAE was 1.77, RMSE was 3.01. That values show very good performance of the algorithm, an attention is especially drawn by very high accuracy (R² metric) almost equal to 100% for both macro-parameters.

Random Forest has another advantage called the feature importance. Feature importance is one of the best qualities of RF because it allows to measure the impact each parameter has on the final prediction. Feature importance of the RF for DEM dataset can be seen below (Figure 6).

That results coincide with the results presented in the correlation matrix (Table 1). Macroscopic Young's modulus is the most affected by microscopic Young's modulus, as well as by radii r and r_min. Other microparameters are negligible. In case of UCS the most significant microparameter is cohesion c_b, as well as r and r_min. Small contribution comes from microscopic Young's modulus E_b and tangent of internal friction angle φ_b.

There is no need to check another algorithms because Random Forest presented almost ideal efficiency on the DEM dataset. Calculated metrics are the best proof of this, especially accuracy almost equal to 100% for macroscopic Young's modulus, as well UCS. Judging on the results, it seems that Random Forest algorithm trained on a properly big DEM dataset can be excellent tool to predict macroscopic parameters of the samples from the given micro-parameters with great precision. However, one of the disadvantages of the presented DEM dataset is the constant size of the cylinder used during uniaxial compression strength tests. In the second part of that work the question was raised how certain macro-parameters of the material change with sample size.

3.8.   Scaling of macroscopic parameters

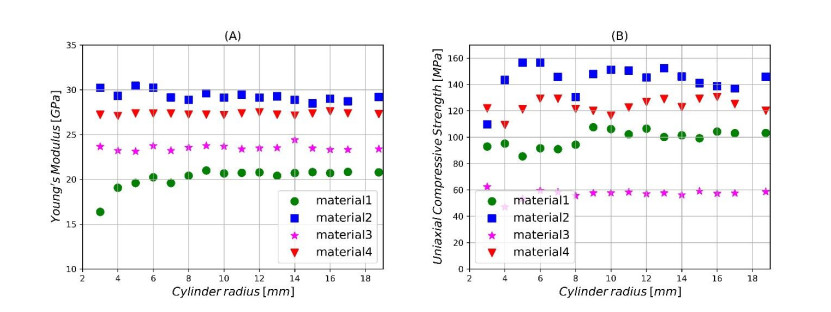
Simulations serving for generating the DEM dataset were carried out for the numerical samples (cylinders) of the same size. It raises the logical question of how the change in sample dimension will affect considered macroscopic parameters. This question is essential from the calibration point of view because it allows to find out whether the model parameters (eg. bonds parameters) found for one model size will also give the same results for larger samples. If this were true, it would save a lot of effort on calibration, as some necessary calculations could be performed on smaller and less time-consuming samples and their results transferred to the actual samples of the original size. Therefore, in the other part, additional tests were carried out concerning scaling of such macroscopic parameters like Young's modulus and UCS in a function of cylinder radius. All the tests were performed for four types of materials, called further shortly material 1, material 2, material 3, material 4. Each material had different density (2429 kg/m³, 2655 kg/m³, 2142 kg/m³, 2448 kg/m³) and distribution of particles radii (0.25–2.0 mm, 0.25–0.5 mm, 0.25–1.0 mm, 0.125–0.5 mm). Those materials created cylindrical samples of height 75 mm and radius 18.75 mm. Such dimensions are typical for real samples used in laboratory uniaxial tests.

Target values (values that should be obtained) in case of material 1 were 20.8 GPa (Young's modulus) and 98 MPa (UCS), in case of material 2–29.2 GPa (Young's modulus) and 136 MPa (UCS), in case of material 3–23.4 GPa (Young's modulus) and 61 MPa (UCS), in case of material 4–27.4 GPa (Young's modulus) and 118 MPa (UCS). Such parameters are typical for sandstone-like materials. Scalablity of macroscopic Young's modulus and UCS was tested for cylindrical samples of radii 3 - 17 mm with resolution of 1 mm. The radius and the height were the only variable parameter, the other parameters were constant for each sample (within each type of material). The DEM simulations of uniaxial compression were carried out in accordance with the international standard ASTM D2938 (Standard Test Method for Unconfined Compressive Strength of Intact Rock Core Specimens), so every cylindrical specimen had a slenderness of 2, where slenderness is the relationship between the height and diameter of the specimen (the consequence of the radius change was a change in height).

The boundary values of the number of particles were as follows. Material 1: radius 3 mm–370 particles, radius 18.75 mm–82266 particles; material 2: radius 3 mm–1275 particles, radius 18.75 mm –339 324 particles; material 3: radius 3 mm–551 particles, radius 18.75 mm–150 563 particles; material 4: radius 3 mm–4525 particles, radius 18.75 mm–82 1 155 851 particles. The biggest DEM models (with radius 18.75 mm and around), equivalents of laboratory samples, were out of the reach of the personal computer. Therefore, DEM simulations of that part of the article were carried out with the help of Supercomputer Cray XC40 "Okeanos" of Interdisciplinary Center for Mathematical and Computational Modelling, Warsaw University. One DEM simulation of uniaxial compression test for a sample with radius 18.75 mm lasted: material 1–287 min (using 92 processors), material 2–667 min (using 228 processors), material 3–335 min (using 93 processors), material 4–1440 min (using 320 processors).

Arrangement of particles and the number of particles were determined by the particle packing algorithm and they depended on the cylinder geometry and particles sizes (radii). Implemented in the ESyS-Particle geometric algorithm places elements according to their geometric relationships using pre-prepared grids. The biggest particles were firstly located in the model domain as the seeds. Then, subsequent particles were inserted in the remaining spaces. This process was completed when the model domain was filled up. The more precise description of the procedure can be found in ^[28].

The best and most promising results were obtained for the Young's modulus (Figure 7a). In this case, it can be seen that this parameter does not depend on the sample size in DEM simulations and the same bonds parameters return similar results as for larger samples. UCS (Figure 7b) is not as well scalable as Young's modulus, but these results are also very similar. Some differences are visible for various types of materials. UCS of material 3 is a practically perfect line, there is no dependence on sample radius. It seems that materials characterized by bigger values of UCS parameter are also characterized by higher discrepancies.

Generally, the results from the set of figures 7 are the most scattered for the smallest values of the considered parameter, it means below radius of 6 mm. Therefore, it seems that samples with radius smaller than 30% of the reference value give less reliable results. Comparison between reference (target) values and results for the samples with radius bigger than 30% of reference radius is as follows: target values in case of material 1 were 20.8 GPa (Young's modulus) against 20.57+/-0.36 for smaller samples and 98 MPa (UCS) against 100.62+/-5.42 for smaller samples; in case of material 2–29.2 GPa (Young's modulus) against 29.16+/-0.44 for smaller samples and 136 MPa (UCS) against 145.21+/-7.04 for smaller samples; in case of material 3 – 23.4 GPa (Young's modulus) against 23.57+/-0.30 for smaller samples and 61 MPa (UCS) against 57.67+/-1.06 for smaller samples; in case of material 4–27.4 GPa (Young's modulus) against 27.32+/-0.13 for smaller samples and 118 MPa (UCS) against 125.18+/-4.33 for smaller samples.

Initially, all the particles inside the material were connected by bonds. Together with progressing compression, some of the bonds disappear due to the acting stresses and a place with lacking bonds can be considered as new fracture. Dependence between number of bonds and cylinder radius is presented in the Figure 8. All the values were scaled (within its material group) to the maximum initial number of bonds of the biggest cylinder. This dependence between number of bonds and sample size is just resulting from the packaging algorithm and the fact that bigger cylinders contain more particles. It is possible to see that this is an exponential relationship with equation f(x) = 0.00014x^3.04, and, very interesting, this dependence is the same for each type of the material.

Other important parameters are kinetic energy (Figure 9a) and potential energy (Figure 9b). Again, that values were scaled against the highest possible energy noted for each type of the material. Kinetic energy can be treated as a sum of all linear and rotational movements of the particles in the material. Potential energy is a sum of all types of energies stored inside the bonds between particles. Again, as in case of number of bonds, this was an exponential dependence with equation f(x) = 0.00027x^2.74 for kinetic energy and f(x) = 0.00009x^3.18 for potential energy. Functions for different types of material were similar, but not identical. In case of kinetic energy at the end of the plot huge differences appeared being probably numerical artifacts.

Concluding, it seems that certain macroscopic parameters show weak or no dependence on sample size, with the threshold ratio between radii defined around 30% (descending below this threshold results in greater differences). It means, for example, that macroscopic Young's modulus of the cylinder of 6 mm radius is basically the same as for the cylinder of almost 19 mm radius. Number of particles inside the cylindrical samples is growing exponentially, therefore using smaller samples during calibration should mean also an exponential time saving. Similar conclusions were drawn for UCS parameter, however, with a slightly larger scatter of results.

4.   Discussion and conclusions

Calibration of DEM models so that the created models correspond to real materials is a difficult, tedious, and time-consuming task ^[29]. Despite the common work on this subject ^[1,2,30], the most typical approach to calibration is the inversion method. The microscopic parameters are selected in trial and error attempt so that the macroscopic parameters generated by them are more or less the same as the macroscopic parameters of the real material. This approach significantly limits the application of the DEM method, especially on a larger, industrial scale. DEM simulations themselves are very time-consuming and generally require the use of a supercomputer, and a significant portion of the time is spent on model calibrating.

Considering the significance of the described problem, this paper attempted to use supervised machine learning to predict macroscopic parameters of the material. Generated DEM dataset, which includes sets of microscopic parameters with corresponding macroscopic parameters, consisted of the results of 6,480 DEM simulations. DEM simulations were a series of uniaxial compression tests on cylindrical samples with a different range of microscopic parameters (parameters of particles and bonds between them), based on which two macroscopic parameters describing the stress-strain curve were calculated, i.e., Young's modulus and Uniaxial Compressive Strength. The generated data were used to train two machine learning models (so-called regressors) - Multiple Linear Regression and Random Forest, using the dataset divided into a training and testing part. Both algorithms were assessed using several basic metrics (assessment was done on the testing part of the dataset), and in the case of Multiple Linear Regression, the degree of fulfillment of the algorithm's basic assumptions was also checked. One of the most basic metrics, i.e. accuracy (R² metric), indicated that Multiple Linear Regression achieves a prediction accuracy of slightly over 80%, which results from not very high linear correlation between independent parameters and dependent parameters. On the other hand, another algorithm, Random Forest, fully confirmed its good reputation, and its accuracy of predictions on the testing dataset reached almost 100% with equally good results of the other metrics.

This clearly demonstrates the feasibility and the possibility of generating a one general DEM dataset with posibly wide range of relevant microscopic parameters and corresponding macro-parameters for training Random Forest algorithm, and such a trained model could later be used by all performing DEM simulations (within one DEM implementation) as a universal method for quick prediction of desired parameters. Unfortunately, the dataset generated for the purposes of this work was still not large enough and complete to satisfied such a role. It would be necessary to expand the range of microscopic parameters, as well as to take into account other macroscopic parameters, such as Poisson's ratio, as well as to include the parameters describing the anisotropic properties of the material. Generating such a dataset once would be quite time-consuming, but its later usefulness would be enormous.

Another issue that was taken up in this paper was an attempt to check whether it is necessary to calibrate DEM models on samples of real dimensions or whether it is possible on smaller, and therefore less time-consuming samples. The macroscopic Young's modulus and Uniaxial Compressive Strength were calculated for the cylindrical DEM models (of the size of real models used in the laboratory), and then it was checked how these two macroscopic parameters behave for models with identical parameters but smaller radii. The obtained results were very promising, and it turned out that if a certain critical value (below 30% of the target radius size) is not exceeded, smaller samples give essentially the same results as a large sample. This can be a handy hint to save a considerable amount of time during calibration, especially since the number of particles in the cylindrical model increases exponentially with the radius of the cylinder, which corresponds to the same increase in computational time.

Acknowledgments

I would like to thank for the support from the statutory funds of the Institute of Geophysics, Polish Academy of Sciences. I would like also to thank the Interdisciplinary Center for Mathematical and Computational Modelling for allowing me to access to the Supercomputer Cray XC40 "Okeanos": Computational Research Grant of Interdisciplinary Center for Mathematical and Computational Modelling, Warsaw University – Project GB79-15. Finally, I would like to thank to all developers of ESyS-Particle and GenGeo software, especially to Dr. Steffen Abe from the Institute for Geothermal Resource Management and Dr. Dion K. Weatherley from The University of Queensland. Thanks are also due to the Reviewers for their comments and improvements.

Conflict of interest

Author declares no conflicts of interest in this paper