Numerical investigation for the nonlinear model of hepatitis-B virus with the existence of optimal solution

Naveed Shahid; Muhammad Aziz-ur Rehman; Nauman Ahmed; Dumitru Baleanu; Muhammad Sajid Iqbal; Muhammad Rafiq; Naveed Shahid; Muhammad Aziz-ur Rehman; Nauman Ahmed; Dumitru Baleanu; Muhammad Sajid Iqbal; Muhammad Rafiq

doi:10.3934/math.2021480

AIMS Mathematics

2021, Volume 6, Issue 8: 8294-8314. doi: 10.3934/math.2021480

Previous Article Next Article

Research article Special Issues

Numerical investigation for the nonlinear model of hepatitis-B virus with the existence of optimal solution

1.
Department of Mathematics, University of Management and Technology, Lahore, Pakistan
2.
Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan
3.
Department of Mathematics, Cankaya University, Balgat 06530, Ankara, Turkey
4.
Institute of Space Sciences, Magurele-Bucharest, Romania
5.
Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
6.
Department of Mathematics, Faculty of Sciences, University of Central Punjab, Lahore, Pakistan

Received: 12 December 2020 Accepted: 06 May 2021 Published: 28 May 2021
MSC : 65N06, 92B99, 37M15

In the recent article, a reaction-advection-diffusion model of the hepatitis-B virus (HBV) is studied. Existence and uniqueness of the optimal solution for the proposed model in function spaces is analyzed. The advection and diffusion terms make the model more generic than the simple model. So, the numerical investigation plays a vital role to understand the behavior of the solutions. To find the existence and uniqueness of the optimal solutions, a closed and convex subset (closed ball) of the Banach space is considered. The explicit estimates regarding the solution of the system for the admissible auxiliary data is computed. On the other hand, for the numerical approximation of the solution, an elegant numerical technique is devised to find the approximate solutions. After constructing the discrete model, some fundamental properties must necessarily be possessed by the proposed numerical scheme. For instance, consistency, stability, and positivity of the solutions. These properties are carefully studied in the current article. To prove the positivity of the proposed scheme, M-matrix theory is used. All the above mentioned properties are verified by sketching the graph via simulations. Furthermore, these plots are helpful to understand the true behavior of the solutions. For this purpose, a fruitful discussion is included about the simulations to justify our results.

Keywords:

Citation: Naveed Shahid, Muhammad Aziz-ur Rehman, Nauman Ahmed, Dumitru Baleanu, Muhammad Sajid Iqbal, Muhammad Rafiq. Numerical investigation for the nonlinear model of hepatitis-B virus with the existence of optimal solution[J]. AIMS Mathematics, 2021, 6(8): 8294-8314. doi: 10.3934/math.2021480

Related Papers:

[1]	Sarbaz H. A. Khoshnaw, Azhi Sabir Mohammed . Computational simulations of the effects of social distancing interventions on the COVID-19 pandemic. AIMS Bioengineering, 2022, 9(3): 239-251. doi: 10.3934/bioeng.2022016
[2]	Mehmet Yavuz, Waled Yavız Ahmed Haydar . A new mathematical modelling and parameter estimation of COVID-19: a case study in Iraq. AIMS Bioengineering, 2022, 9(4): 420-446. doi: 10.3934/bioeng.2022030
[3]	Sarbaz H. A. Khoshnaw, Kawther Y. Abdulrahman, Arkan N. Mustafa . Identifying key critical model parameters in spreading of COVID-19 pandemic. AIMS Bioengineering, 2022, 9(2): 163-177. doi: 10.3934/bioeng.2022012
[4]	Mariem Jelassi, Kayode Oshinubi, Mustapha Rachdi, Jacques Demongeot . Epidemic dynamics on social interaction networks. AIMS Bioengineering, 2022, 9(4): 348-361. doi: 10.3934/bioeng.2022025
[5]	Kayode Oshinubi, Augustina Amakor, Olumuyiwa James Peter, Mustapha Rachdi, Jacques Demongeot . Approach to COVID-19 time series data using deep learning and spectral analysis methods. AIMS Bioengineering, 2022, 9(1): 1-21. doi: 10.3934/bioeng.2022001
[6]	Fırat Evirgen, Fatma Özköse, Mehmet Yavuz, Necati Özdemir . Real data-based optimal control strategies for assessing the impact of the Omicron variant on heart attacks. AIMS Bioengineering, 2023, 10(3): 218-239. doi: 10.3934/bioeng.2023015
[7]	Prasantha Bharathi Dhandapani, Dumitru Baleanu, Jayakumar Thippan, Vinoth Sivakumar . On stiff, fuzzy IRD-14 day average transmission model of COVID-19 pandemic disease. AIMS Bioengineering, 2020, 7(4): 208-223. doi: 10.3934/bioeng.2020018
[8]	Kranthi Kumar Lella, Alphonse PJA . A literature review on COVID-19 disease diagnosis from respiratory sound data. AIMS Bioengineering, 2021, 8(2): 140-153. doi: 10.3934/bioeng.2021013
[9]	Cong Toai Truong, Kim Hieu Huynh, Van Tu Duong, Huy Hung Nguyen, Le An Pham, Tan Tien Nguyen . Model-free volume and pressure cycled control of automatic bag valve mask ventilator. AIMS Bioengineering, 2021, 8(3): 192-207. doi: 10.3934/bioeng.2021017
[10]	Ayub Ahmed, Bashdar Salam, Mahmud Mohammad, Ali Akgül, Sarbaz H. A. Khoshnaw . Analysis coronavirus disease (COVID-19) model using numerical approaches and logistic model. AIMS Bioengineering, 2020, 7(3): 130-146. doi: 10.3934/bioeng.2020013

Abstract

1. Introduction

The emergence of the pandemic COVID-19 in China in the late of 2019 became a critical issue these years globally. In 1930, for the first time the history of coronaviruses recorded when some domesticated chickens were infected by bronchitis virus (IBV) infection. After that in 1960 it was reported in humans for the first time. This disease had a great effect on worldwide economy and people's daily life. Due to the quick outbreak of the virus, specialists tried to refer to the drugs they have already used many years ago for treating SARS and common flu [1]. WHO announced COVID-19 epidemic on 11^th March 2020. By January 20^th, 2022, there were 340,120,476 cases and 5,586,044 of them were deaths and 273,396,004 of them recovered from the disease. It is clear that this disease has not been controlled globally yet and it needs more strategies and preventions to control it.

There were some recently published studies that discussed and analyzed the key critical elements about mathematical models and the spreading of COVID-19 pandemic. There was a study that describes a public data from COVID-19 epidemic in France. It estimates about the model dynamics states of COVID-19 epidemic in France and the regional level SEIR mechanistic model was used. The results showed that a lifting of the lockdown has a great role for further interventions and avoid the epidemic widely [2]. In different studies, a group of researchers developed a mathematical model for this disease, it was defined as a novel Θ-SEIHRD model. This model supports to deal with certain characteristics of this disease that studies the fraction Θ of detected cases for the real total infected cases. It also helps to estimate the required beds in hospitals. The results show that the estimation performed at an early stage of the epidemic could suggest powerful results. These results could be used as a guidance to countries were hugely affected by COVID-19 [3]. A few other researchers conducted some researches on the African continents on COVID-19 epidemic development. The SEIQRDP model was used to establish the realistic estimation of the short-term pandemic condition. The SEIQRDP was a modification of the classical SIR model extensively used in mathematical epidemiology. This model relies on quarantine to a great extent as a productive way of the spread of COVID-19 [4]. Another study sheds light on how social measures such as distance, regional lockdown, quarantine and global public health vigilance, influence the model parameters and the model states. Another critical parameter of COVID-19 is the basic reproduction number called R₀. The global sensitivity analysis is another important technique for infectious diseases. This has been used to observe the impact of different parameters on R₀ [5]. Recently, there was another study that describes local sensitivity analysis of COVID-19 disease. They identified the model critical parameters and considered the relation between model variables and parameters [6].

An effective key element to discuss this disease further and suggest more preventions is data fitting and confirmed cases. This relation between two sets becomes a great step forward to predict this disease further. Data fitting can be used for all infectious disease models, two mathematical models of epidemics have been used to deal with Ebola epidemic in Guinea, Liberia and Sierra Leone. The simulation studies of the model with variable values of sensitive parameters of the spread of the outbreak are undertaken and incorporated in the paper [7]. Recently, there was a compartmental logistic regression and Gaussian model to study and investigate the spread of COVID-19 in Iraq and Egypt by developing SEIR model. The logistic regression and Gaussian models were applied in both countries for the prediction of confirmed cases, and found a very good fitness for incidence data [8]. In addition, there was another study that focused on situation of Saudi Arabia Kingdom for COVID-19. The least square curve fitting was used for the evaluation of the parameters with R₀ ≈ 1.2937 as the number of basic reproduction [9].

There are also many recently published papers on COVID-19 and their impacts in the society. A fractional order of COVID-19 model with Mittag-Leffler kernel was used to analyze this pandemics, the suggested techniques are given in [10]. The stochastic modelling approaches such as transition probabilities and parametric perturbations were applied to calculate some computational dynamics for the SIR model of COVID-19 [11]. The classical SEIR compartment model was used by contact tracing and hospitalization strategies to show the spreading of COVID-19 outbreak [12]. The reader can see more published studies about COVID-19 pandemic in [13]–[20].

Identifying the model critical parameters can be also considered by optimal control analysis that provides more control strategies. This technique has been widely used to COVID-19 pandemics for driving control policies and more interventions. Recently, there was a study that suggested a mathematical model with optimal control to highlight the negative impact of quarantine on diabetic people with Cost-effectiveness presented in [21]. Then, this method was used in analyzing the spread of COVID-19 pandemic with a case study of Brazil and cost-effectiveness, this is given in [22]. More recently, the idea of optimal control analysis was also applied to another suggested model of COVID-19 to show the impact of rapid-tests in controlling this pandemic [23].

Analyzing the suggested SIUWR model based on elasticity of basic reproduction number becomes an important step forward in this study compared to the other existing studies about the confirmed cases of COVID-19 pandemics in Iraq and France. Therefore, we suggest the elasticity coefficient approach to calculate the local sensitivities of basic reproduction number for each model parameters. Another novelty here is the data collection of COVID-19 infected cases for both countries, this provides the future predictions and interventions. Accordingly, we have collected the daily confirmed cases of COVID-19 from January 1^st, 2021 to December 25^th, 2021. The collected real data here give us a great understanding and suggested more interventions and strategies to control this pandemic. Comparing the model results with the real confirmed cases is another novelty for the suggested SIUWR model.

There are some significant contributions in this study. Firstly, we develop and update our previously published model of the COVID-19 pandemic given in [6]. We add more transmission rates to the suggested SIUWR model in order to understand this disease more widely and accurately. Secondly, we compare the model results with the confirmed cases in Iraq and France from January 1^st, 2021 to December 25^th, 2021. Another contribution here is identifying the model critical parameters based on sensitivity of basic reproduction number for each model transmission parameters that helps us to identify the key critical model parameters in spreading this disease.

The organization of this paper is as follows. In Section two, we developed our previously published model and construct the suggested SIUWR model based on our assumptions and model transmissions. Using the next generation matrix to drive the formula of basic reproduction number discussed in Section three. Calculating the model sensitivity based elasticity coefficients is given in Section four. The computational model simulations and the daily infected cases is compared in Section five. Finally, some conclusions and suggestions are given in Section six.

2. A mathematical model for COVID-19 pandemic

The idea of classical kinetic reactions provides an effective tool to represent the biological infectious disease mechanisms in terms of model differential equations with constant rates. There are three important model assumptions in order to define the model equations. They are called model states, parameters, and model equations. We start with n irreversible chemical mechanisms and m chemical species, they are given below:

$\sum_{j = 1}^{m} α_{i j} A_{j} \overset{k_{i}}{\to} \sum_{j = 1}^{m} β_{i j} A_{j}, i = 1, 2, \dots, n$ (1)

where α_ij and β_ij are chemical constant coefficients, A_j for j = 1,2,...,m are chemical components. The chemical reaction rates for equation (1) can be defined as follows:

$v_{i} = k_{i} \prod_{j = 1}^{m} A_{j}^{α_{i j}} (t), i = 1, 2, \dots, n$ (2)

The model differential equations for the chemical reactions (1) are given as follows:

$\frac{d 𝒜}{d t} = \sum_{i \in J \subset ℝ} ℳ_{i} v_{i}, i = 1, 2, \dots, n$ (3)

where $𝒜 \in ℝ^{m}, ℳ_{i} = β_{i j} - α_{i j}$ for i = 1,2,...,n and j = 1,2,...,m. Equation (3) can be also shown as follows:

$\frac{d 𝒜_{j}}{d t} = ℋ_{j} (𝒜) .$ (4)

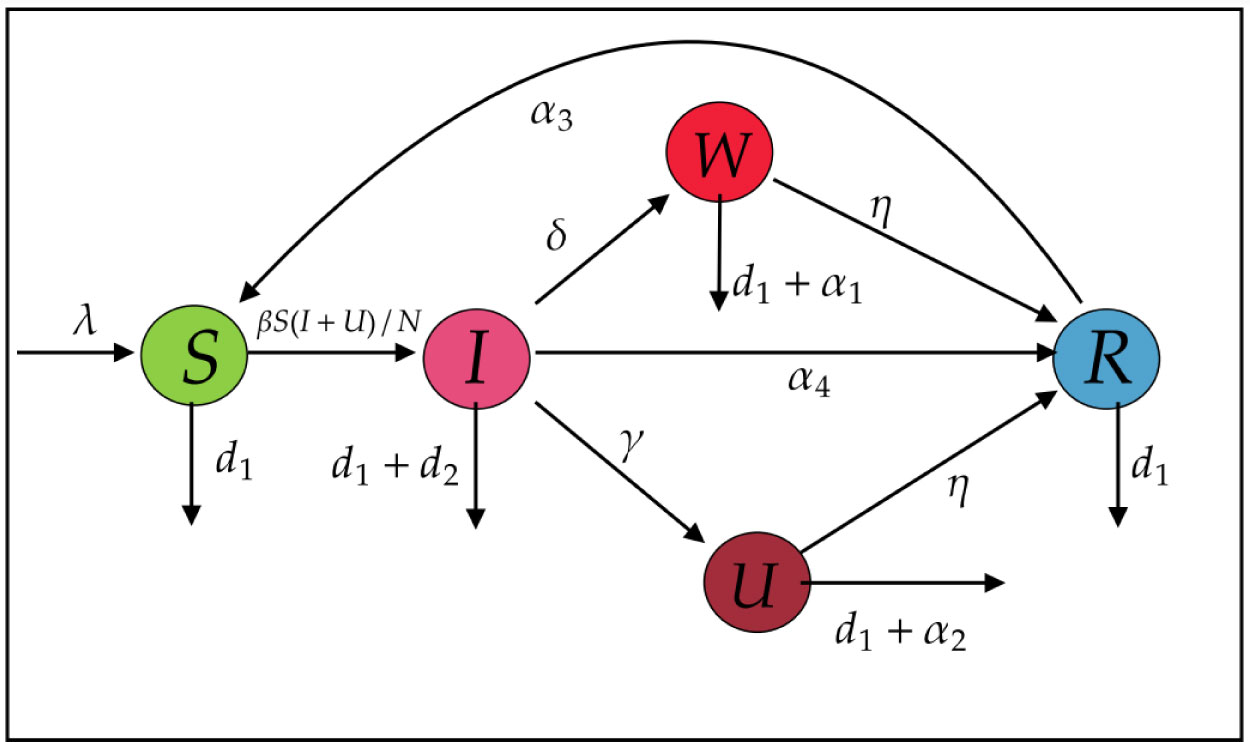
The functions $ℋ_{j}$ , for j = 1,2,...,m are generally non-linear, and model equation (4) may not be solved analytically. Therefore, numerical approaches and computational simulations play an important role in solving such equations. The reader can see more details about the chemical reactions and their applications in systems biology [24]–[27]. Recently, we proposed the SIUWR model to predict the spreading of COVID-19 pandemic. We used the model to find some critical model parameters based on the local sensitivities, the reader can see more details about our previously published paper in [6]. In this paper, we developed the model and added some more transmission rates. For example, we added the natural birth rate λ, the natural death rate d₁, the asymptomatic infected death rate d₂, the unreported symptomatic infected death rate α₁, the reported symptomatic infected death rate α₂, and the immunity loss rate α₃. The suggested model includes five compartments named susceptible individuals S, asymptomatic infected individuals I, reported symptomatic infected individuals W, unreported symptomatic infected individuals U, and recovered individuals R. The model transmission rates and compartments are shown in Figure 1.

Figure 1. The model transmission network for COVID-19 pandemic.

DownLoad: Full-Size Img PowerPoint

All model compartments and parameters are shown in Table 1. Using the mass action law, the model differential equations are defined below:

$\begin{matrix} \frac{d S}{d t} = λ - \frac{β S (I + U)}{N} - d_{1} S + α_{3} R, \\ \frac{d I}{d t} = \frac{β S (I + U)}{N} - (γ + δ + d_{1} + d_{2} + α_{4}) I, \\ \begin{matrix} \frac{d U}{d t} = δ I - (η + α_{1} + d_{1}) U, \\ \frac{d W}{d t} = γ I - (η + α_{2} + d_{1}) W, \\ \frac{d R}{d t} = η W + η U + α_{4} I - (α_{3} + d_{1}) R . \end{matrix} \end{matrix}}$ (5)

With initial model populations S(0) >0, I(0) > 0, U(0) > 0, W(0) > 0, R(0) ≥ 0.

Table 1. Description of the model states and parameters with their estimated values in Iraq and France.

Symbols	Biological definitions	Estimated values - Iraq	Estimated values - France	Sources
S(0)	Initial population of susceptible people	40584909	65063283	[28]
I(0)	Initial population of asymptomatic infected people	789	17523	[28]
U(0)	Initial population of unreported symptomatic infected people	395	9000	Assumed
W(0)	Initial population of reported symptomatic infected people	394	8523	Assumed
R(0)	Initial population of recovered people	581634	25000968	[28]
N	Total population	41179351	67564251	Estimated
λ	Recruitment rate	1482.5537	2241.554	Assumed
β	Constant rate between susceptible people and asymptomatic infected people	0.552	0.558	Assumed
γ	Constant rate between asymptomatic infected people and reported symptomatic infected people	0.2	0.2	Assumed
δ	Constant rate between asymptomatic infected people and unreported symptomatic infected people	0.1	0.1	Assumed
η	Constant rate between reported-unreported symptomatic infected people and recovered people	0.1428	0.1428	Assumed
d₁	Natural death rate	0.001	0.001	Assumed
d₂	The asymptomatic infected death rate	1.5 × 10⁻²	1.5 × 10⁻²	Assumed
α₁	The unreported symptomatic death rate	1.5 × 10⁻⁴	1.5 × 10⁻⁴	Assumed
α₂	The reported symptomatic death rate	1.7826 × 10⁻²	1.7826 × 10⁻²	Assumed
α₃	The immunity loss rate	0.03	0.03	Assumed
α₄	Transition rate between asymptomatic infected and recovered individuals	0.488	0.538	Assumed

| Show Table

DownLoad: CSV

3. Basic reproduction number

The quantity of basic reproduction number, R₀ has a great role in spreading of COVID-19. It defines as the number of secondary infections that infected by a single primary infection in the population. According to the recently published works of epidemiological models, R₀ can provide a wide range of critical model parameters identification. The next-generation matrix is an effective method to derive the basic reproduction number for infectious disease models. This technique was discussed in more details in [29]–[32]. If the individuals are infected in a compartment, then the compartment is classified as an infected compartment. This compartment includes both asymptomatic and symptomatic individuals. Suppose that an infectious disease model has m compartments (x₁, x₂,...,x_m). The model equations are given as follows:

$\frac{d x_{i}}{d t} = f_{i} (x), for i = 1, 2, \dots, m .$ (6)

These compartments can be split into n disease compartments (infected individuals) and k non-disease compartments (non-infected individuals) as follows:

$(x_{1}, x_{2}, \dots, x_{m}) = (\underset{n - infected}{\underset{︸}{x_{1}, x_{2}, \dots, x_{n}}}, \underset{m - noninfected}{\underset{︸}{x_{n + 1}, x_{n + 2}, \dots, x_{m}}}) .$

Let F_i(x) be the rate of appearance of new infections in i^th compartment and the transfer rate is given below:

$V_{i} (x) = V_{i}^{-} (x) - V_{i}^{+} (x),$

where $V_{i}^{+}$ is the rate of transfer of individuals into the i^th compartment and $V_{i}^{-}$ is the rate of transfer of individuals out of the i^th compartment, they are shown in Figure 2.

Figure 2. Input and output fluxes related to compartment $x_{i}^{I}$ .

DownLoad: Full-Size Img PowerPoint

Again, we denote the subpopulations by $x^{I} \in R^{n}$ and $x^{N} \in R^{K}$ . The grouping of new infections from all other model compartments is essential. It helps in determining the basic reproduction number R₀. The compartmental model Equation (6) can be put in the following form:

${\begin{array}{l} \frac{d x_{i}^{I}}{d t} = F_{i} (x^{I}, x^{N}) - V_{i} (x^{I}, x^{N}), i = 1, 2, \dots, n \\ \frac{d x_{j}^{N}}{d t} = M_{j} (x^{I}, x^{N}) . j = 1, 2, \dots, k \end{array}$ (7)

Now, we define the Jacobian matrices F and V as follows:

$F = [\frac{\partial F_{i} (x_{0})}{\partial x_{j}^{I}}] and V = [\frac{\partial V_{i} (x_{0})}{\partial x_{j}^{I}}], 1 \leq i, j \leq n$ (8)

where x₀ is the free equilibrium point for Equation (6), F is the entry wise non-negative and V is a non-singular matrix. The basic reproduction ratio R₀ is given by the spectral radius (dominant eigenvalue) of the next generation matrix FV⁻¹ given below:

$R_{0} = ρ (F V^{- 1})$ (9)

where ρ denotes the spectral radius. The reader can see more details regarding to the next generation matrix and the basic reproduction ratio with their applications in the infection disease models given in [33]–[38].

Taking the right-hand side of system (5) and equating it to zero, the disease-free equilibrium point is given below:

$E_{0}^{1} = (\frac{λ}{d_{1}}, 0, 0, 0, 0) .$

$\frac{d}{d t} [\begin{matrix} I \\ W \\ U \end{matrix}] = [\begin{matrix} \frac{β S (I + U)}{N} \\ 0 \\ 0 \end{matrix}] - [\begin{matrix} (d_{1} + d_{2} + γ + δ + α_{4}) I \\ (η + α_{2} + d_{1}) W - γ I \\ (η + α_{1} + d_{1}) U - δ I \end{matrix}]$ (10)

For system (10) and using the equilibrium point $E_{0}^{1} = (\frac{λ}{d_{1}}, 0, 0, 0, 0)$ , the matrices F and V are defined below:

$\begin{matrix} F = [\begin{matrix} \begin{matrix} \frac{λ β}{N d_{1}} & 0 & \frac{λ β}{N d_{1}} \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \end{matrix}], \\ V = [\begin{matrix} γ + δ + d_{1} + d_{2} + α_{4} & 0 & 0 \\ - γ & η + α_{2} + d_{1} & 0 \\ - δ & 0 & η + α_{1} + d_{1} \end{matrix}] . \end{matrix}$

Therefore, the next generation matrix is as follows:

$F V^{- 1} = [\begin{matrix} \begin{matrix} \frac{λ β}{N d_{1} (γ + δ + d_{1} + d_{2} + α_{4})} + \frac{β λ δ}{N d_{1} (γ + δ + d_{1} + d_{2} + α_{4}) (η + α_{1} + d_{1})} & 0 & \frac{λ β}{N d_{1} (η + α_{1} + d_{1})} \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \end{matrix}] .$

Thus, FV⁻¹ has one dominant eigenvalue. The equation of the basic reproduction number for system (5) with the free equilibrium point $E_{0}^{1} = (\frac{λ}{d_{1}}, 0, 0, 0, 0)$ is given below:

$R_{0} = \frac{β λ (α_{1} + d_{1} + δ + η)}{N d_{1} (γ + δ + d_{1} + d_{2} + α_{4}) (η + α_{1} + d_{1})} .$ (11)

4. Elasticity of R₀

The concept of elasticity for infectious disease models has an effective role in determining sensitivity between R₀ and the model parameters. This technique was discussed in more details in [31],[36],[38]. For calculating such coefficients, the following essential formula is used,

$Γ_{ω}^{R_{0}} = \frac{\partial R_{0}}{\partial ω} * \frac{ω}{R_{0}},$ (12)

where ω is the set of all parameters, we calculate the elasticity index of R₀ for each model parameter. They are given below:

$\begin{array}{l} Γ_{λ}^{R_{0}} = 1, \\ Γ_{β}^{R_{0}} = 1, \\ Γ_{γ}^{R_{0}} = - \frac{γ}{γ + δ + d_{1} + d_{2} + α_{4}}, \\ Γ_{δ}^{R_{0}} = \frac{δ (γ + d_{2} + α_{4} - α_{1} - η)}{(α_{1} + d_{1} + δ + η) (γ + δ + d_{1} + d_{2} + α_{4})}, \\ Γ_{η}^{R_{0}} = - \frac{η δ}{(α_{1} + d_{1} + δ + η) (η + α_{1} + d_{1})}, \\ Γ_{d_{1}}^{R_{0}} = \frac{(\begin{matrix} - 2 d_{1}^{3} + (- d_{2} - 4 η - 4 δ - γ - 4 α_{1} - α_{4}) d_{1}^{2} - \\ 2 (η + δ + α_{1}) (η + d_{2} + δ + γ + α_{1} + α_{4}) d_{1} - \\ (η + α_{1}) (η + δ + α_{1}) (d_{2} + δ + γ + α_{4}) \end{matrix})}{(α_{1} + d_{1} + δ + η) (γ + δ + d_{1} + d_{2} + α_{4}) (η + α_{1} + d_{1})}, \\ Γ_{d_{2}}^{R_{0}} = - \frac{d_{2}}{γ + δ + d_{1} + d_{2} + α_{4}}, \\ Γ_{α_{1}}^{R_{0}} = - \frac{α_{1} δ}{(α_{1} + d_{1} + δ + η) (η + α_{1} + d_{1})}, \\ Γ_{α_{2}}^{R_{0}} = 0, \\ Γ_{α_{3}}^{R_{0}} = 0, \\ Γ_{α_{4}}^{R_{0}} = - \frac{α_{4}}{γ + δ + d_{1} + d_{2} + α_{4}}, \end{array}$

Using the estimated parameters, we can compute the model elasticity; see Table 2.

Table 2. Elasticity coefficient value of R₀ regarding to model parameters.

Elasticity coefficients	Iraq	France
$Γ_{λ}^{R_{0}}$	1	1
$Γ_{β}^{R_{0}}$	1	1
$Γ_{γ}^{R_{0}}$	−0.24875621	−0.23419203
$Γ_{δ}^{R_{0}}$	0.28554195	0.29282404
$Γ_{η}^{R_{0}}$	−0.40664526	−0.40664526
$Γ_{d_{1}}^{R_{0}}$	−1.00409143	−1.00401861
$Γ_{d_{2}}^{R_{0}}$	−0.01865671	−0.01756440
$Γ_{α_{1}}^{R_{0}}$	−0.00042714	−0.00042714
$Γ_{α_{2}}^{R_{0}}$	0	0
$Γ_{α_{3}}^{R_{0}}$	0	0
$Γ_{α_{4}}^{R_{0}}$	−0.60696517	−0.62997658

| Show Table

DownLoad: CSV

Results given in Table 2 show the positive and negative relation for the model elasticity. These give us the direct or indirect relation between R₀ and the model parameters. For example, this coefficient is positive for the set of parameters {λ, β, δ}. This means that when the parameters {λ, β, δ} are increased, the value of R₀ is increased too and this virus spreads further. On the other hand, the signs of {γ, η, d₁, d₂, α₁, α₄} are negative. It means that the value of basic reproduction number can be reduced by increasing such parameters. However, the reproduction number does not have relation with the parameters {α₂, α₃} that means increasing or decreasing the value of {α₂, α₃} do not make a significant effect on the value of R₀.

5. Computational results and discussions

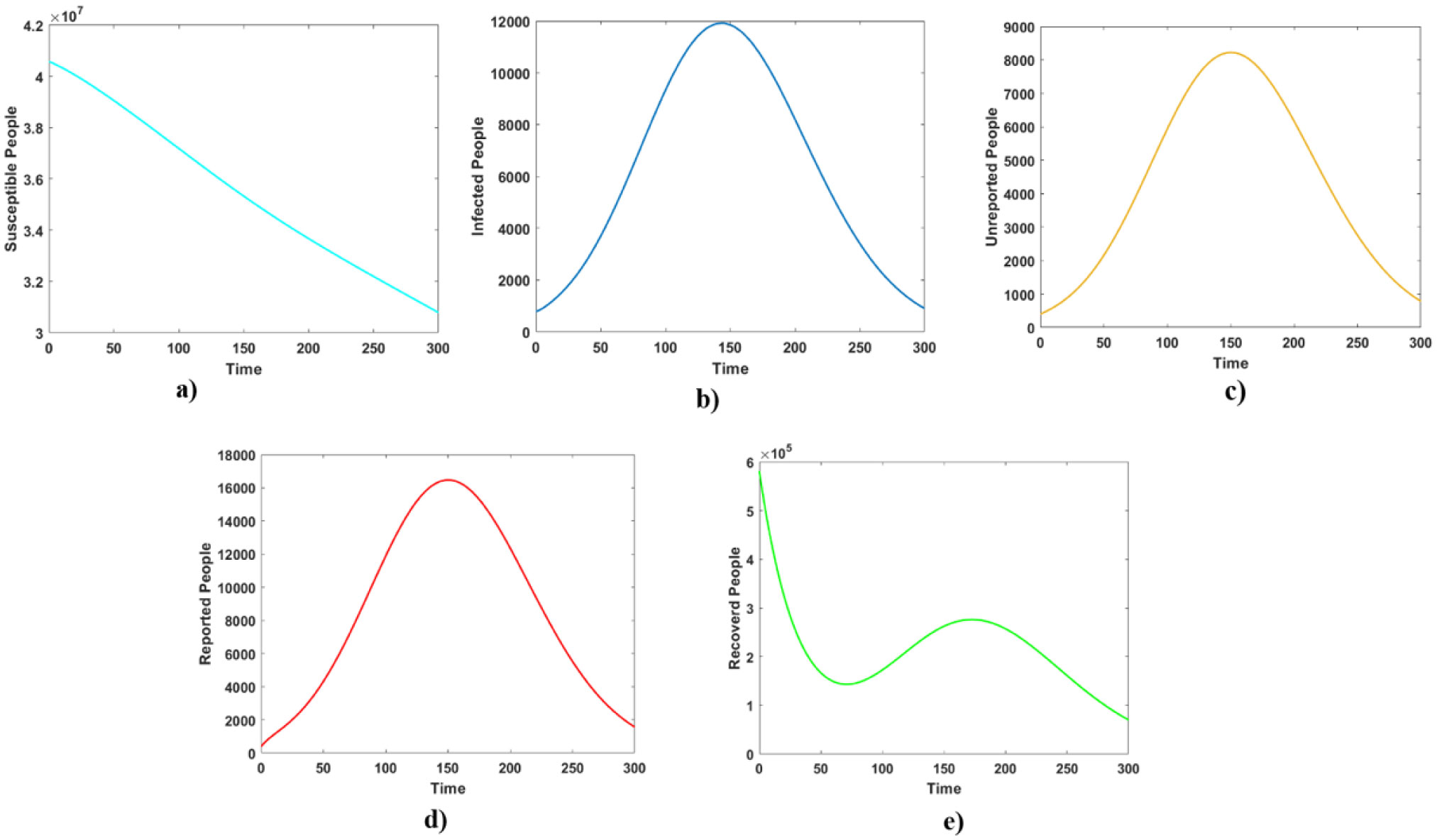
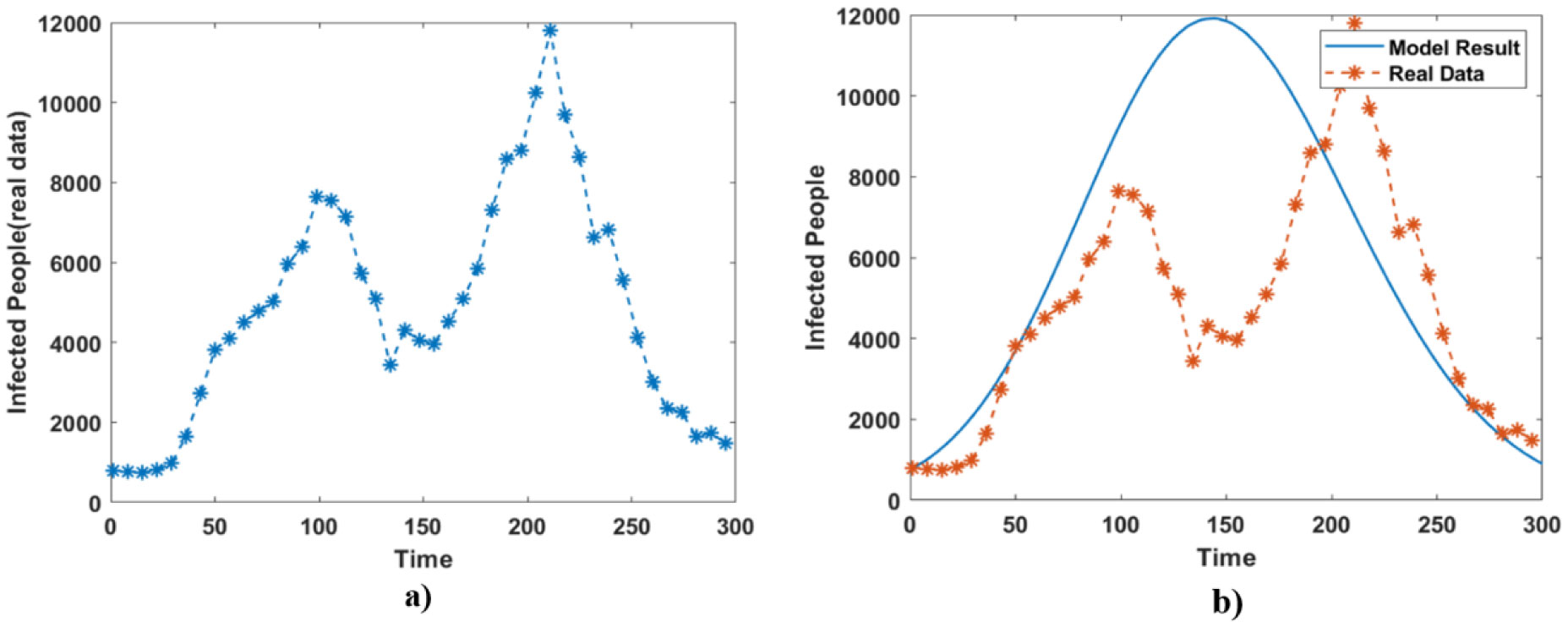
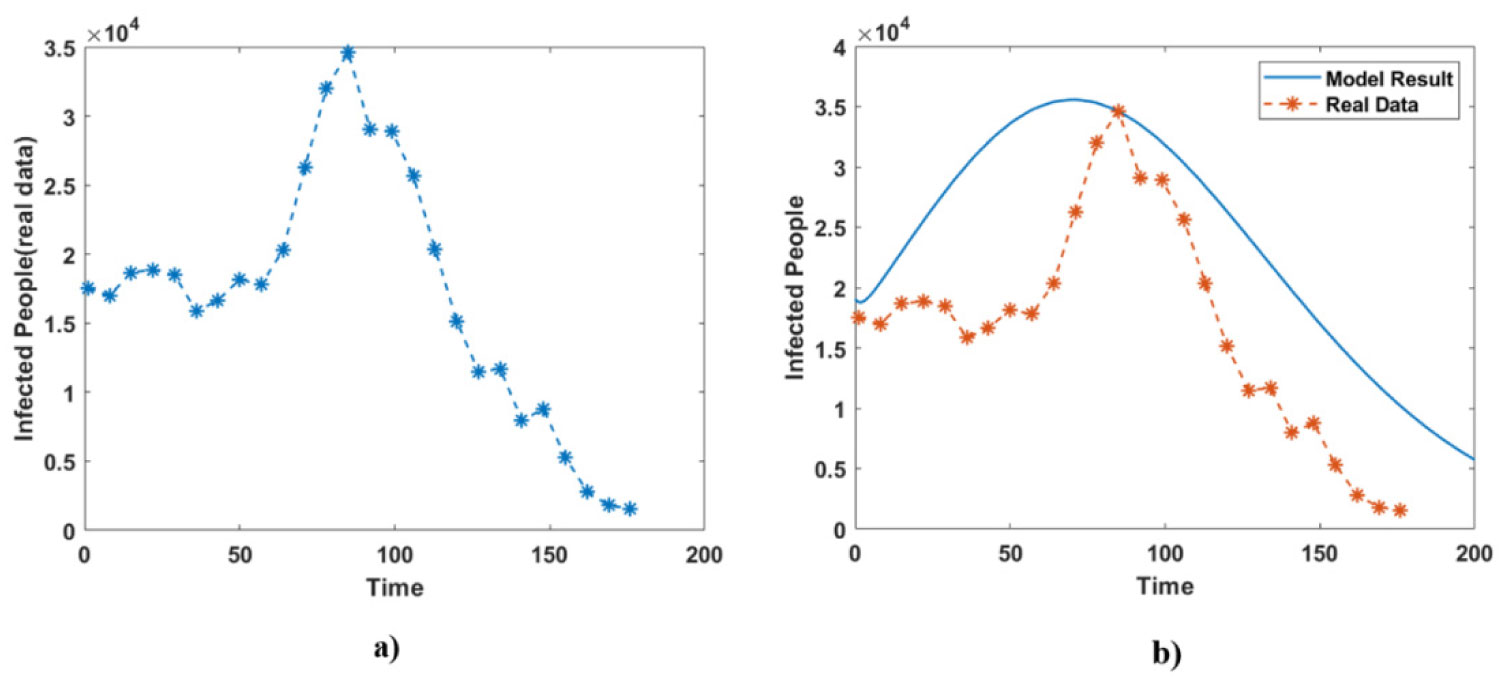
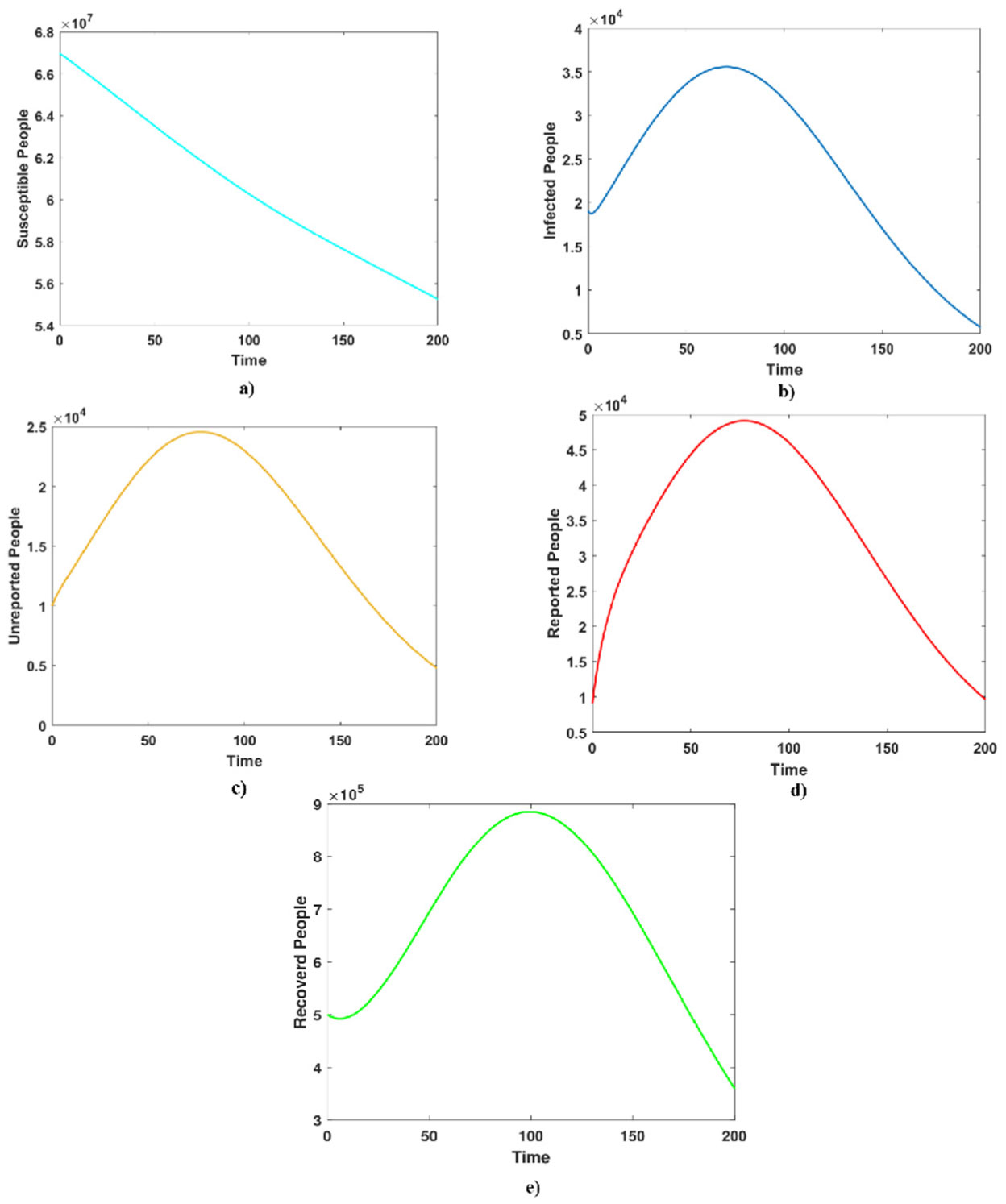
Using computational tools are essential for analyzing complex infectious disease models. Here in this study, we have used MATLAB tools to compute the predicated values for the populations of the spreading COVID-19. We collected the real data of this disease in Iraq and France from 1^st of January 2021 to 25^th of December 2021. All the confirmed cases for both countries are given in the supplementary files (Tables 3 and 4). The estimated variables and parameters given in Table 1 for Iraq and France are used in computational simulations using MATLAB. Figures 3 and 6 show the model results using the initial states and parameters given in Table 1 for Iraq and France, respectively. The total populations of susceptible, symptomatic infected, unreported symptomatic infected, reported symptomatic infected and recovered individuals are computed. In addition, Figure 4(a) shows the total number of infected cases in Iraq using real data given in Table 3. Accordingly, the model results and confirmed infected cases are compared in Figure 4(b), it is clear that there is a good agreement between both model results and the real data. In this vein, Figure 5(a) shows the total infected people in France using the real data given in Table 4. On the other hand, Figure 5(b) shows both model results and real data of the number of infected individuals in France. It is seen that the model results have a good agreement with the real data. Therefore, the suggested SIWUR model can be further used for future predictions and estimations.

Numerical results here give more biological interpretations. As it is clear that computational simulations help international efforts for controlling this pandemic significantly. The dynamics of each compartment can be clearly shown, such model dynamics provide an important environment to predict the future spreading of this virus. For instance, the number of asymptomatic infected, reported symptomatic, unreported symptomatic individuals are simply shown in the computational results here. Accordingly, our model results show that the number of infected people in Iraq has been dramatically changed for the months of February to October. While, there was a big change in the number of confirmed cases in France between March and July. Interestingly, the number of infected people in both countries were significantly declined at the end of 2021.

Figure 3. Computational simulations for the model states given in system (5) of the COVID–19 using MATLAB for the estimated values in Iraq given in Table 1; (a) Susceptible individuals, (b) Asymptomatic infected individuals, (c) Unreported symptomatic infected individuals, (d) Reported symptomatic infected individuals, (e) Recovered individuals.

DownLoad: Full-Size Img PowerPoint

Figure 4. The number of infected people, a) The real confirmed cases in Iraq, b) The model results and the confirmed cases in Iraq.

DownLoad: Full-Size Img PowerPoint

Figure 5. The number of infected people, a) The real confirmed cases in France, b) The model results and the confirmed cases in France.

DownLoad: Full-Size Img PowerPoint

Figure 6. Computational simulations for the model states given in system (5) of the COVID–19 using MATLAB for the estimated values in France given in Table 1; (a) Susceptible individuals, (b) Asymptomatic infected individuals, (c) Unreported symptomatic infected individuals, (d) Reported symptomatic infected individuals, (e) Recovered individuals.

DownLoad: Full-Size Img PowerPoint

6. Conclusions

Analyzing and studying the spreading of COVID-19 pandemic has become a global topic and many studies have been proposed. Comparing the confirmed cases with the model results provide a wide range of environment to predict and give suggestions for further preventions.

In this study, we developed and updated our previously published model of the COVID-19 pandemic and added more transmission rates in order to understand this disease more widely and accurately. In addition, we compared the model results and the confirmed cases in Iraq and France from January 1^st, 2021 to December 25^th, 2021. Then, the model critical parameters based on sensitivity of basic reproduction number for each model transmission parameters are identified. This helps us to identify the key critical model parameters in spreading this disease.

The suggested model here is more appropriated and fitted to the real confirmed cases in Iraq and France. Accordingly, the computational results show that there are good agreements between the model dynamics and daily cases in both countries. This is an effective forward step to study this model more widely and accurately. Identifying the critical model parameters based on sensitivity and elasticity techniques help us to understand such global issues theoretically and practically. Interestingly, the suggested model can be also used to further predications and give more control strategies.

References

[1]	A. Neumaier, Mathematical model building, In: J. Kallrath, Modeling Languages in Mathematical Optimization, Applied Optimization, Boston: Springer, 88 (2004), 37–43.
[2]	N. Shahid, N. Ahmed, D. Baleanu, A. S. Alshomrani, M. S. Iqbal, M. Aziz-ur Rehman, et al., Novel numerical analysis for nonlinear advection-reaction-diffusion systems, Open Phys., 18 (2020), 112–125. doi: 10.1515/phys-2020-0011
[3]	N. Ahmed, M. Rafiq, M. A. Rehman, M. S. Iqbal, M. Ali, Numerical modeling of three dimensional Brusselator reaction diffusion system, AIP Adv., 9 (2019), 015205. doi: 10.1063/1.5070093
[4]	M. Rafiq, J. E. M. Diaz, A. Raza, N. Ahmed, Design of a nonlinear model for the propagation of COVID-19 and its efficient nonstandard computational implementation, Appl. Math. Modell., 89 (2021), 1835–1846. doi: 10.1016/j.apm.2020.08.082
[5]	N. Ahmed, Z. Wei, D. Baleanu, M. Rafiq, M. A. Rehman, Spatio-temporal numerical modeling of reaction-diffusion measles epidemic system, Chaos, 29 (2019), 103101. doi: 10.1063/1.5116807
[6]	A. Chekroun, M. N. Frioui, T. Kuniya, T. M. Touaoula, Global stability of an age-structured epidemic model with general Lyapunov functional, Math. Biosci. Eng., 16 (2019), 1525–1553. doi: 10.3934/mbe.2019073
[7]	G. J. Lan, Z. Y. Lin, C. J. Wei, S. W. Zhang, A stochastic SIRS epidemic model with non-monotone incidence rate under regime-switching, J. Franklin Inst., 356 (2019), 9844–9866. doi: 10.1016/j.jfranklin.2019.09.009
[8]	M. Chaudhary, P. R. Sodani, S. Das, Effect if COVID-19 on econom in India: Some reflections for policy and programme, J. Health Managemant, 22 (2020), 169–180.
[9]	N. Dimitri, The economics of epidemic diseases, Plos One, 10 (2015), e0137964. doi: 10.1371/journal.pone.0137964
[10]	L. Zou, W. Zhang, S. Ruan, Modeling the transmission dynamics and control of hepatitis B virus in China, J. Theor. Biol., 262 (2010), 330–338. doi: 10.1016/j.jtbi.2009.09.035
[11]	F. A. Milner, R. Zhao, SIR model with directed spatial diffusion, Math. Popul. Stud., 15 (2008), 160–181. doi: 10.1080/08898480802221889
[12]	X. Zhou, J. Cui, Analysis of stability and bifurcation for an SEIV epidemic model with vaccination and nonlinear incidence rate, Nonlinear Dyn., 63 (2011), 639–653. doi: 10.1007/s11071-010-9826-z
[13]	T. Khana, G. Zamana, M. I. Chohanb, The transmission dynamic and optimal control of acute and chronic hepatitis B, J. Biol. Dyn., 11 (2016), 172–189.
[14]	M. Zhang, Z. Lin, A reaction-diffusion-advection model for Aedes aegypti mosquitoes in a time periodic environment, Nonlinear Anal.: Real World Appl., 46 (2019), 219–237. doi: 10.1016/j.nonrwa.2018.09.014
[15]	N. Ahmed, S. S. Tahira, M. Imran, M. Rafiq, M. A. Rehman, M. Younis, Numerical analysis of auto-catalytic glycolysis model, AIP Adv., 9 (2019), 085213. doi: 10.1063/1.5112831
[16]	J. Wang, F. Xie, T. Kuniya, Analysis of a reaction-diffusion cholera epidemic model in a spatially heterogeneous environment, Commun. Nonlinear Sci. Numer. Simul., 80 (2020), 104951. doi: 10.1016/j.cnsns.2019.104951
[17]	K. N. Nabi. C. N. Podder, Sensitivity analysis of chronic hepatitis C virus infection with immune response and cell proliferation, Int. J. Biomath., 13 (2020), 2050017. doi: 10.1142/S1793524520500175
[18]	B. A. Danquah, F. Chirove, J. Banasiak, Effective and ineffective treatment in a malariamodel for humans in an endemic region, Afr. Mat., 30 (2019), 1181–1204. doi: 10.1007/s13370-019-00713-z
[19]	K. Goel, Nilam, A mathematical and numerical study of a SIR epidemic model with time delay, nonlinear incidence and treatment rates, Theory Biosci., 138 (2019), 203–213. doi: 10.1007/s12064-019-00275-5
[20]	M. M. Hikal, W. K. Zahra, On fractional model of an HIV/AIDS with treatment and time delay, Progr. Fract. Differ. Appl., 2 (2016), 55–66. doi: 10.18576/pfda/020106
[21]	V. A. F. Costa, On the stability and convergence of numerical solutions, In: Numerical Heat Transfer, Part B: Fundamentals, 79 (2020), 55–69.
[22]	R. E. Mickens, Positivity preserving discrete model for the coupled ODE modeling glycolysis, Proceeding of the Fourth International Conference on Dynamical Systems and Differential Equations, USA, (2002), 623–629.
[23]	R. S. Cantrell, C. Cosner, Spatial Ecology via Reaction-Diffusion Equations, UK: John Wiley and Sons, 2003.
[24]	X. He, W. M. Ni, The effects of diffusion and spatial variation in Lotka-Volterra competition-diffusion system II: The general case, J. Differ. Equations, 254 (2013), 4088–4108. doi: 10.1016/j.jde.2013.02.009
[25]	P. Zhou, On a Lotka-Volterra competition system: Diffusion vs advection, Calculus Var. Partial Differ. Equations, 55 (2016), 1–29. doi: 10.1007/s00526-015-0942-y
[26]	A. K. Mojtabi, M. Deville, One dimensional linear advection-diffusion equation: An alytical and finite element solutions, Comput. Fluids, 107 (2015), 189–195. doi: 10.1016/j.compfluid.2014.11.006
[27]	A. V. Mamonov, Y. H. R. Tsai, Point source identification in nonlinear advection-diffusion-reaction systems, Inverse Probl., 29 (2013), 035009. doi: 10.1088/0266-5611/29/3/035009
[28]	V. J. Ervin, J. E. M. Diaz, J. Ruiz-Ramirez, A positive and bounded 439 finite element approximation of the generalized Burgers-Huxley equation, J. Math. Anal. Appl., 424 (2015), 1143–1160. doi: 10.1016/j.jmaa.2014.11.047
[29]	I. Boztosuna, A. Charafi, An analysis of the linear advection-diffusion equation using mesh free and mesh-dependent methods, Eng. Anal. Boundary Elem., 26 (2002), 889–895. doi: 10.1016/S0955-7997(02)00053-X
[30]	T. Fujimoto, R. Ranade, Two characterizations of inverse positive matrices: The Hawkins-Simon condition and the Le Chatelier-Braun principle, Electron. J. Linear Algebra, 11 (2004), 59–65. doi: 10.1002/nla.333

This article has been cited by:

Alaa Falih Mahdi, Hussein K. Asker, A Sensitivity Analysis of the PSITPS Epidemic Model’s Parameters for COVID-19, 2024, 11, 2518-0010, 79, 10.31642/JoKMC/2018/110210

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)