Exponential stabilization of fixed and random time impulsive delay differential system with applications

1.   Introduction

The time delay plays an important role in various fields such as biology, economics, chemistry, physiology, neural network, engineering, etc. Indeed, the presence of delay in models often results in chaos, instability, and poor performance. The effect of time delay on nonlinear models has been the objective of many researchers in the last decades. For instance in ^[1], Mackey and Glass investigated the time delay nonlinear model of blood cell production for patients with Leukemia. However in ^[2], Ikeda studied the chaotic nature of delay of the optical bistable resonator.

On other direction, time delay systems which describe real phenomena might undergo sudden changes in their nature. This case is best described by incorporating the action of impulses to time delay systems which provides more adequate interpretation for real situations. It has been realized that the action of the impulses may cause chaos and instability in systems. Alternatively, impulses can be used as a control to stabilize and synchronize the chaotic delayed systems. We refer here to the papers ^[3,4] where impulsive stabilization results for chaotic systems are studied and to the paper ^[5] where the impulsive stabilization and impulsive synchronization for Lorenz system are proved. In ^[6], it was shown that the impulsive controller guarantees the exponential convergence rate and exponential stability of chaotic time delay systems. Recently, several types of stability results are obtained based on impulsive control theory ^{[7,8,9,10,11]}. For more impulsive stability and synchronization results, we refer the reader to the literature ^{[12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]}.

The study of delay differential systems with impulses has attracted the attention of many researchers due to their practical applicability in describing the nature of occurrences in real-world systems that often require past history and change from one state to another. However, most works have been conducted for systems with fixed impulses. Never the less, it has been realized that the impulsive arrival taken at random times leads to the solutions that are stochastic in nature and is different from the deterministic impulses. The literature has witnessed the appearance of some works on differential systems with random impulses. The existence, uniqueness, and stability of differential systems with random impulses have been carried out in ^[31]. The study of $p-$th moment exponential stability of differential systems with randomly occurring impulses has been done in ^[32]. Recently in ^[33], the authors investigated the applicability of random impulse control to make the unstable time-delay systems stable. Particularly, the exponential stability for stochastic differential systems under the impulsive effects taken at random time points was investigated in ^[34,35,36]. To the best of our observation, however, there is no paper has addressed the concepts of global exponential stability (GES) for random impulsive scalar delayed equation (RIDDEs) and random impulsive scalar chaotic delayed equation (RISCDEs) by using Lyapunov and Razumikhin technique. Most of the impulsive stabilization and impulsive synchronization results published in the literature have involved fixed time impulsive effects ^{[37,38,39,40,41,42,43,44,45]}.

The objective of this paper is to fill in this gap and investigate functional differential equations and scalar chaotic delayed equations under the effects of impulses taken at fixed and random times. For this purpose, we consider the effects of impulses taken at random time points and assume the waiting time between two consecutive impulses to follow an exponential distribution. The Lyapunov-Razumikhin technique is employed to obtain $p-$th moment GES. Moreover, the $p-$th moment global exponential synchronization(GESy) for the given systems is addressed. For the purpose of applications, we examine the validity of our results by applying them to the Mackey-Glass blood cell production and Ikeda optical bistable resonator models. Comparing to the above mentioned results, we claim that our results are new and discusses different approach. The current paper extends and improves the results reported in ^[46].

The structure of the paper is as follows: In section $2$, essential preliminaries and model formulation are adressed. In Section $3$, we prove $p-$th moment GES and $p-$th moment GESy for the proposed systems. In section $4$, the obtained results are applied to Mackey-Glass blood cell production and Ikeda optical bistable resonator models. The effectiveness of fixed and random impulses are illustrated via graphical representations. We end the paper by a conclusion.

Notations: Let $\mathbb{R} = (-\infty, \infty)$, $\mathbb{R}_{+} = [0, \infty)$, and $\mathbb{Z}_{+} = \left\{1, 2, \dots\right\}$. Let $\mathbb{R}^{n}$ be the Euclidean space and $(\Omega, \mathcal{F}, P)$ be a probability space. Let $\mathcal{PC}\left(\left[-r, 0\right], \mathbb{R}^{n}\right) = \{\varphi: [-r, 0] \rightarrow \mathbb{R}^{n}\}$ be the set of all piecewise right continuous real valued random variables, and $E\|\varphi \| = \sup\limits_{\theta \in [-r, 0]} E\| \varphi (\theta)\|$, denotes the norm of function $\varphi \in \mathcal{PC}\left(\left[-r, 0\right], \mathbb{R}^{n}\right)$, where $E$ is the expectation operator and $r > 0$. We use $PC\mathcal{B}(t)$ to denote set of all bounded piecewise right continuous real valued random variables $\varphi$. Let $\{\tau_m^{'}\}_{m = 1}^{\infty}$ be a sequence of independent exponentially distributed random variable with parameter $\gamma$ defined on sample space $\Omega$ and $\{\tau_m\}_{m = 1}^{\infty}$ be a sequence of points, where $\tau_m$ are arbitrary values of the random variable $\tau_m^{'}, \forall \; m\in \mathbb{Z}_{+}$. Let $\{\chi_{m}^{'}\}_{m = 0}^{\infty}$ be an increasing sequence of random variables and $\{\chi_{m}\}_{m = 0}^{\infty}$ be an increasing sequence of points, where $\chi_{m}$ is an value of the corresponding random variable $\chi_{m}^{'}, \forall \; m\in \mathbb{Z}_{+}$. Note that $\chi_{0}^{'} = t_0$, where $t_0\geq 0$ is a fixed point and $\tau_m^{'} = \chi_{m}^{'}-\chi_{m-1}^{'}$ for $m \in \mathbb{Z}_{+}$, and $\tau_m^{'}$ define the waiting time between two consecutive impulses such that $\sum\limits_{m = 1}^{\infty} \tau_m^{'} = \infty$ with probability 1.

2.   Preliminaries

Consider the random impulsive functional differential equations

where $g\in C([0, \infty)\times \mathcal{PC}\left(\left[-r, 0\right], \mathbb{R}^{n}\right), \mathbb{R}^{n})$, $g(t, 0) = 0$ and $\phi\in PC\mathcal{B}(t)$. For every $t\geq t_{0}, \; \; y_{t} = \{y(t+\theta), \theta\in [-r, 0]\}$, where $r > 0$. For each $m\in \mathbb{Z}_{+}, \; \; I_{m}(t, y) \in C([0, \infty)\times \mathbb{R}^{n}, \mathbb{R}^{n}), \; \; I_{m}(\chi_{m}^{'}, 0) = 0$ and for any $\rho > 0$, there exists $\rho_{1} > 0\; \; (\rho_{1} < \rho)$ such that $y\in S(\rho_{1})$ which implies that $y+I_{m}(\chi_{m}^{'}, y)\in S(\rho)$, where $S(\rho) = \left\{y:\left\|y\right\| < \rho, \; y\in \mathbb{R}^{n} \right\}$. The quantities $y(\chi_{m}^{'+})$ and $y(\chi_{m}^{'-})$ denote the right and left limits at $\chi_{m}^{'}$, respectively. Let $\varphi(\theta) = y(t+\theta)$ then it implies $\varphi(0) = y(t)$.

For convenience, we define $\chi_{0} = t_0$ and $\tau_m = \chi_{m}-\chi_{m-1}, \; \forall \; m\in \mathbb{Z}_{+}$, where $\tau_m$ denote the value of the waiting time. Then, system $(2.1)$ becomes

where $y(t; t_{0}, \phi, \left\{\tau_m\right\})$ is the solution of system $(2.2)$ which depends on the impulses $\chi_{m}, \; \; m \in \mathbb{\mathbb{Z}_{+}}$ with the initial condition $(t_{0}, \phi)$. We will say that $y(t; t_{0}, \phi, \left\{\tau_m\right\})$ is a sample path solution of system $(2.1)$ and we will assume that $\lim\limits_{t\rightarrow \chi_{m}-0} y(t; t_{0}, \phi, \left\{\tau_m\right\}) = y(\chi_{m}; t_{0}, \phi, \left\{\tau_m\right\})$. Moreover, the set of all solutions $y(t; t_{0}, \phi, \left\{\tau_m\right\})$ of systems $(2.2)$ generates a stochastic process. We will denote it by $y(t; t_{0}, \phi, \left\{\tau_m^{'}\right\})$ and we will say that it is a solution of system $(2.1)$.

For the initial value problem system $(2.1)$, we assume its solution is exists and unique. Moreover and since $g(t, 0) = 0$, and $I_{m}(\chi_{m}^{'}, 0) = 0, \; \; m\in \mathbb{Z}_{+},$ we can conclude that $y(t) = 0$ is the trivial solution of system $(2.1)$.

Lemma 2.1. ^[32,33], Assume there exist exactly $m$ impulses until the time $t, t \geq t_0$, and $\tau_m^{'} = \chi_{m}^{'}-\chi_{m-1}^{'}, \; \forall\; m \in \mathbb{Z}_{+}$, then the probability

where the events $\Delta_{m}(t) = \{ \omega \in \Omega: \chi_{m}^{'}(\omega) < t < \chi_{m+1}^{'}{(\omega)} \}, m \in \mathbb{Z}_{+}$.

Definition 2.2. ^[46], The function $W:[-r, \infty) \times \mathcal{PC}\left(\left[-r, 0\right], \mathbb{R}^{n}\right) \longrightarrow \mathbb{R}_{+}$ belongs to class $\omega_{0}$ if

(i) $W$ is continuous differentiable almost every where function.

(ii) $W(t, y)$ is locally Lipschitzian in $y$ and $W(t, 0)\equiv 0$.

Definition 2.3. ^[46], For given $W\in \omega_{0}$, $D^{+}W$ is defined as

for $(t, \varphi)\in \mathbb{R}_{+} \times \mathcal{PC}\left(\left[-r, 0\right], \mathbb{R}^{n}\right)$.

Definition 2.4. Let $p > 0$. Then the trivial solution of system $(2.1)$ is said to be $p-$th moment GES, if there exist $\lambda > 0$ and $\mathcal{L}\geq 1$, such that $E\left\|y(t)\right\|^{p}\leq \mathcal{L} E\left\|\phi\right\|^{p} e^{-\lambda(t-t_{0})}, \; t\geq t_{0},$ for any initial value $\phi \in PC\mathcal{B}(t_{0}).$

Theorem 2.5. Assume there exist a function $W(t, y)\in \omega_{0}$, and constants $a_{1} > 0, \; a_{2} > 0\; \; (a_{1}\leq a_{2}), \; p > 0, q > 0, \mathcal{M} > 1, \; \lambda > 0, w_m > 0, \; \kappa > 0$, such that $E\left[w_{m}\right]\leq\kappa, m\in \mathbb{Z}_{+}$. Then the following conditions hold:

(i) $a_{1}\left\|y\right\|^{p}\leq W(t, y) \leq a_{2}\left\|y\right\|^{p}, \; \; (t, y)\in [-r, \infty)\times \mathbb{R}^{n};$

(ii) For any $t\geq t_{0}$ and $\varphi \in \mathcal{PC}\left(\left[-r, 0\right], \mathbb{R}^{n}\right)$, if $\mathcal{M} W(t, \varphi(0))\geq W(t+\theta, \varphi(\theta))e^{\lambda \theta}, -r \leq \theta \leq 0, \; \; \chi_{m}^{'} < t < \chi_{m+1}^{'}$, then $D^{+}W(t, \varphi(0))\leq q W(t, \varphi(0))$.

(iii) For every $(\chi_{m}^{'}, \varphi)\in \mathbb{R}_{+}\times \mathcal{PC}\left(\left[-r, 0\right], \mathbb{R}^{n}\right), \; \; W(\chi_{m}^{'}, \varphi(0)+I_{m}(\chi_{m}^{'}, \varphi))\leq \mathcal{M}^{-1}w_{m}W(\chi_{m}^{'-}, \varphi(0))$, with $\mathcal{M} = \left\{\prod\limits_{i = 1}^{\infty} E\left[w_i\right]\right\} < \infty;$

(iv) $\frac{ln \mathcal{M}}{q} > \tau^{'}$, where $\tau^{'} = \max\limits_{m \in \mathbb{Z}_{+}}\left\{\chi_{m}^{'}-\chi_{m-1}^{'}\right\} < \infty$. Then the trivial solution of system $(2.1)$ is $p-$th moment GES.

Proof. Let $y(t), t\geq t_{0}$ be a solution of system $(2.1)$. We shall show that

where $\eta = min\left\{\lambda, 0.5\tau^{*}\right\}$. From (iv), we define positive constant $\tau^{*} = \frac{ln\mathcal{M}-q\tau}{\tau} > 0$, where $\tau$ is the value of $\tau^{'}$. Set $W(t) = W(t, y(t))$, and we define

then we shall prove that

It is equal to show that

Assume $k = 0$. First, we prove for $t\in [t_{0}, \chi_{1})$,

Suppose on the contrary it is not, then there exists some $t \in [t_{0}, \chi_{1})$ such that $\Lambda(t) > \mathcal{M} a_{2} \left\|\phi\right\|^{p}$. Note that $\Lambda(t_{0}) < \mathcal{M} a_{2} \left\|\phi\right\|^{p}$.

We define

then $\hat t > t_{0}$, $\Lambda(\hat t) = \mathcal{M} a_{2} \left\|\phi\right\|^{p}$ and $\Lambda(t)\leq \mathcal{M} a_{2} \left\|\phi\right\|^{p}, \; \; t\in [t_{0}, \hat t)$.

Since

Furthermore, we note that $\Lambda(\hat{t}) = \mathcal{M} a_{2} \left\|\phi\right\|^{p} > a_{2} \left\|\phi\right\|^{p}\geq \Lambda(t_{0})$. So we define

then $\hat{\hat {t}} < \hat{t}, \Lambda(\hat{\hat {t}}) = a_{2} \left\|\phi\right\|^{p}$ and $a_{2} \left\|\phi\right\|^{p} < \Lambda(t), \; \; t\in (\hat{\hat {t}}, \hat{t}]$. Combining with Eq $(2.4)$, we have

From $(ii)$, $D^{+}W(t)\leq qW(t)$ holds for $t\in[\hat{\hat {t}}, \hat{t}]$. Hence, we have

Thus

However, noting that

This is a contradiction. Hence, $\Lambda(t)\leq \mathcal{M}a_{2} \left\|\phi\right\|^{p}, \; t\in [t_{0}, \chi_{1})$.

We assume it is true for $k = m-1$,

which implies

Next we shall prove for $k = m$,

Suppose that this assertion is not true, then there exists some $t\in[\chi_{m}, \chi_{m+1})$ such that

It follows from Eq $(2.5)$ that $\Lambda(\chi_{m}) < \mathcal{M}a_{2} \left\|\phi\right\|^{p}\mathscr{W}(\chi_{m})$. Thus we define

then $t^{*} > \chi_{m}, \; \Lambda(t^{*}) = \mathcal{M}a_{2} \left\|\phi\right\|^{p}\mathscr{W}(\chi_{m})$ and $\Lambda(t)\leq \mathcal{M}a_{2} \left\|\phi\right\|^{p}\mathscr{W}(\chi_{m}), \; \; t\in[\chi_{m}, t^{*})$. Also, from Eq $(2.5)$, we know that

Noting that

and

Further, we define

Then $t^{**} < t^{*}, \Lambda(t^{**}) = a_{2} \left\|\phi\right\|^{p}\mathscr{W}(\chi_{m})$ and $\Lambda(t) > a_{2} \left\|\phi\right\|^{p} \mathscr{W}(\chi_{m}), \; \; t\in[t^{**}, t^{*}]$. We can deduce that

from condition (ii)

which implies that

Thus

However, we note that

This is a contradiction. Thus, Eq $(2.6)$ holds. Then by the definition of $\Lambda(t)$ and $\mathscr{W}(t)$, we get

from the condition $(i)$, we obtain

where $\mathcal{L} = \frac{a_{2}}{a_{1}} \mathcal{M}\geq 1$. This solution generates a stochastic process, and it denoted by

By using Lemma $2.1$, and taking expectation, we have

where $[\eta+\gamma(1-\kappa)] > 0$ is exponential convergent rate.

3.   Chaotic delayed equations

In this section, Theorem $2.5$ will be applied to study the $p-$th moment GES and $p-$th moment GESy results for RISCDEs.

3.1.   Exponential stability of RISCDEs

Consider the following RISCDEs

where $\phi\in PC\mathcal{B}(t)$, $a, b, c$ are positive scalar constants, $r > 0$ is delay constant and the nonlinear functions $g$ and $h$ satisfy the conditions $| g(y)| \leq N|y|$ and $|h(y)|\leq L|y|$ where $N, L > 0$.

Corollary 3.1. Assume that there exist constants $\mathcal{M} > 1, \lambda > 0, p > 0, w_{m} > 0, \kappa > 0$, such that $E(w_{m})\leq \kappa$. Let the following conditions hold:

(i) $p[-a+b N+c L \mathcal{M}^{\frac{1}{p}} e^{\frac{\lambda r}{p}}] > 0$.

(ii) $\tau^{'} < \frac{ln\mathcal{M}}{p[-a+b N+c L \mathcal{M}^{\frac{1}{p}} e^{\frac{\lambda r}{p}}]}$, where $\tau^{'} = \max\limits_{m \in Z_{+}}\left\{\chi_{m}^{'}-\chi_{m-1}^{'}\right\} < \infty$.

Then the trivial solution of Eq $(3.1)$ is $p-$th moment GES.

Proof. Choose the Lyapunov function $W(t) = \left|y(t)\right|^{p}$. From Eq $(3.1)$, we have

From Theorem $2.5$, the Razumikhin condition $\mathcal{M} e^{-\lambda \theta}W(t, \varphi(0))\geq W(t+\theta, \varphi(\theta)), \theta \in [-r, 0]$, implies that $\mathcal{M}^{\frac{1}{p}}e^{\frac{\lambda r}{p}}\left|y(t)\right|\geq \left|y(t-r)\right|$. Then calculating $D^{+}W$ along the solution of Eq $(3.1)$, we get

where $q = p\left[-a+b N+c L \mathcal{M}^{\frac{1}{p}} e^{\frac{\lambda r}{p}}\right]$. By using Theorem $2.5$, we end up with

Hence the trivial solution of Eq $(3.1)$ is $p-$th moment GES.

3.2.   Exponential synchronization of RISCDEs

Consider the following RISCDEs,

where $\Phi\in PC\mathcal{B}(t)$. To inspect the synchronization problem through random impulsive control, we define the following response system:

where $\phi\in PC\mathcal{B}(t)$. Let $\vartheta(t) = x(t)-y(t)$ be the synchronization error condition. Then we define the following error system between Eqs $(3.2)$ and $(3.3)$:

where $f$ is a nonlinear bounded function, defined by $f[\vartheta(t)] = g[\vartheta(t)+y(t)]-g[y(t)]$, $f[\vartheta(t-r)] = h[\vartheta(t-r)+y(t-r)]-h[y(t-r)]$, where $a, b, c$ are constants.

Corollary 3.2. Assume that then there exist constants $\mathcal{M} > 1, \lambda > 0, p > 0, w_{m} > 0, \kappa > 0$, such that $E(w_{m})\leq \kappa$. Let the following conditions hold:

(i) $p[-a+b N+c L \mathcal{M}^{\frac{1}{p}} e^{\frac{\lambda r}{p}}] > 0$.

(ii) $\tau^{'} < \frac{ln\mathcal{M}}{p[-a+b N+c L \mathcal{M}^{\frac{1}{p}} e^{\frac{\lambda r}{p}}]}$, where $\tau^{'} = \max\limits_{m \in Z_{+}}\left\{\chi_{m}^{'}-\chi_{m-1}^{'}\right\} < \infty$.

Then the trivial solution of system $(3.4)$ is $p-$th moment GESy.

The proof is similar to the proof of Corollary $3.1$ and hence it is omitted.

4.   Applications

In this part, we shall discuss the stability results for nonlinear scalar time delay model under fixed and random time impulses.

4.1.   Blood cell production model

Leukemia means cancer that starts in the blood forming cells of the bone marrow. It is nothing but the increase of abnormal white blood cells produced by the bone marrow that is relatively mature. This results in the excess production of abnormal white blood cells compared to the normal production rate. The patients with Leukemia may take treatments (with fixed or at random time period) such as chemotherapy, monoclonal antibodies, supportive care, leukapheresis, surgery and radiotherapy, the patient may be curative. The following random impulsive model reflects the effectiveness of the treatments.

Example 4.1. From ^[1,47], the blood cell production model can be represented by nonlinear first order random impulsive control system of the form

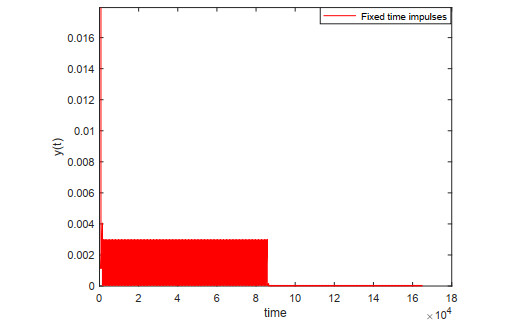
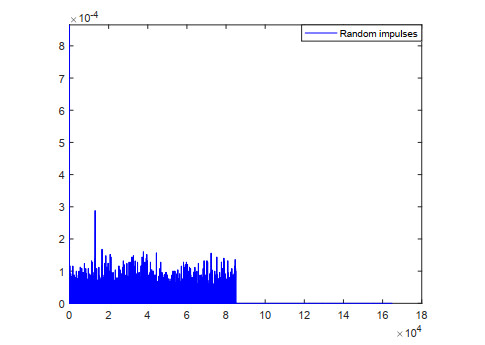
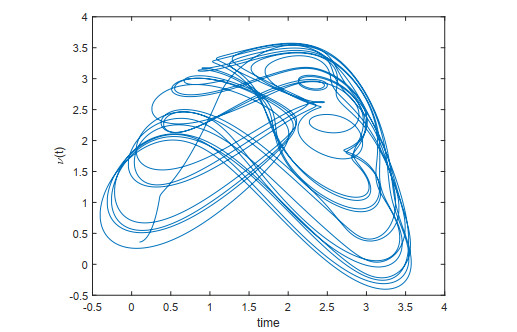
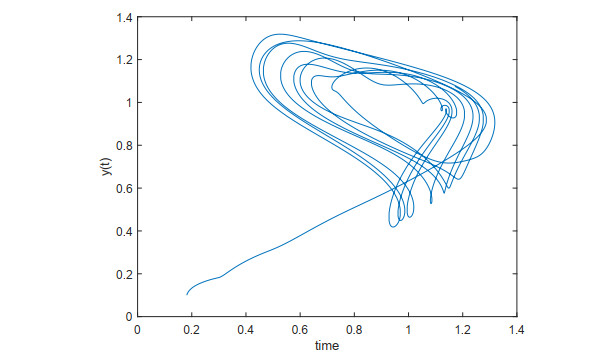
where $y(t)$ represents the density of mature cells at time $t$, $y(t -r)$ represents the density of abnormal white blood cells and $r$ is the time-delay between the production of abnormal white blood cells in the bone marrow and their release of the mature cells in to the blood streams. In patients with leukemia, when the time $r$ is large, the rapid increase in the density of abnormal white blood cells may vary chaotically. There are various kinds of treatments $w_{m}$ like chemotherapy, monoclonal antibodies, supportive care, leukapheresis, surgery and radiotherapy. The aim of the treatment is to control the production of abnormal white blood cells which provides the cure of the disease. Here, $a$ is the average density independent death rate of the population and the constants $a, b$, and $c$ are obtained from ^[1,47]. Consider the particular values $a = 0.1, \; b = 0.2, \; c = 10, \; \phi(\theta) = 0.1$, $r = 17$ and $w_{m} = 0.011$ in Eq (4.1). Then Eq $(4.1)$ exhibits a chaotic behavior illustrated in Figure 1.

Proposition 4.2. If $\tau^{'} < 0.1591$. Then the solution of system $(4.1)$ is GES.

Proof. Consider the Lyapunov function $W(t) = \left|y(t)\right|$. From Corollary $3.1$, we take $p = 1, \mathcal{M} = 16, \lambda = \frac{1}{10}$ and use Razumikhin condition to obtain $16 e^{\frac{1}{10}\times 17} \left|y(t)\right|\geq \left|y(t-17)\right|$. Then we have

where $q = 17.4166$. By using Corollary $3.1$, we get $\frac{ln16}{17.4166} = 0.1591 > \tau^{'}$. Therefore, the solution of system $(4.1)$ is GES.

Remark 4.3. Proposition 1 says that in patients with leukemia, the treatment like chemotherapy, monoclonal antibodies, supportive care, leukapheresis and radiotherapy is taking at random within the maximum duration between two consecutive treatments is less than 0.1591 days, then the patient may cure.

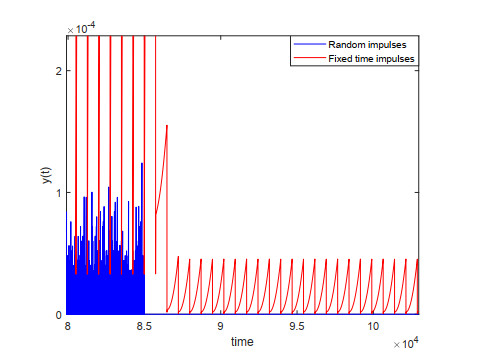
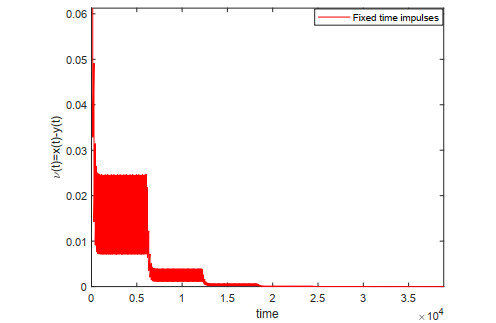
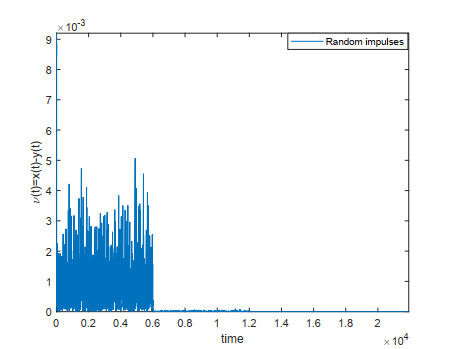
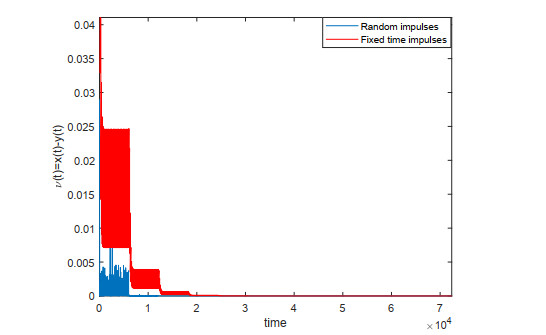
Remark 4.4. Figures 2 and 3, show that the effective of the treatment like chemotherapy, monoclonal antibodies, supportive care, leukapheresis and radiotherapy is taking at fixed and random. Furthermore, Figure 4 demonstrates the effective of random time treatment compared to the fixed time treatment.

Example 4.5. ^[2], When the intensity of the incident light is increased in the optical bistable resonator the transmitted light from a ring cavity containing a nonlinear dielectric medium undergoes a transition from a stationary state to other states. Ikeda addressed the optical bistable resonator with time delay in the following system:

where, $x$ is the phase lag of the electric field across the resonator and $a$ is the relaxation coefficient, $b$ is the laser intensity and $r$ is the round-trip time of the light in the resonator. Then, system $(4.2)$ exhibits a chaotic behavior as shown in Figure 5. Let $w_{m}$ be the amount of external cavity, it fit at the random way in system $(4.2)$, then we obtain the following form of random impulsive system:

where $a = 1, \; b = 4, \; \phi(\theta) = 0.1, \; r = 2$ and $w_{m} = 0.29$.

Proposition 4.6. If $\tau^{'} < 0.0558$. Then the error value of Eqs $(4.2)$ and $(4.3)$ is GESy.

Proof. Consider the Lyapunov function $W(t) = \left|\nu(t)\right|$. From Corollary $3.2$, we take $\mathcal{M} = 5, \lambda = \frac{1}{5}, p = 1$ and use the Razumikhin condition to obtain $5 e^{\frac{1}{5}\times 2}\left|y(t)\right|\geq\left|y(t-2)\right|$. Hence, we have

where $q = 28.8364$. By Corollary $3.2$, we get $\frac{ln5}{28.8364} = 0.0558 > \tau^{'}$. Therefore, the error value of Eqs $(4.2)$ and $(4.3)$ is GESy.

Remark 4.7. Figures 6 and 7 illustrate the external cavity that controls the transmitted light with fixed and random times. Besides, the comparative results on external cavity (fixed and random time) is depicted in Figure 8.

5.   Conclusions

In this paper, the $p-$th moment global exponential stability and $p-$th moment global exponential synchronization are studied for functional differential equations and scalar chaotic delayed equations. We propose the main equations under random impulsive effects and show the effeteness of impulses to stabilize and synchronize the solutions of the proposed equations. Our approach is based on the Lyapunov-Razumikhin techniques which help establishing new sufficient conditions that are extending the existing results in the literature. The blood cell production and optical bistable resonator models are proposed to examine the validity and applicability of the theoretical results. We illustrate the main theorems by graphical simulations that demonstrate the fast convergence of the random impulsive control compared to the fixed impulsive control.

The applications of random impulsive control can be extended to investigate many physical phenomena that involve delay systems. For future consideration, the consideration of random impulsive control for neural network time-delay systems could be a promising topic.

Acknowledgments

This work was supported by Science & Engineering Research Board (DST-SERB) project file number: ECR/ 2015/000301 in India. J. Alzabut would like to thank Prince Sultan University for supporting and funding this work.

Conflict of interest

The authors declare that they have no competing interests.