Dynamics of a stochastic HBV infection model with cell-to-cell transmission and immune response

1.   Introduction 

Hepatitis B, including acute and chronic disease, is caused by the hepatitis B virus (HBV) infection and has become a major global health problem. World Health Organization (WHO) estimates that in 2019,325 million people globally live with hepatitis B and/or C, while in 2015,257 million people were living with chronic hepatitis B infection (defined as hepatitis B surface antigen positive), of them, 887,000 deaths, mostly from cirrhosis and hepatocellular carcinoma (i.e., primary liver cancer)^[1].

Generally, cellular immunopathological reaction plays an important role in controlling HBV infection. For example, cytotoxic T lymphocytes (CTLs) can specifically attack the target infected host cells ^[2], which will induce hepatocyte damage. And more and more attentions have been paid to the study of virus dynamics within-host, which can provide insights into virus infection and dynamics, as well as to how an infection can be reduced or even eradicated, see ^[3,4,5,6,7] and the references therein.

Studies have shown that human immunodeficiency virus (HIV) and hepatitis C virus (HCV) can spread by two fundamental modes within-host, one by virus-to-cell infection through the extracellular space and the other by cell-to-cell transfer involving direct cell-to-cell contact ^{[4,8,9,10,11,12,13,14,15,16]}. Especially, Sourissea et al. ^[17] had reported that viral transfer in vitro via cell-to-cell contact is much more rapid and efficient than infection by free virus because it avoids several biophysical and kinetic barriers. Monel et al. ^[18] showed that direct cell-to-cell transmission in vivo is also more potent and more efficient. And Yang and co-authors ^[19] showed a previously unappreciated role of exosomes in HBV transmission and natural killer cells dysfunction during chronic hepatitis B (CHB) infection. These results showed that cell-to-cell transmission is reasonable apart from virus-to-cell mode in HBV infection because exosomes can transfer genetic material between cells. Therefore, during HBV infection, uninfected hepatocytes can be infected not only by newly released free virus, but also by contacting with infected hepatocytes. Combining with the CTLs population, to describe HBV from a single patient's point of view, we first propose the following HBV infection model:

where $x$, $y$, $v$ and $z$ denote the total numbers of uninfected hepatocytes, infected hepatocytes, free virus and CTLs, respectively. It is assumed that normal hepatocytes are produced by bone marrow and other organs at a constant rate of $\lambda_{1}$ and the natural death rate is $d_{1}x$. $\beta_{1}$ is the effective contact rate between uninfected hepatocytes and virus, $\beta_{2}$ stands for the effective contact rate between uninfected and infected hepatocytes, $a$ represents the natural death rate of the infected hepatocytes. Infected hepatocytes are eliminated by CTLs at rate $pyz$, free virus are produced from infected cells at rate $ky$ and die at rate $\gamma v$. CTLs are produced at a constant $\lambda_{2}$ from the thymus, and at rate $qyz$ due to the stimulation of infected cells ^[20], and die at rate $d_{2}z$.

Note that there are inevitably random disturbances in the process of HBV infection within-host, such as temperature fluctuation, mood fluctuation and other physiological rhythm changes, which may affect the dynamics of HBV infection. Thus, in addition to the traditional ordinary differential equations (ODEs), such as model (1), more attention has been paid to the stochastic differential equations (SDEs) which takes Brownian motion into consideration ^{[21,22,23,24,25,26,27,28,29,30,31]} and the references therein). Concretely, ^[31] was about HIV infection and did not consider cell-to-cell transmission. Especially, references ^[5,26,32] investigated the stochastic dynamics of HBV infection. After assuming the total number of hepatocytes is constant, Bertacchi et al. ^[5] proposed a stochastic HBV model for the infection within a patient which was treated with two drugs, either sequentially or contemporaneously, developed a two-step mutation which was resistant to both drugs, and studied the deterministic approximation of the stochastic model and gave a biological interpretation of its asymptotic behaviour. Luzyanina and Bocharov ^[26] considered a reduced ODEs model which only describes the interaction between the HBV and the CTL response, and Xie et al. ^[32] investigated the stochastic HBV dynamics. Unfortunately, these studies had not considered the CTL response and cell-to-cell transmission in their SDE HBV model.

Thanks to the insightful work of Luzyanina and Bocharov ^[26], we know that the variations can affect either the replication of the virus or its elimination kinetics, e.g., via parameters $\beta_2$, $\gamma$ and $d_2$, respectively. And we can explore their impacts on the dynamics of HBV infection could be the extension of the deterministic description of the virus—CTL interaction to include the stochastic forcing in a multiplicative way.

To investigate the influence of fluctuating (vs. constant) rates $\beta_2$, $\gamma$ and $d_2$ on the model solutions, following ^[26], we randomize these parameters as follows.

Let $p\in[p_1, p_2]$ be a parameter being randomized and $p_1, p_2$ are its low and upper bounds. We assume that $p$ varies randomly according to $p(t) = \tilde{p} + \sigma p\xi(t)$, where $\tilde{p}$ is the value of $p$ around which we randomize, $\xi(t)$ is a standard Gaussian random variable for each $t$ and $\sigma p > 0$ is the intensity of the noise. We adopt $\sigma p$ as

to ensure that $p$ remains in the interval $[p_1, p_2]$ with probability 0.997. This implies that about 99.7% of values drawn from a normal distribution are within three standard deviations $\sigma p$ away from the mean.

More precisely, let

then, corresponding to the deterministic model (1), we can further derive the following SDE HBV model:

where $\sigma_{i}\, (i = 1, 2, 3)$ represent the intensities of the white noises, and $B_{i}(t)\, (i = 1, 2, 3)$ are independent standard Brownian motions.

It is worthy to note that, if the number of individuals in the population gets very large, Kurtz ^[33,34] proved that if there is a density-dependent stochastic jump process (such as the number of viral particles, the infected/uninfected hepatocytes etc..), then the process that we obtain when rescaling by a constant and large quantity can be approximated by the solution of the corresponding ODE.

The purpose of the present study is to elaborate the virus infection dynamics to random perturbations in the virus replication and immune responses parameters. In the next section, we give the global dynamics of the deterministic HBV model (1), including the basic reproduction number and global stability of infection-free equilibrium and infection equilibrium. In Section 3, we show the existence and uniqueness of the global positive solutions of the SDE HBV model (2). In Section 4, we give the asymptotic property of the positive solution of model (2) around infection-free equilibrium. And in Section 5, the dynamics of the stochastic model around infection equilibrium is obtained. In Section 6, numerical simulations of model (2) illustrate the correctness of the theoretical results and the correlation between fluctuation amplitude and intensity of the white noise is further studied. In Section 7, we discuss our new findings in the view of epidemiological implications.

2.   Global threshold dynamics of the deterministic model (1) 

We are interested in the dynamics of viral infection rather than the initial processes of infection. The initial condition of model (1) is assumed as the form $x(0) > 0, y(0) > 0, v(0) > 0$ and $z(0) > 0$. Based on the initial conditions, it is clear that the solutions of model (1) are non-negative and ultimately bounded.

Model (1) always has an infection-free equilibrium $E_{0} = \left(x_0, 0, 0, z_0\right)$, where $x_0 = \frac{\lambda_{1}}{d_{1}}, \; z_0 = \frac{\lambda_{2}}{d_{2}}$. According to the definition and algorithm of the basic reproduction number of virus in ^[35], we can obtain the basic reproduction number of model (1) as follows:

Obviously, $R_0$ increases as $\beta_1$ and $\beta_2$ increasing.

After some algebraic operations, it is easy to know that, if $R_{0} > 1$, model (1) has an infection equilibrium $E^{*} = (x^{*}, y^{*}, v^{*}, z^{*})$, where

and $y^{*}$ is the positive root of Eq (4) in $\left(0, \dfrac{(R_{0}-1)d_{1}}{\beta}\right)$:

On the global stability of the equilibria of model (1), we have the following results.

Theorem 2.1. For model (1), if $R_{0}\leq 1$, $E_{0}$ is globally asymptotically stable. If $R_{0} > 1$, $E^{*}$ is globally asymptotically stable and $E_{0}$ is unstable.

Proof. We first prove the global stability of the disease-free equilibrium $E_0$.

Define a Lyapunov function

where $m$ will be determined below.

Taking the time derivative of $L_1(x, y, v, z)$ with respect to the solution of model (1), we can obtain:

When $R_0\leq1$, we obtain $\frac{\beta_1x_0}{\gamma}\leq\frac{a+pz_0-\beta_2x_0}{k}$, so there exists $m$ satisfying

such that

Then

Let $M_1 = \{(x, y, v, z)\mid L'_1|_{(1)}\}$. We can know that $L'_1|_{(1)} = 0$ if and only if $x = x_0$, $y = 0$, $v = 0$, $z = z_0$. Hence, $M_1 = \{E_0\}$. Therefore it follows from Lyapunov-Lasalle invariance principle that $E_0$ is globally asymptotically stable when $R_0\leq1.$

Next, we prove the global stability of the positive equilibrium $E^*.$

Consider the following Lyapunov function:

At the infection equilibrium $E^*$, we can get:

Taking the time derivation of $L_2(x, y, v, z)$ along with the solution of model (1), and considering Eq (5), we can obtain:

Let $x_1 = \dfrac{x}{x^*}, y_1 = \dfrac{y}{y^*}, v_1 = \dfrac{v}{v^*}, z_1 = \dfrac{z}{z^*}$, then

Since the arithmetical mean $\frac{m+n}{2}$ of $m$ and $n$ is greater than or equal to their geometrical mean $\sqrt{mn}$, it follows that $L'_2|_{(1)}\leq0$. Let $M^* = \left\{(x, y, v, z)\mid L'_2|_{(1)} = 0\right\}.$ We note that $L'_2|_{(1)} = 0$ if and only if $x_1 = 1$, $y_1 = v_1$, $z_1 = 1$, i.e., $x = x^*$, $\dfrac{y}{y^*} = \dfrac{v}{v^*}$, $z = z^*$. Easy to know, $y = y^*$, $v = v^*$. So the largest invariant set of model (1) on the set $M^*$ is the singleton $\{E^*\}$. By the Lasalle principle, when $R_0 > 1$, the infection equilibrium $E^*$ is globally asymptotically stable.

The proof is completed.

Remark 1. From Theorem 2.1, we know that $R_0$ can be used to govern the threshold dynamics of deterministic HBV model (1). That is, if $R_{0}\leq 1$, the HBV infection will go to extinction; while if $R_{0} > 1$, the HBV infection will persist.

3.   The existence and uniqueness of the solution of the SDE model (2) 

Theorem 3.1. For any initial value $X(0) = (x(0), y(0), v(0), z(0))\in \mathbb{R}^{4}_{+}$, there exist positive constants $N_1$ and $N_2$ such that the set $\Omega$ is almost surely positively invariant of the SDE HBV model (2), where

and

Proof. It is clear that all solutions of model (2) starting from $\mathbb{R}_{+}^{4} = \{(x, y, v, z):x(0) > 0, y(0) > 0, v(0) > 0, z(0) > 0\}$ are non-negative. From the first two equations of model (2), we have

which implies

From the third equation of model (2), we have

It follows that

where

and

Clearly, $A_{1}(t)$ and $C_{1}(t)$ are continuous adapted increasing process on $t\geq 0$ with $A_{1}(0) = C_{1}(0) = 0.$ By [36,Theorem 1.3.9,p.14], we can obtain

That is, $\lim\limits_{t\to+\infty}v(t) < \infty\; \; a.s.,$ which means that there is a positive constant $N_{1}$ such that

From the first two and the fourth equations, we have

It follows that

where

and

Clearly, $A_{2}(t)$ and $C_{2}(t)$ are continuous adapted increasing process on $t\geq 0$ with $A_{2}(0) = C_{2}(0) = 0.$ By [36,Theorem 1.3.9,p.14], we can obtain

That is, $\lim\limits_{t\to+\infty}\left(x(t)+y(t)+\dfrac{p}{q}z(t)\right) < \infty\; \; a.s.,$ which means that there is a positive constant $N_{2}$ such that

Summarize the discussions above, we can conclude that the invariant set of model (2) is given as follows:

The proof is completed.

Theorem 3.2. For any initial value $X(0) = (x(0), y(0), v(0), z(0))\in \mathbb{R}^{4}_{+}$, model (2) has a unique globally positive solution $X(t) = (x(t), y(t), v(t), z(t)), t\geq0$, and the solution will remain in $\mathbb{R}^{4}_{+}$ with probability one.

Proof. It is obvious that the coefficients of model (2) satisfy the local Lipschitz conditions. Then, there is a unique local solution $X(t)$ on $(t\in[0, \tau_{e}))$ for any given initial value $X(0)\in \mathbb{R}^{4}_{+}$, where $\tau_{e}$ is the explosion time. In order to show this solution is global, we next prove $\tau_{e} = \infty \; a.s.$

Set $n_{0} > 0$ large enough for any initial value $(x(0), y(0), v(0), z(0))$ lying within the interval $\left[\frac{1}{n_{0}}, n_{0}\right]$. Define the following stopping time

where $n\geq n_{0}$. Set $\inf\phi = \infty$, clearly, when $n\rightarrow\infty$, $\tau_{k}$ is increasing. Let $\tau_{\infty} = \lim\limits_{k\to\infty}\tau_{k}$, we can get $\tau_{\infty}\leq\tau_{e} \; a.s.$ If there is $\tau_{\infty} = \infty \; a.s.$, we can complete the proof at $\tau_{e} = \infty \; a.s.$ Let us put it in another way, we can prove $(x(t), y(t), v(t), z(t))\in \mathbb{R}_{+}^{4}, (t\geq 0) \; a.s.$

Suppose there are constants $T > 0$ and $\varepsilon\in(0, 1)$ such that $P\{\tau_{\infty}\leq T\} > \varepsilon$. So, if $n_{1}\geq n_{0}$ exists, when $n\geq n_{1}$, we have $P\{\tau_{n}\leq T\}\geq\varepsilon$.

Define a $C^{2}$-function $V$: $\mathbb{R}_{+}^{4}\rightarrow \mathbb{R}_{+}$:

where $a_{1}, a_{2}, c_{1}, c_{2}$ are positive constants to be determined.

Using the Itô's formula, we get:

where

Choose $a_{1} = \frac{(a+p)\gamma}{\beta_{2}\gamma+\beta_{1}k}, a_{2} = \frac{d_{2}}{q}, c_{1} = \frac{(a+p)\beta_{1}}{\beta_{2}\gamma+\beta_{1}k}$ and $c_{2} = \frac{p}{q}$ such that

Then,

where $K'$ is a positive constant. Therefore, we have

Thus,

Then taking the expectation on both sides, we obtain

Let $\Omega_{n} = \{\tau_{n}\leq T\}$, where $n\geq n_{1}$, then $P(\Omega_{n})\geq \varepsilon$. Note that $\forall \omega \in \Omega_{n}$. By the definition of stopping time, there is at least one of ($x(\tau_{n}, \omega)$, $y(\tau_{n}, \omega)$, $v(\tau_{n}, \omega)$ and $z(\tau_{n}, \omega)$) equal to $n$ or $\dfrac{1}{n}$. Therefore,

It then follows that

where $1_{\Omega_{n}(\omega)}$ is the indicator function of $\Omega_{n}$. Letting $n\rightarrow\infty$ leads to the contradiction $\infty > {V(x(0), y(0), v(0), z(0))}+K'T = \infty$, so we can conclude that $\tau_{\infty} = \infty,$ which completes the proof.

4.   Stochastic extinction of the HBV infection 

In this section, in order to investigate whether the HBV infection is stochastically extinct, we study the dynamics around $E_0$.

Theorem 4.1. For any given initial value $X(0) = (x(0), y(0), v(0), z(0))\in \Omega$, if $\sigma_1^2 < \dfrac{2d_1}{4\Lambda^2+\frac{\Lambda^2}{2}\left(\frac{d_1}{\lambda_1}+\frac{1}{\Lambda}\right)\left(1+\frac{\lambda_1}{d_1}\right)}, \; \sigma_{2}^{2} < 2\gamma, \; \sigma_{3}^{2} < d_{2},$ and $R_{0}\leq1$, then the solution of model (2) has the following property:

where

Proof. Set $\omega = x-\dfrac{\lambda_{1}}{d_{1}}, \, Q = z-\dfrac{\lambda_{2}}{d_{2}},$ then model (2) can be rewritten as:

Let

By the Itô's formula, we get:

Noting that

then we can obtain:

Consider a new Lyapunov function

where $n$ is positive constant, we compute

When $R_{0}\leq1$, we get

We choose $n$ satisfying

Then,

Define $V = V_{1}+V_{2},$ then

Let

Consequently,

Then

So we obtain

Considering the definition of $\xi$ in Eq (8), we obtain the conclusion (7). This ends the proof.

Remark 2. From Theorem 4.1, we know that, when $R_{0}\leq1$, if the white noise intensity is small and satisfies

the solution of the stochastic model (2) is fluctuating around the disease-free equilibrium point $E_{0}$ of model (1). Epidemiologically speaking, the HBV infection dies out with probability one.

5.   Stochastic persistence of the HBV infection 

In this section, we discuss the stochastic dynamics around the positive equilibrium $E^*$ of the ODE HBV model (1) when $R_0 > 1$.

Theorem 5.1. For any given initial value $X(0) = (x(0), y(0), v(0), z(0))\in \Omega$, if $\sigma_1^2 < \dfrac{d_1}{2\Lambda^2},$ $\sigma_{2}^{2} < \gamma$, $\sigma_{3}^{2} < \dfrac{d_{2}}{2}$ and $R_{0} > 1$, then the solution of model (2) has the following property:

where

Proof. Let

By using Itô's formula, we can obtain:

Consider the following Lyapunov function

By Itô's formula, when $\sigma_2^2 < \gamma$, we can obtain:

Define $W_{1} = V_{1}+\dfrac{a(\gamma-\sigma_2^2)}{2k^2}V_{2},$ then

Consider a new Lyapunov function

Applying Itô's formula, we get:

where

Define $W_{2} = W_{1}+hV_{3},$ then

Choosing

such that $\dfrac{(a+d_{1})^{2}}{a}+\dfrac{(d_{1}+d_{2})^{2}}{2d_{2}} = \dfrac{d_{1}h}{\Lambda}$, we have:

Because $a^{2}\leq2(a-b)^{2}+2b^{2}$, we can get:

Let

and we can derive that

As a result,

By integrating both sides from 0 to $t$ and then taking the expectation on both sides, it yields

Then, we can get

And hence, there is

Let

then

Remark 3. From Theorem 5.1, we know that, when $R_{0} > 1$, if the noise intensity is small and satisfies

then the solution of the stochastic model (2) fluctuates around the infection equilibrium $E^{*}$ of the deterministic model (1). Epidemiologically, the HBV infection persist with probability one.

6.   Numerical simulations 

In this section, we continue to study the SDE model (2) through a numerical approach. We aim to investigate how environmental fluctuations affect disease spreading on the HBV dynamics.

We employ the Milstein's method ^[37] to simulate the SDE model (2), whose numerical scheme for the SDE model (2) is given by

where $\varsigma_i, \zeta_{i}, \vartheta_{i}, i = 1, 2, ..., n$ are Gaussian random variables. We choose $\Delta t = 0.01.$

As an example, the parameters are taken as follows:

Then we obtain

and the corresponding deterministic model (1) has a disease-free equilibrium $E_0 = (1.2, 0, 0, 2.0)$ and a unique epidemic equilibrium $E^* = (1.140, 0.025, 0.015, 2.077),$ which is globally asymptotically stable according to Theorem 2.1.

Next, we use different values of $\sigma_i(i = 1, 2, 3)$ to understand the role of the noise strength in the resulting HBV dynamics for the SDE model (2).

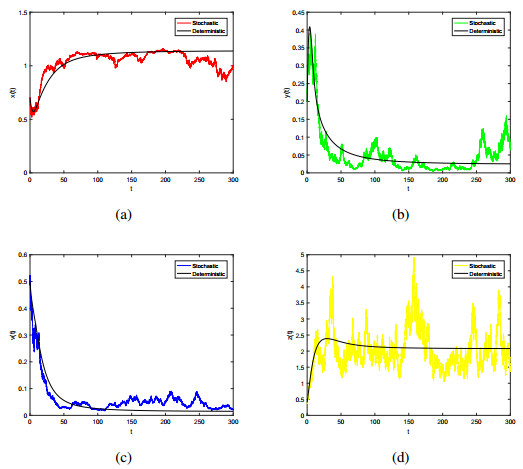
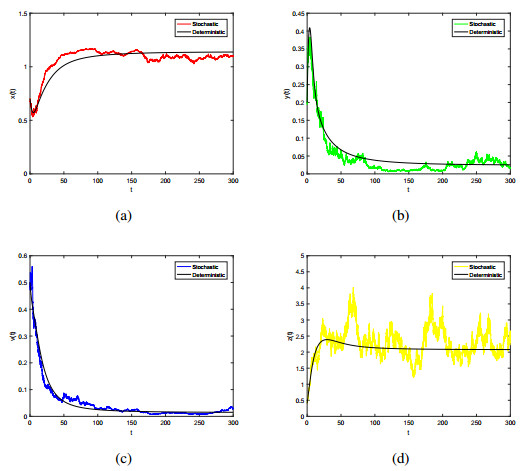
Example 1: We adopt $(\sigma_1, \sigma_2, \sigma_3) = (0.15, 0.08, 0.1)$ and $(0.2, 0.1, 0.15)$, respectively, then simple computations show that $\sigma_1^2 < 0.056, \sigma_2^2 < 0.100, \sigma_3^2 < 0.050$, hence the conditions in Theorem 5.1 hold. From Theorem 5.1, we know that the HBV persist with probability one. The numerical results are shown in Figures 1 and 2, we know that, after some initial transients the solutions $x(t), y(t), v(t), z(t)$ of the SDE model (2) fluctuation around the endemic equilibrium $E^* = (1.140, 0.025, 0.015, 2.077)$ of the deterministic model (1). Comparing Figures 1 and 2, we can see that, if the noise is lower, the amplitude of fluctuation is small (Figure 1); while if the noise is higher, the amplitude of fluctuation is big (Figure 2).

For the sake of learning the impact of random perturbation on the HBV disease dynamics, we have repeated the simulation 10000 times keeping all parameters fixed and never observed any extinction scenario up to $t = 100.$ And we give the histogram of the approximate stationary distributions of $x(t)$ (a), $y(t)$ (b), $v(t)$ (c) and $z(t)$ (d) at $t = 100$ for the stochastic model (2) with $\sigma_1 = 0.15, \sigma_2 = 0.08$ and $\sigma_3 = 0.1$ (Figure 3) and $\sigma_1 = 0.2, \sigma_2 = 0.1$ and $\sigma_3 = 0.15$ (Figure 4), respectively (the numerical method can be found in ^[23]). One can find that $x(t), y(t), v(t)$ and $z(t)$ distributes normally, and also the solution to the SDE model (2) suggests for lower $\sigma_i (i = 1, 2, 3)$, the amplitude of fluctuation is slight and the oscillations are more symmetrically distributed (Figure 3); while for higher $\sigma_i$ that the amplitude of fluctuation is remarkable and the distribution of the solution is skewed (Figure 4).

Example 2: If we adopt $(\sigma_1, \sigma_2, \sigma_3) = (0.8, 0.65, 0.6),$ then $\sigma_1^2 > 0.056, \sigma_2^2 > 0.100, \sigma_3^2 > 0.050$, obviously, the conditions of Theorem 5.1 are not satisfied. The numerical results are shown in Figure 5, which suggest that {the HBV infection dies out} with probability one. That is, in the case of $R_0 > 1$, if the environmental forcing intensity $\sigma_i (i = 1, 2, 3)$ is so large that the conditions of Theorem 5.1 are not satisfied, the HBV could die out with probability one. Obviously, the extinction of the HBV is induced by the noise.

Form Example 2, we know that in the case of $R_0 > 1$, there exists extinction of the HBV infection in the SDE model (2). Next, we will focus on the extinction time of the HBV infection in the stochastic model (2).

Example 3: We adopt $(\sigma_2, \sigma_3) = (0.65, 0.6)$, then $\sigma_2^2-\gamma = 0.32$, $\sigma_3^2-\frac{d_2}{2} = 0.31$. Obviously, the conditions of Theorem 5.1 are not satisfied. And we repeat 10,000 simulations with the same parameters as in Figure 5, we can calculate the average extinction time of $y(t)$ with $\sigma_1$, and the results are shown in Figure 6. For example, when $\sigma_1 = 0.4$, the average extinction time for $y(t)$ is 196.6; when $\sigma_1 = 0.8$, it is 79.6. We can conclude that the average extinction time decreases with the increase of noise intensity $\sigma_1$.

Finally, we will investigate the effect of the effective contact rate $\beta_2$ on the HBV dynamics of the SDE HBV model (2) with fixed forcing intensity.

Example 4: We fix $(\sigma_1, \sigma_2, \sigma_3) = (0.1, 0.1, 0.1),$ and choose $\beta_2 = 0.15, \; 0.2, 0.25, 0.35, \; 0.4, 0.45,$ other parameters are taken as in parameter set (11). In this case, we can obtain

and the values of $R_0$ are given in Table 1. Obviously, the cases of $\beta_2 = 0.15, 0.2, 0.25$ satisfy the conditions of Theorem 4.1, and the cases of $\beta_2 = 0.35, 0.4, 0.45$ satisfy the conditions of Theorem 5.1. The numerical results of the stochastic extinction and persistence of model (2) are shown in Figure 7.

7.   Conclusions 

For the study of an HBV infection model, much attention is usually paid to the persistence and extinction of HBV infection. In the deterministic HBV model, the value of the basic reproductive number is usually the key to determining the persistent and extinction of the HBV. When $R_{0}\leq1$, the HBV will die out; when $R_{0} > 1$, the HBV will persist (see Theorem 2.1). But the SDE HBV model, such as model (2), does not have any equilibrium, so we have to study the asymptotic behavior of the solution of the SDE model around the equilibrium of the deterministic HBV model to reflect the trend of the HBV infection to some extent.

In the present paper, we investigate the stochastic dynamics of an HBV infection model with cell-to-cell transmission and CTL immune response, and analyze the stochastic fluctuation of positive solutions of SDE model (2) around the infection-free equilibrium $E_0$ (Figures 7(a)–7(c)) and the infection equilibrium $E^*$ (Figures 1, 2 and Figure 7(d)–7(f)) of the deterministic model (1), respectively, which reveals that the influence of the white noise on HBV dynamics. More precisely, when the deterministic model (1) is disturbed by small white noise $\sigma_i\, (i = 1, 2, 3)$, the {HBV infection} is extinct (see Theorem 4.1 and Remark 2) or persist (see Theorem 5.1 and Remark 3), and the solutions of model (2) will fluctuate around the infection equilibrium $E^*$ of the deterministic model (1). Furthermore, via numerical simulations, we find that the fluctuation amplitude is positively related to the intensity of the white noise, which means, epidemiologically, as the intensity of white noise decreases, the fluctuation of the solution of model (2) around the equilibrium of the corresponding deterministic model (1) becomes smaller and smaller (Figures 1–4). In these cases, to a great extent, we can ignore the noise and use the deterministic model (2) to describe the HBV infection dynamics. However, when the noise $\sigma_i\, (i = 1, 2, 3)$ is sufficiently large, the infected hepatocytes $y(t)$ on relatively large disturbance of white noise goes to extinction, and the uninfected hepatocytes $x(t)$ generates persistence (Figure 5). In these cases, we cannot ignore the effect of noise, that is, we should use the stochastic HBV model (2) rather than the deterministic model (1) to describe the HBV infection dynamics. In addition, it should be pointed out that the increase in $\beta_2$ results in the corresponding increase in $R_0$. From the biological point of view, one can find that under certain forcing intensity, reducing the value of the effective contact rate $\beta_2$ so that the value of $R_0$ is less than unity could lead to the stochastically extinction of the HBV infection. These results can provide us with some useful control strategies to regulate HBV infection dynamics.

Acknowledgements 

The authors would like to thank the anonymous referees for very helpful suggestions and comments which led to improvements of our original manuscript. This research was supported by the National Natural Science Foundation of China (Grant numbers 61672013, 11601179 and 12071173), and the Huaian Key Laboratory for Infectious Diseases Control and Prevention (HAP201704). K.F. Wang was supported by the National Natural Science Foundation of China (Grant number 11771448).

Conflict of interest 

The authors declare that they have no competing interests.