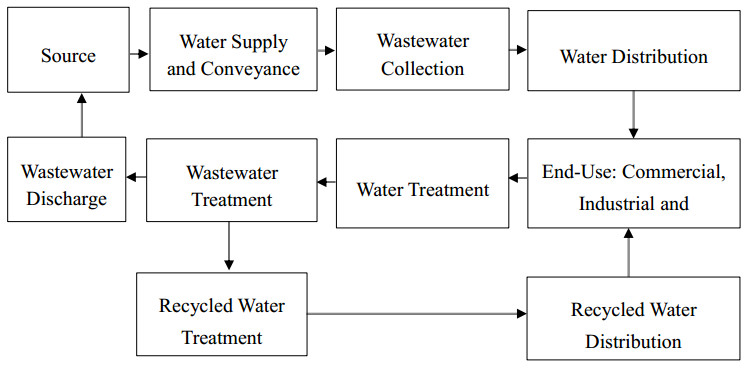
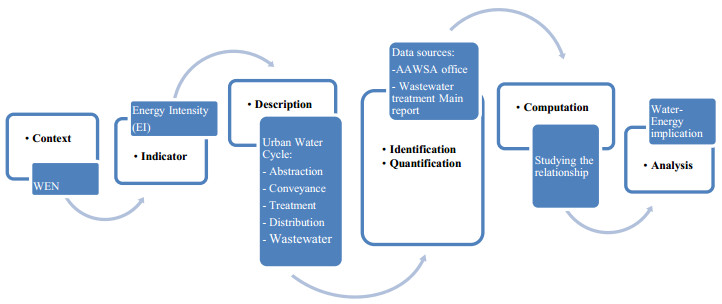
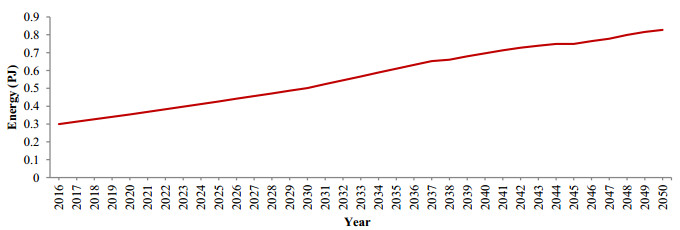
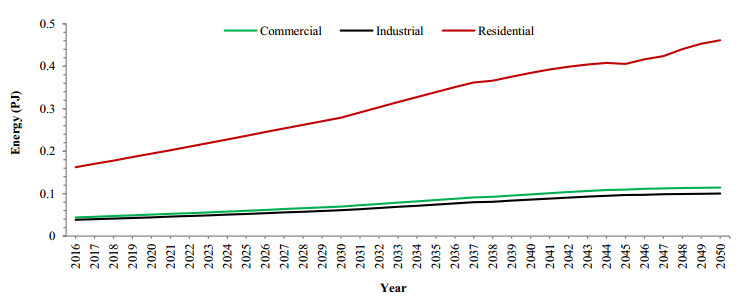
The complex interdependency between water and energy poses new challenges for policymakers to achieve a safe, secure, and sustainable supply of water and energy in the future. The water-energy nexus can be typically characterized by efficient use of energy and water resources. Hence, this paper aims to explore quantitative results of the nexus in terms of energy intensity on existing water systems within urban water cycles. The energy requirement for water treatment and water conveying to the city (from Legadadi water treatment, Gefersa water treatment and wastewater treatment area) as well as the energy requirement for water distribution within the city were quantified. The energy intensity for groundwater extraction, water transmission and water distribution were computed using Energy Intensity method. This led to identify the best technologies to insure the security of water-energy nexus. The annual energy demand and energy intensity values for groundwater extraction were estimated to be 0.6 PJ and 1.2 kWh/m3 respectively. These values for operating all pumps in the water transmission were 0.13 PJ and 0.32 kWh/m3 respectively. Similarly, the energy intensity value for water distribution was 0.27 kWh/m3 and distributes water to residential, commercial and industrial end-users. Determining the energy intensity predicts the future energy demand in urban water system. In 2030 and 2050, the predicted energy demand will be 0.50 and 0.83 PJ respectively for water transmission whereas it will be 0.41 and 0.67 PJ for water distribution.
1.
Introduction
In the modern era of technology and applied sciences, numerous physical phenomena are inherently intricate. Classical calculus has traditionally been employed to mathematically model various aspects of these phenomena. However, with the rapid advancements in technology and the increasing complexity of certain physical phenomena, classical calculus may not always provide accurate models within the constraints of time and computational resources. Consequently, researchers [1,2,3] have redirected their focus towards fractional calculus, which proves more adept at capturing and representing the complexities of these phenomena that elude the accuracy of classical calculus. Conventional derivatives are effective for analyzing changes in a local region near a point, whereas the Caputo fractional derivative enables the analysis of changes over an interval, making it a nonlocal approach. Due to this nonlocal nature, the Caputo fractional derivative is better suited for modeling various physical phenomena, such as earthquakes, atmospheric physics, ocean climate, vibrations, dynamical systems, and polymers, etc. [4].
Significant efforts have been dedicated to the development of versatile and reliable numerical and analytical methods for solving PDEs encompassing both fractional and integer orders. These equations are of great interest in the field of physics and engineering, such as for the fractional-order Burgers' and KdV equations [5], fractional-order anomalous solute transport model [6], fractional-order Fishers' equations in traveling waves [7], fractional-order Cauchy reaction-diffusion model [8], fractional-order option pricing models [9,10], fraction order Sobolev equation [11], the generalized fractional-order Gardner equation being used in plasma physics to study the nonlinear propagation of ion-acoustic waves [12], multi-dimensional hyperbolic telegraph equations [13], Hirota-Satsuma coupled system [14], and others [15,16,17,18,19,20].
Here, in our present investigation, we initiate by studying the Drinfeld-Sokolov-Wilson (DSW) system involving the fractional operator of Caputo, given as follows:
Whereas U(x,τ) and V(x,τ) are unknown functions, and their fractional derivatives are denoted as ∂βU(x,τ)∂τ and ∂βV(x,τ)∂τ in the Caputo sense, and 0<β≤1.
When β = 1, then (1.1) reduces to the standard DSW equation [21,22]. The utilization of the fractional nonlinear DSW system as a mathematical model enables the investigation of dispersive water waves, making it a crucial component in the domain of fluid mechanics [21,22]. Numerous numerical and analytical methodologies have been suggested by researchers to solve the Drinfeld-Sokolov-Wilson system, including the F-expansion method [23], the Homotopy analysis method [24,25], the decomposition method [26] and the Tan method [27], etc.
The Harry Dym equation is attributed to Harry Dym by his unpublished paper, and was introduced by Kruskal and Moser [28] and the time-fractional form is given as
This equation is important because it follows the conservation laws, models the system in which the dispersion is coupled with the nonlinearity, and the Painleve property does not hold in this equation. Researchers have proposed numerous numerical and analytical techniques for solving the fractional order Harry Dym equation [29,30].
Fractional order PDEs often have complex and laborious closed form solutions, making it difficult to use existing methods to calculate them. As a result, it is often more effective to use computational techniques to approximately solve these equations. Among these techniques, meshless techniques have proven to be highly efficient and accurate in addressing a wide range of fractional and non-fractional order PDEs. There are several types of meshless methods, including the radial basis function (RBF) method, the smoothed particle hydrodynamics technique, the element-free Galerkin approach, the diffuse element method, the Fibonacci polynomials, Lucas and Fibonacci polynomials, etc.
Meshless methods are numerical techniques used to solve problems with complex geometries without relying on a fixed mesh. Every technique has its unique strengths and limitations, making it more suitable for specific problem scenarios. The meshless methods based on RBFs are a popular type that interpolate data values at scattered data points and approximate the solution of the PDE. Meshless methods are available in two variants, namely local and global approaches. Nevertheless, the global meshless method has two notable disadvantages: a dense ill-conditioned matrix and susceptibility to variations in shape parameters. Despite these challenges, RBF-based meshless methods remain popular in solving PDEs in various fields [31,32,33,34]. To address these limitations, researchers have turned to the local meshless method [35,36]. The local RBFs meshless have a compact support around each data point, resulting in better conditioned sparse matrices. Consequently, selecting an appropriate value for the shape parameter becomes more straightforward, resulting in improved accuracy and efficiency when solving the linear equations. Unlike global methods, local RBF methods do not require the solution of dense matrices, resulting in a sparse system of linear equations that can be efficiently solved using sparse linear algebra techniques. Local RBF methods are typically more accurate and computationally efficient than global RBF methods, particularly for large-scale problems.
In recent years, researchers have utilized various polynomial-based techniques to tackle nonlinear partial differential equations (PDEs). For instance, the authors in [37] employed B-polynomial bases to solve nonlinear PDEs. Additionally, Davari et al. [38] investigated the application of Legendre polynomials in addressing various types of PDEs (see [38,39,40]). The main objective of this study is to utilize two effective meshless numerical algorithms based on radial basis functions and polynomial methods to obtain an approximate solution for a nonlinear fractional-order DSW equation and Harry Dym equation. The Caputo definition is used to estimate the time fractional component, while RBF and polynomial are used to estimate the space derivatives.
The subsequent sections of this paper are structured in the following manner:
● In Sections 2 and 3, we discuss the primary objective of the study and introduce some fundamental definitions related to fractional calculus.
● Section 4 presents the proposed methodologies.
● In Section 5, we furnish numerical examples, while in Section 6, we offer our conclusions.
2.
Motivation
The motivation for this article arises from the challenging nature of computing analytical solutions for nonlinear PDEs, which find applications in various scientific and engineering domains and offer valuable insights into complex physical phenomena. However, due to their nonlinear characteristics, obtaining exact solutions remains difficult. To address the challenges associated with analytical solutions, researchers have resorted to numerical methods as a feasible alternative. Numerical solutions involve dividing the problem domain into discrete elements and employing iterative algorithms to approximate the solutions at these points, proving to be efficient and practical for a wide range of problems. In this context, the article aims to present two meshless numerical schemes for the class of PDE models discussed. The first method utilizes RBFs, which are distance-dependent functions with excellent approximation capabilities. By adopting RBFs, the numerical scheme avoids the need for a structured mesh, simplifying implementation and enhancing computational efficiency. The second approach depends on polynomials as the basis for approximating solutions, offering researchers an alternative option that complements the RBF-based method. Notably, both methods exhibit a "meshless" property, eliminating the need for structured grids, thereby providing flexibility in handling complex geometries and reducing computational efforts in grid generation. The article emphasizes the high accuracy achieved by these numerical schemes, a critical aspect for reliable results in numerical simulations. The proposed methods can be designed for efficient implementation in higher dimensions, expanding their applicability to complex real-world problems involving multi-dimensional systems.
2.1. Basic definitions
Fractional derivatives are essential in fractional calculus. The following are some fundamental definitions of fractional derivatives that are commonly utilized.
Definition 2.1. The Riemann-Liouville derivative [41,42]
where 0<β<1.
Definition 2.2. Caputo's fractional derivative [43]
where 0<β<1.
Definition 2.3. The Atangana and Baleanu fractional derivative [44]
where 0<β<1.
Definition 2.4. He's fractional derivative [45]
where 0<β<1.
3.
Theoretical framework for time discretization
Initially, we present the essential concepts from functional analysis that will be utilized for the discretization of the time variable.
3.1. Introduction to applied functional analysis: a preliminary overview
Let Ω be a bounded and open domain in R2, and let dx represent the Lebesgue measure on R2. For a finite value of p, the space Lp(Ω) encompasses all measurable functions U: Ω⟶R that meet the condition
This Banach space can be denoted using the norm
The Hilbert space Lp(Ω) is equipped with the inner product defined as
using the norm defined in L2
Additionally, let Ω be an open domain in Rd, where γ=(γ1,…,γd) represents a d-tuple of non-negative integers, and
In accordance with this, we define the following expression:
In this context, it is possible to acquire
Here, we present the definition of an inner product within the context of a Hilbert space
which gives rise to the norm
The Sobolev space X1,p(I) is characterized as
Furthermore, in this paper, we establish the definitions of the following inner product and the corresponding energy norms L2 and H1.
and
by inner products of L2(Ω) and H1(Ω)
respectively.
Let us define Δτ=TM as the mesh size in time, and τi=iΔτ,i∈N+, are the total M temporal discretization points.
Lemma 3.1. Let us suppose η(t)∈C2[0,T] and 0<β<1. Then, it holds that
and
Proof. See Sun et al. [46].□
Lemma 3.2. Let 0<β<1,
and
then,
Proof. Directly follows from Lemma 3.1.□
Lemma 3.3. Let
where 0<β<1,p=0,1,2,…, then b0>b1>b2>⋯>bp→0, as p→∞.
Proof. See Sun et al. [46].□
4.
Formulation of the schemes
Here are the formulations for the discretization of the underlying fractional-order PDE models. In order to discretize the space derivatives appearing in Eqs (1.1) and (1.2), the following methods are used:
(1) Local meshless radial basis function method (MRBFM).
(2) Meshless polynomial method (MPM).
4.1. Local meshless radial basis function method
The problem under consideration involves the discretization of N distinct center points denoted as
in the domain R. These centers, which can be positioned freely without any restrictions on the problem domain's structure, play a crucial role in the local RBF approach. At each of these N centers, a local interpolant of the form is considered as follows: insert the form of the local interpolant here
where λ represents a vector of expansion coefficients, χ be a RBF, and Ii be the vector associated with center i, which includes the center number and the indices of its n−1 nearest neighboring centers. We refer to each center and its n−1 neighbors as a stencil.
and the following n×n linear systems are generated for each stencil, giving N
The expansion coefficients of the above linear system can be determined. The system matrix or interpolation matrix is the term referring to the matrix B. The elements of the local system matrices are
Any type of RBFs can be taken into account, but in this article our choice is the multiquadric (MQ) RBF, which is given as
Applying a linear differential operator L to Eq (4.1) and evaluating it at the center, on which the stencil is based, yields an approximation of the derivatives of a function v at the center locations
The above equation, when simplified, can be expressed as follows:
where λ represents the RBF expansion coefficients vector of order n×1, whereas K is of order 1×n, consisting of the components
By realizing that, the coefficients of the RBF expansion can be eliminated from Eq (4.7) as
where W=KB−1 is the stencil weights. The function values in the stencil's center are therefore multiplied by the weights to approximate the space derivatives.
4.2. Meshless polynomial method
We select N nodes (xi,i=1,2,⋯,N) within the domain Ω∪δΩ, where Na nodes are located in Ω, and Nb nodes are positioned on the boundary δΩ (N=Na+Nb). The approximated representation of the function U(x,τ) is denoted as UN(x,τ). Let us consider the following:
where P(x,r) is a polynomial and
Let UN(xi,τ)=Ui, then Eq (4.10) can further be written as
where
and
From (4.11), we have
It follows from Eqs (4.10) and (4.12) that
where
So far, we have utilized the meshless polynomial approach to approximate the space derivative, resulting in a system of time-fractional ODEs for the underlying PDE models. Our next step is to apply the fractional operator of Caputo to solve this system of ODEs.
4.3. Temporal approximation schemes
The time derivative denoted by ∂βU(x,τ)∂τβ using Caputo's method, where 0<β≤1, is
Taking into account M+1 equidistant time points τ0,τ1,…,τM within the interval [0,τ], where the time step is denoted by Δτ and τi=iΔτ for i=0,1,2,⋯,M, we utilize a first-order finite difference scheme to approximate the time fractional derivative term as follows:
The approximation for ∂U(x,ζp)∂ζ is given by the following expression:
Next,
Let
and
This equation can be written in a more precise manner as
Utilizing Eq (4.18), the time fractional part of the underlying system of Eq (1.2) can be discretized as follows:
4.4. Mathematical framework for the θ-weighted scheme
In this section, we implement the θ-weighted procedure to Eq (1.2) and take into account the time fractional derivative value from Eq (4.19), resulting in the following outcome:
Next, we utilize the suggested meshless method and use RBFs to interpolate U(x,τi+1). Substituting the value from Eq (4.9) into Eq (4.20), we obtain the following expression
We get
In this context, the symbol I denotes an identity matrix, while the matrix L represents the weight matrix associated with the specific differential operator L
where
and
Here,
and
whereas gi+11 and gi+12 represent specific known functions provided in the boundary conditions. Equation (4.21) enables us to compute the solution at any given time level τi.
4.5. Theoretical foundations of stability and convergence
The approach described by (4.21) represents a recurrence relation used to compute the solution values at time τi+1 based on the solution at time τi. The matrix M=D−1E is referred to as the amplification matrix, and its elements rely on the constant κ=Δτhς, where h represents the distance between consecutive nodes, Δτ denotes the time step, and ς corresponds to the order of the spatial differential operator. Let the exact solution of Eq (1.2) be ui at time τi.
Theorem 4.1. [47] Let Ω⊆Rr be an open and bounded set that satisfies an interior cone condition. Assume that Φ∈C2k(Ω×Ω) of order m on Rr is a symmetric and strictly conditionally positive definite function. Let χ be the (m−1)-unisolvent set, and consider the interpolant Pf of the function f∈Nϕ(Ω) over χ. Take β∈Nr0 with |β|≤k. Then, there exist positive constants C and h0 (independent of x, f, and Φ) such that
provided that hχ,Ω≤h0. Here,
Proof. See [47].□
Utilizing Theorem 4.1 on infinitely differentiable functions, such as the Gaussian or MQ functions, results in achieving arbitrarily rapid algebraic convergence rates. In other words, it holds for any natural number k and |β|≤k that
Whenever a function f belongs to the native space Nϕ(Ω), where Nϕ(Ω) denotes the native space of RBFs, extensive research has been conducted to explore the relationship between the constant Ck and the index k [48]. In this study, the MQ RBF is utilized, leading to the following conclusion:
Assuming that the scheme (4.21) exhibits spatial accuracy up to the qth order, then
Let us define the residual as ϵi=ui−Ui. Afterward,
The stability of scheme (4.21) is ensured by adhering to Lax-Richtmyer's condition [49]:
When the vector M follows a normal distribution, its norm ||M|| is equal to β(M). Otherwise, for all cases, the inequality β(M)≤||M|| holds true, provided that the step size h is chosen to be sufficiently small, and the result as well as the initial conditions of the given problem are suitably smooth. In order to maintain a constant value of κ=Δτhq, we take the limit Δτ→0. Consequently, a constant C exists, such that
where i=0,1,2,⋯,T×M. Given that the residual ϵi fulfills zero initial and boundary conditions, it follows that ϵ0=0. Thus, employing mathematical induction,
where i=0,1,2,⋯,T×M, using the condition given in Eq (4.25),
where i=0,1,2,⋯,T×M. Hence, the scheme is convergent.
5.
Results and discussions
The primary objective of this section is to conduct a comprehensive evaluation of the effectiveness of the two suggested numerical methods by subjecting them to rigorous testing on a carefully chosen test problems. To quantitatively assess the performance and efficiency of these computational approaches, we employ the absolute error (Labs) and maximum error (L∞) norms. Subsequently, we compare the computed results with exact solutions and results obtained through a previously established method. This comparative analysis allows us to gain valuable insights into the accuracy and reliability of the proposed methods in solving the targeted PDEs.
Test problem 5.1. Let us examine the test problem associated with the coupled Drinfeld's-Sokolov-Wilson system (1.1). The analytical solution for this problem has been documented in [26]:
Tables 1 and 2 display the numerical outcomes of the proposed methods for the coupled Drinfeld's-Sokolov-Wilson system in test problem 5.1. These results are obtained by varying the final time τ and the spatial point x. Upon analyzing these tables, it becomes apparent that both suggested methods yield highly favorable results. However, when comparing the results of the two methods, it becomes apparent that the MPM method demonstrates higher accuracy and consistency in solving this particular test problem.
Tables 3 and 4 present the numerical results of the suggested approaches for the coupled Drinfeld's-Sokolov-Wilson system in test problem 5.1. These results are obtained by varying the final time τ and the fractional-order β. Upon examining these tables, it becomes clear that both suggested approaches yield highly favorable results. Nevertheless, when comparing the results of the two methods, it becomes apparent that the MPM method demonstrates higher accuracy and consistency in solving this particular test problem.
Figures 1 and 2 depict the Labs error norm for both the MRBFM and MPM, considering a fractional-order β=0.7.
Test problem 5.2. Consider the test problem related to the Harry Dym equation (1.2) with β=1. The analytical solution for this specific problem has been previously documented in [50]:
Table 5 presents the numerical results of the suggested techniques, which are compared with both the exact solution and the method described in [51], for test problem 5.2. Moreover, Table 6 demonstrates the comparison between the proposed methods and [52] for various values of β. Both tables serve as clear evidence of the superior performance of the proposed methods when compared to the methods presented in [51,52]. Additionally, Figure 3 illustrates the MRBFM results for various time values τ.
Comparisons between numerical solutions obtained using MRBFM and MPM, along with the exact solution, are depicted in Figures 4 and 5 as well. These figures also include the Labs error norm. Both methods demonstrate commendable accuracy, although MPM exhibits greater accuracy compared to MRBFM. Furthermore, Figure 6 illustrates the outcomes obtained at various time points, while Figure 7 displays the comparison between exact and numerical results.
6.
Conclusions
In this study, we have implemented two numerical methods, namely the meshless radial basis function method and the meshless polynomial method, to solve the time-fractional Harry Dym equation and Drinfeld-Sokolov-Wilson system. We have successfully solved two test problems through the proposed approaches. A critical aspect of our investigation involved conducting a comprehensive comparison between the computed solutions obtained from our suggested methods, exact solutions, and other methods provided in [51,52], as illustrated in the tables. The results of this comparative analysis have unequivocally demonstrated that the meshless radial basis function method and the meshless polynomial method offer better accuracy in solving these particular PDEs.
Additionally, when comparing the two suggested methods, we have observed that the results obtained from the MPM are better than those from the MRBFM. This observation strengthens the case for adopting the MPM as a preferred numerical tool for similar types of problems in the future. The graphical representations and tabulated data derived from our computations provide further compelling evidence of the effectiveness and suitability of our proposed schemes in tackling these types of PDEs. The excellent agreement between the computed solutions and the exact solutions highlights the robustness and reliability of the MRBFM and MPM in addressing fractional-order problems. In the future, this strategy can be extended to tackle higher dimensional, more complex, and challenging multi-term fractional-order problems.
Use of AI tools declaration
The authors declare they have not used artifiial intelligence tools in the creation of this article.
Conflict of interest
Authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: