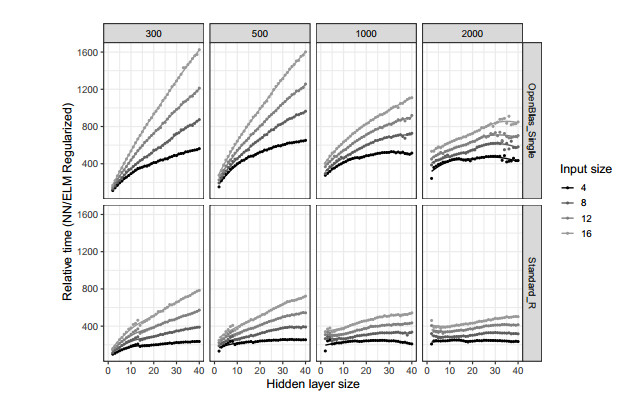
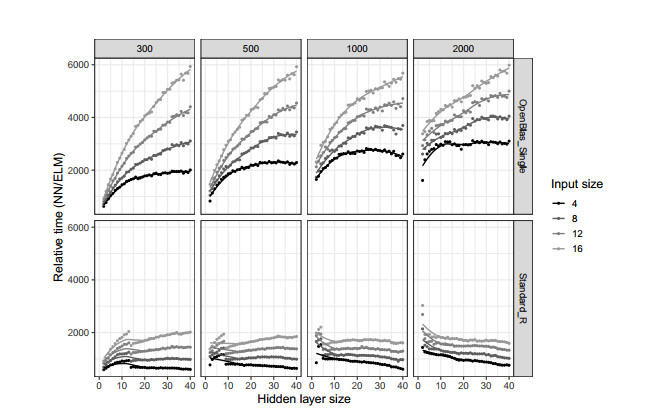
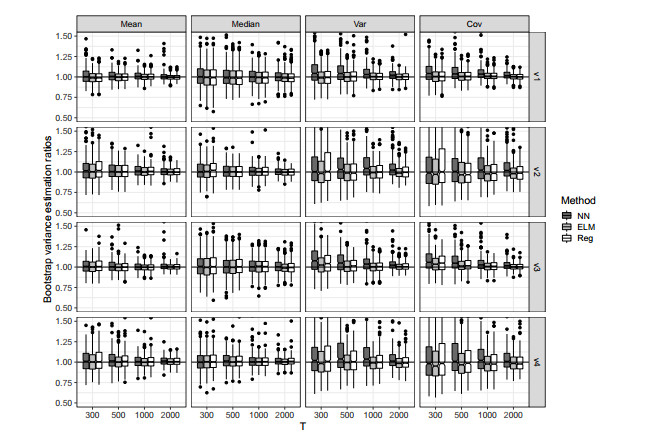
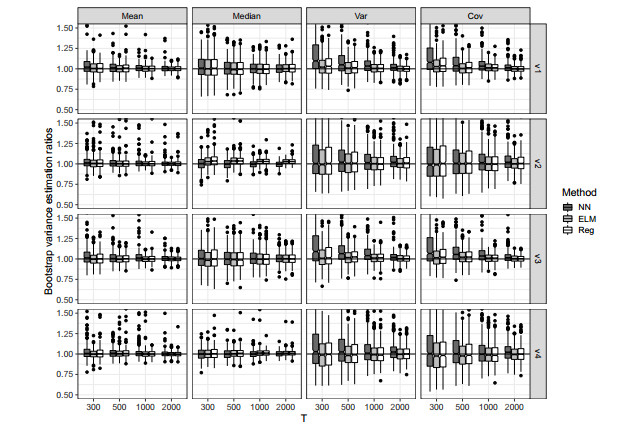
The aim of the paper is to propose and discuss a sieve bootstrap scheme based on Extreme Learning Machines for non linear time series. The procedure is fully nonparametric in its spirit and retains the conceptual simplicity of the residual bootstrap. Using Extreme Learning Machines in the resampling scheme can dramatically reduce the computational burden of the bootstrap procedure, with performances comparable to the NN-Sieve bootstrap and computing time similar to the ARSieve bootstrap. A Monte Carlo simulation experiment has been implemented, in order to evaluate the performance of the proposed procedure and to compare it with the NN-Sieve bootstrap. The distributions of the bootstrap variance estimators appear to be consistent, delivering good results both in terms of accuracy and bias, for either linear and nonlinear statistics (such as the mean and the median) and smooth functions of means (such as the variance and the covariance).
1.
Introduction
In the present paper, we proved the existence of a ground state solution of the following nonlinear Choquard equation
on lattice graph ZN. This equation can be viewed as a discrete version of the following Choquard equation
where α∈(0,N), p>1 and Iα:RN→R is the Riesz potential defined at x∈RN∖{0} by
with Γ being the Euler gamma function.
In the past few decades, many mathematicians have been devoted to studying the Eq (1.2), for example, see [1,2,3,4,5,6]. In particular, if N=3, V=1 and p=2, i.e., −Δu+u=(I2∗|u|2)u, appeared in the literature at least as early as in 1954's work by Pekar on quantum theory of a Polaron at rest [7]. Later in the 1970s, Choquard utilized model (1.2) to describe an electron caught in its own hole, in an approximation to Hartree-Fock theory of one-component plasma [1]. Particularly, the equation is also knows as the Schrödinger-Newton equation, which was used to a model of self-gravitating matter [8]. Also, the article [9] used this system to study the pseudo-relativistic boson stars. In a pioneering work, Lieb [1] proved the existence and uniqueness of the ground state to the Eq (1.2) in R3 with V=1, α=2 and p=2. In the paper [3], Moroz and Van Schaftingen first obtained the sharp range of the parameter for the existence of solutions of the Eq (1.2) with N+αN<p<N+αN−2. If V is the periodic function, since the nonlocal term is invariant under translation, the paper [10] got the existence results. Furthermore, Alves [11] proved the existence and convergence of nontrivial solutions of the nonlocal Choquard equation. There are tremendous results on this direction in [12,13,14,15,16,17,18] and the references therein.
On the other hand, the analysis on the graph has become more and more popular, for example, see [19,20,21,22,23,24,25,26,27]. In a series of work of Grigor'yan et al. [19,20,21], they studied the Yamabe type equations, Kazdan-Warner equation and some other nonlinear equations on graph by using the variational methods. In [27], Zhang and Zhao investigated the existence of nontrivial solution of the equation −Δu+(λa(x)+1)u=|u|p−1u on the locally finite graphs by using Nehari methods (see [28]) and the asymptotic properties of the solution. Later, the paper [22] generalized the results of [27] to higher order. Furthermore, Hua and Xu [] obtained the existence results of nonlinear equation −Δu+V(x)u=f on the lattice graph ZN. Recently, Huang et al. investigated extensively the Mean field equation and the relativistic Abelian Chern-Simons equations on the finite graphs by using the variational method in [23]. For other related results about the graph, we refer the reader to [29,30,31,32,33,34] and references therein.
Inspired by the poineering works, in this paper we study the existence and asymptotical behavior of solution for the Choquard equation (1.2) on the lattice graph ZN. For clarity, let us introduce the basic setting on the lattice graph ZN. The graph ZN consists of the set of vertices
and the set of edges
For any two vertices x,y∈ZN, the distance d(x,y) between them is defined by
where we write y∼x if and only if the edge {x,y}∈E. Assume Ω⊂ZN, we say Ω is bounded if d(x,y) is uniformly bounded for any x,y∈Ω. It is easy for us to see that a bounded domain of ZN can contain only finite vertices. We denote the boundary of Ω is
C(ZN) denotes the set of real-valued functions on ZN. For any u∈C(ZN), its support set is defined as supp(u)={x∈ZN,u(x)≠0}. Let Cc(ZN) denote the set of all functions of finite support. We can define the associated gradient for any function u,v∈C(ZN) by
In particular, let Γ(u)=Γ(u,u) for simplicity. The length of the gradient of u is written by
Let μ be the counting measure on ZN, i.e., for any subset A⊂ZN, μ(A):= #{x:x∈A}. For any function f on ZN, we write
whenever it makes sense. ℓp is a space endowed with the norm
Assume u∈C(ZN), the Laplacican on ZN is defined as
The inner product of the Hilbert space H1(ZN) is given by
Therefore, the corresponding norm reads
For a bounded uniformly positive function V:ZN→R, it is natural for us to consider the equivalent norm in H1(ZN) as
Then we have the conclusions for the Eq (1.1).
Theorem 1.1. Let N∈N∗, α∈(0,N) and p∈(N+αN,∞). Suppose that V(x):ZN→R satisfies the conditions:
(i) V is bounded uniformly positive, i.e. there exist constant C1,C2>0 satisfying C1<V(x)<C2 for any x∈ZN.
(ii) V is T-periodic, i.e. for the positive integer T, we have V(x+Tei)=V(x), ∀x∈ZN,1≤i≤N, where ei is the unit vector in the i-th coordinate.
Then there exists a ground state solution of (1.1).
Remark 1.2. The preceding theorem is a discrete version of the results in [3]. As in the paper [24], we use the Concentration-Compactness Principle (P. L. Lions [35,36]) to recover the compactness and prove the existence of ground state solution of (1.1). Interestingly, since the discreteness of the graph, the Sobolev embedding on the lattice graph is different from that in the continuous setting, which allows us to remove the upper critical exponents N+αN−α in the continuous case.
Next we turn to studying the convergence of the solution for the nonlinear Choquard equation. The results of Schrödinger type equation is already considered in the Euclidean space (see [11,37]). We may expect that the nonlocal Choquard equation on lattice graphs has some similar results. As the paper [22,27], we also consider the confining potential V=λa(x)+1, i.e.,
To study the problem (1.3), we introduce the following subspace of H1(ZN):
It is easy to recognize that the scalar product of Eλ(ZN) is
Then we have the following conclusions.
Theorem 1.3. Let N∈N∗, α∈(0,N) and p∈[N+αN,∞). Suppose that a(x):ZN→R satisfying
(A1) a(x)≥0 and the potential well Ω={x∈ZN:a(x)=0} is a non-empty, connected and bounded domain in ZN.
(A2) There exists a point x0 satisfying a(x)→∞ when d(x,x0)→∞.
Then (1.3) has a ground state solution uλ for any constant λ>1.
In order to observe the asymptotical properties of uλ as λ→∞, we first study the following Dirichlet problem.
We study the Eq (1.4) in the H10(Ω) with the norm:
Similarly, the Eq (1.4) also possess a ground state solution.
Theorem 1.4. Let N∈N∗, α∈(0,N) and p∈(1,∞). Suppose Ω is a non-empty, connected and bounded domain in ZN. Then the Eq (1.4) has a ground state solution u∈H10(Ω).
Finally, we show that the solutions uλ of (1.3) converge to a solution of (1.4) as λ→∞ when the domain in (1.4) is the set of satisfying a(x)=0. On the other words, we obtain the following conclusions.
Theorem 1.5. Let N∈N∗, α∈(0,N) and p∈[2,∞). Assume that a(x) satisfies (A1) and (A2), then for any sequence λk→∞, up to a subsequence, the corresponding ground state solutions uλk of (1.3) converge in H1(ZN) to a ground state solution of (1.4).
The remaining parts of this paper are organized as follows. In Section 2, we give basic definitions and Lemmas on the lattice graph. In Section 3, we establish the discrete Brézis-Lieb Lemma for the nonlocal term and some important conclusions. Section 4 is devoted to proving Theorem 1.1. Then we complete the proof of Theorems 1.3 and 1.4 in Section 5. Finally, we prove Theorem 1.5 in Section 6.
2.
Preliminary results
In this section we give some basic results on the lattice graph. Firstly, we present the formula of integration by parts on lattice graph, which is the basic conclusion when we apply variational methods. Here we omit the concrete proofs and one can refer to [22] for more details.
Lemma 2.1. Suppose that u∈H1(ZN). Then for any v∈Cc(ZN), we obtain
Lemma 2.2. Suppose Ω⊂ZN is a bounded domain and u∈H10(Ω). Then for any v∈Cc(Ω), we have
Now we are ready to define the weak solution as follows.
Definition 1. Assume u∈H1(ZN). A function u is called a weak solution of (1.1) if for any φ∈H1(ZN),
Definition 2. Assume u∈Eλ(ZN). A function u is called a weak solution of (1.3) if for any φ∈Eλ(ZN),
Definition 3. Assume u∈H10(Ω). A function u is called a weak solution of (1.4) if for any φ∈H10(Ω),
Notice that if u is a weak solution of (1.1), we infer from Lemma 2.1 that for any test function φ∈H1(ZN),
For any fixed x0∈ZN, choosing a test function φ:ZN→R in (2.6) which is defined as
we obtain
which implies that u is a point wise solution of (1.1). Thus, we have the following conclusion for the relationship between the weak solution and the point wise solution.
Proposition 2.3. If u is a weak solution of (1.1), then u is a point wise solution. Similarly, if u is a weak solution of (1.3) or (1.4), then u is also a point wise solution of the corresponding equation.
Finally, we state the following conclusions for the Sobolev embedding.
Lemma 2.4. ([38]) H1(ZN) is continuously embedded into ℓq(ZN) for any q∈[2,∞]. Namely, for any u∈H1(ZN), there exists a constant Cq depending only on q such that
Lemma 2.5. ([27,Lemma 2.6]) Assume that λ>1 and a(x) satisfies (A1) and (A2). Then Eλ(ZN) is continuously embedded into ℓq(ZN) for any q∈[2,∞] and the embedding is independent of λ. Namely, there exists a constant Cq depending only on q such that for any u∈Eλ(ZN), ‖u‖ℓq(ZN)≤Cq‖u‖Eλ(ZN). Moreover, for any bounded sequence {uk}∈Eλ(ZN), there exists u∈Eλ(ZN) such that, up to a subsequence,
Lemma 2.6. ([27,Lemma 2.7]) Assume that Ω is a bounded domain in ZN. Then H10(Ω) is continuously embedded into ℓq(Ω) for any q∈[1,∞]. Namely, there exists a constant Cq depending only on q such that for any u∈H10(Ω), ‖u‖ℓq(Ω)≤Cq‖u‖H10(Ω). Moreover, for any bounded sequence {uk}∈H10(Ω), there exists u∈H10(Ω) such that, up to a subsequence,
3.
Discrete Brézis-Lieb Lemma
In this section, we give a proof of the discrete Brézis-Lieb Lemma(see [3,39,40] for the continuous case) for the nonlocal term on the lattice graph. First, let us recall the discrete Brézis-Lieb Lemma [38] for the local case.
Lemma 3.1. ([38,Lemma 9]) Let Ω⊂ZN be a domain and {un}⊂ℓq(Ω) with 0<q<∞. If {un} is bounded in ℓq(Ω) and un→u pointwise on Ω as n→∞, then
From Lemma 3.1 and [38,Corollary 10], it is not hard for us to get the following corollary.
Corollary 3.2. Assume V is a uniformly bounded positive function. If {un} is bounded in H1(ZN) and un→u pointwise on ZN, then
Next, we prove a variant of the discrete Brézis-Lieb Lemma.
Lemma 3.3. Let Ω⊂ZN be a domain, 1≤q<∞. If the sequence {un} is bounded in ℓr(Ω) and un→u pointwise on Ω as n→∞, then for every q∈[1,r],
Proof. Applying the Fatou's Lemma, we obtain
Fix ε>0 and for all a,b∈R, there exists Cε satisfying
Hence we obtain
Thus
It follows from the Dominated Convergence Theorem that
From the definition of fεn, we obtain
Moreover, one deduces from the basic inequality (a+b)p≤Cp(ap+bp)(∀a,b,p>0) that
Therefore, from (3.6) and (3.7), we get
Then let ε→0,
This finishes the proof.
Next, we state the discrete Brézis-Lieb type Lemma.
Lemma 3.4. Suppose Ω⊂ZN and 1≤p<∞. If the sequence {un} is bounded in ℓp(Ω) and un→u pointwise on Ω as n→∞, then for every x∈ZN, we have
Proof. Since x≠y and x,y∈ZN, we obtain |x−y|≥1 and it follows that
Thus the proof is complete as n→∞ from Lemma 3.3.
Now we are in position to establish the discrete Brézis-Lieb Lemma for the nonlocal term of the functional. To this purpose we first present an important inequality on the lattice graph which is studied by many authors in the continuous setting.
Lemma 3.5. ([41]) (Discrete Hardy-Littlewood-Sobolev Inequality) Let 0<α<N, 1<r,s<∞ and 1r+1s+N−αN≥2. Assume f∈ℓr(ZN) and g∈ℓs(ZN). Then there exists a positive constant Cr,s,α depending only on r,s,α such that
The paper [38] also give the following equivalent form of (3.9).
Lemma 3.6. Let 0<α<N, 1<r,t<∞ and 1t+αN≤1r. Assume f∈ℓr(ZN), then there exists a positive constant Cr,t,α depending only on r,t,α such that
The next lemma states the discrete Brézis-Lieb Lemma for the nonlocal term.
Lemma 3.7. Let 1≤p<∞ and the sequence {un} is bounded in ℓ2NpN+α(ZN). Suppose un→u pointwise on ZN as n→∞, then
Proof. For every n, we can divide the left-hand side of (3.11) into two parts,
where
By Lemma 3.3, taking q=p, r=2NpN+α, one has
We first give the estimate for the term J1. From the Hardy-Littlewood-Sobolev inequality (Eq 3.9), one deduces that
From (3.13) and ‖u‖ℓ2NpN+α(ZN)≤lim infn→∞‖un‖ℓ2NpN+α(ZN)<∞, it gives that
Now we give the estimate for J2. From the Banach-Alaoglu theorem, |un−u|p⇀0 weakly in ℓ2NN+α(ZN) as n→∞ and (3.9), we deduce that
We infer from (3.10) that
Moreover, |un−u|p⇀0 in ℓ2NN+α(ZN). Hence we know that
Then one deduces from (3.13) that limn→∞J2=0. This together with (3.14), we get the results.
4.
Proof of the Theorem 1.1
In the present section we are devoted to the proof of Theorem 1.1. Obviously, for any function u:ZN→R, the energy functional related to (1.1) is given by
Notice that the functional J is well defined in H1(ZN). Indeed, assume that u∈ℓ2NPN+α(ZN), then by applying the Hardy-littlewood-Sobolev inequality (Eq 3.9) to the function f=|u|p∈ℓ2NN+α(ZN), we obtain
It sufficient for us to confirm when the condition u∈ℓ2NPN+α(ZN) is satisfied. According to the Lemma 2.4, H1(ZN) is continuously embedded into ℓ2NpN+α(ZN) if and only if p≥N+αN. Moreover, we infer from the inequality (Eq 3.9) that
where the constant CN,p,α depends only on N,α and p. Based on the previous argument, the function J is meaningful.
Next, we define the Nehari manifold related to (4.1) by
Let
If there exists a function u∈N satisfying J(u)=m, then the function u is called a ground state solution. Obviously, u is a critical point of J.
Next, we shall find the critical point of the functional (4.1).
Proposition 4.1. Let N∈N∗, α∈(0,N) and p∈(1,∞). If u∈H1(ZN)∩ℓ2NpN+α(ZN)∖{0} and V is a uniformly bounded positive function, there holds
where
Proof. For any t>0, we set
By a direct computation,
When s′(t)=0, we can obtain a unique tu such that s′(tu)=0. Moreover, one has
Since as 0<t<tu, s′(t)>0 and as t>tu, s′(t)<0, thus
This finishes the proof.
Note that the ground state energy of J can be characterized as
In the next conclusion we show the infirmum of S(u) can be achieved by some nontrivial function.
Proposition 4.2. Let N∈N∗, α∈(0,N) and p∈(N+αN,∞). Suppose that V is a uniformly bounded positive function, then there exists u∈H1(ZN) satisfying
Combining with Propositions 4.1 and 4.2, we complete the proof of Theorem 1.1. Then we only need to focus on the proof Proposition 4.2 in the next. In the Euclidean space, we are familiar with the different kinds of the proof of Proposition 4.2. For example, a strategy consists in minimizing among radial functions and then prove with the symmetrization by rearrangement that a radial minimizer is a global minimizer. In our setting, the main difficulty for the analysis is that there is no proper counterpart for radial functions on ZN and moreover we do not have the compactness in this problem. To overcome the difficulty we borrow an idea of [42,Section 4](also see [24]) and use the constraint method to prove Proposition 4.2.
Proof of Proposition 4.2. Set
then we can get
Let {un} be a minimizing sequence in H1(ZN) such that
and limn→∞1S(un)=1m. By the discrete Hardy-Littlewood-Sobolev inequality (Eq 3.9), we obtain
Taking the limit from both sides, one can see
Since p>N+αN, we obtain
Hence, there exists a subsequence {un} and a sequence {yn}⊂ZN such that |un(yn)|≥C for each n. By translations, we define ˜un=:un(y+knT) with kn=(k1n,⋯kNn) to ensure that (yn−knT)⊂Ω where Ω=[0,T)N∩ZN is a bounded domain in ZN. Then for each ˜un,
Moreover, by translation invariance, we infer from V(x) is T-periodic in x that
and
Without loss of generality, we can get a minimizing sequence {un} satisfying ‖un‖ℓ∞(Ω)≥C>0. Since Ω is bounded, there exists at least one point, say x0, such that un(x0)→u(x0)≥C>0. Since the sequence {un} is bounded in H1(ZN), it follows that un⇀u in H1(ZN) and un→u≠0 pointwise on ZN. Then it follows from Corollary 3.2 and Lemma 3.7 that
For every n, we have
Since u≠0, one has
which yields
By (4.7), one has
By Fatou's Lemma, one gets
Then it is enough for us to prove that ∫ZN(|∇un|2+V(x)u2n)dμ=1. Using a contradiction argument, suppose that
then by
However, (a+b)p>ap+bp if a,b>0. This yields a contradiction by (4.7).
5.
Proof of Theorems 1.3 and 1.4
In this section we shall prove the existence result for (1.3) and (1.4) by using the standard variational methods. Obviously, the functional associated with the problem (1.3) is given by
where p≥N+αN. The corresponding Nehari manifold is defined as
We define the least energy level mλ by
Then we first prove the Nehari manifold Nλ is nonempty.
Lemma 5.1. The Nehari manifold Nλ is non-empty.
Proof. For t∈R and fix a function u∈Eλ(ZN)∖{0} and, we define
Since p>1 and u≠0, it is obvious that γ(t)>0 for small t>0 and that limt→∞γ(t)=−∞. Then there exists t0∈(0,∞) such that γ(t0)=0, which implies that t0u∈Nλ.
Next, we prove the least energy level mλ is positive.
Lemma 5.2. We have mλ=infu∈NλJλ(u)>0.
Proof. Since u∈Nλ, then
By Lemma 2.5 and (3.9), we obtain
where C is independent of λ. It follows from p>1 that
This gives
The next lemma states that the least energy mλ can be achieved.
Lemma 5.3. The value mλ can be achieved by some uλ∈Nλ. Namely, there exists some uλ∈Nλ such that Jλ(uλ)=mλ.
Proof. Take a minimizing sequence {uk}⊂Nλ such that limk→∞Jλ(uk)=mλ. Since
we have that {uk} is bounded in Eλ(ZN), where limk→∞ok(1)=0. By Lemma 2.5, we can assume that there exists some uλ∈Eλ(ZN) such that
From the discrete Hardy-Littlewood-Sobolev inequality (Eq 3.9), we infer that
Therefore, one has
Then from the Lemma 3.7, we get
Since the Eλ norm is weakly lower semi-continuous, one has
Next it suffices to show that uλ∈Nλ. We infer from (5.1) that
This together with (5.2) which implies that
Therefore uλ≠0. Since uk∈Nλ, we infer that
We use the contradiction argument to obtain our results. Assume that
Similar as the proof of Lemma 5.1, there would exist a t∈(0,1) such that tuλ∈Nλ. This implies that
This contradicts the fact that mλ=infu∈NλJλ(u). Therefore we have uλ∈Nλ. Moreover, we infer from (5.3) that mλ is achieved by uλ.
The following Lemma finishes the proof of Theorem 1.3.
Lemma 5.4. uλ∈Nλ is a critical point for Jλ.
Proof. It is enough for us to prove that for any ϕ∈Eλ(ZN), there holds
Since uλ≢0, we can choose a constant ε>0 such that uλ+sϕ≢0 for all s∈(−ε,ε). Furthermore, for every given s∈(−ε,ε), we can find some t(s)∈(0,∞) satisfying t(s)(uλ+sϕ)∈Nλ. Indeed, t(s) can be taken as
Obviously, we can get t(0)=1. Take a function γ(s):(−ε,ε)→R which is defined as
For t(s)(uλ+sϕ)∈Nλ and Jλ(uλ)=infu∈NλJλ(u), γ(s) achieves its minimum at s=0. Together with uλ∈Nλ and J′λ(uλ)uλ=0, it follows that
Next we focus on the proof of Theorem 1.4. The functional associated with the Eq (1.4) is given by
We remark that ‖u‖ℓq(Ω)≤C‖u‖H10(Ω) for q∈[1,∞] by Lemma 2.6. Therefore, the functional JΩ(u) is well defined as p≥N+α2N. The corresponding Nehari manifold is defined as
Let mΩ be
Since Ω contains only finite vertices, the proofs of the previous results can be easily applied to the Eq (1.4). Moreover, p>1 is enough for us to prove Theorem 1.4. Here we omit the details of the proofs.
6.
Convergence of the ground state solution
In the current section, we mainly focus on the asymptotical properties of the solution. That is, we show that the ground state solutions uλ of (1.3) converge to a ground state solution of (1.4) as λ→∞. To accomplish this we first prove that any solution of (1.3) is bounded away from zero.
Lemma 6.1. There exists a constant σ>0 which is independent of λ, such that for any critical point u∈Eλ(ZN) of Jλ, we have ‖u‖Eλ(ZN)≥σ.
Proof. From Lemma 2.5 and the inequality (Eq 3.9), one has
where C is independent of λ. Then we can choose σ=(1C)pp−1 and Lemma 6.1 is proved.
The next lemma studies the property of (PS)c sequence of Jλ.
Lemma 6.2. For any (PS)c sequence {uk} of Jλ, there holds
Furthermore, there would exist a constant C1>0 independent of λ, such that either c≥C1 or c=0.
Proof. Since Jλ(uk)→c and J′λ(uk)→0 as k→∞, we have
which gives (6.1). By Lemma 2.5 and (3.9), for any u∈Eλ(ZN), we obtain
Take ρ=(12C2p)12p−2. If ‖u‖Eλ(ZN)≤ρ, we get
Take C1=p−12pρ2 and suppose c<C1. Since {uk} is a (PS)c sequence, it yields
Hence, for large k, we have
which implies that ‖uk‖Eλ(ZN)→0 as k→∞. It follows immediately that Jλ(uk)→c=0 and the positive constant can be taken as C1=p−12pρ2=(12C2p)1p−1.
Remark 6.3. If we take c=mλ, then there would exist a (PS)c sequence uk such that uk⇀uλ when proving the existence of a ground state solutions uλ. Since the Eλk norm of uλk is weakly lower semi-continuous, then ‖uλ‖Eλ(ZN) is bounded by 2pp−1mλ.
Next, we study the relationship between the ground states mλ and mΩ.
Lemma 6.4. mλ→mΩ as λ→∞.
Proof. Notice that mλ≤mΩ for every positive λ owing to NΩ⊂Nλ. Take a sequence λk→∞ satisfying
where mλk is the ground state and uλk∈Nλk is the corresponding ground state solution of (1.3). Then it follows M>0 from Lemma 6.2. According to Remark 6.3, we know that the Eλk norm of uλk is controlled by the constant 2pp−1mΩ, which is independent of λk. Up to a subsequence, we can assume that uλk(x)→u0(x) on ZN and for any q∈[2,+∞), uλk→u0 in ℓq(ZN). Moreover, we get that u0≢0 from Lemma 6.1.
We first claim that u0|Ωc=0. If it is not true, we can find a point x0 satisfying u0(x0)≠0. Since uλk∈Nλk, then
Since a(x0)>0,uλk(x0)→u0(x0)≠0 and λk→∞, we get
which contradicts with the conclusion mλk≤mΩ. Since the norm ‖⋅‖H1(ZN) is weakly lower semi-continuous and (5.2), we get
Noticing that u0|Ωc=0, we get
Then there exists α∈(0,1] such that αu0∈NΩ, i.e.,
This implies that
Consequently, M≥mΩ. Combining with (6.3), we get that
Next, we are devoted to proving Theorem 1.5.
Proof of Theorem 1.5. We need to prove that for any sequence λk→∞, the corresponding uλk∈Nλk satisfying Jλk(uλk)=mλk converges in H1(ZN) to a ground state solution uΩ of (1.4) along a subsequence. According to Remark 6.3, the Eλk norm of uλk is uniformly bounded by the constant 2pp−1mΩ, which is independent of λk. Consequently, we can assume that there would exist some u0 satisfying uλk(x)→u0(x) in ZNand for any q∈[2,+∞), uλk→u0 in ℓq(ZN). Moreover, we get that u0≢0 from Lemma 6.1. As what we have done in Lemma 6.4, we can prove that u0|Ωc=0.
First, we claim that
and
If for some δ>0, there holds
we have
Then there exists α∈(0,1) such that αu0∈NΩ. On the other hand, if
we also have ∫Ω∪∂Ω(|∇u0|2+u20)dμ<∫Ω(∑y≠xy∈Ω|u0(y)|p|x−y|N−α)|u0|pdμ. Then in both cases, we can find α∈(0,1) such that αu0∈NΩ. Consequently, we have
which arrives at a contradiction.
To prove Theorem 1.5, we also need verify that u0 is a ground state solution of (1.4). The first step is to prove that u0 is a critical point of JΩ. Since J′λk(uλk)ϕ=0, for any ϕ∈H10(Ω)⊂H1(ZN), we have
Since a(x)=0 in Ω and ϕ=0 in Ωc, there holds
Let k→∞, the above equality becomes
Since uλk→u0 in ℓp(ZN) with p≥2 and Lemma 3.4, we obtain
which yields u0∈NΩ, and u0 is a solution of (1.4).
Finally, we prove that u0 achieves the infimum of JΩ in NΩ.
Since Jλk(uλk)=mλk, we get JΩ(u0)=mΩ by Lemma 6.4. Hence the function u0 is a ground state solution of (1.4).
Finally, we have the following lemma for the convergence of the sequence {uλk}.
Corollary 6.5. Furthermore, we have limk→∞‖uλk−u0‖Eλk(ZN)=0.
Proof. Indeed, since uλk∈Nλk and u0|Ωc=0, we have
which finishes the proof.
Acknowledgments
This work was supported by NNSF of China (Grants 11971202), Outstanding Young foundation of Jiangsu Province No. BK20200042.
Conflict of interest
The authors declare no conflict of interest.













 DownLoad:
DownLoad: