Mathematical modeling the dynamics of Clonorchiasis in Guangzhou City of China

1.   Introduction

An estimated 15 million people are infected with clonorchiasis, predominantly in east Asia (ie, China, South Korea, northern Vietnam, and parts of Russia) ^[1,2]. Clonorchiasis infection is primarily related to liver and biliary disorders, especially cholangiocarcinoma.

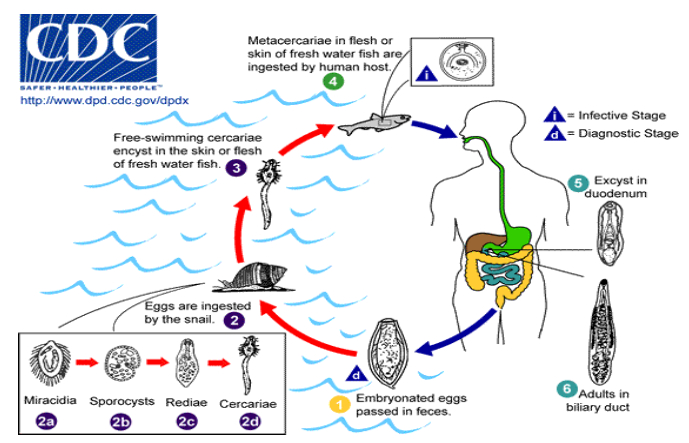
The first report on clonorchiasis in the medical literature was published in the Lancet on August 21, 1875 ^[3]. In 1910, Kobayashi first proved that freshwater fish act as the second intermediate host, and Muto discovered in 1918 that freshwater snails serve as the first intermediate host ^[4]. The life cycle of clonorchiasis is characterised by an alternation of sexual and asexual reproduction in different hosts ^[5,6,7]. Eggs laid by hermaphroditic adult worms, which can reach the intestine with bile fluids and are taken away with the faeces ^[8]. After freshwater snails ingest the eggs, miracidia hatch in the intestine and penetrate into the intestinal wall. By asexual reproduction, sporocysts, rediae, and then cercariae are produced. Cercariae escape from the snails, adhere to freshwater fish, and then develop into mature metacercariae in the subcutaneous tissues or muscles of the fish. When people eat raw or insufficiently cooked infected fish, metacercariae will enter the human body through gastric juice digestion as the final host (Figure 1).

Mathematical models have played significant roles for understanding and controlling of infectious diseases since the publication ^[9]. This work was motivated by the recent work for mathematical modeling of clonorchiasis ^[10], which had considered the transmission dynamic of clonorchiasis among human beings, snails and fish. However, snails are infected only after ingested eggs in faeces produced by parasitic worms in the bile ducts of infectious human being, fish are infected only after cercariae escaped from infectious snails and adhere to freshwater fish. In order to investigate the efficient strategies to control clonorchiasis, we must set up a mathematical model which responds the basic life cycle of clonorchiasis, and consider eggs both in an infected individual and in freshwater, cercariae both in infectious snails and in freshwater. Praziquantel and albendazole are recommended drugs for treatment of clonorchiasis. The efficacy of those drugs depends on the treatment schedule and infection intensity. We will consider the treatment (or recovery) rate in our mathematical model of clonorchiasis such that we can compare the efficacy of different control strategy.

This paper is organized as follows. In section 2, we will set up a mathematical model to describe the transmission dynamic of clonorchiasis, calculate the basic reproductive number, and analyze the relationship between the the basic reproductive number and the global property of the model. In section 3, we will fit the data of human clonorchiasis infection ratios of Guangzhou City of Guangdong Province in China from 2006-2012 by using the Genetic Algorithm and calculate the 95% confidence intervals of infection ratios of human. In section 4, we will give the prevention and control strategy of clonorchiasis.

2.   Mathematical modeling of clonorchiasis

2.1.   Mathematical modeling

Both clonorchiasis and schistosomiasis have an important intermediate medium snail as vector. There are many papers to study the infectious mechanisms and control strategies of schistosomiasis ^{[11,12,13,14,15,16,17]}. They use the qualitative and the quantitative analysis to study the human$-$snail transmission of schistosomiasis. Especially, Chen et. al ^[12] investigated the human$-$cattle$-$snail transmission of schistosomiasis.

In order to investigate the control strategies of clonorchiasis, we set up the following $S_hI_hR_h$ $ES_sI_sCS_fI_f$ model by the the life cycle of clonorchiasis:

where $S_h(t)$, $I_h(t)$ and $R_h(t)$ denote the number of the susceptible, the infectious and the recovered for human beings, $E(t)$ and $C(t)$ denote the number of eggs and cercariae, $S_s(t)$ and $I_s(t)$ denote the number of the susceptible and the infectious for snails, $S_f(t)$ and $I_f(t)$ denote the number of the susceptible and the infectious for freshwater fish.

Parameters in system (2.1) are summarized in Table 1 and all parameters are assumed to be nonnegative. $\delta_e$ and $\delta_c$ denote the consumption rate of eggs per snail and consumption rate of cercariae per fish, respectively. $p_e$ denotes the egg proliferation rate by hermaphroditic adult worms in an infected individual, those eggs are attached with the faeces. Only a part of the faeces flows into fresh water. Parameter $\theta_e$ denotes the ratio of eggs in fresh water. Similarly, $p_c$ denotes the cercaria proliferation rate per infected snail in fresh water. $\theta_c$ denotes the proportion of cercariae survival in fresh water.

The number of eggs consumed by snails compared to the number of eggs in the environment is too small ^[17]. Thus, the term $\delta_e\beta_sS_s(t)E(t)$ can be removed from the fourth equations of system (2.1). Similarly, the term $\delta_c\beta_fS_f(t)C(t)$ can be removed from the seventh equations of system (2.1). System (2.1) can be written in the following form:

In this paper, we assume that all solutions of system (2.2) satisfy the following initial conditions:

Let

Lemma 2.1. The solutions of system (2.2) are positive if all initial values are positive and $\Omega$ is a positively invariant set of system (2.2).

Proof. At first, we will prove the positivity of the solution of system (2.2). By system (2.2), we have

for $t\geq 0.$ Considering the following auxiliary system:

We can obtain

By the comparison principle, we have obtained that all solutions of system (2.2) are positive when their initial values are positive. Therefore, $R^9_+ = \{(S_h(t), I_h(t), R_h(t), E(t), S_s(t), I_s(t),$ $C(t), S_f(t), I_f(t))\in R^9\mid S_h(t)\geq 0, I_h(t)\geq0, R_h(t)\geq 0, E(t)\geq0, S_s(t)\geq 0, I_s(t)\geq0, C(t)\geq0, S_f(t)\geq 0, I_f(t)\geq0\}$ is positive invariant with respect to system (2.2).

And then, we will prove that $\Omega$ is a positively invariant set of system (2.2). Let $X(t) = (S_h(t), I_h(t), R_h(t), E(t), S_s(t), I_s(t), C(t), S_f(t), I_f(t))$ be any positive solution of system (2.2) with initial condition $X(0)\in \Omega$. Let $N_h(t) = S_h(t)+R_h(t)+I_h(t)$, $N_s(t) = S_s(t)+I_s(t)$, and $N_f(t) = S_f(t)+I_f(t)$ denote the total population of human beings, the total population of snails, and the total population of fish, respectively. The total population of human beings satisfies the differential equation:

This implies that $N_h(t)\rightarrow \frac{\lambda_h}{\mu_h}$ as $t\rightarrow +\infty,$ or $\lim_{t\rightarrow +\infty}(S_h(t)+I_h(t)+R_h(t)) = \frac{\lambda_h}{\mu_h}$. Similarly, we have

$N_s(t)\rightarrow \frac{\lambda_s}{\mu_s}$ and $N_f(t)\rightarrow \frac{\lambda_f}{\mu_f+q}$ as $t\rightarrow +\infty,$ or $\lim_{t\rightarrow +\infty}(S_s(t)+I_s(t)) = \frac{\lambda_s}{\mu_s}$ and $\lim_{t\rightarrow +\infty} (S_f(t)+I_f(t)) = \frac{\lambda_f}{\mu_f+q}.$

By the 4th and 7th equation of system (2.2), we have

$\lim_{t\rightarrow +\infty} E(t) \leq \frac{\theta_ep_e\lambda_h}{\mu_e\mu_h}$, $\lim_{t\rightarrow +\infty} C(t) \leq \frac{\theta_cp_c\lambda_s}{\mu_c\mu_s}.$ Thus, $\Omega$ being a positively invariant set of system (2.2) has been proven.

2.2.   The basic reproduction number

The basic reproduction number of system (2.2) can be derived by the next generation matrix as in Diekmann et al. ^[18,19], Van den Driessche and Watmough ^[20]. Let $x = (I_h, I_s, I_f, E, C, S_h, R_h,$ $S_s, S_f)^T$. System (2.2) can be written as the following form:

where $\mathscr{V}(x) = \mathscr{V}^-(x)-\mathscr{V}^+(x),$ which denotes the transfer rate of individuals into or out of each population set and $\mathscr{F}(x)$ denotes the rate of occurrence of new infections and

According to the method in Diekmann et al. ^[18], the derivatives $D \mathscr{F}(x)$ and $D \mathscr{V}(x)$ are partitioned as

where $F, V, J_1$ and $J_2$ are given by

We can obtain the inverse matrix of $V$ as

The basic reproduction number is defined as the spectral radius of the nonnegative matrix $FV^{-1}$ ^[20]. Therefore, we have obtained the formula of the basic reproduction number:

2.3.   Global stability of the system (2.2)

At first, we will prove that the system (2.2) admits a unique endemic equilibrium $x^* = (S_h^{*}, I_h^{*}, R_h^{*},$ $E^{*}, S_s^{*}, I_s^{*}, C^{*}, S_f^{*}, I_f^{*})$. And then, we will prove that $x^*$ is globally asymptotically stable in the region $R^9_{+}.$ Here $S_h^{*}, I_h^{*}, R_h^{*}, E^{*}, S_s^{*}, I_s^{*}, C^{*}, S_f^{*}, I_f^{*}$ satisfy the following equilibrium equations:

By solving equations (2.4), we have

It is obvious to follow that $I_f^{*} > 0$ if and only if $R_0 > 1$. By the equations (2.4) and $R_0 > 1$, there is only one $x^* \in \Omega$ for system (2.2). We have the following result.

Theorem 2.2. If $R_0 > 1,$ then the endemic equilibrium $x^*$ is globally asymptotically stable in the interior of $R^9_{+}.$

Proof. The existence of $x^*$ of system (2.2) has been shown in above. We will only prove that $x^*$ of system (2.2) is globally asymptotically stable in the interior of $R^9_{+}$ when $R_0 > 1$. Let $g(a) = 1-a+\ln{a}$. It is easy to verify that for $\forall a > 0$,

and the equality holds if and only if $a = 1$.

Let $L_1 = \int_{S_h^{*}}^{S_h}\frac{z-S_h^{*}}{z}dz+I_h-I_h^{*}-\ln{\frac{I_h}{I_h^{*}}}, L_2 = \int_{S_s^{*}}^{S_s}\frac{z-S_s^{*}}{z}dz+I_s-I_s^{*}-\ln{\frac{I_s}{I_s^{*}}}, L_3 = \int_{S_f^{*}}^{S_f}\frac{z-S_f^{*}}{z}dz+I_f-I_f^{*}-\ln{\frac{I_f}{I_f^{*}}}, L_4 = E-E^{*}-E^{*}\ln{\frac{E}{E^{*}}}, L_5 = C-C^{*}-C^{*}\ln{\frac{C}{C^{*}}}.$ Differentiating $L_1, L_2, L_3, L_4$ and $L_5$ with respect to t along solution curves of system (2.2), we have

where $1-\frac{S_h^{*}}{S_h}\leq -\ln{\frac{S_h^{*}}{S_h}}$, $1-\frac{S_hI_fI_h^{*}}{S_h^{*}I_f^{*}I_h} \leq -\ln{\frac{S_hI_fI_h^{*}}{S_h^{*}I_f^{*}I_h}}$.

Hence, we can define the following Lyapunov function:

It follows that

Moreover, the equality $L^{'} = 0$ holds if and only if $I_h = I_h^{*}, I_s = I_s^{*}, I_f = I_f^{*}, E = E^{*}, C = C^{*}, S_h = S_h^{*}, R_h = R_h^{*}, S_s = S_s^{*}$ and $S_f = S_f^{*}.$ Therefore, $x^*$ of system (2.2) is globally asymptotically stable in the region $R^9_{+}$ if $R_0 > 1.$

If $R_0 < 1$, the endemic equilibrium $x^*$ of system (2.2) does not exist. There is only the disease-free equilibrium $x^0$, where $x^{0} = (S_h^{0}, 0, 0, 0, S_s^{0}, 0, 0, S_f^{0}, 0)$. We have the following result.

Theorem 2.3. If $R_0 < 1,$ then the disease-free equilibrium $x^0$ of system (2.2) is globally asymptotically stable in the region $R^9_{+}$.

Proof. In order to prove the Theorem 2.3, at first we will prove that the origin of a subsystem of system (2.2) is globally asymptotically stable in $R^5_+$, where $R^5_+ = \{(I_h(t), I_s(t), I_f(t), E(t), C(t))\in R^5 \mid I_h(t)\geq 0, I_s(t)\geq 0, I_f(t)\geq 0, E(t)\geq 0, C(t)\geq 0\}$. And then, we will prove that the $x^0$ of system (2.2) is globally asymptotically stable in the region $R^9_{+}$.

Step 1 Let $x = (I_h, I_s, I_f, G, C)^T$. By system (2.2), we have the following subsystem.

The origin $\overline{x_{0}} = (0, 0, 0, 0, 0)$ is an equilibrium of the subsystem (2.5). All solutions of system (2.5) remain nonnegative and

is positively invariant for system (2.5). If the origin $\overline{x_{0}}$ is globally stable for $\forall x \in \Omega_0$, then, $\overline{x_{0}}$ is globally stable for $\forall x \in R^5_+$.

By system (2.5), for $\forall x \in \Omega_0$ we can obtain the following inequalities

where $F$ and $V$ are expressed as (2.3). We construct a new linear system

where $x \in R^5_+$. By the Perron-Frobenius Theorem ^[21], there is a nonnegative left eigenvector $\nu$ of the nonnegative matrix $V^{-1}F$ corresponding to the eigenvalue $\rho(V^{-1}F) = R_0,$ that is $\nu^TV^{-1}F = R_0\nu^T.$ Define a Lyapunov function

Then the derivative of $V_0$ along with system (2.7) is

If $R_0 < 1,$ then $V_0^{'}\leq0.$ Let

If $R_0 < 1,$ $V_0^{'} = 0$ implies that $\nu^Tx = 0.$ Thus, $I_h = 0, I_s = 0, I_f = 0, G = 0, C = 0.$ Therefore, the largest invariant set of $\Psi$ is the point $\{\overline{x_{0}}\}.$ By LaSalle Invariance Principle ^[22], $\overline{x_{0}}$ of the new linear system (2.7) is globally asymptotically stable in $R^5_+$. By inequalities (2.6) and the comparison theorem of ordinary differential equation, each component of the system (2.5) must approach to zero when its initial value in $\Omega_0$. We have finished the proof that the origin of the system (2.5) is globally asymptotically stable in the region $\Omega_0$ when $R_0 < 1.$

Step 2 Now, we will prove that $x^0$ of system (2.2) is globally asymptotically stable in the region $R^9_{+}$. By Step 1, for $\forall \varepsilon > 0,$ there exists a $T > 0$ such that for $t > T,$ we have

When $t > T,$ by the first equation of system (2.2), we have

We construct the following equations:

By the comparison theorem of ordinary differential equation, we have

Let $\varepsilon > 0$ be sufficiently small. We have

Similarly, from the third, fifth and eighth equations of system (2.2), we can prove

It follows that the disease-free equilibrium $x^{0} = (\frac{\lambda_h}{\mu_h}, 0, 0, 0, \frac{\lambda_s}{\mu_s}, 0, 0, \frac{\lambda_f}{p+\mu_f}, 0)$ of system (2.2) is globally asymptotically stable.

3.   Data and numerical simulations

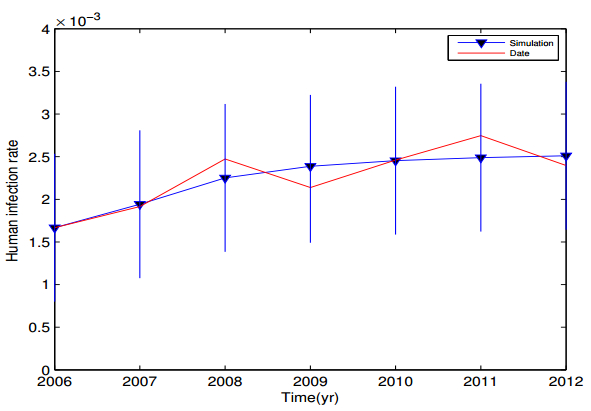
The data are infection ratios of human in Guangzhou City of Guangdong Providence in China from 2006-2012 ^[23] (see Figure 2). The infection ratio of human in model (2.2) is determined by the formula $\frac{I_h(t)}{N_h(t)}$. The initial values of system (2.2) are given by $S_h(0) = 9.4652\times 10^6, I_h(0) = 1.968\times 10^4, R_h(0) = 2.33 \times 10^6, E(0) = 120, S_s(0) = 6.95\times 10^3, I_s(0) = 130, C(0) = 100, S_f(0) = 2.2628\times 10^5, I_f(0) = 1.87 \times 10^4$. Some parameter values are cited from references, the other parameter values are estimated by calculating the minimum sum of square (MSS):

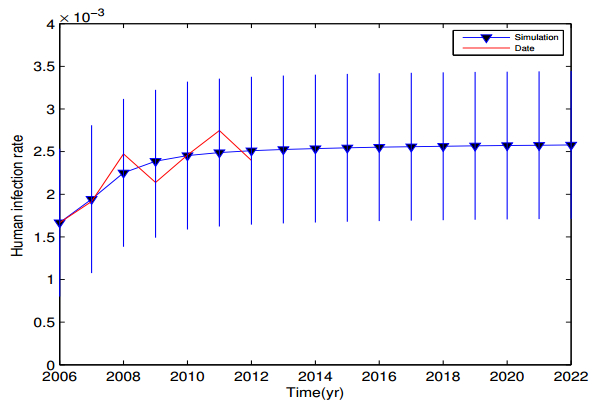
The minimum sum of square (MSS) can be regarded as an optimization problem which is solved using Genetic Algorithm ^[24,25]. The efficiency of Genetic Algorithm depends on the appropriate choice of the starting population along with other associated parameters. The initial population size plays an important role in the quality and efficiency of the algorithm, and small population size results in local convergence or requirement of large generations. To avoid this, the population size 1000 and the gene size 50 are chosen. A crossover probability of 0.55 and mutation probability of 0.15 are chosen to maitain diversity in the population. By the parameter values in Table 1, we can estimate that the basic reproduction number of human clonorchiasis is $R_0 = 1.41$. This result is shown that clonorchiasis will be epidemic in Guangzhou City. Figure 3 presents the prediction of human clonorchiasis infection ratios and of the 95% confidence intervals.

4.   Conclusion and discussion

By simulation of the data of human clonorchiasis infection ratios of Guangzhou City of Guangdong Province from 2006–2012 (see Figure 2), we have obtained that the basic reproduction number is $R_0 = 1.41$ which indicates that clonorchiasis will be epidemic in Guangzhou City. The wide distribution of intermediate hosts and reservoir hosts, human eating habits, the lack of the food safety supervision of freshwater fish, and relatively undeveloped techniques for detection and treatment are contributing to the prevalence of clonorchiasis ^[23]. Therefore, it is very difficult to eradicate clonorchiasis even if some chemotherapy and control programmes have been implemented over several years in a few endemic areas ^[26,27].

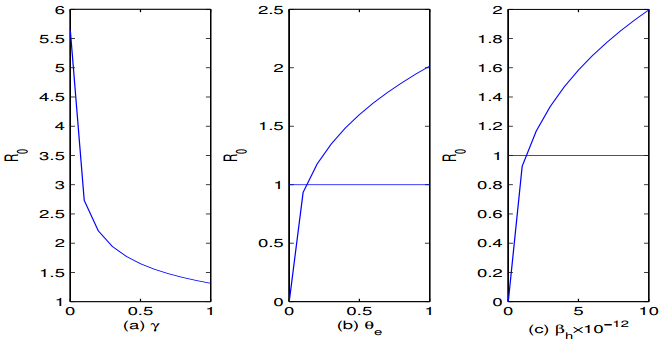
In Table 2, we have proposed seven types of control strategies dealing with three parameters $\beta_h$, $\gamma$, $\theta_e$ which mean decreasing the transmission rate from infected fish to human, increasing the recovery rate of human being, and decreasing the ratio of the eggs in fresh water. If we decrease by half of the transmission rate from infected fish to human, increase to one for the recovery rate of human being, and decrease by half of the ratio of the eggs in fresh water, respectively, it is still impossible to eradicate the clonorchiasis, which means that single measure is difficult to eradicate the clonorchiasis. However, increasing the recovery rate has small effect on the epidemic of the clonorchiasis (see Figure 4(a)), decreasing the transmission rate from infected fish to human or decreasing the ratio of the eggs in fresh water has obvious effect on the epidemic of the clonorchiasis (see Figure 4(b), (c)).

The prevention and control strategy of clonorchiasis must be a combination of two or more measures, including health education, health promotion, chemotherapy and environmental reconstruction ^[28,29]. Health education includes the broadcast of educational programmes on television, broadcast and VCDs, billboard/propaganda paintings, the distribution of health guide booklets, and the transmission of disease-related knowledge to residents and school children. The contents of health education are avoid to eat raw or undercooked freshwater fish. Health promotion includes the investigation of the infection rates and distribution of freshwater fish and snails in endemic areas, under surveillance of the infected ponds, rapid, convenient and accurate detection of metacercaria-tainted fish. Environment reconstruction includes removing toilets and pigsties from fishpond areas.

Acknowledgments

This research was partially supported by the National Nature Science Foundation of China (No.11871238, No.11871235, No.11471133), by self-determined research funds of CCNU from the colleges'basic research and operation of MOE (Grant No.CCNU16JCZX10, No.CCNU16A02009). We thank the anonymous reviewers very much for their valuable opinions on the original manuscript.

Conflict of interest

The authors declare no competing interests.