1. Introduction

Due to inadequate medical facilities in developing countries, they face difficulties to prevent the spread of new and re-emerging infectious diseases. Thus, on the emergence of any new infectious disease, these countries focus on the alternate of medical facilities to slow down its spread. Awareness, which brings the behavioral changes among the population, can be seen as partial treatment at no cost. Apart from this, awareness regarding the spread of any infectious disease also reduces the economic burden required for medication [24,31]. The correct and timely knowledge about the disease has the capacity to halt its spread. To disseminate awareness, several modes, like Television, radio, posters, social media, etc., can be used. Nowadays social media is an important platform to propagate information regarding the risk of infection and its control mechanisms. In India, the number of Smartphone users are predicted to reach $340$ million and could reach almost $468$ million by $2021$ [40]. Due to low literacy rates in rural population, especially in developing countries, the print and social media are less effective in comparison to TV and radio. Thus, Television and radio are powerful modes of transmission of any information to the public as they are accessible to most of the population. When an advertisement regarding the spread of any new infectious disease is broadcasted, people change their perception and adopt precautionary measures to halt its spread.

In the recent past, some studies have been conducted to assess the impact of media to control the spread of infectious diseases [11,13,27,28,29,41,37,38,36,43,44]. In particular, Sun et al. [41] have studied an SIS model to see the effect of media-induced social distancing on disease prevalence in two patch. Authors have assumed that the contact rate decreases as the number of infected individuals in respective patch increases. Their finding suggests that the media coverage reduces the disease prevalence and shorten the duration of infection. Misra et al. [29] have proposed an SIS model to see the effects of awareness through media campaigns on the prevalence of infectious diseases by considering media campaigns as a dynamic variable whose growth is proportional to the number of infected individuals. In the modeling process, it is assumed that media campaigns induce behavioral changes among susceptible individuals and they form an isolated aware class, which is fully protected from infection. The model analysis reveals that the number of infectives decreases as the media campaigns increases. Samanta et al. [37] have extended this model by assuming that aware susceptibles are also vulnerable to infection but at a lower rate than unaware susceptibles. In this model, authors have assumed that the growth rate of media campaigns is proportional to the mortality rate due to the disease. It is shown that the rate of execution of awareness programs has enough impact on the endemic state and sustained oscillations may arise through Hopf-bifurcation. Further, Dubey et al. [11] have studied the role of media and treatment on the emergence of an infectious disease. It is shown that media plays an important role to eliminate the disease in presence of treatment. As the information regarding the disease driven by media campaigns modifies the human behavior towards the disease [9,12,35]. Therefore, Funk et al. [14] have studied the impact of public awareness and local behavioral response, where the proportion of both the susceptible and infected individuals is aware and aware susceptibles are less vulnerable to infection whereas awareness among infected individuals reduces the infectivity due to pharmaceutical interventions. Kiss et al. [22] have proposed an SIRS model with treatment compartment by considering two classes of susceptible and infected individuals (responsive and non-responsive towards the information). Authors have assumed that the responsive infected individuals search treatment faster in comparison to non-responsive infected individuals and the rate of disease transmission among responsive susceptibles is less due to the impact of information. It is shown that if the dissemination rate is fast enough, the infection can be eradicated. Here, it may be noted that information provided to the population through media changes the human behavior and population adopt the precautionary measures, like the use of bed nets for Malaria [3,33], condoms for HIV/ AIDS [1,8,20,34], wearing of face masks for influenza [19,23], vaccination [4,5,39], voluntary quarantine [17], etc., to prevent the spread of such diseases. Buonomo et al. [5] have studied the effect of information on vaccination of an infectious disease and it is shown that for low media coverage, the endemic state is globally stable and for higher media coverage, this endemic state becomes unstable and sustained oscillations occur. The effect of media-related information on the spread of any infectious disease is also studied by considering the decrease in the contact rate between susceptibles and infectives as (ⅰ) the exponential decaying function of infectives [6,26], (ⅱ) saturated function of infectives [7,27,42]. In these studies, it is found that media coverage does not affect basic reproduction number of the disease but controls the prevalence of the disease in the population.

For some infectious diseases, mathematical models are also proposed to see the effect of time delay in the implementation of awareness programs [15,30,32] and it is shown that incorporation of time delay in the modeling process destabilizes the system. Recently, Kumar et al. [24] have proposed an SIRS model to see the role of information and limited optimal treatment on disease prevalence. Authors have considered that the growth rate of information is proportional to a saturated function of infected individuals. It is shown that combined effects of information and treatment are more fruitful and economical during the course of infection. Agaba et al. [2] have proposed a SIRS - type model to see the impact of awareness by considering private awareness, which reduces the contact rate between unaware and aware population and public information campaigns on disease prevalence. It is shown that both the private and public awareness have the capacity to reduce the size of epidemic outbreaks.

It may be noted that the change in human behavior towards the diseases through print media, social media, internet are limited only to educated people but TV ads have the capacity to impact large population (less educated people too) in a very short period of time and thus are more effective. In previous studies, it is assumed that the awareness programs are implemented proportional to the number of infected individuals by considering media campaigns as a dynamic variable or transmission rate as decreasing function of infected individuals due to media alerts. However, it is plausible to assume that the cumulative number of TV and social media ads increases proportional to number of infected individuals and their growth rate decreases with the increase in number of aware individuals as cost is also involved in broadcasting the information. In this regard, Kim and Yoo [21] have presented the cost effective analysis for the implementation of TV campaigns to promote vaccination against seasonal influenza in an elderly population and the remarkable increment in vaccination coverage is found due to TV campaigns.

Keeping in mind the importance of information provided through social media and TV ads to the population regarding the protection against any infectious disease and cost involved in TV advertisements, in the present, we formulate and analyze a nonlinear mathematical model to study the effect of TV and social media ads which includes internet information as well as print media for the control of an infectious disease. In the modeling process, it is assumed that the cumulative number of TV and social media ads increases proportional to the number of infected individuals and their growth rate decreases with the increase in number of aware individuals.

---

2. Mathematical model

Let in the region under consideration, $N(t)$ be the total population at any time $t$, which is divided into three sub-populations; namely $S(t)$-susceptible population, $I(t)$-infected population and $A(t)$-aware population. Let $\Lambda$ be the constant immigration in the class of the susceptible population at any time $t$ in the region. It is assumed that the population is homogeneously mixed and susceptible individuals contract the infection via the direct contact with infected individuals. Further, the variable $M(t)$ addresses the cumulative number of TV and social media advertisements, which includes internet information as well as print media etc., in the region at time $t$. The information regarding the protection against the disease is propagated through TV and social media ads and the growth rate of cumulative number of TV and social media ads is assumed to be proportional to the number of infected individuals. However, this growth rate decreases with a factor $f(A) = r\theta\frac{A}{\omega+A}$. In this case, the net growth rate of TV and social media ads to aware the population becomes $r\left(1-\theta\frac{A}{\omega+A}\right)$. The constant $\theta$ is the decay in advertisements due to increase in the number of aware individuals. Further, it is assumed that $M_0$ is the baseline number of TV and social media ads, which are always broadcasted. The constant $\omega$ represents the half saturation point [27] for this interaction as $f(A)$ attains half of its maximum value $r\theta$ when due to the effect of TV and social media ads, the aware population arrives at $\omega$. Here, it may be pointed out that for the feasibility of model, the value of $\theta$ lies between $0$ and 1. It is often observed that as time passes, the TV and social media ads lose their impact, which leads to the diminution in TV and social media ads. In this view, depletion in the cumulative number of TV and social media ads is also incorporated in the model. It is also assumed that TV and social media ads induce behavioral changes among susceptible individuals and they avoid their contact with infected individuals by forming an isolated class known as aware class, which is fully protected from infection as aware individuals use precautionary measures for their protection during the infection period. It may be noted that individuals in aware class may lose awareness with the passage of time and become susceptible again, this aspect has been considered by incorporating the term $\lambda_0 A$. Further, it is assumed that TV and social media ads have limited impact on the susceptible population and thus the susceptible population becomes aware at a rate $\lambda S\frac{M}{p+M}$ and moves to the aware class. Here, the constant $p$ represents the half saturation point for the impact of TV and social media ads on susceptible individuals and it attains half of its maximum value $\lambda S$ when the cumulative number of ads to aware the population arrives at $p$. The interaction between susceptible and infected individuals is assumed to follow the simple law of mass action.

Taking into account above facts, the dynamics of the problem is governed by the following system of nonlinear ordinary differential equations:

$\frac{dS}{dt} = \Lambda-\beta S I- \lambda S \frac{M}{p+M}+\nu I+\lambda_0 A-d S , \nonumber \\ \frac{dI}{dt} = \beta S I-(\nu+\alpha+d)I, \\ \frac{dA}{dt} = \lambda S \frac{M}{p+M}-(\lambda_0+d)A, \nonumber \\ \frac{dM}{dt} = r\left(1-\theta \frac{A}{\omega+A}\right)I-r_0(M-M_0), \nonumber$

(1)

where, $S(0)>0$, $I(0)\geq0$, $A(0)>0$ and $M(0)\geq M_0.$

In the above model system (1), $\beta$ is the contact rate between susceptibles with infectives and the constant $\lambda$ represents the dissemination rate of awareness among susceptible individuals due to which they form a different class and keep themselves away from infected individuals. The constants $\nu$, $\alpha$ and $d$ denote the recovery rate, disease-induced death rate and natural death rate, respectively. The constant $\lambda_0$ denotes the rate of transfer of aware individuals to susceptible class. The constant $r$ is the growth rate in TV and social media ads whereas the constant $r_0$ represents the diminution rate of TV and social media ads due to inefficiency and psychological barriers etc. [18].

Using the fact that $S+I+A = N$, the above system reduces to the following system:

$\frac{dI}{dt} = \beta I\left(N-I-A\right)-(\nu+\alpha+d)I, \nonumber \\ \frac{dA}{dt} = \lambda \frac{M}{p+M}\left(N-I-A\right)-(\lambda_0+d)A, \nonumber\\ \frac{dN}{dt} = \Lambda-d N-\alpha I, \\ \frac{dM}{dt} = r\left(1-\theta\frac{A}{\omega+A}\right)I-r_0(M-M_0).\nonumber$

(2)

As the study of model system (1) is equivalent to the study of model system (2), so we study model system (2).

For the solutions of model (2), the region of attraction [29] is given by the set:

$\Omega = \{(I, A, N, M)\in \mathbb{R}_+^4 : 0\leq I, A \leq\ N \leq \frac{\Lambda}{d}, 0\leq\ M \leq \left(M_0+\frac{r\Lambda}{r_0 d}\right) = M_r \}.\nonumber$

and attracts all solutions initiating in the interior of the positive orthant.

Proof. From the third equation of model system (2), we have

$\frac{dN}{dt} \leq \Lambda-dN$

and

$\frac{d}{dt}\left(N e^{dt}\right)\leq \Lambda e^{dt}.$

Now integrating the above equation from $0$ to $t$, we have

$N(t)\leq N_0 e^{-dt}+\frac{\Lambda}{d}$

Therefore, by using the theory of differential inequalities [25], we obtain, $\lim_{t\to\infty} \sup N(t)\leq \frac{\Lambda}{d}$, i.e., the human population can not be more than $N(t)\to N_\infty\leq \frac{\Lambda}{d}$. Since $S = N-I-A\geq0$, therefore $0\leq I, A\leq N\leq \frac{\Lambda}{d}$ for large $t\geq0$.

Further, from the fourth equation of model system (2) and using the fact, $I\leq \frac{\Lambda}{d}$ for large $t>0$, we obtain

$\frac{dM}{dt}+r_0 M\leq \left(r_0 M_0+r\frac{\Lambda}{d}\right).$

From the theory of differential inequality, we obtain

$\lim\limits_{t\to\infty}\sup M(t)\leq\left(M_0+\frac{r\Lambda}{r_0 d}\right).$

This implies that $0\leq M(t)\leq\left(M_0+\frac{r\Lambda}{r_0 d}\right)$ for large $t\geq0$.

---

3. Equilibrium analysis

In this section, we show the feasibility of all equilibria by setting the rate of change with respect to time '$t$' of all dynamical variables to zero. The model system (2) has two feasible equilibria, which are listed as follows:

(ⅰ) The disease-free equilibrium (DFE) $E_0\left(0, \frac{\lambda \Lambda M_0}{d(\lambda M_0+(\lambda_0+d)(p+M_0))}, \frac{\Lambda}{d}, M_0\right)$.

(ⅱ) The endemic equilibrium (EE) $E^*(I^*, A^*, N^*, M^*)$.

Let us denote $\displaystyle R_0 = \frac{\beta \Lambda}{d(\nu+\alpha+d)}$, the quantity $R_0$ is known as basic reproduction number when there is no TV and social media ads, the number of newly infected individuals produced by an infected individual during his / her whole infectious period in completely susceptible population [10], i.e., the infection persists in population if on average an infected individual infects more than one susceptible individuals during his / her whole infectious period. In the presence of TV and social media ads, this basic reproduction number is modified and becomes $R_1 = \frac{\beta\Lambda}{d(\nu+\alpha+d)}\left(\frac{(\lambda_0+d)(p+M_0)}{\lambda M_0+(\lambda_0+d)(p+M_0)}\right)$. It is easy to see that $R_1 <R_0$. The basic reproduction number ($R_1$) is obtained by using next generation matrix approach [10], for the proof, see Appendix A.

The feasibility of the equilibrium $E_0$ is trivial. Here, we show the feasibility of endemic equilibrium $E^*$.

Feasibility of equilibrium $E^*$:

In equilibrium $E^*(I^*, A^*, N^*, M^*)$, the values of $I^*$, $A^*$, $N^*$ and $M^*$ are obtained by solving following set of algebraic equations:

$\beta(N-I-A)-(\nu+\alpha+d) = 0,$

(3)

$\lambda \frac{M}{p+M}(N-I-A)-(\lambda_0+d)A = 0,$

(4)

$\Lambda-dN-\alpha I = 0,$

(5)

$r\left(1-\theta \frac{A}{\omega+A}\right)I-r_0(M-M_0) = 0.$

(6)

From equation (5), we obtain

$N-I = \frac{\Lambda-(\alpha+d)I}{d}.$

(7)

From equations (3) and (7), we get

$A = \frac{\beta(\Lambda-(\alpha+d)I)-d(\nu+\alpha+d)}{\beta d}.$

(8)

Here, it may be noted that for $A$ to be positive, we must have $I <\left(\frac{\beta \Lambda-d(\nu+\alpha+d)}{\beta(\alpha+d)}\right) = I_1$ (say) and clearly $I_1>0$, if $R_1>1$ as $R_0>R_1$.

From equation (8), we obtain

$G(I) = \left(1-\theta\frac{A}{\omega+A}\right) = \frac{\beta d \omega+(1-\theta)[\beta(\Lambda-(\alpha+d)I)-d(\nu+\alpha+d)]}{\beta d \omega+\beta(\Lambda-(\alpha+d)I)-d(\nu+\alpha+d)}.$

(9)

Differentiating above equation with respect to $I$, we get

$G^\prime(I) = \frac{\theta \beta^2 d \omega(\alpha+d)}{[\beta d \omega+\beta(\Lambda-(\alpha+d)I)-d(\nu+\alpha+d)]^2}.$

(10)

From the above equation, it is clear that, $G^\prime(I)>0$.

Further, from equation (6), we have

$\frac{M}{p+M} = \frac{r_0 M_0+r I G(I)}{(p+M_0)r_0+r I G(I)}.$

(11)

Substituting equations (8) and (11) in equation (4), we obtain an equation in $I$ as:

${ F(I) = \lambda\left(\frac{r_0 M_0+r I G(I)}{(p+M_0)r_0+r I G(I)}\right)\left(\frac{\nu+\alpha+d}{\beta}\right)-(\lambda_0+d)\left(\frac{\beta(\Lambda-(\alpha+d)I)-d(\nu+\alpha+d)}{\beta d}\right)}.$

(12)

From, equation (12), we may easily note that

(ⅰ) $\beta$ $F(0) = \left\{\lambda\frac{ M_0}{p+M_0}(\nu+\alpha+d)-(\lambda_0+d)\left(\frac{\beta \Lambda}{d}-(\nu+\alpha+d)\right)\right\} <0$, if $\displaystyle R_1>1$.

(ⅱ)$\beta F(I_1) = \left\{\lambda\left(\frac{r_0 M_0+r I_1}{(p+M_0)r_0+r I_1}\right)(\nu+\alpha+d)\right\}>0$, (ⅲ) $F^\prime(I)>0$ in $(0, I_1)$.

Thus, clearly $F(I) = 0$ has a unique positive root $I = I^*$ (say) in $\left( 0, I_1\right)$, provided $R_1>1$. Now using $I = I^*$ in equations (7), (8) and (11), we obtain positive values of $N^*$, $A^*$ and $M^*$, respectively. Thus, equilibrium $E^*(I^*, A^*, N^*, M^*)$ is feasible provided $R_1>1$ and $I^*\in \left( 0, I_1\right)$.

Remark 1. From equation (12), it is easy to see that $\frac{dI^*}{dr} <0$, $\frac{dI^*}{d\lambda} <0$ and $\frac{dI^*}{dM_0} <0$. This implies that the equilibrium number of infected individuals decreases as the growth rate of TV and social media ads ($r$), dissemination rate of awareness among susceptible individuals ($\lambda$) and the baseline number of TV and social media ads ($M_0$) increases. Further, we may see that $\frac{dI^*}{dp}>0$, i.e., the equilibrium number of infected individuals increases as the value of $p$ increases.

Remark 2. From equation (12), it is also easy to note that $\frac{dI^*}{d\theta}>0$ and $\frac{dI^*}{d\omega} <0$. This implies that the equilibrium number of infected individuals increases as the decay in advertisements due to increase in aware individuals ($\theta$) increases whereas it decreases as the value of $\omega$ increases.

For the details of remarks 1 and 2, see Appendix B.

---

4. Local stability analysis

In this section, we summarize the results of linear stability of the model system (2) by finding the sign of eigenvalues of the Jacobian matrix around the equilibrium $E_0$ and $E^*$. The stability conditions of equilibria $E_0$ and $E^*$ are stated in the following theorem:

Theorem 4.1. (i) The equilibrium (DFE) $E_0$ is always feasible and unstable if $R_1>1$, whereas it is locally asymptotically stable if $R_1 <1$.

(ii) The equilibrium (EE) $E^*$ is feasible if $R_1>1$ and locally asymptotically stable provided the following condition is satisfied:

$B_3(B_1B_2-B_3)-B_1^2B_4>0.$

(13)

For the proof of this theorem, see Appendix C.

The above theorem tells that if $E^*$ is feasible, then $E_0$ is saddle point with stable manifold locally in $N-A-M$ space and unstable manifold locally in $I$-direction. Thus, $E_0$ is unstable whenever $E^*$ is feasible.

The local stability analysis of the endemic equilibrium tells that if the initial values of any trajectory are near the equilibrium $E^*(I^*, A^*, N^*, M^*)$, the solution trajectories approach to the equilibrium $E^*$ under the condition (13). Thus, the initial values of the state variables $I$, $A$, $N$ and $M$ are near to the corresponding equilibrium levels, the equilibrium number of infected individuals get stabilized if condition (13) is satisfied.

---

5. Global stability analysis

In this section, we provide the result of the nonlinear stability of the model system (2). The nonlinear stability analysis of the endemic equilibrium follows from the following theorem:

Theorem 5.1. The endemic equilibrium $E^*$, if feasible, is non-linearly stable in the region $\Omega$, if following inequalities are satisfied:

$\left(G_{11}\right)^2 < \frac{16}{45}\min\left\{\frac{1}{5}\left(\frac{d}{\theta \Lambda}\right)^2, G_{12}\right\}$

(14)

$\left(\frac{\lambda M^*}{\lambda M^*+(p+M^*)(\lambda_0+d)}\right)^2 < \frac{16}{75}\min\left\{\frac{1}{3}, \frac{d}{\alpha}\right\}$

(15)

where, $G_{11} = \frac{\lambda\Lambda r}{r_0d(\omega+A^*)(\lambda M^*+(p+M^*)(\lambda_0+d))},$ $G_{12} = \frac{\beta(p+M^*)}{3m_1(\omega+A^*(1-\theta))^2(\lambda M^*+(p+M^*)(\lambda_0+d))}.$ The inequality (15) is a condition for determining $m_1>0$.

For the proof of this theorem, see Appendix D.

Remark 3. From the nonlinear stability conditions (14) and (15) of the endemic equilibrium, it is clear that the growth rate of TV and social media ads and dissemination rate of awareness among susceptible individuals (i.e., $r$ and $\lambda$) may have destabilizing effect on the system. It is noted that on increasing the value of $r$ and $\lambda$, the local stability condition stated in Theorem 4.1 is violated and thus there is a possibility of Hopf - bifurcation as the value of $r$ and $\lambda$ cross a threshold value and the endemic equilibrium may become unstable and periodic solutions may arise.

---

6. Existence of Hopf-bifurcation

In this section, we derive the conditions for the existence of Hopf-bifurcation around the endemic equilibrium $E^*(I^*, A^*, N^*, M^*)$ by taking '$r$' as a bifurcation parameter. Since all the coefficients of characteristic equation (50) can be written as a function of $r$, we have

$\eta^4 + B_1(r)\eta^3 + B_2(r)\eta^2 + B_3(r) \eta+B_4(r) = 0.$

(16)

It is clear that $B_j(r)>0$ ($j = 1, 2, 3 , 4$) for any $r>0$. Let at $r = r_c$,

$B_3(r_c)(B_1(r_c)B_2(r_c)-B_3(r_c))-B_1^2(r_c)B_4(r_c) = 0.$

(17)

Then at $r = r_c$, the characteristic equation can be written as

$\left(\eta^2+\frac{B_3}{B_1}\right)\left(\eta^2+B_1\eta+\frac{B_1B_4}{B_3}\right) = 0.$

(18)

This equation has four roots, say $\eta_j$ ($j = 1, 2, 3, 4$), with pair of purely imaginary roots $\eta_{1, 2} = \pm i \omega_0$, where $\omega_0 = (\frac{B_3}{B_1})^{1/2}$. For the existence of Hopf-bifurcation, all the roots except $\pm i \omega_0$ (i.e., $\eta_3$ and $\eta_4$) should lie in the left half of the complex plane. To identify the nature of remaining two roots, we have

$\eta_3+\eta_4 = -B_1$

(19)

$\omega_0^2+\eta_3\eta_4 = B_2$

(20)

$\omega_0^2(\eta_3+\eta_4) = -B_3$

(21)

$\omega_0^2\eta_3\eta_4 = B_4.$

(22)

If, $\eta_3$ and $\eta_4$ are complex conjugate, then from equation (19), we have $2\Re(\eta_3) = -B_1$, i.e., $\eta_3$ and $\eta_4$ have negative real parts. If, $\eta_3$ and $\eta_4$ are real roots, then from (19) and (22), we find that $\eta_3$ and $\eta_4$ are negative. Thus, the roots $\eta_3$ and $\eta_4$ lie in the left half of the complex plane. Further, we find the transversality condition under which Hopf-bifurcation may occur. For this let at any point $r\in(r_c-\epsilon, r_c+\epsilon)$, $\eta_{1, 2} = \kappa \pm i\vartheta$. Putting this in equation (16), we have

$\kappa^4+B_1\kappa^3+B_2\kappa^2+B_3\kappa+B_4+\vartheta^4-6\kappa^2\vartheta^2-3B_1\kappa\vartheta^2-B_2\vartheta^2 = 0,$

(23)

$4\kappa\vartheta(\kappa^2-\vartheta^2)-B_1\vartheta^3+3B_1\kappa^2\vartheta+2B_2\kappa\vartheta+B_3\vartheta = 0.$

(24)

As $\vartheta(r)\neq0$, from equation (24), we have

$-(4\kappa+B_1)\vartheta^2+4\kappa^3+3B_1\kappa^2+2B_2\kappa+B_3 = 0.$

Using the value of $\vartheta^2$ in equation (23) we have

$-64\kappa^6-96B_1\kappa^5-16\left(3B_1^2+2B_2\right)\kappa^4-8\left(B_1^3+4B_1B_2\right)\kappa^3\nonumber\\ -4\left(B_2^2+2B_1^2B_2+B_1B_3-4B_4\right)\kappa^2-2B_1(B_1B_3+B_2^2-4B_4)\kappa\nonumber\\ -(B_3(B_1B_2-B_3)-B_1^2B_4) = 0.$

Differentiating above equation with respect to $r$ and use the fact that $\kappa(r_c) = 0$, we get

$\left[\frac{d\kappa}{dr}\right]_{r = r_c} = \left[\frac{\frac{d}{dr}(B_3(B_1B_2-B_3)-B_1^2B_4)}{-2B_1\left(B_1B_3+B_2^2-4B_4\right)}\right]_{r = r_c}.$

Using the value of $B_4(r_c) = \left(\frac{B_1(r_c)B_2(r_c)B_3(r_c)-B_3^2(r_c)}{B_1^2(r_c)}\right)$ from equation (17) in above equation we have

$\left[\frac{d\kappa}{dr}\right]_{r = r_c} = \left[\frac{\frac{d}{dr}(B_3(B_1B_2-B_3)-B_1^2B_4)}{-2B_1\left(B_1B_3+\left(\frac{2B_3}{B_1}\right)^2-2\left(\frac{2B_3}{B_1}\right)B_2+B_2^2\right)}\right]_{r = r_c}.$

This implies that

$\left[\frac{d\kappa}{dr}\right]_{r = r_c} = \left[\frac{\frac{d}{dr}(B_1B_2B_3-B_3^2-B_1^2B_4)}{-2B_1(B_1B_3+(2B_3/B_1-B_2)^2)}\right]_{r = r_{c}}\neq0$

if $[\frac{d}{dr}(B_1B_2B_3-B_3^2-B_1^2B_4)]_{r = r_c}\neq0$. Thus, the transversality condition is $[\frac{d}{dr}(B_1B_2B_3-B_3^2-B_1^2B_4)]_{r = r_c}\neq0$. Hence, we have following theorem for the existence of Hopf-bifurcation.

Theorem 6.1. The reduced model system (2) undergoes Hopf-bifurcation around the endemic equilibrium $E^*$ if there exists $r = r_c$ such that:

(i) $B_3(r_c)(B_1(r_c)B_2(r_c)-B_3(r_c))-B_1^2(r_c)B_4(r_c) = 0.$

(ii) $\left[\Re\frac{d\eta_j(r)}{dr}\right]_{r = r_c}\neq0$ for $j = 1, 2$

i.e., $\left[\frac{d}{dr}(B_1B_2B_3-B_3^2-B_1^2B_4)\right]_{r = r_c}\neq0.$

---

7. Stability and direction of Hopf-bifurcation

In this section, we present the result for the direction of bifurcating periodic solutions. The following theorem provides the information about the direction and stability of the periodic solutions.

Theorem 7.1. The Hopf-bifurcation is forward (backward) if $\mu_2>0$ ($\mu_2 <0$) and the bifurcating periodic solution exist for $r>r_c$ ($r <r_c$). The periodic solutions are stable or unstable according as $\beta_2 <0$ or $\beta_2>0$ and period increases or decreases according as $\tau_2>0$ or $\tau_2 <0$.

For the proof of this theorem see, Appendix E.

---

8. Numerical simulation

In the previous sections, we have presented the qualitative analysis of the model system (2) and obtained results regarding the stability of equilibria and Hopf-bifurcation analysis of the endemic equilibrium. In this section, we conduct numerical simulation of model system (2) using MATLAB, regarding the feasibility of our analysis and its stability conditions.

For the set of parameter values, we have checked that the condition for the feasibility of the endemic equilibrium (i.e., $R_1>1$) is satisfied. The equilibrium values are obtained as:

${I^ * } = {\rm{ }}932, \;\;{A^ * } = {\rm{ }}57151, \;\;{N^ * } = {\rm{ }}124767, \;\;{M^ * } = {\rm{ }}1618.$

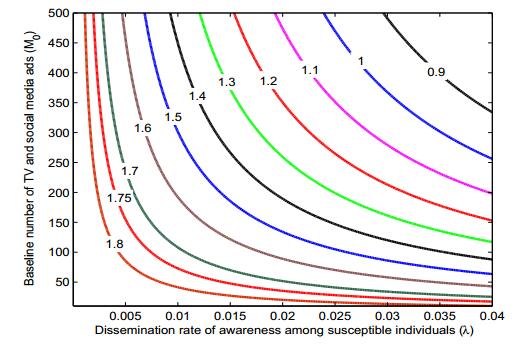
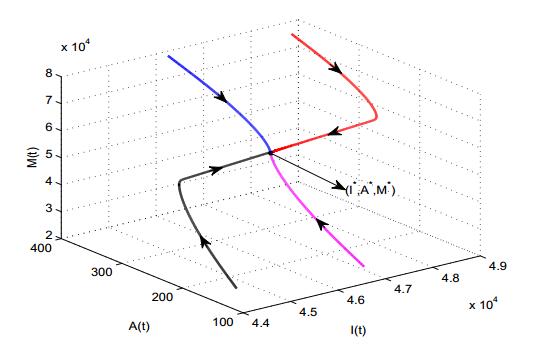
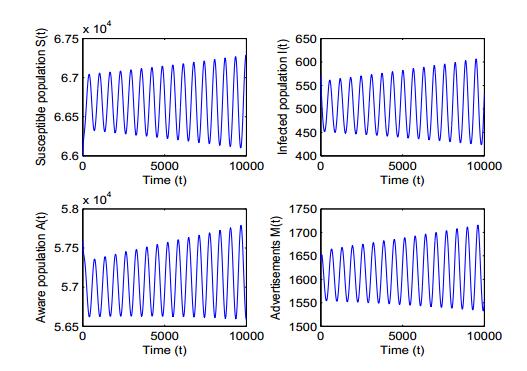
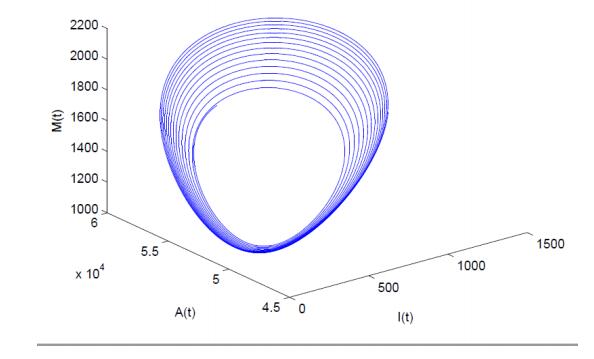
For the set of parameter values given in Table 1, the value of basic reproduction number $R_0$ is found to be $1.87$ and the value of modified basic reproduction number $R_1$ is $1.30$. We have made contour plots of $R_1$ for different values of $\lambda$ and $M_0$, which are shown in Fig. 1. From this figure, it may be noted that for small values of dissemination rate of awareness among susceptible individuals ($\lambda$) and baseline number of TV and social media ads ($M_0$), the value of $R_1$ is higher but on increasing the values of these parameters, $R_1$ becomes less than unity and endemic equilibrium loses its feasibility, showing the importance of TV and social media ads. The eigenvalues of the Jacobian matrix corresponding to the equilibrium $E^*$ are $-0.02208$, $-0.00004$, $-0.00032+0.00984i$ and $-0.00032-0.00984i$. We note that two eigenvalues of the Jacobian matrix are negative and the other two eigenvalues have negative real part. This implies that the endemic equilibrium is locally asymptotically stable. Further, it may be checked that the stability condition stated in Theorem 4.1 is satisfied. Fig. 2 is drawn for the solution trajectories of model system (2) with different initial starts in $I-A-M$ space for $\lambda = 0.00003$, keeping rest of parameter values same as given in Table 1. We may see that all solution trajectories starting in positive orthant inside the region of attraction are approaching towards its equilibrium value. This shows the non-linear stability of the endemic equilibrium in $I-A-M$ space. The non-linear stability conditions stated in the Theorem 5.1 is also satisfied, which shows disease remains endemic in the region for smaller values of $r$ and $\lambda$.

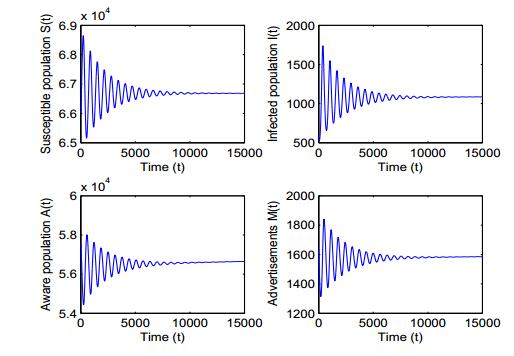
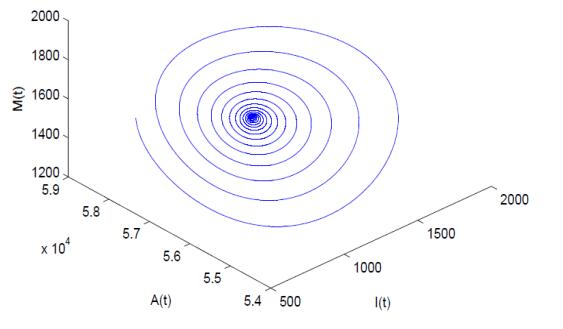
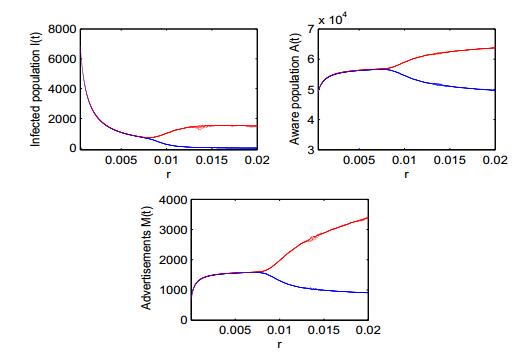
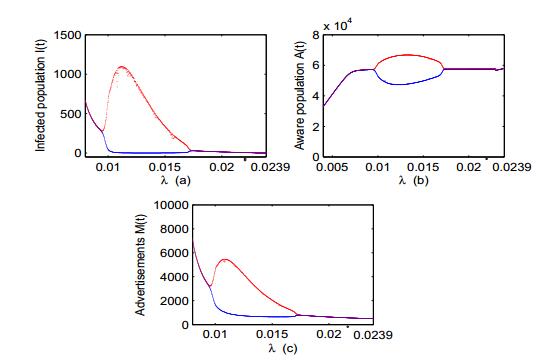
For the chosen set of parameter values given in Table 1, the dynamics near the endemic equilibrium changes as the growth rate of TV and social media ads ($r$) increases. For small values of $r$, the endemic equilibrium is stable while an increase in the growth rate of TV and social media ads destabilizes the endemic equilibrium and sustained oscillations arise, which clearly states that Hopf-bifurcation occurs as the values of $r$ increases after a threshold. Numerically, we have obtained the critical value of growth rate of advertisements parameter (i.e., $r = r_c$) at which change in stability occurs and this is $r_c = 0.01011$. It may be noted that for $r\in [0, r_c)$, all the eigenvalues of Jacobian matrix lie in the left half of the complex plane showing that the endemic equilibrium of model system (2) is stable for small values of $r$ while loss of stability occurs for $r = 0.011(>r_c)$ and endemic equilibrium becomes unstable. The conditions stated in Theorem 6.1 are also satisfied, which shows that model system (2) undergoes Hopf-bifurcation around the endemic equilibrium at $r = r_{c}$. Further, the sign of $\mu_2$, $\beta_2$ and $\tau_2$ at $r = r_{c}$ are found to be $1.48\times10^{-15}$, $-3.06\times10^{-15}$ and $4.47\times 10^{-15}$, respectively. Using Theorem 7.1 we can say that the Hopf-bifurcation is forward and bifurcating periodic solutions exist for $r>r_{c}$. The periodic solutions are stable and period increases as $\mu_2>0$, $\beta_2 <0$ and $\tau_2>0$. Now, we discuss the variation of susceptible population $S(t)$, infected population $I(t)$, aware population $A(t)$ and cumulative number of TV and social media ads $M(t)$ with respect to time $t$ for $r = 0.005\ ( <r_{c})$, which is shown in Fig. 3. This diagram reveals that for $r\in [0, r_c)$, all the variables attain their equilibrium values. In Fig. 4, we plot a phase portrait for $r = 0.005\ ( <r_{c})$, which demonstrates that the endemic equilibrium is stable, i.e., the solution trajectory starting from outside approaches towards its equilibrium $E^*$. Further, we have plotted the variation of $S(t)$, $I(t)$, $A(t)$ and $M(t)$ with respect to time $t$ for $r = 0.011\ (>r_{c})$. This diagram clarifies that all the variables show oscillatory behavior, which is shown in Fig. 5. In Fig. 6, we draw a phase portrait in $I-A-M$ space to show that the endemic equilibrium is unstable for $r = 0.011\ (>r_{c})$. To get the more clear picture, we have drawn a bifurcation diagram shown in Fig. 7, by taking r as a bifurcation parameter. Form Fig. 7, it can be easily seen that for small values of the growth rate of TV and social media ads, all variables settle down to their equilibrium values. However, as the growth rate of TV and social media ads increase after a threshold, periodic solutions of increasing amplitude are observed and endemic equilibrium changes its stability from stable to unstable. In addition, for $r = 0.05$, $\omega = 60$, keeping rest of parameter values same as given in Table 1, the dynamics near the endemic equilibrium changes as the dissemination rate of awareness among susceptible individuals ($\lambda$) increases. For small values of $\lambda$, the endemic equilibrium is stable while an increase in dissemination rate destabilizes the endemic equilibrium. Further increase in dissemination rate again stabilizes the endemic equilibrium, which clearly states that Hopf-bifurcation occurs twice as the value of $\lambda$ increases. Numerically, we have obtained the critical values of dissemination parameter $\lambda$ (i.e., $\lambda_{c_1}$ and $\lambda_{c_2}$) at which the change in stability occurs are given by $\lambda_{c_1} = 0.00997$ and $\lambda_{c_2} = 0.01779$. For $r = 0.05$, $\omega = 60$ and rest of parameter values as given in Table 1, the endemic equilibrium is stable if $\lambda \in [0, \lambda_{c_1})\cup(\lambda_{c_2}, \lambda_{\max})$ and unstable for $\lambda \in (\lambda_{c_1}, \lambda_{c_2})$. Furthermore, increase in the value of $\lambda(>\lambda_{c_2})$, after a threshold (i.e., $\lambda = \lambda_{\max} = 0.0239$), the endemic equilibrium loses its feasibility (i.e., $R_1$ becomes less than unity) and in this case only disease-free equilibrium will be feasible. This states that if dissemination rate of awareness among the susceptible individuals is fast enough then disease can be effectively controlled in the population. To get the more clear picture, we have plotted a bifurcation diagram shown in Fig. 8 (a -c), by taking $\lambda$ as a bifurcation parameter. These figures demonstrate the interesting dynamics of the system as the dissemination rate of awareness among susceptible individuals ($\lambda$) increases. From Fig. 8 (a), it can be easily seen that for small values of the dissemination rate, the number of infected individuals settles to their equilibrium value but as the dissemination rate increases, the periodic oscillations in the number of infected individuals with increasing amplitude are observed. Further increase in dissemination rate leads to decrease in the amplitude of these oscillations and finally, they die out for large values of dissemination rate and again the number of infected individuals settles down to their lower equilibrium value. From Figs. 8 (a-c), it is also apparent that for $\lambda \in [0, \lambda_{c_1})\cup(\lambda_{c_2}, \lambda_{\max})$, the endemic equilibrium shows stable character; however for $\lambda \in (\lambda_{c_1}, \lambda_{c_2})$, the endemic equilibrium is unstable and Hopf-bifurcation occurs at $\lambda = \lambda_{c_1}$ and $\lambda_{c_2}$. Thus, we have observed that the endemic equilibrium of model system (2) switches from stability to instability to stability as dissemination rate of awareness among susceptible individuals ($\lambda$) increases.

---

9. Conclusion

In this paper, we have proposed and analyzed a nonlinear mathematical model to assess the impact of TV and social media ads on the spread of an infectious disease. In the model formulation, it is assumed that cumulative number of TV and social media ads increases proportional to the number of infected individuals and their growth rate decreases with the increase in number of aware individuals. It is also assumed that susceptible individuals contract infection due to the direct contact with infected individuals.

The analysis of proposed model reveals that only two equilibria; namely disease-free equilibrium (DFE) $E_0$, and endemic equilibrium (EE) $E^*$ are feasible. The linear and non-linear stability of endemic equilibrium, existence of Hopf-bifurcation and result for the direction of bifurcating periodic solutions are discussed. Model analysis shows that the increase in growth rate of cumulative number of TV and social media ads after a threshold value destabilizes the system and periodic oscillations arise through Hopf-bifurcation. It is also found that the dissemination rate of awareness among susceptible individuals gives rise to interesting result about the stability of endemic equilibrium. It is noted that for small values of dissemination rate, the endemic equilibrium is stable and the increase in dissemination rate destabilizes the system; however further increase in this rate again stabilizes the endemic equilibrium. This means that the endemic equilibrium changes its stability from stable to unstable to stable state as the dissemination rate of awareness among susceptible individuals increases and further increase in dissemination rate after a threshold (i.e., $\lambda_{\max}$), ceases the feasibility of endemic equilibrium (i.e., $R_1 <1$) and only disease-free equilibrium is feasible, which is stable. It is also noted that in absence of baseline number of TV and social media ads, the basic reproduction number $R_0$ is same as obtained for classical SIS models considered in other articles [29,37,30]. The incorporation of baseline number of TV and social media ads modifies this basic reproduction number to $R_1$, which is less than $R_0$. This infers that the TV and social media ads have the potential to reduce the number of infected individuals but for the eradication of the disease from the community, some other efforts, like treatment, sanitation, maintaining the baseline number of TV and social media ads are also important.

The above discussion in terms of epidemiology states that the augmentation in the dissemination rate of awareness among susceptible individuals increases the number of aware individuals, which leads to decrease in the number of TV and social media ads and thus increases the number of infected individuals. Further, this increase in number of infected individuals increases the TV and social media ads, which increases the aware individuals. This interplay between the number of infected individuals and dissemination of awareness through TV and social media gives rise to oscillatory solution. It may be noted that when number of infected individuals become low and aware population reaches its saturated level, the oscillatory behavior dies out and further increase in dissemination rate provides the stable solution. Further increase in dissemination rate of awareness among the susceptible individuals after a threshold (i.e., $\lambda_{\max}$) leads to the feasibility of only disease-free equilibrium.

---

Acknowledgments

Authors are grateful to reviewers for their useful suggestions. The second author thankfully acknowledge the University Grants Commission, New Delhi, India for providing financial assistance during the research period.

---

Appendix A

Here, we will find the basic reproduction number $(R_1)$ of model system (2) using next generation matrix approach. we have the matrix of new infection $\mathcal{F}(x)$ and the matrix of transfer $\mathcal{V}(x)$. Let $x = (I, A, N, M)^T$, the model system (2) can be rewritten as:

$\frac{dx}{dt} = \mathcal{F}(x)-\mathcal{V}(x),$

where $\mathcal{F}(x) = \left(\begin{array}{c} \beta I(N-I-A)\\ 0 \\ 0 \\ 0 \end{array}\right)$ and $\mathcal{V}(x) = \left( \begin{array}{c} (\nu+\alpha+d)I \\ -\lambda \frac{M}{p+M}(N-I-A)+(\lambda_0+d)A \\ -\Lambda+dN+\alpha I \\ -r\left(1-\theta\frac{A}{\omega+A}\right)I+r_0(M-M_0) \\ \end{array} \right).$

The Jacobian matrix of $\mathcal{F}(x)$ and $\mathcal{V}(x)$ at disease-free equilibrium $E_0\left(0, \right. \left.\frac{\lambda\Lambda M_0}{d(\lambda M_0+(\lambda_0+d)(p+M_0))}, \frac{\Lambda}{d}, M_0\right)$ are $J\mathcal{F}(E_0) = \left( \begin{array}{cccc} \frac{\beta\Lambda}{d}\left(\frac{(\lambda_0+d)(p+M_0)}{\lambda M_0+(\lambda_0+d)(p+M_0)}\right)&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ \end{array} \right)$

and

$J\mathcal{V}(E_0) = \left( \begin{array}{cccc} (\nu+\alpha+d)&0&0&0 \\ \lambda \frac{M_0}{p+M_0}&\left(\lambda \frac{M_0}{p+M_0}+\lambda_0+d\right)&-\lambda \frac{M_0}{p+M_0}&-\frac{\lambda p}{(p+M_0)^2}\left(\frac{\Lambda}{d}-A_0\right) \\ \alpha&0&d&0\\ -r\left(1-\theta\frac{A_0}{\omega+A_0}\right)&0&0&r_0 \\ \end{array} \right),$

where $A_0 = \frac{\lambda\Lambda M_0}{d(\lambda M_0+(\lambda_0+d)(p+M_0))}$. The next generation matrix $\mathcal{K}_L = J\mathcal{F}(E_0) J\mathcal{V}(E_0)^{-1}$ is given by

$\mathcal{K}_{L} = \left( \begin{array}{cccc} \frac{\beta\Lambda}{d(\nu+\alpha+d)}\left(\frac{(\lambda_0+d)(p+M_0)}{\lambda M_0+(\lambda_0+d)(p+M_0)}\right)&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ \end{array} \right).$

Therefore, basic reproduction number is $R_1 = \rho(\mathcal{K}_L) = \max\left(|\mu|; \mu\in\rho(\mathcal{K}_L)\right)$ is spectral radius of matrix $\mathcal{K}_L$ and basic reproduction number ($R_1$) is obtained as follows,

$R_1 = \frac{\beta\Lambda}{d(\nu+\alpha+d)}\left(\frac{(\lambda_0+d)(p+M_0)}{\lambda M_0+(\lambda_0+d)(p+M_0)}\right).$

---

Appendix B

Here, we proof the results for $\frac{dI^*}{dr} <0$, $\frac{dI^*}{d\lambda} <0$, $\frac{dI^*}{dM_0} <0$, $\frac{dI^*}{dp}>0$, $\frac{dI^*}{d\theta}>0$ and $\frac{dI^*}{d\omega} <0$ stated in remarks 1, 2.

(ⅰ) Variation of $I^*$ with respect to $r$:

Here we show the variation of $I^*$ with respect to $r$. Since at the equilibrium point $E^*(I^*, A^*, N^*, M^*)$, the rate of change of all dynamical variables with respect to time '$t$' is zero. Thus we have following system of equations:

$\beta(N^*-I^*-A^*)-(\nu+\alpha+d) = 0, \label{eq38b}$

(25)

$\lambda \frac{M^*}{p+M^*}(N^*-I^*-A^*)-(\lambda_0+d)A^* = 0, \label{eq39b}$

(26)

$\Lambda -dN^*-\alpha I^* = 0, \label{eq40b}$

(27)

$r\left(1-\theta \frac{A^*}{\omega+A^*}\right)I^*-r_0(M^*-M_0) = 0.\label{eq41b}$

(28)

Using equation (27) in equation (25), we have

${\rm{Let}}\ \ \mathbb{F}_1(r, I^*, A^*): = \beta\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)-(\nu+\alpha+d) = 0.$

(29)

And using equations (27) and (28) in equation (26), we have

$\mathbb{G}_1(r, I^*, A^*) : = \lambda\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)\nonumber\\ -(\lambda_0+d)A^* = 0.$

(30)

Differentiating $\mathbb{F}_1(r, I^*, A^*)$ and $\mathbb{G}_1(r, I^*, A^*)$ partially with respect to $r$, $I^*$ and $A^*$, we get $\frac{\partial\mathbb{F}_1}{\partial r} = 0$, $\frac{\partial \mathbb{F}_1}{\partial I^*} = -\frac{\beta(\alpha+d)}{d}$, $\frac{\partial\mathbb{F}_1}{\partial A^*} = -\beta,$

$\frac{\partial \mathbb{G}_1}{\partial r} = \frac{\lambda p r_0\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*}{\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2}\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right), \label{eq44b} \\ $

(31)

$\frac{\partial \mathbb{G}_1}{\partial I^*} = -\frac{\lambda(\alpha+d)}{d}\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\nonumber\\ +\frac{\lambda pr_0r\left(1-\theta\frac{A^*}{\omega+A^*}\right)}{\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2}\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right), \label{eq45b}$

(32)

$\frac{\partial \mathbb{G}_1}{\partial A^*} = -\lambda\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\nonumber\\ -\left(\frac{\lambda pr_0r\theta\omega I^*}{(\omega+A^*)^2\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2}\right)\nonumber\\ \times\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)-(\lambda_0+d)\label{eq46b}.$

(33)

Since $\mathbb{F}_1(r, I^*, A^*) = 0$, and differentiating it with respect to $r$, we have

$\frac{\partial \mathbb{F}_1}{\partial r}+\frac{\partial\mathbb{F}_1}{\partial I^*}\frac{dI^*}{dr}+\frac{\partial\mathbb{F}_1}{\partial A^*}\frac{dA^*}{dr} = 0.$

Using the values of $\frac{\partial \mathbb{F}_1}{\partial r}$, $\frac{\partial\mathbb{F}_1}{\partial I^*}$ and $\frac{\partial\mathbb{F}_1}{\partial A^*}$ in above equation, we have

$\frac{dA^*}{dr} = -\left(\frac{\alpha+d}{d}\right)\frac{dI^*}{dr}.$

(34)

Since $\mathbb{G}_1(r, I^*, A^*) = 0$, and differentiating it with respect to $r$, we have

$\frac{\partial \mathbb{G}_1}{\partial r}+\frac{\partial\mathbb{G}_1}{\partial I^*}\frac{dI^*}{dr}+\frac{\partial\mathbb{G}_1}{\partial A^*}\frac{dA^*}{dr} = 0.$

Using equations (31)-(33) and (34), we get

$\frac{dI^*}{dr} = -\left(\frac{A_{11}}{A_{12}}\right).$

where, $A_{11} = \lambda pr_0\left(1-\theta\frac{A^*}{\omega+A^*}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)I^*$ and $A_{12} = \lambda pr_0r\left(1-\right. \left.\theta\frac{A^*}{\omega+A^*}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)+\frac{\lambda pr_0r\theta\omega(\alpha+d)I^*}{d(\omega+A^*)^2}\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)+\frac{(\alpha+d)(\lambda_0+d)}{d} \left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2$.

Thus, from above equation it is clear that $\frac{dI^*}{dr} <0$.

(ⅱ) Variation of $I^*$ with respect to $\lambda$:

${\rm{Let}} \ \ \mathbb{F}_2(\lambda, I^*, A^*): = \beta\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)-(\nu+\alpha+d) = 0,$

(35)

and

$\mathbb{G}_2(\lambda, I^*, A^*) : = \lambda\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)\nonumber\\ -(\lambda_0+d)A^* = 0.$

(36)

Differentiating $\mathbb{F}_2(\lambda, I^*, A^*)$ and $\mathbb{G}_2(\lambda, I^*, A^*)$ partially with respect to $\lambda$, $I^*$ and $A^*$, we get $\frac{\partial\mathbb{F}_2}{\partial \lambda} = 0$, $\frac{\partial \mathbb{F}_2}{\partial I^*} = -\frac{\beta(\alpha+d)}{d}$, $\frac{\partial\mathbb{F}_2}{\partial A^*} = -\beta$, $\frac{\partial \mathbb{G}_2}{\partial \lambda} = \left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right) \left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ $\frac{\partial\mathbb{G}_2}{\partial I^*} = \frac{\partial\mathbb{G}_1}{\partial I^*}$ and $\frac{\partial\mathbb{G}_2}{\partial A^*} = \frac{\partial\mathbb{G}_1}{\partial A^*}$. Since $\mathbb{F}_2(\lambda, I^*, A^*) = 0$, and differentiating it with respect to $\lambda$, we have

$\frac{\partial \mathbb{F}_2}{\partial \lambda}+\frac{\partial\mathbb{F}_2}{\partial I^*}\frac{dI^*}{d\lambda}+\frac{\partial\mathbb{F}_2}{\partial A^*}\frac{dA^*}{d\lambda} = 0.$

Using the values of $\frac{\partial \mathbb{F}_2}{\partial \lambda}$, $\frac{\partial\mathbb{F}_2}{\partial I^*}$ and $\frac{\partial\mathbb{F}_2}{\partial A^*}$ in above equation, we have

$\frac{dA^*}{d\lambda} = -\left(\frac{\alpha+d}{d}\right)\frac{dI^*}{d\lambda}.$

(37)

Since $\mathbb{G}_2(\lambda, I^*, A^*) = 0$, and differentiating it with respect to $\lambda$, we have

$\frac{\partial \mathbb{G}_2}{\partial \lambda}+\frac{\partial\mathbb{G}_2}{\partial I^*}\frac{dI^*}{d\lambda}+\frac{\partial\mathbb{G}_2}{\partial A^*}\frac{dA^*}{d\lambda} = 0.$

Using the values of $\frac{\partial \mathbb{G}_2}{\partial \lambda}$, $\frac{\partial\mathbb{G}_2}{\partial I^*}$, $\frac{\partial\mathbb{G}_2}{\partial A^*}$ and $\frac{dA^*}{d\lambda}$ in above equation, we have

$\frac{dI^*}{d\lambda} = -\left(\frac{A_{21}}{A_{22}}\right),$

where, $A_{21} = \left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0\right)\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right) \times\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ and $A_{22} = A_{12}$.

Thus, from above equation it is easy to note that $\frac{dI^*}{d\lambda} <0$. Hence the proof.

(ⅲ) Variation of $I^*$ with respect to $M_0$:

Here we show the variation of $I^*$ with respect to $M_0$.

${\rm{Let}} \ \ \mathbb{F}_3(M_0, I^*, A^*): = \beta\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)-(\nu+\alpha+d) = 0,$

(38)

and

$\mathbb{G}_3(M_0, I^*, A^*)\nonumber\\ : = \lambda\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)\nonumber\\ -(\lambda_0+d)A^* = 0.$

(39)

Differentiating $\mathbb{F}_3(M_0, I^*, A^*)$ and $\mathbb{G}_3(M_0, I^*, A^*)$ partially with respect to $M_0$, $I^*$ and $A^*$, we get $\frac{\partial\mathbb{F}_3}{\partial M_0} = 0$, $\frac{\partial \mathbb{F}_3}{\partial I^*} = -\frac{\beta(\alpha+d)}{d}$, $\frac{\partial\mathbb{F}_3}{\partial A^*} = -\beta$, $\frac{\partial \mathbb{G}_3}{\partial M_0} = \frac{\lambda pr_0^2\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)}{\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2},$ $\frac{\partial\mathbb{G}_3}{\partial I^*} = \frac{\partial\mathbb{G}_1}{\partial I^*}$ and $\frac{\partial\mathbb{G}_3}{\partial A^*} = \frac{\partial\mathbb{G}_1}{\partial A^*}$. Since $\mathbb{F}_3(M_0, I^*, A^*) = 0$, and differentiating it with respect to $M_0$, we have

$\frac{\partial \mathbb{F}_3}{\partial M_0}+\frac{\partial\mathbb{F}_3}{\partial I^*}\frac{dI^*}{dM_0}+\frac{\partial\mathbb{F}_3}{\partial A^*}\frac{dA^*}{dM_0} = 0.$

Using the values of $\frac{\partial \mathbb{F}_3}{\partial M_0}$, $\frac{\partial\mathbb{F}_3}{\partial I^*}$ and $\frac{\partial\mathbb{F}_3}{\partial A^*}$ in above equation, we obtain

$\frac{dA^*}{dM_0} = -\left(\frac{\alpha+d}{d}\right)\frac{dI^*}{dM_0}.$

(40)

Since $\mathbb{G}_3(M_0, I^*, A^*) = 0$, and differentiating it with respect to $M_0$, we have

$\frac{\partial \mathbb{G}_3}{\partial M_0}+\frac{\partial\mathbb{G}_3}{\partial I^*}\frac{dI^*}{dM_0}+\frac{\partial\mathbb{G}_3}{\partial A^*}\frac{dA^*}{dM_0} = 0.$

Using the values of $\frac{\partial \mathbb{G}_3}{\partial M_0}$, $\frac{\partial\mathbb{G}_3}{\partial I^*}$, $\frac{\partial\mathbb{G}_3}{\partial A^*}$ and $\frac{dA^*}{dM_0}$ in above equation, we get

$\frac{dI^*}{dM_0} = -\left(\frac{A_{31}}{A_{32}}\right),$

where, $A_{31} = \lambda pr_0^2\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ and $A_{32} = A_{12}$.

Thus, it is clear that $\frac{dI^*}{dM_0} <0$. Hence the proof.

(ⅳ) Variation of $I^*$ with respect to $p$:

${\rm{Let}} \ \ \mathbb{F}_4(p, I^*, A^*): = \beta\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)-(\nu+\alpha+d) = 0,$

(41)

and

$\mathbb{G}_4(p, I^*, A^*) : = \lambda\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)\nonumber\\ -(\lambda_0+d)A^* = 0.$

(42)

Differentiating $\mathbb{F}_4(p, I^*, A^*)$ and $\mathbb{G}_4(p, I^*, A^*)$ partially with respect to $p$, $I^*$ and $A^*$, we obtain $\frac{\partial\mathbb{F}_4}{\partial p} = 0$, $\frac{\partial \mathbb{F}_4}{\partial I^*} = -\frac{\beta(\alpha+d)}{d}$, $\frac{\partial\mathbb{F}_4}{\partial A^*} = -\beta$,

$\frac{\partial \mathbb{G}_4}{\partial p} = -\frac{\lambda r_0\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0\right)}{\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2}\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ $\frac{\partial\mathbb{G}_4}{\partial I^*} = \frac{\partial\mathbb{G}_1}{\partial I^*}$ and $\frac{\partial\mathbb{G}_4}{\partial A^*} = \frac{\partial\mathbb{G}_1}{\partial A^*}$.

Since $\mathbb{F}_4(p, I^*, A^*) = 0$, and differentiating it with respect to $p$, we have

$\frac{\partial \mathbb{F}_4}{\partial p}+\frac{\partial\mathbb{F}_4}{\partial I^*}\frac{dI^*}{dp}+\frac{\partial\mathbb{F}_4}{\partial A^*}\frac{dA^*}{dp} = 0.$

Using the values of $\frac{\partial \mathbb{F}_4}{\partial p}$, $\frac{\partial\mathbb{F}_4}{\partial I^*}$ and $\frac{\partial\mathbb{F}_4}{\partial A^*}$ in above equation, we get

$\frac{dA^*}{dp} = -\left(\frac{\alpha+d}{d}\right)\frac{dI^*}{dp}.$

(43)

Since $\mathbb{G}_4(p, I^*, A^*) = 0$, and differentiating it with respect to $p$, we have

$\frac{\partial \mathbb{G}_4}{\partial p}+\frac{\partial\mathbb{G}_4}{\partial I^*}\frac{dI^*}{dp}+\frac{\partial\mathbb{G}_4}{\partial A^*}\frac{dA^*}{dp} = 0.$

Using the values of $\frac{\partial\mathbb{G}_4}{\partial p}$, $\frac{\partial\mathbb{G}_4}{\partial I^*}$, $\frac{\partial\mathbb{G}_4}{\partial A^*}$ and $\frac{dA^*}{dp}$ in above equation, we obtain

$\frac{dI^*}{dp} = \left(\frac{A_{41}}{A_{42}}\right),$

where, $A_{41} = \lambda r_0\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ and $A_{42} = A_{12}$. Thus, from above equation, it is clear that $\frac{dI^*}{dp}>0$. Hence the proof.

(ⅴ) Variation of $I^*$ with respect to $\theta$:

Here, we show the variation of $I^*$ with respect to $\theta$.

${\rm{Let}} \ \ \mathbb{F}_5(\theta, I^*, A^*): = \beta\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)-(\nu+\alpha+d) = 0,$

(44)

and

$\mathbb{G}_5(\theta, I^*, A^*) : = \lambda\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)\nonumber\\ -(\lambda_0+d)A^* = 0.$

(45)

Differentiating $\mathbb{F}_5(\theta, I^*, A^*)$ and $\mathbb{G}_5(\theta, I^*, A^*)$ partially with respect to $\theta$, $I^*$ and $A^*$, we get $\frac{\partial\mathbb{F}_5}{\partial \theta} = 0$, $\frac{\partial \mathbb{F}_5}{\partial I^*} = -\frac{\beta(\alpha+d)}{d}$, $\frac{\partial\mathbb{F}_5}{\partial A^*} = -\beta$,

$\frac{\partial \mathbb{G}_5}{\partial \theta} = -\left(\frac{\lambda pr_0rI^*A^*}{(\omega+A^*)\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ $\frac{\partial\mathbb{G}_5}{\partial I^*} = \frac{\partial\mathbb{G}_1}{\partial I^*}$ and $\frac{\partial\mathbb{G}_5}{\partial A^*} = \frac{\partial\mathbb{G}_1}{\partial A^*}$. Since $\mathbb{F}_5(\theta, I^*, A^*) = 0$, and differentiating it with respect to $\theta$, we have

$\frac{\partial \mathbb{F}_5}{\partial \theta}+\frac{\partial\mathbb{F}_5}{\partial I^*}\frac{dI^*}{d\theta}+\frac{\partial\mathbb{F}_5}{\partial A^*}\frac{dA^*}{d\theta} = 0.$

Using the values of $\frac{\partial \mathbb{F}_5}{\partial \theta}$, $\frac{\partial\mathbb{F}_5}{\partial I^*}$ and $\frac{\partial\mathbb{F}_5}{\partial A^*}$ in above equation, we obtain

$\frac{dA^*}{d\theta} = -\left(\frac{\alpha+d}{d}\right)\frac{dI^*}{d\theta}.$

(46)

Since $\mathbb{G}_5(\theta, I^*, A^*) = 0$, and differentiating it with respect to $\theta$, we have

$\frac{\partial \mathbb{G}_5}{\partial \theta}+\frac{\partial\mathbb{G}_5}{\partial I^*}\frac{dI^*}{d\theta}+\frac{\partial\mathbb{G}_5}{\partial A^*}\frac{dA^*}{d\theta} = 0.$

Using the values of $\frac{\partial\mathbb{G}_5}{\partial \theta}$, $\frac{\partial\mathbb{G}_5}{\partial I^*}$, $\frac{\partial\mathbb{G}_5}{\partial A^*}$ and $\frac{dA^*}{d\theta}$ in above equation, we have

$\frac{dI^*}{d\theta} = \left(\frac{A_{51}}{A_{52}}\right),$

where, $A_{51} = \frac{\lambda pr_0rI^*A^*}{\omega+A^*} \left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ and $A_{52} = A_{12}$. Thus, from above equation, it is easy to note that $\frac{dI^*}{d\theta}>0$. Hence the proof.

(ⅵ) Variation of $I^*$ with respect to $\omega$:

${\rm{Let}} \ \ \mathbb{F}_6(\omega, I^*, A^*): = \beta\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)-(\nu+\alpha+d) = 0,$

(47)

and

$\mathbb{G}_6(\omega, I^*, A^*) : = \lambda\left(\frac{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0M_0}{r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right)\nonumber\\ -(\lambda_0+d)A^* = 0.$

(48)

Differentiating $\mathbb{F}_6(\omega, I^*, A^*)$ and $\mathbb{G}_6(\omega, I^*, A^*)$ partially with respect to $\omega$, $I^*$, $A^*$, we get $\frac{\partial\mathbb{F}_6}{\partial \omega} = 0$, $\frac{\partial \mathbb{F}_6}{\partial I^*} = -\frac{\beta(\alpha+d)}{d}$, $\frac{\partial\mathbb{F}_6}{\partial A^*} = -\beta$,

$\frac{\partial \mathbb{G}_6}{\partial \omega} = \left(\frac{\lambda pr_0r\theta I^*A^*}{(\omega+A^*)^2\left(r\left(1-\theta\frac{A^*}{\omega+A^*}\right)I^*+r_0(p+M_0)\right)^2}\right)\left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ $\frac{\partial\mathbb{G}_6}{\partial I^*} = \frac{\partial\mathbb{G}_1}{\partial I^*}$ and $\frac{\partial\mathbb{G}_6}{\partial A^*} = \frac{\partial\mathbb{G}_1}{\partial A^*}$. Since $\mathbb{F}_6(\omega, I^*, A^*) = 0$, and differentiating it with respect to $\omega$, we have

$\frac{\partial \mathbb{F}_6}{\partial \omega}+\frac{\partial\mathbb{F}_6}{\partial I^*}\frac{dI^*}{d\omega}+\frac{\partial\mathbb{F}_6}{\partial A^*}\frac{dA^*}{d\omega} = 0.$

Using the values of $\frac{\partial \mathbb{F}_6}{\partial \omega}$, $\frac{\partial\mathbb{F}_6}{\partial I^*}$ and $\frac{\partial\mathbb{F}_6}{\partial A^*}$ in above equation, we have

$\frac{dA^*}{d\omega} = -\left(\frac{\alpha+d}{d}\right)\frac{dI^*}{d\omega}.$

(49)

Since $\mathbb{G}_6(\omega, I^*, A^*) = 0$, and differentiating it with respect to $\omega$, we have

$\frac{\partial \mathbb{G}_6}{\partial \omega}+\frac{\partial\mathbb{G}_6}{\partial I^*}\frac{dI^*}{d\omega}+\frac{\partial\mathbb{G}_6}{\partial A^*}\frac{dA^*}{d\omega} = 0.$

Using the values of $\frac{\partial\mathbb{G}_6}{\partial \omega}$, $\frac{\partial\mathbb{G}_6}{\partial I^*}$, $\frac{\partial\mathbb{G}_6}{\partial A^*}$ and $\frac{dA^*}{d\omega}$ in above equation, we obtain

$\frac{dI^*}{d\omega} = -\left(\frac{A_{61}}{A_{62}}\right),$

where, $A_{61} = \frac{\lambda pr_0r\theta I^*A^*}{(\omega+A^*)^2} \left(\frac{\Lambda-(\alpha+d)I^*}{d}-A^*\right),$ and $A_{62} = A_{12}$. Thus, from above equation, it is clear that $\frac{dI^*}{d\omega} <0$. Hence the proof.

---

Appendix C

Proof. Here, we show the local stability of equilibrium $E_0$ and $E^*$ by finding the eigenvalues of corresponding Jacobian matrices $J_0$ and $J^*$. The general Jacobian matrix '$J$' of model system (2) is as follows:

$J = \left( \begin{array}{cccc} a_{11}&-\beta I&\beta I&0 \\ -\frac{\lambda M}{p+M}&-\frac{\lambda M}{p+M}-(\lambda_0+d)& \frac{\lambda M}{p+M}&\frac{\lambda p(N-I-A)}{(p+M)^2} \\ -\alpha&0&-d&0 \\ r\left(1-\frac{\theta A}{\omega+A}\right)&-\frac{r\theta \omega I}{(\omega+A)^2}&0&-r_0 \\ \end{array} \right).$

where,

$a_{11} = \beta(N-2I-A)-(\nu+\alpha+d).$

Let $J_0$ and $J^*$ be Jacobian matrices evaluated at the equilibrium $E_0$ and $E^*$, respectively. Now the Jacobian matrix at equilibrium $E_0$ is given by:

$J_0 = \left( \begin{array}{cccc} a_{11}^0-(\nu+\alpha+d)&0&0&0 \\ -\frac{\lambda M_0}{p+M_0}&-\frac{\lambda M_0}{p+M_0}-(\lambda_0+d)& \frac{\lambda M_0}{p+M_0}&a_{24}^0\\ -\alpha&0&-d&0 \\ r\left(1-\frac{\theta A_0}{\omega+A_0}\right)&0&0&-r_0 \\ \end{array} \right).$

where,

$A_0 = \frac{\lambda \Lambda M_0}{d(\lambda M_0+(\lambda_0+d)(p+M_0))}$, $a_{11}^0 = \frac{\beta \Lambda}{d}\left(\frac{(\lambda_0+d)(p+M_0)}{\lambda M_0+(\lambda_0 +d)(p+M_0)}\right)$ and $a_{24}^0 = \frac{\lambda p\Lambda}{d(p+M_0)^2} \left(\frac{(\lambda_0+d)(p+M_0)}{\lambda M_0+(\lambda_0+d)(p+M_0)}\right)$.

From the Jacobian matrix evaluated at $E_0$, it is observed that one of the eigenvalue of this matrix is $\left(a_{11}^0-(\nu+\alpha+d)\right)$, which is positive if $R_1>1$ and negative if $R_1 <1$. It is also easy to see that all other eigenvalues of $J_0$ are -$\left(\frac{\lambda M_0}{p+M_0}+\lambda_0+d\right)$, $-d$ and $-r_0$. Thus, the equilibrium $E_0$ is locally asymptotically stable if $R_1 <1$. $E_0$ becomes unstable whenever $E^*$ is feasible (i.e., $R_1>1$). Thus, $E_0$ is saddle point with stable manifold locally in $N-A-M$ space and unstable manifold locally in $I$-direction whenever $E^*$ is feasible.

Now, we show the local stability of the endemic equilibrium $E^*$ using Routh-Hurwitz criterion. The characteristic equation for the matrix $J^*$ is given as follows:

$\eta^4 + B_1\eta^3 + B_2\eta^2 + B_3 \eta+B_4 = 0.$

(50)

where, $B_1 = a_{21}^*+\lambda_0+2d+r_0+\beta I^*$, $B_2 = r_0(a_{21}^*+\lambda_0+d)+a_{24}^*\frac{r\theta \omega I^*}{(\omega+A^*)^2}+\beta I^*(\lambda_0+r_0+d)+\alpha \beta I^*+d(a_{21}^*+\lambda_0+r_0+d)+d\beta I^*$.

$B_3 = \beta I^*r_0(\lambda_0+d)+\beta I^* a_{24}^*\frac{r\theta \omega I^*}{(\omega+A^*)^2}+\beta I^*a_{24}^*r\left(1-\frac{\theta A^*}{\omega+A^*}\right)+\alpha \beta I^*(\lambda_0+r_0+d)+dr_0(a_{21}^*+\lambda_0+d)+d a_{24}^*\frac{r\theta \omega I^*}{(\omega+A^*)^2}+\beta d I^*(\lambda_0+r_0+d)$, $B_4 = \beta dI^*r_0(\lambda_0+d)+d\beta I^* a_{24}^*\frac{r\theta \omega I^*}{(\omega+A^*)^2}+d\beta I^* a_{24}^*r\left(1-\frac{\theta A^*}{\omega+A^*}\right)+\alpha \beta I^*(\lambda_0+d)r_0+\alpha \beta I^* a_{24}^*\frac{r\theta \omega I^*}{(\omega+A^*)^2}$, $a_{21}^* = \frac{\lambda M^*}{p+M^*}$, $a_{24}^* = \frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}$. Here, we see that $B_1$, $B_2$, $B_3$ and $B_4$ all are positive. Thus, by using Routh-Hurwith criterion for above characteristic equation, we say that all the eigenvalues of the Jacobian matrix $J^*$ will be in left-half of the complex plane if following condition is satisfied:

$B_3(B_1B_2-B_3)-B_1^2B_4>0.$

Hence, the endemic equilibrium $E^*$ is locally asymptotically stable provided the above condition is satisfied.

---

Appendix D

Proof. To establish the non-linear stability of equilibrium $E^*$, consider the following positive definite function corresponding to reduced model system (2), about the equilibrium $E^*(I^*, A^*, N^*, M^*)$:

$\begin{align}\label{eq21b} G = &I-I^*-I^*\ln\left(\frac{I}{I^*}\right)+\frac{1}{2}m_1(A-A^*)^2+\frac{1}{2}m_2(N-N^*)^2\nonumber\\&+\frac{1}{2}m_3(M-M^*)^2. \end{align}$

(51)

where, the coefficient $m_1$, $m_2$ and $m_3$ are positive constants to be chosen appropriately.

Differentiating equation (51) with respect to time '$t$', along the solutions of model system (2) and choosing $m_2 = \frac{\beta}{\alpha}$, after rearranging the terms, we have

$\frac{dG}{dt} = -\beta(I-I^*)^2-m_1\left(\frac{\lambda M^*}{p+M^*}+(\lambda_0+d)\right)(A-A^*)^2-\frac{\beta d}{\alpha}(N-N^*)^2\nonumber \\ -m_3r_0(M-M^*)^2-\beta(A-A^*)(I-I^*)-m_1\frac{\lambda M^*}{p+M^*}(I-I^*)(A-A^*) \nonumber\\ +m_1\frac{\lambda p(N-I-A)}{(p+M)(p+M^*)}(M-M^*)(A-A^*)\nonumber \\ -m_3\frac{r\theta \omega I}{(\omega+A)(\omega+A^*)}(M-M^*)(A-A^*)\nonumber \\ +m_1\frac{\lambda M^*}{p+M^*}(N-N^*)(A-A^*) \nonumber \\ +m_3r\left(1-\theta\frac{ A^*}{\omega+A^*}\right)(I-I^*)(M-M^*).$

Thus, $\frac{dG}{dt}$ will be negative definite inside the region of attraction $\Omega$ provided the following inequalities are satisfied:

$\beta < \frac{4}{15}m_1\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right), \label{eq22b}$

(52)

$m_1\left(\frac{\lambda M^*}{p+M^*}\right)^2 < \frac{4\beta}{15}\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right), \label{eq23b}$

(53)

$m_1\left(\frac{\lambda M^*}{p+M^*}\right)^2 < \frac{4\beta d}{5\alpha}\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right), \label{eq24b}$

(54)

$m_1\left(\frac{\lambda \Lambda}{d(p+M^*)}\right)^2 < \frac{4r_0}{15}m_3\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right), \label{eq25b}$

(55)

$m_3\left(\frac{r\theta \Lambda}{d(\omega+A^*)}\right)^2 < \frac{4r_0}{15}m_1\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right), \label{eq26b}$

(56)

$m_3r^2\left(1-\frac{\theta A^*}{\omega+A^*}\right)^2 < \frac{4\beta r_0}{9}.\label{eq27b}$

(57)

From inequalities (52)-(54), we may choose the positive value of $m_1$, provided condition (15) is satisfied. Now, using this value of $m_1$, we may choose the positive value of $m_3$ from inequalities (55)-(57), provided condition (14) is satisfied.

Thus, $\frac{dG}{dt}$ will be negative definite inside the region of attraction $\Omega$, if the inequalities (14) and (15) are satisfied.

---

Appendix E

Proof. In this section, we proof the result for direction of bifurcating periodic solutions. For this, we translate the origin of the co-ordinate system to the Hopf-bifurcation point $E^*(I^*, A^*, N^*, M^*)$, by substituting $I = I^*+z_1$, $A = A^*+z_2$, $N = N^*+z_3$, $M = M^*+z_4$.

Where, $z = (z_1, z_2, z_3, z_4)^T$, where $T$ represents the transpose of matrix. Now we have the following system:

$\left( \begin{array}{c} \frac{dz_1}{dt} \\ \frac{dz_2}{dt} \\ \frac{dz_3}{dt} \\ \frac{dz_4}{dt} \\ \end{array} \right) = \left( \begin{array}{c} f_1(z_1, z_2, z_3, z_4)\\ f_2(z_1, z_2, z_3, z_4)\\ f_3(z_1, z_2, z_3, z_4)\\ f_4(z_1, z_2, z_3, z_4) \end{array} \right)+O(|z|^3).$

where, $f_1(z_1, z_2, z_3, z_4) = -\beta I^* z_1-\beta I^*z_2+\beta I^*z_3-\beta z_1^2-\beta z_1z_2+\beta z_1z_3$,

$f_2(z_1, z_2, z_3, z_4) = -\frac{\lambda M^*}{p+M^*}z_1-\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right)z_2+\frac{\lambda M^*}{p+M^*}z_3+\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}z_4, \\ -\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^3}z_4^2-\frac{\lambda p}{(p+M^*)^2}z_1z_4-\frac{\lambda p}{(p+M^*)^2}z_2z_4+\frac{\lambda p}{(p+M^*)^2}z_3z_4,$

$f_3(z_1, z_2, z_3, z_4) = -\alpha z_1-d z_3$,

$f_4(z_1, z_2, z_3, z_4) = r\left(1-\frac{\theta A^*}{\omega+A^*}\right)z_1-\frac{r\theta\omega I^*}{(\omega+A^*)^2}z_2-r_0z_4+\frac{r \theta \omega I^*}{(\omega+A^*)^3}z_2^2-\frac{r \theta \omega}{(\omega+A^*)^2}z_1z_2$.

In the above expression, we are not interested in the coefficient of the third, forth and higher order terms as they make no contribution in the further calculation.

Now, system takes the form:

$\dot{z} = Pz+H(z).$

(58)

where, $z = \left(\begin{array}{c} z_1 \\ z_2 \\ z_3 \\ z_4 \\ \end{array}\right)$,

$P = \left( \begin{array}{cccc} -\beta I^*&-\beta I^*&\beta I^*&0 \\ -\frac{\lambda M^*}{p+M^*}&-\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right)&\frac{\lambda M^*}{p+M^*}&\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2} \\ -\alpha&0&-d&0 \\ r\left(1-\frac{\theta A^*}{\omega+A^*}\right)&-\frac{r\theta \omega I^*}{(\omega+A^*)^2}&0&-r_0 \\ \end{array} \right).$ and

$H(z) = \left( \begin{array}{c} h_1 \\ h_2 \\ h_3 \\ h_4 \\ \end{array} \right)$

$= \left( \begin{array}{c} -\beta z_1^2-\beta z_1z_2+\beta z_1z_3 \\ -\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^3}z_4^2-\frac{\lambda p}{(p+M^*)^2}z_1z_4-\frac{\lambda p}{(p+M^*)^2}z_2z_4+\frac{\lambda p}{(p+M^*)^2}z_3z_4\\ 0 \\ \frac{r \theta \omega I^*}{(\omega+A^*)^3}z_2^2-\frac{r \theta \omega}{(\omega+A^*)^2}z_1z_2\\ \end{array} \right) .$

The eigenvectors $v_1$, $v_2$ and $v_3$ of the Jacobian matrix $P$ corresponding to the eigenvalues $i \omega_0$, $\eta_3$ and $\eta_4$, respectively, at $r = r_c$ are obtained as follows:

$v_1 = \left( \begin{array}{c} v_{11}-i v_{12} \\ v_{21}-i v_{22}\\ v_{31}-i v_{32} \\ v_{41}-i v_{42} \\ \end{array} \right)$, $v_2 = \left( \begin{array}{c} v_{13} \\ v_{23} \\ v_{33} \\ v_{43} \\ \end{array} \right)$ and $v_3 = \left( \begin{array}{c} v_{14} \\ v_{24} \\ v_{34} \\ v_{44}\\ \end{array} \right).$

where, $v_{11} = \frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}\frac{r\theta\omega I^*}{(\omega+A^*)^2}+r_0\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right)-\omega_0^2,$

$v_{12} = -\left\{\omega_0\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right)+r_0\omega_0\right\},$

$v_{21} = r\left(1-\frac{\theta A^*}{\omega+A^*}\right)\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}-\frac{\lambda M^*}{p+M^*}\left(\frac{r_0(\alpha+d)d+\omega_0^2(\alpha+r_0)}{d^2+\omega_0^2}\right),$

$v_{22} = \frac{\lambda M^*}{p+M^*}\left(\frac{\omega_0((\alpha+d)d+\omega_0^2)-r_0\omega_0\alpha}{d^2+\omega_0^2}\right),$

$v_{31} = -\left\{\frac{\alpha \lambda p d(N^*-I^*-A^*)}{(d^2+\omega_0^2)(p+M^*)^2}\frac{r \theta \omega I^*}{(\omega+A^*)^2}+\frac{\alpha d r_0}{d^2+\omega_0^2}\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right)+\frac{\alpha \omega_0^2r_0}{d^2+\omega_0^2}\right.\\ \left.+\frac{\alpha\omega_0^2}{d^2+\omega_0^2}\left(\frac{\lambda M^*}{p+M^*}+\lambda_0\right)\right\},$

$v_{32} = \left\{\frac{\alpha \omega_0^3}{d^2+\omega_0^2}+\frac{\alpha d \omega_0}{d^2+\omega_0^2}\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right)-\frac{\alpha \omega_0}{d^2+\omega_0^2}\left(\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}\right)\frac{r \theta \omega I^*}{(\omega+A^*)^2}\right.\\ \left.-\frac{\alpha \omega_0 r_0}{d^2+\omega_0^2}\left(\frac{\lambda M^*}{p+M^*}+\lambda_0\right)\right\},$

$v_{41} = \frac{\lambda M^*}{p+M^*}\left(1+\frac{\alpha d}{d^2+\omega_0^2}\right)\frac{r\theta \omega I^*}{(\omega +A^*)^2}+r\left(1-\frac{\theta A^*}{\omega+A^*}\right)\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d\right),$

$v_{42} = \frac{\lambda M^*}{p+M^*}\left(\frac{\alpha \omega_0}{d^2+\omega_0^2}\right)\frac{r \theta \omega I^*}{(\omega+A^*)^2}-r\omega_0\left(1-\frac{\theta A^*}{\omega+A^*}\right),$

$v_{13} = \frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}\frac{r\theta\omega I^*}{(\omega+A^*)^2}+(r_0+\eta_3)\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d+\eta_3\right),$

$v_{23} = r\left(1-\frac{\theta A^*}{\omega+A^*}\right)\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}-(r_0+\eta_3)\left(\frac{\alpha+d+\eta_3}{d+\eta_3}\right)\frac{\lambda M^*}{p+M^*},$

$v_{33} = -\frac{\alpha}{d+\eta_3}\left\{\frac{\lambda p (N^*-I^*-A^*)}{(p+M^*)^2}\frac{r \theta \omega I^*}{(\omega+A^*)^2}+(r_0+\eta_3)\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d+\eta_3\right)\right\},$

$v_{43} = \frac{\lambda M^*}{p+M^*}\left(\frac{\alpha+d+\eta_3}{d+\eta_3}\right)\left(\frac{r\theta \omega I^*}{(\omega+A^*)^2}\right)+r\left(1-\frac{\theta A^*}{\omega+A^*}\right)\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d+\eta_3\right),$

$v_{14} = \frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}\frac{r\theta\omega I^*}{(\omega+A^*)^2}+(r_0+\eta_4)\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d+\eta_4\right),$

$v_{24} = r\left(1-\frac{\theta A^*}{\omega+A^*}\right)\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^2}-(r_0+\eta_4)\left(\frac{\alpha+d+\eta_4}{d+\eta_4}\right)\frac{\lambda M^*}{p+M^*},$

$v_{34} = -\frac{\alpha}{d+\eta_4}\left\{\frac{\lambda p (N^*-I^*-A^*)}{(p+M^*)^2}\frac{r \theta \omega I^*}{(\omega+A^*)^2}+(r_0+\eta_4)\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d+\eta_4\right)\right\},$

$v_{44} = \frac{\lambda M^*}{p+M^*}\left(\frac{\alpha+d+\eta_4}{d+\eta_4}\right)\left(\frac{r\theta \omega I^*}{(\omega+A^*)^2}\right)+r\left(1-\frac{\theta A^*}{\omega+A^*}\right)\left(\frac{\lambda M^*}{p+M^*}+\lambda_0+d+\eta_4\right)$.

Define, $V = (Re(v_1), -Im(v_1), v_2, v_3)$,

$V = \left( \begin{array}{cccc} v_{11}&v_{12}&v_{13}&v_{14} \\ v_{21}&v_{22}&v_{23}&v_{24} \\ v_{31}&v_{32}&v_{33}&v_{34} \\ v_{41}&v_{42}&v_{43}&v_{44} \\ \end{array} \right).$

The matrix $V$ is non-singular such that

$V^{-1}PV = \left( \begin{array}{cccc} 0&-\omega_0&0&0 \\ \omega_0& 0&0&0 \\ 0&0&\eta_3&0 \\ 0&0&0&\eta_4 \\ \end{array} \right).$

Inverse of matrix $V$ is given by:

$V^{-1} = \left( \begin{array}{cccc} w_{11}&w_{12}&w_{13}&w_{14} \\ w_{21}&w_{22}&w_{23}&w_{24} \\ w_{31}&w_{32}&w_{33}&w_{34} \\ w_{41}&w_{42}&w_{43}&w_{44} \\ \end{array} \right).$

where,

$w_{11} = \frac{1}{\Delta}\left[v_{22}(v_{44}v_{33}-v_{43}v_{34})+v_{23}(v_{42}v_{34}-v_{44}v_{32})+v_{24}(v_{43}v_{32}-v_{42}v_{33})\right],$

$w_{12} = \frac{1}{\Delta}\left[v_{12}(v_{43}v_{34}-v_{44}v_{33})+v_{13}(v_{32}v_{44}-v_{34}v_{42})+v_{14}(v_{33}v_{42}-v_{43}v_{32})\right],$

$w_{13} = \frac{1}{\Delta}\left[v_{12}(v_{44}v_{23}-v_{43}v_{24})+v_{13}(v_{42}v_{24}-v_{44}v_{22})+v_{14}(v_{43}v_{22}-v_{23}v_{42})\right],$

$w_{14} = \frac{1}{\Delta}\left[v_{12}(v_{24}v_{33}-v_{23}v_{34})+v_{13}(v_{22}v_{34}-v_{32}v_{24})+v_{14}(v_{23}v_{32}-v_{33}v_{22})\right],$

$w_{21} = \frac{1}{\Delta}\left[v_{21}(v_{34}v_{43}-v_{44}v_{33})+v_{23}(v_{44}v_{31}-v_{34}v_{41})+v_{24}(v_{41}v_{33}-v_{31}v_{43})\right],$

$w_{22} = \frac{1}{\Delta}\left[v_{11}(v_{33}v_{44}-v_{34}v_{43})+v_{13}(v_{34}v_{41}-v_{44}v_{31})+v_{14}(v_{31}v_{43}-v_{33}v_{41})\right],$

$w_{23} = \frac{1}{\Delta}\left[v_{11}(v_{43}v_{24}-v_{44}v_{23})+v_{13}(v_{21}v_{44}-v_{24}v_{41})+v_{14}(v_{41}v_{23}-v_{43}v_{21})\right],$

$w_{24} = \frac{1}{\Delta}\left[v_{11}(v_{23}v_{34}-v_{24}v_{33})+v_{13}(v_{31}v_{24}-v_{34}v_{21})+v_{14}(v_{33}v_{21}-v_{23}v_{31})\right],$

$w_{31} = \frac{1}{\Delta}\left[v_{21}(v_{32}v_{44}-v_{42}v_{34})+v_{22}(v_{34}v_{41}-v_{31}v_{44})+v_{24}(v_{31}v_{42}-v_{32}v_{41})\right],$

$w_{32} = \frac{1}{\Delta}\left[v_{11}(v_{42}v_{34}-v_{44}v_{32})+v_{12}(v_{44}v_{31}-v_{34}v_{41})+v_{14}(v_{41}v_{32}-v_{42}v_{31})\right],$

$w_{33} = \frac{1}{\Delta}\left[v_{11}(v_{44}v_{22}-v_{42}v_{24})+v_{12}(v_{41}v_{24}-v_{21}v_{44})+v_{14}(v_{41}v_{32}-v_{42}v_{31})\right],$

$w_{34} = \frac{1}{\Delta}\left[v_{11}(v_{32}v_{24}-v_{34}v_{22})+v_{12}(v_{21}v_{34}-v_{24}v_{31})+v_{14}(v_{22}v_{31}-v_{21}v_{32})\right],$

$w_{41} = \frac{1}{\Delta}\left[v_{21}(v_{42}v_{33}-v_{43}v_{32})+v_{22}(v_{43}v_{31}-v_{33}v_{41})+v_{23}(v_{41}v_{32}-v_{31}v_{42})\right],$

$w_{42} = \frac{1}{\Delta}\left[v_{11}(v_{43}v_{32}-v_{42}v_{33})+v_{12}(v_{33}v_{41}-v_{31}v_{43})+v_{13}(v_{42}v_{31}-v_{32}v_{41})\right],$

$w_{43} = \frac{1}{\Delta}\left[v_{11}(v_{42}v_{23}-v_{43}v_{22})+v_{12}(v_{21}v_{43}-v_{23}v_{41})+v_{13}(v_{41}v_{22}-v_{21}v_{42})\right],$

$w_{44} = \frac{1}{\Delta}\left[v_{11}(v_{33}v_{22}-v_{32}v_{23})+v_{12}(v_{31}v_{23}-v_{21}v_{33})+v_{13}(v_{32}v_{21}-v_{31}v_{22})\right].$

$\Delta = det(V)$. Consider the transformation $z = Vy$, i.e., $y = V^{-1}z$.

Where,

$y = (y_1, y_2, y_3, y_4)^T.$

Under this linear transformation system (58), takes the form:

$\dot{y} = (V^{-1}P V)y+f(y).$

(59)

where, $f(y) = V^{-1}H(Vy)$. This can be written as:

$\dot{y_1} = -\omega_0 y_2+f^1(y_1, y_2, y_3, y_4), \\ \dot{y_2} = \omega_0 y_1+f^2(y_1, y_2, y_3, y_4), \\ \dot{y_3} = \eta_3 y_3+f^3(y_1, y_2, y_3, y_4), \\ \dot{y_4} = \eta_4 y_4+f^4(y_1, y_2, y_3, y_4).$

where,

$f = (f^1, f^2, f^3, f^4)^T.$

$\begin{align*} f^1 = & w_{11}h_1+w_{12}h_2+w_{13}h_3+w_{14}h_4, \\ f^2 = & w_{21}h_1+w_{22}h_2+w_{23}h_3+w_{24}h_4, \\ f^3 = & w_{31}h_1+w_{32}h_2+w_{33}h_3+w_{34}h_4, \\ f^4 = & w_{41}h_1+w_{42}h_2+w_{43}h_3+w_{44}h_4, \\ h_1 = & -\beta(v_{11}y_1+v_{12}y_2+v_{13}y_3+v_{14}y_4)^2\\ \nonumber &-\beta(v_{11}y_1+v_{12}y_2+v_{13}y_3+v_{14}y_4)(v_{21}y_1+v_{22}y_2+v_{23}y_3+v_{24}y_4)\\ \nonumber &+\beta(v_{11}y_1+v_{12}y_2+v_{13}y_3+v_{14}y_4)(v_{31}y_1+v_{32}y_2+v_{33}y_3+v_{34}y_4), \\ h_2 = & -\frac{\lambda p(N^*-I^*-A^*)}{(p+M^*)^3}(v_{41}y_1+v_{42}y_2+v_{43}y_3+v_{44}y_4)^2 \\ \nonumber &-\frac{\lambda p}{(p+M^*)^2}(v_{11}y_1+v_{12}y_2+v_{13}y_3+v_{14}y_4)(v_{41}y_1+v_{42}y_2+v_{43}y_3+v_{44}y_4)\\ \nonumber &-\frac{\lambda p}{(p+M^*)^2}(v_{21}y_1+v_{22}y_2+v_{23}y_3+v_{24}y_4)(v_{41}y_1+v_{42}y_2+v_{43}y_3+v_{44}y_4)\\ \nonumber &+\frac{\lambda p}{(p+M^*)^2}(v_{31}y_1+v_{32}y_2+v_{33}y_3+v_{34}y_4)(v_{41}y_1+v_{42}y_2+v_{43}y_3+v_{44}y_4), \\ h_3 = & 0, \\ h_4 = & -\frac{r\theta \omega}{(\omega+A^*)^2}(v_{11}y_1+v_{12}y_2+v_{13}y_3+v_{14}y_4)(v_{21}y_1+v_{22}y_2+v_{23}y_3+v_{24}y_4)\\ \nonumber &+\frac{r\theta \omega I^*}{(\omega+A^*)^3}(v_{21}y_1+v_{22}y_2+v_{23}y_3+v_{24}y_4)^2. \end{align*}$

Furthermore, we can calculate $h_{11}$, $h_{02}$, $h_{20}$, $H_{21}$, $H_{110}^1$, $H_{110}^2$, $H_{101}^1$, $H_{101}^2$, $\sigma_{11}^1$, $\sigma_{11}^2$, $\sigma_{20}^1$, $\sigma_{20}^2$ following the procedure given in Hassard et al. [16].

Using above, we can find following quantities:

$h_{21} = H_{21}+2\left(H_{110}^1\sigma_{11}^1+H_{110}^2\sigma_{11}^2\right)+H_{101}^1\sigma_{20}^1+H_{101}^2\sigma_{20}^2, \\ c_1(0) = \frac{i}{2\omega_0}\left(h_{11}h_{20}-2 |h_{11}|^2-\frac{|h_{02}|^2} {3}\right)+\frac{h_{21}}{2}, \\ \mu_2 = -\frac{Re (c_1(0))}{\phi^\prime(0)}, \\ \tau_2 = -\frac{Im (c_1(0))+\mu_2 \sigma^\prime(0)}{\omega_0}, \\ \beta_2 = -2\mu_2 \phi^\prime(0).$

where, $\phi^\prime(0) = \frac{d}{dr}(Re(\eta_1(r)))|_{r = r_c}$ and $\sigma^\prime(0) = \frac{d}{dr}(Im(\eta_1(r)))|_{r = r_c}.$

---