Partial differential equations from theory to applications: Dedicated to Alberto Farina, on the occasion of his 50th birthday

1.   Introduction

Conformance checking is used to compare process instances documented in event logs with existing reference models. This technique determines the conformity of the lived process with the reference process and identifies deviations. State-of-the-art conformance checking approaches work for many event types and can successfully identify deviations. Even deviations from events in a loop can be detected and identified by some approaches ^[1]. However, if the process models contain 1-loops, then not all deviations can be identified. 1-loops describe a subclass of events-in-a-loop, which are loops that contain only one activity ^[2]. Thus, they can only detect deviations in single events, but in sequences of repetitive events, they are not able to calculate the exact number of missing events that causes the violation. This problem intensifies if the process is of high complexity and also contains temporal rules. There are process modelling languages like BPMN, Declare and DPN which are multi-perspective and thus can be used to check for temporal rules. A problem arises if a conformance check with an alignment should be conducted using these process modelling languages. Here, most conformance checking algorithms are able to calculate alignments for simple temporal rules like checking if a given event was executed in a given time frame or check if an event happens after a given point in time. ^[3,4,5] However, complex temporal rules like checking how many events should have been taken place in a given time frame is not possible without extensive manual modelling. Especially in healthcare monitoring processes, such as blood pressure monitoring or oncological and postoperative follow-up processes, 1-loops defined by complex temporal rules are an integral part of the processes and thus prevent conformance checking using native process mining approaches. For example, in the case of two consecutive missed follow-up appointments in the follow-up process of an oncological disease with a follow-up interval of three months, most approaches can only identify one deviation. This is due to the fact that in an alignment the defined temporal rule is only checked for the event that appeared in the log and not for the events that are missing. Currently, only the approach of Rinner et al. ^[6] addresses the problem of conformance checking on event logs containing 1-loops in combination with complex temporal rules. The approach is based on a preprocessing method called time boxing and relabels events according to their expected time of occurrence. However, time boxing comes with limitations, e.g. the application of time boxing leads to very complex process models, a multiplication of activities in the model and requires complex event log preprocessing.

In this paper, we present an approach and formalization towards dealing with events in 1-loops in conformance checking, called RIDE (Reconstructing Invisible Deviating Events). The approach is based on the basic assumption that the absence of a planned event can also be interpreted as an event. Thus, for example, the nonattendance of an appointment can be mapped directly to an event "appointment not attended". Taking advantage of this assumption, the approach reconstructs the events that identify the absence of an event in the preprocessing step ^[7]. These events are called invisible deviating events and are therefore events that are not included in the process log and violate the process model ^[20]. These are used to calculate deviations of the traces using established conformance checking algorithms. Furthermore, multi-perspective conformance checking is used and the approach does not require complex modifications of the process models like time boxing. We demonstrate the applicability of the approach in the medical domain in a case study to determine guideline compliance of follow-up care for patients with malignant melanoma. The approach can generally be used for recurring events with complex temporal rules. This means that it can also be used if other events occur between the recurring events. For this reason, we refer to recurring events in the following and mean both 1-loops and recurrences in which other events occur in between.

According to the challenges proposed by the Process Mining Manifesto, this paper addresses challenge C2, described as dealing with complex event logs with different characteristics. ^[8] To this end, the following research questions are examined:

RQ1: How to perform conformance checking on event logs containing recurring activities by reconstructing the events?

RQ2: What are the limitations and advantages of reconstructing recoverable invisible deviating events directly in the event log concerning conformance checking?

The structure of the paper is as follows. In Section 2, we provide the theoretical fundamentals needed to reconstruct invisible deviating events in the event log, in Section 3, recurring activities are analyzed in detail as well as problems this event type implies to conformance checking. Next, we introduce the $\texttt{RIDE}$ (Reconstructing Invisible Deviating Events) approach used for reconstructing invisible deviating events in Section 4. In Section 5, the $\texttt{RIDE}$ approach is applied in a case study for conformance checking on a medical event log and the results of the conformance check are also discussed. In section 6 the paper is concluded.

2.   Fundamentals

2.1.   Event Logs

Process mining approaches are based on event logs. Event logs are a collection of cases and thus can be interpreted as multi-sets. Each case contains a sequence of events, called a trace. Events represent the execution of an activity, hence a work package, which is executed in the process instance. Note that an execution of an activity can be represented by several events (e.g. if both start and end of the activity are represented by one event) ^[9]. In addition to control-flow related data, event logs may use attributes to represent other perspectives, such as the data perspective or the resource perspective. In the following, we define events, event logs, cases and traces, and operations on event logs.

Definition 1. (Universes) We define the following universes to be used in this paper:

● $\mathcal{C}$ is the universe of all possible case identifiers

● $\mathcal{E}$ is the universe of all possible event identifiers

● $\mathcal{A}$ is the universe of all possible activity identifiers

● $\mathcal{AN}$ is the universe of all possible attribute identifiers

Definition 2. (Attributes, Classifier) Attributes can be used to characterize events and cases, e.g. an event can be assigned to a resource or have a timestamp. For any event $e\in\mathcal{E}$, any case $c\in\mathcal{C}$ and name $n\in\mathcal{AN}$, $\#_n(e)$ is the value of attribute $n$ for event $e$ and $\#_n(c)$ is the value of attribute $n$ for case $c$. $\#_n(e) = \perp$ if event $e$ has no attribute $n$ and $\#_n(c) = \perp$ if case $c$ has no attribute $n$. We assume the classifier $\underline{e} = \#_{activity}(e)$ as the default classifier.

Definition 3. (Trace, Case) Each case $c\in\mathcal{C}$ has a mandatory attribute trace, with $\hat{c} = \#_{trace}(c)\in\mathcal{E^*}\setminus \{\langle\rangle\}$. A trace is a finite sequence of events $\sigma\in\Sigma^*$ where each event occurs only once, i.e. $1 \leq i < j \leq | \sigma |: \sigma(i) \neq \sigma(j)$. By $\sigma \oplus e = \sigma$ we denote the addition of an $e$ event to a trace $\sigma$.

Definition 4. (Event log) An event log is a set of cases $\mathcal{L}\subseteq\mathcal{C}$, in the form that each event is contained only once in the event log. If an event log contains timestamps these should be ordered in each trace. $\hat{\mathcal{L}} = \{e|c\in\mathcal{L}\land e \in\hat{c}\}$ is the set of all events appearing in the log $\mathcal{L}$.

Definition 5. (Operations on event logs) Let $\mathcal{L}$ be an event log with $c\in\mathcal{L}$ and $\#_{trace}(c) = \sigma = \langle e_1, ..., e_n\rangle$ be a trace from $\mathcal{L}$.

● The trace, that contains an event $e$ is denoted by

● The latest event before an event occurred, with the given activity parameter as attribute value or the first event of the trace:

● $createEvent:\mathcal{AN}\times TIME \rightarrow \mathcal{E}$ creates a new event with the given name and timestamp.

2.2.   Petri Nets

In process mining, Petri nets are used to model the control flow perspective. They can be viewed as a directed bipartite graph that uses places and transitions to create a static process model. Transitions refer to the activities of a process, and tokens are used to determine the current state of the process. ^[10]

Definition 6. (Petri net ^[10]) A Petri net is a triplet consisting of $N = (P, T, F)$ with

● $P = \{p_1, \, p_2, \, p_3\, .. \, p_m\}$, the finite set of places,

● $T = \{t_1\, , t_2\, , t_3\, .. \, t_n\}$, the finite set of transitions and

● $F \subseteq (P\, \times\, T) \cup (T\, \times \, P)$, the set of arcs between places and transitions.

The state of a Petri net is expressed by the distribution of tokens over places. All the possible states or behaviour of the Petri net can be expressed as a multi set of its places, which can be formalized as $M \in \mathbb{B}(P)$ and is called marking.

Labeled Petri nets extend Petri nets by the possibility to label transitions, while several transitions can also have the same label. Furthermore, they allow expressing transitions that are unobservable or invisible.

Definition 7. (Labeled Petri Net) A Labeled Petri Net is a five-tuple $N = (P, T, F, A, l)$ where the Petri net $(P, T, F)$ is extended by activity labels $A\subseteq \mathcal{A}$ and labeling function $l\ : T\rightarrow A$, where $l(t) = \tau$ with $t\in T$ represents an unobservable or invisible transition ^[10].

2.3.   Alignments and Conformance Measure

In conformance checking, alignments are used to identify discrepancies between the desired behaviour of the process depicted by the process model and the real behaviour depicted by the event log ^[11]. An alignment is created by mapping the viable process steps depicted in the process model to the events recorded in the event log. For events of the event log that cannot be mapped to an event in the process model, the alignment algorithm performs a so-called log move. If the model requires an event that is not present in the log, then a model move is performed. ^[12] Otherwise, if everything matches, the movement is defined as correct synchronous movement. Thus, an alignment can be thought of as a sequence of alignment moves. ^[13,14]

To calculate a real executions' conformance with a process model, costs can be assigned to the specific alignment moves. These can then be used to select an optimal alignment from the set of possible alignments, i.e. an alignment with the lowest costs. The most used conformance measure is fitness, which describes to what extent the model reflects the recorded behavior in the event log ^[10,15]. Fitness is calculated by comparing the costs of the optimal alignment with the trace length and the shortest path through the process model. By using fitness as a conformance measure, it is possible to compare traces corresponding to the same process but with different length.

3.   Problem analysis

1-loops are loops, that only contain a single activity and have no other activities in between ^[2,18]. The term recurring activities refers to activities that recur at certain time intervals, e.g. days, months or years. These can be 1-loops or loops with other activities between the recurring activities. This kind of activities can be found in many areas, where it is necessary to check, if an event is executed in regular intervals. For example, elevator inspections or drinking water testing. In the medical domain, 1-loops can arise from regular monitoring of heart rates, blood pressure, and other vital signs ^[16] or in the process of melanoma surveillance ^[17].

In a process model, recurring or repeated activities are easily described by a loop structure in which the same activity of a process is repeated ^[18]. It is important not to confuse recurring activities with duplicate events. Duplicate events refer to a data quality issue of event logs, where the same activity is executed falsely multiple times and thus generates inaccurate event logs ^[19]. On the other hand, recurring activities are not considered as a data quality issue because these activities are intended to be repeated in a process.

For conformance checking on models containing simple loops or recurring activities, there are native process mining approaches that can calculate alignments. A particular problem further arises when recurring activities occur in combination with complex temporal rules, i.e. activities whose interval changes over time. This concerns both sudden interval changes, e.g., due to changes in certain environmental factors, as well as known changes, such as intervals that change gradually. Although the interval change is known, when deviations from the process occur, native conformance checking approaches cannot create a correct alignment. In this case, the native algorithms cannot determine the correct number of missing events. Missing events are events that are intended in the model, but are missing in the trace at the corresponding position ^[19].

One approach to address recurring activities with complex temporal rules is to fully model out the recurrences in the process model. A method that accomplishes this is proposed by Rinner et al. and is called time boxing ^[6]. When using time boxing, a separate activity, also called a time box, is generated for each repetition and thus for each interval. Preprocessing is used to assign the events in the event log to a time box by renaming the activity attribute to the time boxes' identifier. By replacing the loops in the process model with the time boxes, a complex process model is generated, which enables the conformance check. Time boxing thus requires complex preprocessing as well as extensive manual modelling, which can result in a process model that is difficult to maintain.

In this paper, a new approach to conformance checking on process models containing recurring activities is proposed. In contrast to the approach of Rinner et al., this approach is based on the basic assumption that even the absence of an expected event is actually an event, which in most cases is not recorded in the event log. Examples of this could be events that indicate that an examination or an installment payment was not made within the specified time period. This assumption allows the reconstruction of these events (see figure 1), thus enabling the use of native conformance checking algorithms for models containing recurring activities at time intervals, while the process model itself remains unchanged.

In this paper, we refer to these events as recoverable invisible deviating events ^[20]. The name is derived from vanden Broucke's event classification framework ^[20]. The term Invisible Event indicates that these events actually occurred (actual business event) but were not recorded in the event log. The terms recoverable and deviating indicate that the events are recoverable using other data sources for e.g. timestamps or background knowledge and deviate from the process model. Based on our assumption that the absence of a planned event can be interpreted as an actual business event, the recoverable invisible deviating event can be thought of as a dummy event that was inserted into the event log to represent a recurring activity that was missed.

Note, these events are not to be interchanged with non-events. Referring to event 3 in figure 1, the event "a" would be a non-event, since it did not occur. The event "missed a", on the other hand, has taken place and is only derived from the absence of "a" and thus from the non-event ^[21].

4.   Methods

The RIDE approach is based on the idea of making invisible deviating events in the event log visible by reconstructing them. The reconstruction process uses a Backtracing Algorithm (BTA) approach. This algorithm ensures the chronologically correct reconstruction of the invisible events by taking into account time-related attributes and rules. Thus, a conditional reconstruction of the invisible events based on complex time-related rules and local conformance checking is enabled. In the first step, the structure of the time-related attributes and the definition of the rules are explained, while in the second step the Backtracing algorithm is specified.

4.1.   Time-related properties

Application of the approach described here allows reconstruction of invisible deviating events in the case of (1) activities that repeat at defined time intervals, (2) activities that repeat at defined time intervals and exhibit sudden interval changes after a defined period of time, and of (3) activities that repeat at defined time intervals and exhibit interval changes that is dependent on the occurrence of a previously defined event. Thereby, it is independent if the event occurs as 1-loop or if other activities occur between the single events. To address cases 1-3, it is necessary to be able to include certain temporal properties of individual events in the reconstruction rules. The following properties were identified as necessary in the work:

● Between Event Time (bet) defines the time between two consecutive events of the same type or the trace's first event.

● Cumulative Between Event Time (cbet) defines the cumulative value of bet over each event of the same type, i.e. the time between the current event and the trace's first event.

● Cumulative Time From Event ($ctfe_{x}$) is the cumulative bet calculated for each event, since the occurrence of a given activity $x$. If the given activity $x$ occurs, the value of $ctfe_{x}$ is reset to 0.

Definition 8. (bet, cbet, ctfe) Let $L\subseteq\mathcal{C}$ be an event log and $a\in\mathcal{A}$ an activity. Then for $\forall e\in\hat{L}$ holds

4.2.   Reconstruction rules

Reconstruction rules are logical expressions and determine whether one or more events must be reconstructed. $R_a$ defines the set of rules for activity $a$. Each rule consists of a logical expression and a threshold, which specifies the time interval between a current event and a possible event to be reconstructed. The rules can be specified based on the complete universe of variables $V$ as well as the time-related attributes $(bet, ctfe_{x}, cbet)$ in the rule definition (see examples Table 1).

Definition 9. (Reconstruction Rules) Following Mannhardt et al., we denote the universe of all Boolean expressions over variables $V$ and the time-relevant attributes $TA$ as $EXPR(V\cup TA)$. An expression $expr \in EXPR(V\cup TA)$ is a Boolean formula that evaluates to $true$ or $false$. Based on this, we define $R_{a} \subseteq \{(c, th) \in EXPR(V\cup TA)\times \mathbb{R}\}$ be the set of rules for all events $e\in\sigma$ for which holds $\#_{activity}(e) = a$, where each rule is a tuple of a condition $c$ and a threshold $th$.

Definition 10. (Reconstruction Rule evaluation function) Based on Mannhardt, let $V_P\subset V$ be a subset of all process variables and $TA_P$ be a subset of all time-related attributes. The truth value of the logical expression $expr\in EXPR(V_P\cup TA_P)$ is determined with an evaluation function:

The function $eval$ maps the set $\{true, false\}$ and determines the truth value of the expression, taking into account the current values of the variables and time-related attributes. While values of variables are fixed at runtime, values of time-related attributes are calculated at the time of execution of the $eval$ function, since their values may change at runtime.

We do not go further into the logical expressions, since they are only based on the basic algorithms and the basic logic.

4.3.   Algorithm formalization

In this section, we present a technique to perform a conformance check for events repeating at temporal intervals, and to detect so-called missing events ^[20] and thus events that should have occurred but did not. As previously described, current conformance checking approaches cannot handle these events. The Reconstructing Invisible Deviating Events (RIDE) approach addresses the problem of recurring activities in conformance checking by reconstructing the related events in the event log as Invisible Deviating Events. The RIDE approach is based on the idea of using previously defined rules to determine exactly when events are missing and reconstruct them. This means that established conformance checking algorithms can be used to calculate conformance. The RIDE approach is based on sequential forward viewing and evaluation of events and recursive backward evaluation and reconstruction of missing events. The required inputs are an Event Log $\mathcal{L}$, the set of reconstruction rules $R$ and the reconstructed event identifier $IdeID$ (Invisible Deviating Event Identifier), which defines a suffix that is appended to the name of the recurring invisible event and is defined in a way, that no preferred activity ends on the $IdeID$. The output of the algorithm is an event log $\mathcal{L}_{Rec}$ that contains all the reconstructed invisible events.

Algorithm 1 shows the RIDE approach. The algorithm takes an event log $\mathcal{L}$ and set of reconstruction rules $R$ as input and returns a reconstructed event log containing all invisible events identified based on the rules $R$. The algorithm assumes that the $IdeID$ suffix is chosen to ensure that none of the reconstructed events are part of the process model.

Starting with an empty output event log $\mathcal{L}_{Rec}$, the RIDE iterates over all traces and all events contained in $\mathcal{L}$. For each event, the Backtracing function checks whether any of the rules from the given set of rules $R$ are violated. In this case, a new event is generated, whose time interval to the current event is calculated with the threshold of the used rule. The Backtracing function is now called for the reconstructed event to check if there are any missing events before the current event. This is repeated until a reconstruction rule from $R$ is no longer violated. The event log with the reconstructed event is then composed of the return of the Backtracing function.

Reconstruction of the non-compliant events whose classifier is not part of the process model results in a violation. Thus, native conformance checking algorithms can be used to detect deviations and create alignments without having to implement complex temporal rules.

5.   Melanoma surveillance case study

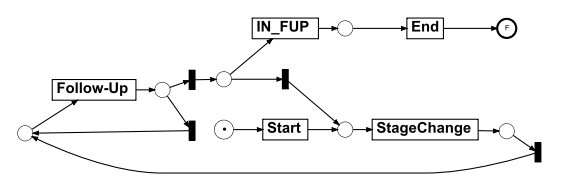
In this section, we describe how the RIDE approach was applied in a specific case study. The case study is built on a melanoma surveillance dataset and was provided by the Department of Dermatology, Medical University of Vienna (DDMUV). The data are particularly characterized by the occurrence of missing events referencing on recurring activities and the occurrence of complex temporal rules. These are derived from the guideline for the treatment of malignant melanoma, which prescribes follow-up examinations at specific time intervals depending on the severity of the tumor disease and the time elapsed. The process of melanoma surveillance begins with excision of the primary tumor, which is referred to as $\texttt{Excision}$ in the process model shown in Figure 2. After excision, the severity of the cancer is determined using the American Joint Committee on Cancer (AJCC) staging system in four stages (Ⅰ - Ⅳ). This is based on tumor thickness, the presence of an ulcer, and the presence of metastases. ^[22] In the process model, this is represented by $\texttt{state change}$. Patients then cycle through follow-up examinations at the previously defined intervals for each AJCC stage. The process ends if the patient attended follow-up examinations for 10 years without a stage change. Because each follow-up visit may reveal that the tumor disease is progressing negatively, each visit may also be followed by a stage change. Stage changes during tumor surveillance always describe a change to a higher stage. Changes to a lower stage are not possible. A change in stage also introduces an interval change, as the melanoma surveillance period of 10 years is reset and the intervals between follow-up examinations change.

5.1.   Event log

The melanoma surveillance event log was collected from the DDMUV and was first used by Rinner et al. to verify guideline compliance using a time boxing approach. It consists of 1023 melanoma surveillance cases distributed among 146 variants, 6 activities, and 10,320 events, of which 58.45 percent are follow-ups and 11.81 percent are stage changes. The event log covers a period of seven years, starting in January 2010 and ending in June 2017. Since seven years do not cover the entire melanoma surveillance process, which is at least ten years, the patient is still compliant if the last follow-up visit was before the end of the study in June 2017. It is important to note that only patients who have at least one follow-up appointment at the DDMUV were included ^[6]. Due to the General Data Protection Regulation (GDPR) of Electronic Healthcare Records (EHR) it was not possible to obtain the data directly recorded by the information system of the DDMUV. It has to be ensured, that the data from the EHR is anonymized. Thus, each timestamp is rounded to the first of the month. To maintain the right order of events, the timestamp of each event in a trace is incremented by 1 millisecond. Thus, it is not possible that two events of the same trace have the same timestamp. The anonymized event log was provided in the MXML format. By using ProM the MXML event log was transformed into a XES event log. Table 2 shows the structure of the traces in the melanoma surveillance event log. It shows a sample trace consisting of a start and an end event and various follow-ups, lost to follow-ups and stage changes in between.

The event log consists of the following events. $\texttt{Start}$, which indicates the beginning of the melanoma surveillance process. The event $\texttt{Stage Change}$ describes a stage change as explained in the previous section. This event is always followed by the follow-up event that describes the activity of the follow-up examination. Furthermore, the $\texttt{Stage Change}$ event has a global attribute (Stage dpa), which contains the value of the stage the patient is in. Since Stage dpa is a global attribute, it is only recorded if a $\texttt{Stage Change}$ is executed. After the last $\texttt{Follow-Up}$ the events $\texttt{IN}\_\texttt{FUP}$ (In Follow-Up) or $\texttt{LTFU}$ (Lost to Follow-Up) have to occur. The patient is in the follow-up process $\texttt{IN}\_\texttt{FUP}$ when the last follow-up visit is attended in June 2017. However, patients are considered "Lost to Follow-Up" $\texttt{LTFU}$ if the monitoring process is terminated early. This could mean that the patient has changed hospitals or no longer wishes to participate in melanoma surveillance. The last event is always the $\texttt{End}$ event that indicates the end of the process and always occurs after $\texttt{IN}\_\texttt{FUP}$ or $\texttt{LTFU}$.

5.2.   Implementation

The RIDE approach is implemented in Python. The suffix for reconstructed events was set to "_REC". The input is the described XES event log for melanoma surveillance and a rule set $R_{follow-up}$ (see table 3), which is derived by the guideline for the treatment of malignant melanoma and is used to reconstruct missing follow-up events. Rule $R_1$ describes that patients in Stages Ⅱ to Ⅵ should attend a follow-up visit every 3 months in the first 5 years, and then (Rule $R_2$) every 6 months in the following 5 years if no stage change has occurred. Rules $R_3$ and $R_4$ refer to patients in Stage Ⅰ, who should come for follow-up every 6 months in the first 5 years and once a year in the following 5 years.

Table 4 shows the application of the defined rules to an event of the event log. Starting from event $5$ and the global attribute $\texttt{stage dpa}$ with value $3$, the missing events between this and event $4$ are reconstructed. First, rule $R_2$ is validated as true, indicating that a followup is missing, which is reconstructed with an interval of 180 days (threshold) from the current event in the timestamp attribute. Recursively, the Backtracing algorithm is applied to the new created event (R90) and rule $R_1$ is evaluated as true, which in turn leads to the reconstruction of a follow-up date. The recursion is terminated when all rules are validated as false. In total, 3 events are reconstructed in this example.

After applying the algorithm to the whole event log, in summary, 5634 invisible deviating events are reconstructed with the RIDE approach. Also, on average 5.5 events are reconstructed per trace. The event $\texttt{Follow-Up}$ occurs 6032 times in the event log. After the algorithm is applied the event log consists of seven event types and 15963 events. Thus, each trace contains 15.6 events on average. The output of the RIDE is an event log with reconstructed invisible deviating events. This log is created as XES file and for the activity name of each reconstructed invisible event the suffix _REC is appended.

5.3.   Reconstruction model implementation

This chapter shows the implementation of the $N_{REC}$ process model used for the reconstructed event log. To show how the alignment is computed, native Petri nets are chosen as the modelling language. The Peri net is implemented using the PM4PY library. The implemented model does not need any guards, since the existing constraints have already been implemented in the RIDE. Thus, the Petri net defines only the allowed behavior of the melanoma surveillance process. Figure 3 displays the $\texttt{Reconstruction Model}$, which is used to calculate an alignment between the process model and event log. It can be seen that the transition LTFU is also not modelled, because this transition should not occur.

5.4.   Evaluation

In the following section, the evaluation is explained. For evaluation, alignments are chosen because it can verify the global conformance of a process model, which is vital in the case study ^[3]. The conformance check was conducted by using the native alignment algorithm implemented in the PM4PY library. As process model the in section 5.3 defined $Reconstruction$ $model$ is used and as event log the in section 5.2 reconstructed event log $L_{Rec}$ is applied. The costs for a log move and a model move were set to 1, with the exception for a log move of the event $\texttt{LTFU}$ (Lost to Follow-up), which was set to 0, because only the missing $\texttt{IN}\_\texttt{FUP}$ should be considered in the calculation of the conformance measure. In this case study, the conformance measure of fitness is chosen. For calculating the fitness, the following function is used:

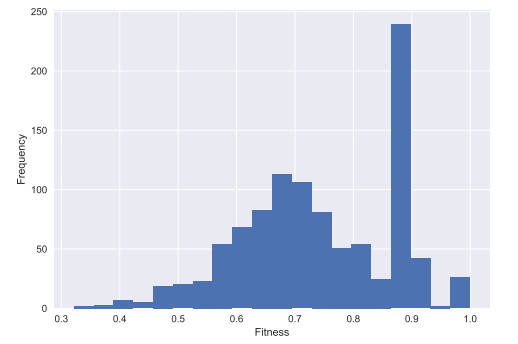
Herein, $K(\gamma^{opt}_{\sigma})$ defines the cost of the optimal alignment concerning trace $\sigma$ under the utilized cost function. $K(\gamma^{ref}_{\sigma})$ denotes the sum of the cost of all model moves needed for the alignment of an empty trace and the cost for each log move to create the empty trace. The cost of all log moves is equal to the number of events in the trace and their event specific cost associated with them. The costs of all model moves needed for the alignment of an empty trace, describes the shortest path through the model. The average fitness of the complete event log is 0.743. Figure 4 illustrates the fitness distribution of the complete event log. It is visible that there is a peak around 0.9 fitness, this is because 148 of the 1023 patients have the same sequence of activities, which only consists of six events. Except for the peak at 0.9 the fitness distribution reflects the average fitness of 0.743 and corresponds to the expectations. This shows that few patients follow-up without deviation from the guideline. However, many of the patients have only minor deviations.

Note that a high fitness only indicates the degree to which the original trace matches the process model. A statement about the quality of the alignment cannot be automatically derived from this. In the context of the case study, however, the boundary conditions are so tight that the alignment is always optimal under the assumption that no data writes are performed. This is due to the complete modelling of the cases (level Ⅰ to Ⅵ) and the absence of erroneous synchronous moves. Figure 5 shows an alignment that was calculated.

Overall, 9655 synchronous moves, 6308 log moves and 665 model moves are made. Note, that the number of log moves is high because each of the 5634 reconstructed events correspond to a log move in the alignment (see figure 5). To further evaluate the correctness of this approach, random sampling is used. Therefore, a test event log of 100 random traces was extracted from the reconstructed event log $\mathcal{L}_{Rec}$ and extended to include all 43 cases, deviating after an interval change from the event log. This was done to ensure that the proposed approach can handle recurring activities with complex temporal rules. An optimal alignment was manually constructed for each of the 143 cases. Manual creation of the optimal alignments was possible without direct involvement of medical professionals because the statements in the medical guideline in this case were clear if-then statements that left no room for interpretation or deviation. For this purpose, the alignments were each created in duplicate by two process analysts and then checked for accuracy by a third process analyst. In the event of deviations or errors, these were discussed among the process analysts in workshops, corrected and revalidated. In case of ambiguities, a domain expert was available to clarify domain-specific questions. The resulting gold standard was then used to compare these alignments to those computed using $\mathcal{L}_{Rec}$. In all cases, the alignments computed using the proposed approach are identical to the perfect alignments. Thus, it can be concluded that the proposed approach works as intended.

5.5.   Discussion

A fitness-based comparison of the RIDE approach with other approaches based is not possible. One reason for this is that the focus of RIDE is on reconstructing the correct number of events. However, if RIDE detects, for example, three divergent events while native conformance checking algorithms would detect only one, the fitness of the RIDE approach is always lower in such cases. This is because it only detects a difference in fitness values, not a significance. Figure 6 illustrates the difference between native multi-perspective conformance checking and the RIDE approach. It can be seen that native conformance checking without extensive modelling is not able to perform meaningful alignment in this case. It is only possible to detect the event that causes a violation because there are too many days between these two follow-ups. However, the native approach is not able to detect the missing events. Therefore, only a qualitative comparison is possible.

Furthermore, it was not possible to utilize the fitness to compare the RIDE approach with the approach from Rinner et al. The reason is, that due to the GDPR of EHR it was not possible to obtain the exact same timestamps recorded by the information system of the DDMUV. As explained in Section 5.1 the timestamps needed to be anonymized. Thus, this case study does not use the same timestamps as Rinner et al. Therefore, the fitness calculated by Rinner et al. and the RIDE approach is different and cannot be used as a valid measure for comparing these approaches.

In contrast to the approach of Rinner et al. ^[6], this method keeps the structure of the process model simple by conducting the conformance check of the data and time perspective in the RIDE. For comparison, the model created by Rinner et al. used 106 places and 306 transitions including invisible ones. On contrast our model needs 8 places and 9 transitions including invisible ones. Thus, the process model stays easily maintainable as shown in Figure 3. Moreover, the model shown in Figure 3, can also be easily extended or integrated in a more complex process if necessary.

Another advantage of this approach in contrast to time boxing, is that RIDE can be used independently of the modelling language, since the invisible deviating events are reconstructed in the event log. Thus, this approach is not depending on a specific process modelling language. However, a limitation is that a complex preprocessing is a requirement to conduct a conformance check, since this approach is not integrated in an existing process framework. A further limitation is that temporal rules must be defined in an external configuration that is independent of the process model. This increases the complexity of preprocessing. Moreover, the definition of the temporal rules is also more complex than the definition of guards that are included in a process model. At the moment, there is also no way to determine if the defined temporal rules contradict each other. In the future, an approach to verify the rule base needs to be developed. Furthermore, the approach currently focuses on recurring events and therefore loops over single activities, 2-loops or n-loops are not supported yet.

Another problem that occurs by using crisp conformance checking algorithms in a setting with recurring activities are meaningful fitness values. A meaningful value of a conformance measure can be defined as a value that should be considered as meaningful by a domain expert. In a crisp setting, a deviation of a variable, independent how small it is, is considered as full violation. In this scenario, a follow-up that was missed by one day is just as severe as a follow-up that was missed by 100 days. To create a meaningful fitness value and make different cases comparable, a fuzzy conformance checking is needed that considers the degree of violation. Thus, the fuzzy conformance checking algorithm proposed by Zhang et al. could be utilized ^[5].

6.   Conclusion

In this paper, we have presented an approach to enable conformance checking on event logs containing missing events, referencing on recurring activities, by reconstructing them. To the best of our knowledge, this study is the first one that provides a comprehensive analysis of recurring activities and provides methods to overcome their limitations in conformance checking. By combining the Event Classification Framework ^[20] and the Framework for Data Quality Issues ^[19], it is possible to classify events and derive solutions for handling event categories that cause issues for native alignment algorithms. In the case of invisible deviating events, it enabled us to derive the reconstruction approach described here.

Answering research question 1, the study shows that the approach is able to identify reliably invisible preferred events, referencing on recurring activities, and reconstruct them, and handle them in a meaningful way, e.g., during alignment. In addition, complex temporal rules such as interval changes dependent on temporal rules can be handled efficiently. With respect to research question 2, it can be said that the approach simultaneously preserves maintainability and extensibility of the process model. Limitations are, among others, that there is still no approach for checking inconsistencies in the rule base, that the approach has only been developed and evaluated for recurring events, and that the creation of temporal rules is complex. Since no approach for handling invisible recurring activities is currently available in a process mining framework, we aim to provide an implementation of the RIDE approach in a framework in the future. In addition, an extension of the multi-perspective conformance checking is to be developed based on the approach, which should integrate this approach such that the preprocessing is conducted during runtime of the conformance checking algorithm.

Acknowledgments

The healthcAIre project is funded by the ministry of science and health of the German state Rhineland-Palatinate and the Pre-OnkoCase project is funded by the National Care Conference on Skin Cancer (NVKH) e.V.

Conflict of interest

The authors declare there is no conflict of interest.