Telehealth during COVID-19: why Sub-Saharan Africa is yet to log-in to virtual healthcare?

1.   Introduction

A set $\mathfrak{C}\subseteq\mathbb{R}$ is said to be convex, if

A mapping ${{\bar{\Xi}}}:\mathfrak{C}\to\mathbb{R}$ is said to be convex, if

Convex analysis is a vital and extensive branch of mathematics that investigates convex sets and mappings defined over them, as well as their properties. It encompasses both geometric and classical aspects of the problem and has numerous applications in functional analysis, topology, optimization theory, fixed-point theory, economics, engineering, and other fields. The theory of convex mappings is closely linked with the theory of inequalities. Inequalities are crucial in mathematical analysis due to their vast applications. In recent years, the theory of inequalities has attracted many researchers, as it presents various intriguing problems. The development of this theory, in conjunction with convex mapping, has been remarkable over the past few decades. Numerous inequalities can be derived directly from the application of convex mappings. One of the most widely studied results in this context is the Hermite-Hadamard (also known as trapezium) inequality, which provides a necessary and sufficient condition for a mapping to be convex. It reads as:

Let ${{\bar{\Xi}}}:I = [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\subseteq\mathbb{R}\to\mathbb{R}$ be a convex mapping, then

One of the fruitful results pertaining to the convexity property of the mappings is Jensen's inequality, which reads as:

Theorem 1.1. ^[1] Let $0 < x_{1}\leq x_{2}\leq x_{3}\leq \ldots.\leq x_{n}$ and let $\mu = (\mu_{1}, \mu_{2}, \ldots, \mu_{n})$ nonnegative weights such that $\sum\limits_{i = 0}^{n}\mu = 1$. If ${{\bar{\Xi}}}:I = [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\subseteq\mathbb{R}\to\mathbb{R}$ is a convex mapping, then

where $x_{i}\in [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$ and $\mu_{i}\in[0, 1]$, $(i = \overline{1, n})$.

In 2001 Mercer, ^[2] derived the discrete version of the Jensen inequality known as the Jensen-Mercer inequality, and is given as:

Theorem 1.2. Let ${{\bar{\Xi}}}:I = [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\subseteq\mathbb{R}\to\mathbb{R}$ be a convex mapping, then

for each $x_{i}\in[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$ and $\mu_{i}\in[0, 1]$, $(i = \overline{1, n})$ with $\sum_{i = 1}^{n}\mu = 1$.

Convex mapping theory has numerous applications in approximation theory, particularly in obtaining error bounds using inequalities. The Hermite-Hadamard inequality (HHI) plays a crucial role in some trapezoidal quadrature rules and estimations. Specifically, the left and right estimations of HHI provide the error bounds for the midpoint rule and trapezoidal rule, respectively. For details, see ^[3].

Building upon inequality (1.1), Kian and Moslehian ^[4] proposed a new refinement and extension of the trapezium inequality. Subsequently, Ogulmus et al. ^[5] derived fractional analogues of TJM-like inequalities based on their work. There have been several recent publications on this inequality. For example, see ^[6,7,8,9,10].

The $h$ and ${\mathfrak{q}}$ calculus was introduced by Euler in the 18th century, and since then has undergone significant developments and gained much attention. It is a type of time scale calculus that focuses on the $0 < {\mathfrak{q}} < 1$ domain, with major areas of study including ${\mathfrak{q}}$-derivatives, ${\mathfrak{q}}$-integrals, and their generalizations using various techniques such as $pq$-calculus, interval valued technique, and trapezoidal strips. This calculus has numerous applications in special mappings, physics, number theory, combinatorics, cryptography, and other fields.

In recent years, the study of inequalities based on ${\mathfrak{q}}$-calculus has become a prominent subject in mathematical analysis. Many researchers have dedicated their efforts to obtaining new ${\mathfrak{q}}$-analogues of classical inequalities. For example, Sudsutad et al. ^[11] discussed ${\mathfrak{q}}$-Hölder's inequality and Hermite-Hadamard's inequalities via quantum calculus, while Noor et al. ^[12] derived some ${\mathfrak{q}}$-variants of integral inequalities. In 2018, Alp et al. ^[13] corrected the ${\mathfrak{q}}$-HHI derived some ${\mathfrak{q}}$-mid-point type inequalities. Other recent developments include Zhang et al. ^[14] formulating ${\mathfrak{q}}$-integral inequalities via $(\alpha, m)$ convex mappings, Deng et al. ^[15] investigating a stronger version of ${\mathfrak{q}}$-integral inequalities in terms of preinvex mappings, Kunt ^[16] deriving fractional quantum variants of HHI, and Cortez et al. ^[17] deriving fractional quantum integral inequalities involving new generalized convex mappings.

Further research in this field has resulted in Iftikhar et al. ^[18] proposing new quantum analogies of Simpson's type inequalities, Wang ^[19] presenting some ${\mathfrak{q}}$-outcomes related to ${\mathfrak{s}}$-preinvexity, Chu et al. ^[20] introducing the concept of generalized right ${\mathfrak{q}}$-derivatives and integrals and developing new Ostrowski's type inequalities involving $n$-polynomial convex mappings, and authors in ^[21] deducing some parametric quantum inequalities with respect to preinvex mappings. Additionally, Kalsoom et al. ^[22] analyzed the generalized quantum integral inequalities involving preinvex mappings, Ali et al. ^[23] incorporated with some ${\mathfrak{q}}$-mid-point HHI and derived some trapezoidal type inequalities, and Bin-Mohsin et al. ^[24] established some new generalized TJM type inequalities in the light of ${\mathfrak{q}}$-calculus. The quantum and post quantum variants of TJM inequalities have also been proven in ^[25,26], which has opened new avenues for researchers. For more information, refer to ^[27,28,29].

Our paper aims to explore the mid-point-TJM inequality by utilizing ${\mathfrak{q}}$-concepts and majorization techniques. The theory of majorization plays a significant role in mathematical analysis and has a wide range of applications in information theory and inequality theory. It encompasses both discrete and continuous forms of inequalities, which are detailed in ^[30,31,32]. Our work is organized as follows: the first section serves as an introduction to the topic, while the subsequent section provides a review of essential definitions and facts that are instrumental in proving our main results. The third section discusses quantum TJM inequalities and presents two new ${\mathfrak{q}}$-integral identities in the first subsection, followed by the presentation of new associated bounds in the third subsection. In the final section, we delve into the applications of our findings, including numerical examples and graphical analysis. The novelty of the current study is that we develop some new generalized TJM inequalities in the frame of quantum calculus by linking the concepts of majorization theory. Results obtained in the current study unifies many known and new results in both continuous and discrete form. We hope that our approach and methods will stimulate further research in this field.

2.   Preliminaries

In this section, we discuss some preliminaries which will be helpful during the study of this paper. First of all, we recall some basic concepts from quantum calculus. Tariboon and Ntouyas have defined the $\mathfrak{q}$-derivative as:

Definition 2.1. ^[33] Assume ${{\bar{\Xi}}}:J = [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\subseteq\mathbb{R}\to \mathbb{R}$ is a continuous mapping and suppose $\mathfrak{u}\in J$, then

We say that ${{\bar{\Xi}}}$ is ${\mathfrak{q}}$-differentiable on $J$ provided $_{{{\varsigma_{1}}}}\mathfrak{D}_{{\mathfrak{q}}}{{\bar{\Xi}}}(\mathfrak{u})$ exists for all $\mathfrak{u}\in J$. Note that if ${{\varsigma_{1}}} = 0$ in (2.1), then $_{0}\mathfrak{D}_{{\mathfrak{q}}}{{\bar{\Xi}}} = \mathfrak{D}_{{\mathfrak{q}}}{{\bar{\Xi}}}$, where $\mathfrak{D}_{{\mathfrak{q}}}$ is the well-known classical ${\mathfrak{q}}$ -derivative of the mapping ${{\bar{\Xi}}}(\mathfrak{u})$ defined by

Also, here and further we use the following notation for ${\mathfrak{q}}$-number

Jackson gave the definition of the ${\mathfrak{q}}$-Jackson integral from $0$ to ${{{\varsigma_{2}}}}$ for $0 < {\mathfrak{q}} < 1$ as follows:

provided the sum converges absolutely. Jackson also gave the ${\mathfrak{q}}$-Jackson integral on a generic interval $[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$ as:

We now give the definition of the ${\mathfrak{q}}_{{{\varsigma_{1}}}}$-definite integral.

Definition 2.2. ^[33] Let ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow {\mathbb{R}}$ be a continuous mapping. Then, the ${\mathfrak{q}}_{{{\varsigma_{1}}}}$-definite integral on $[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$ is defined as:

Now we recall some more important results, which will help us in deriving our main result.

Theorem 2.1. ^[33] If ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow \mathbb{R}$ is a CM and $\mathfrak{u}\in[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$, then

Now we recall the definitions of the ${\mathfrak{q}}^{{{{\varsigma_{2}}}}}$ derivative and definite integrals.

Definition 2.3. ^[34] Let ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow \mathbb{R}$ be a CM and $\mathfrak{u}\in [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$, then

Definition 2.4. ^[34] Let ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow {\mathbb{R}}$ be a continuous mapping. Then, the ${\mathfrak{q}}^{{{{\varsigma_{2}}}}}$-definite integral on $[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$ is defined as:

Now we rewrite some further results.

Theorem 2.2. ^[34] If ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow \mathbb{R}$ is a CM and $\mathfrak{u}\in[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$, then

Lemma 2.1. ^[34] For a continuous mappings ${{\bar{\Xi}}}, {\Phi}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow \mathbb{R}$, then

Using the Definition 2.4, one can have the following quantum version of the Hermite-Hadamard's inequality.

Theorem 2.3. ^[13] Let ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow {\mathbb{R}}$ be a convex mapping, then for $0 < {\mathfrak{q}} < 1$, we have

Inspired by ongoing research, Ali et al. ^[23] calculated a new quantum version of the mid-point trapezium inequality.

Theorem 2.4. ^[23] Let ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow \mathbb{R}$ be a convex mapping then

Now we recall some known definitions and results regarding majorization theory.

Definition 2.5. ^[35] Let ${{\varsigma_{1}}} = ({{\varsigma_{1}}}_1, {{\varsigma_{1}}}_2, \ldots, {{\varsigma_{1}}}_l)$ and ${{{\varsigma_{2}}}} = ({{{\varsigma_{2}}}}_1, {{{\varsigma_{2}}}}_2, \ldots, {{{\varsigma_{2}}}}_l)$ be two $l$-tuples of real numbers and ${{\varsigma_{1}}}_{[1]}\geq {{\varsigma_{1}}}_{[2]}\geq\ldots\geq {{\varsigma_{2}}}_{[l]}, {{{\varsigma_{2}}}}_{[1]}\geq {{{\varsigma_{2}}}}_{[2]}\geq\ldots\geq {{{\varsigma_{2}}}}_{[l]}$ be their ordered components, then ${{\varsigma_{1}}}$ is said to majorize ${{{\varsigma_{2}}}}$ (symbolically ${{{\varsigma_{2}}}}\prec {{\varsigma_{1}}}$), if

and

Majorization is a partial ordered relation of two $l$-tuples ${{\varsigma_{1}}} = ({{\varsigma_{1}}}_1, {{\varsigma_{1}}}_2, \ldots, {{\varsigma_{1}}}_l)$ and ${{{\varsigma_{2}}}} = ({{{\varsigma_{2}}}}_1, {{{\varsigma_{2}}}}_2, \ldots, {{{\varsigma_{2}}}}_l)$ which explains that ${{\varsigma_{1}}}$ is more nearly equal to ${{{\varsigma_{2}}}}$. Now we recall majorization theorem due to Hardy, Littlewood and Polya ^[36].

Theorem 2.5. Let ${{\varsigma_{1}}} = ({{\varsigma_{1}}}_1, {{\varsigma_{1}}}_2, \ldots, {{\varsigma_{1}}}_l)$ and ${{{\varsigma_{2}}}} = ({{{\varsigma_{2}}}}_1, {{{\varsigma_{2}}}}_2, \ldots, {{{\varsigma_{2}}}}_l)$ be two real $l$-tuples such that ${{\varsigma_{1}}}_{\mathfrak{s}}, {{{\varsigma_{2}}}}_{\mathfrak{s}}\in I = [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]$. Then

is valid for each continuous convex mapping ${{\bar{\Xi}}}:I\rightarrow \mathbb{R}$ if and only if ${{{\varsigma_{2}}}}\prec {{\varsigma_{1}}}$.

The weighted version of the above theorem is given as:

Theorem 2.6. ^[37] Let ${{\bar{\Xi}}}:I\rightarrow \mathbb{R}$ be a continuous convex mapping and ${{\varsigma_{1}}} = ({{\varsigma_{1}}}_1, {{\varsigma_{1}}}_2, \ldots, {{\varsigma_{1}}}_l), {{{\varsigma_{2}}}} = ({{{\varsigma_{2}}}}_1, {{{\varsigma_{2}}}}_2, \ldots, {{{\varsigma_{2}}}}_l)$ and $p = (p_1, p_2, \ldots, p_l)$ be the three $l$-tuples such that ${{\varsigma_{1}}}_{\mathfrak{s}}, {{{\varsigma_{2}}}}_{\mathfrak{s}}\in I, p_{\mathfrak{s}}\geq0, {\mathfrak{s}}\in\{1, 2, 3, \ldots., l\}$. If ${{{\varsigma_{2}}}}$ is a decreasing $l$-tuple, then

then

Theorem 2.7. ^[38] Suppose that ${{\bar{\Xi}}}:[{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow \mathbb{R}$ be a real valued convex mapping $(x_{ij})$ is a $n\times m$ real matrix and $\mathfrak{u} = (\mathfrak{u}_1, \mathfrak{u}_2, \ldots, \mathfrak{u}_l)$ is a $l$-tuple such that $\mathfrak{u}_j, x_{ij}, w_i\geq0$ for $i = 1, 2, 3, \ldots, n$ with $\sum_{i = 1}^nw_i = 1$. If $\mathfrak{u}$ every row of $x_{ij}$ then

3.   Main results

In this section, we derive ${\mathfrak{q}}$-TJM inequality associated with convex mapping. Furthermore, we also establish ${\mathfrak{q}}$-TJM like inequalities with the help of auxiliary results.

3.1.   TJM inequality

In the following section, we established a new mid-point TJM- inequality involving convexity and ${\mathfrak{q}}$-integrability of ${{\bar{\Xi}}}$.

Theorem 3.1. Suppose that ${{\bar{\Xi}}}:I = [{{\varsigma_{1}}}, {{{\varsigma_{2}}}}]\rightarrow \mathbb{R}$ is real valued convex mapping and $\varpi = (\varpi_1, \varpi_2, \ldots, \varpi_l), \xi = (\xi_1, \xi_2, \ldots, \xi_l), \eta = (\eta_1, \eta_2, \ldots, \eta_l)$ are three $l$-tuples $\varpi_{\mathfrak{s}}, \xi_{\mathfrak{s}}, \eta_{\mathfrak{s}}$ for all ${\mathfrak{s}}\in\{1, 2, 3, \ldots, l\}$. If $\xi\prec \varpi$ and $\eta\prec \varpi$, then

and

Proof. To use Theorem 2.7 we show that $\varpi$ majorizes $r$ and $z$ where $r = (r_1, r_2, \ldots, r_l), z = (z_1, z_2, \ldots, z_l), r_j = \frac{{\vartheta}}{2}\xi_{\mathfrak{s}}+\frac{(2-{\vartheta})}{2}\eta_{\mathfrak{s}}$ and $z_j = \frac{{\vartheta}}{2}\eta_{\mathfrak{s}}+\frac{(2-{\vartheta})}{2}\xi_{\mathfrak{s}}$ for ${\mathfrak{s}} = \{1, 2, 3, \ldots, l\}$.

For this, let $\sum_{j = 1}^k\xi_{[j]} = \beta_{1k}$ and $\sum_{j = 1}^k\eta_{[j]} = \beta_{2k}$ for $k = 1, 2, \ldots, l-1$. Then

Since $\xi\prec \varpi$ and $\eta\prec \varpi$ then by definition of majorization, we have $\sum_{j = 1}^k\xi_{[j]}\leq \sum_{j = 1}^k\varpi_{[j]}$ and $\sum_{j = 1}^k\eta_{[j]}\leq \sum_{j = 1}^k\varpi_{[j]}$ that is

and

Multiplying (3.3) by $\frac{{\vartheta}}{2}$ and (3.4) by $\frac{2-{\vartheta}}{2}$ and then adding the resulting inequalities, we get

But $\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{\mathfrak{s}} = \sum_{{\mathfrak{s}} = 1}^{l}\xi_{\mathfrak{s}}$ and $\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{\mathfrak{s}} = \sum_{{\mathfrak{s}} = 1}^{l}\eta_{\mathfrak{s}}$, then by using $(3.5)$, we have

Hence $r\prec \varpi$. Similarly, we can show that $z\prec \varpi$. Then by using Theorem 3.2 for $w_1 = w_2 = \frac{1}{2}$, we have

Now taking the ${\mathfrak{q}}$-integration of (3.6), we have

After simplifying, we obtain the left inequality of (3.1).

For the right inequality of (3.1), using (2.4), we have

Adding $\sum_{{\mathfrak{s}} = 1}^{l-1}{{\bar{\Xi}}}(\varpi_{{\mathfrak{s}}})$ on both sides of (3.7), we obtain our required result. In this way, we complete the proof of our (3.1).

To prove (3.2), we apply the definition of convex mapping, we have

Now, taking the ${\mathfrak{q}}$-integration of (3.8) on both sides over $[0, 1]$ and using the definitions (2.1) and (2.3), then

Hence we complete the proof of our first inequality of (3.2).

To prove, our second inequality, we use the notion of convex mappings,

Adding (3.9) and (3.10), then ${\mathfrak{q}}$-integration of resulting inequality yields the required inequality.

$\bullet$ If we choose $l = 2$, then

and

For further demonstration, we discuss a numeric example in the support of Theorem 3.1.

Example 3.1. Considering ${{\bar{\Xi}}}(\mathfrak{u}) = \mathfrak{u}^2$, with $\varpi_{1} = -1, \xi_{1} = 1, \eta_{1} = 2, \varpi_{2} = 3$ and ${\mathfrak{q}} = 0.5$, then

From above calculations, we can infer that $0.25 < 0.31 < 7.5$.

3.2.   New ${\mathfrak{q}}$-identities

In the following subsection, our first target is to derive two new quantum integral identities involving $_{{{\varsigma_{1}}}}{\mathfrak{q}}$ and $^{{{\varsigma_{2}}}}{{\mathfrak{q}}}$ differentiability of the mappings and ordered $n$-tuples. Here, we propose a new general identity of mid-point type which will play a critical role in order to compute some new error bounds of mid-point schemes.

Lemma 3.1. Let $\varpi = (\varpi_1, \varpi_2, \varpi_3, \ldots, \varpi_l)$, $\xi = (\xi_1, \xi_2, .., \xi_l)$ and $\eta = (\eta_1, \eta_2, \ldots, \eta_l)$ be the three $l$-tuples such that $\varpi_{\mathfrak{s}}, \xi_{\mathfrak{s}}, \eta_{\mathfrak{s}}\in[I]$ for all ${\mathfrak{s}}\in\{1, 2, \ldots, l\}, {\vartheta}\in[0, 1]$ and ${{\bar{\Xi}}}:J\rightarrow \mathbb{R}$ be a CM and $0 < {\mathfrak{q}} < 1$. If $^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}{{\bar{\Xi}}}$ and $_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}{{\bar{\Xi}}}$ an integrable mapping on $J^{\circ}$, then

where

Proof. Consider the right-hand side of (3.11) as

By Lemma 2.1, we have

Similarly, we get

Combination of (3.12)–(3.14) yields the required result.

$\bullet$ If we choose $l = 2$ in Lemma 3.1, then we have

Now, we establish a general Dragomir-Agarwal-type inequality, which is crucial to establish some error bounds of the trapezoidal rule.

Lemma 3.2. Let $\varpi = (\varpi_1, \varpi_2, \varpi_3, \ldots, \varpi_l)$, $\xi = (\xi_1, \xi_2, .., \xi_l)$ and $\eta = (\eta_1, \eta_2, \ldots, \eta_l)$ be the three $l$-tuples such that $\varpi_{\mathfrak{s}}, \xi_{\mathfrak{s}}, \eta_{\mathfrak{s}}\in[I]$ for all ${\mathfrak{s}}\in\{1, 2, \ldots, l\}, {\vartheta}\in[0, 1]$ and ${{\bar{\Xi}}}:J\rightarrow \mathbb{R}$ be a CM and $0 < {\mathfrak{q}} < 1$. If $^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}{{\bar{\Xi}}}$ and $_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}{{\bar{\Xi}}}$ an integrable mapping on $J^{\circ}$, then

where

Proof. Consider the right-hand side of (3.15) as

By Lemma 2.1, we have

Similarly, we get

Comparing (3.16)–(3.18), we conclude our required result.

$\bullet$ If we choose $l = 2$ in Lemma 3.2, then

3.3.   ${\mathfrak{q}}$-Estimations of TJM inequality

In this section, we propose some new generalized left and right estimations connecting to newly proved ${\mathfrak{q}}$-TJM inequality proved in the previous section. We use auxiliary results, the convexity property of the mappings, and some well-known inequalities to obtain new refinements of existing results.

Theorem 3.2. Under the assumptions of Lemma 3.1 and if $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$ are convex mappings, then

Proof. Using Lemma 3.1, property of modulus and the convexity of $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$, we have

After simple calculations, we achieve our final result.

$\bullet$ If we choose $l = 2$ in Theorem 3.2, then

Theorem 3.3. Under the assumptions of Lemma 3.1 and if $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ are convex mappings with $\frac{1}{r}+\frac{1}{{\mathfrak{s}}} = 1$, then we have

Proof. Using Lemma 3.1, property of modulus, power-mean inequality and the convexity property of $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ with $\frac{1}{r}+\frac{1}{{\mathfrak{s}}} = 1$, we have

After simple calculations, we achieve our final result.

$\bullet$ If we choose $l = 2$ in Theorem 3.3, then

Theorem 3.4. Under the assumptions of Lemma 3.1 and if $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ are convex mappings with $\frac{1}{r}+\frac{1}{{\mathfrak{s}}} = 1$, then we have

Proof. Using Lemma 3.1, property of modulus, Hölder's inequality and using the convexity property of $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ with $\frac{1}{r}+\frac{1}{{\mathfrak{s}}} = 1$, we have

After simple calculations, we achieve our final result.

$\bullet$ If we choose $l = 2$ in Theorem 3.4, then

Now we derive some new results related to the right side of TJM inequality using Lemma 3.2.

Theorem 3.5. Under the assumptions of Lemma 3.2 and if $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$ are convex mappings, we have

Proof. Using Lemma 3.2, property of modulus and the convexity property $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|$, we have

After some calculations, we obtain our required result.

$\bullet$ If we choose $l = 2$ in Theorem 3.5, then

where $\frac{1}{r}+\frac{1}{{\mathfrak{s}}} = 1$.

Theorem 3.6. Under the assumptions of Lemma 3.2 and the convexity property of $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$, we have

Proof. Using Lemma 3.2, property of modulus, power-mean inequality and the convexity property of $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$, we have

After simple calculations, we achieve our final result.

$\bullet$ If we choose $l = 2$ in Theorem 3.6, then

where $\frac{1}{r}+\frac{1}{{\mathfrak{s}}} = 1$.

Theorem 3.7. Under the assumptions of Lemma 3.2 and if $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ are convex mappings, we have

where $\frac{1}{r}+\frac{1}{{\mathfrak{s}}} = 1$.

Proof. Using Lemma 3.2, property of modulus, Hölder's inequality and using the convexity property of $|^{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\xi_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$ and $|_{\sum_{{\mathfrak{s}} = 1}^{l}\varpi_{{\mathfrak{s}}}-\sum_{{\mathfrak{s}} = 1}^{l-1}{\eta_{\mathfrak{s}}}}\mathfrak{D}_{{\mathfrak{q}}}|^r$, we have

After simple calculations, we achieve our final result.

$\bullet$ If we choose $l = 2$ in Theorem 3.7, then

4.   Applications

Finally, we present some applications to bivariate means of non-negative real numbers in the support of main results. For more visualization, we check the validity through numeric examples and a graphical explanation is also mentioned. The arithmetic mean: $A({{\varsigma_{1}}}, {{{\varsigma_{2}}}}) = \frac{{{\varsigma_{1}}}+{{{\varsigma_{2}}}}}{2}$,

The generalized $\log$-mean: $L_{p}({{\varsigma_{1}}}, {{{\varsigma_{2}}}}) = \left[\frac{{{{\varsigma_{2}}}}^{p+1}-{{{\varsigma_{1}}}}^{p+1}}{ (p+1)({{{\varsigma_{2}}}}-{{\varsigma_{1}}})}\right]^{\frac{1}{p}}$.

where $p\in \mathbb{R}\setminus\{-1, 0\}$, ${{\varsigma_{1}}}, {{{\varsigma_{2}}}} \in \mathbb{R}$, ${{\varsigma_{1}}}\neq {{{\varsigma_{2}}}}$.

Proposition 4.1. Assume that all the assumptions of Theorem 3.2 are held. Then

where

Proof. The assertion follows directly from Theorem 3.2 for ${{\bar{\Xi}}}(\mathfrak{u}) = \mathfrak{u}^2$.

Now we give the numerical verification of Theorem 3.2.

Example 4.1. Taking $\varpi_{1} = 0, \xi_{1} = 1, \eta_{1} = 2$ and $\varpi_{2} = 3$ in Proposition 4.1, we have $0.0595 < 0.5357$.

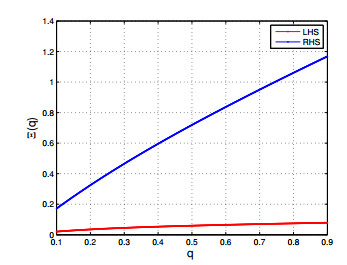
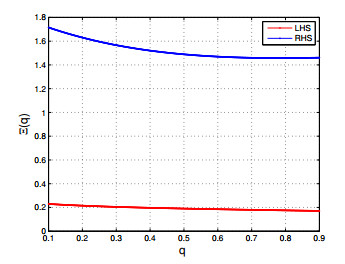
For the graphical explanation of Theorem 3.2, we have

Figure 1 clearly emphasizes the correctness of Theorem 3.2, where the red and blue colours indicate the left-hand and right-hand sides respectively.

Proposition 4.2. Assume that all the assumptions of Theorem 3.3 are held. Then

where

Proof. The assertion follows directly from Theorem 3.3 for ${{\bar{\Xi}}}(\mathfrak{u}) = \mathfrak{u}^2$.

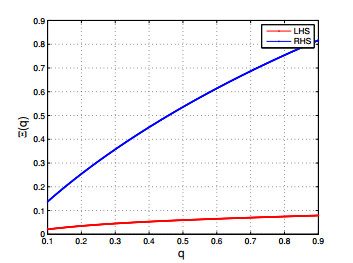
Now we give the numerical verification of Theorem 3.3.

Example 4.2. Taking $\varpi_{1} = 0, \xi_{1} = 1, \eta_{1} = 2$ and $\varpi_{2} = 3$ in Proposition 4.2, we have $0.0595 < 0.7191$.

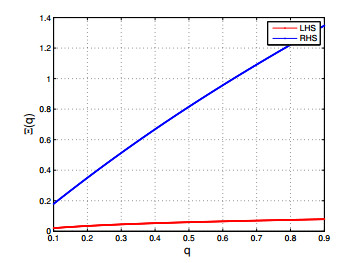
For the graphical explanation of Theorem 3.3 are held. Then

Figure 2 clearly emphasizes the correctness of Theorem 3.3, where the red and blue colours indicate the left-hand and right-hand sides respectively.

Proposition 4.3. Assume that all the assumptions of Theorem 3.4 are held. Then

$B^r(z, \xi_{1})$ and $C^r(z, \eta_{1})$ are defined by (4.3) and (4.4) respectively.

Proof. The assertion follows directly from Theorem 3.4 for ${{\bar{\Xi}}}(\mathfrak{u}) = \mathfrak{u}^2$.

Now we give the numerical verification of Theorem 3.4.

Example 4.3. Taking $\varpi_{1} = 0, \xi_{1} = 1, \eta_{1} = 2$ and $\varpi_{2} = 3$ in Proposition 4.3, we have $0.0595 < 0.8157$.

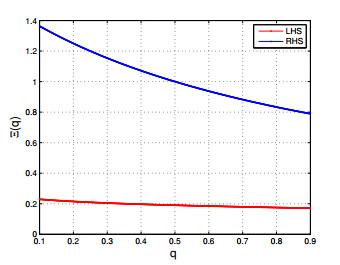
For the graphical explanation of Theorem 3.4, we have following expression

Figure 3 clearly emphasizes the correctness of Theorem 3.4, where the red and blue colours indicate the left-hand and right-hand sides respectively.

Proposition 4.4. Assume that all the assumptions of Theorem 3.5 are held. Then

where $B(z, \xi_{1})$ and $C(z, \eta_{1})$ are defined by (4.1) and (4.2) respectively.

Proof. The assertion follows directly from Theorem 3.5 for ${{\bar{\Xi}}}(\mathfrak{u}) = \mathfrak{u}^2$.

Now we give the numerical verification of Theorem 3.5.

Example 4.4. Taking $\varpi_{1} = 0, \xi_{1} = 1, \eta_{1} = 2$ and $\varpi_{2} = 3$ in Proposition 4.4, we have $0.1905 < 1.0000$.

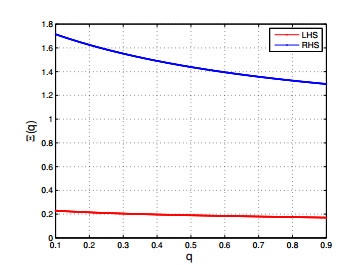
For the graphical explanation of Theorem 3.5, we have following expression

Figure 4 clearly emphasizes the correctness of Theorem 3.5, where the red and blue colours indicate the left-hand and right-hand sides respectively.

Proposition 4.5. Assume that all the assumptions of Theorem 3.6 are held, Then

where $B^r(z, \xi_{1})$ and $B^r(z, \eta_{1})$ are defined by (4.3) and (4.4) respectively.

Proof. The assertion follows directly from Theorem 3.6 for ${{\bar{\Xi}}}(\mathfrak{u}) = \mathfrak{u}^2$.

Now we give the numerical verification of Theorem 3.6.

Example 4.5. Taking $\varpi_{1} = 0, \xi_{1} = 1, \eta_{1} = 2$ and $\varpi_{2} = 3$ in Proposition 4.5, we have $0.1905 < 1.4387$.

For the graphical explanation of Theorem 3.6, we have following expression

Figure 5 clearly emphasizes the correctness of Theorem 3.6, where the red and blue colours indicate the left-hand and right-hand sides respectively.

Proposition 4.6. Assume that all the assumptions of Theorem 3.7 are held. Then

$B^r(z, \xi_{1})$ and $B^r(z, \eta_{1})$ are defined by (4.3) and (4.4) respectively.

Proof. The assertion follows directly from Theorem 3.7 for ${{\bar{\Xi}}}(\mathfrak{u}) = \mathfrak{u}^2$.

Now we give the numerical verification of Theorem 3.7.

Example 4.6. Taking $\varpi_{1} = 0, \xi_{1} = 1, \eta_{1} = 2$ and $\varpi_{2} = 3$ in Proposition 4.6, we have $0.1905 < 1.4892$.

For the graphical explanation of Theorem 3.7, we have following expression

Figure 6 clearly emphasizes the correctness of Theorem 3.7, where the red and blue colours indicate the left-hand and right-hand sides respectively.

5.   Conclusions

The Trapezium-Jensen-Mercer (TJM) inequality is a well-researched and extensively studied result in the literature. Various versions of this inequality have been derived using different concepts of convexity, including fractional and ${\mathfrak{q}}$-calculus. In this study, we have introduced new continuous and discrete quantum versions of TJM and established some new bounds of inequality through convex mapping. Additionally, we have provided several applications and graphical analyses to support our findings. Moving forward, we plan to derive ${\mathfrak{q}}$-fractional and $(p, {\mathfrak{q}})$-analogues of TJM, Simpson-Mercer, and Ostrowski-like inequalities that involve different categories of convexity.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are thankful to the editor and anonymous reviewers for their valuable comments and suggestions. This research is supported by "Researchers Supporting Project number (RSP2023R158), King Saud University, Riyadh, Saudi Arabia." Muhammad Uzair Awan is thankful to HEC Pakistan for 8081/Punjab/NRPU/R & D/HEC/2017.

Conflict of interest

The authors declare that they have no competing interests.