1.
Introduction
The concept of type-2 fuzzy sets (T2 FSs) was first proposed by Zadeh [1] and a detailed introduction was given in [2]. T2 FSs are an extension of the type-1 fuzzy set (T1 FS) and further considers the fuzziness of the fuzzy set. Since the definition of T2 FSs was proposed, most scholars have mainly studied the operations and properties of T2 FSs [3,4]. Until the 1990s, Prof. Mendel redefined T2 FSs and proposed the type-2 fuzzy logic system (T2 FLS) [5,6].
As an extension of T1 FSs, T2 FSs overcome the limitations of T1 FSs in dealing with the uncertainties of actual objects. However the definition of T2 FSs is complicated, and the corresponding graph must be a spatial graph. Due to the complexity of the expression of T2 FSs, Mendel introduces the definition of interval T2 FSs (IT2 FSs) as a special case of T2 FSs. The secondary membership grade of IT2 FSs is constant one, which is more simpler than T2 FSs. In general, IT2 fuzzy logic system (IT2 FLS) are used in most theories and applications [7,8].
In the field of fuzzy control, solving fuzzy relation equations (FREs) plays an important role in the design of fuzzy controller and fuzzy logic reasoning. Most algorithms for solving FREs can obtain some specific solutions, such as the minimum or maximum solution [9], or can describe the solution theoretically [10]. In the existing methods, most of them are used for solving type-1 fuzzy relation equations (T1 FREs), while few methods are used for solving interval type-2 fuzzy relation equations (IT2 FREs). The main work of this paper is to propose a new method to obtain the entire solution set of IT2 FREs.
On the other hand, Prof. Cheng proposed a new matrix product-semi-tensor product (STP) of matrices, which is the generalization of the conventional matrix product and retains almost all the main properties of the conventional matrix product. As a novel mathematical technique for handling logical operations, STP has been successfully applied to logical systems [11,12,13,14] and, based on this, a new algorithm for solving FREs has been devised. For example, in T1 FREs, the STP is used to solve fuzzy relation equalities and fuzzy relation inequalities [15,16,17,18]. In type-2 fuzzy relational equations (T2 FREs), only some simple algorithms have been proposed to study the solution of type-2 single-valued fuzzy relation equations and type-2 symmetry-valued fuzzy relation equations [19,20]. However, the ordinary STP cannot be used directly to solve IT2 FREs. Therefore, we extend the STP to interval matrices and propose the STP of interval matrices, then discuss the solutions of IT2 FREs.
In the rest of this paper, section two introduces the basic concepts of the STP of interval matrices. Section three mainly gives the relevant definitions of interval-valued logic and gives its matrix representation. Section four discusses the solvability of IT2 FREs and designs an algorithm to solve IT2 FREs. Section five explains the viability of the proposed algorithm with a numerical example. Section six gives a brief summary of the paper.
2.
Preliminaries
2.1. Basic concept
First, in order to express conveniently, we introduce some notations used throughout the paper.
●
where α_,¯α∈R. If α=[α_,α_](or α=[¯α,¯α]), this is a point interval and α degenerates into a real number.
●
A_=(α_i)m and ¯A=(¯αi)m are two m-dimensional vectors and [a_i,¯ai]∈I[0,1], i=1⋯m.
●
A_=(α_ij)m×n and ¯A=(¯αij)m×n are two m×n dimensional matrices and [α_ij,¯αij]∈I[0,1], i=1⋯m, j=1⋯n.
● δir : the ith column of unit matrix In.
● [δir,δjr] : a bounded closed interval, where δin represents its lower bound and δjn represents its upper bound, abbreviated as δr[i,j].
● Coli(M): the ith column of interval matrix M.
● Rowj(M): the jth row of interval matrix M.
Next, we define ∧,∨ and ¬ in I[0,1].
Definition 2.1. [21] (1) Let
then,
(2) Let
then their max-min composition operation is defined as
where
where i=1,⋯,m, j=1,⋯,k.
Definition 2.2. [22] Let
then the partial order ≥,≤ and = are defined as
(1) If a_ij≥b_ij,¯aij≥¯bij, we say A≥B.
(2) If a_ij≤b_ij,¯aij≤¯bij, we say A≤B.
(3) If a_ij=b_ij,¯aij=¯bij, we say A=B.
Property 2.1. [15] Let
Assume A≤B and C≤D, then
Definition 2.3. [22] (1) Let
then the four operations of intervals α and β are as follows.
1) Addition operation
2) Subtraction operation
3) Multiplication operation
4) Division operation
Note that 0∉β=[β_,¯β].
(2) If
then the product of interval α and interval matrix A is
(3) If
then the product of interval matrices A and B is
where
Based on Definition 2.3, we give the relevant definition of the STP of interval matrices.
Definition 2.4. (1) If
then the kronecker product of interval matrices A and B is
(2) If
then the STP of interval matrices A and B is
where t=lcm(n,p) is the least common multiple of n and p.
(3) If
then the khatri-rao product of interval matrices A and B is
Remark 2.1. In Definition 2.4, if n=p, then the STP of interval matrices degenerates to the ordinary interval matrix multiplication. Therefore, the STP of interval matrices is a generalization of interval matrices multiplication. In the context, the STP of interval matrices is ⋉, which is omitted by default.
Example 2.1. Given the interval matrices A and B,
The kronecker product of the interval matrix A and the unit interval matrix I2 is
The STP of interval matrices A and B is
The khatri-rao product of interval matrices A and B is
According to the definition of STP of interval matrices, we can get the following properties.
Property 2.2. (1) Let A,B∈I([0,1]m×n),C∈I([0,1]p×q), then
(2) Let A∈I([0,1]m×n),B∈I([0,1]p×q) and C∈I([0,1]r×s), then
(3) Let A∈I([0,1]m×n), C∈I([0,1]s) and R∈I([0,1]s) are column and row interval vectors, respectively, then
2.2. Problem formulation
Let the interval type-2 fuzzy relation ˜R∈F(V×W), where the domain V={v1,v2,⋯,vn} and W={w1,w2,⋯,wp}, then the matrix form of interval type-2 fuzzy relation ˜R can be defined as
μ˜R(vi,wk) and f˜R(vi,wk) represent the primary membership grade and secondary membership grade of IT2 FSs, respectively. For primary membership grade, it is composed of upper membership grade and lower membership grade; that is,
The secondary membership grade of IT2 FSs equals one; that is, f˜R(vi,wk)=1, then the matrix form of interval type-2 fuzzy relation ˜R can be further described as
Two common types of FREs exist in practical application [20]. One type is that the fuzzy relation is unknown, which is commonly used for designing fuzzy controllers. The other type is that the fuzzy input is unknown, which is commonly used for diagnosing diseases based on the symptom similarity. In terms of the aforementioned situations, it can be assumed that there are similar two types of IT2 FREs, as shown in Figures 1 and 2.
Type 1: assume ˜A∈F(U×V),˜B∈F(U×W). We seek an interval type-2 fuzzy relation ˜X∈F(V×W) such that it satisfies
Type 2: assume ˜R∈F(V×W),˜B∈F(U×W). We seek an interval type-2 fuzzy input ˜X∈F(U×V) such that it satisfies
Remark 2.2. Take a transpose of both sides of (2.19) to get ˜RT∘˜XT=˜BT. (2.19) is equivalent to (2.18), so we only need to consider the solvability of (2.18).
3.
Interval-valued logic and its matrix representation
Definition 3.1. (1)
is called the domain of interval-valued fuzzy logic, and the interval-valued fuzzy logic variable is P∈If. When α=[0,0] (orα=[1,1]), α degenerates into a classical logic variable.
(2)
i=1,⋯,k, then Ik is called the domain of k-valued interval-valued fuzzy logic.
(3) Mapping
is called r-ary k-valued interval-valued logic function.
If
put the different upper and lower bounds of all interval-valued fuzzy logic variables in Ik into the ordered set Θ. If Θ does not contain zero and one, it needs to add zero or one:
In order to facilitate matrix calculation, each variable in Ik is represented as an interval vector. If α_i=am (1≤m≤s,m∈Z+) and ¯αi=an (1≤n≤s,n∈Z+), then the lower bound α_i can be represented by vector δms and the upper bound ¯αi can be represented by vector δns. Therefore,
Similar to the proof of theorem in paper [23], we can obtain Theorem 3.1.
Theorem 3.1. f is a r-ary k-valued interval-valued logic function, then there exists a unique structural matrix Mf, whose algebraic form is
Remark 3.1. Structure matrix is also a special interval matrix that can be used to replace ∧,∨ and ¬ for algebraic operations.
In the following, we give the structure matrix of ∧,∨ and ¬.
Let
The ordered set Θ generated by Ik contains s different elements. To simply represent the structure matrix of ∧,∨ and ¬, we introduce a set of s-dimensional vectors
(1) The structure matrix of ∨:
When s = 3, we have
(2) The structure matrix of ∧:
When s = 3, we have
4.
Main results
4.1. Decomposition of IT2 FRE
Definition 4.1. [20] In (2.17), the matrix constructed by the primary membership grade μ˜R(vj,wk) is called primary fuzzy matrix of interval type-2 fuzzy relation, denoted as ˜Rμ(μ˜R(vj,wk)) and abbreviated as ˜Rμ:
Similarly, in (2.17), the matrix constructed by the secondary membership grade f˜R(vj,wk) is called secondary fuzzy matrix of interval type-2 fuzzy relation, denoted as ˜Rf(f˜R(vj,wk)) and abbreviated as ˜Rf:
Clearly, (2.18) is composed of the primary fuzzy matrix equation and secondary fuzzy matrix equation.
Definition 4.2. The IT2 FRE (2.18) can be divided into two parts: primary fuzzy matrix equation and secondary fuzzy matrix equation.
(1) The primary fuzzy matrix equation is
where ˜Aμ∈I([0,1]m×n), ˜Bμ∈I([0,1]m×p), ˜Xμ∈I([0,1]n×p) and ˜Xμ is unknown.
If
satisfies (4.1), then we call that ˜Xμ is the solution of (4.1). X_μ, ¯Xμ are lower and upper bound matrices of ˜Xμ, respectively.
If
is a solution of (4.1), and for any solution ˜Xμ of (4.1), there is ˜Xμ≤˜Hμ, then ˜Hμ is called the maximum solution of (4.1).
If
is a solution of (4.1), and for any solution ˜Xμ of (4.1), there is ˜Xμ≥˜Jμ, then ˜Jμ is called the minimal solution of (4.1).
If
is a solution of (4.1), and for any solution ˜Xμ of (4.1), as long as ˜Xμ≤˜Qμ is satisfied, there is ˜Xμ=˜Qμ, then ˜Qμ is called the minimum solution of (4.1).
(2) The secondary fuzzy matrix equation is
where ˜Af∈Mm×n, ˜Bf∈Mm×p, ˜Xf∈Mn×p and ˜Xf is unknown.
The matrix ˜Xf satisfying (4.2) is called the solution of this equation. In (4.2), the elements of ˜Af and ˜Bf are all one, then the elements of ˜Xf are all one.
4.2. Solvability of primary fuzzy matrix equation
The primary fuzzy matrix Eq (4.1) is equivalent to
The conditions for the establishment of (4.3) are relatively difficult, so we first need to determine whether (4.1) has solutions.
Lemma 4.1. [24] Let
The T1 FRE A∘X=B has solutions if, and only if, ATαB is a solution of this equation and ATαB is the maximum solution of this equation. The α composition operation between fuzzy matrices is
where (aki)α(bij)={bij,aki>bij,1,aki≤bij.
Theorem 4.1. If the primary fuzzy matrix Eq (4.1) has solutions then
is a solution of this equation and ˜Hμ is the maximum solution of this equation.
In (4.4),
when
When ∃ h_ik>¯hik, we replace all elements of H_ that do not satisfy h_ik≤¯hik with ¯hik; thus, generating a new lower bound matrix H_μ′.
Proof. The primary fuzzy matrix Eq (4.1) has solutions, then T1 FREs
must have solutions. Lemma 4.1 implies that H_μ and ¯Hμ are solutions of T1 FREs
respectively. H_μ and ¯Hμ must exist in either of the following two cases.
(1) For ∀ h_ij≤¯hij, we known that H_μ≤¯Hμ. H_μ and ¯Hμ are solutions of T1 FREs
respectively. Hence,
satisfies (4.3) and ˜Hμ is a solution of the primary fuzzy matrix equation.
From Lemma 4.1, it follows that H_μ and ¯Hμ are maximum solutions of T1 FREs
respectively. Clearly, X_μ≤H_μ and ¯Xμ≤¯Hμ, so
is the maximum solution of the primary fuzzy matrix equation.
(2) For ∃ h_ij>¯hij, we know that the newly generated matrix is H_μ′ and the matrix satisfies
According to
H_μ′ is a solution of T1 FRE
From Lemma 4.1, it follows that ¯Hμ is a solution of T1 FRE ¯Aμ∘¯Xμ=¯Bμ, respectively. Hence,
satisfies (4.3) and ˜Hμ is a solution of the primary fuzzy matrix equation.
From Lemma 4.1, it is known that H_μ and ¯Hμ are, respectively, maximum solutions of T1 FREs
According to the requirement that X_μ≤¯Xμ, we construct a new matrix H_μ′ based on H_μ. Clearly, X_μ≤H_μ′ and ¯Xμ≤¯Hμ, so
is the maximum solution of the primary fuzzy matrix equation.
In summary, ˜Hμ is a solution of the primary fuzzy matrix Eq (4.1) and is the maximum solution of this equation. □
If the primary fuzzy matrix Eq (4.1) has solutions, the next step is to explore how to construct parameter set solutions I∗(˜Xμ) and I∗(˜Xμ) of this equation.
First, take all the elements in ˜Aμand ˜Bμ and place the different upper and lower bounds of these elements in the the ordered set Θ:
Construct an ordered interval-valued set Ψ by the ordered set Θ, defined as
Next, according to the order interval-valued set Ψ, we define two mappings necessary to construct the parameter set solution I∗(˜Xμ) and I∗(˜Xμ) of primary fuzzy matrix Eq (4.1).
Definition 4.3. Assuming x∈If, [ξi,ξj]∈Ψ.
(1) I∗: [x_,¯x]→Ψ is
(2) I∗: [x_,¯x]→Ψ is
Note that 1) When x_=ξi∈Ξ, ¯x=ξj∈Ξ,
2) When x_∉Ξ, ¯x=ξj∈Ξ, there exists a unique i such that ξi<x<ξi+1, then
3) When x_=ξi∈Ξ, ¯x∉Ξ, there exists a unique j such that ξj<x<ξj+1, then
4) When x_∉Ξ, ¯x∉Ξ, there exists a unique i and j such that ξi<x<ξi+1, ξj<x<ξj+1, then
By Definition 4.3, it is not difficult to derive the following properties.
Property 4.1. Let
then,
(1) I∗(aij)=I∗(aij)=aij;I∗(bik)=I∗(bik)=bik.
(2) I∗(˜Aμ)=I∗(˜Aμ=˜Aμ;I∗(˜Bμ)=I∗(˜Bμ)=˜Bμ.
(3) I∗(˜Aμ∘˜Xμ)=I∗(˜Bμ)=˜Bμ;I∗(˜Aμ∘˜Xμ)=I∗(˜Bμ)=˜Bμ.
(4) ˜Xμ≤I∗(˜Xμ),I∗(˜Xμ)≤˜Xμ.
Property 4.2. Let x,y∈If, xi,yi∈If, i=1,⋯,n, then
(1) I∗(x)∨I∗(y)=I∗(x∨y); I∗(x)∨I∗(y)=I∗(x∨y).
(2) I∗(x)∧I∗(y)=I∗(x∧y); I∗(x)∧I∗(y)=I∗(x∧y).
(3) n∨i=1[I∗(xi)∧I∗(yi)]=I∗[n∨i=1(xi∧yi)].
(4) n∨i=1[I∗(xi)∧I∗(yi)]=I∗[n∨i=1(xi∧yi)].
Property 4.3. Let
then,
(1) I∗(˜Aμ∘˜Xμ)=I∗(˜Aμ)∘I∗(˜Xμ).
(2) I∗(˜Aμ∘˜Xμ)=I∗(˜Aμ)∘I∗(˜Xμ).
Theorem 4.2. ˜Xμ is a solution of the primary fuzzy matrix Eq (4.1) if, and only if, I∗(˜Xμ) is a solution of the primary fuzzy matrix equation.
Proof. (Necessity) Assuming that ˜Xμ is a solution of the primary fuzzy matrix equation, it is clear that ˜Aμ∘˜Xμ=˜Bμ. By Property 4.1, it follows that
According to the Property 4.3, we know that
From (4.7) we have
By the Property 4.1, it is not difficult to obtain I∗(˜Aμ)=˜Aμ. From (4.8) we have
Formula (4.9) shows that I∗(˜Xμ) is a solution of the primary fuzzy matrix equation.
(Sufficiency) Assuming that I∗(˜Xμ) is a solution of the primary fuzzy matrix equation, it is clear that ˜Aμ∘I∗(˜Xμ)=˜Bμ. By Property 4.1, it follows that
Using Property 2.1, we can get
Formula (4.11) shows that ˜Xμ is a solution of the primary fuzzy matrix equation.
Therefore, the conclusion is correct.
Similarly, ˜Xμ is a solution of the primary fuzzy matrix Eq (4.1) if, and only if, I∗(˜Xμ) is a solution of the primary fuzzy matrix equation.
By Theorem 4.2, we can obtain the following corollary.
Corollary 4.1. (1) The interval matrix ˜Hμ is the maximum solution of primary fuzzy matrix Eq (4.1) if, and only if, I∗(˜Hμ) is the maximum solution of this equation.
(2) The interval matrix ˜Jμ is the minimum solution of primary fuzzy matrix Eq (4.1) if, and only if, I∗(˜Jμ) is the minimum solution of this equation.
(3) The interval matrix ˜Qμ is the minimal solution of primary fuzzy matrix Eq (4.1) if, and only if, I∗(˜Qμ) is the minimal solution of this equation.
If the primary fuzzy matrix Eq (4.1) has solutions, we next explore how to obtain parameter set solutions of this equation. By Theorem 4.2, the ordered interval-valued set Ψ is sufficient to inscribe the entire parameter set solutions of the primary fuzzy matrix equation.
First, the primary fuzzy matrix equation can be rewritten to
where k=1,⋯,p.
In (4.12), the kth equality is equivalent to
where i=1,⋯,m.
Second, the logical form of the primary fuzzy matrix equation is converted to algebraic form.
For simplicity of presentation, let
With the help of Theorem 3.1, the left hand side (LHS) of (4.13) can be expressed in algebraic form:
where i=1,⋯,m.
By Property 2.2, we know that
According to (4.15), (4.14) is simplified to
From Property 2.2, it follows that
According to (4.17), (4.16) is further simplified to
Repeating the process of (4.15)–(4.18), (4.14) is finally expressed as
where i = 1, \cdots, m, and
then (4.19) can be simplified to
where i = 1, \cdots, m.
Equation (4.20) is equivalent to
where
where "*" denotes the khatri-rao product of interval matrices.
According to the above procedure, the value of the kth row of {\widetilde X_\mu } can be determined. Let k = 1, 2, \cdots, p , and we can obtain the parameter set solutions of the primary fuzzy matrix equation.
A specific algorithm for solving all solutions of IT2 FRE (2.18) is given in the following.
Algorithm 4.1. The following steps are used to solve the solution set of IT2 FRE (2.18).
Step. 1. Decompose IT2 FRE (2.18) to construct the primary fuzzy matrix Eq (4.1).
Step. 2. Use Theorem 4.1 to determine if there are solutions to the primary fuzzy matrix equation. If the primary fuzzy matrix equation has solutions, then proceed as follows; otherwise, IT2 FRE (equ:IT2 FRE(a)) has no solution.
Step. 3. Construct an ordered set \Theta from {\widetilde A_\mu} and {\widetilde B_\mu}
We specify
The elements in {\widetilde A_\mu} and {\widetilde B_\mu} can be represented as vectors to facilitate algebraic operations.
Step. 4. Construct (4.12) and convert it into the form of (4.21) to solve for the parameter set solutions of Co{l_k}\left({{{\widetilde X}_\mu }} \right).
Step. 5. Let k = 1, 2, \cdots, p , and we can get all parameter set solutions of \left({{{\widetilde X}_\mu }} \right) . Determine the maximum and minimum (or minimal) solutions of the primary fuzzy matrix equation.
Step. 6. Finally, based on the solution set of the primary fuzzy matrix equation and secondary fuzzy matrix equation, the solution set \widetilde X of IT2 FRE is constructed.
5.
Application
Consider the following IT2 FRE,
where
First, taking a transpose on both sides of (5.1), we get
By decomposing IT2 FRE (5.2), we can obtain the primary fuzzy matrix equation and the secondary fuzzy matrix equation. From Definition 4.1, we only need to solve the primary fuzzy matrix equation to obtain the solution set of IT2 FRE. The primary fuzzy matrix equation of (5.2) can be expressed as
where
Next, use Theorem 4.1 to determine if (5.3) has solutions.
According to the above calculation, {\underline H _\mu } \le {\overline H _\mu } , {\widetilde H_\mu } is a solution of (5.3) and {\widetilde H_\mu } is the maximum solution of this equation.
Let
which needs to satisfy the following logical equation.
However, solving (5.4) directly is relatively difficult, so it needs to be converted into algebraic form.
Construct the ordered set \Theta based on {\widetilde A_\mu } and {\widetilde B_\mu } :
Represent the elements in \Theta as vectors
Convert (5.4) into an algebraic equation
Let
which is equivalent to
Let
This leads to
The MATLAB program provided in the literature [15] is improved so that it can calculate the STP of the interval matrix. (5.5) is calculated as
Solving for (5.5), we get
where i = 41, 42, 48, \ j = 18, 19, 20, 21.
From the values of [\underline x_1, \overline x_1] , there are 3 \times 4 = 12 parameter set solutions for Co{l_1}\left({\widetilde X}_\mu^T \right) , two of which do not satisfy {\underline {\rm{x}} _{i1}} \le {\overline x _{i1}}\left({i = 1, 2} \right) ; then
Assuming
we have
where the value of L has been obtained in (5.5),
Solving for (5.6), we get
where i = 29, 30, 31 , j = 15, 16, 22, 23, 29, 30, 36.
Depending on the value of [\underline x_2, \overline x_2] , it follows that Co{l_2}\left({{{\widetilde X}_\mu^T }}\right) has 3 \times 7 = 21 parameter set solutions, six of which do not satisfy {\underline {\rm{x}} _{i2}} \le {\overline x _{i2}}\left({i = 1, 2} \right) ; then
In summary, we can conclude that:
(1) The primary fuzzy matrix Eq (5.3) has a total of 10 \times 15 = 150 parameter set solutions.
(2) The maximum solution of this equation is
(3) The equation has no minimum solution and only two minimal solutions,
(4) Based on the maximum and minimal solutions of the primary fuzzy matrix equation, we can work out all the parameter set solutions of the primary fuzzy matrix equation.
(5) The solution set of IT2 FRE is
6.
Conclusions
This paper focused on the solution of IT2 FRE \widetilde A \circ \widetilde X = \widetilde B . First, the STP of interval matrices and its properties were introduced, and the matrix representation of the interval-valued logic was given. Then, the IT2 FRE was considered as the primary fuzzy matrix equation and secondary fuzzy matrix equation. The solution of secondary fuzzy matrix is known, so only the primary fuzzy matrix equation needs to be solved. Moreover, the solvability of the primary matrix equation was studied, and a specific algorithm for solving IT2 FREs based on the STP of interval matrices was given. Finally, a numerical example was given to verify the effectiveness of the proposed method.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported in part by the Research Fund for the Taishan Scholar Project of Shandong Province of China under Grant tstp20221103, and in part by the National Natural Science Foundation of China under Grant 62273201.
Conflict of interest
The authors declare that there are no conflicts of interest in this paper.
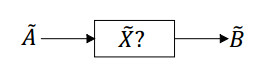








 DownLoad:
DownLoad: