High-order rational-type solutions of the analogous (3+1)-dimensional Hirota-bilinear-like equation

Wenting Li; Ailing Jiao; Wei Liu; Zhaoying Guo; Wenting Li; Ailing Jiao; Wei Liu; Zhaoying Guo

doi:10.3934/mbe.2023856

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 11: 19360-19371. doi: 10.3934/mbe.2023856

Previous Article Next Article

Research article Special Issues

High-order rational-type solutions of the analogous (3+1)-dimensional Hirota-bilinear-like equation

1.
Qiongtai Normal University, Haikou 571127, China
2.
School of Mathematics, Heilongjiang University, Harbin 150080, China

Academic Editor: Xiaodi Li

Received: 11 August 2023 Revised: 10 October 2023 Accepted: 13 October 2023 Published: 18 October 2023

In this article, a new dynamical system equation named the (3+1)-dimensional Hirota-bilinear-like equation (HBLE) was constructed. The generalized Hirota bilinear method was applied to obtain this new HBLE in (3+1) dimensions. This new HBLE possesses a similar bilinear form to the original (3+1)-dimensional Hirota bilinear equation, but with additional nonlinear terms. A set of high-order rational solutions is constructed for the given equation, generated from polynomial solutions to the associated generalized bilinear equation. The analyticity conditions of the resulting solutions were investigated and six groups of general solutions were derived. In addition, the shape and surface of the high-order rational function solutions and their dynamic behaviors were studied by utilizing Maple.

Keywords:

Citation: Wenting Li, Ailing Jiao, Wei Liu, Zhaoying Guo. High-order rational-type solutions of the analogous (3+1)-dimensional Hirota-bilinear-like equation[J]. Mathematical Biosciences and Engineering, 2023, 20(11): 19360-19371. doi: 10.3934/mbe.2023856

Related Papers:

[1]	Hong-Yang Guan, Jian-Guo Liu . Propagation of lump-type waves in nonlinear shallow water wave. Mathematical Biosciences and Engineering, 2023, 20(11): 19553-19564. doi: 10.3934/mbe.2023866
[2]	James M. Hyman, Jia Li . Epidemic models with differential susceptibility and staged progression and their dynamics. Mathematical Biosciences and Engineering, 2009, 6(2): 321-332. doi: 10.3934/mbe.2009.6.321
[3]	Qian Ding, Yunfeng Liu, Yuming Chen, Zhiming Guo . Dynamics of a reaction-diffusion SIRI model with relapse and free boundary. Mathematical Biosciences and Engineering, 2020, 17(2): 1659-1676. doi: 10.3934/mbe.2020087
[4]	Xinyu Bai, Shaojuan Ma . Stochastic dynamical behavior of COVID-19 model based on secondary vaccination. Mathematical Biosciences and Engineering, 2023, 20(2): 2980-2997. doi: 10.3934/mbe.2023141
[5]	Napoleon Bame, Samuel Bowong, Josepha Mbang, Gauthier Sallet, Jean-Jules Tewa . Global stability analysis for SEIS models with n latent classes. Mathematical Biosciences and Engineering, 2008, 5(1): 20-33. doi: 10.3934/mbe.2008.5.20
[6]	Hongbin Guo, Michael Yi Li . Global dynamics of a staged progression model for infectious diseases. Mathematical Biosciences and Engineering, 2006, 3(3): 513-525. doi: 10.3934/mbe.2006.3.513
[7]	Andrzej Swierniak, Jaroslaw Smieja . Analysis and Optimization of Drug Resistant an Phase-Specific Cancer. Mathematical Biosciences and Engineering, 2005, 2(3): 657-670. doi: 10.3934/mbe.2005.2.657
[8]	James M. Hyman, Jia Li . Differential susceptibility and infectivity epidemic models. Mathematical Biosciences and Engineering, 2006, 3(1): 89-100. doi: 10.3934/mbe.2006.3.89
[9]	Hui Cao, Yicang Zhou, Zhien Ma . Bifurcation analysis of a discrete SIS model with bilinear incidence depending on new infection. Mathematical Biosciences and Engineering, 2013, 10(5&6): 1399-1417. doi: 10.3934/mbe.2013.10.1399
[10]	Baojian Hong . Bifurcation analysis and exact solutions for a class of generalized time-space fractional nonlinear Schrödinger equations. Mathematical Biosciences and Engineering, 2023, 20(8): 14377-14394. doi: 10.3934/mbe.2023643

Abstract

1. Introduction

The study of nonlinear partial differential equations has gained significant attention in various fields of nonlinear sciences, including physics, biology, chemistry and plasma physics. This is particularly evident in the areas of nonlinear optics, harbor dynamics, chemical reactions, Bose-Einstein condensates, and coastal structures^[1,2,3,4,5]. In recent times, various types of rational function solutions have demonstrated their significance in interpreting the wave characteristics of appropriate equations.

One important task in mathematical physics is the search for exact solutions to nonlinear partial differential equations. There are several important methods for finding exact solutions to nonlinear partial differential equations, such as the inverse scattering method ^[6], Bäcklund transformation method ^[7], Painlev $\acute{e}$ analysis method ^[8], Darboux transformation method ^[9], the Hirota bilinear method ^[10], the extended direct algebraic method^[11], the Tikhonov regularization method ^[12], the adaptive nonlinear numerical method^[13] and others. Many types of solutions can be found using these methods. Particularly, the solitary wave solutions, the lump solutions and the optical solitons, along with many other rational solutions that can describe wave motion that have garnered significant attention in the scientific research community ^{[14,15,16,17,18,19]}. Many kinds of nonlinear differential equations have been studied, such as fractional evolution equations ^[20], nonlinear fractional integro-differential equations ^[21], the nano-ionic currents equation ^[22] and the stochastic longitudinal wave equation ^[23].

The Hirota bilinear method is an important method to deal with complex systems. The Hirota bilinear equation can be used to describe and analyze some wave systems, electromagnetic fields, mathematical models and more, including a series of finite difference equations, as well as multidimensional and multi-parameter mathematical models. One of its important features is that it can solve complex problems involving time-varying systems without requiring additional computation. It also has been applied to many scientific fields, such as electromagnetic field theory, heat conduction theory, acoustic theory, fluid mechanics and so on. Its theoretical research can also provide important guidance for application research. Jia investigated the generalized coupled nonlinear Hirota equations with additional effects using the Hirota method ^[29]. Dong used the homoclinic test method to obtain the rational breather wave and rogue wave solutions of the (3+1)-dimensional Hirota bilinear equation ^[30]. Chen investigated the matrix Riemann-Hilbert problem of the Hirota equation with nonzero boundary conditions ^[31].

By extending the Hirota bilinear operators, Ma ^[24,25] introduced a novel type of bilinear differential equation. Meanwhile, the linear superposition principle is an important principle for solving generalized bilinear differential equations. The (3+1)-dimensional Boiti-Leon-Manna-Pempinelli-like equation ^[26], (3+1)-dimensional Jimbo-Miwa-like equation ^[27], and Kadomtsev-Petviashvili-Boussinesq-like equation ^[28] were derived using Ma's method. These "like" equations have some terms in common with the original equations, as well as additional nonlinear terms that can better describe nonlinear phenomena. However, the study of high-order rational solutions was less extensive. In this study, our focus is not only to establish the HBLE but to also contribute high-order rational solutions to this new equation.

The paper will be arranged as follows. In section two, a new equation called the (3+1)-dimensional HBLE will be derived by introducing the general Hirota bilinear operators and the dependent variable transformation. In section three, some types of the high-order rational solutions of the (3+1)-dimensional HBLE will be studied. Finally, a few concluding remarks will be provided.

2. The (3+1)-dimensional HBLE

In this paper, we primarily focus on the following dynamical model, which can be utilized to describe certain intriguing (3+1)-dimensional physical wave models:

$\begin{equation} u_{yt}-u_{xxxy}-3(u_{x}u_{y})_{x}-3u_{xx}+3u_{zz} = 0, \end{equation}$

(2.1)

where $u = u{(x, y, z, t)}$ . The (3+1)-dimensional Hirota bilinear equation (HBE) (2.1) is an extension of the Korteweg-de Vries equation, which serves as a mathematical model for waves on shallow water surfaces ^[30]. The model has been mentioned to be completely integrable and possess N-soliton. If we substitute $t$ with $T$ , $x$ with $X$ , $y$ with $X$ , $z$ with $X$ , and $u$ with $U$ , then Eq (2.1) reduces to the classical KdV equation.

Under the transformation

$\begin{equation} u = 2[\ln F(x, y, z, t)]_{x} = \frac{2 F_{x}(x, y, z, t)}{F(x, y, z, t)}, \end{equation}$

(2.2)

where $F = F(x, y, z, t)$ is an unknown real function that will be determined later.

Substituting (2.2) into (2.1) and integrating once with respect to $x$ yields

$\begin{equation} F_{ty}F-F_tF_y-F_{xxxy}F+3F_{xxy}F_x-3F_{xx}F_{xy}+F_{xxx}F_y-3F_{xx}F+3F_x+3F_{zz}F-3F^2_z = 0. \end{equation}$

(2.3)

Equation (2.3) can be rewritten as

$\begin{equation} (D_{t}D_{y}- D_{x}^{3}D_{y}-3D_{x}^{2}+3D_{z}^{2})F\cdot F = 0, \end{equation}$

(2.4)

under the definition of the bilinear derivative operators as follows

$\begin{equation} (D_{x}^{m}D_{y}^{n}D_{z}^{r}D_{t}^{s}) = (\partial_{x}-\partial_{x'})^{m}(\partial y-\partial_{y'})^{n}(\partial_{z}-\partial_{z'})^{r}(\partial t-\partial_{t'})^{s}|_{x' = x, y' = y, z' = z, t' = t}. \end{equation}$

(2.5)

Using the same form of (2.4), the (3+1)-dimensional HBE (2.1) can be transformed into the generalized Hirota bilinear form

$\begin{equation} (D_{p, t}D_{p, y}- D_{p, x}^{3}D_{p, y}-3D_{p, x}^{2}+D_{p, z}^{2})F\cdot F = 0. \end{equation}$

(2.6)

The generalized bilinear differential operator $D_{p}$ is introduced as follows ^[24]

$\begin{equation} \begin{aligned} (D_{p, x}^{m}D_{p, y}^{n}D_{p, z}^{r}D_{p, t}^{s})F\cdot F = &(\partial_{x}+\alpha_{p}\partial_{x'})^{m}(\partial y+\alpha_{p}\partial_{y'})^{n}(\partial_{z}+\alpha_{p}\partial_{z'})^{r}(\partial t+\alpha_{p}\partial_{t'})^{s}\\ &F(x, y, z, t)F(x', y', z', t')|_{x' = x, y' = y, z' = z, t' = t}, \end{aligned} \end{equation}$

(2.7)

where $m, n, r, s\geq0$ , $\alpha_{p}^{\mu} = (-1)^{\nu_{p}(\mu)}, \;$ $\mu\equiv r_{p}(\mu)\mod p$ .

While taking $p = 3$ , the operator $D_{p, i}$ could be expressed as a prime order bilinear operator $D_{3, x}, \; D_{3, y}, \; D_{3, z}, \; D_{3, t}$ correspondingly, and

$\begin{equation} \alpha_{3} = -1, \quad \alpha_{3}^{2} = 1, \quad \alpha_{3}^{3} = 1, \quad \alpha_{3}^{4} = -1, \quad \alpha_{3}^{5} = 1, \quad \alpha_{3}^{6} = 1, \quad \ldots \end{equation}$

(2.8)

which leads to

$\begin{equation} \begin{array}{lll} D_{3, x}D_{3, t}F\cdot F = 2F_{xt}F-2F_{x}F_{t}, &\quad &D_{3, x}D_{3, y}F\cdot F = 2F_{xy}F-2F_{x}F_{y}, \\ D_{3, t}D_{3, y}F\cdot F = 2F_{ty}F-2F_{t}F_{y}, &\quad &D_{3, x}^{3}D_{y}F\cdot F = 6F_{xy}F_{xx}, \\ D_{3, x}^{2}F\cdot F = 2F_{xx}F-2F_{x}^{2}, &\quad &D_{3, z}^{2}F\cdot F = 2F_{zz}F-2F_{z}^{2}. \end{array} \end{equation}$

(2.9)

By submitting (2.9) into (2.6), the generalized HBE is obtained

$\begin{equation} \begin{aligned} &(D_{3y}D_{3t}-D_{3x}^{3}D_{3y}-3D_{3x}^{2}+D_{3z}^{2})F\cdot F\\ & = F_{yt}F-F_{y}F_{t}-3F_{xy}F_{xx}-3F_{xx}F+3F_{x}^{2}+3F_{zz}F-3F_{z}^{2} = 0. \end{aligned} \end{equation}$

(2.10)

Based on the Bell polynomial theory and linear superposition principle, a new nonlinear equation is formed from the bilinear equation (2.10). Under the inverse transformation of (2.2) $F = e^{\int{\frac{1}{2}u}dx}$ , Eq (2.10) could be changed into a nonlinear partial equation about the dependent variable $u$ , and three independent variables $x, y, z, t$ . The nonlinear wave equation could be called (3+1)-dimensional generalized HBLE

$\begin{equation} 8v_{t}-12u_{x}u_{y}-6u^{2}u_{y}-3u^{3}v-6u v u_{x}-24u_{x}+24w_{z} = 0, \end{equation}$

(2.11)

where $v_{x} = u_{y}$ , $w_{x} = u_{z}$ .

3. Rational solutions of the (3+1)-dimensional HBLE

In this section, we will search for some higher-order rational function solutions to the (3+1)-dimensional HBLE (2.11). Although it is often difficult to find exact polynomial solutions to nonlinear partial differential equations while overcoming the problem by solving the enormous and complex algebra equations, fortunately some mathematical software can help to overcome this difficulty. To obtain the high-order polynomial function solution, $F$ is constructed as

$\begin{equation} F = \sum\limits_{i = 0}^{2}\sum\limits_{j = 0}^{4}\sum\limits_{k = 0}^{2}\sum\limits_{l = 0}^{1}c_{i, j, k, l}x^{i}y^{j}z^{k}t^{l}, \end{equation}$

(3.1)

where $c_{i, j, k, l}$ are arbitrary constants. $F$ solves the generalized bilinear equation (2.10), when implies $u = 2(\ln F)_{x}$ and solves the HBLE (2.11). By using Maple to perform calculations, we obtained the following six sets of polynomial solutions to Eq (2.10):

$\begin{equation} \begin{aligned} F_{1} = \frac{1}{c_{0, 0, 0, 1}^{2}}&(c_{0, 0, 0, 1}^{3} t +\left(\left(x +z \right)^{2} c_{2, 0, 0, 0}+c_{1, 0, 0, 0} x +c_{0, 0, 1, 0} z +c_{0, 0, 0, 0}\right) c_{0, 0, 0, 1}^{2}\\ &-12 \left(\left(x +z \right) c_{2, 0, 0, 0}+\frac{c_{0, 0, 1, 0}}{4}+\frac{c_{1, 0, 0, 0}}{4}\right) y \left(c_{0, 0, 1, 0}-c_{1, 0, 0, 0}\right) c_{0, 0, 0, 1}\\ &+36 \left(2 c_{2, 0, 0, 0}+y \left(c_{0, 0, 1, 0}-c_{1, 0, 0, 0}\right)\right) c_{2, 0, 0, 0} y \left(c_{0, 0, 1, 0}-c_{1, 0, 0, 0}\right)), \end{aligned} \end{equation}$

(3.2)

$\begin{equation} \begin{aligned} F_{2} = \frac{1}{c_{1, 0, 0, 1}^{2}}&(t \left(x -z \right) c_{1, 0, 0, 1}^{3}+(\left(x +3 z \right) \left(x -z \right) c_{2, 0, 0, 0}+c_{0, 3, 0, 1} y^{3} t+c_{0, 1, 0, 1} y t\\ &+c_{0, 0, 0, 1} t -c_{0, 0, 1, 0} x +c_{0, 0, 1, 0} z ) c_{1, 0, 0, 1}^{2}+(\left(6+\left(-24 x +24 z \right) y \right) c_{2, 0, 0, 0}^{2}\\ &+\left(c_{0, 3, 0, 1} \left(x +3 z \right) y^{3}+c_{0, 1, 0, 1} \left(x +3 z \right) y +4 x c_{0, 0, 0, 1}\right) c_{2, 0, 0, 0}\\ &-c_{0, 0, 1, 0} \left(y^{3} c_{0, 3, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right)) c_{1, 0, 0, 1}\\ &-24 \left(y c_{2, 0, 0, 0}-\frac{c_{0, 0, 0, 1}}{8}\right) \left(y^{3} c_{0, 3, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right) c_{2, 0, 0, 0}), \end{aligned} \end{equation}$

(3.3)

$\begin{equation} \begin{aligned} F_{3} = \frac{1}{c_{1, 0, 0, 1}^{2}}&(t \left(x +z \right) c_{1, 0, 0, 1}^{3}+(\left(x +z \right)^{2} c_{2, 0, 0, 0}+c_{0, 2, 0, 1} y^{2} t\\ &+c_{0, 1, 0, 1} y t+c_{0, 0, 0, 1} t +c_{0, 0, 1, 0} x +c_{0, 0, 1, 0} z ) c_{1, 0, 0, 1}^{2}\\ &+(6 c_{2, 0, 0, 0}^{2}+y \left(y c_{0, 2, 0, 1}+c_{0, 1, 0, 1}\right) \left(x +z \right) c_{2, 0, 0, 0}\\ &+c_{0, 0, 1, 0} \left(y^{2} c_{0, 2, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right)) c_{1, 0, 0, 1}\\ &-c_{0, 0, 0, 1} c_{2, 0, 0, 0} \left(y^{2} c_{0, 2, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right)), \end{aligned} \end{equation}$

(3.4)

$\begin{equation} \begin{aligned} F_{4} = \frac{1}{c_{1, 0, 0, 1}^{2}}&(t \left(x +z \right) c_{1, 0, 0, 1}^{3}+(\left(x +z \right) \left(x -3 z \right) c_{2, 0, 0, 0}+c_{0, 2, 0, 1} y^{2} t \\ &+c_{0, 1, 0, 1} y t +c_{0, 0, 0, 1} t +c_{0, 0, 1, 0} x +c_{0, 0, 1, 0} z ) c_{1, 0, 0, 1}^{2}\\ &+(\left(6+\left(-24 x -24 z \right) y \right) c_{2, 0, 0, 0}^{2}+(c_{0, 2, 0, 1} \left(x -3 z \right) y^{2}\\ &+c_{0, 1, 0, 1} \left(x -3 z \right) y+4 x c_{0, 0, 0, 1}) c_{2, 0, 0, 0}\\ &+c_{0, 0, 1, 0} \left(y^{2} c_{0, 2, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right)) c_{1, 0, 0, 1}\\ &-24 \left(y^{2} c_{0, 2, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right) c_{2, 0, 0, 0} \left(y c_{2, 0, 0, 0}-\frac{c_{0, 0, 0, 1}}{8}\right)), \end{aligned} \end{equation}$

(3.5)

$\begin{equation} \begin{aligned} F_{5} = \frac{1}{c_{1, 0, 0, 1}^{2}}&(t \left(x +z \right) c_{1, 0, 0, 1}^{3}+(\left(24 t y +x^{2}-2 x z -3 z^{2}\right) c_{2, 0, 0, 0}\\ &+c_{0, 0, 0, 1} t+x c_{0, 0, 1, 0}+c_{0, 0, 1, 0} z +c_{0, 0, 0, 0}) c_{1, 0, 0, 1}^{2}\\ &+4 c_{2, 0, 0, 0} \left(-24 y z c_{2, 0, 0, 0}+x c_{0, 0, 0, 1}+6 y c_{0, 0, 1, 0}\right) c_{1, 0, 0, 1}\\ &-576 c_{2, 0, 0, 0}^{3} y^{2}+48 y c_{0, 0, 0, 1} c_{2, 0, 0, 0}^{2}), \end{aligned} \end{equation}$

(3.6)

$\begin{equation} \begin{aligned} F_{6} = \frac{1}{c_{1, 0, 0, 1}^{2}}&(t \left(x +z \right) c_{1, 0, 0, 1}^{3}+(\left(x +z \right)^{2} c_{2, 0, 0, 0}+c_{0, 3, 0, 1} y^{3} t\\ &+c_{0, 1, 0, 1} y t +c_{0, 0, 0, 1} t +c_{0, 0, 1, 0} x +c_{0, 0, 1, 0} z ) c_{1, 0, 0, 1}^{2}\\ &+(6 c_{2, 0, 0, 0}^{2}+y \left(y^{2} c_{0, 3, 0, 1}+c_{0, 1, 0, 1}\right) \left(x +z \right) c_{2, 0, 0, 0}\\ &+c_{0, 0, 1, 0} \left(y^{3} c_{0, 3, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right)) c_{1, 0, 0, 1}\\ &-c_{0, 0, 0, 1} c_{2, 0, 0, 0} \left(y^{3} c_{0, 3, 0, 1}+y c_{0, 1, 0, 1}+c_{0, 0, 0, 1}\right)), \end{aligned} \end{equation}$

(3.7)

where $c_{i, j, k, l}$ is an arbitrary constant, subject to the given condition, and $F$ is ensured to have significance.

By applying the transformation (2.2), we obtain six groups of rational solutions for the (3+1)-dimensional HBLE, where $u_i = 2F_{ix}/F_i$ for $i = 1, 2, 3, 4, 5, 6$ .

(ⅰ) The first group of solutions is given by $u_1 = \dfrac{2 c_{0, 0, 0, 1} f_1}{F_1}$ , where

$\begin{equation} \begin{aligned} f_1 = 4 \left(\left(\left(x +z \right) c_{2, 0, 0, 0}+\frac{c_{1, 0, 0, 0}}{2}\right) c_{0, 0, 0, 1}-6 c_{2, 0, 0, 0} y \left(c_{0, 0, 1, 0}-c_{1, 0, 0, 0}\right)\right) c_{0, 0, 0, 1}. \end{aligned} \end{equation}$

(3.8)

(ⅱ) The second group of solutions is given by $u_2 = \dfrac{2 c_{1, 0, 0, 1} f_2}{F_2}$ , where

$\begin{equation} \begin{aligned} f_2 = &2 (t c_{1, 0, 0, 1}^{2}+\left(\left(2 x +2 z \right) c_{2, 0, 0, 0}-c_{0, 0, 1, 0}\right) c_{1, 0, 0, 1}+c_{2, 0, 0, 0} (y^{3} c_{0, 3, 0, 1}+y c_{0, 1, 0, 1}\\ &-24 y c_{2, 0, 0, 0}+4 c_{0, 0, 0, 1})) c_{1, 0, 0, 1}. \end{aligned} \end{equation}$

(3.9)

(ⅲ) The third group of solutions is given by $u_3 = \dfrac{2 c_{1, 0, 0, 1} f_3}{F_3}$ , where

$\begin{equation} \begin{aligned} f_3 = 2 t c_{1, 0, 0, 1}^{3}+2 \left(2 \left(x +z \right) c_{2, 0, 0, 0}+c_{0, 0, 1, 0}\right) c_{1, 0, 0, 1}^{2}+2 y \left(y c_{0, 2, 0, 1}+c_{0, 1, 0, 1}\right) c_{2, 0, 0, 0} c_{1, 0, 0, 1}. \end{aligned} \end{equation}$

(3.10)

(ⅳ) The fourth group of solutions is given by $u_4 = \dfrac{2 c_{1, 0, 0, 1} f_4}{F_4}$ , where

$\begin{equation} \begin{aligned} f_4 = &2 (t c_{1, 0, 0, 1}^{2}+\left(\left(2 x -2 z \right) c_{2, 0, 0, 0}+c_{0, 0, 1, 0}\right) c_{1, 0, 0, 1}+c_{2, 0, 0, 0} (y^{2} c_{0, 2, 0, 1}+y c_{0, 1, 0, 1}\\ &-24 y c_{2, 0, 0, 0}+4 c_{0, 0, 0, 1})) c_{1, 0, 0, 1}. \end{aligned} \end{equation}$

(3.11)

(ⅴ) The fifth group of solutions is given by $u_5 = \dfrac{2 c_{1, 0, 0, 1} f_5}{F_5}$ , where

$\begin{equation} f_5 = 2 c_{1, 0, 0, 1} \left(t c_{1, 0, 0, 1}^{2}+\left(\left(2 x -2 z \right) c_{2, 0, 0, 0}+c_{0, 0, 1, 0}\right) c_{1, 0, 0, 1}+4 c_{0, 0, 0, 1} c_{2, 0, 0, 0}\right). \end{equation}$

(3.12)

(ⅵ) The sixth group of solutions is given by $u_6 = \dfrac{2 c_{1, 0, 0, 1} f_6}{F_6}$ , where

$\begin{equation} \begin{aligned} f_6 = 2 c_{1, 0, 0, 1} \left(t c_{1, 0, 0, 1}^{2}+\left(\left(2 x +2 z \right) c_{2, 0, 0, 0}+c_{0, 0, 1, 0}\right) c_{1, 0, 0, 1}+y \left(y^{2} c_{0, 3, 0, 1}+c_{0, 1, 0, 1}\right) c_{2, 0, 0, 0}\right). \end{aligned} \end{equation}$

(3.13)

To illustrate the high-order rational solutions of HBLE (2.11), random parameters are selected as follows.

(1) $c_{0, 0, 0, 0} = 1, c_{0, 0, 0, 1} = 1, c_{0, 0, 1, 0} = 2, c_{1, 0, 0, 0} = 1, c_{2, 0, 0, 0} = 1,$

$\begin{equation} u_{1} = \frac{4 x +4 z +2-24 y}{x^{2}+\left(-12 y +2 z +1\right) x +36 y^{2}+\left(-12 z +63\right) y +z^{2}+t +2 z +1}, \end{equation}$

(3.14)

(2) $c_{0, 0, 0, 1} = 1, c_{0, 0, 1, 0} = 1, c_{0, 1, 0, 1} = 1, c_{0, 3, 0, 1} = 1, c_{1, 0, 0, 1} = 1, c_{2, 0, 0, 0} = 1,$

$\begin{equation} u_{2} = \frac{2 y^{3}+2 t +4 x -46 y +4 z +6}{-24 y^{4}+\left(t +x +3 z +2\right) y^{3}-24 y^{2}+\left(t -23 x +27 z -22\right) y +x^{2}+\left(t +2 z +3\right) x -3 z^{2}+\left(-t +1\right) z +t +8}, \end{equation}$

(3.15)

(3) $c_{0, 0, 0, 0} = 1, c_{0, 0, 0, 1} = 1, c_{0, 0, 1, 0} = 1, c_{0, 1, 0, 1} = 1, c_{0, 2, 0, 1} = 1, c_{1, 0, 0, 0} = 1, c_{1, 0, 0, 1} = 1, c_{2, 0, 0, 0} = 1,$

$\begin{equation} u_{3} = \frac{2 y^{2}+2 t +4 x +2 y +4 z +2}{\left(t +x +z \right) y^{2}+\left(t +x +z \right) y +x^{2}+\left(t +2 z +1\right) x +z^{2}+\left(t +1\right) z +t +6}, \end{equation}$

(3.16)

(4) $c_{0, 0, 0, 1} = 1, c_{0, 0, 1, 0} = 1, c_{0, 1, 0, 1} = 1, c_{0, 2, 0, 1} = 1, c_{1, 0, 0, 1} = 1, c_{2, 0, 0, 0} = 1,$

$\begin{equation} u_{4} = \frac{2 y^{2}+2 t +4 x -46 y -4 z +10}{{-24 y^{3}+\left(t +x -3 z -20\right) y^{2}+\left(t -23 x -27 z -20\right) y +x^{2}+\left(t -2 z +5\right) x-3 z^{2}+\left(t +1\right) z +t +10}}, \end{equation}$

(3.17)

(5) $c_{0, 0, 0, 0} = 1, c_{0, 0, 0, 1} = 1, c_{0, 0, 1, 0} = 1, c_{1, 0, 0, 1} = 1, c_{2, 0, 0, 0} = 1,$

$\begin{equation} u_{5} = \frac{2 t +4 x -4 z +10}{-3 z^{2}+\left(t -2 x -96 y +1\right) z +\left(x +24 y +1\right) t +x^{2}-576 y^{2}+5 x +72 y +1}, \end{equation}$

(3.18)

(6) $c_{0, 0, 0, 1} = 1, c_{0, 0, 1, 0} = 1, c_{0, 1, 0, 1} = 1, c_{0, 3, 0, 1} = 1, c_{1, 0, 0, 1} = 1, c_{2, 0, 0, 0} = 1,$

$\begin{equation} u_{6} = \frac{2 y^{3}+2 t +4 x +2 y +4 z +2}{\left(t +x +z \right) y^{3}+\left(t +x +z \right) y +x^{2}+\left(t +2 z +1\right) x +z^{2}+\left(t +1\right) z +t +6}, \end{equation}$

(3.19)

Six sets of the high-order rational solutions of the (3+1)-dimensional HBLE were obtained from the polynomial solution of the bilinear equation with the link $u = 2({\rm ln} F)_x$ .

4. Conclusions

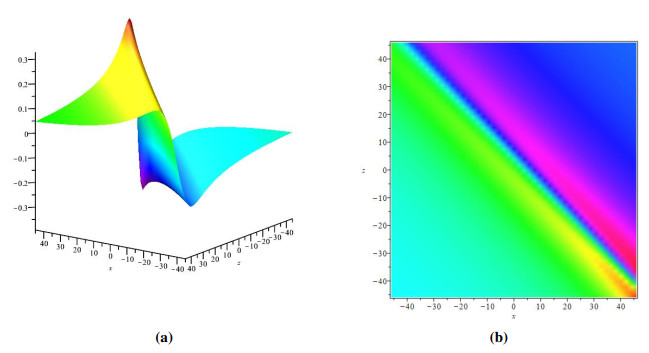
Using the generalized bilinear method with the prime number $p = 3$ and applying the linear superposition principle, a new equation called the (3+1)-dimensional HBLE was constructed. The new equation possesses a similar bilinear form to the bilinear equation of the (3+1)-dimensional HBE, but it includes additional nonlinear terms and higher nonlinearity. In addition, the study investigated the highest-order rational function solutions and their dynamic motion of the high-dimensional HBLE using the mathematical software Maple. The analyticity conditions of the resulting solutions were investigated, and six groups of high-order rational-type solutions which were set by the highest degree of $x, y, z, t$ to be 2–4–2–1, were derived. By observing the above solutions, it can be seen that the highest power of $x$ is second and the highest power of $y$ is fourth. However, the highest order of $z$ and $t$ are two and one respectively. It is hard to say that the HBLE does not have any other types of high-order solutions. Due to the fact that all six groups of solutions are rational types, the solutions $u_i(i = 1, ...6)$ are computed and plotted as examples, using specific values of the parameters. It is easy to see that the rational-type solutions can have various shapes. – showed the physical appearance of the rational solution $u_i(i = 1, ...6)$ (3.14–3.19) under some appropriate parameter selection. 3D plots and density plots of these solutions were presented with special values respectively. We also observed that rational solutions can exhibit various forms. Significantly, all of these rational solutions have the property that $\lim_{x\rightarrow \infty}u = 0$ , $\lim_{y\rightarrow \infty}u = 0$ , $\lim_{z\rightarrow \infty}u = 0$ . This means that the rational component of the wave will gradually diminish as it propagates. Figure 1 represented a kink soliton solution. Figures 2 and 5 both depicted two cross solitons solutions. Figure 3 showed a periodic-singular soliton solution. Figure 4 resembled optical soliton solutions. In Figure 6, the rational solutions demonstrated the interaction between two cross solitons and one lump. Some interactive phenomena may occur in all three dimensions over a period of time. It could be assumed that two waves collided and separated, maintaining similar shapes in a very short time. There are many other types of solutions to the (3+1)-dimensional HBLE that are worth studying, such as N-solitons, lump solutions, rogue wave solutions, and so on. These solutions will be explored in the next work. It is hoped that the results obtained in this paper can be helpful in explaining the nonlinear phenomenon in the field of mathematical physics and engineering.

Figure 1. 3D plot (a) and density plot (b) of

$u_1$ (3.14) at

$t = 1, y = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. 3D plot (a) and density plot (b) of

$u_2$ (3.15) at

$t = 0.2, y = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. 3D plot (a) and density plot (b) of

$u_3$ (3.16) at

$t = 0.2, y = 3$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. 3D plot (a) and density plot (b) of

$u_4$ (3.17) at

$t = 1, z = 60$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. 3D plot (a) and density plot (b) of

$u_5$ (3.18) at

$t = 1, y = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. 3D plot (a) and density plot (b) of

$u_6$ (3.19) at

$t = 1, x = 1$ .

DownLoad: Full-Size Img PowerPoint

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by Hainan Provincial Natural Science Foundation of China grant number 122QN332.

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	Y. Zhou, Lump and rogue wave solutions to (1+1)-dimensional evolution equations, Partial Differ. Equations Appl. Math., 5 (2022), 100252. https://doi.org/10.1016/j.padiff.2021.100252 doi: 10.1016/j.padiff.2021.100252
[2]	Q. Li, W. Shan, P. Wang, H. Cui, Breather, lump and N-soliton wave solutions of the (2+1)-dimensional coupled nonlinear partial differential equation with variable coefficients, Commun. Nonlinear Sci. Numer. Simul., 106 (2022), 106098. https://doi.org/10.1016/j.cnsns.2021.106098 doi: 10.1016/j.cnsns.2021.106098
[3]	A. Tripathy, S. Sahoo, H. Rezazadeh, Z. P. Izgi, M. S. Osman, Dynamics of damped and undamped wave natures in ferromagnetic materials, Optik, 281 (2023), 170817. https://doi.org/10.1016/j.ijleo.2023.170817 doi: 10.1016/j.ijleo.2023.170817
[4]	H. F. Ismael, T. A. Sulaiman, H. R. Nabi, W. Mahmoud, M. S. Osman, Geometrical patterns of time variable Kadomtsev-Petviashvili (Ⅰ) equation that models dynamics of waves in thin films with high surface tension, Nonlinear Dyn., 111 (2023), 9457–9466. https://doi.org/10.1007/s11071-023-08319-8 doi: 10.1007/s11071-023-08319-8
[5]	L. Akinyemi, A. Houwe, S. Abbagari, A. M. Wazwaz, H. M. Alshehri, M. S. Osman, Effects of the higher-order dispersion on solitary waves and modulation instability in a monomode fiber, Optik, 288 (2023), 171202. https://doi.org/10.1016/j.ijleo.2023.171202 doi: 10.1016/j.ijleo.2023.171202
[6]	M. A. Ablowitz, P. A. Clarkson, Solitons, Nonlinear Evolution Equations and Inverse Scattering, Cambridge University Press, London, 1991. https://doi.org/10.1017/CBO9780511623998
[7]	C. Rogers, W. K. Schief, Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory, Cambridge University Press, Cambridge, 2022. https://doi.org/10.1017/CBO9780511606359
[8]	S. Malik, H. Almusawa, S. Kumar, A. M. Wazwaz, M. S. Osman, A (2+1)-dimensional Kadomtsev–Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions, Results Phys., 23 (2021), 104043. https://doi.org/10.1016/j.rinp.2021.104043 doi: 10.1016/j.rinp.2021.104043
[9]	C. Gu, H. Hu, Z. Zhou, Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry, Springer Science & Business Media, Dordrecht, 2005. https://doi.org/10.1007/1-4020-3088-6
[10]	R. Hirota, The Direct Method in Soliton Theory, Cambridge University Press, Cambridge, 2004. https://doi.org/10.1017/CBO9780511543043
[11]	F. Tasnim, M. A. Akbar, M. S. Osman, The extended direct algebraic method for extracting analytical solitons solutions to the cubic nonlinear schrödinger equation Involving beta derivatives in space and time, Fractal Fractional, 7 (2023), 426. https://doi.org/10.3390/fractalfract7060426 doi: 10.3390/fractalfract7060426
[12]	S. Djennadi, N. Shawagfeh, M. Inc, M. S. Osman, J. F. Gómez-Aguilar, O. A. Arqub, The Tikhonov regularization method for the inverse source problem of time fractional heat equation in the view of ABC-fractional technique, Phys. Scr., 96 (2021), 094006. https://dx.doi.org/10.1088/1402-4896/ac0867 doi: 10.1088/1402-4896/ac0867
[13]	S. Qureshi, M. A. Akanbi, A. A. Shaikh, A. S. Wusu, O. M. Ogunlaran, W. Mahmoud, et al., A new adaptive nonlinear numerical method for singular and stiff differential problems, Alexandria Eng. J., 74 (2023), 585–597. https://doi.org/10.1016/j.aej.2023.05.055 doi: 10.1016/j.aej.2023.05.055
[14]	K. Hosseini, M. Mirzazadeh, D. Baleanu, S. Salahshour, L. Akinyemi, Optical solitons of a high-order nonlinear Schrödinger equation involving nonlinear dispersions and Kerr effect, Opt. Quant. Electron., 54 (2022), 177. https://doi.org/10.1007/s11082-022-03522-0 doi: 10.1007/s11082-022-03522-0
[15]	L. Akinyemi, E. Morazara, Integrability, multi-solitons, breathers, lumps and wave interactions for generalized extended Kadomtsev-Petviashvili equation, Nonlinear Dyn., 111 (2023), 4683–4707. https://doi.org/10.1007/s11071-022-08087-x doi: 10.1007/s11071-022-08087-x
[16]	A. Houwe, S. Abbagari, L. Akinyemi, H. Rezazadeh, S. Y. Doka, Peculiar optical solitons and modulated waves patterns in anti-cubic nonlinear media with cubic-quintic nonlinearity, Opt. Quant. Electron., 55 (2023), 719. https://doi.org/10.1007/s11082-023-04950-2 doi: 10.1007/s11082-023-04950-2
[17]	D. Ntiamoah, W. Ofori-Atta, L. Akinyemi, The higher-order modified Korteweg-de Vries equation: Its soliton, breather and approximate solutions, J. Ocean Eng. Sci., (2022). https://doi.org/10.1016/j.joes.2022.06.042 doi: 10.1016/j.joes.2022.06.042
[18]	H. F. Ismael, H. Bulut, C. Park, M. S. Osman, M-lump, N-soliton solutions, and the collision phenomena for the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation, Results Phys., 19 (2020), 103329. https://doi.org/10.1016/j.rinp.2020.103329 doi: 10.1016/j.rinp.2020.103329
[19]	S. Kumar, M. Niwas, M. S. Osman, M. A. Abdou, Abundant different types of exact soliton solution to the (4+1)-dimensional Fokas and (2+1)-dimensional breaking soliton equations, Commun. Theor. Phys., 73 (2021), 105007. https://dx.doi.org/10.1088/1572-9494/ac11ee doi: 10.1088/1572-9494/ac11ee
[20]	R. Ur-Rahman, M. M. M. Qousini, A. Alshehri, S. M. Eldin, K. El-Rashidy, M. S. Osman, Evaluation of the performance of fractional evolution equations based on fractional operators and sensitivity assessment, Results Phys., 49 (2023), 106537. https://doi.org/10.1016/j.rinp.2023.106537 doi: 10.1016/j.rinp.2023.106537
[21]	K. K. Ali, M. A. A. E. Salam, E. M. H. Mohamed, B. Samet, S. Kumar, M. S. Osman, Numerical solution for generalized nonlinear fractional integro-differential equations with linear functional arguments using Chebyshev series, Adv. Differ. Equations, 494 (2020), 2020. https://doi.org/10.1186/s13662-020-02951-z doi: 10.1186/s13662-020-02951-z
[22]	M. A. Chowdhury, M. M. Miah, M. A. Iqbal, H. M. Alshehri, D. Baleanu, M. S. Osman, Advanced exact solutions to the nano-ionic currents equation through MTs and the soliton equation containing the RLC transmission line, Eur. Phys. J. Plus Vol., 138 (2023), 502. https://doi.org/10.1140/epjp/s13360-023-04105-y doi: 10.1140/epjp/s13360-023-04105-y
[23]	M. M. Miah, M. A. Iqbal, M. S. Osman, A study on stochastic longitudinal wave equation in a magneto-electro-elastic annular bar to find the analytical solutions tension, Commun. Theor. Phys., 75 (2023), 085008. https://dx.doi.org/10.1088/1572-9494/ace155 doi: 10.1088/1572-9494/ace155
[24]	W. Ma, Generalized bilinear differential equations, Stud. Nonlinear Sci., 2 (2011), 140–144. https://api.semanticscholar.org/CorpusID:6958538
[25]	W. Ma, Bilinear equations, Bell polynomials and linear superposition principle, J. Phys. Conf. Ser., 411 (2013), 012021. https://doi.org/10.1088/1742-6596/411/1/012021 doi: 10.1088/1742-6596/411/1/012021
[26]	K. Shi, B. Ren, Dynamics of mixed lump-soliton solutions to the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli like equation, Partial Differ. Equations Appl. Math., 5 (2022), 100276. https://doi.org/10.1016/j.padiff.2022.100276 doi: 10.1016/j.padiff.2022.100276
[27]	S. Batwa, W. Ma, A study of lump-type and interaction solutions to a (3+1)-dimensional Jimbo-Miwa-like equation, Comput. Math. Appl., 76 (2018), 1576–1582. https://doi.org/10.1016/j.camwa.2018.07.008 doi: 10.1016/j.camwa.2018.07.008
[28]	Y. Sun, W. Ma, J. Yu, C. M. Khalique, Dynamics of lump solitary wave of Kadomtsev-Petviashvili-Boussinesq-like equation, Comput. Math. Appl., 78 (2019), 840–847. https://doi.org/10.1016/j.camwa.2019.03.001 doi: 10.1016/j.camwa.2019.03.001
[29]	T. Jia, Y. Chai, H. Hao, Multi-soliton solutions and Breathers for the generalized coupled nonlinear Hirota equations via the Hirota method, Superlattices Microstruct., 105 (2017), 172–182. https://doi.org/10.1016/j.spmi.2016.10.091 doi: 10.1016/j.spmi.2016.10.091
[30]	M. Dong, S. Tian, X. Yan, L. Zou, Solitary waves, homoclinic breather waves and rogue waves of the (3+1)-dimensional Hirota bilinear equation, Comput. Math. Appl., 75 (2018), 957–964. https://doi.org/10.1016/j.camwa.2017.10.037 doi: 10.1016/j.camwa.2017.10.037
[31]	S. Chen, Z. Yan, The Hirota equation: Darboux transform of the Riemann-Hilbert problem and higher-order rogue waves, Appl. Math. Lett., 95 (2019), 65–71. https://doi.org/10.1016/j.aml.2019.03.020 doi: 10.1016/j.aml.2019.03.020

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematical Biosciences and Engineering

3.9

Metrics

Article views(1267) PDF downloads(75) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Mathematical Biosciences and Engineering

High-order rational-type solutions of the analogous (3+1)-dimensional Hirota-bilinear-like equation

Related Papers:

Abstract

1. Introduction

2. The (3+1)-dimensional HBLE

3. Rational solutions of the (3+1)-dimensional HBLE

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. The (3+1)-dimensional HBLE

3. Rational solutions of the (3+1)-dimensional HBLE

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Mathematical Biosciences and Engineering

High-order rational-type solutions of the analogous (3+1)-dimensional Hirota-bilinear-like equation

Related Papers:

Abstract

1. Introduction

2. The (3+1)-dimensional HBLE

3. Rational solutions of the (3+1)-dimensional HBLE

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. The (3+1)-dimensional HBLE

3. Rational solutions of the (3+1)-dimensional HBLE

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References