Dynamics analysis of strangles with asymptomatic infected horses and long-term subclinical carriers

1.   Introduction

The equine industry has a long history across the world and horses have been successfully trained for more than 6000 years. Over the years, the horse industry has been modernized, and now consists of horse breeding, horse products and horse activities, such as horse racing and horseback riding ^[1]. This has led to a secondary industry and contributes a lot to economic and social development. However, the prevention and control of horse diseases is connected to severe economic loss, causing widespread concern.

Strangles is an acute infectious disease in horses and is caused by streptococcus equi (noted as S equi) ^[2]. Strangles is one of the most prevalent horse diseases, which was first described by Jordanus Ruffus in 1251 ^[3]. Typical symptoms of strangles include fever, nasopharyngeal mucosal inflammation, acute suppurative swelling and suppuration of mandibular lymph nodes and respiratory obstruction. Once healthy horses become infected, there will be an incubation period, lasting approximately one week. Following this, they may either be asymptomatic while carrying S equi or immediately present with symptoms, which varies from horse to horse ^[4]. Generally, clinical symptoms can be divided into three types:

$\bullet$ General strangles: Horses exhibit mild signs, such as nasal discharge, small abscesses and rapid resolution of the disease. Infected horses with general strangles can self-cure with good care in about 1 week.

$\bullet$ Typical strangles: Horses present with a serious onset of symptoms, characterized by fever, acute catarrh in nasal mucosa and lymphadenopathy. Infected horses with typical strangles need immediate treatment and can recover within 2–3 weeks.

$\bullet$ Bastard strangles: This causes the worst symptoms and can even lead to further complications, such as throat capsulitis, purulent peritonitis and death. Hence, horses need long-term antimicrobial treatments and therapy. Most horses can recover if they are provided good veterinary care; for example, in the presence of purpura, the mortality of horses is only between 8 and 25% ^[5,6,7].

Strangles mostly occurs during cold periods, (i.e., from about September this year to March or April of next year) and sporadically during other periods. Each year, approximately 1000 outbreaks of strangles cases are recorded in the UK alone ^[8]. Strangles outbreaks of can be serious, which may involve up to hundreds of horses and lead to associated economic costs exceeding £300,000 ^[9]. In China, strangles is a disease found on "The list of three categories of epidemic animal diseases", which was formulated by the Agricultural Ministry of China ^[10].

Strangles can infect horses of all ages and spread by either direct or indirect contact ^[11]. Indirect contact mainly includes contact through infectious food, water, horse stables, troughs, and workers' clothes. It can be decreased or even eliminated by implementing stringent farm regulations and restricting activities, such as raising health awareness and improving environmental hygiene. Therefore, this paper only considers the direct contact between horses.

If infected horses exhibit symptoms, they will be isolated until they recover. The majority of the recovered may develop a resistance to strangles ^[12,13]; however, up to 10% of these horses can continue to shed S. equi intermittently and spread strangles, which instills the their classification as long-term subclinical S equi carriers ^{[14,15,16,17]}. These carriers present as asymptomatic but carrying infectious pathogens. Thus, they are regarded as one of the main reasons for a strangles outbreak. As for their diagnosis, instead of relying on clinical symptoms, an accurate diagnosis is based on laboratory-based detection methods, such as bacterial culture, Polymerase Chain Reaction (PCR) determination and serological tests (or Enzyme-linked Immunosorbent Assay test kits) ^[18]. Healthy horses on a horse farm always refer to those without an onset symptoms because the horse farm rarely obtains an official diagnosis based on laboratory tests, thereby only focusing on clinical symptoms. Hence, identifying clinically healthy horses that carrying infectious S equi, which includes asymptomatic horses and long-term subclinical carriers, is essential for controlling strangles.

Currently, vaccination and implementing regular screening are the two main measures for the prevention and control of strangles. One-time vaccination of horses can reduce the number of susceptible horses at the initial moment. Hence, this paper considers the screening procedures conducted on healthy horses and further studies the effect of the screening intensity on strangles epidemics.

Genuinely, mathematical models have been an effective tool to solve the problem of disease spreading ^[19]. The compartmental model can study the occurrence and development of infectious diseases and further guide the prevention, control and elimination. There are numerous works aimed at understanding the influence of asymptomatic infected individuals among the human population, such as individuals infected with COVID-19, influenza, ebola, dengue and malaria ^{[20,21,22,23,24,25]}. Meanwhile, there are also numerous works aimed at understanding diseases among animals such as scrapie, swine fever, and brucellosis ^{[26,27,28,29]}. These works stressed the strong influence of these asymptomatic individuals the spread and outbreak of diseases. Similarly, this result is also applicable in strangles. However, the transmission of strangles was mainly investigated from a data and statistical perspective and rarely mathematically ^[30]. Therefore, based on the existence of asymptomatic infected horses and long-term subclinical carriers, we construct a mathematical model to investigate the transmission and control of strangles.

The organization of this paper is as follows. Section 2 formulates an extended compartmental model and computes its basic reproduction number. Through Lyapunov functions, section 3 studies the stability of a disease-free equilibrium and an endemic equilibrium. Furthermore, based on a real stud farm outbreak in England in 2012, section 4 highlights a parameter estimation and sensitivity analysis. Finally Section 5 summarizes the paper with a discussion and the conclusion.

2.   Mathematical model formulation

This section constructs a strangles model that describes the transmission process with population dynamics and screening procedures at a real stud farm.

2.1.   Model formulation

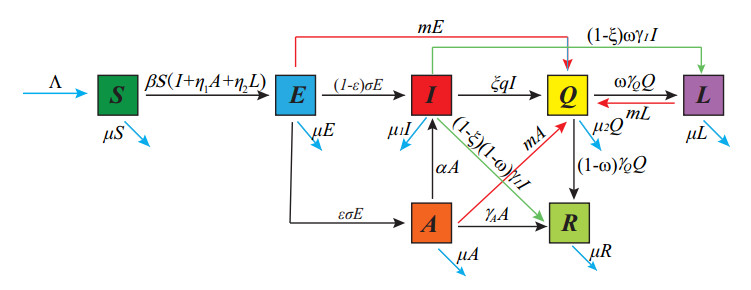
Herein, according to the different statuses of strangles, we classify the whole horses into 7 categories: susceptible horses $(S)$, exposed horses $(E)$, symptomatic infected horses $(I)$, asymptomatic infected horses $(A)$, quarantined horses $(Q)$, long-term subclinical carriers $(L)$ and recovered horses without S equi $(R)$. The compartments $I, A$ and $L$ are all infectious and can spread disease; however, the later two compartments have a decreased transmission rate compared with $I$ for a decreased load of S equi.

The transmission process is as follows. When $S$ becomes infected, it transfers into $E$. After the incubation period, $E$ comes into a period of illness. Then, having no symptoms, it transfers into $A$; otherwise, it transfers into $I$. $A$ can recover to $R$ by self-healing or display clinical signs of $I$ before it recovers. $I$ will be immediately isolated, which is much quicker than it recovers. Thus, we assume a higher proportion $\xi$ of $I$ entering into $Q$ than it recovers to either $R$ or $L$. If $Q$ recovers, a proportion of $\omega$ continues to carry the infectious pathogen, $L$, and the other is truly recovered, $R$. We assume $R$ has permanent immunity and cannot be infected again.

Moreover, the horse population dynamics are considered, containing either newly born or bought horses, the sale of horses and death due to illness. We take a constant input rate and assume that all new inputs are susceptible. The rate of horse sales is proportional to the number of horses and the sale of horses is only conducted on clinically healthy horses (i.e., S, E, A, L and R). $I$ and $Q$ may be dead due of illness. Meanwhile, the force of screening measures implemented on those clinically healthy horses are the same; therefore, compartments $E, A$ and $L$ have the same flow rate coefficient to $Q$. Thus, we extend the classical Susceptible-Infected-Recovered (SIR) model to a Susceptible-Exposed-Infected-Asymptomatic-Quarantined-Longterm subclinical carrier-Recovered (SEIAQLR) model. The transmission flow chart is displayed in Figure 1.

Correspondingly, the SEIAQLR model can be described by the following ordinary differential equations:

where $\beta$ represents the efficient contact rate when $I$ contacts and transmits strangles to $S$. Compared with I, $\eta_1$ and $\eta_2$ display the relative transmission ability of $A$ and $L$. Their values are between [0, 1]. $\Lambda$ is constant input rate, while $\mu$ is the sales coefficient of clinically healthy horses. $\mu_1$ and $\mu_2$ are the death rates of $I$ and $Q$, respectively. $1/\sigma$ is the mean incubation period, $1/\gamma_Q$ is the mean period of isolation and $1/\gamma_A$ is the mean course of horses that presented as asymptomatic. $\varepsilon$ is the ratio of asymptomatic infected horses to all infected horses. $\omega$ is the proportion of long-term subclinical carriers among all recovered horses. $\xi$ is the proportion of isolated symptomatic horses among all symptomatic horses. $\alpha$ is the rate of asymptomatic horses displaying clinical signs. $q$ represents the rate of isolation. $m$ is the rate of detection and isolation of clinically healthy horses with the infectious pathogen, which represents the strength of the horse screening. All the parameters in system (2.1) are nonnegative constants.

2.2.   Positivity and boundedness of solution

For system (2.1), we need to verify if its solutions are positive and bounded, which guarantees the well-posedness of this model, both mathematically and epidemiologically.

Lemma 1. For any nonnegative initial value $\left\{ S(0), E(0), I(0), A(0), Q(0), L(0), R(0) \right\} \geq 0$, the solution of system (2.1) is unique, nonnegative and bounded for all t $\geq$ 0. Meanwhile,

is the positively invariant set of system (2.1), where $\tilde{\mu} = \min \{ \mu, \mu_1, \mu_2\}$.

Proof. Applying the constant variation method to solve the first equation of system (2.1), we drive that

where $\lambda(t) = \beta \left [ I(t)+\eta_1 A(t) + \eta_2 L(t) \right ].$ Hence, if $S(0)\geq0$, then $S(t)\geq0$ for $\forall t \geq 0$.

Then, we prove the nonnegativity of $E(t), I(t), A(t), Q(t), L(t)$ and $R(t)$ for $\forall t\geq0$. Denote

Let

Without a loss of generality, we might take $E(T_0) = 0$. Considering the second equation of system (2.1) at time $T_0$,

Hence, $E(t)$ is nonnegative. Similarly $I(t), A(t), Q(t), L(t)$ and $R(t)$ have the same property. Therefore, the solution of system (2.1) is nonnegative for $\forall t\geq 0$.

Let

Summing the equations of system (2.1), we obtain the following:

leading to $N(t) \rightarrow \frac{\Lambda}{{\tilde{\mu}}}$ as $t\rightarrow +\infty.$ Thus, the solution of system (2.1) is bounded and $\Omega$ is the positively invariant set of system (2.1).

If no epidemic occurs, all compartments with infectious horses are 0 and all horses are susceptible. Therefore, in this case, $\frac{\text{d} N(t)}{d t} = \Lambda-\mu N$ and $N \rightarrow \frac{\Lambda}{\mu}$, as $t\rightarrow +\infty.$ □

2.3.   The basic reproduction number

Clearly, system (2.1) always have a disease-free equilibrium $\mathcal {E} ^0\left(\frac{\Lambda}{\mu}, 0, 0, 0, 0, 0, 0 \right).$ We use the next-generation matrix method to compute the basic reproduction number^[31].

Denote $X = (E, I, A, Q, L, S, R)^\text{T}$, where $\text{T}$ denotes transposition. Then, system (2.1) is equivalent to $\dot{X} = \mathcal{F}(X)-\mathcal{V}(X),$ where

According to method in ^[31], we need to check the hypotheses A(1)–A(5). The first four hypotheses are easily verified. As for A(5), it is necessary that all eigenvalues of $DX(x)$ have negative real parts, where $x$ satisfies $\mathcal{F}(x) = 0$. Actually,

where $b_1 = \sigma+m+\mu$, $b_2 = \xi q+(1-\xi)\gamma_I+\mu_1$, $b_3 = \alpha + \mu + \gamma_A +m$.

Obviously, matrix (2.2) has five negative real eigenvalues: $\lambda_1 = -b_1 < 0$, $\lambda_2 = -b_2 < 0$, $\lambda_3 = -b_3 < 0$, $\lambda_4 = \lambda_5 = -\mu < 0,$ and the other two eigenvalues of matrix (2.2) are determined by the following $2\times2$ matrix,

Based on tr$(J) = -(\gamma_Q+\mu_2+m+\mu) < 0$ and $\det(J) = \left (m(1-\omega)+\mu \right) \gamma_Q+\mu_2(m+\mu) > 0$, the two eigenvalues are all negative, which means that $\lambda_6 < 0$ and $\lambda_7 < 0.$ Hence, A(5) is satisfied.

Hereafter, by calculation, we obtain the Jacobian matrix of $\mathcal{F}$ and $\mathcal{V}$ at $\mathcal{E}^0$ as follows:

where,

Then, we have

and

where

$k_1 = (1-\varepsilon)+\frac{\varepsilon\alpha}{(\alpha+\mu+\gamma_A+m)}$, $k_2 = \left(\xi q \frac{ \gamma_Q}{\gamma_Q+\mu_2}+(1-\xi)\gamma_I \right) \frac{\sigma k_1}{\xi q+(1-\xi)\gamma_I +\mu_1}$ $+ \frac{m\gamma_Q}{\gamma_Q+\mu_2}\left(1+\frac{\varepsilon\sigma}{(\alpha+\mu+\gamma_A+m)}\right)$. $b_1, b_2, b_3$ are defined as before. $b_4 = \gamma_Q+\mu_2,$ $b_5 = (m+ \mu)b_4-m\omega \gamma_Q,$ $b_6 = \xi q+(1-\xi)\omega\gamma_I,$ $b_7 = \xi q \gamma_Q+(1-\xi)b_4\gamma_I,$ $s_0 = b_2(\varepsilon\sigma+b_3)m^2+[(1-\varepsilon) b_3 b_6+\varepsilon(\alpha b_6+b_2 \mu)]m +b_3 k_1 \xi \sigma \mu q$.

Therefore, $\rho(FV^{-1}) = \mathcal{R}_0$. Applying Theorem 2 in ^[31], we can derive that $\mathcal{R}_0$ is the basic reproduction number of system (2.1). Recall that the basic reproduction number describes the average number of secondary infected individuals produced by a single infectious individual during its course of disease among completely susceptible individuals. The factor $\frac{1}{\mu}\times\frac{1}{(\mu+\sigma+m)}$ denotes the mean period that one newly input susceptible horse staying at $S$ multiplies to that of $E$. The first term in brackets depicts the transmission caused by $I$ horses through two ways: one is when $E$ directly removes to $I$ and the other one is when $E$ first transfers to $A$ and then to $I$. Similarly, the second term is the transmission caused by $A$ and the third term means that of $L$. Therefore, $\mathcal{R}_0$ is the basic reproduction number of system (2.1) because of its biological interpretability.

2.4.   The existence of endemic equilibrium

Suppose system (2.1) has an endemic equilibrium $\mathcal {E}^* (S^*, E^*, I^*, A^*, Q^*,$ $L^*,$ $R^*) \in \Omega$, where it must satisfy the following system:

From the first equation, we have the following:

Adding the first two equations, we obtain the following:

From the forth equation,

Substitue it into the third equation,

Combing with the fifth and sixth equations, we derive the following:

Therefore,

From the last equation,

Considering the second equation of system (2.4),

If $\mathcal{R}_0 > 1$, then $E^* > 0$ and the other states are all positive. Therefore, the endemic equilibrium $\mathcal {E}^*$ of system (2.1) uniquely exists if $\mathcal{R}_0 > 1$.

3.   Stability analysis

In this section, we study the global stability of the two equilibria by constructing Lyapunov functions ^[32,33].

Theorem 1. The disease-free equilibrium $\mathcal{E}^0$ is globally and asymptotically stable if $\mathcal{R}_0 < 1$, while it is unstable if $\mathcal{R}_0 > 1$.

Proof. Applying Theorem 2 in ^[31], we derive that $\mathcal{E}^0$ is locally asymptotically stable if $\mathcal{R}_0 < 1$ and it is unstable if $\mathcal{R}_0 > 1$. Hereafter, we study the global stability of $\mathcal{E}^0$ using the matrix-theoretic method in ^[32].

Note that $V^{-1}F$ is reducible (because the first column is a total zero column); therefore, the Perron-Frobenius Theorem is not applicable here ^[34]. For simplify, let $c_1 = (\alpha b_7+m b_2 \gamma_Q)\omega /b_2 b_3 b_5,$ $c_2 = \sigma k_1/ b_1 b_2$, $c_3 = \varepsilon \sigma/ b_1 b_3,$ $c_4 = s_0/ b_1 b_2 b_3 b_5,$ $c_5 = \omega k_2 b_4/ b_1 b_5$, the first column of $V^{-1}$ is $(1/b_1, c_2, c_3, c_4, c_5)^\text{T}$. By calculation we have the following:

$\mathcal{R}_0 = \beta \frac{\Lambda}{\mu} (c_2 + \eta_1 c_3 + \eta_2 c_5)$ is the maximum eigenvalue of matrices $V^{-1}F$ and $FV^{-1}$. Therefore, we can solve the left eigenvector $\xi$ corresponding to $R_0$ of matrix $V^{-1}F$, where $\xi$ satisfies,

which implies $\xi = (0, 1, \eta_1, 0, \eta_2).$

$Y = (E, A, I, Q, L)^\text{T}$ denotes all infectious compartments, then

where $f(Y, S) = \beta \left(\frac{\Lambda}{\mu}-S\right) (I+\eta_1 A+ \eta_2 L).$ Obviously, $f(Y, S)\geq 0, F\geq0, V^{-1}\geq0$ and $\mathcal{R}_0\leq1$ in $\Omega$. Based on Theorem 2 in ^[32], we can construct the Lyapunov function $\Phi$ as follows:

By a simple calculation,

Compute the derivation of $\Phi$ along system (2.1) under Eq (3.1),

It is easily seen that $\frac{\text{d}\Phi}{dt} {\text{|}}_{(2.1)} \leq 0$ provided $\mathcal{R}_0\leq1$ in $\Omega$.

Furthermore, $\frac{d\Phi}{dt} = 0$ implies that $I = 0, A = 0, L = 0$ or $S = \frac{\Lambda}{\mu}$. It can be shown that the only invariant set where $I = 0, A = 0, L = 0$ or $S = \frac{\Lambda}{\mu}$ is the singleton $\{ \mathcal{E}^0 \}.$ Hence, using LaSalle's invariance principle ^[33], the disease-free equilibrium $\mathcal{E}^0$ is globally and asymptotically stable, which demonstrates that if $\mathcal{R}_0 < 1$, strangles will eventually die out no matter how many asymptomatic, symptomatic infected horses or long-term subclinical carriers horses there are at the initial time. □

Theorem 2. The endemic equilibrium $\mathcal{E}^*$ uniquely exists and is globally asymptotically stable in $\Omega$ if $\mathcal{R}_0 > 1$.

Proof. From Section 2.4, we derive that system (2.1) has a unique endemic equilibrium $\mathcal{E}^*$ if $\mathcal{R}_0 > 1$. Hereafter, we only need to prove the global asymptotic stability of $\mathcal{E}^*$. To this end, we define a Lyapunov function as follows:

where

Because $\mathcal{E}^*$ satisfies system (2.4), we have the following:

In order to complete the proof, we need the following two propositions.

Proposition 1.

Proposition 2.

From the Proposition 1, we derive that $\mathcal{L} \geq 0$, and the equality holds if and only if $(S, E, I, A, Q, L) = (S^*, E^*, I^*, A^*, Q^*, L^*)$. Next, we need to verify $\frac{d\mathcal{L}}{dt}\leq0$ along the positive solution of system (2.1).

Combing with Eq (3.4) and taking the derivation of $\mathcal{L}$, we have the following:

where,

Applying Proposition 2, we derive the following:

Sum both sides and arrange the same items as follows:

Moreover, $\frac{\text{d}\mathcal{L}} {dt} = 0$ holds when $(S, E, I, A, Q, L) = (S^*, E^*, I^*, A^*, Q^*, L^*)$ and the endemic equilibrium $\mathcal{E^*}$ is the only invariant set of system (2.1) in int$(\Omega)$. Therefore, by the Lasalle's invariance principle ^[33], $\mathcal{E^*}$ is globally asymptotically stable in $\Omega$ when $\mathcal{R}_0 > 1$. □

As for the bifurcation study, we further conclude that there exists a Transcritical Bifurcation of system (2.1) under $\mathcal{R}_0 = 1$. Basically, this kind of bifurcation analysis can be conducted by using the universal method in ^[35]. However, our model is a high-dimension system and is too complicated for computing. By means of the numerical simulation, the Transcritical Bifurcation occurs in system (2.1) under $\mathcal{R}_0 = 1$, which is displayed in Figure 2.

4.   Case study on a real standard bred farm

4.1.   Parameter estimation

There are numerous works on the outbreak of strangles ^{[36,37,38,39]}. Here, for example, we take a standardbred breeding farm a capacity of 1,400 horses on average. The reference ^[36] recorded a weekly strangles epidemic at the clinical and pathogenic level (i.e., symptomatic cases and asymptomatic cases). This paper considers the outbreak during the period from April, 30 2012, to December, 09 2012, including 48 clinically infected horses (with an approximate morbidity of 3.43%), and takes one week as the unit time. The weekly incidence data is displayed in Table 1.

The strangles outbreak is a natural evolution process without implementing a screen procedure (i.e., $m = 0$). The parameters that need to be estimated are the transmission rate $I, A,$ and $L$ infects $S$. The other epidemiology parameters of strangles are given by the actual outbreak data. Because the floating size of this farm is 300 horses, we roughly assume that the input number for each week is 9 for $300/32 = 9.375$ and $\mu = 9/1400$. As for $q$, we assume the frequency of isolation of symptomatic infected horse is once daily because of the daily feeding, therefore $q = 7$. Meanwhile, this farm permits that all symptomatic horses are isolated, which means $\xi = 100%$. Based on theses values, we use the Least Square Method (LSM) for the parameter estimation by minimizing the error of cumulative symptomatic infected horses outputted from the model (noted as C) and the real incidence data.

Let $(S(t_0), E(t_0), I(t_0), A(t_0), Q(t_0), L(t_0), R(t_0)) = (1385, 8, 2, 1, 0, 4, 0)$, where the real data used for data fitting is starts from $C(t_0) = 2$ and ends at $C(t_0+31) = 49$. By LSM simulation, we obtain the optimal parameters shown in Table 2 and the fitting plot displayed in Figure 3, which demonstrates that the model matches perfectly with the real outbreak event. The result means that the transmission rate between the susceptible and asymptomatic horses is $16.436%$, while that of long-term subclinical carriers is $4.831 \times 10^{-4}$. It confirms that asymptomatic horses plays a more hazardous role in strangles transmission and can clarify why these horses are the main reasons for losing strangles control.

Under this set of parameters, we can depict the prevalence curve of each state, which is shown in Figure 4. It demonstrates that $S$ first decreases and then increases, while the curve of $R$ is the inverse of S. They are both mainly caused by the infection at first and then later by the constant input. $E, I$ and $A$ directly cut down from their initial values to a very low level, nearly close to 0. $Q$ reaches to the peak with a value of nearly 9, followed by a decrease to about 0, which is just corresponding to a single strangles outbreak. $L$ is regarded as an absorption state that displays the nondecreasing trend and finally stay at about 6.5 accounting for 0.46% among the whole horses.

These results illustrate that strangles experienced an outbreak and eventually died out. Actually, from the perspective of $\mathcal{R}_0$, we can compute $\mathcal{R}_0 = 0.8416 < 1$. This mathematically assures the strangles will finally die out and can not form an endemic, even with the different initial state of infection. However, the number of cumulative cases (i.e., the final size) shows absolutely different initial values. Their relationship is displayed in Figure 5. The left figure shows that the final size will augment when the initial value increases. Compared with the others, the curves with different $L(0)$ differ a little because they seem the same at first, and followed by increased differences, which means the influence of $L(0)$ only displays after a long period. This means that the long-term carriers can be regarded as a source of infection for the next outbreak. The right figure shows the increasing rate of the final size with respect to initial value. It is extremely obvious that $E$ is the most influential, followed by $I, A$ and $L$. Therefore, besides the symptomatic infected horses, identifying these infected horses without any clinical signs is also vital for strangles control, both at the present and in the future.

4.2.   Sensitivity analysis

It is well known that the basic reproduction number $\mathcal{R}_0$ is a fundamental index to depict the epidemic and the final steady states of the disease. $\mathcal{R}_0 < 1$ means that the disease will eventually die out and can determine the final size, peak value, peak time, and prevalence span. $\mathcal{R}_0 > 1$ corresponds to an endemic and is also associated with the value of an endemic equilibrium. In this section, as an example, we take $\mathcal{R}_0$ and the final size and further adopt the sensitivity analysis to ascertain the influence of each model parameter on them.

Here, we use an Elasticity Index to quantity how these model parameters locally influence $\mathcal{R}_0$. We define

where $p_i (i = 1, 2, \cdots, 12)$ are the parameters in Table 2. From Eq (2.3), $\mathcal{R}_0$ is an explicit function of all related parameters and $\Upsilon_{p_i}^{\mathcal{R}_0}$ is an analytic expression that can provide some insights on how to cut down $\mathcal{R}_0$ and control strangles. Meanwhile, considering that $m = 0$, we just directly apply the derivation of $\mathcal{R}_0$ with $m$ to show the sensitivity. By a simple calculation and taking the values of parameters from Table 2, we compute their Elasticity Indices, which are summarized in the left of Figure 6. At the same time, we use a Partial Rank Correlation Coefficient (PRCC) analysis to assess how these parameters globally influence the final size. The result is shown in the right of Figure 6.

Figure (6) shows that increasing $\beta, \eta_1, \eta_2$ and $\varepsilon$ are beneficial for promoting a strangles outbreak, regardless of either the aspects of $\mathcal{R}_0$ or the final size. It mainly attributes to the increased enforced disease transmission rate. On the contrary, increasing $\xi, \gamma_A$ and $q$ suppress the strangles spread by reducing the number of infectious horses through either recovering or being isolated. Meanwhile, a bigger $\Lambda$ and a smaller $\mu$ can accelerate strangles, which is interpreted as the less susceptible horses caused by an increased input and a decreased removal of the susceptible horses. It's worth nothing that an increased $\omega$ is good for improving $\mathcal{R}_0$, whereas it has no significance in the final size. An increased $\omega$ signifies a larger proportion of long-term subclinical carriers among all recovered horses. Combing with their infectivity, the whole transmission ability enhances and $\mathcal{R}_0$ increases accordingly. In terms of the final size, the period we simulate is just one outbreak and $L$ rarely has an effect within the short time; therefore, $\omega$ almost has no effect on the final size of this outbreak scene.

Herein, we consider an special scenario that $\xi = 1$, which indicates that once the infected horses displays clinical signs, we isolate them unexceptionally. However, there are many farms either taking no isolation measures or just selectively isolating those infected horses presenting with a serious illness. Let $\xi$ be the ratio of severe illnesses to all symptomatic horses and satisfy the uniform distribution from [0, 1]. At this time, the value of $\xi$ and the period of course $1/\gamma_I$ play an essential role in strangles epidemics. Similarly, we study the impact of $\xi$ and $1/\gamma_I$ on $\mathcal{R}_0$ and the final size. Basically, with the parameters determined above, we can get the following:

It is a negative function with respect to $\xi$ and $\gamma_I$, respectively, demonstrating that with a decreased isolation ratio and longer infection time, $\mathcal{R}_0$ will be larger and cause more severe strangles outbreaks. The final size shows the similar result that is displayed in Figure 7.

If there is no isolation measure for all symptomatic horses, there will be nearly 2,000 infected horses; alternatively, there is less than 50 infected horses with 100% isolated proportion of symptomatic horses. That means that the isolation proportion of symptomatic horses shows a great ability in controlling strangles.

4.3.   Control measures

Generally vaccinations and regular screening procedures are mainly used to control strangles. Vaccinations can help horses produce antibody immunity and prevent them from becoming infected. Mathematically, this leads to a reduction in the number of initial susceptible horses. Here, we take $p$ as the percentage of horses receiving vaccinations, so the number of whole susceptible horses is $(1-p)S(t_0)$. As for the screening procedure, it can help us find those clinically healthy horses with infectious pathogen by laboratory detection and isolate them, which makes $E, A$ and $L$ move to $Q$ at rate $m$. Besides, there is a natural isolation rate $q$ that permits $I$ transfers to $Q$, where $q$ can quantify the management capability of a horse yard. Thus, in this section, we consider three kinds of measurements, including vaccination, screening and isolation, to control the strangles outbreak in this section. Specially, we study the influence of $p$, $m$ and $q$ on the final size, either singely or in pairs.

Taking the fitted parameters as the baseline, $S(t_0) = 1385, m = 0$ and $q = 7$. Let $r$ be the enhanced ratio, then

Scaling $r$ from $0$ to $0.9$, we derive the final size curve with respect to these three parameters, the results of which are displayed in Figure 8. The figure in the upper left corner shows the adoption of three control measures, with a single final size being conducive to restrain strangles. With an increase for $p, m$ and $q$, the final size demonstrates a decreasing trend and finally tends to a stable value. Moreover, screening clinically healthy horses has a more effective effect on decreasing the final size compared to the other two measures, although vaccination can achieve the same result under a very high percentage. In fact, the essence of them are different. Screening procedures are aimed at finding and decreasing those potential sources of infection, whereas vaccination is protecting those susceptible horses that are potentially infected. In this case, decreasing infectious horses exhibits a stronger superiority in strangles control. Additionally, the isolation of symptomatic horses is beneficial for strangles control because it can reduce the number of infected horses. However, this measure can not cover those asymptomatic horses and long-term subclinical carriers, which leads to a limited efficiency of suppressing strangles and is weaker than the other two measures.

The other three figures show the effect of a combined action among two of the three measures, respectively. The results show that they all have different modes of action and the contour line of each figure are obviously distinguished. However, the different combinations of the three measures can obtain the same value of the final size, even with different values, which demonstrates that there are lots of choices for farmer managers to choose for strangles control.

Additionally, we consider the expression of the basic reproduction number $\mathcal{R}_0$ associated with $m$ and $q$. Based on the parameter values of the parameters in Table 2, $\mathcal{R}_0$ has the following form:

Similarly, we study the influence of a single parameter on $\mathcal{R}_0$ by taking the other parameter as a constant, such as varying $m$ in $[0, 0.9]$ by keeping $q = 7$ and varying $q$ in $[4, 7.6]$ by keeping $m = 0$. The results are displayed in Figure 9. The left of Figure 9 demonstrates the same decreasing trend of $\mathcal{R}_0$ versus with $m$ and $q$. At this farm, it corresponds to the red star that $q = 7$ and $\mathcal{R}_0 = 0.8416$, which means that the epidemic of strangles of this farm is just an outbreak and mainly attributes to the larger $q$. In order to ensure $\mathcal{R}_0 < 1$, $q$ is not less than 5.72 (i.e., the isolation measure must be conducted within at least $1.2238$ day); otherwise, there will be an endemic. From the right of Figure 9, it is easily seen that a larger $q$ and $m$ leads to a smaller $\mathcal{R}_0$. Similarly, there are lots of selections of $(q, m)$ pairs to keep $\mathcal{R}_0 < 1$. For example, if $q = 4.74, m = 0.42$, then $\mathcal{R}_0 = 0.799$, which can still ensure that there is no strangles endemic in this farm.

4.4.   Extended scenarios

Here, based on the fitted parameters of the real farm from Table 2, we consider some extended scenarios.

Case 1: Considering horse farms of different sizes, how will strangles evolve and develop? To this end, based on eight levels of horse farms that started at the same density of each state, we focus on the prevalence of density of symptomatic horses and investigate the final size curve when $\mathcal{R}_0 < 1$ and epidemic curve of $I$ when $\mathcal{R}_0 > 1$, respectively. The results are shown in Figure 10. It is obviously seen that when $\mathcal{R}_0 < 1$, no matter how large the horse farm is, the strangles experiences an outbreak, though the final size differs. As $N$ increases, the strangles spreads more faster, leading to more infected horses, and eventually leads to nearly 90% of horses infected. This means that the horse farm with a bigger size is more likely to cause more infected horses. When we amplify the value of $\beta$ ten times and lead to $\mathcal{R}_0 > 1$, the strangles case will be an endemic. The right of Figure 10 shows that the bigger size the horse farm is, the quicker and higher peak value of density of $I$ has and the smaller value of steady density of $I$ has. This depicts that the smaller horse farm is more likely to cause more severe strangles endemics.

Case 2: Studying the efficiency of isolation measure, what will happen if there is no isolation measure adopted? How the starting time and strength of conducting the isolation measurements influence the strangles spread? Therefore, we study the strangles development with and without isolation measurements under different values of $\xi$. Furthermore, we also derive the counter plot of the final size with respect to the strength and starting time of the isolation measurement when fixing $\xi$.

The results are displayed in Figure 11. The left graph shows that the isolation measurement outstandingly decreases the final size and the effect shows an increased significance with an increase of $\xi$. A bigger $\xi$ and $q = 0$ means that there are more symptomatic horses that need to be isolated, but not measurement, which causes more severe strangles outbreak. As for the starting time of adopting isolation measure, when the isolation rate is less than the recovery rate of $I$, noted as the white dashed line (i.e., $q < \gamma_I$), the value of $q$ has almost no effect on strangles control. When $q > \gamma_I$, it is easily seen that the quicker isolation rate $q$ and the earlier starting time $T$ are all beneficial for controlling strangles. Hence, we need ensure that the isolation rate is quicker than the recover rate and conduct an isolation measurement as early as possible.

Case 3: Considering the scenario of the strangles epidemic as an endemic by letting $\xi = 0.5$, $\beta = 0.409$, i.e. $\mathcal{R}_0 = 14.64 > 1$. We focus on the impact of the isolation rate $q$ and screening strength $m$ on the value of steady states, new incidence cases and the equivalence between these incidence cases, both numerically and theoretically. The results of numerical simulations are displayed in Figure 12.

The left two graphs show that both the basic reproduction number $\mathcal{R}_0$ and the value of the steady state $I$ have similar decreasing trends versus with the two parameters. The right two graphs are focused on the new incidence cases. All new incidence cases represent the number of newly real infected horses that enters into the incubation periods. It can not be observed directly. The new incidence of $I$ refers to the number of the new onset horses presented with clinical signs and can be observed and reported. The results demonstrate that all these incidences are sensitive with both $q$ and $m$.

Actually, for any pair of $(m_0, q_0)$, there must be $(0, \tilde{q})$ and $(\tilde{m}, 0)$ that can derive the same result of all new incidences and the incidence of $I$. The former is computed as follows:

and the later is

where the steady-state values $S^*, E^*, I^*, A^*$ and $L^*$ of $\mathcal{E}^*$ are the function of $m$ and $q$. Then, there must exist

and

From the perspective of simulation, the same contour line represents the same value and the point $(0, \tilde{q})$ and $(\tilde{m}, 0)$ are the intersection points with the coordinate axis $x$ and $y$, respectively.

5.   Discussions and conclusions

Based on the existence of asymptomatic horses and long-term subclinical S equi carriers among the infected horses with strangles, this paper established a SEIAQLR model with the screening procedure on clinically healthy horses. By applying a next-generation method, we derived the expression of the basic reproduction number $\mathcal{R}_0$. Furthermore, we constructed Lyapunov functions and concluded with the global asymptotical stability of a disease-free equilibrium and an epidemic equilibrium. Based on a real standard bred farm, we conducted a parameter estimation by adopting the cumulative number of symptomatic horses; then, we implemented a sensitivity analysis about these parameters on $\mathcal{R}_0$ and the final size through numerical simulations. These conclusions above are as follows:

$\spadesuit$ The basic reproduction number $\mathcal{R}_0 = 0.8416 < 1$, which mathematically assured that the strangles epidemic is an outbreak rather than an endemic;

$\spadesuit$ The relative transmission rate of asymptomatic horses was 16.436% and that of long-term subclinical carriers was 0.05% comparing with symptomatic horses. Both of them can promote the value of $\mathcal{R}_0$, which makes it increasingly difficult for strangles control if those horses are neglected;

$\spadesuit$ The existence of asymptomatic horses stimulated the strangles outbreak and increased the final size at this outbreak, while the long-term subclinical carriers were the main source of the next outbreak because they can sustain the infectious state for long time. This result is consistent with prior studies that these carriers can be a source of either new or recurrent disease in a well-managed groups of horses ^[40,41];

$\spadesuit$ Weakening the transmission rate, decreasing the number of infectious horses and reducing the input of susceptible horses can all suppress the strangles outbreak, which can be used to inhibit strangles spreading;

$\spadesuit$ Implementing the three control measures, including vaccinations, implementing screen procedures and isolating symptomatic horses, were all good for controlling strangles. Among them, screening seems the most effective strategy, followed by vaccination and isolation. Meanwhile, the different combinations can produce the same result of the final size, which provides the farmer management with more choices;

$\spadesuit$ Aimed at some possible scenarios, such as how the size of horse farm, the starting time, the strength of the isolation measurements and the interaction action of $q$ and $m$ influence strangles epidemics were studied. We believe that these results can provide some clues to strangles management.

There are still some limitations. As for a horse farm, the economic benefit is always the key factor to be considered. Hence, taking the cost of implementing control measures into consideration and then proposing an optimal control question can be studied in the future. Meanwhile, the period that we consider and simulate is just a strangles outbreak and neglects to consider the recurrence of strangles after a long period because of the existence of long-term subclinical carriers. Thus, modeling a long-time horse transmission process is also needed. As for the infected horses that presented with different degrees of illness, they may have various transmission abilities and recover rates. Therefore, the heterogeneity of transmission and recovery also needed to be noted. In a word, it is needed to construct a more precise model to describe strangles transmission and to provide a more intelligent combination of control measurements.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12231012, 91846302, 12101373, 61873154). Shanxi Key Laboratory (No. 201705D111006). Key R & D projects of Shanxi Province (No. 202003D31011/GZ). Health Commission of Shanxi Province (No. 2020XM18). Research of Technological Important Programs in the city of Lvliang, China (No. 2022GXYF18).

Conflict of interest

The authors declare there is no conflict of interest.