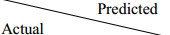Improved support vector machine classification for imbalanced medical datasets by novel hybrid sampling combining modified mega-trend-diffusion and bagging extreme learning machine model

1.   Introduction

The imbalanced data classification problem frequently occurs in medical applications, including diabetes classification ^[1,2], cancer diagnosis ^[3,4,5] and biomedical data classification ^[6,7,8,9]. An imbalanced medical dataset indicates that the number of negative examples such as healthy individuals drastically exceed the number of positive examples or patients with diseases. Researchers thus often place much effort towards learning patterns in those minority patients with cancer or other rare diseases. Under this circumstance, traditional machine learning and deep learning models are often distorted towards the majority class on prediction results. As a result, these models often exhibit lower classification performance for the minority class. Under this scenario, these learning models fail to provide credible prediction results for doctors to make correct treatment decisions according to a patient's conditions. Consequently, we note researchers have devoted significant efforts for developing effective methods to overcome the imbalanced dataset problem in academic and real-world applications.

To deal with imbalanced datasets, some researchers proposed sampling techniques for balancing class distributions to improve overall classification accuracy of learning models. These sampling approaches can be classified into three categories: 1) under-sampling method; 2) over-sampling method; and 3) hybrid sampling method.

The 1) under-sampling method aims at reducing learning bias towards the majority class by removing some negative examples. Babar and Ade ^[10], for example, proposed an under-sampling technique based on the multi-layer perceptron (MLP) model to identify valuable samples and eliminate noise in the majority class. In ^[10], they divided majority class examples into several clusters and filtered critical examples according to stochastic measure evaluation. To improve breast cancer prediction with imbalanced data, Zhang et al. ^[11], for example, proposed an under-sampling method which utilizes k-means algorithm to select representative examples close to original examples in the majority class. Vuttipittayamongkol and Elyan ^[12] suggested an overlap-based under-sampling method that utilizes k-nearest neighbor (KNN) algorithm to find dangerous minority class examples (i.e., positive examples) that are surrounded by most of the majority class examples (i.e., negative examples). They excluded these negative examples to enhance prediction for positive examples.

The 2) over-sampling method directly raises the quantity of examples in the minority class by creating synthetic samples. The synthetic minority oversampling technique (SMOTE) proposed by Chawla et al. ^[13] is the most representative technique among over-sampling methods. In ^[13], they create new minority class examples using a linear interpolation method. In addition, they use the KNN algorithm to select new examples belonging to the minority class. To avoid synthetic examples falling into the majority class area, Bunkhumpornpat et al. ^[14] proposed the safe-level-SMOTE method to generate safe positive examples close to original positive examples. To reduce false positive rates, Cieslak et al. ^[15] proposed a clustering-based SMOTE sampling method (cluster-SMOTE), which partitions the original dataset into several subsets and generates new minority class examples using SMOTE with these subsets. Other than generating examples within the safe minority class region, de la Calleja et al. ^[16] proposed the synthetic multi-minority oversampling (SMMO) method, which resamples misclassified positive examples as new instances to improve prediction accuracy of learning models for the minority class. Furthermore, Farquad and Bose ^[17] employed the support vector machines (SVM) model as a pre-processor (named the SVM-balance method) to resample misclassified data close to the raw minority class example as new samples for pushing the decision boundary toward the majority class.

The 3) hybrid sampling method is a combination of under-sampling and over-sampling methods. For instance, Wang ^[18] proposed a hybrid sampling SVM method which removes negative examples that are far from SVM's decision boundary and uses the SMOTE algorithm to create minority class examples with several training subsets. To improve SVM imbalanced classification on breast cancer diagnosis, Zhang and Chen ^[19] presented a hybrid of random over sampling example (ROSE), k-means and support vector machine (RK-SVM) methods, which consists of using ROSE to resample samples in the minority class and using k-means clustering method for keeping informative samples in the majority class.

As previously stated, the kernel-based over-sampling methods can effectively push SVM's decision boundary toward the majority class. However, when the margin on the hypersphere is very short, linearly interpolated examples using SMOTE may become dangerous new examples in the minority class, since they are very proximate to the area of the majority class. As a result, new examples of minority class may be regarded as noise or outliers that worsen classification accuracy of SVM for the minority class. Conversely, when the margin is wide, although safer examples of the minority class can be created, this softly shifts the SVM decision boundary toward the majority class. This may have tiny effects for improving SVM classification of skewed datasets. Overall, based on the above-mentioned problem, we note two challenging research questions (RQs), as follows:

RQ1: According to the above-mentioned studies, kernel-based SVM is prone to misclassifying minority class examples located near the decision boundary. To improve SVM classification for minority class examples, some studies aimed to generate kernel-based synthetic minority class examples to adjust SVM's decision boundary towards the region of majority class. We consulted the findings in ^[18] and ^[19], finding a hybrid sampling method can more effectively improve classification performances of SVM as compared to using a single under-sampling or over-sampling method. But which kind of hybrid sampling methods for creating synthetic examples of minority class and screening representative examples of majority class can further improve SVM imbalanced classification?

RQ2: The kernel-based oversampling methods aimed to create virtual samples of minority class nearby the SVM decision boundary. However, the generated virtual samples may be surrounded by most of the majority class examples. They are considered as danger minority class examples or noise, which distort learning of SVM. What kind of learning models can be used to monitor the similarity between synthetic examples and original data to screen acceptable minority class examples?

In order to address SVM imbalanced classification on RQ1 and RQ2, we develop a novel hybrid sampling method termed modified mega-trend-diffusion-extreme learning machines (MMTD-ELM) to adjust the SVM decision boundary to achieve improvement of SVM classification for imbalanced datasets. The major contributions of this paper are as follows:

a) To reduce bias of majority class examples for SVM models, based on a fuzzy triangular membership function (MF), we propose an under-sampling method using α-cut fuzzy number to screen representative SVs of majority class. The MF value of the example represents the possibility that the example belongs to the majority class. The higher MF value indicates that the example has more representations for constructing the SVM decision boundary of the majority class. When the example has a higher value, it indicates a higher effect in predicting majority class.

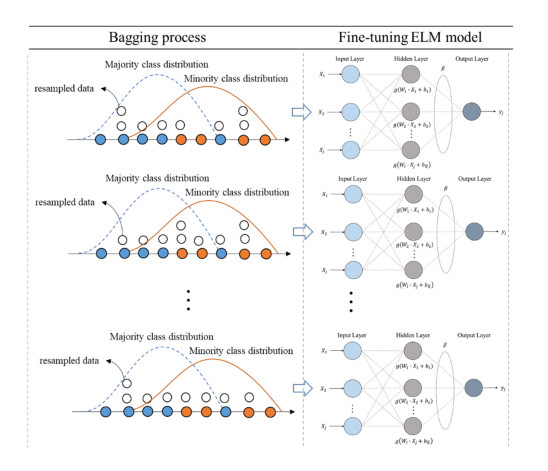
b) To avoid generated new examples falling into the area of majority class, we proposed a modified MTD method, in which, MTD as proposed by Li et al. ^[20], is deployed to estimate the data range of support vectors of the minority class and generate the virtual data's inputs within the estimated data range. To predict labels corresponding to the virtual data's inputs, we construct a bagging-based extreme learning machine (ELM) model. In this paper, we feed the ELM using different datasets resampled from an original dataset. The bagging method, proposed by Breiman ^[21], can enable the ELM model to capture diverse patterns between inputs and output. With a bagging strategy, the prediction accuracy of the ELM model can be improved at identifying the virtual data's output.

c) Some studies about hybrid sampling methods ^[18,19] measured distance of majority class examples from each other and removed unrepresentative examples that were far from the SVM's decision boundary. However, the distance-based sampling method is easily impacted by noise or outliers. Differing from their papers, we developed a hybrid sampling method named MMTD-ELM, which consists of a under-sampling α-cut fuzzy number technique for screen representative examples of the majority class and a over-sampling MMTD technique for producing synthetic examples of minority class. In the proposed under-sampling method, we use MF value to measure the representation of the majority class example with low impact of noise, in which, MF value is used to measure potential information of majority class examples. By removing some examples and creating new examples near the decision boundary, we can effectively shift the SVM decision boundary towards the region of the majority class. By this shift, more minority class examples can be correctly predicted but only a few majority class examples may be misclassified. As a result, the proposed method can further improve SVM classification of the minority class.

In this paper, three medical datasets obtained from the Knowledge Extraction based on Evolutionary Learning (KEEL) dataset repository ^[22] and one medical dataset obtained from microarray gene expression cancer data ^[23] are used to test efficacy of the proposed MMTD-ELM method. Based on the four datasets, we compared the MMTD-ELM method with the IMB (using imbalanced datasets) method, which only uses an original imbalanced dataset without generating new examples, and three other sampling methods. The three sampling methods include the SMOTE method for interpolating examples of minority class, the SVM-balance method ^[17] for randomly generating SVs in the minority class, and the cluster-SMOTE method ^[15] for a distance-based hybrid sampling for imbalanced datasets. We construct two types of SVM models: SVM with polynomial kernel (SVM_poly) and SVM with radial basis function kernel (SVM_rbf) to test classification performance using these methods. Four evaluation metrics: geometric mean (G-mean) as seen in ^[24], F-measure (F1), index of balanced accuracy (IBA) as seen in ^[25] and area under curve (AUC) as seen in ^[26] are used to measure classification results with imbalanced datasets. Additionally, the paired t-test is used to examine whether the proposed MMTD-ELM method has statistically significant differences from the other methods in terms of four evaluation indicators. According to our experimental results, the proposed MMTD-ELM method outperforms the other four methods. For instance, when imbalance ratio between majority class and minority class is at 9:1, based on the four datasets, the proposed MMTD-ELM method achieves the best average values in terms of G-mean (0.901 and 0.914), F1 (0.877 and 0.885), IBA (0.719 and 0.742) and AUC (0.841 and 0.854) metrics for SVM_poly and SVM_rbf models, respectively.

The remainder of this paper is organized as follows: Section 2 introduces the SVM model; Section 3 illustrates the complete implementation procedure for the proposed MMTD-ELM method; Section 4 provides the description of four medical datasets and discusses the experimental results; and Section 5 concludes and discusses future work.

2.   Related works

In this section, we present a literature review of sampling techniques for improving SVM imbalanced classification. Additionally, we introduce the SVM model for classification tasks.

2.1.   Sampling approaches for improving SVM imbalanced classification

SVM proposed by Cortes and Vapnik ^[27], is a typical kernel-based learning algorithm to address classification work in many fields, such as air quality classification ^[28,29], medical diagnosis ^[19,30,31] and speech recognition ^[32,33]. The kernel-based SVM model maps original data onto a high-dimensional feature space to identify examples between different classes. The decision boundary is constructed by SVM that can effectively separate examples of different classes while minimizing training error. The examples located on SVM's decision boundary are called support vectors (SVs). The classification ability of the SVM model depends on the quantity of support vectors on the decision boundary. However, with skewed datasets, prediction results of SVM often tend towards the majority class because the learning model is trained using tiny examples of the minority class. To improve SVM classification performance for imbalanced datasets, some research has suggested employing sampling techniques to generate artificial minority class examples to balance data class distributions. However, randomly generating artificial examples cannot significantly improve SVM classification accuracy for skewed datasets since SVM's decision boundary may be slightly shifted towards the majority class. To deal with this issue, Zeng and Gao ^[34] addressed a kernel-based SMOTE method to generate virtual samples near the decision boundary of SVM on the minority class side to extend the margin of SVM's hyperplane. Other than over-sampling methods with SVs, Luo et al. ^[35] presented a hybrid sampling support vector data description (SVDD) method, which randomly deletes SVs in the majority class and generates SVs in the minority class using SMOTE to obtain balanced training datasets. However, eliminating SVs of the majority class may omit critical information for classifying majority class. At the same time, generating SVs using SMOTE might lead to new SVs surrounded by most majority class examples that become noise or outliers in the minority class.

2.2.   SVM

Given a dataset of n samples: $({\vec x_{\text{1}}}, {y_1})$, $({\vec x_{\text{2}}}, {y_{\text{2}}})$, ..., $({\vec x_i}, {y_i})$, i = 1, 2, ..., n, where ${\vec x_i} \in {\mathbb{R}^m}$ is the input vector and ${y_i}$$\in${−1, +1} is the label of ith sample. According to the formula in ^[27], SVM classification satisfies the following condition:

where ${\bf{w}}$ represents weight vector, b is the bias and φ(‧) is the mapping function for projecting original inputs onto a high-dimensional feature space. Based on Eq (1), SVM classification for these samples with different classes can be determined by Eq (2).

According to the principle of structural risk minimization, the construction of SVM can be defined as a primal optimization problem, as follows:

where ${\left\| {\bf{w}} \right\|^2} = {{\bf{w}}^T} \cdot {\bf{w}}$, C is the error penalty parameter to control trade-off between acceptable classification error and maintaining decision boundary with maximum margin and ${\xi _i}$ is a slack variable to allow tolerance for misclassification errors. According to Karush-Kuhn-Tucker (KKT) optimality conditions, we can reformulate Eq (3) as a quadratic optimization problem. To solve this optimization problem, we derive the problem with Lagrange multipliers ${\alpha _i}$, as:

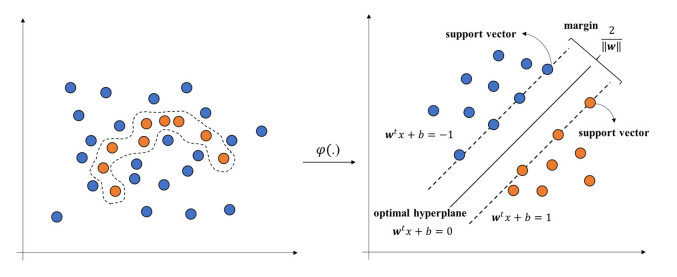
where when ${\alpha _i}$ is not equal to zero, it is called a support vector (SV) on the decision boundary and $k({\vec x_i}, {\vec x_j})$ is a kernel function noted as $\left\langle {\varphi ({{\vec x}_i})} \right.$, $\left. {\varphi ({{\vec x}_j})} \right\rangle$, $\forall i \ne j$ for mapping non-linear ${\vec x_i}$ onto a high-dimensional space, as depicted in Figure 1.

There are four categories of $k\left({{{\vec x}_i}, {{\vec x}_j}} \right)$: linear kernel $\vec x_i^T \cdot {\vec x_j}$, polynomial kernel ${[\gamma \cdot (\vec x_i^T \cdot {\vec x_j}) + r]^d}$, radial basis function kernel $\exp (- \gamma ||{\vec x_i} - {\vec x_j}|{|^2})$ and sigmoid kernel $\tanh (\gamma (\vec x_i^T \cdot {\vec x_j}) + r)$, in which, $d \in \mathbb{N}$, $r \in \mathbb{N}$ and $\gamma \in {\mathbb{R}^ + }$.

3.   The proposed MMTD-ELM method

In this paper, we develop a unique hybrid sampling technique for improving SVM classification for skewed datasets. We explain the proposed method in depth in the following sections.

3.1.   Method

Given a dataset has n samples with m input variables ${X_1}$, ${X_2}$, ..., ${X_m}$ and one output variable $Y$, which are denoted as {$({\vec x_{\text{1}}}, {y_1})$, $({\vec x_{\text{2}}}, {y_{\text{2}}})$, ..., $({\vec x_i}, {y_i})$}, i = 1, 2, ..., n. The ${\vec x_i}$ expresses ith data vector, and ${y_i}$ is its label. We utilize the min-max data normalization to eliminate effects between m input variables ${X_1}$, ${X_2}$, ..., ${X_m}$ with different scales before implementing the suggested MMTD-ELM technique. The data normalization formula is expressed as:

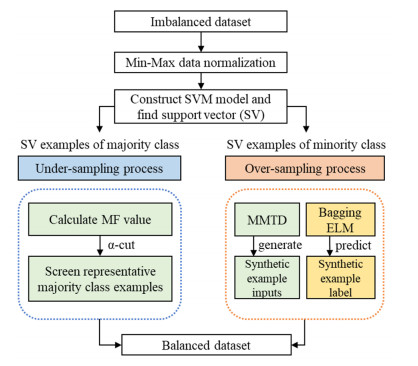
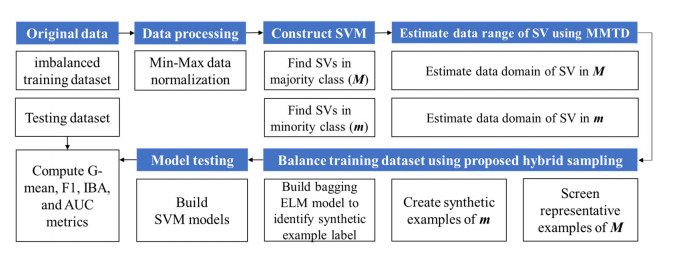
where ${\tilde x_{i, j}}$ is normalized data, max(${X_j}$) is the maximum value of the jth input variable and min(${X_j}$) is the minimum value of the jth input variable. To address classification problems posed by imbalanced datasets, the proposed MMTD-ELM hybrid sampling method consists of two stages: under-sampling and over-sampling stages. To balance skewed class distribution, in the under-sampling stage, we screen representative support vectors (SVs) in the majority class; in the over-sampling stage, we create new minority class examples. By implementing the proposed MMTD-ELM method, a new balanced dataset is obtained. The designed hybrid sampling procedure is illustrated in Figure 2.

3.2.   Implementing MMTD-ELM technique

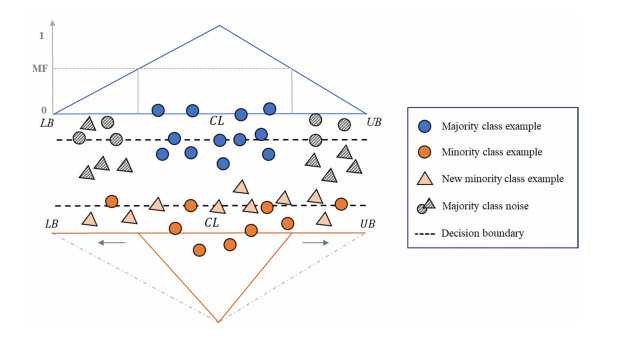
The proposed method is aimed at effectively shifting the SVM model decision boundary towards the majority class to improve SVM classification for imbalanced datasets. The proposed method is developed to select significant majority class SVs and create artificial minority class SVs within the estimated data domain. First, we employ the MMTD method to estimate data range of SVs in both the majority and minority classes, respectively. Based on estimation of SVs in the majority class, we calculate MF values of SVs and find valuable majority class SVs with an α-cut. In addition, we generate new SVs close to original SVs in the minority class within the estimated data range of minority class SVs. Additionally, we depict data domain estimation of SVs using the MMTD method and proposed hybrid sampling approach in Figure 3.

3.3.   Estimate data range using MMTD method

In this paper, we use MMTD method to estimate data range [LB, UB] of SVs on the decision boundary. They are calculated by Eqs (6) and (7), respectively.

where LB and UB are the lower and upper bound, respectively. ${N_{{\text{LB}}, j}}$(${N_{{\text{UB}}, j}}$) is the number of values smaller (greater) than ${\text{CL}}(X_j^{SV})$ for jth input variable. If the ${N_{{\text{LB}}, j}}$(${N_{{\text{UB}}, j}}$) is zero, the lower bound ${\text{L}}{{\text{B}}_j}$ (the upper bound ${\text{U}}{{\text{B}}_j}$) cannot be defined, and we set them as ${\text{min(}}X_j^{SV}{\text{)}}$ and $\max (X_j^{SV})$, respectively. The φ is set to ${10^{ - 20}}$, ${\hat s^2}(\cdot)$ represents sample variance and ${\text{CL}}(\cdot)$ is the median of samples. They are presented as follows:

In addition, ${\text{Ske}}{{\text{w}}_{{\text{LB}}, j}}$ (${\text{Ske}}{{\text{w}}_{{\text{UB}}, j}}$) is defined as coefficients of skewness on left (right) side of CL, which are calculated as follows:

in which, σ is a shape parameter for adjusting the degree of data skewness. In this paper we set σ to one. By the MMTD method, the data range of the SVs set can be estimated.

3.4.   The under-sampling method using α-cut

To screen representative instances in the majority class, we employ the MMTD method to evaluate the data domain of majority class SVs. Based on a triangular MF, the MF value of the support vector(s) is calculated as follows:

where x is the support vector(s) of majority class and MF(x)$\in$[0, 1]. In this paper, we utilize α-cut $\in$[0, 1] for selecting valuable SVs according to MF value. The α-cut is a crisp set represented as follows:

in which, from Eq (12), α-cut can be derived as follows:

where ${A_{\alpha, lower{\text{ }}bound}} = LB_j^{SV, M} + \alpha \cdot (CL_j^{SV, M} - LB_j^{SV, M})$ and ${A_{\alpha, upper{\text{ }}bound}} = UB_j^{SV, M} - \alpha \cdot (UB_j^{SV, M} - CL_j^{SV, M})$. By ${A_\alpha }$, we can implement the under-sampling process to find representative SVs of the majority class. The derivation of Eq (14) is shown as follows:

and

As a result, from Eq (14), valuable majority class SVs can be kept within data range $[{A_{\alpha, {\text{lower bound}}}}, {A_{\alpha, {\text{upper bound}}}}]$.

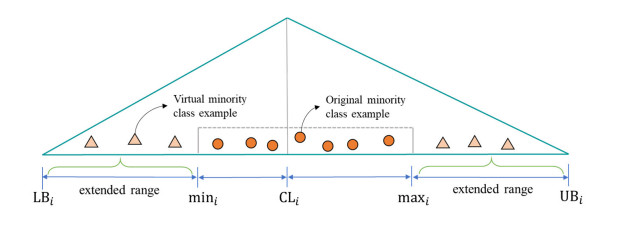
3.5.   The over-sampling method using bagging ELM model

The data range [LB, UB] of SV in the minority class can be estimated by MMTD method in Section 3.3. We randomly generate virtual SVs inputs within estimated [LB, UB], as shown in Figure 4.

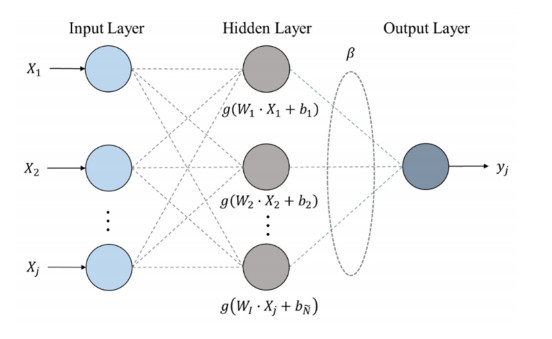
As for prediction of virtual SV output, we deploy the extreme learning machines (ELM) proposed by Huang et al. ^[36] to monitor virtual SV output. The ELM is a feed-forward neural network, which consists of an input layer, hidden layer and output layer. The ELM model architecture is depicted in Figure 5.

In Figure 5, the ELM's outcome can be expressed as follows:

where $\tilde N$ is the quantity of neurons in the hidden layer, ${\beta _i}$ is weight between hidden layer and output layer, f is activation function, ${W_i}$ is weight between input layer to hidden layer, ${b_i}$ is a bias and ${y_j}$ is model outcome. The detailed steps for training the ELM model are listed as follows:

Step 1. Randomly assign initial values of weight ${W_i}$ and bias ${b_i}$ in the hidden layer.

Step 2. Calculate hidden layer output matrix H, as follows:

Step 3. Solve the following formula to find the weight ${\beta _i}$, as:

where T is the target value in the output layer.

In this paper, we employ the sigmoid function as the activation function, as follows:

In addition, we use classification error rate to measure ELM model prediction accuracy. If model prediction is greater than 0.5, it is considered positive class. Conversely, if predicted value is less than or equal to 0.5, it is considered negative class. To optimize overall ELM model weights, we employ the bagging method ^[21] to resample original datasets to create multiple training datasets for retraining the ELM model. The bagging method is beneficial for training datasets with skewed class, since it creates several datasets by resampling from original datasets that allow the ELM model to learn different patterns between inputs and output. In the fine-tuning process, we update these weights for 10 epochs each iteration at a learning rate of 1 × 10^–3 until a total of 100 epochs, as illustrated in Figure 6.

3.6.   Proposed MMTD-ELM procedure

In this section, the hybrid sampling scheme for the proposed MMTD-ELM method is depicted as Figure 7. After completing the proposed implementation procedure for balancing the imbalanced training dataset, we constructed two SVM models using the balanced training dataset. Finally, we measure prediction accuracy of SVM model for testing dataset in terms of G-mean, F1, IBA and AUC metrics.

In the following, we summarize the implementation procedure explaining the MMTD-ELM method in steps as described in Table 1.

4.   Experiment

In this section, we will describe four benchmark datasets used in our experiments as well as their experimental results. The experiment was executed with a computer equipped with Intel(R) Core(TM) i7-13700KF and 64 GB memory. Under the Ubuntu 22.04.1 LTS operating system, the experiment is implemented using Python 3.10.6 programming language for data processing and constructing SVM predictive models. In this paper, we configure SVM models with the scikit-learn package (version 1.3.0) ^[37].

4.1.   Dataset description

We used the four datasets to test prediction performance using the proposed MMTD-ELM method. The four datasets consist of new-thyroid1, Ecoli2, and Wisconsin (Diagnostic) obtained from the KEEL dataset repository, and one high-dimensional lung cancer microarray dataset downloaded from microarray gene expression cancer data ^[23]. We summarized the number of input features, the amount of data and other information for the four datasets in Table 2, in which, #instances represents the amount of data, #features represents the quantity of input features and #class indicates the number of categories. In addition, #M and #m indicate the quantity of majority and minority class examples, respectively. The imbalanced ratio (IR) is defined as #M/#m.

4.2.   Evaluation metrics

When a training dataset has imbalanced class distributions, the accuracy rate metric is not suitable to fully evaluate classification performance. As a result, we use the confusion matrix to evaluate classification performance of predictive models for imbalanced datasets. The confusion matrix consists of the predictive model's outcome and the actual output as presented in Table 3.

In this paper, we define positive class (minority class) as 1 and negative class (majority class) as 0. Considering classification accuracy for both negative class and positive class, four evaluation metrics, G-mean, F1, IBA and AUC, are used to measure classification performance for imbalanced datasets. The G-mean is defined as the geometric mean of Recall and Specificity as in Eq (19), in which, Recall (Specificity) represents the proportion of correctly predicted positive (negative) class examples to actual positive (negative) class examples. They are calculated as TP / (TP + FN) and TN / (TN + FP), respectively. F1 is the harmonic mean of Precision and Recall as calculated in Eq (20), where Precision = TP / (TP + FP). In addition, IBA and AUC have comprehensive evaluations for overall classification results for imbalanced datasets as presented in Eqs (21) and (22). In Eq (22), $Ran{k_i}$ represents the ranking of the ith instance in the TP set. In addition, |TP| and |TN| represent the amount of TP and TN, respectively.

4.3.   Experiment design

In order to test effects of the proposed method for imbalanced datasets, we create imbalanced dataset scenarios for the four datasets. We randomly draw 100 data from an original dataset as training datasets according to IR values of 4 and 9, respectively. The remaining data is set as a testing dataset. Based on the four datasets, we compare prediction performance between the proposed MMTD-ELM method for hybrid sampling examples near the SVM's decision boundary, IMB method for only using imbalanced datasets and three sampling methods: SMOTE for generating new minority class examples by interpolating between original minority class examples, SVM-balance for generating minority class examples nearby the SVM's decision boundary and Cluster-SMOTE for generating new minority class examples and excluding unrepresentative majority class examples. In addition, we construct two types of SVM models with polynomial kernel (SVM_poly) and radial basis kernel (SVM_rbf) as predictive models to compare prediction performance across these five methods. The two SVM models are constructed with scikit-learn tool (version 1.3.0) ^[37]. The SVM_poly model is configured with {kernel: poly; cost penalty C:10; degree:2} and the SVM_rbf model is configured with {kernel: rbf; cost penalty C:10; gamma: "auto"}, where "auto" is defined as 1/the number of input features.

4.4.   An example using the proposed MMTD-ELM method

In this section, to explain the proposed MMTD-ELM method in depth, based on the Ecoli2 dataset, we create a training dataset with IR = 9 as an example. The training dataset has 10 minority class data and 90 majority class data as listed in Table 4. The minority (m) class is labeled as "Positive" and the majority (M) class is labeled as "Negative". Seven variables: Mcg, Gvh, Lip, Chg, Aac, Alm1 and Alm2 are set as input features. The implementing steps for the MMTD-ELM method are explained, as follows:

Step 1. Convert training data into domain [0, 1] by min-max data normalization given by Eq (5).

Step 2. Find support vectors using the SVM_poly model. We listed the support vectors for negative class and positive class in Tables 5 and 6, respectively.

Step 3. Estimate data range of each input feature of majority class support vectors using MMTD method, as listed in Table 7.

Step 4. Calculate ${A_\alpha } = [{A_{\alpha = 0.{\text{2}}5, lower{\text{ }}bound}}, {A_{\alpha = 0.25, upper{\text{ }}bound}}]$ as seen in Eq (14), where α is set at 0.25. The ${A_{\alpha = 0.{\text{2}}5, lower{\text{ }}bound}}$ is calculated as $L{B_M} + {\text{0}}{\text{.25}} \cdot (C{L_M} - L{B_M})$ and ${A_{\alpha = 0.25, upper{\text{ }}bound}}$ is calculated as $U{B_M} - 0.25 \cdot (U{B_M} - C{L_M})$. The calculations are shown in Table 8.

Step 5. Remove majority class examples outside the range ${A_\alpha }$. The deleted examples are listed in Table 9.

Step 6. Estimate data range of each input feature of minority class support vectors using MMTD method, as listed in Table 10.

Step 7. Create synthetic minority class example within the estimated range [$L{B_m}$, $U{B_m}$] and input them into the trained bagging ELM model to determine if it belongs to the minority class.

Step 8. Repeat Step 7 until 75 ( = 90 – 5 − 10) synthetic examples of the minority class are created. These generated examples are listed in Table 11.

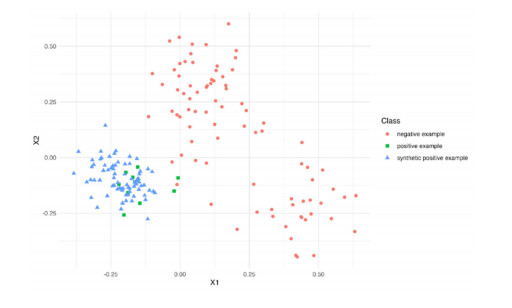
Step 9. Add synthetic minority class dataset into original training dataset to build up a balanced training dataset. We depict them in Figure 8.

4.5.   Statistical tests with experimental results

In this section, we use the paired t-test to assess whether there are significant differences between the proposed MMTD-ELM method and the ith method in IMB, SMOTE, SVM-balance and Cluster-SMOTE. In the paired t-test procedure, we set the null hypothesis ${H_0}$ and the alternative hypothesis ${H_1}$ as:

where ${\mu _{MMTD - ELM}} - {\mu _{ith}}$ indicates the average of differences of classification results between the MMTD-ELM method and ith method for G-mean, F1, IBA or AUC metric with 50 experiments. In addition, we set the significance level α at 0.05. When p-value is less than the significance level α, the hypothesis ${H_0}$ is rejected, indicating there is a significant difference for G-mean, F1, IBA or AUC metric. We used the symbol "^*" to indicate that the classification capability of the proposed MMTD-ELM method has statistically significant effects over the other methods.

4.6.   Experimental results

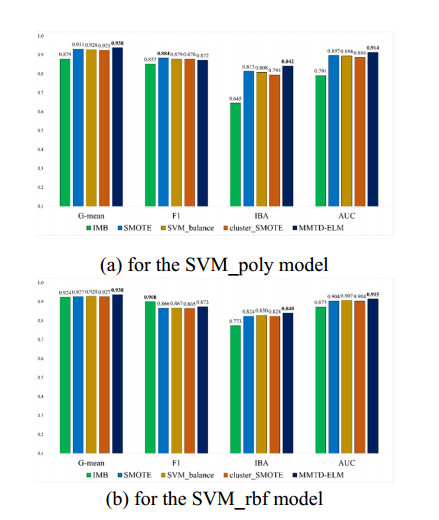
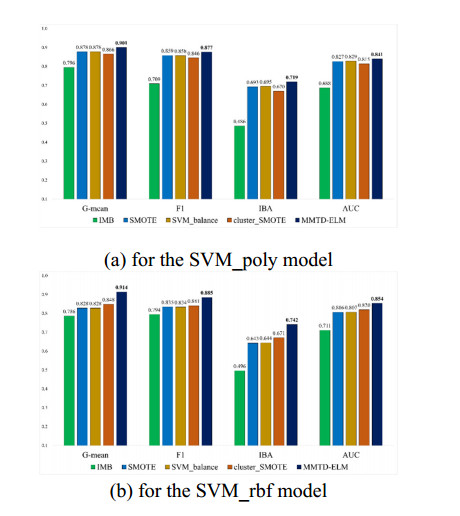
In this section, we implemented a total of 50 experiments to compare classification results among the five methods on the four datasets. In Figure 9(a) and (b), for example, when IR value was set at 4, classification results using the proposed MMTD-ELM method (deep blue line) are better than those of IMB (green line), SMOTE (blue line), SVM-balance (earthy yellow line) and Cluster-SMOTE (orange line) methods on SVM_poly and SVM_rbf models, respectively. When IR value is increased from 4 to 9, the MMTD-ELM method still outperforms the other four methods in terms of the four evaluation metrics, as displayed in Figure 10.

Additionally, in Tables 12 and 13, we list other experimental results for the four datasets with IR values of 4 and 9. In these tables, the values in bold represent the best classification results among five methods in items of G-mean, F1, IBA and AUC metrics. In Table 12, for example, the proposed MMTD-ELM method in terms of AUC metric can achieve the best average scores of 0.958 and 0.973 on the SVM_poly and SVM_rbf models for new-thyroid1 dataset, respectively. Note that, on the SVM_poly and SVM_rbf models, the prediction accuracy using the suggested MMTD-ELM method can achieve improvement of 0.919 − 0.543 = 0.376 and 0.947 − 0.852 = 0.095 in terms of IBA metric, respectively.

4.7.   Analysis of the experimental results

In this section, based on the four datasets, we calculate the average (Avg) and standard deviation (SD) of classification accuracy in terms of G-mean, F1, IBA and AUC metrics as seen in Tables 14 and 15. In Table 14, for example, the values of "0.938" and "0.023" indicate Avg and SD of prediction results using the proposed MMTD-ELM method for G-mean metric on the SVM_poly model, respectively. Additionally, we rank the five methods, to select the best methods in terms of G-mean, F1, IBA and AUC metrics. In Tables 14 and 15, we can see that the proposed method has the best ranking averages on the four evaluation metrics. In Table 15, for example, on the SVM_poly and SVM_rbf models, the proposed MMTD-ELM method achieves better ranking value among the five methods in terms of G-mean (1.830 and 2.005), F1 (1.755 and 1.885), IBA (1.930 and 2.125) and AUC (1.935 and 2.115), respectively.

In order to further analyze classification results using these methods, we used paired t-test to demonstrate if these experimental results exhibit statistically significant differences between the proposed MMTD-ELM method and the other methods on G-mean, F1, IBA and AUC metrics. In Tables 14 and 15, the symbol "^*" indicates that the MMTD-ELM method enjoys statistically significant differences (p-value < 0.05) from IMB, SMOTE, SVM-balance and cluster-SMOTE methods. In Table 14, for example, on the SMV_rbf model, the classification results using the proposed MMTD-ELM method have significant improvements (p-value = 0.003^* < 0.05) as compared to the IMB method for terms of F1 metric.

4.8.   Summary

According to the experimental results using all five methods: IMB, SMOTE, SVM-balance, Cluster-SMOTE, and our proposed MMTD-ELM methods, listed in Tables 12–16, the findings can be summarized as follows:

a) Based on the four datasets, when IR values are set at 4 and 9, our suggested MMTD-ELM method can achieve the best classification accuracy among these methods on two types of SVM models in terms of G-mean, F1, IBA and AUC metrics, as seen in Tables 12 and 13. From these results, we can see that with increasing IR values, the proposed MMTD-ELM method consistently achieves the best classification performance in terms of G-mean, F1, IBA and AUC metrics.

b) From these experimental results listed in Tables 14 and 15, we can see that most Avg and SDs using the MMTD-ELM method obtain the best performance in terms of G-mean, F1, IBA and AUC metrics. Additionally, the proposed MMTD-ELM method has the best ranking score in terms of G-mean, F1, IBA and AUC metrics. Furthermore, most p-values are less than 0.05 at IR values of 4 and 9.

c) Although a few experimental results indicate the MMTD-ELM method does not have statistically significant prediction accuracy compared to the IMB method, the proposed MMTD-ELM method still outperforms the other methods in terms of G-mean, F1, IBA and AUC metrics.

d) In Table 16, in terms of the Recall (i.e., true positive rate) metric, we can see that the MMTD-ELM method outperforms the other methods for four experimental datasets indicating that our proposed method has better prediction accuracy for minority class (which is defined as positive class). Additionally, in terms of the Specificity (i.e., true negative rate) metric, there are only slight differences among the five methods indicating that the five methods have similar prediction performance to each other for majority class (which is defined as negative class).

In sum, the suggested MMTD-ELM method has more improvement effects and is shown to be superior to the other methods for four imbalanced datasets.

5.   Conclusions

The sampling approach has been proposed as an effective technique to improve prediction accuracy in traditional machine learning and deep learning models for imbalanced datasets. This technique directly creates new examples of minority class to balance skewed data distribution. For SVM imbalanced classification, some researchers suggested generating synthetic minority class examples adjusting the SVM's decision boundary to correctly predict minority class examples as seen in ^[15,17,38]. Farquad and Bose ^[17], for example, proposed the SVM-balance method, which randomly over-samples misclassified examples near the decision boundary as new examples, to improve prediction accuracy of SVM for minority class examples. However, generated examples may be surrounded by most of the majority class examples that are thus regarded as danger examples of minority class or noise. These may lead to distortion of SVM learning. To effectively adjust SVM's decision boundary, Cieslak et al. ^[15] proposed the distance-based cluster-SMOTE hybrid sampling method, which creates new minority class examples and eliminates unrepresentative majority class examples. However, the cluster-SMOTE method based on distance between examples is easily impacted by noise or outliers. Differing from their papers, based on a fuzzy triangular MF, we developed a new hybrid sampling method named MMTD-ELM to screen representative majority class examples and generate synthetic minority class examples. In order to screen informative support vectors of the majority class, we developed an α-cut technique to measure representation of the majority class example. Furthermore, to create better synthetic minority class examples, we deploy a bagging ELM model to monitor the similarity between synthetic examples and original data of the minority class. As a result, when compared to the oversampling SVM-balance and distance-based hybrid sampling cluster-SMOTE methods, the proposed MMTD-ELM method achieves better prediction accuracy of SVM for skewed datasets.

In this paper, four biomedical datasets were used to elucidate effectiveness of the suggested MMTD-ELM method for SVM classification with imbalanced datasets. These experimental results demonstrate the suggested MMTD-ELM method successfully outperforms other sampling methods in imbalanced datasets. As for research limitations, the proposed MMTD-ELM approach can be utilized to estimate the data range of numerical datasets, but it is not appropriate for datasets with discrete variables. In the future, we will further consider three directions: 1. using the proposed method for addressing other high-dimensional imbalanced microarray cancer data; 2. developing a sampling method for handling imbalanced datasets with discrete features; 3. developing a sampling method or deep learning model for imbalanced but small-sample-size datasets.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Data availability

Data available in a publicly accessible repository. The experimental datasets presented in this paper are openly available at the KEEL dataset repository ^[22] and the Microarray Gene Expression Cancer Data ^[23].

Conflict of interest

The authors declare that there are no conflicts of interest.

Acknowledgments

The National Taipei University of Nursing and Health Sciences and the National Science and Technology Council both provided funding for this research. The National Science and Technology Council, Taiwan financed this study pursuant to contract number NSTC 112-2221-E-227-003.