MUNIX repeatability evaluation method based on FastICA demixing

1.   Introduction

Motor neuron disease (MND) has received a lot of attention in recent years due to its high incidence. The clinical manifestations of this disease are upper and lower motor neuron damage, resulting in progressive muscle atrophy in the extremities, trunk, chest and abdomen and a progressive decrease in the number of motor units in the muscles as the disease progresses ^[1,2]. To assess the progression of the disease, Nandedkar's team proposed the motor unit number index (MUNIX) technique, which provides a neurophysiological index related to the number of motor units in the muscle, the MUNIX, and characterizes the trend in the number of motor units over time by detecting changes in the index ^[3]. MUNIX is calculated using the compound muscle action potential (CMAP) generated by neuroelectrical stimulation and the surface interferential pattern (SIP) recorded during voluntary muscle contraction ^[4,5]. This method has the advantage of being non-invasive, rapid and easy to use compared to the traditional motor unit number estimation (MUNE) method [6−8]. Several studies have demonstrated that MUNIX can be used as a biomarker to monitor the progression of various neuronal diseases such as amyotrophic lateral sclerosis (ALS) [4, 9−12].

For the techniques of motor unit number index evaluation, reproducibility is the primary condition that needs to be met. Good reproducibility of the method and stability of the retest results are required to provide a reliable basis for disease diagnosis ^[13]. According to the National Institute of Standards and Technology, reproducibility is defined as the degree of dispersion of repeated measurements under the same experimental conditions (same measurement steps, observer, location, measurement instrument and short time period). The coefficient of variation (CV) and correlation coefficient (CC) are two metrics commonly used to evaluate the reproducibility of test methods. MUNIX has been measured in healthy individuals ^[10,14,15] and in patients with neuronal diseases ^[9,16,17], respectively, and it was found that the mean value of MUNIX was lower in patients with diseases than in healthy subjects, and its mean value gradually decreased as the disease worsened, indicating that MUNIX is meaningful for disease assessment. However, in patients with neuromuscular diseases, although more CCs were used to evaluate reproducibility, CV values were higher, especially in ALS patients, in some cases up to 69.9% ^[9,14,16]. The phenomenon suggests that the repeatability of MUNIX is worse in patients with neurological diseases compared to healthy controls and that the index CV is influenced by the health status of the test subject ^[18,19]. Therefore, there is a need to refine the MUNIX experimental method to further improve its reproducibility and reduce the negative effects.

Traditional motor unit counting methods use mostly single-electrode sEMG signals, but single-electrode channels can only measure surface electromyography (sEMG) signals at a fixed point in the muscle, and the large variability of muscle shapes in different subjects, especially in patients with neurological diseases, affects the precise localization of electrode locations ^[20]. In recent years, the development of high-density sEMG (HD-sEMG) measurement techniques have provided the conditions for recording more comprehensive EMG information within a specific muscle region ^[11,21]. Peng et al. enhanced the MUNE technique by decomposing HD-sEMG signals, yielding favorable outcomes in assessing disease progression among patients using motor unit counting methods. Their experiments showed that the use of high-density electrodes and the demixing of sEMG signals facilitated the assessment of motor unit count ^[22]. Cao et al. tried to use high-density electrodes instead of single electrodes to acquire and record sEMG signals, then calculated the MUNIX index and achieved excellent results, but there was still a phenomenon that the CV value increased instead with the increase in the number of channels ^[23]. Combined with Peng et al.'s study, it was speculated that high-density electrodes have coupling crosstalk factors between adjacent channels due to the small spacing of each channel, so that the individual signals in the sEMG signal are mixed with each other to become an important factor affecting the experimental results ^[21,24].

For the demixing of sEMG signals, fast independent component analysis (FastICA) was proposed by Hyvarinen et al. ^[25]. A method was presented as a graph structure learning by the natural evolution theory ^[26]. Existing studies have shown that the source signals acquired by sEMG electrode arrays are independent of each other at each release time point ^[27]. For the separation of independent signals the more applied method is independent component analysis (ICA) ^[28]. Compared with the traditional independent component analysis method, the FastICA method estimates the independent components of the source signal one by one according to the characteristics of the signal independence, which avoids the tedious calculation of the whole demixing matrix ^[29] and does not require estimating the number of source signals ^[30]. For the independence evaluation and validity judgment of the demixed signal, negative entropy is a widely recognized metric ^[31]. At present, FastICA has been widely used in speech signal separation, biomedical signal processing, face recognition, etc. Some scholars ^[32] used the FastICA algorithm based on negative entropy to separate human speech signals, and the results were more satisfactory.

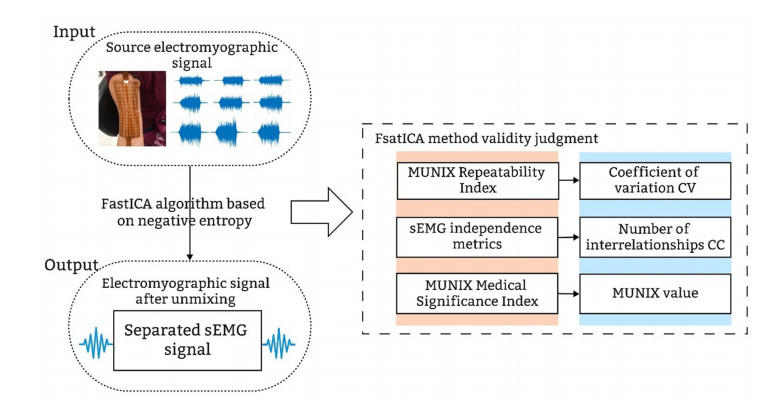
In the field of HD-sEMG signals, FastICA has been frequently employed in the MUNE technique to effectively decompose the number of motor units (MUs) within sEMG signals, yielding promising outcomes ^[30,31,33]. Meanwhile, research on the application of the MUNIX technique is still in a limited stage. Studies have shown that the MUNIX assessment technique possesses almost the same effect as the MUNE method in assessing motor unit loss and is favored by many clinical physiologists ^[19,34]. Therefore, in this paper, the FastICA algorithm based on negative entropy was used to separate the confounding components of the acquired HD-sEMG signals, and the effect of unmixing on the reproducibility of MUNIX was verified by comparative analysis.

The applications of deep learning methods and sensor technologies are increasing interest in the field of pattern analysis and recognition [35−39]. These studies indicate that artificial intelligence technology can be applied to bioelectric signal processing, and further research is needed. The main contributions of this paper are as follows.

● The FastICA algorithm for HD-sEMG signal demixing was presented, and the effect of the degree of signal mixing between high-density channels on MUNIX repeatability was investigated, combined with MUNIX values and coefficients of variation.

● The negative entropy index was used for the evaluation of signal independence after unmixing, and the Pearson correlation coefficient was selected for statistical analysis to verify the effectiveness of the FastICA method.

● The coefficient of variation of the MUNIX value shows a decreasing trend with the increase of the number of channels on the basis of ensuring the validity, and the degree of signal mixing between channels has been effectively removed. This work provides the potential application value of the MUNIX index in clinical practice.

2.   Methods

The acquired EMG signals underwent denoising using the negative entropy-based FastICA algorithm for de-mixing iterations. To assess the independence and validity of the demixed signals, we utilized coefficient of variation (CV), number of correlations (CC), and MUNIX value as repeatability, sEMG independence and medical significance indices respectively. The methodological steps are illustrated in Figure 1.

2.1.   Experimental paradigm

The experimental protocol followed existing studies ^[4,14,22] and selected the biceps muscle of the arm for MUNIX measurements, as it is one of the muscles commonly used for MUNIX measurements ^[10,40]. Before the experiment, the skin was wiped with medical alcohol to remove skin flakes, and the study used flexible 8*8 high-density grid electrodes with 4.5 mm electrode diameter and 8.5 mm electrode spacing, and two high-density grid electrodes were attached adjacent to each other above the muscle belly along the muscle fiber direction, and the schematic diagram is shown in Figure 2(a). The patching method of high-density electrodes is shown in Figure 2(b). The electrodes were connected to a 136-channel Refa amplifier that acquires sEMG signals at 2048 Hz. The reference electrode was placed above the elbow of that arm, and the ground electrode was placed at the wrist of the other arm. The subject was comfortably seated in an adjustable Biodex chair (Biodex, Shirley, NY) with the dominant arm and wrist secured inside a fiberglass casting, a position that minimizes interference forces from other muscles, as shown in Figure 2(c). The proximal myocutaneous nerve of the arm was stimulated with a DS7 current stimulator (Digitimer Ltd, Welwyn Garden city, United Kingdom), and the stimulation current was a rectangular pulse with a width of 0.2 ms. The position of the stimulating electrode was adjusted in an attempt to find the stimulation site where the maximum CMAP amplitude appeared, and then the stimulation was continued at that location in 5 mA increments of stimulation intensity at that location until the CMAP amplitude no longer increased ^[41]. Subjects performed three sets of isometric elbow flexion movements at different levels of force ^[42]. The force levels (10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 100%) are measured by first measuring the set of contractions with the highest force level according to the subject's condition and then feeding back to the subject and the operator through the on-screen monitor when other levels of force are measured, in order to control the muscle force signal and its stability. During each of the two voluntary contractions or stimulations, the subject was allowed to rest sufficiently to reduce muscle fatigue. Contraction forces greater than 50% MVC were considered medium to high grade contraction forces, and those less than 50% MVC were considered low grade contraction forces in this study.

2.2.   FastICA unmixing based on maximum negative entropy

Negentropy-based FastICA is an ICA algorithm that enables the processing of non-linear mixture models and multiple signal sources by optimizing the orthogonal rotation matrix based on various non-Gaussianity measures to achieve efficient signal separation. In contrast, other ICA algorithms are limited to linear mixed models and two signal sources, utilizing only one non-Gaussianity measure. It is worth noting that the algorithm assumes a linear combination of multiple independent components from a non-Gaussian distribution in the data, which may not hold true in certain cases and consequently impact the efficacy of signal separation ^[20]. However, within this study, the negative entropy-based FastICA algorithm proves more suitable for separating sEMG signals compared to other algorithms due to their pronounced nonlinearity and non-Gaussianity.

2.2.1.   FastICA algorithm for sEMG

Let $\mathit{\boldsymbol{X}} = {\left[{{x_1}, {x_2}, \cdots {x_n}} \right]^T}$ be an n-dimensional observation signal obtained with an array of n sensors and $\mathit{\boldsymbol{S}} = {\left[{{s_1}, {s_2}, \cdots {s_m}} \right]^T}$ be the m mutually-passed statistically independent source signals that generate the observation signal, and the observation signal X is the source signal generated by linear mixing, which can be expressed as follows.

The FastICA algorithm aims to discover a transformation matrix W that can linearly convert X into an n-dimensional output vector $\mathit{\boldsymbol{Y}} = {\left[{{y_1}, {y_2}, \cdots {y_n}} \right]^T}$, which serves as an estimate of the independent component S and closely approximates the source signal, i.e.,

given that the mixing matrix A and the source signal S are unknown, which can be seen in Figure 3.

2.2.2.   FastICA algorithm based on negentropy

Negentropy is a valid objective function that can be used to measure the non-Gaussianity of a random variable. For a continuous random variable with probability density function $p\left(x \right)$, the differential entropy of x is defined as

where the entropy is always nonnegative, $H\left(x \right) \geqslant 0$, and is zero for events that occur with certainty or that never occur.

The independence of the separated sEMG signal can be assessed in terms of non-Gaussianity, as per the central limit theorem ^[43]. This is because the distribution of means for arbitrarily distributed independent random variables tends to follow a Gaussian distribution, which has higher entropy value than non-Gaussian distributions. Therefore, our objective is to identify the projection direction that minimizes the entropy of the projected signal. The current FastICA algorithm employs a non-Gaussianity measure based on negative entropy, which represents the deviation from maximum entropy corresponding to Gaussian distribution. A lower negative entropy indicates greater non-Gaussianity and closer proximity of the signal to its original source.

In general, the greater the entropy of a random variable is, the greater its uncertainty, and for a random variable with equal variance, the entropy is greatest when it satisfies a Gaussian distribution (mean power-constrained maximum entropy theorem) ^[20]. Based on this theorem, one can use negative entropy to describe the degree of difference between a distribution $p\left(x \right)$ and a Gaussian distribution ${p_G}\left(x \right)$, where $p\left(x \right)$ and ${p_G}\left(x \right)$ have the same mean and variance.

Since the probability p-value of x needs to be estimated and is computationally intensive, a reasonably efficient approximation to the negative entropy using a non-polynomial function L converging to the negative entropy with zero mean and unit variance is considered by referring to ^[20] as follows.

Typically, a non-polynomial function $L\left(y \right) = \log \left({\cosh \left(y \right)} \right)$ is employed, and v follows a standard normal distribution of random variables, rendering v the strongest non-Gaussian variable and $L\left(v \right)$ the maximum. Therefore, the problem can be further simplified to finding W that maximizes negative entropy $J\left(y \right)$, where $y = {w^T}x$.

^[32] gives a solution to the above equation based on the theory of fixed-point algorithms, namely, the FastICA algorithm.

The algorithm estimates one independent component w of the unmixing matrix at a time, as shown in Eq (7). To compute additional components, the orthogonalization method can be employed.

2.2.3.   FastICA demixing of EMG signals

For the denoised sEMG signal X (INPUT), the negative entropy based FastICA technology for separating mixed sEMG signals is elaborated in detail as follows. Here, x, y, w denote the components of the matrices X, Y, W, respectively.

Step 1. Perform mean subtraction and whitening on X.

Step 2. Choose non-quadratic function $L\left(x \right) = \log \left({\cosh \left(x \right)} \right)$ as the approximate function of negentropy.

Step 3. Initialize the vector ${w_j}\left(i \right)$ of the demixing matrix by taking $\left\| {{w_i}\left(0 \right)} \right\| = 0$, where i is the number of independent components, $i = 1, 2, \cdots, m$, and j is the current source signal sequence number to be demixed, $j = 1, 2, \cdots, n$.

Step 4. Calculate the k+1 components of the unmixing matrix W iteratively according to the principle of negentropic entrenchment ^[25].

Step 5. Orthogonalize the independent components.

Step 6. Normalize the components of the matrices.

Step7. The input sEMG signal for each channel is iteratively processed using Eqs (8−10) to calculate the components of the unmixing matrix. Finally, according to Eq (2), Y = W^TX, we can obtain the unmixing result Y (OUTPUT).

To make the algorithm steps clear, the process of the negative entropy-based FastICA is illustrated in Figure 4. The optimal processing result is obtained until the objective function result converges. If it does not converge, the iterative algorithm is repeated. The proposed algorithm is based on the FastICA algorithm with negative entropy as the comparison function, which can yield approximate Newtonian iterations ^[20,44]. Thus, our algorithm inherits the convergence properties of the FastICA algorithm, with guaranteed convergence under mild conditions and a quadratic convergence rate.

A total of 9 levels of sEMG signals of muscle force were collected and acquired in the experiment, and each level was processed according to the above steps.

Distinguishing the processing of various levels of myoelectric signals is crucial. Specifically, upon inputting EMG signal data segments with different contraction force levels, the magnitude of the contraction force level is initially assessed, and if it is low, the signal is directly demixed. Theoretically, FastICA exhibits enhanced accuracy in demixing iterations of sEMG signals characterized by lower grade contraction force. To ensure the absence of distortion pre- and post-unmixing of medium and high-grade contraction force signals, the motion unit action potential sequence matrix for low-grade contraction force signals can be extracted when the contraction force level is medium or high grade. This low-grade sequence matrix can then serve as a template for unmixing the medium and high-grade contraction force signals.

2.3.   MUNIX medical significance indicators

To compute MUNIX, SIP data pools need to be constructed by extracting the sEMG interference phases - referred to as SIP data segments - that were recorded during autonomous muscle contractions from the sEMG signal at each level of contraction intensity.

In accordance with the SIP inclusion criteria described by Nandedkar's team ^[4], H SIP data segments with a duration of T ms each were divided at moderate intervals across n levels of muscle force. Figure 5(a) illustrates an example of this method applied to a subject, where 10 SIP signal data segments were obtained at 30% MVC. Since the number of SIP data segments does not significantly affect the repeatability of MUNIX ^[27], and the difference in MUNIX calculated using different SIP segments is within an acceptable range, the SIP pool is constructed at this time by selecting the first SIP data segment from each class of muscle power, as shown in the black rectangular window in Figure 5(b), provided that the results are reliable. Each SIP pool consists of 1*n SIP data segments, as shown in Figure 5(c), for an example of 9 muscle strength levels in 30% MVC for a subject.

The MUNIX calculation method is based on the mathematical model developed by Nandedkar's team ^[3,4], which computes the area and power of each SIP signal as well as the area and power of CMAP. We assume that a muscle comprises N identical motor units, with ${P_M}$ and ${R_M}$ denoting the power and area of each motor unit potential, respectively. CMAP represents the sum of all superimposed motor unit potentials, which can be obtained using the following equations.

Assuming that the SIP signal consists of D kinematic units discharging at a frequency of "F" Hz, the power and area of the SIP can be determined as follows.

Based on the variables, the ideal case motor unit count (ICMUC) is derived as follows.

The ideal scenario is characterized by the superposition of identical motion units and the absence of motion unit potentials in the SIP signal. Subsequently, a power regression fitting modeling analysis is conducted for all ICMUC and SIParea, yielding the following relationship.

The CAMP signal reflects the response of all low-threshold motor units. When SIParea = 20 mV/ms, the ICMUC is approximately considered the MUNIX ^[3,4].

Inspired by ^[21,45], where MUNIX was calculated using the high-density optimal myoelectricity weighted average method, the authors proposed in their paper a method to estimate the number of motor units using HD-sEMG signals. According to Eqs (15) and (16) for calculating MUNIX, it is known that SIParea is directly proportional to the value of MUNIX. SIParea signals at the best myoelectric force in multiple channels are weighted and summed using SIParea as a weighting variable to define the weights.

where k is the electrode channel sequence number, w(k) is the weight value in each channel, and the denominator in this equation corresponds to a descending order of CMAP magnitudes across 128 channels. Specifically, it involves taking the squares of SIParea values for K channels with the highest CMAP magnitudes and summing them up.

As MUNIX techniques do not provide a direct estimate of the specific number of motor units but rather calculate an index proportional to the number of motor units contained in the muscle ^[46], monitoring disease progression requires observing trends in changes within the same muscle. Therefore, the FastICA method is evaluated by analyzing the trend of changes in MUNIX before unmixing.

2.4.   MUNIX repeatability index

● Coefficient of variation (CV)

The CV is calculated as follows.

where ${\mu _1}$ is the mean of the data to be calculated, and ${\sigma _1}$ is the standard deviation of the data in that segment.

In Eq (18), it can be seen that the smaller the fluctuation of the data segment is, the smaller the standard deviation of the data segment and the smaller the CV obtained, which leads to the conclusion that the repeatability is better. The greater the instability and volatility of the data segment is, the greater its standard deviation becomes, thereby compromising repeatability.

2.5.   Independence index of EMG signal

● Correlation coefficient (CC)

The Pearson correlation coefficient (CC), initially introduced by Karl Pearson as a statistical measure for quantifying the degree of association between variables, has been extensively employed in statistical computations. In order to assess the independence of adjacent sEMG signal channels, their mutual correlation can be computed to determine the presence of a linear relationship and thereby establish their independence.

There exist diverse approaches to defining the correlation coefficient, with Pearson's correlation coefficient being commonly employed. The equation for its computation is presented as follows.

where $Cov\left({E, Q} \right)$ is the covariance of E and Q, $Var\left[E \right]$ is the variance of E and $Var\left[Q \right]$ is the variance of Q. E and Q denote signals between neighboring channels respectively. The strength of correlation is directly proportional to the absolute value of the correlation coefficient, with a stronger correlation resulting in a coefficient closer to 1 or -1, and weaker correlations approaching 0.

3.   Analysis of results and discussion

This experimental protocol is based on previous studies ^[5,14,21,42]. Considering the difficulty of recruiting patients with neurological disorders and the ethical issues involved, we recruited eight healthy subjects (two females and six males, mean age 27 ± 4 years) without neurological history. The experimental procedure and purpose of the study were thoroughly explained to all participants, who were also provided with comprehensive information regarding potential risks. Informed consent forms were signed by all subjects prior to their participation. Approval for the experimental protocol was obtained from the local medical ethics committee.

3.1.   EMG signal preprocessing

There was preprocessing of the acquired EMG signals. First, the baseline drift of all signals was corrected in the time domain by a sliding average method, so that the signal average value was around 0. Second, to account for varying levels of contraction movements in EMG signals, a Butterworth filter was employed for band-pass filtering within the range of 10 to 500 Hz to eliminate high and low frequency interference. Additionally, a notch filter at 60 Hz was utilized to mitigate industrial frequency noise. The denoised EMG signals were de-mixed. According to the previous study ^[5], the above pre-processing was able to achieve the desired results and extract the effective components of the EMG signal.

The propagation of the compound muscle action potential (CMAP) signal occurs from the site of motor unit activation, typically within a narrow region located midway between the two electrode pads, where an increased CMAParea is commonly observed. Figure 6(a) displays a map of the CMAParea for subject 1, illustrating the distribution of 128 channels. The horizontal and vertical coordinates correspond to the number of electrodes, with a total of 8 electrodes on the horizontal axis and 16 electrodes on the vertical axis, respectively. Each rectangle represents each channel electrode, 16*8 = 128 rectangles, representing the 128 channel electrodes in the experiment. The blue rectangle in the top right corner is channel 1, and the bottom left channel is channel 65. Channel 1 is the reference electrode. The red region depicted in the diagram represents areas with higher CMAParea, while the periphery is indicated by green shading.

It is worth noting that the wide coverage of the two electrode pads results in a time delay in the conduction of the CMAP signal from the site where the motor unit is activated to the edge of the electrode pads, causing a discrepancy in onset timing for CMAP signals across all 128 channels and making it challenging to intercept these signals ^[5]. For instance, Figure 6(b) illustrates how CMAP signals from all channels were superimposed for subject #1.

Figure 6 shows that the signal pre-processing has the expected effect. The weighted values of MUNIX and its coefficient of variation were calculated for different numbers of channels, using the unmixing of the high-density EMG data combined with the weighted average best contraction force method ^[21], to assess the variability of MUNIX repeatability under multiple channels.

3.2.   MUNIX comparative analysis

In the experiments, 9 levels (10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 100%) of myoelectric signals were sampled in each group, and according to the SIP inclusion criteria described by Nandedkar's team, 10 SIP data segments were selected at moderate intervals for each level of myoelectricity, with each data segment lasting 300 ms, in 9 levels of MVC. The 10 SIP signal data segments were selected among the sEMG signals obtained, and a total of 3*9*10 SIP data segments were obtained for the 3 sets of experimental data. It should be noted that both healthy and diseased subjects maintained a relatively short duration when performing maximal voluntary contractions, and thus only 5 SIP data segments could be extracted in 100% MVC, and these 5 SIPs were replicated to obtain 10 SIP data segments for ease of calculation. The first SIP data segment is selected from each level of muscle power to construct the SIP pool. The constructed SIP pool is used for the MUNIX calculation.

The comparison results of MUNIX values before and after unmixing for subjects 1 and 3 are listed in Table 1. As can be seen in Figure 7, there is a slight decrease in the value of MUNIX after unmixing, and the coefficient of variation between groups of MUNIX in subjects tends to decrease with the increase in the number of channels. However, this does not affect the diagnostic results of the disease, because the ultimate concern is the trend of this indicator of MUNIX over time. The change of MUNIX value is valuable for reference ^[5].

3.3.   Comparative analysis of coefficient of variation CV

The coefficients of variation of MUNIX at the number of n channels before FastICA demixing when n = 2, 4, 8, 16, 32, 64,128 are shown in Table 2.

In Table 2, the coefficients of variation between the three groups of MUNIX at the corresponding numbers of channels are calculated. The repeatability of MUNIX became worse, which is not what we would like to see. Incorporating multichannel EMG signals can provide richer and more comprehensive spatio-temporal information for MUNIX assessment, but we do not expect a decrease in MUNIX repeatability, which could be the result of introducing some kind of signal interference that reduces MUNIX repeatability.

The line graph illustrates a decreasing trend in the coefficient of variation after unmixing, as depicted in Figure 8. This is primarily attributed to the fact that when the number of channels is limited, the unmixing operation becomes more susceptible and thus may result in an increased coefficient of variation among the channels ^[42]. Figure 8 shows that the trend of the coefficient of variation follows strictly the pattern of smaller coefficients with a higher number of channels. When the signals of all 128 channels are included in the calculation of MUNIX, it can be found that the coefficient of variation becomes smaller. For example, the coefficient of variation of subject 1 decreases from 3.28 to 1.74, and the repeatability of MUNIX demonstrates a slight improvement.

3.4.   Comparative analysis of interrelationship number CC

In order to measure the degree of signal intermixing between channels, the number of interrelationships was introduced as a metric in the experiment. The comparison of CC between adjacent channels before and after the demixing process for 40% of MVC contractile EMG signals in subjects is presented in Table 3. From the table, it can be found that after the FastICA demixing, the mutual correlation number CC between adjacent channels is reduced, and the mixing components are removed to different degrees.

Several studies have shown that MUNIX values correlate well with CMAP magnitudes ^[4,14,17]. To validate the robustness of the findings, MAP plots illustrating CMAP and MUNIX values for subjects 1 and 3 subsequent to sEMG unmixing were generated and are depicted in Figure 9.

It is evident that the color shades of the CMAP and MUNIX maps for both subjects demonstrate a significant degree of similarity, indicating a robust correlation between MUNIX and CMAP values. This finding is consistent with ^[42], which suggests that even after the demixing process of EMG signals, MUNIX and CMAP remain highly correlated. Therefore, the results obtained from this experiment are considered reliable.

3.5.   Summary of results

The demixing of EMG signals, while preserving their integrity, facilitates the acquisition of pure source signals with enhanced clarity and waveform information, thereby enabling a more realistic representation of central motor neuron activity for clinical physiological analysis. The high-density sEMG signal of this experiment has undergone demixing processing to effectively mitigate channel coupling and minimize the impact of signal crosstalk and other confounding factors, thereby ensuring the accuracy of the data employed for MUNIX evaluation to a considerable extent.

4.   Conclusions

In this study, we proposed a negative entropy-based FastICA demixing method for assessing the reproducibility of MUNIX in high-density surface EMG signals. The utilization of a non-Gaussian metric enables the identification of an orthogonal rotation matrix, facilitating the projection of EMG signals with minimal negative entropy and thereby achieving the separation of nonlinear high-density surface EMG signals. The method's feasibility and effectiveness were validated through data analysis techniques, including the cross-correlation criterion, coefficient of variation and MUNIX. This study discovered that while maintaining a high correlation between MUNIX and CMAP, the inter-group variation coefficient of MUNIX and the inter-channel cross-correlation index of MUNIX tended to decrease. Additionally, as the number of channels increased, the repeatability of MUNIX improved. The limitations of the study, such as the lack of diversity among subjects, could be extended further. A more expansive discourse on how this constraint affects the results and ways to mitigate its effects would be beneficial in future studies. Future research endeavors could consider including individuals with neurological diseases or a history thereof as subjects, in order to determine whether similar findings are present in patients and to enhance the efficacy and generalizability of the research. In summary, our work is valuable for the sEMG signal processing methods and potential applications in the field of neurological disease diagnosis and management, as well as the prevention and control of neurological disorders.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Zhejiang Provincial Natural Science Foundation of China (No. LY20E050011) and the Zhejiang Provincial Innovative Incubation Projects for University Students (Emerging Artists Talent Program) (No. 2021R407016). The authors would like to thank Dr. Yingchun Zhang at the University of Houston for helpful discussions on this subject.

Conflict of interest

The authors declare there is no conflict of interest.