Synchronization analysis of coupled fractional-order neural networks with time-varying delays

1.   Introduction

In the past decades, neural networks (NNs), as a kind of nonlinear network model similar to brain intelligence, have been the focus of research because of their rich contents and wide applications ^[1,2,3]. As a famous physicist in the USA, Hopfield published two papers related to artificial NNs in the Proceedings of the National Academy of Sciences in 1982 and 1984 respectively, which caused a huge response ^[4]. Subsequently, many researchers have conducted further analyses based on Hopfield's exploration. Since then, different types of NNs have been put forward, such as Hopfield NNs, bidirectional associative memory NNs, fuzzy cell NNs, recurrent NNs and so on ^{[5,6,7,8,9,10,11]}. In particular, coupled neural networks (CNNs) have attracted widespread attention, because the brain can be regarded as multiple coupled neurons; so, the dynamic behaviors of CNNs are a vital step to further comprehend the science of the human brain ^[12].

Fractional calculus began to appear in the 17th century, and its applications are very wide; not only can it solve any order of differential problems, but it can also deal with any order of integral problems ^{[13,14,15,16]}. In fact, fractional-order calculus can be combined with NNs to form a new model called fractional-order NNs (FONNs). When the order of FONNs is equal to 1, the FONNs can be transformed into integer-order NNs. In particular, FONNs can solve more practical problems than integer-order NNs because it has the special characteristics of heredity and infinite memory ^[17]. Hence, FONNs are widely used in fluid mechanics, biological engineering, cell detection, signal processing, etc. So, the dynamic behaviors of FONNs, such as chaos, different types of synchronization and stability have always been the focus of our discussion ^{[18,19,20,21,22]}. It is worth noting that many dynamic analyses of coupled FONNs have been reported in recent years ^{[13,20,23,24]}. A large number of nodes interact with each other to form CFONNs, and each node can be regarded as a fractional-order dynamic system. Therefore, the dynamic analysis of CFONNs is meaningful.

CFONNs are classically complex networks, and their synchronization phenomenon is the main problem that has been explored by many researchers in the past decades ^[23]. There are many kinds of synchronization, such as pinning synchronization, adaptive synchronization, finite time synchronization, multi-quasi-synchronization and out lag synchronization and so on ^{[13,24,25,26,27,28]}. On the one hand, in ^[18] and ^[28], the stability and synchronization of FONNs with delay are studied. Adaptive synchronization of CFONNs has been established based on ouput quantization control ^[25]. The system studied by the authors of ^[10,11] has no coupling term. On the other hand, in ^[29] the authors discussed the Mittag-Leffler synchronization of FONNs. In ^[17], the Mittag-Leffler synchronization of fractional-order memristive NNs with delays under linear and nonlinear adaptive control are studied respectively. Although the complete synchronization and Mittag-Leffler synchronization of NNs have been discussed, these two types of synchronization for CFONNs with time-varying delays (CDFONNs) are rarely reported. In addition, because of the complexity of NNs, CNNs themselves may not achieve synchronization; therefore, for the sake of solving the synchronization problem, many references provide feasible control schemes ^{[24,28,30,31,32]}. For example, ^[24] provides pinning impulsive control; in ^[28], a feedback control scheme is given; and, in ^[30], the authors offer a delay-dependent distributed impulsive control scheme. And in order to choose fewer nodes to control, the related references put forward pinning control schemes ^[3,26,33,34]. Inspired by these reports, this article analyzes the complete synchronization of CFONNs under a pinning controller. But how many or which nodes should be selected for control? Moreover, it is worth noting that most of the time the control parameters play an important role in the controller. Hence, an adaptive control method with good performance and self-adjusting control parameters has been reported ^[17,35]. The design of adaptive control is related to the construction of the Lyapunov function; so, we aimed to answer the questions of how to design the controller and how to choose the appropriate Lyapunov function to make the neural network synchronization faster. These are the difficulties of this paper.

In addition, time delays are inevitable in life, and they include constant delays, discrete delays, mixed delays and time-varying delays, which are inevitable when a neuronal signal is transmitted. We can see that the dynamic behaviors of NNs will be more complex and changeable due to the effect of time delays ^{[13,25,36,37,38]}. In ^[36], the fractional-order complex network is composed of systems with linear terms without delays and coupling terms with delays; then, the linear matrix inequality criterion is used to solve the synchronization problem of this network. As for the synchronization problem of NNs with time delays, in ^[37] synchronization of NNs with time delays is discussed by using the method of centralized data sampling. The highlight of ^[38] is that the system investigated has kernel function, choosing an appropriate kernel function simplifies the calculation process and makes it easier to achieve synchronization. Therefore, it is valuable to choose the NN with time delays for analysis.

From what has been discussed above, the primary contents of this article are a discussion of complete synchronization under a pinning controller and a study of the Mittag-Leffler synchronization under an adaptive controller of CDFONNs. This article has the following three highlights:

(1) The idea of pinning control is to control part of the nodes and make the error system achieve stability so that the original system can attain synchronization. Compared to a normal linear controller that controls all nodes, the resource cost of this method is lower, and it is more attractive and desirable to choose fewer nodes to control the network.

(2) By designing a new adaptive controller, an important theorem is proposed to guarantee Mittag-Leffler synchronization of CDFONNs. The application of the controller is clever.

(3) The results show that pinning control and adaptive control have positive effects on the synchronization of CDFONNs. Under certain conditions, by controlling the gain coefficient and coupling strength, the synchronization speed will change accordingly.

Here is the framework of the remaining sections: Section 1 ends with the basic notations to be used in this paper. Section 2 not only gives the preparatory knowledge of fractional calculus, but it also provides the relevant definitions and lemmas, as well as the hypothesis required for the discussion in this paper. In Section 3, two controllers are designed to obtain theorems about two types of synchronization. In Section 4, two examples and simulation results verify the feasibility of the theorems. Finally, Section 5 provides a summary.

Notations: For the rest of this article, we present the following notation descriptions. $\mathbb{Z}^+$ is the set of positive integers, $\mathbb{R}$ and $\mathbb{R} ^n$ are the sets of real numbers and the $n$-dimensional real Euclidean space, respectively, and $\mathbb{R} ^{n\times n}$ denotes the set of $n\times n$ real matrices. $\mathfrak{L}_1[a, b]$ is the set of absolute integrable functions on $[a, b]$. Denote $\mathfrak{C}^\ell ([t_0, +\infty), \mathbb{R})$ as the space of continuous and differentiable functions of $\ell$-order from $[t_0, +\infty)$ to $\mathbb{R}$. The transpose of $\Lambda$ is denoted by $\Lambda ^\mathrm{T}$. $\Lambda_1\otimes \Lambda_2$ denotes the Kronecker product of matrices $\Lambda_1$ and $\Lambda_2$. For the matrix $\Lambda\in \mathbb{R} ^{n\times n}$, the minimum eigenvalue of $\Lambda$ is represented by $\lambda _{\min }(\Lambda)$, and similarly, $\lambda _{\max }(\Lambda)$ denotes the maximum eigenvalue. $\mathcal{T} = \{1, 2, \cdot\cdot\cdot, N\}$. $I_m$ is the $m\times m$ identity matrix. $||\cdot||$ is the Euclidean norm.

2.   Preliminaries and model

2.1.   Preliminaries

The fractional integral of order $\mathfrak{q}$ for a function $\mathfrak{F}(t) \in \mathfrak{L}_1[t_0, b]$ with $t\geq t_0$ is defined by

where $\mathfrak{q} > 0$, $\Gamma{(\mathfrak{q})} = \int_{0}^{\infty}{t^{\mathfrak{q}-1}e^{-t}\mathrm{d}t}$ and $\Gamma{(\mathfrak{q})}$ is a gamma function.

The $\mathfrak{q}$-order Caputo fractional derivative of the function ${\mathfrak{F}}(t)\in\mathfrak{C}^{\imath +1}([t_0, +\infty), \mathbb{R})$ is defined as

where $t\geq t_0 > 0$ and $\imath \in\mathbb{Z}^{+}$ such that $\imath -1\leq\mathfrak{q} < \imath$.

In this paper, we apply Caputo's fractional derivative; because the initial value in the sense of Caputo is of the integer order, the initial value of the derivative of the integer order is easy to obtain and the meaning is relatively clear, which is convenient for practical application modeling. More information about fractional derivatives can be found in ^[24,37,39].

2.2.   Model

CNNs have strong applicability and have been widely used to describe physical models in the fields of natural science and bioengineering; coupling between nodes can be used to express the connections and influences between some things. Compared with integer-order NNs, FONNs can more accurately describe the changing process of a system because of their characteristics. And in real life, many activities or things are affected by the time delays, so it is essential to consider the time delays. So it is valuable to investigate the synchronization of CDFONNs.

Throughout this paper, consider a class of CDFONNs composed of $N$ nodes governed by

where $i\in \mathcal{T}$ and $N\geq2$ is the number of subnetworks. ${\mathfrak{x} }_i(t) = {({\mathfrak{x} }_{i1}(t), \cdot\cdot\cdot, {\mathfrak{x} }_{in}(t))}^\mathrm{T}\in \mathbb{R} ^n$ denotes the $i$th state vector of the NN, ${\mathfrak{P} } = diag(\hat p_1, \hat p_2, \cdot\cdot\cdot, \hat p _n) > 0$ represents the self-feedback term of the $j$th neuron and $\breve{\mathcal{F} }({\mathfrak{x} }_i(t)) = (\breve{\mathcal{F} }_1({\mathfrak{x} }_{i1}(t)), \cdot\cdot\cdot, \breve{\mathcal{F} }_n({\mathfrak{x} }_{in}(t)))^\mathrm{T}\in \mathbb{R} ^n$ is the activation function. $\mathfrak{Q} = (\hat q_{ij})_{n\times n}$ is the connection weight matrix and $\mathfrak{R} = (\hat r_{ij})_{n\times n}$ is the delayed connection matrix; $\varrho (t) = (\varrho_1(t), \cdot\cdot\cdot, \varrho_n(t))^\mathrm{T}$ is the transmission delay vector with $0\leq \varrho_1(t), \cdot\cdot\cdot, \varrho_n(t)\leq \varrho$, $\sigma > 0$ is the coupling coefficient and the coupling matrix $\hat{\mathcal{G}} = (\hat{{g}}_{ij})_{N\times N}$, where $\hat{{g}}_{ij} > 0$ $(i\neq j)$ if there are direct connections from node $j$ to $i$, otherwise, $\hat{{g}}_{ij} = 0$. $\Gamma\in \mathbb{R} ^{n\times n}$ is a diagonal matrix denoting the inner connecting matrix, and its diagonal elements are $\gamma_1, \gamma_2, \cdot\cdot\cdot, \gamma_n$; $\mathfrak{J}$ represents the external inputs.

The initial conditions of CFONN (2.1) are described by

The isolated node of CFONN (2.1) satisfies the following equation:

where $\ddot { \mathfrak{z}} (t) = (\ddot { \mathfrak{z}} _1(t), \ddot { \mathfrak{z}} _2, \cdot\cdot\cdot, \ddot { \mathfrak{z}} _n(t))^\mathrm{T}$ represents the state target trajectory.

Correspondingly, the controlled network-related system (2.1) is given by

where $\mathfrak{U} _i(t)$ is a controller that needs to be designed later in this article.

Define $\breve{ \mathfrak{d}} _i(t) = {\mathfrak{x} }_{i}(t)-\ddot { \mathfrak{z}} (t)$; one has $\breve{ \mathfrak{d}} _i(t-\varrho(t)) = {\mathfrak{x} }_{i}(t-\varrho(t))-\ddot { \mathfrak{z}} (t-\varrho(t))$.

Combining (2.3) and (2.4), we can describe the error system as follows:

where $i\in \mathcal{T}$.

2.3.   Definitions and properties

First, several lemmas are introduced; then, some definitions of synchronization are given, and finally we present the hypothesis that we will need later in the discussion.

Lemma 1 ^[39]. Let $\Lambda(t)\in \mathbb{R} ^n$ be a derivable vector; then, for any positive matrix $\Sigma$, the following formula is correct:

Lemma 2 ^[39]. For any $\Lambda _1, \Lambda _2\in \mathbb{R} ^n$ and $\varepsilon > 0$, there exists a positive matrix $\mathcal{Q}\in \mathbb{R} ^{n\times n}$ that makes the following inequality true:

Lemma 3 ^[19]. Suppose that we have a system

This is a Caputo fractional differential system. Let $\overline{w} _1$ and $\overline{w} _2$ be two continuous non-decreasing functions; $\overline{w} _1(s)$ and $\overline{w} _2(s)$ are positive for $s > 0$, and $\overline{w} _1(0) = \overline{w} _2(0) = 0$. $\overline{w} _2$ is strictly increasing. If there is a continuously differentiable function $\overline{W}:\mathbb{R} \times \mathbb{R} ^n\rightarrow \mathbb{R}$ that makes $\overline{w} _1(||\aleph ||)\leq \overline{W}(t, \aleph)\leq \overline{w} _2(||\aleph ||)$, for $t\in \mathbb{R}, \aleph \in \mathbb{R} ^n$. Besides, there exist $\varsigma _1 > \varsigma _2 > 0$ such that

for $t\geq t_0$; then, the given Caputo system is globally uniformly asymptotically stable.

Lemma 4 ^[17]. Define two continuous non-negative functions $\mathfrak{g} (t)$ and $\mathfrak{h} (t)$, and one has

where $\hat{\mathfrak{y}}$ is a positive number. Then there exists a $T > 0$ and any positive constant $\ell$ such that

Definition 1 ^[24]. System (2.4) is said to obtain synchronization if the following condition is satisfied

Definition 2 ^[26]. Define the Mittag-Leffler function with two parameters $E_{\mathfrak{q}, \overline{\mathfrak{q}} }(\cdot)$ as follows:

where $\mathfrak{q} > 0$, $\overline{\mathfrak{q}} > 0$ and $s$ is a complex number.

In particular, if $\overline{\mathfrak{q}} = 1$, then the Mittag-Leffler function with one parameter is denoted by

Definition 3 ^[17]. The controlled system (2.4) is said to be Mittag-Leffler synchronized for any $\gamma > 0$ if there are $\mathcal{M}(\gamma) > 0, ||\varpi||\leq \gamma, \ell > 0$ and $T > 0$ such that

where $d > 0$ and $\mathfrak{q}\in (0, 1)$.

For generality, the assumption required in this paper is given as follows:

Assumption (A1) The activation functions $\breve{\mathcal{F} }_i(\cdot)$ in the NN are continuous and satisfy

for any $\hat\eth, \check\eth \in \mathbb{R}$, where $\mathfrak{w}_i > 0$ is the Lipschitz constant. Let $L = diag\{\mathfrak{w}_1, \mathfrak{w}_2, \cdot\cdot\cdot, \mathfrak{w}_N\}$.

For convenience, the following definitions are given

3.   Main results

Here, we will introduce several conditions to ensure the complete synchronization of system (2.4) under a pinning controller. First of all, the pinning controller is designed as follows:

where $\mathfrak{h}_i$ is the control gain; if node $i$ is selected to be pinned, then $\mathfrak{h}_i > 0$, if not, $\mathfrak{h}_i = 0$. Let $H = diag\{\mathfrak{h}_1, \mathfrak{h}_2, \cdot\cdot\cdot, \mathfrak{h}_N\}$.

For a complex dynamic network, it is a challenge to choose what kind of pinning scheme is required to achieve synchronization and how many nodes need to be controlled. For this paper, we referred to ^[40] and ^[41] and selected nodes whose out-degree is bigger than the in-degree as pinned nodes.

Next, from the above controller (3.1), we get the important theorem as below.

Theorem 1. Under Assumption (A1) and controller (3.1), if there is a diagonally positive definite matrix $\mathcal{Q}\in \mathbb{R} ^{n\times n}$ such that

where $\mathcal{P}\in \mathbb{R} ^{n\times n}$ is a positive diagonal matrix, then the CDFONN (2.4) is synchronized under controller (3.1).

Proof. First, consider the following Lyapunov function:

From (2.5) and Lemma 2 we can simplify (3.2) as follows

On the one hand, from Assumption (A1) and Lemma 2, there is a diagonal positive definite matrix $\mathcal{P}$ that yields

and

On the other hand, from the Kronecker product we can get the following two equations:

From (3.4)–(3.7), we know that (3.3) can be reduced as below:

where

So

Let $\lambda_1 = \frac{2\hat\lambda_1}{\lambda_{max}(\mathcal{Q})}, \lambda_2 = \frac{2\hat\lambda_2}{\lambda_{min}(\mathcal{Q})}$; then,

From the above inequality, using Lemma 3, we can know that system (2.5) is globally asymptotically stable; so, $\breve{ \mathfrak{d}} (t)$ converges asymptotically to 0. That is, under the controller (3.1), system (2.4) can achieve synchronization, and this completes the proof.

Remark 1. Looking at Theorem 1, we used pinning control; only some nodes need to be controlled to reach synchronization. Choosing some nodes for control can reduce resource waste compared with controlling all nodes. In ^[38,42], the controller considered for the system with time delays needs to control all nodes to realize synchronization. In ^[25] and ^[33], the synchronization of CFONNs is discussed, but the system under study has no time delays. In ^[34], the synchronization of FONNs with a delayed memristive network under pinning control is investigated. In contrast, the NN discussed in this paper is fractional, with both time delays and coupling terms. In addition, the control node selection scheme is different. In ^[26,43], the graph is divided into several subgraphs by using the pinned node selection scheme, and then the nodes control are selected. The aim of pinned nodes in Theorem 1 is to choose the nodes whose out-degree is bigger than the in-degree. Hence, the conclusions discussed in this paper under controller (3.1) for systems with time-varying delays are more widely applied.

Remark 2. If fractional-order $\mathfrak{q} = 1$, model (2.1) can be written as $\dot{\mathfrak{x} } _{i}(t) = -{\mathfrak{P} } {\mathfrak{x} }_{i}(t)+\mathfrak{Q} \breve{\mathcal{F} }({\mathfrak{x} }_{i}{(t)})+\mathfrak{R} \breve{\mathcal{F} }({\mathfrak{x} }_{i}{(t-\varrho(t))})+\sigma \sum_{j = 1}^{N} \hat{{g}}_{ij}\Gamma{\mathfrak{x} }_{j}(t)+\mathfrak{J}$; ^[3] and ^[30] discuss the synchronization of NNs under pinning control. Therefore, the result of Theorem 1 can be generalized to the corresponding integer-based NNs; then, the synchronization criteria are available. In addition, the coupling matrix in this article is not necessarily symmetric, irreducible or Laplace transformed. Therefore, the conditions in this paper are more favorable.

Remark 3. Assumption (A1) is commonly used in many studies in which the Lipschitz constant is always positive ^[25,37,38]. In fact, Assumption (A1) can be generalized as follows, namely Assumption (A2):

where $\breve{\mathfrak{w}} _i^{-}$ and $\breve{\mathfrak{w}} _i^{+}$ can be negative, zero or positive. In this case, letting $\breve{\mathfrak{w}} _i^{'}$ denote the maximum values of $|\breve{\mathfrak{w}} _i^{-}|$ and $|\breve{\mathfrak{w}} _i^{+}|$ and ${L}'$ be a diagonal matrix whose elements $\breve{\mathfrak{w}} _i^{'} > 0$, $i\in \mathcal{T}$, then

From Assumption (A2), we quickly arrive at the following conclusion.

Corollary 1. Under Assumption (A2) and controller (3.1), if there exists an $n\times n$ positive definite matrix $\mathcal{Q}$ satisfying the following conditions:

where $\mathcal{P}$ is a positive diagonal matrix and $\mathcal{P}\in \mathbb{R} ^{n\times n}$, then the controlled system (2.4) is synchronized under controller (3.1).

Now, we shall discuss Mittag-Leffler synchronization for CDFONNs. An adaptive-type feedback controller $\mathfrak{U} _i(t)$ is described below:

where $\eta$ and $h$ are arbitrary positive constants.

Theorem 2. Under Assumption (A1) and controller (3.8), if there are two positive definite diagonal matrices $\mathcal{P}, \mathcal{Q}\in\mathbb{R} ^{n\times n}$ such that

then the CDFONN (2.4) is Mittag-Leffler synchronized under controller (3.8).

Proof. Consider an auxiliary function as below:

Then

where $\mathfrak{k}^* = \min_{1\leq i\leq N}{ \mathfrak{k}_i^*}$; now, choose an appropriate constant $\mathfrak{k}_i^*$ such that $\sigma \mathfrak{k}^*||\Gamma||\geq ||\mathfrak{R} ||\; ||L||$; thus,

Therefore

where

so

let $\lambda_3 = \frac{2\hat\lambda_3}{\lambda_{max}(\mathcal{Q})}$; then,

From Lemma 4 and (3.10) we know that for any $\ell > 0$, there is $T > 0$ which gives

so

for $t\geq t_0+T$ when $||\varpi||\leq\gamma$, where

Thus, according to Definition 3, the controlled system (2.4) can realize Mittag-Leffler synchronization under controller (3.8); this completes the proof.

Remark 4. Adaptive control means that the controller can adjust its own parameters to adapt to the controlled network itself, or that the controlled network is affected by the environmental disturbance. From Theorem 2 we can see that the choice of Lyapunov function is related to the adaptive controller; the CFONNs can realize Mittag-Leffler synchronization by adjusting the control gain and coupling strength coefficient and using Razumikhin-type theory. In ^[17], an adaptive linear controller is setup to discuss the Mittag-Leffler synchronization of FONNs. The NN studied in this paper has coupling terms. And when model (2.1) is converted into an integral order model, we modify the adaptive controller; then,

After computing $\dot{\mathcal{W}} (t)$, we can still get the same conclusion by using a similar derivation of Theorem 2.

Remark 5. In Theorem 2, the controller we choose is linear. Note that in ^[17], the synchronous use of nonlinear controllers for FONNs is explored. However, the system studied in this article contains coupling, so we consider whether the system (2.5) can still achieve Mittag-Leffler synchronization if a nonlinear adaptive controller is used. The following is a description of this nonlinear-type adaptive discontinuous controller.

In our opinion, the nonlinear controller is more difficult than the linear controller, so it is more complicated to discuss the synchronization of system (2.5) under the nonlinear controller, which needs to be investigated more carefully in future research.

Remark 6. In ^[26], the authors point out that when the CFONN has no delay, and under the pinning controller, the CFONN has Mittag-Leffler synchronization. But when the CFONN has delays, it cannot guarantee Mittag-Leffler synchronization. This means that time delay affects the synchronization speed of CFONNs. Thus, we designed a linear adaptive controller, which allows CDFONNs to achieve Mittag-Leffler synchronization.

4.   Numerical examples

In this section, two examples are provided to illustrate the feasibility of our theoretical conclusion. And in the simulation process, we can see that the conditions of the main theorems are not difficult to obtain.

Example 1. Consider a 3-dimensional delayed NN given by (2.1)

where $i = 1, 2, 3$, $\varrho (t) = 1$, $\mathfrak{q} = 0.99$, $\mathfrak{P} = diag\{1, 2, 3\}$ and $\breve{\mathcal{F} }_j(\cdot) = 0.02tanh(\cdot)$. Let $\Gamma = diag\{1, 1, 1\}$; the connection weight matrices are as below:

the external input $\mathfrak{J} = (0, 0, 0)^\mathrm{T}$, and the coupling matrix is taken as

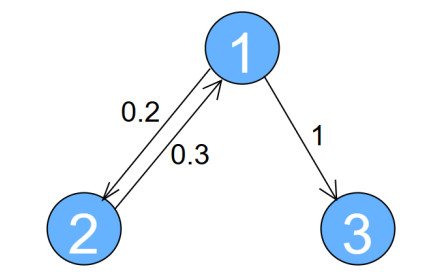
The topological structure of NN (2.1) is depicted in Figure 1.

Virtually, $\breve{\mathcal{F} }_j(\cdot)$ $(j = 1, 2, 3)$ satisfies Assumption (A1) and $\mathfrak{w} _i = 0.02$, so the matrix $L = \begin{pmatrix}0.02 & 0 & 0 \\0 & 0.02 & 0 \\0 & 0 & 0.02 \end{pmatrix}.$ In what follows, the dynamics of the system in Example 1 are discussed for a pinning controller. Select nodes 1 and 2 whose out-degrees are bigger than the in-degrees as controlled; let $\mathfrak{h}_1 = \mathfrak{h}_2 = 0.1$ and $\mathfrak{h}_3 = 0$, so $H = diag\{0.1, 0.1, 0\}$. Choose the coupling strength $\sigma = 2$. Then through the use of the MATLAB LMI toolbox, we found that the matrices $\mathcal{Q}$ and $\mathcal{P}$ satisfy

By simple calculation, we obtain $I_N\otimes\Phi+\Lambda > 0$, $\frac{L^\mathrm{T}L\otimes \mathcal{P}}{2} > 0$ and $\frac{\lambda_{min}(I_N\otimes\Phi+\Lambda)}{\lambda_{max}(\mathcal{Q})} = 0.0251 > \frac{\lambda_{max}(L^\mathrm{T}L\otimes \mathcal{P})}{2\lambda_{min}(\mathcal{Q})} = 9.934\times 10^{-6} > 0$. From Theorem 1 and the above calculation, one can accurately obtain that system (2.4) is synchronized. And Figure 2 displays the simulation results of Example 1.

Example 2. We discuss the CDFONNs with $n = 2$ and $\mathfrak{q} = 0.99$, that is

where $i = 1, 2$, $\breve{\mathcal{F} }_j(\cdot) = 0.01tanh(\cdot)$, $\varrho(t) = 1$ and $\mathfrak{P} = diag\{1, 1\}$. And the connection weight matrices are as follows:

Virtually, $\breve{\mathcal{F} }_j(\cdot)$ $(j = 1, 2)$ satisfies Assumption (A1) and $\mathfrak{w} _i = 0.01$, so the matrix $L = \begin{pmatrix}0.01 & 0 \\0 & 0.01 \end{pmatrix},$ let $\Gamma = diag\{1, 1\}$, the external input $\mathfrak{J} = (0, 0)^\mathrm{T}$ and the coupling matrix be described as

In what follows, the dynamics of the system in Example 2 are discussed for an adaptive controller with time delays. Select the coupling strength $\sigma = 0.1$ and control parameters $\eta = 0.001$, $h = 0.001$. Through the use of the MATLAB LMI toolbox, the solutions can be derived as follows:

In view of Theorem 2, we can calculate that $\Omega < 0$. So from the above, it can be obtained that the error system is Mittag-Leffler synchronized under an adaptive controller with time delays. And Figure 3 shows the simulation results of Example 2. The initial conditions $\mathfrak{k}_1(t) = 0.2$, $\mathfrak{k}_2(t) = 0.4$, $m_1(t) = 0.2$ and $m_2(t) = 0.2$; then, the adaptive feedback gains $\mathfrak{k}_i(t)$ and $m_i(t)$ are given in Figure 4, respectively.

5.   Conclusions

In this article, the two types of synchronization of CDFONNs are introduced based on a pinning controller and an adaptive controller. First, the Kronecker product and Lyapunov direct method were used to get some sufficient conditions for complete synchronization of the CDFONNs in which the pinning controller only needs to control part of the nodes to make the system achieve synchronization. Second, by designing a new adaptive controller, CDFONNs can achieve Mittag-Leffler synchronization using the Razumikhin-type method and Mittag-Leffler stability theory. In fact, many phenomena in life can be explained by complete synchronization and Mittag-Leffler synchronization. For example, to study the situation of water pollution spreading along rivers and causing pollution to surrounding cities, urban water pollution can be abstracted as nodes, which can form a network. If certain levels of pollution are synchronized, then a study of pollution in one city shows that similar levels are found in cities around a river. For another example, the urban transport network can be seen as a dynamic complex network, which is affected by the traffic behavior of its participants. Our results extend those of the available literature.

It is worth noting that the synchronization of integer order NNs has been introduced by many scholars, who showed that the adaptive controller without delays can achieve synchronization for the system. However, there is no relevant literature to show that these results and methods can be generalized to fractional order. Hence, it is still possible to design an adaptive controller without delays to make CDFONNs realize Mittag-Leffler synchronization. This will be one of our important research topics in the future.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

This work was supported by the Natural Science Foundation of China (62072164 and 11704109).

Conflict of interest

The authors declare that there is no conflict of interest.