A lightweight dual-path cascaded network for vessel segmentation in fundus image

1.   Introduction

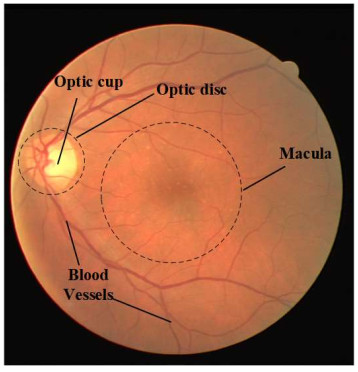
Retinal image assessment is indispensable for the identification of retinal pathology. It illustrates retina structure, such as blood vessels tree, optic cup, disc, and macula (shown in Figure 1). Fundus vessel segmentation is an essential step for diagnosing ophthalmic diseases. It requires manual segmentation by experienced ophthalmologists. However, this process faces many challenges. For example, the topological structure of vessels and the bending shape are complex, and there are many pathological areas around the branches of blood vessels. Besides, the collected images can be affected by the illumination and focus of the camera, which results in uneven brightness. These factors restrict ophthalmologists' segmentation accuracy and cause manual segmentation remains challenging.

Computer-aided medical image processing can assist the doctor in making an accurate and efficient diagnosis and taking proper treatment. Therefore, developing an efficient method for retinal vessel segmentation is of great value. With the development of computer hardware, a mass of automatic retinal vessel segmentation methods has been proposed. However, these methods are still unsatisfactory in terms of accuracy and time consumption. Therefore, this paper presents an LDPC-Net for retinal vessel segmentation. Its main contributions are as follows:

➢     Design a SD convolution block in the encoding and decoding parts to alleviate the over-fitting problem.

➢     Introduce the DSC technology into the structured convolution block to reduce the number of parameters.

➢     Construct a residual atrous spatial pyramid pooling (ASPP) in the connection layer to integrate multi-scale information and expand the receptive field.

The following Section 2 gives an introduction to related work. Section 3 details the proposed method, Section 4 provides the experimental results and analysis, and the final Section 5 presents the conclusion of this paper.

2.   Related works

2.1.   Matched filter

Chaudhuri et al. ^[1] introduced a two-dimensional matched filter into the fundus vessel segmentation task. However, due to the complex shape of fundus blood vessels, single-scale matched filters cannot identify variable blood vessels. To solve this problem, Li et al. ^[2] established the response relationship of matched filters on three scales and proposed a simple and efficient multi-scale matched filtering method. Sreejini et al. ^[3] provided the particle swarm optimization algorithm in the multi-scale matched filter method. Saroj et al. ^[4] proposed a novel matched filter approach based on Fréchet probability distribution function for blood vessel segmentation.

The matched filter method for fundus vessel segmentation is easy to implement, and the amount of calculation is relatively tiny. However, these methods are severely restricted by factors such as image contrast and noise, and the ability to distinguish blood vessel pixels from background pixels is relatively poor.

2.2.   Vessel tracking

Aibinu et al. ^[5] proposed a method with a better segmentation effect at the intersection and branch of vessels. They use the mixed intersection number method to identify vessels' intersection and branch points and realize blood vessel tracking and extraction. On the other hand, the linear multi-scale tracking method proposed by Vlachos et al. ^[6] adopts the initial seed node as a blood vessel pixel block and tracks according to the grayscale characteristics of the blood vessel pixels. When the condition of the cross-sectional outline of the blood vessel is invalid, the tracking is stopped, and then the meshed extraction of the blood vessel is formed. Therefore, the vessel tracking method can obtain a very accurate width of the segmented target. Still, the segmentation effect largely depends on the selection of the initial seed node. It is also susceptible to noise interference, which may cause the problem of segmented blood vessels to be broken.

2.3.   Morphology

Zana et al. ^[7] first determined the Gaussian-like contours of vessels, combined morphological processing with cross-curvature evaluation, and segmented blood vessel images. Fraz et al. ^[8] further obtained the vessel skeleton based on detecting the vessel's centerline, got the direction map through morphological plane slices, and simultaneously generated the vessel's shape. The vessel neutral line image is reconstructed through the orientation map and vessel shape, and finally, the segmented vessel choroid map is obtained. Yang et al. ^[9] applied mathematical morphology and fuzzy clustering algorithm to propose a hybrid method to extract vessels. The morphological-based process has fast calculation speed and strong anti-interference ability. However, the selection of structural elements limits the segmentation effect of these methods without considering the delicate features of blood vessels, and the accuracy of segmenting blood vessels is low. Mardani et al. ^[10] proposed a new algorithm for segmenting retinal blood vessels in medical images. They used the density-based spatial clustering of applications with noise (DBSCAN) and the morphological reconstruction (MR) techniques.

2.4.   Classification

Staal et al. ^[11] used the K-nearest neighbor algorithm to intercept the first k data for further comparison to determine its category, essentially performing binary classification on each pixel. Soares et al. ^[12] used a two-dimensional Gabor filter to extract the overall features of the retinal image. Then they classified the retinal blood vessels and background through a naive Bayesian classifier. Khowaja et al. ^[13] proposed a framework based on a hybrid feature set and hierarchical classification method. They use random forests for classification and evaluating the performance of each feature category for feature set selection and then combine the selected feature set with the classification method for vessel segmentation.

2.5.   Neural network

The proposal of U-Net ^[14] makes the U-shape network an efficient segmentation framework. The U-Net stitches coarse features with fine features through skip connections, showing its applicability in medical image analysis. U-Net is a convolutional neural network architecture designed for biomedical image segmentation, but it has been successfully applied in various other domains as well. The network consists of a contracting path, which encodes the input image into a small feature map, and an expanding path, which produces a segmentation mask of the same size as the input image. The contracting path is designed to capture the context of the input image, while the expanding path uses this context to produce a fine-grained segmentation mask.

Compared to traditional image segmentation algorithms, U-Net has several advantages. First, it can handle complex and irregular object shapes since it uses a convolutional neural network to learn complex image patterns. Second, it can be trained end-to-end, which means that the entire network can be optimized simultaneously for the task of image segmentation. Third, it can be easily adapted to new datasets and segmentation tasks since it only requires a small number of annotated images for training.

Recent works ^[15,16,17] have extended the U-Net architecture by adding various modifications, such as skip connections, attention mechanisms, and multi-scale input. These modifications have improved the performance of U-Net in various tasks, such as semantic segmentation, instance segmentation, and image-to-image translation. Specifically, many retinal vessel segmentation approaches are based on U-Net. For example, Wu et al. ^[18] proposed a multi-scale follower network-MS-NFN model to solve the problem of small blood vessel segmentation. The LadderNet presented by Zhuang et al. ^[19] introduces multiple sets of encoding and decoding structures, and skip connections also increase the path of information flow. Alom et al. ^[20] proposed a recursive residual convolutional neural network R2U-net based on a U-shaped network model, which better preserves feature information and achieves the effect of feature reuse. Li et al. ^[21] proposed a small U-Net multiple iteration segmentation methods, IterNet, which considers the segmentation details while expanding the model depth. Gu et al. ^[22] proposed CE-Net. This model introduces a feature extraction module for cascading context information in the middle layer of the codec, which can ensure the acquisition of complete feature information and extract deeper information. Lin et al. ^[23] combined HR-Net to propose a multi-path high-resolution retinal vessel segmentation method. It discarded the high-low-high architecture, and the feature map kept a high resolution in the network feature extraction process, making the retinal blood vessel probability map more accurate. Li et al. ^[24] proposed a lightweight attention network for retinal image segmentation, significantly reducing network parameters. Its primary network adopted U-Net, and the attention mechanism module was designed for its symmetrical structure. Zhang et al. ^[25] introduced new edge-aware flows into U-Net encoder-decoder architecture to guide the retinal vessel segmentation, which makes the segmentation more sensitive to the delicate edges of the capillaries. Deng et al. ^[26] proposed a D-MNet network combined with an improved PCNN (PulseCoupled Neural Network) model to bring together the advantages of supervised and unsupervised learning to improve the performance of retinal blood vessel segmentation.

In addition, there are other network models developed for high-level segmentation tasks. For example, He et al. ^[27] proposed a generative adversarial framework for COVID-19 infection segmentation. However, due to the complex vessel structure in fundus images, adversarial approaches may not be suitable for vessel segmentation. Alternatively, non-adversarial methods have also been extensively studied. For example, mu et al. ^[28] proposed the Progressive Global Perception and Local Polishing (PCPLP) network for automatically segmenting COVID-19-caused pneumonia infections in CT images. Zhao et al. ^[29] suggested a deep learning model that integrates a feature pyramid with a U-Net++ model for automatic segmentation of coronary arteries in ICAs. Additionally, Liu et al. ^[30] employed a deep, fully convolutional neural network to perform end-to-end segmentation of pathological tissue slices by combining distance maps and contour information, which was difficult to achieve using traditional segmentation methods.

Although the neural network-based methods can automatically learn features, avoid manual participation, have stronger robustness, and achieve promising results in vessel segmentation, the discontinuous phenomenon of vessel segmentation, blurred boundaries, and the identification of microvessels still exist. To summarize, there are three problems in the existing research: (i) Firstly, improving segmentation accuracy often leads to higher computational complexity. (ii) Secondly, some deep neural network models are prone to training overfitting. (iii) Thirdly, the concatenated layers of the encoder and decoder do not fully capture multi-scale information, and continuous pooling and convolution may further cause a decrease in the recognition rate of the vessel ends.

Therefore, it is still necessary to further explore the automatic segmentation method of fundus retinal vessels.

3.   Methods

3.1.   Overview

Figure 2 is the overall flowchart of the training LDPC-Net framework proposed in this paper. The process consists of three stages: 1) fundus image preprocessing and patch extraction. 2) feeding the patches into the LDPC-Net for prediction. 3) reconstructing the prediction results.

3.2.   Image preprocessing

This paper employs grayscale transformation, standardization, contrast-limited adaptive histogram equalization (CLAHE), and gamma correction for image preprocessing. Besides, we utilize the random cropping strategy for image expansion, and the sliced image is randomly flipped and rotated.

3.2.1.   Grayscale transformation

The image in the green channel has higher brightness and stronger foreground-background contrast. However, the image of the green channel still has a large amount of redundant information. Therefore, this paper employs the channel re-weighting strategy to implement the grayscale transform ^[31], which is defined by the following formula:

3.2.2.   Standardization

The data standardization formula is as follows:

where $\mu$ and $\sigma$ represent the mean and variance of the image data.

3.2.3.   CLAHE

To alleviate the problem of the low contrast of fundus images, the image data needs to be further processed by CLAHE after data standardization. First, we clip the unit pixel's peak value of the neighborhood histogram. Then, the redundant pixels are evenly distributed so that the overall area of the histogram does not change, thereby enhancing the contrast of the fundus image under the premise of effectively suppressing noise amplification.

3.2.4.   Gamma correction

The light intensity of the input retinal image is adjusted using the nonlinear gamma transform, and the intensity values are subjected to nonlinear operations so that the intensity values of the input and output images form an exponential relationship:

where A is a constant, γ is a gamma variable, and the V_in and V_out are both non-negative values. In this paper, we empirically select the correction value of γ = 1.2 to perform nonlinear regulation to increase the proportion of high and low gray values in the image and increase the contrast. As shown in Figure 3, the overexposed or too dark retinal images are corrected through nonlinear gamma transformation.

For the preprocessing data parameters, we randomly crop out patches of size 128 × 128 from the original image due to the large size of the fundus image. Then, all patches are normalized before being fed into the neural network. Finally, the probability maps predicted by the model are binarized with a threshold of 0.5 to obtain the final segmentation.

3.3.   Lightweight dual-path cascaded network (LDPC-Net)

In the LDPC-Net, the original input shape is 128 × 128 × 1, and a three-channel probability map with the same shape size is predicted. Since vessel segmentation is a binary classification task, we employed binary cross entropy (BCE) loss for backpropagation to make the prediction results closer to the ground truth through iteration and optimization. Its formula is defined as follows:

where g represents the label value, with two possible values of 0 and 1; p represents the predicted value of the pixel. When g is 0, the first half of the formula equals 0. If a smaller loss value is required, p should be as close to 0 as possible; otherwise, when g is 1, the second half of the formula is 0. For a minor loss, p should be as close to 1 as possible. Besides, the sigmoid activation function is necessary to ensure that the model output is in the range of (0, 1). In addition, the evaluation metrics for model performance are provided in Section 3.3.

The framework of the proposed LDPC-Net is shown in Figure 4, which consists of two cascaded U-shaped units, the rough segmentation unit, and the refinement unit. Each unit consists of two-layer downsampling structures, and the structured discarded (SD) convolutional block forms both the encoding and decoding parts of the model. Firstly, the encoder performs feature extraction via the SD block, and the downsampling operation is followed to extract high-level features. Secondly, the ResASPP model is used in the connection layer to aggregate multi-scale information. Finally, the decoder is deployed to restore the feature map to the same size as the input image and outputs the probability segmentation map.

After the rough segmentation process, the segmentation result is joined with the input image and input to the refinement unit for post-processing. The structure of the refinement unit is the same as that of the rough segmentation unit, except that SD introduces an additional residual process to avoid the problem of gradient disappearance.

3.3.1.   Structured discarded (SD) convolutional block

In the rough segmentation part, the SD shape consists of two repeat units (shown in Figure 5(a)). For the first unit, a 3 × 3 convolution kernel is used for feature extraction, followed by a structured DropBlock ^[32] layer. It is used to discard the continuous area of the feature map, which can effectively suppress the overfitting problem. The third layer is a classic batch normalization (BN) layer, which speeds up the training speed and alleviates the gradient disappearance; The fourth layer is the rectified linear unit (ReLU), employed to improve the expression level of the model. After the first unit, the iteration in the second SD block continues.

As the network structure is gradually complicated, we introduced the residual operation in the SD block, named $\overline{{\mathrm{S}}{\mathrm{D}}}$ (as shown in Figure 5(b)) to avoid network degradation problems in the refinement step.

3.3.2.   Depthwise separable convolution (DSC) module

To reduce the network's parameter amount and computational cost and achieve a lightweight architecture, we employ the depthwise separable convolution (DSC) technology to replace all the ordinary convolution operations in this paper. A schematic diagram of DSC is shown in Figure 6, which was first proposed by Chollet et al. ^[31].

In Figure 3, the DSC first peels off each channel of the input feature map. It uses depthwise convolution to convolve a single track to obtain the feature map of the first stage. Then, the convolution operation with the same number of channels and a convolution kernel size of 1 × 1 is used to perform pointwise convolution on the above feature map. It extracts the spatial information of each feature map at the same position and finally realizes the weighting of the feature map output via depthwise convolution combination.

The above process splits the conventional convolution operation and uses two different forms of convolution operation to reduce the number of parameters significantly. In this way, we built a deeper and more complex model using the same amount of parameters.

3.3.3.   Residual atrous spatial pyramid pooling (ResASPP) module

We designed the ResASPP module at the intermediate connection layer of the network to aggregate multi-scale information (as shown in Figure 7). The ResASPP consists of three parallel atrous spatial branches. The atrous convolution is used to avoid information loss while expanding the receptive field.

The main idea of atrous convolution is to set different atrous rates for feature extraction, which enable atrous convolution to capture multi-scale detail information. Therefore, the atrous ratios of the atrous convolutional layers of the three parallel branches are set to 2, 4 and 8, respectively. In addition, a residual connection is introduced in each branch to improve the information flow and reduce computational complexity. Moreover, we designed a bottleneck structure to reduce the computation of the larger convolutional layer. Therefore, the middle layer of LDPC-Net uses convolution to compress the number of channels of the feature map input to the larger convolutional layer and achieves a reduction of computation.

Figure 7 shows the detailed process of the bottleneck structure designed in this paper. First, it is processed using a 1 × 1 convolutional layer with 128 channels, followed by an atrous convolutional layer with a 3 × 3 kernel. After that, it is handed over to 1 × 1 convolutional layer with 256 channels. Through these operations, The bottleneck structure makes the network achieve a deeper level and improves the feature extraction ability accordingly.

3.4.   Evaluation metrics

1) Acc: It measures the proportion of correctly classified pixels, a representative evaluation metric for the vessel segmentation task.

2) Spe: It refers to the proportion of correctly classified non-vessel pixels to actual non-vessel pixels.

3) Sen: It is also known as the recall rate (Recall), which refers to the proportion of correctly classified blood vessel pixels to the actual blood vessel pixels.

4) PR: It refers to the ratio of the blood vessel pixels correctly classified to those classified as positive cases.

5) F1_Score: It can be seen as the harmonic mean of model precision and recall, and it will show satisfactory results only when the values of Sen and PR are high.

6) IoU: It represents the ratio of the intersection and union of the segmentation results of a specific method and the ground truth.

7) FLOPs: The Floating Point Operations (FLOPs) indicate the amount of floating-point operations the model performs during an information transmission process. FLOPs are mainly used to measure the computational complexity of the network.

8) Params: The number of parameters (Params) indicates the number of parameters stored in the network, reflecting the space complexity of the model. The parameters of the convolutional layer and the densely connected layer can be calculated by formulas (13) and (14).

Among them, H, W, and C_t represent the output feature map's height, width, and number of channels. Likewise, F_h and F_w represent the height and width of the convolution kernel, respectively. Finally, C_i is the number of channels of the input feature map, representing the densely connected layer's input and output dimensions.

4.   Experiments and results

4.1.   Datasets and implementation

All the experiments in this paper are implemented on three public fundus databases, including DRIVE, STARE, and CHASE_DB1 (DRIVE dataset (https://drive.grand-challenge.org/) STARE dataset (http://cecas.clemson.edu/~ahoover/stare/) CHASE_DB1 dataset (https://blogs.kingston.ac.uk/retinal/chasedb1/)). Table 1 lists the specific ways to divide the training and test sets.

We performed the proposed method using the Keras framework. Experiments and tests are implemented in Ubuntu 18.04 operation system with GPU 2080Ti. In the experiment, the BCE is used as the loss function, the Adam optimizer is used for iterative calculation, and the learning rate is set to 0.001. The batch size is set to 32, the epoch is set to 50, and an early stop mechanism is introduced during the training process. Based on these configurations, our training time on the three datasets is 47m 21s, 49m 56s, and 1h 12m 40s, respectively.

As shown in Figure 8, during the training stage, the loss value and accuracy rate changes on the validation sets of the three datasets are visualized separately. It can be found that at the 400th batch, the curve converges and becomes stable.

4.2.   Ablations

This section verified the gain of each module to the proposed framework on the public dataset. We set the cascaded UNet as the baseline and tested the improved framework performance after adding the SD and ResASPP modules. As shown in Table 2, adding the proposed modules to the baseline can improve the network performance, and all evaluation metrics are superior to the baseline.

Table 2 shows that compared with the baseline, the Acc and AUC values are not significantly improved after adding the SD block. It is because the DSC technology in the SD convolution is used for a lightweight purpose, which results in a loss of accuracy. However, compared with the single module, the integrated LDPC-Net model has improved in all evaluation metrics except for a slight decrease in specificity. It thus proved that the proposed model could combine each module's advantages and improve the overall segmentation performance.

4.3.   Quantitative comparison and analysis

To verify the effectiveness of the cascaded network, we evaluate the performance of the proposed model and the U-Net model for qualitative and quantitative analysis on the DRIVE, STARE and CHASE databases. The training and testing parameters, configuration, and datasets are consistent in the comparative experiment.

Table 3 lists the quantitative segmentation results. It can be seen that the Sen, Spe, Acc, and AUC values of the LDPC-Net on the DRIVE, STARE, and CHASE datasets are all higher than those of the U-Net model. Although the overall performance of the proposed method is superior to that of U-Net, the performance on the CHASE dataset, especially the AUC value, is not significantly improved compared with the U-Net model. The reason is that the proposed method focuses more on segmenting small blood vessels. Besides, some small blood vessels manually segmented by the second expert were not marked by the first, resulting in false negatives/positive errors.

Figure 9 presents a comparison of the two methods in a histogram. It can be observed that the sen of the proposed LDPC-Net is significantly higher than the U-Net, mainly due to our method's superior ability to deal with microscopic blood vessels.

4.4.   Qualitative comparison and analysis

We compare the qualitative segmentation results of the proposed model and the U-Net model on DRIVE, STARE, and CHASE databases. From Figures 10–12, we can see that the proposed model result in fewer artifacts at the mask boundary, and the false negative rate is also lower. Specifically, in the DRIVE dataset's third column and the STARE dataset's first column, the blood vessels that U-Net failed to segment were successfully extracted by our proposed LDPC-Net, which is also consistent with the ground truth.

In addition, from the second column of the CHASE dataset, we found that the segmentation results of U-Net are discontinuous; however, the blood vessels segmented by LDPC-Net show better connectivity. Compared with U-Net, the proposed method can detect blood vessels more completely while considering the segmentation of small blood vessels. The reason is that the proposed SD block enables the model to more accurately identify the edges of blood vessels and extract more positional information. Moreover, the ResASPP makes the model more capable of obtaining multi-scale information through a larger receptive field.

Finally, we can also observe from the area framed by the light green oval circle that, although the U-Net model identified most of the main blood vessels, it is ineffective in segmenting small vessels and areas with dense blood vessels. In contrast, our proposed LDPC-Net showed a higher segmentation recognition rate for small blood vessels and better connectivity at the vascular end.

4.5.   Comparisons with SOTA methods

To further verify the effectiveness of the proposed method in retinal vascular segmentation, we selected four metrics (Acc, Sen, Spe and AUC) to compare the proposed model with the state-of-the-art (SOTA) methods on the DRIVE, STARE, and CHASE databases. Table 4 lists the comparative result.

It can be seen from the table that compared with the SOTA method, the proposed LDPC-Net achieved superior performance on the three datasets. Specifically, it showed that it reached the best value on Acc, AUC, and Spe in the DRIVE datasets. In addition, the proposed method exceeds the average of all approaches in each metric, mainly because the proposed method's purpose is to significantly reduce the number of parameters while retaining relatively high accuracy as much as possible.

4.6.   Test on the generalization ability

The method's generalization ability is also essential from the application point of view. Therefore, we train the proposed LDPC-Net on the DRIVE dataset, save the model weights, and test it on the STARE dataset.

Figure 13 shows the segmentation results of the generalization experiment. It can be seen that the detection of blood vessels is relatively complete, and the ends and bifurcations were also segmented entirely, which verifies the consistency of the proposed method in different data distributions and its good generalization ability.

4.7.   Analysis of parameters and complexity

This section gives different model parameters and floating-point operations (FLOPs). In Table 5, we listed the model parameters, the complexity, and the AUC on the DRIVE dataset. Generally, the number of parameters of a model is directly proportional to its computational complexity. However, too few model parameters will also significantly affect the network performance. Compared with the SOTA models, our proposed model's number of parameters is considerably reduced. It can be seen that the proposed method is second only to that of ^[24] in terms of the number of parameters, mainly because the proposed network LDPC-Net has more layers. Still, it is acceptable, considering the improvement of the AUC value. Since the proposed LDPC-Net requires fewer model parameters and lower computational complexity, with superior segmentation performance compared with other models, the proposed model is competitive in considering both model performance and scale. The main reason is that the proposed LDPC-Net employs a structured discarding (SD) convolution module to alleviate over-fitting and utilizes the depthwise separable convolution (DSC) technique to reduce model parameters. In addition, the residual atrous spatial pyramid pooling (ResASPP) model effectively aggregates multi-scale information. Therefore, the proposed method could be a promising tool in rapidly diagnosing fundus diseases.

4.8.   Application

To enable cross-platform single-device high-speed online inference, we deployed LDPC-Net on the web using the Django (https://github.com/django/django) framework and ONNX (https://github.com/onnx/onnx) technology. Figure 14 presents a screenshot of the application system of the proposed method.

Accurate and efficient segmentation of eye fundus images is critical for diagnosing and monitoring diseases such as diabetic retinopathy, age-related macular degeneration, and glaucoma. The method proposed in this paper takes into account both accuracy and lightweight. Specifically, this paper's dual-path structure and multi-scale aggregation model could inspire society in network structure design, thereby promoting the development of automatic fundus image segmentation technology. In addition, it is worth noting that the proposed framework could also be deployed and applied in other image processing and analysis, such as thermographic fault diagnosis based on the analysis of thermal images [43.44].

5.   Conclusions

This paper proposes a lightweight dual-path cascaded network (LDPC-Net) for automatic and fast vessel segmentation in fundus images, which is crucial in clinical ophthalmic diseases. The LDPC-Net employs a structured discarding (SD) convolution module to alleviate over-fitting, a depthwise separable convolution (DSC) technique to reduce model parameters, and a residual atrous spatial pyramid pooling (ResASPP) model to effectively aggregate multi-scale information. We performed qualitative and quantitative experiments on public datasets to verify the effectiveness of the proposed network. First, we demonstrate the model combination's effectiveness through ablation analysis. Then, through the comparative experimentation with SOTA methods, we prove that LDPC-Net can retain the accuracy as much as possible, meanwhile significantly reducing the number of parameters. In addition, the generalization experiments also verify the model's generalization ability. Finally, the comparative analysis of the parameter amount and computational complexity further proves the lightweight and efficiency of the LDPC-Net. However, although the proposed method effectively achieves lightweight, there is still room for improvement in segmentation accuracy. Therefore, in the future, we will consider choosing a better compromise between lightweight and accuracy to improve the networks. Besides, we also plan to test the proposed model on other medical images tasks, such as vessel classification and auxiliary diagnosis of ophthalmic diseases.

Conflict of interest

The authors declare there is no conflict of interest in this study.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China (No. 61701178), the Scientific Research Fund of Hunan Provincial Education Department (No. 22B0653) and Innovation and Entrepreneurship Project for College Students in Heilongjiang Province (No. 202210214042).