Stochastic sensitivity analysis and feedback control of noise-induced transitions in a predator-prey model with anti-predator behavior

1.   Introduction

In a population system, when a population preys on another population in order to survive, the preyed species will have a sense of self-protective, and this self-protective behavior is called anti-predation behavior. Species use a variety of methods to protect themselves, such as camouflage, avoiding confrontation, changing body color and releasing toxins in the form of chemical defense, and different species tend to protect themselves by using different methods ^[1]. But anti-predation behavior not only refers to prey attacking relatively weak predators, as it also includes prey killing stronger predators together, such as the phenomenon of herd defense, which occors when the prey is in sufficient numbers, the ability of the prey to better defend or camouflage itself increases, leading to reduced or even completely blocked predation ^[2,3,4]. For instance, Huang et al. ^[5] mentioned that when the prey species are spider mites, a possible source of disturbance is the web produced by these mites, which reduces the predator's walking speed and chances of catching prey. Therefore, predators not adapted to walking on the web may also starve to death in the presence of spider mites.

Using mathematical language to describe the relationship between predator and prey can provide a theoretical basis for problems encountered in real world. The interactions between biological populations are often characterized by functional response functions. In the predator-prey model, the intensity of the functional response of predators to prey is critical, as it enriches the dynamics of the predator-prey system ^[6]. Many researchers have investigated predator-prey models with the Holling type IV functional response function ^[7,8,9,10]. For example, Ruan and Xiao ^[8] studied the global dynamics of a predator-prey model with such a non-monotonic functional response function and proved that saddle-node bifurcation, Hopf bifurcation and B-T bifurcation would occur. Based on ^[8], Tang and Xiao ^[11] considered the influence of anti-predator behavior and proposed the following model with the Holling type IV functional response function:

where all parameters are positive. $r$ is the intrinsic growth rate of the prey. $k$ is the environmental capacity. $\beta$ is the capture rate of the predator. $\mu$ is the rate of conversion of prey to predator. $d$ is the natural death rate of the predator population. $\eta$ is the anti-predator behavior rate of the prey in response to the predator population. It is worth emphasizing that most works describe anti-predator behavior only through functional response functions, whereas the model (1.1) not only describes the phenomenon that the predation rate decreases with increasing prey density through the Holling IV functional response function, but it also characterizes the phenomenon that adult prey can kill weak predators. In ^[11], Tang and Xiao analyzed the existence and stability of all possible equilibria of the predator-prey model (1.1) with anti-predator behavior, and they conducted a detailed and complete bifurcation analysis, including saddle-node bifurcation, Hopf bifurcation, homoclinic bifurcation and B-T bifurcation of codimension 2.

The results of the deterministic model can indeed provide us with some theoretical reference, but the dynamics of the deterministic model depends closely on the initial value and model parameters, which are extremely sensitive to environmental fluctuations ^[12,13,14]. Obviously, the establishment of deterministic models is based on several identified populations, consistent patterns of behavior, and specific environments ^[15]. But real life is full of randomness and unpredictability. A series of biological and environmental factors in the ecosystem will cause population fluctuations, and environmental uncertainty, which is influenced by factors such as the temperature, the climate, and rainfall will lead to noise ^[16]. Fluctuations of the environment can even dramatically change the dynamic behavior of the model ^[17]. For example, Bawa et al. ^[18] experimentally demonstrated that extreme temperatures negatively affected Helicoverpa punctigera pupae. It was found that the application of heat stress to pupae could affect Helicoverpa punctigera population dynamics by reducing fecundity and prolonging pre-oviposition and affecting adult development. Due to heat exposure, the parent did not produce offspring. Therefore, in order to accurately characterize the impact of environmental fluctuations, many scholars have carried out a series of studies by incorporating stochastic factors into deterministic models ^{[19,20,21,22,23,24]}. For instance, Liu et al. ^[23] studied a state-transition predator-prey model with anti-predator behavior and higher-order perturbations, and they obtained the ergodic property by constructing a suitable stochastic Lyapunov function. Zhang et al. ^[24] proposed a stochastic predator-prey model with habitat complexity and prey aggregation efficiency, proved the existence, uniqueness and stochastic uniformity of the global positive solution of the model, and found sufficient conditions for the existence of ergodic stationary distributions. It is worth emphasizing that most of the existing literature on stochastic predator-prey models mainly pay attention to the long-term qualitative behavior of the model and the existence of an ergodic stationary distribution, while our work in this paper provides a quantitative analysis of how noise affects the system.

The research on the impact of environmental noise on the system has also attracted the attention of many scholars ^{[25,26,27,28]}. For example, Zhou et al. ^[25] studied stationary distribution, extinction and probability density functions for stochastic vegetation-water models in arid ecosystems, verified the theoretical results through numerical simulation based on the data and studied the impact of random noise on vegetation dynamics. Bashkirtseva et al. ^[29] proposed a novel method based on the stochastic sensitivity function technique to construct an analytical description of the stochastic forced equilibrium and loops of discrete-time models. Further, Yuan et al. ^[30] used the stochastic sensitivity function technique to analyze the noise-induced state transition phenomenon in a non-smooth producer-grazer model with stoichiometric constraints. They found that stochastic trajectories jump frequently between two stochastic attractors. From a biological point of view, people often prefer species to maintain a high biomass state to enrich the diversity and stability of ecosystems. Therefore, it is necessary to control the sensitivity of the ecosystem to environmental noise. In order to suppress the stochastic sensitivity of equilibrium points and limit cycles, Ryashko and Bashkirtseva ^[31,32] proposed control principles of stochastic sensitivity for equilibrium points and limit cycles respectively, and carried out numerical simulations with examples. In this study, we used the stochastic sensitivity function technique to respectively construct the corresponding confidence ellipses and confidence bands for equilibrium points and limit cycles, and then estimated the critical noise intensity at the noise-induced system state transitions. Next, different control methods were applied to stabilize the biomass at the attraction region of the coexistence equilibrium point and the coexistence limit cycle, respectively.

The rest of this paper is structured as follows. We outline the main results of the deterministic model (1.1) and formulate the corresponding stochastic predator-prey model with anti-predator behavior in Section 2. In Section 3, we analyze the state transitions between the equilibrium point and the equilibrium point (or the limit cycle and the equilibrium point) induced by noise; we also estimate the critical thresholds for state transitions by using confidence ellipses and confidence bands, respectively. According to the feedback control principle, we control the sensitivity between the two equilibrium points (or the limit cycle and the equilibrium point) in Section 4. Finally, we give a brief summary of this paper in Section 5 to conclude our study.

2.   Model formulation

2.1.   Restate the main results of the deterministic model

We briefly revisit some results from ^[11]: the system (1.1) has two boundary equilibria $E_0 = (0, 0)$ and $E_k = (k, 0)$, and up to two coexisting equilibrium points $E_{i} = (x_{i}, y_{i})$, $i = 1, 2$, where

where $A = d^{2}-3\eta(\eta a-\mu \beta)$, $B = d(\eta a-\mu \beta)-9\eta ad$, $\theta = \arccos{T}$ and $T = \dfrac{2Ad-3\eta B}{2\sqrt{A^{3}}}$. Further, we have the following lemma.

Lemma 1. For $k > x_{2}$, if there is a stable boundary equilibrium point $E_k = (k, 0)$, a stable node $E_{1}$, and a saddle point $E_{2}$, but $E_{1}$ gradually loses its stability as $k$ increases, then a locally stable limit cycle $\Gamma^{'}$ appears. In other words, the system (1.1) has two types of bistability: the coexistence of two stable equilibrium points $E_k$ and $E_1$ or a stable equilibrium point $E_k$ and a stable $\Gamma^{'}$.

For the purpose of our study, in this paper, we mainly focus on the parameter domains when the system admits bistability. Therefore, we treat the environmental capacity $k$ as a control parameter and fix other parameters of the model as follows:

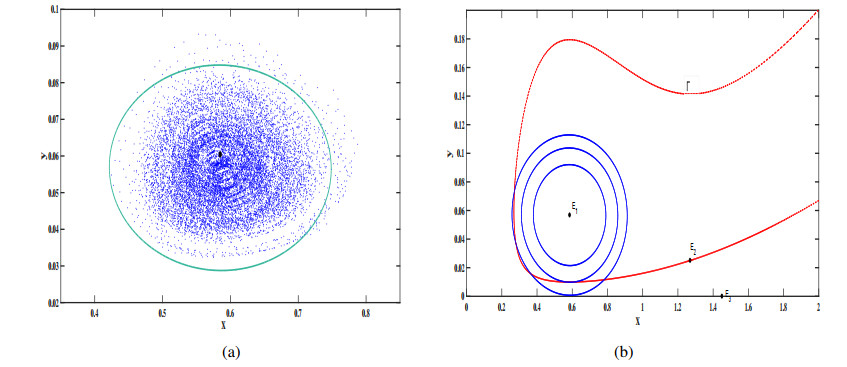
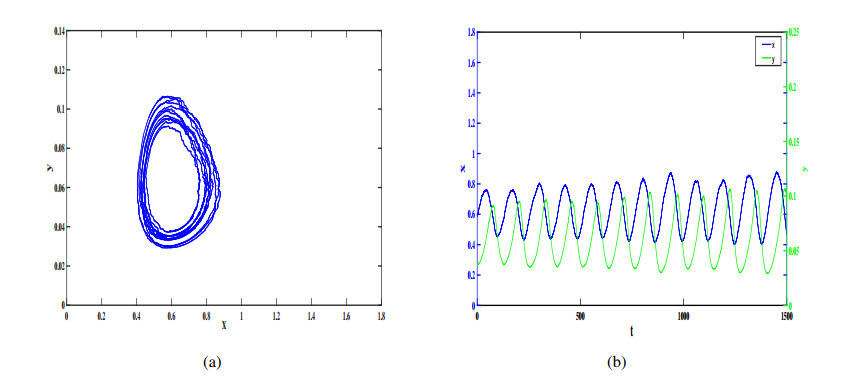
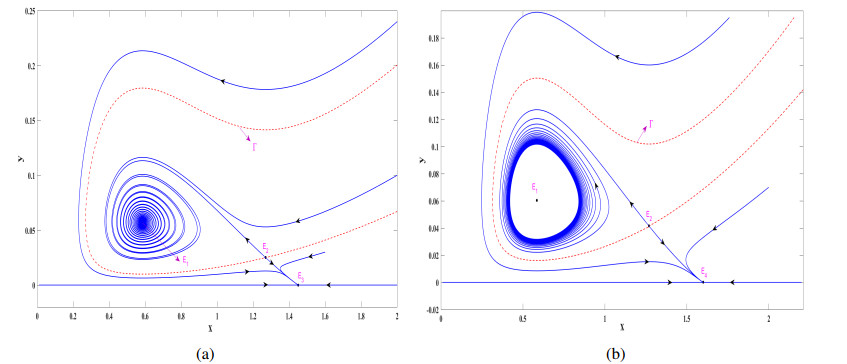
In this set of parameters, we take $k = 1.45$, and then system (1.1) has a stable coexistence equilibrium point $E_{1} = (0.58509, 0.05678)$, a saddle point $E_{2} = (1.26925, 0.02505)$ and a stable boundary equilibrium point $E_3 = (1.45, 0)$, as shown in Figure 1(a). The red dotted line $\Gamma$ in the figure is the separatrix between two domains of attraction in the first quadrant. The trajectories starting from the interior of the separatrix finally converge to the coexistence equilibrium point $E_{1}$, and the trajectories starting from the outside of the separatrix tend to the predator extinction equilibrium point $E_3$. That is, depending on the initial value, the final population will tend to the coexistence equilibrium $E_{1}$ or the predator extinction equilibrium $E_3$. When $k = 1.6$, as shown in Figure 1(b), the system (1.1) has a stable boundary equilibrium point $E_4 = (1.6, 0)$ and a saddle point $E_{2}$. $E_1$ loses stability resulting in a stable limit cycle $\Gamma^{'}$. In this case, the species biomass exhibits a periodic oscillation pattern.

2.2.   Stochastic model

Since the deterministic systems are inevitably affected by various environmental noises, which will further affect or even change the original properties of the deterministic model, we use the idea of small perturbation to incorporate the noise into the model. Thus, based on the model (1.1), we consider the following stochastic differential equation

where $B_{1}(t)$ and $B_{2}(t)$ are independent standard one-dimensional Brownian motions, which are defined in a complete probability space ($\Omega$, $\big\{\mathcal{F}_{t} \big\}_{t\geq 0}$, $Prob$) with a fltration $\big\{\mathcal{F}_{t} \big\}$ satisfying the usual normal conditions (right continuous and increasing while $\mathcal{F}_{0}$ contains all probability-null sets). $\sigma_{1}$ and $\sigma_{2}$ represent noise intensities. For simplicity, we assume $\sigma_{1} = \sigma_{2} = \sigma$ in our study. Next, we study the properties of the model (2.2).

3.   Analysis of noise-induced transitions

3.1.   Sensitivity analysis of noise-induced transitions between attractors

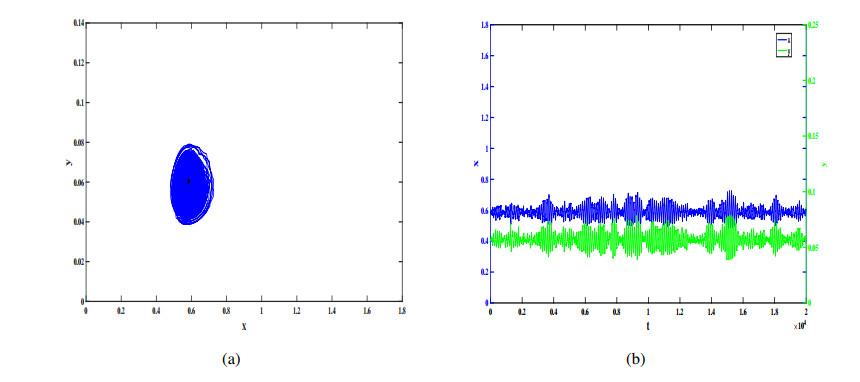
As mentioned earlier, for a deterministic model, the evolution of the solution is completely determined by the initial values and model parameters. But, for stochastic models, the behavior of stochastic trajectories can be very complex and interesting. Next, we will explore the dynamical behavior of the stochastic model (2.2) in the presence of noise. Take $\sigma = 0.004$ and the initial value $(0.5851, 0.0568)$ near $E_{1}$; the trajectory from this initial value will hover around $E_{1}$ (see Figure 2).

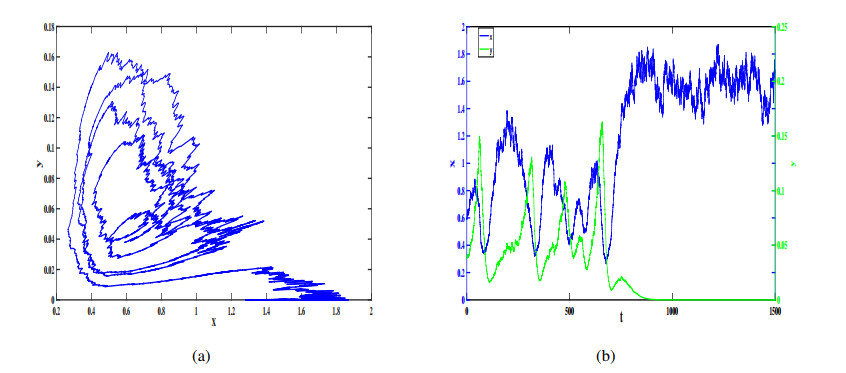
But when the noise intensity gradually increases and becomes large enough, the solution of the stochastic model (2.2) will behave very different from the behavior shown in Figure 2. Here, we take $\sigma = 0.0175$, and the stochastic trajectory escapes from the domain of attraction of $E_1$ and enters the domain of attraction of $E_3$. That is, in this case, the predator biomass tends to extinction while the prey biomass increases significantly (Figure 3). These noise-induced transitions suggest that the coexistence of the two species is disrupted and predators can be forced to extinction.

From the above analysis, it can be seen that the critical noise intensity $\sigma^{*}$ of the noise-induced stochastic model (2.2) state transitioning from the coexistence state to the prey-only state is between $0.004$ and $0.0175$. When $0.004 < \sigma < \sigma^{*}$, the stochastic model (2.2) has persistence; thus, the predator and prey coexist. To further determine the critical threshold $\sigma^{*}$ for noise-induced model state transitions, using the stochastic sensitive function technique in ^[33], we construct confidence ellipses for the equilibrium point $E_1$.

For the coexistence equilibrium point $E_1 = (x_{1}, y_{1})$ of the deterministic model (1.1), let $F = \left(\begin{array}{cccc} f_{11} & f_{12}\\ f_{21} & f_{22} \\ \end{array}\right)$ be the Jacobian matrix at $E_1 = (x_{1}, y_{1})$, where

we define $g_{11} = x$, $g_{22} = y$, and $G = \left(\begin{array}{cccc} g_{11} & 0 \\ 0 & g_{22} \\ \end{array}\right)$. After solving the following system of linear equations for $w_{ij}$, $i, j = 1, 2$,

we get the stochastic sensitive matrix as $W = \left(\begin{array}{cccc} w_{11} & w_{12}\\ w_{21} & w_{22} \\ \end{array}\right)$.

Given a noise intensity $\sigma$ and fiducial probability $P$, the confidence ellipse equation at $E_1 = (x_{1}, y_{1})$ can be obtained by applying Formula $A.3$ in ^[33] as

Applying the above method to the coexistence equilibrium point $E_{1} = (0.58509, 0.05678)$, we respectively obtain the corresponding stochastic sensitivity matrix and its inverse as

The confidence ellipse equation of $E_1$ is

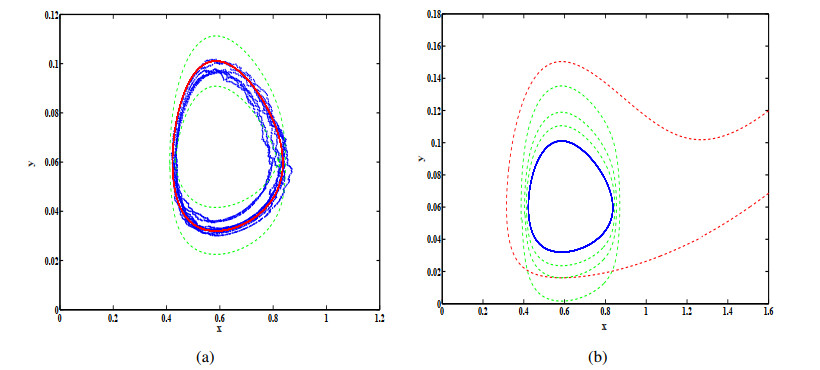
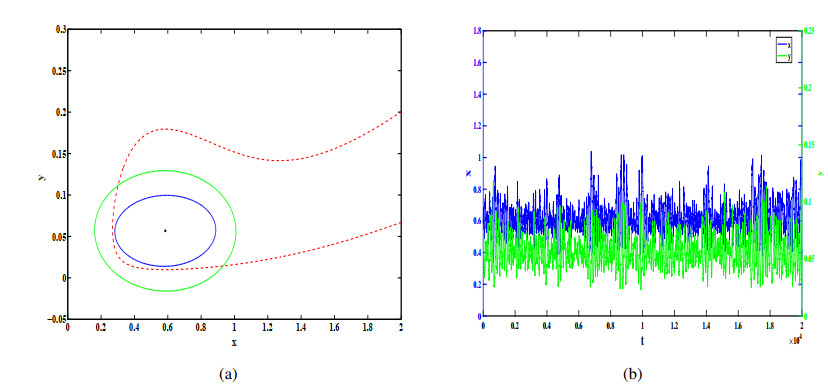
Fixing the fiducial probability at $P = 0.95$, we vary the noise intensity and observe the effect of the noise intensity on the confidence ellipse. The corresponding stochastic states and confidence ellipses of the system (2.2) with $\sigma = 0.00675$ are shown in Figure 4(a). This figure shows that the stochastic states are distributed around the deterministic equilibrium point $E_1$ and have a probability of $0.95$ of lying inside the confidence ellipse.

Next, we select different noise levels $\sigma = 0.0085$, $0.0113$ and $0.0135$, which respectively correspond to the small, medium and large confidence ellipses of the solid blue line in Figure 4(b). Obviously, with the continuous increase of the noise intensity, the confidence ellipse continues to increase and exceeds the separatrix $\Gamma$ of the two attraction domains; it contains the domain of attraction of the partial predator extinction equilibrium point $E_3$. When the confidence ellipse is tangent to the separatrix $\Gamma$, the corresponding noise intensity is the estimated value of the critical noise $\sigma^{*}$ of the noise-induced stochastic model state transition, where $\sigma^{*}\approx0.0113$. In Figure 3, a typical example is that the trajectory of the system (2.2) starting near the coexistence equilibrium $E_1$ converges to the prey-only equilibrium $E_3$ with $\sigma = 0.0175 > \sigma^{*}$.

3.2.   Sensitivity analysis of noise-induced transitions between the limit cycle and equilibrium point

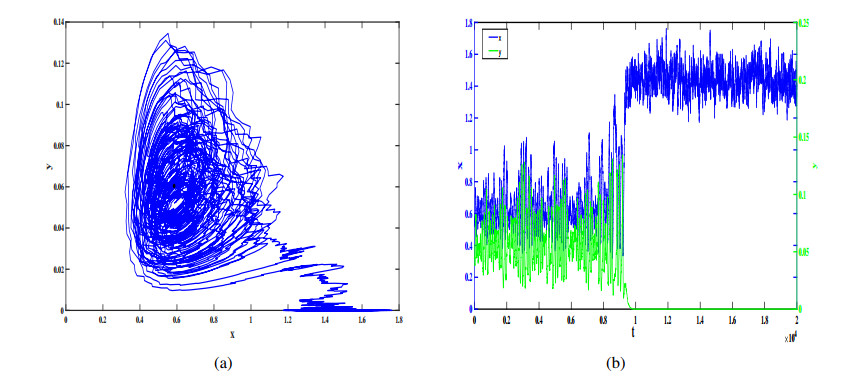
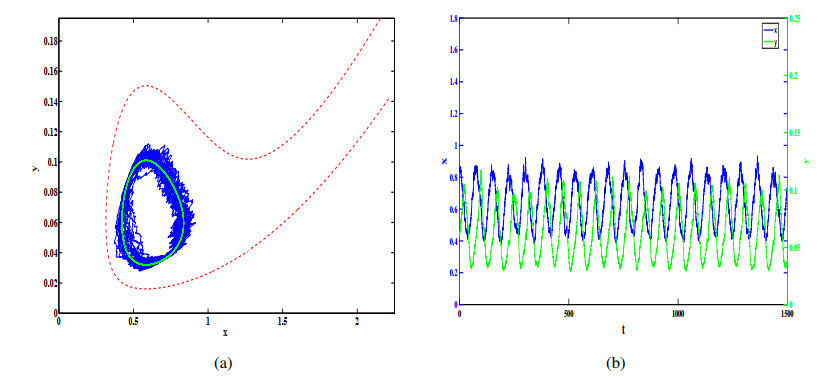
Similarly, we explore another dynamical behavior of the stochastic model (2.2) in the presence of noise. Take $\sigma = 0.004$ and the initial value $(0.5851, 0.0378)$ near the limit cycle $\Gamma^{'}$; the trajectory from this initial value will hover around the limit cycle (Figure 5).

But, when the noise intensity gradually increases and becomes large enough, the solution of the stochastic model (2.2) will behave very differently from the behavior shown in Figure 5. Here, we take $\sigma = 0.03$; the stochastic trajectory escapes from the domain of attraction of $\Gamma^{'}$ and enters the domain of attraction of $E_4$. In this case the predator biomass tends to extinction, while the prey biomass increases significantly (Figure 6). That is, the model (2.2) undergoes a state transition and finally converges to the prey-only equilibrium point $E_4$.

From the above analysis, it can be seen that the critical noise intensity $\sigma^{'}$ of the noise-induced stochastic model (2.2) transitioning from the coexistence state to the prey-only state is between 0.004 and 0.03. When $0.004 < \sigma < \sigma^{'}$, the stochastic model (2.2) exhibits persistence, which means that the predator and prey coexist. To further determine the critical threshold $\sigma^{'}$ for noise-induced model state transitions, using the stochastic sensitive function technique in ^[33], we construct corresponding confidence bands for the stochastic system (2.2).

For ease of calculation, define

Let $\Gamma^{'}(x(t), y(t))$, $t\in [0, T]$, where $T$ is the period, and denote the limit cycle of a deterministic model. According to the principle of confidence bands in ^[33], we can write

where

We know that the random sensitive function $\mu(t)$ satisfies the following boundary value problem ^[33]:

where

Here,

are the components of the vector function $p(t) = (p_{1}(t), p_{2}(t))^{T}$ orthogonal to the vector $(F_{1}(x, y), F_{2}(x, y))^{T}$. According to $A.5$ in ^[33], the boundary $\Gamma_{1, 2}^{'}(t)$ of the confidence band can be obtained as

where the parameter $k = erf^{-1}(P)$, $P$ is the fiducial probability, and $erf(x) = \dfrac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^{2}}dt$ is the error function.

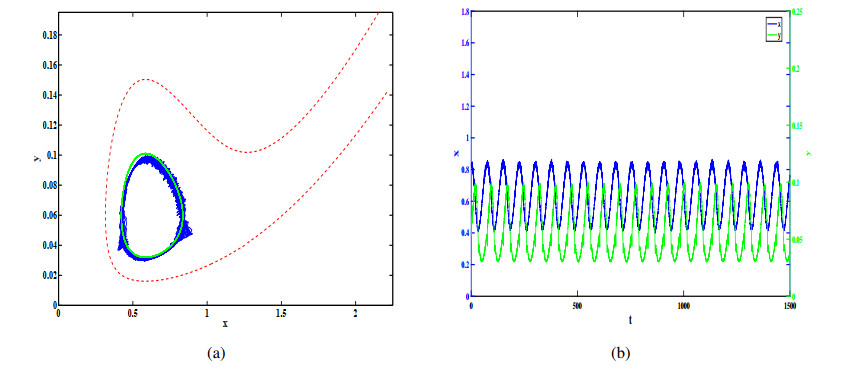
In Figure 7(a), $\sigma = 0.004$, $P = 0.95$, the red line is the deterministic limit cycle $\Gamma^{'}$, the blue points are the stochastic state of the stochastic model (2.2) and the two green dotted lines are the boundaries of the confidence band. Obviously, the stochastic state oscillates around the deterministic limit cycle $\Gamma^{'}$, and their probability within the confidence band interval is $0.95$.

In fact, judging whether the model has a state transition only requires attention to the outer boundary of the confidence band. As shown in Figure 7(b), the blue solid line is the deterministic limit cycle $\Gamma^{'}$, the red dashed line is the separatrix between the domains of attraction of the limit cycle $\Gamma^{'}$ and the predator extinction equilibrium point $E_4$ and the green dashed lines are the outer boundaries of the confidence band corresponding to $\sigma = 0.005$ (small), $\sigma = 0.0094$ (middle) and $\sigma = 0.018$ (large) with $P = 0.95$. It can be seen in the Figure 7(b) that, with the continuous increase of noise intensity, the outer boundary of the confidence band continues to increase to exceed the separatrix $\Gamma$ of the two attractive domains, and it contains the domain of attraction of the partial predator extinction equilibrium point $E_4$. When the outer boundary of the confidence band is tangent to the separatrix $\Gamma$, the corresponding noise intensity is the estimated value $\sigma^{'}$ of the critical noise of noise-induced transitions from coexistence limit cycles to the extinction equilibrium point. Here $\sigma^{'}\approx0.0094$. The case of $\sigma = 0.03 > \sigma^{'}$ in Figure 6 validates our conclusion.

4.   Feedback control of noise-induced system from coexistence to extinction

After the analysis in Section $3$, we find that there are two situations in which predator extinction occurs. As shown in Figure 3, when the noise intensity $\sigma = 0.0175$, the trajectory of the uncontrolled system (2.2) will escape from the attraction domain of the coexistence equilibrium point $E_1$, and eventually converge to the prey-only equilibrium point $E_3$. And, in Figure 6, when the noise intensity $\sigma = 0.03$, the trajectory of the uncontrolled stochastic model (2.2) starting from the attraction domain of the coexistence limit cycle $\Gamma^{'}$ will also pass through the separatrix of the two attraction domains, eventually tending toward the predator extinction equilibrium point $E_4$. But from a biological point of view, people often prefer species to maintain a high biomass state to enrich the diversity and stability of ecosystems. Therefore, we will study the sensitivity control problem of the equilibrium point or limit cycle next.

4.1.   Sensitivity control of the coexistence equilibrium point

From the analysis in Section $3.1$, it can be seen that the critical threshold for the state transition of the noise-induced system from the coexistence equilibrium point $E_1$ to the predator extinction equilibrium point $E_3$ is $\sigma^{*}\approx0.0113$. When $\sigma = 0.0175 > \sigma^{*}$, the trajectory starting from the vicinity of the equilibrium point $E_1$ finally converges to the prey-only equilibrium point $E_3$. In order to avoid the noise-induced state transition of the population from the coexistence equilibrium point $E_1$ to the predator extinction equilibrium point $E_3$, we introduce a feedback control strategy to make the corresponding confidence ellipse smaller and completely within the domain of attraction of the coexistence equilibrium point $E_1$. We consider the following model with controls:

where $(u_{1}(x, y), u_{2}(x, y))^{T}$ is the control factor and has the following linear form

Here, $K$ is the feedback matrix, and $(\bar{x}, \bar{y})$ is the locally stable equilibrium point $E_1$ of the system (1.1). Next, we will examine the following three control strategies:

According to the control method in ^[31], we note that for stochastic systems with added controls

where $f(x, u(x))$ is a sufficiently smooth vector function, $\epsilon$ is the scalar parameter of perturbation intensity, $\sigma(x, u(x))$ is a sufficiently smooth $n \times n$ matrix function characterizing the state and control, and $\omega(t)$ is an $n$-dimensional Wiener process.

Further, the system can be simplified as

The aim of the control is to provide an assigned stochastic sensitivity matrix $W$ by choosing a suitable feedback matrix $K$, where $K$ satisfies $Re\lambda_{i}(A+BK) < 0$. The matrix $W$ is the solution of the equation

If the rank $B = n$, then for the selected assigned positive definite matrix $W$, the feedback matrix $K$ is

If the rank $B < n$, the matrix $W$ satisfies the equation

where $B^{+}$ is the generalized inverse of $B$. Then the feedback matrix $K$ is

We take the parameters in (2.1), $k = 1.45$, $P = 0.95$ and the same noise intensity $\sigma = 0.0175$ as that applied in Figure 3. When we apply Strategy $1)$, the matrix $B = \left(\begin{array}{cccc} 1 & 0\\ 0 & 1 \\ \end{array}\right)$; then, we respectively choose the stochastic sensitive matrix and its inverse as

which is a symmetric positive definite matrix. Because $rankB = 2$, the feedback matrix is known from (4.2) as

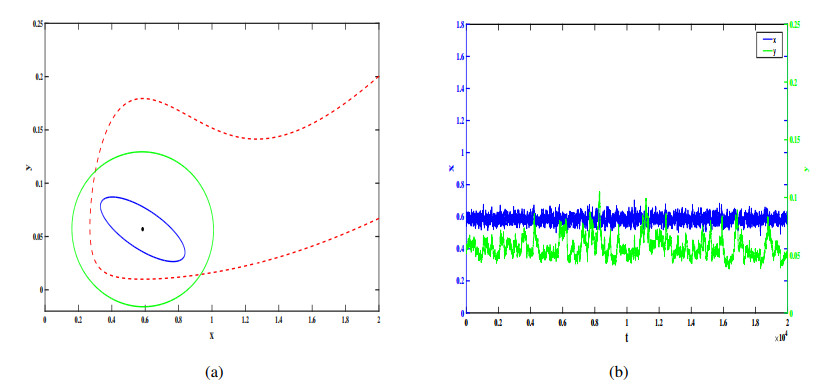
Then, the confidence ellipses of the uncontrolled system (2.2) and the controlled system (4.1) at the equilibrium point $E_1$ are as indicated by the green line and the blue line in Figure 8(a), respectively. Obviously, the confidence ellipse controlled by Strategy $1)$ is completely within the domain of attraction of the coexistence equilibrium point $E_1$. It can be seen in Figure 8(b) that the corresponding time series is maintained around high biomass. Unlike the extinction situation shown in Figure 3, the stochastic model after adopting the control strategy $1)$ avoids the extinction of predators.

When we apply Strategy $2)$, the matrix $B = \left(\begin{array}{cccc} 1 & 0\\ 0 & 0 \\ \end{array}\right)$; because $rankB = 1 < 2$, according to $P_{1} = BB^{+}$ and $P_{2} = I-P_{1}$, we have

We can respectively assign the stochastic sensitive matrix and its inverse as

satisfying (4.3); according to (4.4), the feedback matrix $K$ can be known as

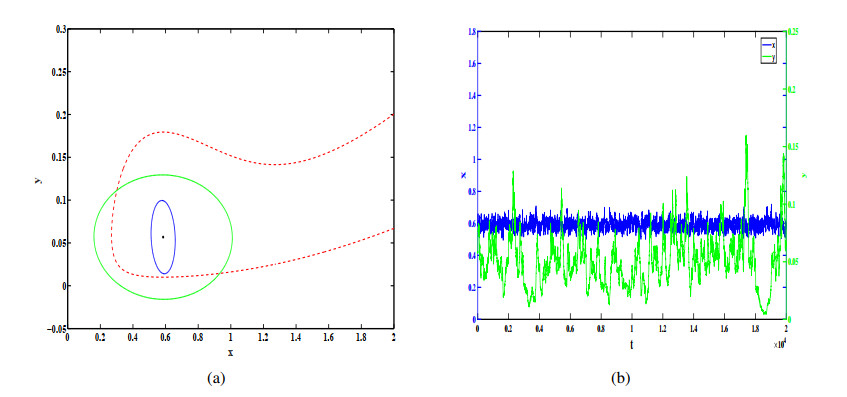
Then, the confidence ellipses of the uncontrolled system (2.2) and the controlled system (4.1) at the equilibrium point $E_1$ are shown as the green line and the blue line in Figure 9(a), respectively. Obviously, the confidence ellipse of the system being controlled by Strategy $2)$ becomes smaller and completely lies within the attraction domain of the equilibrium point $E_1$. Similarly, it can also be seen in Figure 9(b) that the corresponding time series is maintained around high biomass. Unlike the extinction situation shown in Figure 3, the stochastic model after adopting the control strategy $2)$ avoids the extinction of predators.

When we apply Strategy $3)$, the matrix $B = \left(\begin{array}{cccc} 0 & 0\\ 0 & 1 \\ \end{array}\right)$; because $rankB = 1 < 2$, according to $P_{1} = BB^{+}$ and $P_{2} = I-P_{1}$, we have

We can respectively assign the stochastic sensitive matrix and its inverse as

satisfying (4.3); then, according to (4.4), the feedback matrix $K$ can be known as

The confidence ellipse corresponding to the controlled system (4.1) is shown in Figure 10(a). Similar to the results of adopting Strategy $2)$, the confidence ellipse becomes smaller and completely lies within the attraction domain of the equilibrium point $E_1$. It can also be seen in Figure 10(b) that the corresponding time series is maintained around high biomass. Unlike the extinction situation shown in Figure 3, the stochastic model after adopting the control strategy $3)$ avoids the extinction of predators.

4.2.   Sensitivity control of coexistence limit cycles

According to the previous analysis, it can be seen that the critical noise intensity for the state transition of the noise-induced system from the stable limit cycle $\Gamma^{'}$ to the predator extinction equilibrium point $E_4$ is $\sigma^{'}\approx0.0094$. Here $\sigma = 0.03 > \sigma^{'}$; the trajectory starting from the vicinity of the limit cycle $\Gamma^{'}$ finally converges to the predator extinction equilibrium point $E_4$. To avoid noise-induced transitions from coexistence to extinction, we introduce a feedback control strategy to keep the solution of the system (2.2) in an oscillatory state, and then we consider the following control model similar to model (4.1):

where we take the parameters in (2.1), $k = 1.6$, $P = 0.95$, and the same noise intensity $\sigma = 0.03$ as that applied in Figure 6. $u_{3}(x, y)$, $u_{4}(x, y)$ represent the control function.

According to the control principle in ^[32], consider a stochastic control system

where $x$ is the $n$-dimensional state variable, $u$ is the $r$-dimensional control function vector, $f(x, u), \sigma(x, u)$ is the vector function, $\omega(t)$ is the $n$-dimensional Wiener process, and $\varepsilon$ is the noise intensity. Assuming $\varepsilon = 0$, $u = 0$, the system has a T-periodic solution $x = \xi(t)$, and the phase diagram trajectory is $\gamma$. The feedback control function $u(x)$ satisfies the following conditions:

$(a)$ $u(x)$ is sufficiently smooth and $u|_{\gamma} = 0$;

$(b)$ The deterministic system is

and the solution $x = \xi(t)$ is exponentially stable in the neighborhood $\Gamma$ of the cycle $\gamma$. Our aim is to control the stochastic sensitive function $W$, which satisfies the equation

where $p(t)$ is the normalized orthogonal vector at point $\xi(t)$. It can be seen that controlling $u$ changes only $F(t, u)$, and in fact, the result depends only on the value of the derivative $\dfrac{\partial u}{\partial x}$. Therefore, further consider the Taylor expansion of $u(x)$ at point $\gamma$

For $\gamma = \gamma(x)$, using property $(a)$, we get

where $\bigtriangleup(x) = x-\gamma$(x). It can be approximated as

where $\Phi(\gamma(x))$ is the feedback matrix coefficient; denote $K(t) = \Phi(\xi(t))$ and $t(x) = \xi^{-1}(\gamma(x))$; then, we have

Therefore, the feedback matrix $K(t)$ completely determines the ability of the regulator $u = K(t(x))\bigtriangleup(x)$ to synthesize $W(t)$.

When controlling for the stochastic sensitivity function of 2D-cycles, let the sensitivity function be $\mu$, and it is the solution of the following boundary value problem

Further, it can be seen that

where

According to (4.7), and given $\bigtriangleup = P\bigtriangleup$, $P = p^{T}p$, $k = Kp$, we know that

Then, change the feedback $k(t)$ to construct different stochastic sensitivity functions for the limit cycle. Denote $\bar{\mu}(t)$ as an assignment sensitivity function; then, a cycle $\gamma$ is completely stochastic controllable if and only if $\beta(t)\neq0$, $\forall t\in[0, T]$, and the relationship between $\bar{\mu}(t)$ and the control parameter $k(t)$ is

where

Next, notice the additional optimality criteria

Then the corresponding optimal control has a unique solution

and the corresponding Lyapunov exponent $\lambda$ of the system can be simplified as

Therefore, for any $\bar{\mu}(t) > 0$, we have $\lambda < 0$. That is to say, the selected sensitive function need only satisfy $\bar{\mu}(t) > 0$.

To avoid the extinction of predators, we exploit the limit cycle sensitivity control principle for the system (4.5) and assign the matrix $B = \left(\begin{array}{cccc} 1 & 0\\ 0 & 1 \\ \end{array}\right)$ and $\beta(t)\equiv p(t)$. It then follows from (4.11) that

which can be simplified to the following form

where $\bar{a}_{1}(t)$ is a scalar function of $\bar{\mu}(t)$ taking the following form:

where

and $\xi_{1}(t)$, $\xi_{2}(t)$ are the coordinates of the $T$ periodic vector function $\xi(t) = (\xi_{1}(t)$, $\xi_{2}(t))^{T}$ of the deterministic limit cycle $\Gamma^{'}$.

Next, we consider the two parameter control cases of the system (4.5). For the first one, $\sigma = 0.03$ and $\bar{ \mu} = 0.8$, the phase diagram of the system (4.5) is shown in Figure 11(a). The red dotted line in this figure is the separatrix of the attraction domain between the deterministic limit cycle $\Gamma^{'}$ and the predator extinction equilibrium point $E_4$. The green solid line is the deterministic limit cycle $\Gamma^{'}$. The blue line is the trajectory starting from $(0.836, 0.06)$ near the limit cycle after control. Obviously, the controlled stochastic trajectory oscillates near the deterministic limit cycle $\Gamma^{'}$, and the controlled trajectory is completely inside the attraction domain of the coexistence limit cycle $\Gamma^{'}$; its corresponding time series is shown in Figure 11(b). At this time, the solution of the system (4.5) remains oscillatory and the controlled model (4.5) avoids the occurrence of the predator extinction phenomenon in Figure 6.

Similarly, when $\sigma = 0.03$, $\bar{ \mu} = 0.03$, the phase diagram of the system (4.5) is as shown in Figure 12(a). The red dotted line is the separatrix between the two attracting domains, the green solid line is the deterministic limit cycle $\Gamma^{'}$, and the blue line is a controlled random trajectory starting from $(0.836, 0.06)$ near $\Gamma^{'}$. Obviously, the controlled stochastic trajectory hovers near $\Gamma^{'}$, but the oscillation amplitude is smaller than that for $\sigma = 0.03$, $\bar{ \mu} = 0.8$; the controlled trajectories are all located inside the attraction domain of the deterministic limit cycle $\Gamma^{'}$. The solution of the system (4.5) remains oscillatory, and its corresponding time series is shown in Figure 12(b). The controlled model (4.5) avoids the occurrence of the predator extinction phenomenon that can be seen in Figure 6.

According to the two different control results, unlike the predator extinction case shown in Figure 6, both control strategies can keep the solution of the system oscillating. It can also be seen in Figures 11(a) and 12(a) that the control sensitivity can avoid the occurrence of predator extinction, and that, with the decrease of the selected sensitivity function, the magnitude of population fluctuations is reduced.

5.   Discussion

In this paper, our focus was on noise-induced transitions from the coexistence state to predator extinction for a stochastic predator-prey model with anti-predator behavior. The corresponding deterministic model has two different bistable states under two different sets of parameters. When $k = 1.45$, as shown in Figure 1(a), the system (1.1) has a stable coexistence equilibrium point $E_{1} = (0.58509, 0.05678)$, a saddle point $E_{2} = (1.26925, 0.02505)$ and a stable boundary equilibrium point $E_3 = (1.45, 0)$. At this time, the system (1.1) has a bistable point between $E_{1}$ and $E_3$, the stable manifold of $E_{2}$ is the separatrix between the two domains of attraction. When $k = 1.6$, as shown in Figure 1(b), the system (1.1) has a stable boundary equilibrium point $E_4 = (1.6, 0)$, a saddle point $E_{2}$. At this time, $E_{1}$ is unstable, and there is a stable limit cycle $\Gamma^{'}$, the red dotted line $\Gamma$ in the figure is the separatrix of two domains of attraction. Obviously, there will be a coexistence area and a predator extinction area in both cases. We found that when the system is affected by a certain degree of environmental noise, the trajectory starting from the coexistence area will cross the separatrix and eventually converges to the predator extinction equilibrium. This is shown in Figures 3 and 6.

In order to estimate the critical threshold of the system state switching under the influence of environmental noise, we used the stochastic sensitive function technique to construct corresponding confidence ellipses or confidence bands for the two cases, respectively. Then, when the confidence ellipse (or the outer boundary of the confidence band) is tangent to the separatrix of two attraction domains, the noise intensity is the estimated value of the critical threshold for the state transition from coexistence to extinction.

When the environmental noise continues to increase, the confidence ellipse and the outer boundary of the confidence band will also become larger, gradually increasing to exceed the separatrix of the two attracting domains and contain part of the attracting domain of the predator extinction equilibrium point. But from a biological point of view, people often prefer species to maintain a high biomass state to enrich the diversity and stability of ecosystems. In order to avoid the occurrence of population extinction, we used two different feedback control methods to control the two situations respectively, and the "solution" of the controlled model was maintained around high biomass.

We mainly used the stochastic sensitivity function technique to find the critical threshold for noise-induced state switching, so as to maintain the biomass near high biomass levels, and we applied two different control strategies to the stochastic model. The system studied in this paper is a two-dimensional predator-prey system, so whether the stochastic sensitive function technique and feedback control technology used in this paper are suitable for a high-dimensional food chain system still needs further research.

Acknowledgements

The research was supported by the National Natural Science Foundation of China (12071293).

Conflict of interest

The authors declare there is no conflict of interest.