Dynamics of toxoplasmosis in the cat's population with an exposed stage and a time delay

1.   Introduction

Toxoplasmosis is the main cause of death associated to foodborne illness in the United States. It has been estimated that more than forty million persons in the U.S. carry the Toxoplasma parasite ^[1,2]. Toxoplasmosis disease is caused by the protozoan parasite Toxoplasma gondii (T. gondii). In the United States it is estimated that 11% of the population six years and older have been infected with Toxoplasma. In various places throughout the world, it has been shown that more than 60% of some populations have been infected with Toxoplasma. Infection is often highest in areas of the world that have hot, humid climates and lower altitudes, because the oocysts survive better in these types of environments ^[1,2,3].

The sexual cycle of T. gondii only takes place in members of the Felidae family and most of the studies on the sexual cycle have been carried out in cats ^[3,4,5]. Due to the difficulties in maintaining and sacrificing cats in the laboratory, there are relatively few papers dealing with the cycle of T. gondii in this host ^[4]. It has been recently reported that T. gondii sexual development in the intestinal cells of mice under some particular conditions is feasible ^[4,6]. Following a period of asexual reproduction by tachyzoite forms, the parasite enters a latent phase in the bradyzoite stage that persists for the host's lifetime in pseudocysts, macrophages and neurons of various tissues, notably in the brain ^[7,8].

T. gondii infects terrestrial and aquatic mammals and birds ^[4]. These animals are intermediate hosts because only asexual stages occur in them ^[4,7,8]. The sexual stages are seen only in the members of the family Felidae, including the domestic cat ^[3,4,9,10]. The final or definitive host are the cats, and other warm-blooded vertebrates are just intermediate hosts ^[7,8]. T. gondii can encysts in the brain, and can inhibit apoptosis ^[8]. Interestingly, the T. gondii parasite does not disturb the life of cats. It has been estimated that an infected cat can produce approximately $20$ million oocysts, between $4$ and $13$ days after the cat gets infected ^[11]. Domestic cats are able to excrete oocysts that can infect warm-blooded animals ^[12]. These oocysts contaminate the environment, including water, vegetables and various foods ^[13,14]. However, it has been shown that gamma irradiation can decontaminate food that contains oocysts ^[14]. Nevertheless, oocysts of T. gondii are spreaded in the environment. Therefore, control strategy studies for the toxoplamosis disease have been related to considering cat populations ^{[15,16,17,18]}. For a review of mathematical models for toxoplasmosis the reader can see ^[19].

The seroprevalence related to toxoplasmosis around the world is significantly high with values in the range of $30\%-40 \%$ ^[20]. In addition, cats are very popular in the world and therefore can contribute to the permanence of the toxoplasmosis disease ^[21]. One consequence of a high prevalence is that in 2013 congenital toxoplasmosis was estimated to be 1.2 million ^[19]. The congenital infection affects the eye and it is difficult to diagnose at birth but is present in $20\%-80\%$ of congenitally infected persons ^[1]. In Europe all pregnant women are tested for T. gondii infection, but there have been concerns about the cost–benefit of these tests ^[22].

The study of parasites is very important for the public health ^[23]. There are many studies that have used mathematical models to investigate the dynamics of a variety of parasites, even though models are simplifications of the real-world ^[24,25,26]. For toxoplasmosis dynamics several mathematical models have been proposed ^{[12,27,28,29]}. For instance, in ^[30] the author proposed a model to describe the coinfection dynamics of malaria-toxoplasmosis in the human and feline susceptible host population. In ^[18] the authors developed a differential equation model to investigate the effective transmission pathways of T. gondii and potential control mechanisms. A systematic review of previous mathematical models for the transmission of T. gondii is available in ^[19].

There are a variety of mathematical models with time delays that have been used in many different fields including biology ^{[31,32,33,34]}. In particular, there are many mathematical models for studying the dynamics of infectious diseases that are based on delay differential equations ^{[35,36,37,38]}. For instance, in ^[39] the authors studied an epidemic model with spatial diffusion and time delay and they found two different types of instability. One due to diffusion, and the other one related to the time delay. The time delays are introduced in order to model the effect of processes that are not instantaneous ^{[40,41,42,43]}. In ^[44], the authors studied a SEIS epidemiological model with a saturation incidence rate and a time delay representing the latent period of the disease. There are advantages and disadvantages of using mathematical models based on delay differential equations. For instance, there is more variety of dynamics with delay differential equations in comparison with ordinary differential equations. The introduction of time delays can change the stability of an equilibrium point and periodic solutions can arise ^{[45,46,47,48]}. In addition, in general obtaining the solutions of delay differential equations is more challenging than those of the ordinary differential equations ^{[49,50,51,52]}. There are a variety of analytical and numerical methods that have been developed to find the solutions of delay differential equations ^{[53,54,55,56]}.

In this work, we propose a mathematical model that includes a latent stage for the cats who become infected with the T. gondii parasite, since it is well-known that these cats are not able to produce oocysts instantaneously ^[3,5,7]. We focus on the cats since they are one of the main factors for the permanence of T. gondii in the environment ^[20]. The time delay represents the duration of the latent stage for the cats. The model also includes the oocysts related to the T. gondii in the environment. The oocysts, are of paramount importance in the survival of the T. gondii ^[3,7,57,58]. The model considers lifelong immunity for the recovered cats and vaccinated of cats. In addition, the model considers that cats get infected through an effective contact with the oocysts in the environment. The T. gondii parasite can be vertically transmitted and therefore we include this aspect in the model ^[59]. The model does not consider other intermediate hosts like rodents and birds and this is a limitation of the model. However, the proposed model is an improvement and generalization of the mathematical model presented in ^[60]. In ^[60] a model based on ODEs was developed to study the dynamics of toxoplasmosis on the cat populations and taking into account the oocysts that contain the T. gondii parasite. In ^[61] the authors extended the model to include a time delay between the time from when oocysts become present in the environment and when they become infectious. However, in this study we include the effect of a time delay between the time a cat has an effective contact with the oocysts and the time when the cats become infective and able to shed oocysts in their feces ^[62,63]. The entire enteroepithelial cycle of T. gondii can be completed within 3 to 10 days after ingestion of tissue cysts ^[62]. After the cats ingest sporulated oocysts, the formation of oocysts is delayed until 18 days or more ^[62]. In other words, a cat can undergo a latent period of a few days before casting feces with oocysts, which may last for 10–15 days ^[5,62,63]. In ^[63], the authors assumed a short latent period of three days. Thus, based on these aforementioned facts we propose the introduction of a latent stage in the cats and a time delay.

From a mathematical analysis viewpoint we study the stability of the equilibrium points of the model. We use the next generation method to find the basic reproductive number $\mathcal{R}_{0}$ for the model without the time delay ^[64,65]. Then, we study the model with the time delay and see the effects on the dynamics of toxoplasmosis. We numerically solve the delay differential equation system to corroborate the theoretical results and finally we provide additional numerical results to understand better the impact of the length of the delay on the dynamics.

We organized this paper as follows: In Section 2, we develop the model and present the main assumptions. In Section 3, we perform the local and global stability analysis of the steady states. In Section 4, we present a variety of numerical simulations. Finally, in Section 5 we present the conclusions.

2.   Materials and methods

Here we present a new mathematical model for the transmission of toxoplasmosis in cat populations taking into account the time delay between the time a cat has an effective contact with the oocysts and the time when the cats become infective and able to shed oocysts in the feces ^[3,5,11,62]. As in ^[60] the mathematical model allows the vaccination of the cats and the infection of cats through effective contacts with oocysts shed by cats. Previous studies have included vaccination for cats ^[60,66,67]. The inclusion of vaccines in the mathematical model makes possible the study of the effect of vaccines on the control of toxoplasmosis. The model assumes that the rate of infection depends on the environmental load of the T. gondii parasite ^[68]. The proposed model is based on a system of delay differential equations. For more details about the model see ^[60].

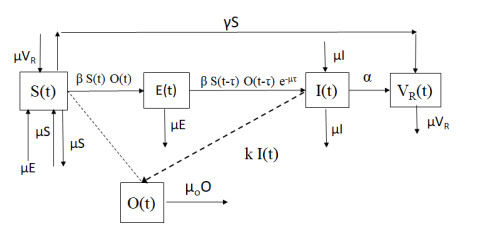
The model divides the cat population into four disjoint subpopulations: susceptible $S(t)$, latent $E(t)$, infected $I(t)$ and recovered $R(t)$ (includes vaccinated cats). The model uses one state variable $O(t)$ for the T. gondii oocysts. The model assumes that vaccinated cats have permanent immunity ^{[16,66,69,70]}. Moreover, the model includes a constant proportional vaccination rate, which is a standard way in mathematical modeling of infectious diseases. However, more realistic and complex vaccination types have been used for modeling for studying COVID-19 pandemic ^[71,72]. The population of cats is assumed constant. Susceptible cats transit to the latent subpopulation $E(t)$ after an effective contact with an oocyst. The latent stage is included as a time delay of $\tau$. The infected stage lasts an average of $\frac{1}{\alpha}$. The increase in the amount of oocysts is proportional to the infectious cats $I(t)$. In particular, the model assumes that the parameter $k$ is related to the oocysts that are shed per infected cat and per unit time. There is a removal rate of oocysts from the environment. It is assumed vertical transmission in the cat population due to congenital transmission ^{[73,74,75,76]}. For instance, in ^[77] the authors studied lactational transmission from infected cats to their kittens.

The mathematical model is based on a nonlinear delay differential equations given by

Without loss of generality, the population of cats is assumed to be ${N}(t) = S(t)+E(t)+I(t)+V_{R}(t) = 1$. The mathematical model flow is depicted in Figure 1. The initial conditions at time $t = 0$ are given by

We can disregard the subpopulation $V_R(t)$ and study the following reduced model

The reduced system (3) satisfies the initial conditions given by

where $\xi_1(s)$ and $\xi_2(s)$ are continuous function defined from the interval $[-\tau, 0]$ to $\mathbb{R}_{+}$, and with the norm $\|\xi_i\| = \sup\limits_{-\tau\leq s\leq 0} |\xi_i(s)|$. The susceptible subpopulation of cats is nonnegative for $t\le0$ and the number of oocysts is nonnegative for $t\le0$.

3.   Stability analysis of the Model

Let's see that in the constructed model the subpopulations are positive for all $t\ge 0$ and that they are bounded.

Theorem 3.1. If the parameters of model (3) are all positive and the initial conditions given by (4) are satisfied, then the solutions of the model (3) given by $\Big(S(t), E(t), I(t), O(t)\Big)$ remain positive and uniformly bounded in $[0, +\infty)$.

Proof. From (3), one gets that

Thus,

Let's suppose that there exists a $t_1 > 0$ such that $I(t_1) = 0,$ $\dot{I}(t_1)\le 0,$ and $I(t) > 0\, \forall \, t\in(0, t_1).$ Then, from the third equation of model (3), it follows that

However, $O(t) > 0$ for all $t\in (0, t_1).$ If this is not the case, there exists a $t_2 > 0$ such that $t_2 < t_1,$ $\dot{O}(t_2)\le 0,$ $O(t_2) = 0$ and $O(t) > 0$ for $t\in (0, t_2).$ From the fourth equation of system (3), it follows that $0\ge kI(t_2).$ This is a contradiction because $I(t) > 0$ for all $t\in(0, t_1).$ Thus, using the continuity of $O(t),$ it follows that $O(t) > 0,$ with $t\in(0, t_1].$ Therefore, (5) is false as $\tau\to 0^{+}$ and thus $I(t)\ge 0$ for $t\ge 0.$ From the fourth equation of system (3), it is concluded that $O(t)\ge 0$ for $t\ge 0.$ Next, the positivity for $E(t)$ it follows from the fact that solutions of the differential equations of $E(t)$ can be written as

Now, the subpopulation $S(t)$ is bounded by $\frac{\mu}{\mu+\gamma}$, because by the standard comparison theorem ^[78], we can show that

In particular, if $S(0)\leq \dfrac{\mu}{\mu+\gamma}$, then $S(t)\leq \dfrac{\mu}{\mu+\gamma}$. Analogously, one gets that $O(t)\leq \dfrac{k}{\mu_{0}}$ if $O(0)\leq \dfrac{k}{\mu_{0}},$ $E(t)\le\dfrac{\beta k}{(\mu+\gamma)\mu_0}$ if $E(0)\le\dfrac{\beta k}{(\mu+\gamma)\mu_0},$ and $I(t)\le \dfrac{\beta \mu k e^{-\mu\tau}}{\alpha\mu_0 (\mu+\gamma)}$ if $I(0)\le \dfrac{\beta \mu k e^{-\mu\tau}}{\alpha\mu_0 (\mu+\gamma)}.$ Thus, the set

is positively invariant.

Based on this previous result, we can study the solutions of model (3) in the restricted region $\mathcal{O}$.

3.1.   Toxoplasmosis-free equilibrium point

The mathematical model (3) has the following toxoplasmosis-free equilibrium point: $F^{*}_{0} = \left(\frac{\mu}{\mu+\gamma}, 0, 0, 0\right)$. This would be the ideal realistic condition where there toxoplasmosis becomes extinct. First, we will analyze the case when there is not time delay (ODE model). Then, we will see the impact of the time delay on the stability of the toxoplasmosis-free equilibrium point. The local stability of $F^{*}_{0}$ is determined by the eigenvalues of the Jacobian of the system (3) at $F^{*}_{0}$:

The eigenvalues are the following $\lambda_{1} = -\mu - \gamma$, $\lambda_{2} = -\mu$, and the roots of

Reordering one gets

where, $a = \alpha+\mu_{0}$, $b = -{\frac{\beta\, \mu\, k}{\gamma+\mu}} +\alpha\, \mu_{0}$. According to the Routh–Hurwitz criterion, if $\frac{k\, \beta\, \mu}{\mu+\gamma} < \alpha\, \mu_{0}$ one obtains that $p(\lambda)$ has only roots with negative real parts and the toxoplasmosis-free equilibrium point $F^{*}_{0}$ is locally asymptotically stable (las). Therefore, one can define the basic reproduction number as

Now we have obtained the following theorem,

Theorem 3.2. The disease-free equilibrium $F^{*}_{0}$ of model (3) with $\tau = 0$ is locally asymptotically stable if $\mathcal{R}_0 < 1$, but unstable if $\mathcal{R}_0 > 1$.

Proof. It follows from the previous computations.

3.2.   Toxoplasmosis-free equilibrium point analysis with the time delay

Calculations show that system (3) has the same toxoplasmosis-free equilibrium $F^{*}_{0} = \left(\frac{\mu}{\mu+\gamma}, 0, 0, 0\right)$, as the system with $\tau = 0$. Linearizing the system (3) one obtains the following characteristic equation

where

After some simple calculations one gets

where,

We can see that two eigenvalues are $\lambda_{1, 2} = -\mu, -\mu-\gamma$ are negative. The other eigenvalues are the roots of $T\left(\lambda\right)$. Now, let's define the basic reproduction number for the delay model (3) as:

Theorem 3.3. The disease-free equilibrium $F^{*}_{0}$ of model (3) is locally asymptotically stable if $\mathcal{R}_0^d < 1$, but unstable if $\mathcal{R}_0^d > 1$.

Proof. We define from Eq. (7) the following function

where, $a = \alpha+\mu_{0}$, $b = -{\dfrac{\beta\, \mu\, k}{\gamma+\mu}}\, e^{-\mu\, \tau} = -R_{0}^d\, \alpha\, \mu_{0}$, and $c = \alpha\, \mu_{0}$. It can be seen that $p$ is a continuous function. Moreover,

and

Then, if $\mathcal{R}_{0}^d > 1$, there is a positive real root, and then the disease free equilibrium is locally unstable. Now, let us consider the case when $\mathcal{R}_{0}^d < 1$. Notice that when $\tau = 0$, $\mathcal{R}_0^d = \mathcal{R}_0$ and one obtains

Thus, all the roots of $p(\lambda)$ have negative real parts by the Routh–Hurwitz criterion. We can see that $p(\lambda)$ does not have nonnegative real solutions because in $p(\lambda)$, it is increasing when $\lambda\ge 0$.

Let us see how the complex roots distribute for the transcendental characteristic equation. If $p(\lambda)$ has roots with nonnegative real parts, they must be complex. Then $p(\lambda)$ must have a pair of purely imaginary solutions. Let us assume that $\lambda = i\, \omega\, (\omega > 0)$ is a root of $p(\lambda)$. Then, using (8) we see that it must satisfy

Separating the real and imaginary part, one obtains

and

Adding up the squares of the previous equations, one obtains that

Here, $a^2-2c = (\alpha+\mu_0)^2-2 \alpha \mu_0 = \alpha^2+\mu_0^2 > 0$ and

if $\mathcal{R}_0^d < 1.$ Thus, all the coefficients of Eq.(9) are positive and therefore Eq.(9) does not have positive real roots. Then, there is no $\omega$ such that $i\omega$ is a solution of Eq.(7). Therefore, the real parts of all the eigenvalues of the characteristic Eq.(7) are negative for all $\tau > 0$ and $\mathcal{R}_0^d < 1$. This implies that disease-free equilibrium $F^{*}_{0}$ is locally asymptotically stable if $\mathcal{R}_{0}^d < 1$ for the delayed model (3).

3.3.   Global stability of the disease-free equilibrium

We propose the following theorem.

Theorem 3.4. The disease-free equilibrium point $F^{*}_{0}$ of system (3) is globally asymptotically stable if $\mathcal{R}_0^d\leq 1.$

Proof. Let us denote by $y_t$ the translation of the solution of the system (3), by $y_t = (S(t +\xi), I (t +\xi), V (t +\xi))$ where $\xi \in [-\tau, 0]$. Define the following Lyapunov function:

Calculating the derivative of $\mathcal{L}(I(t), S(t), O(t))$, one gets that

Since, we know from the restricted region that $S(t) \leq \frac{\mu}{\mu + \gamma}$, one obtains

Thus, $\mathcal{L}' \leq 0$ if $\mathcal{R}_0^d \leq 1$. Moreover, $\mathcal{L}(F^{*}_{0}) = 0$ and $\mathcal{L}(I(t), S(t), O(t)) > 0,$ at any point different than the disease-free equilibrium point $F^{*}_{0}$. Then, $F^{*}_{0}$ is globally asymptotically stable.

3.4.   Local stability analysis of the endemic equilibrium

The endemic equilibrium for the delayed model (3) is

where

Note, that the endemic point $E_{0}^{*}$ exists if and only if $\mathcal{R}_{0}^d > 1$. The characteristic equation is given by

where

The characteristic equation of the system can be factored in a long form expression and it can be obtained that one eigenvalue is $\lambda = -\mu$ and the other roots of characteristic equation are given by

Rewriting, one gets

where

where $A, B, C > 0$. Rewriting Eq.(18), one obtains

Then, one gets

where

These inequalities are valid if $\mathcal{R}_0^d > 1$. Then, the left-hand side of Eq. (19) is positive and the right-hand side is negative for all $\lambda\ge 0$. Therefore, for any $\lambda\ge 0$, Eq. (18) cannot have real non-negative solutions.

Let us consider the complex roots and assume that $\lambda = i\, \omega\, (\omega > 0)$ is a root of Eq.(18). This occurs if and only if $\omega$ is a solution of,

We can obtain the following equations for the imaginary and real parts respectively,

and

Squaring Eqs. (20) and (21), one gets

and

Adding these squares, we get the following result,

Reordering,

Making the change of variable $z = \omega^2$, one gets

Then,

where, $D = A^2-2B$, $E = B^2-2AC-T_1^2$ and $F = C^2-T_2^2$. These particular coefficients are given by

and

The coefficient $D$ is positive for all values of the parameters. On the other hand, $E$ and $F$ are positive for $\alpha\ge {{\rm e}^{-\mu\, \tau}}\mu$. This last inequality is true from biological facts since $\alpha$ is the reciprocal of the average infectious time for the toxoplasmosis disease and $\mu$ is the reciprocal of the average lifespan of the cats.

Lemma 3.5. If $D$, $E$ and $F$ are non-negative, then Eq.(24) has no positive real roots.

Proof. Let $p(\xi) = \xi^{3}+D\, \xi^2+E\, \xi+F.$ Deriving with respect to $\xi$, one obtains that $p'(\xi) = 3\xi^{2}+2D\, \xi+E$. Where $\xi = \omega^2 > 0$, $D\ge 0$, $E\ge 0$ and $F\ge 0$. Thus, $p'(\xi) > 0$, so $p(\xi)$ increases for $\xi\ge0$. Then, since $p(0) = F\ge0$, then Eq.(24) has no positive real roots.

Then we can conclude that there is no complex root of the form $\lambda = i\omega$ such that it is a solution of Eq. (18). Then using Rouché's theorem one can conclude that the real parts of all the roots of Eq.(18) are negative $\forall \tau\ge0$, ^[79]. Thus, if $\alpha\ge {{\rm e}^{-\mu\, \tau}}\mu$ the endemic equilibrium $E_{0}^{*}$ is stable for any time delay $\tau$ (with $\mathcal{R}_0^d > 1$).

From a biological viewpoint we have proven that for any time delay $\tau$ such that $\mathcal{R}_0^d > 1$, the endemic equilibrium point $E_{0}^{*}$ would not loose its stability. This is important to know since it means that even if the exposed stage is large then the crucial parameter is the basic reproduction number $\mathcal{R}_0^d$ for the delayed model (3). We will perform numerical simulations to support the theoretical results obtained in this section.

4.   Numerical simulations

Here, some numerical simulations are presented to support our proposed theoretical results. We vary some of the values of the parameters for the numerical simulations. For some cases we obtain the disease-free equilibrium and for other ones we obtain the endemic steady state depending on the value of the basic reproduction number of the delayed model (3). We also vary the time delays and therefore obtain different values of the basic reproduction number $\mathcal{R}_{0}^d$. In addition, the numerical simulations allow us to explore the dynamics of toxoplasmosis.

We use Matlab to calculate the numerical solutions and the built-in function dde23 for delay differential equations ^[52,55]. We use mostly the parameter values (using weeks as the time unit) provided in Table 1. For instance, for the vaccination rate we use a value of $\gamma = 0.001$ which means that $0.1$% of the susceptible population in some particular region is vaccinated per week. In reality, this could vary depending on many factors such as vaccine availability and willingness to vaccinate the cats. The transmission rate $\beta$ varies for different regions and it is difficult to estimate due to the lack of real data regarding longitudinal data related to toxoplasmosis prevalence in cats. The initial conditions are varied in order to observe the local and global stability behaviors.

4.1.   Stability for the disease-free equilibrium point

Here we set a time delay $\tau\ne0$ and a transmission rate $\beta$ that allows us to obtain $\mathcal{R}_{0}^d < 1$. Fig. 2 depicts the dynamics of the different subpopulations of cats and the oocysts. It can be seen that the system reaches the disease free equilibrium $F_{0}^*$. Fig. 3 shows the dynamics when the time delay is large ($\tau = 10$), $\mathcal{R}_{0} > 1$ and $\mathcal{R}_{0}^d < 1$. We can see that the system again approaches the disease free equilibrium $F_{0}^*$ despite $\mathcal{R}_{0} > 1$. Notice that the endemic equilibrium point $E_{0}^*$ exists, but the system does not approach to it. These results support our previous theoretical results where it was concluded that if $\mathcal{R}_{0}^d < 1$ regardless of the initial conditions the disease becomes extinct (global stability). From a biological viewpoint this means that the duration of the exposed stage can affect the steady state and to the possibility of toxoplasmosis becoming extinct.

4.2.   Stability for the endemic equilibrium point

In this subsection we assume parameter values such that $\mathcal{R}_{0}^d > 1$. Based on the theoretical results the system must reach the endemic steady state $E_{0}^*$. Fig. 4 depicts the dynamics of the subpopulations when $\mathcal{R}_{0}^d > 1$. As our theoretical results predicted, the system reaches the endemic steady state $E_{0}^*$. Notice that despite the time delay in the model the stability of the endemic steady state $E_{0}^*$ is maintained. We consider a hypothetical case where the time delay (duration of the exposed stage) is very large. Fig. 5 shows the dynamics when $\tau = 100$. Note, that the endemic steady state $E_{0}^*$ keeps its stability, but some oscillations appear. All these previous numerical results agree with our theoretical results.

4.3.   Effect of the duration of the exposed stage

The duration of the exposed stage is closely related to the time delay $\tau$. We perform numerical simulations varying the time delay to see the effect of the duration of the exposed stage on the dynamics of the toxoplasmosis disease. Fig. 6 depicts the transient behavior of the system (3). We perform the simulations for the case when $\mathcal{R}_{0} > 1$ since it has more interesting dynamics. It can be seen that the transient behavior of the solutions is different when the time delay is varied.

It can be seen from Fig. 6 that the time delay has some effects on the transient behavior of the different subpopulations as expected. Notice that main changes occur at $t = \tau$. The infected cats and oocysts are the main driven factors of the diseases and they are clearly correlated. For instance, at $t = 100$ and when $\tau = 100$, the infected cats increase abruptly since all the effective contacts between susceptible cats and oocysts at $t = 0$ now appear in the infected subpopulation. Then, right away there is an increase in the amount of oocysts in the environment since infected cats produce oocysts. As a consequence at $t = 100$ the susceptible population starts to decrease again due to the increase of oocysts. This effect is also shown in the exposed subpopulation of cats, but to a lesser degree because some exposed cats are continuously leaving the exposed stage. Notice that if the numerical simulation is performed for a very long time the system will reach the endemic state $E_{0}^*$ since $\mathcal{R}_{0}^d > 1$ for all cases. Thus, we can say that the time delay clearly can affect the transient dynamics. However, the steady state only can be changed if $\mathcal{R}_{0}^d$ increases its value to more than one, as the theoretical results pointed out. However, it is important to remark that increasing the time delay decreases $\mathcal{R}_{0}^d$ and therefore the disease free steady state can be reached.

5.   Conclusions

We proposed a new mathematical model to investigate the effect of the introduction of an exposed stage for the cats who become infected with the T. gondii parasite, but that are not still able to produce oocysts in the environment. We introduce in the model a time delay that represents the duration of the exposed stage. The model includes the cat population and also the oocysts related to the T. gondii in the environment. A key part of the model is the inclusion of the cats since they are the only definitive host. In addition, the spread of the toxoplasmosis is mainly through the oocysts in the environment. As any mathematical model there are certain assumptions that were made. The model considers lifelong immunity for the recovered cats and vaccinated cats. The cats can get infected by contact with the oocyst.

In this study we found the conditions such that the toxoplasmosis disease becomes extinct and also when it persists. We considered a fixed duration for the exposed stage using a time delay in the mathematical model. We analyzed the disease dynamics and in particular on the stability of the equilibrium points. We computed and used the characteristic equations to study the local stability of the equilibrium points. We found the particular basic reproduction number $\mathcal{R}_{0}^d$ of the mathematical model with a time delay. We found this basic reproduction number of the delayed model includes the time delay. We prove that if $\mathcal{R}_{0}^d <$ is less than unity, the disease-free equilibrium is locally asymptotically stable. On the other hand, if $\mathcal{R}_{0}^d > 1$, the endemic equilibrium is locally asymptotically stable. The global stability of the disease-free equilibrium was established by using the Lyapunov-LaSalle theorem. In particular, if $\mathcal{R}_{0}^d < 1$ the disease-free equilibrium is globally asymptotically stable and the toxoplasmosis becomes extinct in the long term. We obtained that if $\mathcal{R}_{0}^d > 1$, then the time delay representing the fixed duration of the exposed stage has no effect on the stability of the endemic equilibrium point and therefore does not induce periodic solutions and Hopf bifurcations cannot occur.

In general, our results allow us to get deeper insight on the dynamics of the toxoplasmosis disease. Some parameters were taken from the literature related to toxoplasmosis. However, some of them have a degree of uncertainty as is common in biological processes. We found that the basic reproduction number $\mathcal{R}_{0}^d$ decreases as the time delay increases and therefore this time delay can help to control the toxoplasmosis disease. It is important to remark that the temperature might have some influence on the duration of the exposed stage and therefore on the time delay. Thus, climate change can modify the time delay and the dynamics of the toxoplasmosis. From the mathematical expression of the basic reproduction number $\mathcal{R}_{0}^d$ we can see that the mean infectious period, the vaccination rate, the removal rate of oocysts and the time delay affect the value of the basic reproduction number and the endemic equilibrium point. For instance, all these parameters increase, the basic reproduction number $\mathcal{R}_{0}^d$ decreases and then this has positive control effects on the toxoplasmosis disease. We numerically solved the delayed mathematical model for a variety of parameters' values and the theoretical numerical results were in good agreement with the theoretical ones. We would like to remark that if $\mathcal{R}_{0}^d > 1$, then the endemic equilibrium didn't lose stability regardless of the time delay. It is important to point out that our theoretical results are valid regardless of the parameter values. We used some particular values to show graphically few toxoplasmosis dynamics that agree with the theoretical results. In reality, the vaccination rate would vary depending on many factors such as vaccine availability and willingness to vaccinate the cats. Regarding the transmission rate this varies for different regions and it is difficult to estimate due to the lack of real data regarding longitudinal data related to toxoplasmosis prevalence in cats.

The proposed mathematical model allows the assessment of various control strategies against toxoplasmosis. For instance, the implementation of vaccination programs for cats can reduce the prevalence of toxoplasmosis. Optimal control can be used to determine the best strategy if costs of each strategy are established. As a good research practice we would like to point out a few limitations of this work, but there are others. The model studied in this work has an important limitation since it does not consider other intermediate hosts. However, since the only definitive host are the cats it is crucial to have models that include them and it is expected that they are the main driving force of toxoplasmosis ^[7,8]. Further studies that include additional intermediate hosts are necessary to get deeper insight in the toxoplasmosis dynamics. In addition, the well-known homogeneous mixing assumption might not represent reality. One key assumption and limitation is the permanent immunity of vaccinated cats. This aspect would need further studies and the design of a new mathematical model and analysis. The mathematical model assumes exponential transitions between most of the subpopulations and this is not exactly what happens in the real world. Some authors have proposed models using gamma distributions, but this requires much more equations ^{[82,83,84,85]}. The value of the crucial transmission rate is unknown and can vary depending on the region. This requires much further biological field study. We expect in future works to consider other hosts. Finally, we would like to point out that this type of studies provide deeper insight into the toxoplasmosis disease and can help health authorities to reduce the prevalence of toxoplasmosis.

Conflict of interest

The authors declare there is no conflict of interest.