Estimation of left ventricular parameters based on deep learning method

1.   Introduction

The dynamic modeling and simulation of cardiac function using patient-specific three-dimensional (3D) geometric heart structure is studied by a large number of researchers ^[1]. Estimating the constitutive parameters non-invasively remains a great challenge for the LV modelling community ^[2].

Various geometric models are used to approximate the shape of the LV. Hanna et al. ^[3] experimentally dissected the LV of a dog and proposed a method to represent the shape of the LV membranes with elliptic curves. To study the transmission of ecg and the structure of the LV myocardial fibers, Pravdin et al. ^[4] improved Hanna's method by fitting the shape of the LV with conic curve formed by spiral curve. To blackuce the complexity of the finite element simulation of the LV, Achille et al. ^[5] used a rotation curve based on elliptic curve to represent the geometric features of the LV.

In general, finite element method (FEM) is applied to the field of cardiac modeling and calculation. Gould et al. ^[6] used FEM to study the stress and strain of the ventricular wall. This is the first time the FME has been applied to cardiac modeling. Sermesant et al. ^[7] calculated the local myocardial stress during systole using MRI images and other cardiac data. Peskin et al. ^[8] proposed the Immersed Boundary (IB) method. The IB method is often used to solve the problem of fluid-structure interaction and has been widely popularized in the field of biomechanics in recent years. Cai et al. ^[9] successfully used IB/FE method to numerically simulate LV at different stages of cardiac cycle.

However, it requires several iterations to obtain the optimal solution of the FEM simulation, and the calculation time is relatively long ^[10,11,12]. Such high computational costs will inhibit the practical use of these methods. In recent years, DL techniques ^[13,14,15] have gained great attention in the field of artificial intelligence^[16]. DL model can establish a complex nonlinear relationship between inputs and outputs. A possible solution to the bottlenecks associated with patient-specific computational modeling is to use DL algorithms to speed up the process of material parameter identification. By designing and training a DL model on large amounts of data, it can automatically generate the desiblack output directly from the necessary inputs, without the need for expensive iterative algorithms. Once the training is complete, the DL model can make the pblackiction instantaneously. Bonnemain et al. ^[17] used deep learning to assess cardiac contractility. Also in another article ^[18], they developed a framework comprising a deep neural network and a 0D model of the cardiovascular system to pblackict parameters of LV systolic function. Ren ^[19] proposed a surrogate model based on the machine learning method to study cardiac mechanical parameters. In conclusion, deep learning can effectively speed up the calculation process of finite element simulation^[20].

This paper presents a standardized geometric model of LV. Based on the previous research ^[19,21], a PV curve parameters pblackiction model of the LV dynamics in diastole based on DL is proposed. Then the DL model is used for solving the inverse problem of finding the constitutive parameters.

2.   Methods

2.1.   Geometric model of LV

2.1.1.   Standardized model

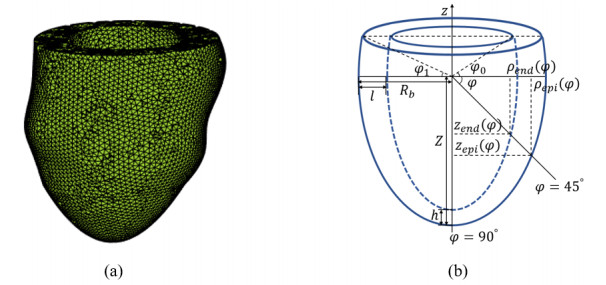
In this study, we obtained 27 healthy LV geometries from a published study ^[22]. All geometries are reconstructed from in vivo cardiac MR images. Details of patient characteristics, imaging protocols and reconstruction procedures can be found in ^[22]. Figure 1(a) shows a reconstructed LV geometry of a healthy volunteer. The shape of the LV is irregular, and the thickness of the heart wall is not uniform. However, it is difficult to obtain a large number of MRI images of the LV. To facilitate follow-up studies, we approximate the LV with a geometric parametric model based on the previous model ^[3,5,23]. Figure 1(b) shows a schematic of an idealized LV geometry annotated with geometric descriptions of the parameters. The inner and outer surfaces of the left ventricle are respectively regarded as the surface of rotation formed by the curve rotating around the $Z$ axis. Each point on the curve has two coordinates, the horizontal axis $\rho$ and the vertical axis $z$. These two coordinates can be controlled by the Angle $\varphi$. The inner surface of $[\varphi_{0}, {\pi }/{2}]$, and outside surface of $\varphi$ value range is $[\varphi_{1}, {\pi }/{2}]$. The parametric model was described by the following relations

The parametric model is determined by six parameters: the maximum radius of the outer surface, $R_{b}$; the wall thickness at the horizontal axis, $l$; The distance between the origin and the lowest point of the outer surface, $Z$; the wall thickness at the vertical axis, $h$; the truncation angle of the inner wall, $\varphi_{0}$; and finally, the degree of bending of the wall curve, $e\in\left[0, 1\right]$. When $e = 0$, the curve geometry becomes a cone; and when $e = 1$, it is an elliptic curve. In particular, $\varphi_{1}$can be calculated by $\varphi_{0}$. According to the MRI image data of the left ventricle, the initial geometric shape can be generated by setting initial values for the geometric model parameters.

2.1.2.   Personalized geometric parameters

Based on the shape and coordinates of the original LV, the cube can be defined with $\left(x_{min}-\xi, x_{max}+\xi\right)$, $\left(y_{min}-\xi, y_{max}+\xi\right)$ and $\left(z_{min}-\xi, z_{max}+\xi\right)$, and the cube was evenly divided with a $128 \times 128 \times 128$ grid. The calculation process will be slow if the mesh is too dense, and the result will not be accurate if the mesh step is too large. $\xi$ is a constant to make the grid space slightly larger than the original LV, as shown in Figure 2. When the grid node is inside the shape of the LV wall, the node is assigned a value of 1; When the grid node is outside the shape of the LV wall, the node is assigned a value of 0. Then the original LV can be approximately represented by a three-dimensional matrix consisting of values 0 and 1, and the total number of nodes with the value of 1 in the matrix represents the shape of the left ventricle. Similarly, the idealized parametric model can also be approximated in the same cube space by a three-dimensional matrix composed of 0-1. Next, we optimize the parameter $\varsigma = \left[R_{b}, Z, l, h, e, \varphi_{0}\right]$ of the geometric model. Establish the objective function $G$, as follows

where $I_ {real}$ represents MRI LV image, $I_ {}\varsigma$ represents geometric model, $C_{real}$ represents the 0-1 three-dimensional matrix of $I_ {real}$, $C_ {\varsigma}$ represents the 0-1 three-dimensional matrix of $I_ {\varsigma}$. $\left | {{C_ {real}}} \right |$ represents the sum of all 1 in $C_{real}$. Similarly, $\left| {{C_\varsigma }} \right|$ is the sum of all 1 in $C_{\varsigma}$. $\varepsilon$ represents a very small constant in case the denominator is 0.

$G$ represents the measure of similarity between the geometric model and MRI image of the LV, and the value range is $[0, 1]$. The higher the degree of overlap between the two, the smaller $G$ will be. The geometric parameter optimization model is established, and the mathematical expression is as follows

Among them, $R$ is one-half of the widest value in the horizontal direction of the MRI LV image, and $H$ is the longest value in the vertical direction of the MRI LV image. The optimization process uses the FMINcon function in MATLAB. The parameter optimization flow chart is shown in Figure 3. Figure 4 shows optimization results and the corresponding LV shape for a representative case.

2.2.   Pressure-volume model

2.2.1.   Constitutive law of LV

The constitutive relation, also known as the constitutive equation, is used to describe the relationship between force and deformation or stress and strain. The constitutive equation expresses the relationship between stress and strain as a function, and different materials have different constitutive relations. The LV myocardium is a non-uniform, thick-walled, incompressible, orthotropic nonlinear hyperelastic material. Myocardial structure strain energy functions are given below, the so-called H-O model ^[24,25]

in which ${{a}, {b}, {{a}_{\text{f}}}, {{b}_{\text{f}}}, {{a}_{\text{s}}}, {{b}_{\text{s}}}, {{a}_{\text{fs}}}, {{b}_{\text{fs}}}}$ are unknown material parameters, The five parameters ${{a}, {b}, {{a}_{\text{f}}}, {{b}_{\text{f}}}, {{a}_{\text{s}}}}$ are mainly used in this paper, and the remaining parameters are fixed with appropriate values based on the group's previous research ^[25]. ${I_{4i}}(i = \mathrm{f}, \mathrm{s}), {I_{8\mathrm{fs}}}$ represent invariants along the fiber, slice and normal directions respectively. The calculation formulas are as follows

in which ${{\bf{f}}_0}$ and ${{\bf{s}}_0}$ are the myofibre and sheet orientations, which are determined by a rule-based method ^[25] and known before numerical simulation (initial conditions). $\mathbb{C}$ is the right Cauchy-Green deformation tensor, defined as $\mathbb{C} = {{\mathbb{F}}^{\rm{T}}}{\mathbb{F}}$, and $\mathbb{F}$ is the deformation gradient that describes the motion of the heart muscle. In other words, the deformation gradient describes how the shape of the heart muscle changes over time in three dimensions. The expression $\frac{1}{2}K{\left({J - 1} \right)^2}$ represents the incompressibility of the material, $K$ is a constant, and $J$ is the determinant of $\mathbb{F}$.

However, Gao ^[21] had found that the sensitivity of these parameters for the changes of volume and PV curves is not quite the same. For example, $a$, $b$, and ${a_{\text{f}}}$ had the highest sensitivity, while ${a_{\text{fs}}}$, ${b_{\text{fs}}}$, and ${b_{\text{s}}}$ have the lowest sensitivity. Therefore, in the following, we selected three groups of parameter combinations for analysis and comparison, which are $\left\{ {a, b, {a_{\text{f}}}, {b_{\text{f}}}} \right\}$, $\left\{ {a, b, {a_{\text{f}}}, {a_{\text{s}}}} \right\}$ and $\left\{ {a, b, {a_{\text{f}}}} \right\}$, respectively. ${a_{\text{s}}}$ and ${b_{\text{f}}}$ were added respectively in the first two combinations to serve as a comparison with the third group of parameters.

2.2.2.   Numerical simulation of LV

The deformation process of the LV diastole can be simulated by numerical simulation. The specific calculation model can be described as the boundary value question below ^[26,27,28].

where $\Omega$ represents the entire LV wall region, $\partial \Omega$ represents the boundary of $\Omega$, the relation between Cauchy stress tensor and Piola Kirchhoff stress of the second kind is $\sigma = \frac{1}{J} {{\bf{FSF}}}^{\top}$ (which can be derived from Formula 2.4), ${\bf{b}}$ represents the surface force of unit volume, ${\bf{n}}$ represents the external normal of the unit of $\partial \Omega$, and $\Gamma^{N}$ and $\Gamma^{D}$ represent the displacement boundary and pressure boundary. The displacement boundary refers to the displacement control of the plane, circumferential direction and vertical axis at the bottom of the left ventricle is 0, and the radial direction can contract or expand, while other regions are free to deform. Meanwhile, the non-sliding boundary condition was applied to the LV wall ^[9]. The pressure boundary condition refers to that the pressure is linearly loaded on the LV wall in 25-time steps with a pressure range from 0 to $8 mmHg$. The pressure of the outer wall of the left heart was set at $0 mmHg$. In the beginning, the left ventricle was regarded as the resting state and the end as the end-diastolic state. The hexahedron element is used to discretize space and solve it by the finite element method. The simulation process was realized by ABAQUS (Simulia, Providence, RI, USA). The volume of the corresponding LV lumen was extracted after each step of the compression process.

3.   Generation of data sets

3.1.   Parameter range

27 sets of geometric parameters were obtained from the Section 2.1. Supposing that each geometric parameter follows a normal distribution $N\left({\mu, {\sigma ^2}} \right)$. The 27 known geometric parameters are samples of the population. Since the sample variance $S_n^{{*^2}}$ is the least variance unbiased estimate of ${{\sigma ^2}}$, ${\sigma}$ can be approximated by $S_n^*$. Then we do an interval estimate of the population mean $\mu$. On the assumption that ${\left({{X_1}, {X_2}, ..., {X_n}} \right)^{\rm{T}}}$ is a sample from population $\overline X$, and we can use $\overline X$ as a point estimate for $\mu$. And the sample means $\overline X$ is the moment estimator of the population mean $\mu$, so $\overline X$ can be used to approximate $\mu$. Therefore, the sample population score of geometric parameters can be obtained, as shown in Table 1. According to the $3{\sigma}$ principle of normal distribution, the probability of sample falling within $[\mu-3\sigma, \mu{{+}}3\sigma]$ is $99.7\%$, so $[\mu-3\sigma, \mu{{+}}3\sigma]$ is taken as the value range of geometric parameter. The range of the constitutive parameters has been obtained from previous studies ^[22], as shown in Table 2.

3.2.   Sampling the parameter space

The multi-dimensional sample space is established according to the result of parameter estimation. According to different combinations of constitutive parameters, three sampling Spaces are established as follows

each sampling space is composed of geometric parameters and constitutive parameters. Due to the high dimension of our sampling space, to ensure the efficiency of sampling and the uniformity of sample distribution, LHS method ^[29] is selected here. LHS is a multi-dimensional stratified sampling method. Its advantage is that the sampling value can fully reflect the overall distribution of the sample and ensure that all probability intervals are coveblack by sampling points. The sampling process is as offeblack:

1) Let the dimension of sampling space be $E$, and define the number of samples to be sampled as $N$.

2) Divide each one-dimensional sampling region into $N$ small regions with equal probability, then generate $E$ group $N$ small region set. Some little region in the group that it's in has a probability of $1/N$.

3) A point in a small region is randomly selected in each dimension. The $E$ points are combined to form a sample, and the small region selected will not participate in the subsequent sampling.

4) Repeat the third step $N$ times, all the small areas are just used up, and $N$ samples are obtained.

10,000 samples were collected in each sampling space, with a total of 30,000 samples. Because the sampling of each parameter is randomly combined, there will inevitably be samples that do not conform to the real physiological situation. Such samples will lead to non-closure of the virtual LV bottom, calculation failure or compression failure in the subsequent ABAQUS simulation. These data will be eliminated.

3.3.   Model of PV curve parameters

The ventricular PV curve represents the relationship between pressure and volume changes in the LV cavity. True cardiac PV relationships can be obtained using catheters and ultrasound monitoring.

Three sample sets $A_1$, $A_2$ and $A_3$ with 30,000 groups of material parameters samples obtained above were simulated using the method in Section 2.2.2. Then 30,000 PV relationship curves were generated. The configuration used for finite element calculation in this paper is a workstation with a 64-bit Windows 7 operating system, using the Intel Core E52609 processor and 32GB memory space. The simulation process of ABAQUS uses 16-thread parallel. Some parameter samples may have problems in the calculation process, as mentioned in Section 3.2. After eliminating through wrong data, 6985, 7742 and 7782 sets of PV curves were left. The process of calculating the relationship between load pressure and volume is shown in Figure 5.

Klotz et al. ^[30] found that the relationship between normalized volume(${v_n}$) and $p$ can be approximated by $p = \alpha {v_n}^\beta$, where $\alpha$ and $\beta$ are coefficients, ${v_n} = \frac{{v - {v_0}}}{{{v_0}}}$ is the normalized volume with respect to the initial volume ${v_0}$. We also use the quadratic polynomial function $p = d{v^2} + qv + c$ approximates the relationship between $v$ and $p$. After the least square fitting processing, the obtained effect is shown in Figure 6. Finally, we get the values of parameters $\alpha$, $\beta$, $d$, $q$ and $c$ corresponding to the three sample sets. The distribution of three-parameter PV curve parameters $\left\{d, q, c\right\}$ and two-parameter PV curve parameters $\left\{\alpha, \beta\right\}$ is shown in Figure 7.

3.4.   Partitioning the dataset

10% data are randomly selected from the entire dataset as the test set, and the remaining data are training and validation set. As a result, in $A_1$, the training and validation set has 6286 input-output pairs, and the test set has 699 input-output pairs; In $A_2$, the training and validation set has 6967 input-output pairs, and the test set has 775 input-output pairs and in $A_3$, the training and validation set has 7003 input-output pairs, the test set has 779 input-output pairs.

4.   Deep learning model for the PV curve parameters

4.1.   The neural network model

The nonlinear mapping system will map the geometric parameters, constitutive parameters to the PV curve parameters. 6 neural networks $N{N_i}\left({i = 1, ..., 6} \right)$ are established. The corresponding input $\mathit{\boldsymbol{x}}$ and ouput $\mathit{\boldsymbol{y}}$ of each neural network are as offeblack

As shown in Figure 8, this is a feedforward fully connected neural network. Each neuron has multiple inputs and one output. For example, take the forward propagation of one neuron, each neuron has a weight r$\omega _{ji}^{\left(l \right)}$ as it passes down the next layer. Namely, the weight of the connection between neuron $i$ at layer $L-1$ and neuron $j$ at layer $l$. The output of neurons in layer $l-1$ to layer $l$ is

where $b_j^{(l)}$ is the offset term and ${f^{(l)}}$ represents the activation. If the offset term is represented as the column vector${\mathit{\boldsymbol{b}}^{(l)}}$, the Eq (4.2) can be expressed as

However, offset terms can also be represented in weights. Add a neuron with output 1 on the input layer and all hidden layers, denoted as $i = 0$, then

The weight $\omega _{j0}^{(l)}$ is introduced between the neuron $i = 0$ at layer $l-1$ and the neuron $j \ne 0$ at layer $l$, then the weight is the bias term. The derivation process is

the Eq (4.3) can be further expressed as

Assume that a neural network consists of $L$ layers, and the model from input $\mathit{\boldsymbol{x}}$ to output $\mathit{\boldsymbol{y}}$ is

$\widehat {\mathit{\boldsymbol{y}}}$ represents the approximation of ${\mathit{\boldsymbol{y}}}$. Using this functional model to fit the data is the mathematical expression of a neural network. And then the training is to find the optimal ${\mathit{\boldsymbol{W}}^{(L)}}$.

The neural network has many activation functions to choose from, we choose ReLU ^[31] as our activation function, which is given by

The neural network model has two hidden layers, take the example of ${NN_1}$ in formula 4.1, the input layer has ten neurons, and the output layer has three neurons. The number of neurons in each layer of the neural network will be determined in subsequent training. Keras is used to implement the neural network.

Before training, the input data and output data are normalized. Here, we use the min-max normalization

4.2.   Training and testing

4.2.1.   10-fold cross validation

Using the training/validation data set, the performance of the nonlinear mapping module is evaluated by cross-validation. The hyperparameters of the neural network are adjusted. The data set is divided into $N$ parts, one of which is taken as the verification set each time. The other $N-1$ parts are put together as the training set. A total of $N$ training sessions are conducted, and the average result is selected as the final training result. In this case, $N$ is equal to 10.

4.2.2.   Search for the optimal number of network nodes

Since the dimension of the input layer and the output layer of our neural network is not large, the stepwise increase method ^[32] is adopted to find the optimal network node number of hidden layers. The method starts from the network with a small number of nodes, and gradually increases the number of hidden nodes according to the speed change of blackucing the network output error. Firstly, the number of nodes on the second hidden layer is fixed at 30. The number of nodes on the first hidden layer gradually increases from 1 to 30. Similarly, fix the first hidden layer to the optimal value just found and increase the number of nodes in the second hidden layer from 1 to 30. It can be found that when the error drops to a certain value, it does not decrease with the increase of nodes, and the optimal number of nodes is obtained. The optimal number of nodes of each neural network is shown in Table 3.

To evaluate the deep learning model and check the accuracy of the pblackicted results, the PV curve's parameters are pblackicted using the data in the test set. The pblackicted parameters are compablack with the parameters in the test set, which process is illustrated in Figure 9.

4.2.3.   Results

Once the network structure is determined, data can be put in for training. The mean absolute error (MAE) is used as the loss function, The training error is shown in Table 4. It can be found that the training error results of the two pressure-volume curve parameters are similar, and both have good performance. The gradient descent algorithm used in this paper is Adam optimization algorithm ^[33]. After training, proper weights, bias and hyperparameters are obtained for the network. Then we plug the data from the test set into the neural network. The actual PV curve parameters versus pblackicted PV curve parameters are shown in Figures 10 and 11. The horizontal axis represents the true value of the parameter, and the vertical axis represents the pblackicted value of the parameter. The closer to the line $y = x$ in the figure, the more accurate the results are. It can be seen that among the three parameters of the PV curve fitted by the quadratic function, the pblackiction result of $c$ is the best, followed by $q$, while the pblackicted value of some points in $d$ is slightly far from the real value. Among the two parameters of the PV curve fitted by the exponential function, $\alpha$ pblackicted better.

The discrepancy between the actual material parameters and pblackicted material parameters in the testing set is quantified by normalized mean absolute error (NMAE) ^[20]. The absolute error (AE) for the ${k^{{\text{th}}}}$ PV parameter is defined by

$y_k^{\left(l \right)}$ and $\widehat y_k^ {\left(l \right)}$ represent the ${k^{{\text{th}}}}$ actual and pblackicted PV parameter, respectively. The NMAE of the ${k^{{\text{th}}}}$ PV parameter is defined by

where $n$ represents the total number of training data. The NMAE for each PV parameter in the testing sets are reported in Table 5. It can be found that $NN_1$ and $NN_4$ have the best pblackiction results, and their errors are lower than $1\%$. The error of all parameters is within $5\%$. The results show that the PV parameters pblackicted by deep learning are in good agreement with the actual PV parameters. The results of the quadratic function PV curve and exponential function PV curve are similar, indicating that within a certain range, the variation relationship of PV can also be approximated by the quadratic function.

Then ${R^2}$ is used to evaluate the pblackiction accuracy, as defined by the following formula

The value of $R^2$ ranges from 0 to 1, and the closer to 1, the more accurate it is. The accuracy of network pblackiction is shown in Table 6. The observation results show that all parameters are highly accurate. It shows that deep learning can replace the calculation process of the finite element method and pblackict relevant parameters. The accuracy of fitting PV parameters with quadratic function is above 0.9, showing good performance.

5.   Deep learning model for the constitutive parameters

5.1.   The neural network model

The calculation of LV constitutive parameters is an inverse problem, which is usually solved by solving an optimization problem with additional conditions ^[19]. Different from the previous methods, we establish the nonlinear mapping relationship between input features and output features by taking geometric parameters and three-parameter PV curves as inputs and constitutive parameters as outputs. Three multiple neural networks are established. The input and output characteristics of each network are as follows

Each network selects a slightly different combination of output characteristics. According to Gao's study ^[22], the constitutive parameters $a$, $b$ and $a_{\text{f}}$ are sensitive, and the PV change has a great influence on them. Meanwhile, parameters $a_{\text{s}}$ and $b_{\text{f}}$ with lower sensitivity are added to the output characteristics of $NN_7$ and $NN_8$ respectively as controls. The other parameters are fixed as in Section 4.

LHS method and deep learning model in Section 4 are used to expand data, and 50,000 sets of data are generated for $NN_7$, $NN_8$ and $NN_9$ respectively, with a total of 150,000 sets of input and output pairs. Next comes data processing, initialization, and selection of hyperparameters.

The ReLU activation function and the MAE loss function are still used here. The number of nodes in each hidden layer is determined by the stepwise increase method, the nodes of each neural network are shown in Table 7.

5.2.   Training and testing

10% of each dataset was randomly selected as the test set, and the remaining data were used for training. As a result, in each neural network, the training and validation set has 45,000 input-output pairs and the test set has 5000 input-output pairs. The training process uses 10-fold cross-validation to ensure accuracy. The loss function decline curve of the training set and verification set of the three neural networks in the learning process is shown in Figure 12. It can be found that the loss function curve of the inverse problem shows a downward trend in general. But the local loss function of the verification set always has a small fluctuation. The MAE training error of each neural network is shown in Table 8. It can be found that the error of $NN_9$ is the smallest, and the error of $NN_7$ and $NN_8$ is slightly larger, because the constitutive parameters $a_{\text{s}}$ and $b_{\text{f}}$ are added into the output characteristics.

Next, test sets are used to test the trained neural network, The comparison between the actual value and the pblackicted value is illustrated in Figure 13. It can be found that among the three groups of pblackicted constitutive parameters, $b$ has the best performance, and most points are close to straight line $y = x$. While the distribution of parameters $a$ and $a_{\mathrm f}$ is slightly loose. $a_{\text{s}}$ in network $NN_7$ and $b_{\text{f}}$ in network $NN_8$ are not sensitive to PV changes, so they cannot be well pblackicted, and the error of the whole network increases. The pblackiction accuracy of each network is measublack by $R^2$, as shown in Table 9. According to the results in the table, the pblackiction accuracy of $a$, $b$ and $a_{\mathrm f}$ with high sensitivity is between 0.7 and 0.9. The result accuracy of 9 is higher than the other two networks, which shows the importance of feature selection. Compablack with the pblackiction accuracy of positive questions in the previous chapter, the accuracy of negative questions decreases obviously, which is related to the unsuitability of negative questions. Estimate the constitutive parameters by a normal method generally need dozens of hours, deep learning can significantly speeds up the results of the output. But the parameter estimation accuracy will be blackuced, so the method is more suitable for lack of experimental data in the inverse problem generated when a large number of data and combined with the finite element calculation, determine the initial value range of parameter iteration to improve iteration efficiency.

6.   Discussion and conclusions

There are some limitations to this paper. 27 real heart data were used in the study, but the expected results were not obtained when the trained model was used to pblackict the parameters of these hearts. That's probably because the characteristic parameters selected in the learning of the inverse problem were insufficient or the data volume was not large enough. Later researchers will try different schemes and continue to improve the model for this problem.

Some other aspects in this paper need to be improved in subsequent research. First, the data used in the test set were generated by statistical methods, not directly from in vivo measurements of the LV. Later, more clinical data can be obtained to verify the accuracy of the model with data independent of the training set. Secondly, patient specificity needs to be consideblack. The geometric characteristics of the LV and myocardial parameters of some patients are not within the normal value range, so the model should detect and indicate abnormal points instead of making direct pblackictions. Third, in numerical simulation, the initial value of pressure on the LV is 0, while the real heart is always under pressure at any time. Future work will need to investigate how existing data can be used to model a more realistic left ventricular state.

Acknowledgments

This work is supported by National Natural Science Foundation of China (11871399) and the UK EPSRC (EP/S030875, EP/S014284/1, EP/S020950/1, EP/R511705/1, EP/T017899/1), which are gratefully acknowledged.

Conflict of interest

The authors declare there is no conflict of interest.