1.
Introduction and position of problem
The study of nonlinear wave processes in real media with dispersion, despite the significant progress in this area in recent years, for example, [1,2,3] and numerous references in these works are still relevant. This, in particular, concerns the dynamics of oscillations in cases where high-energy particle fluxes occur in the medium, which significantly change such parameters of propagating wave structures, such as their phase velocity, amplitude and characteristic length. In recent and earlier years, a fairly large number of works have been devoted to studies of this kind of relativistic effects (see [12,13,14]).
Recently, the great interest on the KP equation has led to the construction and the study of many extensions to the KP equation. These new extended models propelled greatly the research that directly resulted in many promising findings and gave an insight into some novel physical features of scientific and engineering applications. Moreover, lump solutions, and interaction solutions between lump waves and solitons, have attracted a great amount of attentions aiming to make more progress in solitary waves theory. Lump solutions, have been widely studied by researchers for their significant features in physics and many other nonlinear fields[18,19,20].
Let u=u(x,y,t),(x,y,t)∈R3 and α≥4. We consider the initial value problem for the generalized Kadomtsev-Petviashvili I equation,
with
This equation belongs to the class of Kadomtsev-Petviashvili equations, which are models for the propagation of long dispersive nonlinear waves which are essentially unidirectional and have weak transverse effects. Due to the asymmetric nature of the equation with respect to the spatial derivatives, it is natural to consider the Cauchy problem for (1.1) with initial data in the anisotropic Sobolev spaces Hs1,s2(R2), defined by the norm
Many authors have investigated the Cauchy problem for Kadomtsev-Petviashvili equations as in, for instance [4,8,16]. Yan et al. [17] established the local well-posedness of the Cauchy problem for the Kadomtsev-Petviashvili I equation in anisotropic Sobolev spaces Hs1,s2(R) with s1>−α−14, s2≥0 with α≥4 and globally well-posed in Hs1,0(R) with s1>−(α−1)(3α−4)4(5α+3) if 4≤α≤5 also proved that the Cauchy problem is globally well-posed in Hs1,0(R) with s1>−α(3α−4)4(5α+4) if α>5. The authors in [8] proposed the problem
and proved that it is globally well-posed for given data in an anisotropic Gevrey space Gσ1,σ2(R2),σ1,σ2≥0, with respect to the norm
With initial data in anisotropic Gevrey space
and κ⩾1, we will consider the problem (1.1). The spaces Gσ1,σ2,κs1,s2 can be defined as the completion of the Schwartz functions with respect to the norm
where
In addition to the holomorphic extension property, Gevrey spaces satisfy the embeddings Gσ1,σ2s1↪Gσ′1,σ′2s′1 for s1,s′1∈R and σ′i<σi where Gσ1,σ2,1s1,0=Gσ1,σ2s1, which follow from the corresponding estimates
The main aim to consider initial data in these spaces is because of the Paley-Wiener Theorem.
Proposition 1.1. Let σ1>0, s∈R. Then f∈Gσ1x(R) if and only if it is the restriction to the to the real line of a function F which is holomorphic in the strip {x+iy∈C: |y|<σ}, and satisfies
Notation
We will also need the full space time Fourier transform denoted by
In both cases, we will denote the corresponding inverse transform of a function
To simplify the notation, we introduce some operators. We first introduce the operator Aσ1,σ2κ, which we define as
Then, we may then define another useful operator
For x∈Rn, we denote ⟨x⟩=(1+|x|2)1/2. Finally, we write a≲b if there exists a constant C>0 such that a≤Cb, and a∼b if a≲b≲a. If the constant C depends on some quantity q, we denote this by a≲qb.
Function spaces
Since our proofs rely heavily on the theory developed by Yan et al., let us state the function spaces they used explicitly, so that we can state their useful properties which we will exploit in our modifications of their spaces. The main function spaces they used are the so-called anisotropic Bourgain spaces, adapted to the generalized Kadomtsev-Petviashvili I, whose norm is given by
where
with m(ξ,η)=ξ|ξ|α+η2ξ.
Furthermore, we will also need a hybrid of the anlytic Gevrey and anisotropic Bourgain spaces, designated Xσ1,σ2,κs1,s2,b(R3) and defined by the standard
It is well-known that these spaces satisfy the embedding
Thus, solutions constructed in Xσ1,σ2,κs1,s2,b belong to the natural solution space.
When considering local solutions, it is useful to consider localized versions of these spaces. For a time interval I and a Banach space Y, we define the localized space Y(I) by the norm
2.
Main results
The first result related to the short-term persistence of analyticity of solutions is given in the next Theorem.
Theorem 2.1. Let s1>−α−14,s2≥0, α≥4, σ1≥0, σ2≥0 and κ≥1. Then for all initial data f∈Gσ1,σ2,κs1,s2 and |ξ|−1ˆf(ξ,μ)∈L2(R2), there exists δ=δ(∥f∥Gσ1,σ2,κs1,s2)>0 and a unique solution u of (1.1) on the time interval [0,δ] such that
Moreover the solution depends continuously on the data f. In particular, the time of existence can be chosen to satisfy
for some constants c0>0 and γ>1. Moreover, the solution u satisfies
The second main result concerns the evolution of the radius of analyticity for the x-direction is given in the next Theorem. Here
Theorem 2.2. Let σ1>0, s1>−α−14,α=4,6,8,... and assume that f∈Gσ1,0s1, |ξ|−1ˆf(ξ,μ)∈L2(R2). Then the solution u given by Theorem 2.1 extends globally in time, and for any T>0, we have
with ρ=4α−1+ε for ε>0 when α=4 and ρ=1 when α=6,8,10,... and the constant C is a positive.
The method used here for proving lower bounds on the radius of analyticity was introduced in [15] in the study of the non-periodic KdV equation. It was applied to the the higher order nonlinear dispersive equation in [9] and the system of mKdV equation in [10].
Our last aim is to show the regularity of the solution in the time. A non-periodic function ϕ(x) is the Gevrey class of order κ i.e, ϕ(x)∈Gκ, if there exists a constant C>0 such that
Here we will show that for x,y∈R, for every t∈[0,δ] and j,l,n∈{0,1,2,…}, there exist C>0 such that,
i.e, u(⋅,⋅,t)∈Gσ(R)×Gσ(R) in x,y and u(x,y,⋅)∈G(α+1)κ([0,δ]) in time variable.
Theorem 2.3. Let s1>−α−14,s2≥0, α≥4, σ1≥0, σ2≥0 and κ≥1.
If f∈Gσ1,σ2,κs1,s2 then the solution
given by Theorem 2.1, belongs to the Gevrey class G(α+1)κ in time variable.
Corollary 2.4. Let σ1>0,s1>−α−14,α=4,6,8,.... If f∈Gσ1,0s1 then the solution
given by Theorem 2.2, belongs to the Gevrey class G(α+1) in time variable.
The rest of the paper is organized as follows: In section 3, we present all the auxiliary estimates that will be employed in the remaining sections. We prove Theorem 2.1 in subsection 4.1 using the standard contraction method and Theorem 2.2 in subsection 4.2. Finally, in section 5, we prove G(α+1) regularity in time.
3.
Auxiliary estimates
To begin with, let us consider the related linear problem
By Duhamel's principle the solution can be written as
where
We localize it in t by using a cut-off function satisfying ψ∈C∞0(R), with ψ=1 in [−1,1] and suppψ⊂[−2,2].
We consider the operator Φ given by
where ψδ(t)=ψ(tδ). To this operator, we apply the following estimates.
Lemma 3.1. (Linear estimate) Let s1,s2∈R,−12<b′≤0≤b≤b′+1,σ1≥0,σ2≥0,κ≥1 and δ∈(0,1). Then
Proof. The proofs of (3.3) and (3.4) for σ1=σ2=0 can be found in Lemma 2.1 of [17]. These inequalities clearly remain valid for σ1,σ2>0, as one merely has to replace f by Aσ1,σ2κf, F by Aσ1,σ2κF.
The final preliminary fact we must state is the following bilinear estimate, which is Lemma 3.1 of [17].
Lemma 3.2. (Bilinear estimate in Bourgain space.)
Let s1≥−α−14+4αϵ,s2≥0, α≥4, b=12+ϵ and b′=−12+2ϵ. Then, we have
To this result, we apply the following Lemma, which is a corollary of Lemma 3.2.
Lemma 3.3. (Bilinear estimate in Gevrey-Bourgain space.)
Let s1>−α−14+4αϵ,s2≥0,α≥4,σ1≥0,σ2≥0,κ≥1,b=12+ϵ and b′=−12+2ϵ. Then, we have
Proof. It is not hard to see that
By Lemma 3.2, we get
4.
Proof of main results regarding the existence
4.1. Local well-posedness in an anisotropic Gevrey space
The above Lemmas will be used without somtimes mention to prove Theorem 2.1.
Lemma 4.1. Let s1>−α−14+4αϵ,s2≥0,α≥4,σ1≥0,σ2≥0,κ≥1,b=12+ϵ,b′=−12+2ϵ and 0<δ<1. Then
and
Proof. Combining Lemma 3.3 and Lemma 3.1 with the fixed point Theorem. We define
Then, we have
We choose δ such that
We have
Thus, Φ(u) maps B(0,2C‖f‖Gσ1,σ2,κs1,s2) into B(0,2C‖f‖Gσ1,σ2,κs1,s2) which is a contraction, since
Here we choose δ such that
We choose the time of existence where
For appropriate choice of c0, this will satisfy inequalities (4.1) and (4.2).
From Lemma 4.1, we see that for initial data f(x,y)∈Gσ1,σ2,κs1,s2(R2) if the lifespan δ=c0/(1+‖f‖Xσ1,σ2,κs1,s2,b)1ϵ then the map Φ(u) is a contraction on a small ball centered at the origin in Xσ1,σ2,κs1,s2,b. Hence, the map Φ(u) has a unique fixed point u in a neighborhood of 0 with respect to the norm ‖⋅‖Xσ1,σ2,κs1,s2,b.
The rest of the proof follows the standard argument.
4.2. Global well-posedness
In this section, we prove Theorem 2.2. The first step is to obtain estimates on the growth of the norm of the solutions. For this end, we need to prove the following approximate conservation law.
Theorem 4.2. Let σ1>0 and δ be as in Theorem 2.1, there exist b∈(1/2,1) and C>0, such that for any solution u∈Xσ1,00,b(I) to the Cauchy problem (1.1) on the time interval I⊂[0,δ], we have the estimate
with ϱ∈[0,34) if α=4, and ϱ=1 if α=6,8,10,….
Before we may show the proof, let us first state some preliminary Lemmas. The first one is an immediate consequence of Lemma 12 in [15].
Lemma 4.3. For σ>0, 0≤θ≤1 and ξ,ξ1∈R, we have
This will be used to prove the following key estimate.
Lemma 4.4. Let Nσ1,01(u) be as in Eq (1.4) for σ1≥0 and σ2=0. Then for b as in Lemma 3.2, we have
with ϱ∈[0,34) if α=4 and ϱ=1 if α=6,8,10,...
Proof. We first observe that the inequality in Lemma 3.2, is equivalent to
where we denote ϕ(τ,ξ,η)=⟨τ+m(ξ,η)⟩. With this, we observe that the left side of the inequality in Lemma 4.4 can be estimated by Lemma 4.3 as
If we apply Lemma 3.2 with s1=−ϱ, s2=0, it will follow, from the comments above, that
Proof of Theorem 4.2. Begin by applying the operator Aσ1,01 to Eq (1.1). If we let U=Aσ1,01u, then Eq (1.1) becomes
where α=4,6,8,.. and Nσ1,01(u) is defined in Lemma 4.4. Multiplying (4.4) by U and integrating with respect to the spatial variables, we obtain
If we apply integration by parts, we may rewrite the left-hand side as
which can then be rewritten as
By noticing that ∂jxU(x,t)→0 as |x|→∞ (see [15]) we obtaining
Integrating with respect to time yields
Applying Cauchy-Schwarz and the definition of U, we obtain
We now apply Lemma 4.4 and the fact that b=12+ϵ, we can further estimate this by
as desired.
Proof of Theorem 2.2. With the tools established in the previous subsection, we may begin the proof of Theorem 2.2. Let us first suppose that T∗ is the supremum of the set of times T for which
If T∗=∞, there is nothing to prove, so let us assume that T∗<∞. In this case, it suffices to prove that
for all T>T∗. To show that this is the case, we will use Theorem 2.1 and Theorem 4.2 to construct a solution which exists over subintervals of width δ, using the parameter σ1 to control the growth of the norm of the solution. We first prove the case s=0 and then we will generalize the case.
4.2.1. The case s=0
The desired result will follow from the following proposition.
Proposition 4.5. Let T>0, x=0, 0<σ1≤σ0 and δ>0 be numbers such that nδ≤T<(n+1)δ. Then the solution u to the Cauchy problem (1.1) satisfies
and
if
for some constant C>0.
Proof. For fixed T≥T∗, we will prove, for sufficiently small σ1>0, that
We will use the Theorem 2.1 and Theorem 4.2 with the time step
The smallness conditions on σ1 will be
where C>0 is the constant in Theorem 4.2. Proceeding by induction, we will verify that
for n∈{1,⋅⋅⋅,m+1}, where m∈N is chosen, so that T∈[mδ,(m+1)δ). This m does exist, since by Theorem 2.1 and the definition of T∗, we have
We cover now, the interval [0,δ], and by Theorem 4.2, we have
where we used that
since σ1≤σ0. This verifies (4.12) for n=1 and now, (4.13) follows using again
as well as Cσϱ1‖f‖Gσ0,00≤1. Next, assuming that (4.12) and (4.13) hold for some n∈{1,⋅⋅⋅,m}, we will prove that they hold for n+1. We estimate
verifying (4.12) with n replaced by n+1. To get (4.13) with n replaced by n+1, it is then enough to have
But this holds by (4.11), since
Finally, the condition (4.11) is satisfied for σ1∈(0,σ0) such that
Thus, σ1=C1T−1ϱ, where
4.2.2. The general case
For general s, we have
The case s=0 already being proved, we know that there is a T1>0, such hat
and
where ς>0 depends on f,σ0 and ς. We now conclude that
and
The proof of Theorem 2.2 is now completed.
5.
Gevrey's regularity in time
We follow the methods found in [5,6,7,11] to treat the regularity in time in Gevrey sens for unique solution of (1.1).
Proposition 5.1. Let δ>0,s1>−α−14, s2≥0 and
be the solution of (1.1). Then u belong in x,y to Gκ for all times near the zero. In other words,
for all (x,y)∈R2,C>0,t∈[0,δ],l,n∈{0,1,...}.
Proof. We have, for any t∈[0,δ]
We observe that
and
This implies that
Thus,
Since (2l)!κ≤c2l1(l!)2κ and (2n)!κ≤c2n2(n!)2κ, for some c1,c2>0, we have for all l,n∈{0,1,2,…}
where C0=‖u(⋅,⋅,t)‖Gσ1,σ2,κs1,s2 and C1=c20Cσ1,σ2,κ and c0=max(c1,c2), which implies that the solution u is analytic in x,y for all time near zero and s1,s2≥0.
Now, for −α−14<s1<0, s2≥0 and for any 0<ϵ<σ1, there exists a positive constant C=Cs,ϵ>0 such that
This implies that if
then
which allows us to conclude that u is in Gκ in x,y for all s1>−α−14, s2≥0.
In order to prove Theorem 2.3 it is enough to prove the following result.
Lemma 5.2. For j,l,n∈{0,1,2,…}, the next inequality
holds, where L=Cα+1120κ+C40κ, ∀x,y∈R, t∈[0,δ].
In fact, taking l=n=0 we obtain
Proof. We use the induction on j to prove Lemma 5.2.
For j=0 and l,n∈{0,1,2,…}, we have, by (5.1)
For j=1 and l,n∈{0,1,2,…}, we have
The terms of (5.4) can be estimated as
The nonlinear terms are treated as follows
Recalling that for l≥p and n≥k, we have the next inequality
By (5.7), we have
At this stage, we use the fact that
Then,
From (5.5), (5.6) and (5.9), it follows that
We assume that (5.2) is correct for j≥m≥1 where l,n∈{0,1,2,…} and then we prove it for m=j+1 and l,n∈{0,1,2,…}.
We obtain
These terms are estimated as follows
and
The nonlinear terms are treated as follows
Using (5.7) to estimate (5.12)1
We estimate (5.12)2 as
To estimate (5.12)3, we recall that for j≥q, l≥p and n≥k, we have the next inequality
Then
Finally by using (5.13)-(5.15) we arrive at
for all (x,y)∈R2,t∈[0,δ].
The detailed proof of (5.12) for κ=1 is given in [6].
6.
Conclusions
We have discussed the local well-posedness for a generalized Kadomtsev-Petviashvili I equation in an anisotropic Gevrey space. We proved the existence of solutions using the Banach contraction mapping principle. This was done by using the bilinear estimates in anisotropic Gevrey-Bourgain. We used this local result and a Gevrey approximate conservation law to prove that global solutions exist. These solutions are Gevrey class of order (α+1)κ in the time variable. The results of the present paper are new and significantly contribute to the existing literature on the topic.
Acknowledgments
The authors wish to thank deeply the anonymous referee for his/here useful remarks and his/here careful reading of the proofs presented in this paper.
Conflict of interest
The authors declare that they have no conflict of interest.









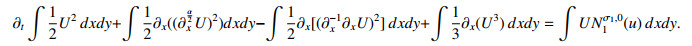









 DownLoad:
DownLoad: