Dynamics of diffusive modified Previte-Hoffman food web model

1.   Introduction

A variety of mathematical models for multi-species interaction, such as predator-prey models, food chain models and food web models, are proposed in literature ^[1,2,3] to satisfy the different environmental factors. Over recent decades, the evolution of the food web has become a major field of ecology and biology ^[4,5]. Complex networks play an significant role in explaining how biological processes are structured ^[6,7]. The higher species on the ecological food web can have a significant impact on the populations of species which are below them. Models of the food web were extensively studied by many researchers ^[8,9,10] such as the most interesting predator-prey models. The authors of ^[8,9,10] have shown that the global stability, longevity, extinction of the top predator, chaos-related systems, existence, uniqueness and stability of positive periodic solution can occur in these models.

Alan Turing ^[11] was among the first scientists who highlighted the role of biomorphogenesis patterns in the nonequilibrium diffusion reaction processes. In a uniform environment, dissipative nonequilibrium processes of random spatial and spatiotemporal pattern creation have been of uninterrupted importance in experimental and theoretical biology and ecology. A lot of researchers have paid attention over the past few decades to consider the evolution of spatiotemporal changes in ecological systems and their potential mechanisms ^{[12,13,14,15,16,17,18,19,20]}. Chaotic oscillations behind diffusive fronts are observed in the prey-predator model ^[21,22]. The appearance of diffusion-induced spatial-temporal chaos along a linear nutrient gradient was described by Pascual et al. ^[23] in the Rosenzweig-MacArthur phytoplankton-zooplankton model. Moreover, several types of stationary patterns such as labyrinthine, hot spots, cold spots, mixture of spots and lines, and chaotic patterns such as moving waves, intermittent traveling waves, spatiotemporal disorder, etc. are reported in ^[24,25,26]. However, contrast to the two-dimensional cases, the research works which consider pattern formations for three-species food chain models are rather limited in number. For example, Petrovskii et al. ^[27] proposed a three-species Lotka-Volterra type competitive spatial model and demonstrated the presence of moving waves and spatiotemporal chaos. Rao ^[28] studied the spatiotemporal pattern of a food web network and demonstrated the transformation of different classes of stationary patterns to turbulent wave patterns based on the magnitudes of the maximal ingestion rate or intermediate predator mortality rate. The authors of ^[29] investigated the case where Holling type Ⅱ and updated Leslie-Gower functional responses are defined over a circular domain of potential sequence configurations in a 3D food chain model. Some further research can be found in this area in ^{[30,31,32,33,34,35]}.

The classical two species predator-prey model introduced by Lotka and Volterra has been considered a cornerstone in mathematical ecology field. This model along with its variants successfully captured the nonlinear interactions of predator and prey populations and interpreted the observed oscillations in their densities. Thus, the two dimensional predator-prey models have been extensively studied in literature where different functional responses are exploited to better simulate real cases in nature. The new Previte-Hoffman model ^[36] introduced a third species, a scavenger, to conventional Lotka-Volterra predation model. In Previte-Hoffman model, the scavenger is a second predator that can eat prey and consume the carcasses of the first predator. The introduced scavenger has no direct negative impact on the predator population which is scavenged yet it has negative inhibitory effects on the prey population only. Note that in real world we can find a scavenger that consumes carcasses of both prey and predator populations in the way that it has no effect on either living prey or predator species. In this work, we intend to focus on the first type of scavenger.

The original model in ^[36] employs the simplest type of functional response, i.e. the Holling-type Ⅰ, and it only considers temporal dynamics of the three species. Consequently, the following challenging research questions emerge and need to be addressed: What are ecological implications of exploiting a more realistic and general functional response such as the Holling-type Ⅱ functional response? Also, what are the influences of such functional response on nonlinear temporal dynamics of the model? Can spatial extension of updated model, via adding random movements of all species, be considered? What are its implications?. In response to these questions, the authors first establish an updated version of original model in ^[36] by adopting Holling type Ⅱ functional response to describe predation of the first predator on the prey species.The next goal of this work is to further extend the model via incorporating random movements for the three species in updated model. The importance of this work from the ecological point of view arises because recent studies in mathematical ecology have highlighted that terrestrial scavenging is a key ecological process that must be accounted for in mathematical formulation of ecological models ^[37]. More specifically, there is a plethora of evidences and verification data which suggest that scavenging is an important factor and it does play a crucial role that was previously underestimated by ecologists. It is observed that a considerable number of species die due to several reasons other than normal predation and therefore they become available food to different scavengers. In fact, a fierce competition emerges among the diverse vertebrate scavengers which consume most available carcasses, particularly in warm environments. On other hand, the proposed model can lead to some new insights into competition and coexistence theory in mathematical biology. Interestingly, results for both the nonspatial and the spatially extended models indicate that coexistence of both predators occurs, despite sharing of a common prey species resource.

In this work, we propose and investigate the dynamics of a modified Previte-Hoffman food web model with spatially with local diffusion. The model includes a scavenger species that scavenges the predator and is also a predator of the common prey. The proposed model considers the mixed functional responses Holling types Ⅰ, Ⅱ. We derived the conditions for local stability of the model system in the absence and presence of diffusion. The criteria for Turing instability is examined. Numerical simulation results are presented and reveal changes in model dynamics from stability to limit cycle, and illustrate also possible types spatiotemporal behaviors of diffusive system.

We organize the paper as follows: In section 2, we introduce a modified Previte-Hoffmann model and discuss the dynamic behaviors of non-diffusive case. Thus, we expand the dynamical analysis in section 3 by adding spatial components and exploring a wide variety of spatiotemporal dynamics it possesses. Finally, a short description of the conclusion of the analysis is given in section 4.

2.   The modified Previte-Hoffman model

The omnivore predator-prey is an ODE model which generalizes the Lotka-Volterra system. Previte and Hoffmann have introduced this model in ^[36]. They proved that this model possesses the biologically attractive property that all solution trajectories remain bounded under some specific conditions on parameters. The model exhibits off-on-off chaotic behavior and cascades of period-doubling bifurcations. We propose a new version of Previte-Hoffman model. Here, the densities of the prey, predator and scavenger populations at the time t are denoted by $u(t)$, $v(t)$ and $w(t)$. In the absence of a predator and scavenger population, the logistic growth rate of prey was considered. Previte-Hoffman ^[36] assumed that the predation rate of prey by predator follows Holling I functional response form. But in our model, it is supposed that the predation rate of prey by predator is of Holling II functional type since it is known that when the population size of prey species considerably increases, the predation rate is almost fixed. The third species in the model represents a kind of scavengers which attacks and eats prey species whereas it just consumes the carcasses of other predator in the food web. Consequently, the scavenger has negative effects on the prey species while it has no immediate negative impact on the predator species. In mathematical formulation of this case, the positive effects of prey and (dead) predator species on scavenger population are included in scavenger equation while its negative influences appears only in prey equation. The proposed model in the presence of mixed functional responses of prey-predator and scavenger is a modified for Previte-Hoffman model. Then the modification Previte-Hoffman model is described by

The parameter $b$ is the reciprocal carrying capacity of $u$. The parameter $c$ reflects the predator's normal death rate in the absence of a prey. The parameter $e$ represents the omnivore's normal death rate in the absence of resources. The $p$ parameter is related to the efficiency that $w$ preys on $u$. The $q$ parameter is related to the efficiency that $w$ gains from carcasses of $v$. The $\beta$ parameter is related to $w$'s reciprocal carrying capacity. Also, the parameter of Holling type Ⅱ functional response is $\varepsilon$. The linear functional response (Holling Type I) presupposes that rate of prey species consumption by predators increases without limits when prey population density rises. However, empirical and laboratory studies show that the consumption rate of prey increases till it asymptotically reaches a constant value at which the rate of consumption is constant regardless of prey population density.

Thus, handling parameter $\varepsilon$ is an invariant value that is utilized to describe the efforts exerted by predator species in searching for, attacking and consuming one prey species when effects of satiation are taken into account. As a result, although it is easier for predator to locate places of prey species when their density increases, the presence of invariant $\varepsilon$ implies that the maximum value reached of prey consumption rate will be (1/$\varepsilon$). By including the handling time parameter $\varepsilon$, the Previte-Hoffman model turns to be just the special case that occurs when $\varepsilon = 0$. Then, the temporal dynamical study of updated model is carried out analytically and numerically to explore its emerging dynamical characteristics.

Notice that all the parameters in this model (2.1) are positive constants. The model (2.1) is also subject to the initial non-negative conditions.

Therefore, the model (2.1) has the following domain:

The solution of system (2.1) is proved to be uniformly bounded in the following theorem.

2.1.   Positivity, boundedness, existence and uniqueness of the solution model (2.1)

To ensure that the model (2.1) is biologically well behaved, we need to demonstrate positivity and boundedness of model (2.1) solutions. In this regard, we have the following theorems:

Corollary 1. Any solution of the model (2.1) that initiates within $\mathbb{R}_{+}^{3}$ remains forever positive.

Proof. We get from the first equation of (2.1):

Consequently,

In the same way,

Also,

Therefore, solutions of system (2.1) are non-negative.

Theorem 1. The solutions of model (2.1) are always non-negative and remain bounded.

Proof. Let $(u(t), v(t), w(t))$ be an arbitrary solution of the model (2.1) with a non-negative initial condition. Then for $\Psi(t) = u(t)+v(t)+\frac{1} {p}w(t),$ we have

Now, we introduce a positive constant $\eta > 0$, then we have

If $\eta = \min\{c, e\},$ hence

The function $\left(\frac{\beta}{p} w^{2}-\frac{q}{p} v w + v^{2} \right)$ is positive definite if $q^{2} < 4p\beta$. Thus,

where $M = \frac{(1+\eta)^{2}}{4b}+\frac{(\eta-c)^{2}}{4}$. Applying Gronwall's Inequality, the following is obtained:

Thus for model (2.1) all solutions are bounded. Hence, it proves the theorem.

The existence and uniqueness of the solutions of the system (2.1) in the region $\Omega \times (0, T]$ can be discussed.

where

$T < +\infty$, $\kappa$ is sufficiently large, the existence of $\kappa$ is ensured by the boundedness of the solution.

Theorem 2. There is a unique solution $U(t)\in \Omega$ of system (2.1) for each initial condition $U_{0} = (u_{0}, v_{0}, w_{0})\in \Omega$, which is defined for all $t\geq 0.$

Proof. The mapping $I (U) = (I_{1}(U), I_{2}(U), I_{3}(U))$ is given by

We are interested to find out the existence and uniqueness the solution of model (2.1). To find this, we need to prove that the mapping $I (U)$ satisfies Lipschitz condition. For any $U$, $\overset{-}{U}$ two solutions in $\Omega$ of the system (2.1), it follows from (2.4) that

where

Therefore, $I(U)$ satisfies the condition of Lipschitz with respect to $U$. Thus, the solution $U(t)$ of the system (2.1) with initial condition $(u_{0}, v_{0}, w_{0})$ exists and it is unique.

It is impossible to find exact solution of the nonlinear autonomous model (2.1). Hence, we are analyzing the qualitative behavior of the solutions in the neighborhood of steady states.

2.2.   Non-negative steady states and their stability

It is easy to see that, the model (2.1) has five steady states. The necessary conditions for the existence of each steady state have been examined below. The trivial steady state is $S_{0}$, corresponds to extinction of all species. The boundary steady state is $S_{1}$ corresponds to the disappearance of predator and scavenger. Planer steady states are $S_{2}$ and $S_{3}$ corresponds to extinction of predator or scavenger respectively. Finally, the coexistence steady state is $S_{4}$ associates to coexistence prey, predator and scavenger.

Define the functions $f, g$ and $h$ as follows:

Jacobian matrix takes the form

where

In this analysis, we are primarily concerned with the system's behaviors around the points of equilibrium.

Theorem 3. The trivial steady state $S_{0}$ of model (2.1) is always unstable saddle point.

Proof. Straightforward computation shows that the Jacobian matrix (2.6) of model (2.1) around the trivial steady state $S_{0}$ has the following eigenvalues:

Accordingly, $c$ and $e$ are nonnegative then the trivial steady state $S_{0}$ is always unstable saddle point.

Theorem 4. The axial steady state $S_{1}$ of model (2.1) is locally asymptotically stable if and only if the

Proof. The Jacobian matrix (2.6) of the model (2.1) evaluated at axial steady state $S_{1}$ is given by

which has the following eigenvalues

These eigenvalues have real parts are negative if and only if

Therefore, $S_{1}$ is locally asymptotically stable if and only if the following condition holds:

Theorem 5. The predator free steady state $S_{2}$ of model (2.1) is locally asymptotically stable if and only if

Proof. The Jacobian matrix (2.6) of the model (2.1) at predator free steady state $S_{2}$ is given by

Consequently, the eigenvalues of $J(S_{2})$ are given by

where

It's clear that, these eigenvalues have real parts that are negative if and only if

Theorem 6. The the scavenger free steady state $S_{3}$ of model (2.1) is locally asymptotically stable if and only if

Proof. The Jacobian matrix (2.6) of the model (2.1) at the scavenger free steady state $S_{3}$ is given by

Consequently, the eigenvalues of $J(S_{3})$ are given by

where

It's clear that, these eigenvalues have real parts are negative if and only if

From a biological point of view, it is of interest to see the stability of the nontrivial steady state $S_{4}$ which ensures that three species coexist. Now, we consider the local stability of coexistence steady state i.e. for $S_{4}.$ In this case, the elements of Jacobian matrix (2.6) at $S_{4}$ are given by

The characteristic equation of matrix $J$ takes the form

where

and the lengthy and complicated expression of $C_{2}$ is completely omitted for brevity.

From Routh-Hurwitz stability criterion ^[38], it is known that $S_{4}$ is locally asymptotically stable if the following necessary and sufficient conditions are satisfied

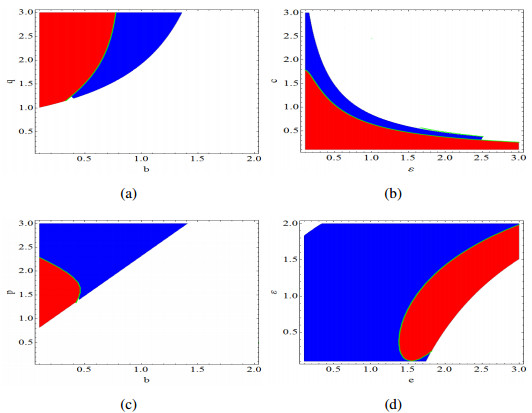
The very complex expressions of these conditions, when they are explicitly written in terms of parameters of the proposed model, render it inevitable to examine them numerically along with aforementioned conditions which ensure the positivity of three species densities at $S_{4}.$ In ^[10], the authors further extended the dynamical and bifurcation study of baseline Previte-Hoffman model ^[36] with Holling-Type I functional response. The present paper investigates the modified model with mixed functional responses in addition to analyze the influences of the spatial extension of the proposed model. Accordingly, the theoretical and numerical results obtained on temporal dynamics of the model in ^[10,36] can be considered as special cases that occur when $\varepsilon = 0$ in modified model. Indeed, significant changes are discerned due to our modification to baseline model. One of the key differences that are found is that pattern formation ceased to exist in Previte-Hoffman model ($\varepsilon = 0$) while its regions of occurrence in space of parameters of modified model are depicted. Also, the nonoccurrence of codimensional two bifurcations for $\varepsilon\neq0$ is figured out in this work. The influences of model's parameters are illustrated in the following scenarios of numerical investigations where the white regions denote the range of selected values of parameters at which one population density or more of three species is negative or zero. The blue and red colored regions indicate the values of parameters associated with local asymptotic stability and unstability of steady state $S_{4}$, respectively.

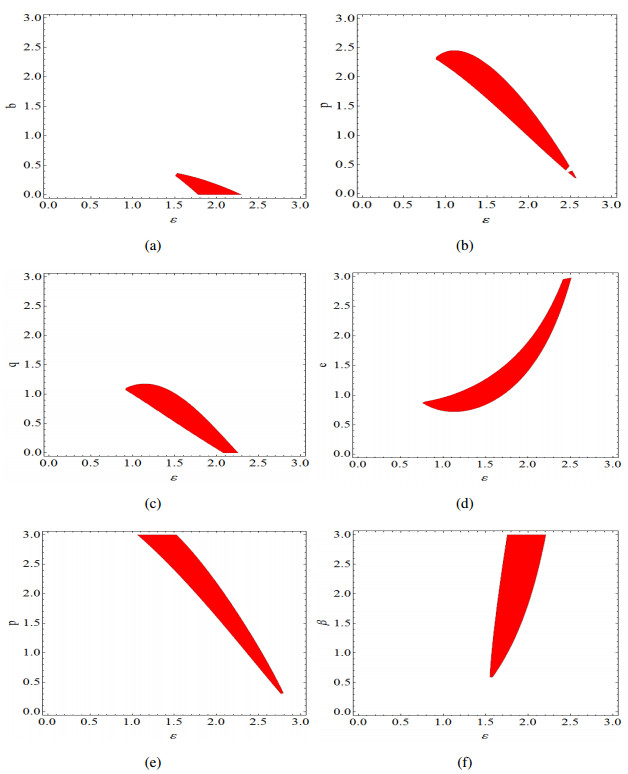
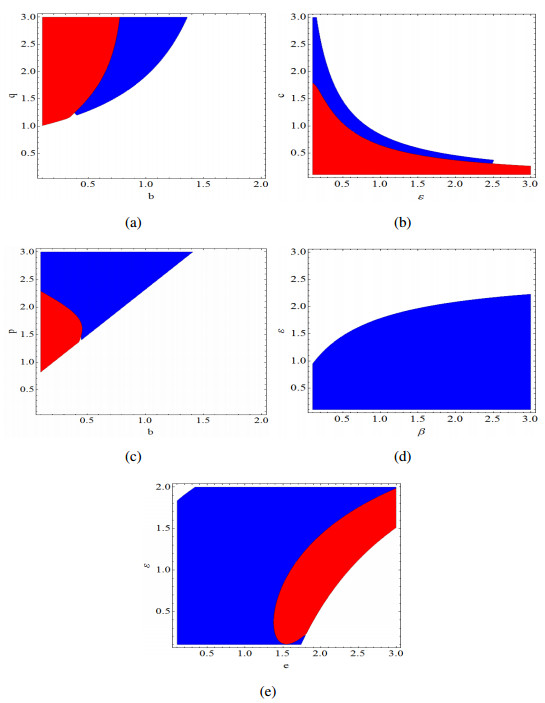
Figure 1 shows results of numerical simulations for different cases. In first case, we take $c = 0.4, e = 1.3, p = 0.2, \beta = 1.3, \varepsilon = 0.5$ whereas the values of parameters $b$ and $q$ are varied in order to explore their effects on stability of $S_{4},$ see Figure 1a. In second case, the fixed values of parameters are $b = 0.1, e = 0.1, p = 0.1, q = 0.6, \beta = 1$ whereas the values of parameters $\varepsilon$ and $c$ are varied to examine their effects on stability of $S_{4}$, see Figure 1b. In third case, we take $c = 0.4, e = 2.1, q = 1, \beta = 1, \varepsilon = 1$ whereas the values of parameters $b$ and $p$ are changed to explore their effects on stability of $S_{4},$ see Figure 1c. Similarly, the fixed parameters for forth case are given by $b = 0.7, c = 0.3, e = 0.8, p = 2.1, q = 1.5$ whereas the values of parameters $\beta$ and $\varepsilon$ are varied, see Figure 1d. Finally, the case of $b = 0.2, c = 0.3, p = 2.5, q = 1, \beta = 1.8$ is considered in Figure 1e and the values of parameters $e$ and $\varepsilon$ are changed. It is observed that the coexistence steady state is stable for the following cases: (ⅰ) The predation rates of $w$ are large enough while the reciprocal carrying capacity of prey takes moderate to large values. (ⅱ) small to moderate values of handling parameter and omnivore's death rate.

Note that colored regions correspond to the region of feasible occurrence of coexistence equilibrium point. The five different parameter sets are chosen in the way that they address possible influences of combination of parameters, in the modified model, on the stability of coexistence equilibrium point. In first case, increasing the value of $b$ implicates that density of prey population decreases and therefore negatively affects both of predator and scavenger species. However, if scavenger has reasonable scavenging efficiency on carcasses of predators, both competitors species can coexist as shown in Figure 1a. Otherwise, the smaller values of $b$ or $q$ imply that the competition between predators and scavengers destabilizes the coexistence equilibrium point i.e. it leads to the extinction of one of the two species. When the value of handling parameter $\varepsilon$ is decreased while the value of $p$ is fixed, as in second case, it results in high predation efficiency of predators and simultaneously considerably reduces some food resources of scavenger species. Consequently, the stable coexistence state of two competitors is observed only when death rate of predators is increased over a certain value, depending on $\varepsilon$, and hence the negative impact on scavengers is compensated, see Figure 1b.

Another interest observation is demonstrated in Figure 1c. It is found that is starting at small values of $b$ and $p$ i.e. relatively large population size of preys and weak predation efficiency of scavenger species, respectively, the stable coexistence state of predators and scavengers competitors ceases to exist. By increasing $p$, and thus improving predation efficiency of scavengers, the stable coexistence of both species is observed. The effects of simultaneous changes in parameters $\beta$ and $\varepsilon$ are demonstrated in Figure 1d. It is obvious that the two competitors coexist for relatively small to moderate values of $\varepsilon$ according to the specific value of $\beta.$ When the value of $\varepsilon$ considerably rises, it results in decaying in predator's hunting efficiency in favor of scavenger species. Consequently, the cohabitation of the two competitors is impossible in this case, see Figure 1d. Finally, from Figure 1e it can be observed that starting from region of stability of $S_{4},$ when the scavenger death rate increases it destabilizes the coexistence equilibrium point. However, for short handling time parameter $\varepsilon,$ the equilibrium point $S_{4}$ is first destabilized then it becomes stable again before it totally disappears. A possible interpretation, from ecological point of view, is that when $e$ increases, the resulting reduction in population size of scavenger species allows cohabitation between predators and scavengers for limited range of $e$ values before $S_{4}$ vanishes (the extinction scavengers). For larger values of $\varepsilon$, the mathematical form of $S_{4}$ renders its restabilization occurs at values of $\varepsilon$ which correspond to infeasible negative densities, hence these irrelevant regions have not been considered in the Figure.

2.3.   Possible scenarios of bifurcations

Suppose that the eigenvalues of matrix $J,$ at steady state $S_4$, for some values of parameters are given by $\lambda _{1, 2, 3}^{h} = -\alpha _{0}, \pm i\omega _{0}$ such that $\alpha _{0}$ and $\omega _{0} > 0.$ Now, the characteristic equation is expressed by

Obviously, from (2.8) it implies that

at critical values of parameters associated to Hopf bifurcation ^[38]. The characteristic Eq (2.7) is very complicated at steady state $S_{4}$ to allow direct analysis of Hopf bifurcation in the model. The matrix $J$ has three eigenvalues and we assume that for a particular values of parameters they take the form

which represents a primary condition for Hopf bifurcation in three dimensional systems. Hence, the aforementioned assumption implies that the characteristic equation can be expressed as

or

Note that Eq (2.10) is just an assumption which need to be verified using appropriate numerical simulations which determine the critical values of parameters (if they exist) which yield $\lambda _{i}^{h}, \; i = 1, 2, 3$. When the values of parameters are slightly perturbed around critical values, the occurrence of Hopf bifurcation requires also that the two complex conjugate eigenvalues of $J$ take the form

such that the real part $r$ vanishes exactly at critical value of bifurcation and changes its sign when transversely crossing the bifurcation curve in space of parameters.

By the aid of numerical evaluations, the Hopf bifurcation curves are obtained in two dimensional space of systems parameters. More specifically, Figure 2 shows the results of numerical simulations where the intersections of green curves and region of presence for $S_{4}$ represent the Hopf bifurcation curves in the model (2.1). It is clear that the Hopf bifurcation curves occur at the boundary between stable and unstable regions in 2D space of parameters. In particular, periodic solutions exist at small reciprocal carrying capacity of prey and small predator death rate.

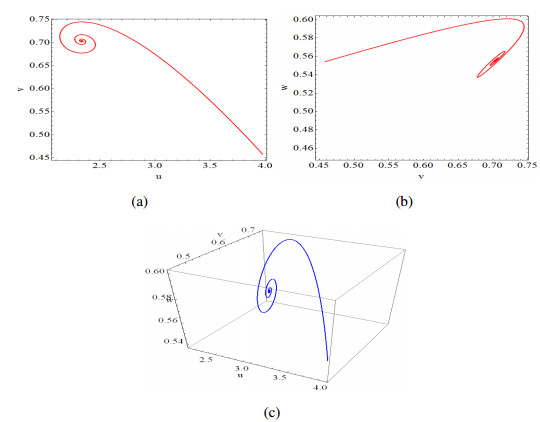
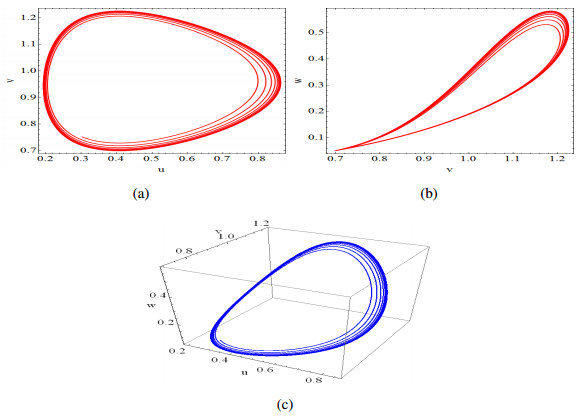
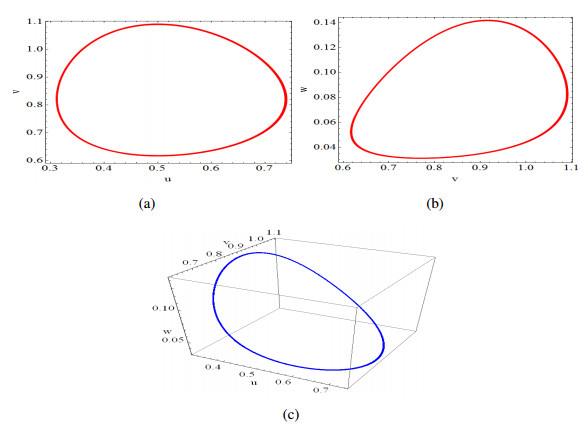
The phase portraits of system (2.1) are obtained to verify the aforementioned results. Firstly, the local asymptotically stable equilibrium point $S_{4}$ is shown in Figure 3 for some selected values of parameters, which can be extracted from Figure 1, such that $b = 0.1, p = 0.1, \beta = 1, q = 0.6, e = 0.1, c = 0.7, \varepsilon = 1.$ Secondly, two examples of stable limit cycles which are generated via Hopf bifurcation are illustrated in Figures 4 and 5.

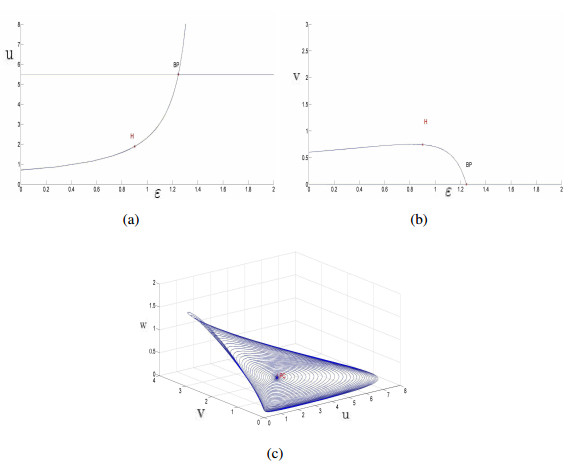
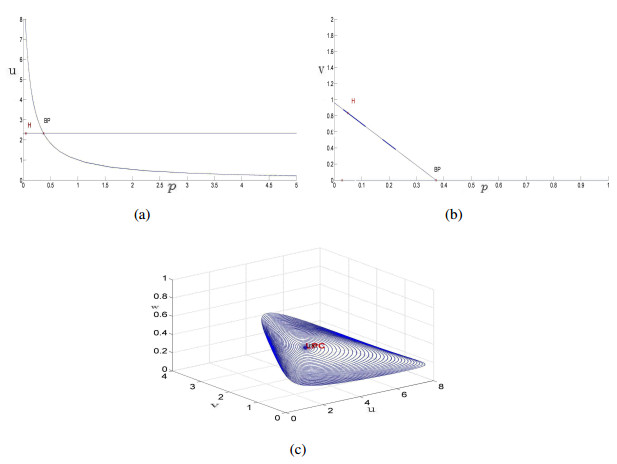
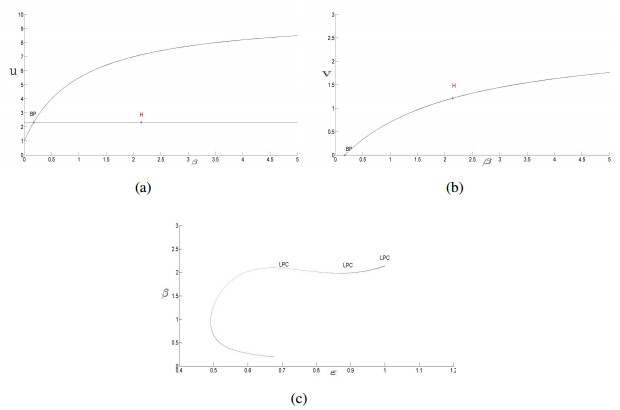
The bifurcation diagrams are employed to further explore the critical dynamical changes in behaviour of model (2.1) that are accompanied by variations in values of parameters. More specifically, numerical continuations of steady state $S_{4}$ versus different parameters of model (2.1) are acquired using Matcont numerical bifurcation analysis tool. Starting at $b = 0.1, p = 0.1, \beta = 1, q = 0.6, e = 0.1, c = 0.7, \varepsilon = 1,$ Figure 6 depicts the possible bifurcations which are encountered with variations in value of $\varepsilon.$ It is obvious that both transcritical bifurcation, denoted by BP at $\varepsilon = 1.247$, and Hopf bifurcation, denoted by H at $\varepsilon = 0.901,$ occur in bifurcation diagram. In particular, the Hopf bifurcation is a supercritical since the first Lyapunov coefficient is found to be $-0.058$ i.e. it has negative value and thus a stable limit cycle is generated. The continuation of Hopf point reveals that a limit point cycle (LPC) or fold bifurcation exist at $\varepsilon = 0.901$ with normal form coefficient equals $-0.726,$ see Figure 6c. In second scenario, Figure 7 illustrates the possible bifurcations that occur as a response to variations in value of $p.$ It is obvious that both transcritical bifurcation, at $p = 0.371$, and Hopf bifurcation, at $p = 0.049,$ occur in bifurcation diagram. In particular, the Hopf bifurcation is a supercritical since the first Lyapunov coefficient is found to be $-0.337$ and hence a stable limit cycle is generated. The continuation of Hopf point reveals that a fold bifurcation of cycles occurs at $\varepsilon = 0.049$ with normal form coefficient equals $-0.051,$ see Figure 7c. In third scenario, the bifurcation diagram is obtained vs. parameter $\beta$ for the same values of parameters. Figure 8a, b clarify the presence of transcritical bifurcation of $S_{4},$ at $\beta = 0.174,$ and supercritical Hopf bifurcation, at $\beta = \; 2.142$ with first Lyapunov coefficient equals $-0.041.$ The continuation of Hopf bifurcation curve in $\varepsilon -\beta$ parameter plane is provided in Figure 8c where three limit point cycles are detected.

The dynamical behaviour of the system (2.1), as shown in these figures, is found to be sensitive to parameter values and initial data. This behaviour shows that the handling parameter $\varepsilon$ has a negative impact on stabilizing the dynamics of the model (2.1).

2.4.   Notes about nonoccurrence of codimensional two bifurcations

The non-occurrence of codimension two bifurcations reveals that there are some complicated dynamics, which relate to local codimension two bifurcations, cannot be observed in modified model's behavior. For example, non-occurrence of zero-Hopf bifurcation implies the non-occurrence of torus bifurcation and the bifurcations of Shil'nikov homoclinic (or heteroclinic) orbits. More interestingly, the local birth of chaotic dynamical behavior in the model, through torus breakdown from regular to chaotic regimes, can then be excluded. The double-Hopf (DH) bifurcation requires at least four dimensional state space of the dynamical system. Thus, it cannot be induced in model (2.1). In this subsection, we describe briefly the reasons for nonoccurrence of the other two basic types of codimension two bifurcation, namely, Bogdanov-Takens (BT) bifurcation and zero-Hopf (ZH) bifurcation.

(1) BT bifurcation The investigation of characteristic equation of matrix $J$, defined in (2.6), at equilibrium point $S_{4}$ shows that two zero eigenvalues occur at the following critical values of parameters in model (2.1)

By applying suitable linear transformation to put the linear part of the matrix in Jordan canonical form, it can be verified that the linear part of transformed model (2.1) is expressed by

which is different from that of BT bifurcation. Furthermore, the second set of critical values of parameters which yield two zero eigenvalues is given by

By using the following transformation matrix

the linear part of resulting standard form of model (2.1) is found to be

which agrees with BT standard form ^[38].

Therefore, proceeding to compute the center manifold which takes the form

it implies that $m_{1} = \frac{(c \varepsilon -1)^2 \left(b^2 c^2 (e+1) \varepsilon +b (c (\varepsilon (c+e) (c \varepsilon -2)-c \varepsilon q+q+1)+e-q)-q (c \varepsilon -1)^2\right)}{(b c e+b c+c e \varepsilon -e)^2}$,

$m_{2} = (b c (e+1)+e (c \varepsilon -1)) (b c (c \varepsilon -q-1)-c \varepsilon q+q) \left(b^2 c \left(e (c \varepsilon -1)^2+c \varepsilon (c \varepsilon -1)-q\right)-q (c \varepsilon -1)^3\right....$

The critical normal form is found to be

where

$\varsigma = -\frac{0.25 (c \varepsilon -1)^3 (b c (c \varepsilon - q-1)-c \varepsilon q+q)}{b^3 c (c (b+\varepsilon)-1) (c \varepsilon e- e+q)}+\frac{0.5 (1-c \varepsilon)}{b^3 c (b c (e+1)+e (c \varepsilon -1))} \; (\frac{b^3 c^2}{c (b+\varepsilon)-1}-\frac{e (c \varepsilon -1)^2 (b c (c \varepsilon -q-1)-c \varepsilon q+q)}{e (c \varepsilon -1)+q}\text{...}).$ Nevertheless, careful investigations indicate that the coefficients of critical normal form (2.15) do not satisfy nondegeneracy conditions of codimension two and codimension three BT bifurcation.

(2) ZH bifurcation A thorough examination of characteristic equation of matrix $J$ (2.7) of steady state $S_{4}$ demonstrates that the matrix has one zero eigenvalue and two purely imaginary eigenvalues at the following sets of critical values

with condition

or

provided that

or

with condition

or

provided that

However, all of the aforementioned conditions contradict those related to presence of $S_{4}$ and positivity of parameters. Thus, the ZH bifurcation cannot be induced in parameter's space of model (2.1).

3.   Spatio-temporal model

The study of the movement and dispersal of organisms has become a key element in the understanding of a number of ecological problems pertaining to the spatiotemporal dynamics of populations ^[39,40,41]. The effects of key parameters in spatial model dynamics, involving Turing instabilities and pattern formations, have become a very attractive field for researchers. Some other works on the existence of spatiotemporal dynamics for different types of diffusive biological systems can be found in ^[42,43,44]. The proposed model (2.1) can lead to some new insights into competition and coexistence theory in mathematical biology. The aim of this section is to further extend the model via incorporating random movements for the three species in updated model. The effects of key parameters in spatial model dynamics, involving Turing instabilities and pattern formations, are traced where it should be taken into account that the subordinate special case of $\varepsilon = 0$ reveals the specific dynamics of spatial Previte-Hoffman model. The space effects on the model (2.1) is to be explored by considering the the random movements of prey, intermediate predators and scavengers (top predators) in some specified domain domain. In particular, the self-diffusion terms are included in the proposed system of reaction diffusion equations as follows:

where $\nabla ^{2}$ denotes the two dimensional Laplacian operator given by $\nabla ^{2} = \frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{ \partial y^{2}}$.

The steady states shown in the diffusion-free system (2.1) also, are diffusion system solutions (3.1) if the variables show no spatial dependency i.e. they are the same. However, this homogenous solution 's linear stability, as we can see now, depends on diffusion.

3.1.   Stability analysis of spatial model system

In this subsection, we are studying the effect of diffusion on the inside uniform steady state of system (3.1). The linearization of the model (3.1) is obtained for small disturbances of the uniform steady state $E(u^{\ast }, v^{\ast }, w^{\ast })$, namely, $U$, $V$ and $W$ such that $u = u^{\ast }+U, v = v^{\ast }+V$ and $w = w^{\ast }+W$. The linear form of the equations is given as

Suppose that the model system (3.2) has a solution of the form

where $A_{1}$, $A_{2}$ and $A_{3}$ are sufficiently small constants. The parameter $\lambda$ is the time growth rate, $\textbf{k}$ is wave vector and $r\equiv (x, y)$ denotes the space vector. The characteristic equation of linearized system is expressed as

where

such as

where

and

Here $M$ is the Jacobian matrix of ODE system at coexistence uniform steady state. Based on Routh–Hurwitz criterion, the spatial system around steady state is stable if

The steady state is destabilized if at least one of these conditions is violated for some value of $k$. Clearly if $k = 0$ then it follows Routh-Hurwitz conditions for stability of steady state without diffusion. Instability of uniform equilibrium points can lead to two main types of bifurcations, namely, breaking symmetry-Hopf and Turing bifurcations, and therefore the appearance of spatio-temporal patterns. Turing bifurcation violates spatial symmetry, resulting in patterns being constant in time and oscillating in space ^{[39,40,41,42,43,44]}.

More specifically, Turing instability arises if the steady state of non-diffusive model is stable but it loses its stability in associated diffusive system such that at least one of the conditions of the inequality (3.3) is violated, i.e.

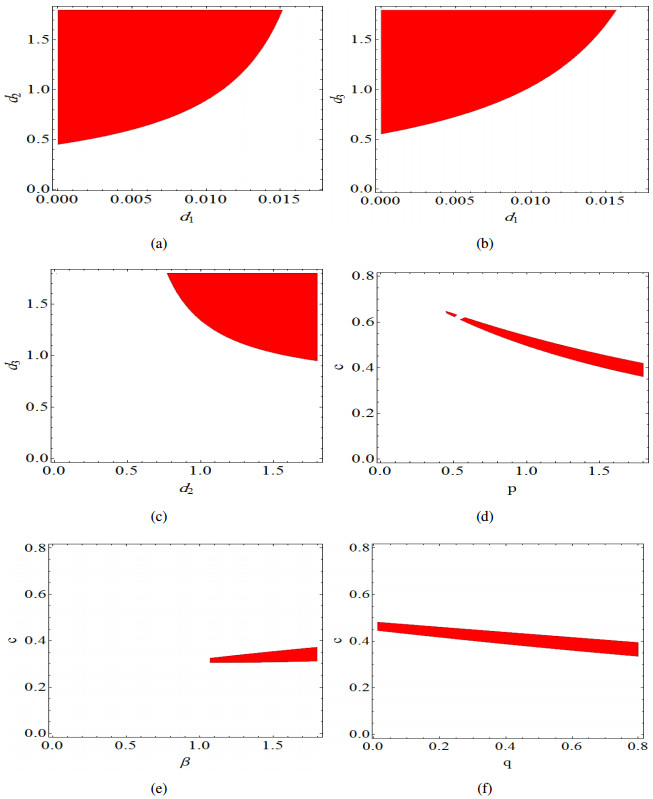
By exploiting a thorough numerical bifurcation analysis in space of parameters, the boundaries between stability and instability regions of uniform equilibrium point can be found out. In Figures 9 and 10, the regions which associate with formation of onset of patterns are marked with red color. On other words, Turing instability of spatially uniform equilibrium point is induced at the values of parameters that occur in red colored region. From Figure 9a–c, the induction of patterns is observed for small values of prey species diffusion coefficient and relatively large values of predators and scavengers diffusion coefficients. For example, if the value of $d_{1}$ is fixed at $0.005$ whereas the values of $d_{2}$ and $d_{3}$ are varied along a vertical upward direction in Figure 9a, b, the boundaries of Turing instability will be attained at approximate values of $0.6$ and $0.7$ for $d_{2}$ and $d_{3}$, respectively. Moreover, when the value of $d_{1}$ is fixed at $0.01$, the boundaries of Turing instability are reached approximately at $d_{2} = 0.9$ and $d_{3} = 1$. It implies that as the value of $d_{1}$ is increased, it requires firstly a bigger values of $d_{2}$ and $d_{3}$ for destabilization of spatially uniform steady state and creation of patterns. Then, by increasing further the value of $d_{1}$, the uniform equilibrium point preserves stability and does not turn into Turing instability regime regardless the value of $d_{2}$ and $d_{3}$. From Figure 9d, it is observed that pattern onset cannot occur at small values of predation rate $p$ of scavengers on prey species. Patterns start to appear if the value of $p$ is boosted while the value of predator death rate $c$ is confined in red strip illustrated in Figure 9d. Note that as the efficiency of scavengers' predation increases, the values of $c$ in red strip gradually decreases. From Figure 9e, it can be demonstrated that Turing instability of spatially uniform steady state is excluded at small values of scavenger species interior competition (i.e small $\beta$). When the value of $\beta$ is increased and the value of predator death rate is taken from the horizontal red strip illustrated in Figure 9e, the formation of patterns is exhibited. Note that the width of red strip is relatively expanded when the interior competition among scavenger species rises. This means that the high competition among scavenger population enables the onset of patterns for bigger values of $c$, provided that $c$ values do not cross the boundaries of red colored region. Moreover, Figure 9f indicates that Turing instability of spatially uniform steady state occurs at wide range of values for $q$ and limited values of $c$ as illustrated by the red colored region. Indeed, the values of feeding efficiency of scavenger from carcasses of predators, i.e. $q$, are inversely proportional to the value of predators' death rate in the aforementioned red strip of Figure 9f.

Figure 10 illustrates Turing instability regions, in red color, for different planes of parameters in the proposed model (3.2). Numerical simulations reveal that the spatial extension of baseline model ($\varepsilon$) cannot exhibit Turing instability such that the different types of patterns, which can arise in the modified model, occur only for $\varepsilon > 0$. This implies that employing the more realistic Holling type Ⅱ functional response in baseline model has remarkable and interesting effects on the model. In order to explore the effects of $\varepsilon$ along with other parameters on creation of patterns, Figure 10 illustrates Turing instability regions, in red color, for different planes of parameters in the proposed model (3.1). Numerical simulations reveal that the spatial extension of baseline model ($\varepsilon = 0$) cannot exhibit Turing instability such that the different types of patterns, which can arise in the modified model, occur only for some particular values of $\varepsilon > 0$ as shown in the figure$.$ This implies that employing the more realistic Holling type Ⅱ functional response in baseline model has remarkable and interesting effects on the baseline model.

Generally, it is observed that spatial patterns always feature both of the two predators. Also, the type of pattern and transitions between them depend on the particular values of parameters in the represented red regions in Figures 9 and 10. It is found that the transitions from cold spots to hot spots or vice versa are accompanied with intermediate stage consists of stripes and spots or stripes only. From the above, we see that diffusion destabilizes the steady state solution and thus generates the spatial patterns of the model (3.1). In the next subsection, we use numerical simulations to locate the regions of spatial patterns through Turing instability in parameters space of the model.

3.2.   Numerical simulations and validation of theoretical results

In this subsection, numerical simulations are carried out for reaction diffusion system (3.1). For each simulation simulations start till there is no significant change in the behavior of the solution. We will show the figures of the three species if there is a notable difference between them, otherwise the results of the prey species are presented. MATLAB software is employed to run this simulation such that no-flux boundary conditions are applied and also the initial conditions take very close values to the equilibria. The size of the system is $Lx\times Lx = 200\times 200$ and the size of the space step and time step are $\delta = \Delta x = \Delta y = 0.25, \Delta t = 0.01$, respectively. For the simulation we apply an explicit finite difference scheme that can be manifested as follows

where $N_{i, j}^{n+1}$ for $N = \{u, v, w\}$ represents the concentration of the species at the point $\left(x_{i}, y_{i}\right)$ at time $n+1$.

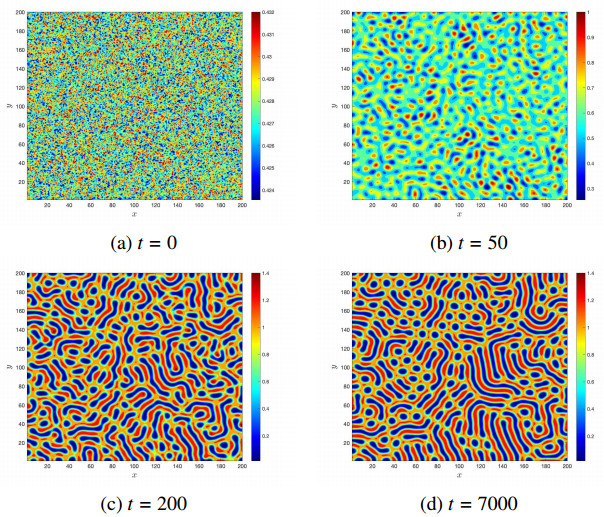
At the beginning of the simulation, we choose the uniform coexistence steady state $u^\star, v^\star, w^\star$ in the autonomous system (3.1) as initial conditions and add sufficiently small perturbation. For very small values of the diffusion coefficients $d_1, d_2$ and $d_3$ there is no Turing patterns appear, as observed in simulations.

Increasing the values of $d_2$ and $d_3$, the evolution of the spatial patterns of the species starts irregular. Then after long time, the spatial patterns are being time independent, see Figure 11.

For system (3.1), different behaviours of the patterns like hot spot and cold spot, mixture of spot and stripes and stripes only are observed. Hot spot used in ^[43] to denote the isolated zones with high density of prey while cold spots denotes the isolated zones with low density of prey and stripes for interlaced stripes of high and low population densities.

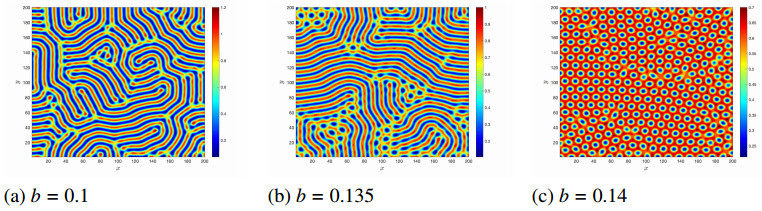
Now, focusing on the impact the reciprocal carrying capacity or domestic competition rate of the prey, i.e $\left(b \right)$, on the spatial distribution of the system. It is noticed that for small value of $b$, say $b = 0.1$, stripes are found. By continuing increase the value of $\: b \:$, the stripes disappear and there are only cold spots, see Figure 12. This can be interpreted as follows: From Figure 12 high density of prey species is distributed over the whole region for large value of $b$ (small value of carrying capacity and low domestic completion) while for higher domestic competition of prey population (small values of $b$) we notice that the most concentrated areas of prey form stripes due to high competition.

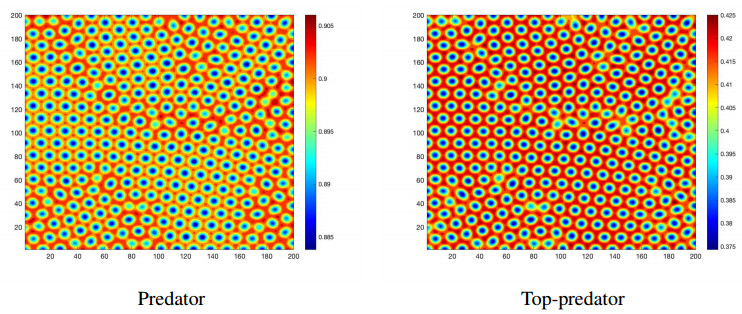
By comparing the distribution of preys, predators and top-predators in the area, it is depicted that the distributions of predators and top-predators densities in the area do not significantly vary from location to another location, see Figure 13.

More precisely, the lowest value of predator population size in the area at $\: t = 7000 \:$ is $\:0.8838 \:$ and the highest value at this time is $\: t = 0.9066 \:$. Also, the difference between the highest and the lowest value of top-predator population size is less than $\: 0.055 \:$. In contrast, the difference between the highest and the lowest numbers of top-predators is bigger than $\: 0.5$. We have noticed this behaviour of distributions of species in the model occurs for different choices of parameters. The possible interpretation is that, the distribution of prey depends mainly on the preys' competition rate and interaction with predators while there is nothing scare predator and top-predators so that they concentrate on the areas where are the prey on.

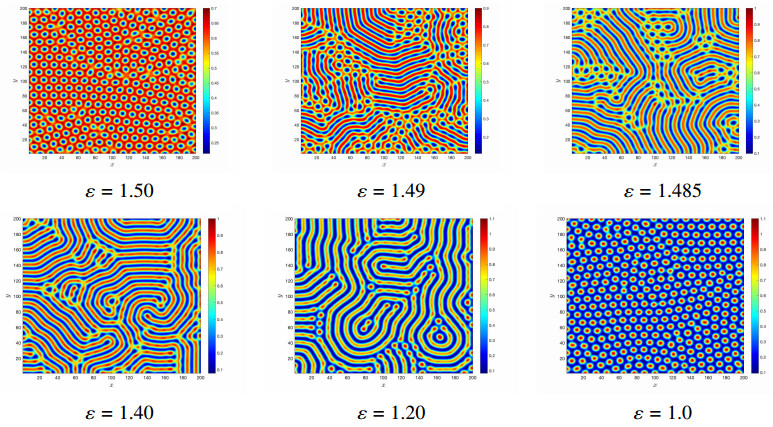
We analyze the influences of $\varepsilon$ in the following way. We fix the parameters in Figure 14 and decrease $\varepsilon$ to monitor the behaviour of the spatial patterns. It is observed that at $\varepsilon = 1.5$, the spatial patterns take a cold spots form. For $\varepsilon = 1.49$ there are stripes and spots while for $\varepsilon = 1.40$ the spatial patterns form a stripes and it forms a hot spots for $\varepsilon = 1.0$.

From above numerical analysis, we observed that the average intensity of prey population size in generated patterns increases with the increase in value of handling parameter $\varepsilon$. This highlights the fact that small $\varepsilon$ results in high consumption rates of preys by predators and thus relatively small prey population density. On the other hand, for bigger values of $\varepsilon$ the consumption rates of preys by predators take relative small values and the prey population intensity increases. The intermediate values of $\varepsilon$ along with possible random motion of species constitute stripes are shown in the figure.

4.   Conclusions

In this work, the dynamics of a proposed Previte-Hoffman model with mixed functional response were explored. In particular, two versions of the model, namely temporal and spatio-temporal, were examined. The stability analysis was firstly presented for steady states of temporal model followed by studying possible bifurcation scenarios of codimension one and codimension two. It has been shown the nonoccurence of BT and ZH bifurcations and presence of supercritical Hopf bifurcation. The stability analysis of uniform coexistence steady state of spatiotemporal was carried out in model's space of parameters to investigate Turing instability and its subsequent two dimensional spatial patterns. The effects of key parameters of the model on its dynamical behaviours were depicted and it was found that a plethora of patterns including hot spots, cold spots and stripes can occur. The results of analytical and numerical study of the proposed model reveal that the realistic case where key scavenging ecological process is considered render the two predators in the model coexist in stable state, at some values of model's parameters, in spite of the competition among them. The influences of parameters in the model on stability of coexistence equilibrium point are thoroughly investigated. The attained results contradict the well-known results of classical Lotka-Volterra model of competition which predict that one species drive the other to extinction, see ^[45] and references therein. Note that in classical Lotka-Volterra model of competition, the effects of scavenging are not taken into account. Also, the results of this work show that the spatial extension of baseline model, which employs the linear functional response, cannot undergo Turing instability. Consequently, the different types of patterns, which can arise in the modified model, occur only for strict positive values of handling time parameter. The regions in parameters' space where Turing instability of spatially uniform steady state occur are found. It is observed that spatial patterns always feature both of the two predators. The transitions from cold spots to hot spots or vice versa are found to be accompanied with intermediate stage consists of stripes and spots or stripes only. Future work may include incorporation of more suitable forms of functional responses such as Holling type Ⅲ and Beddigton De-Angelis functional responses which render the model more biologically feasible. Fractional order derivatives can be also utilized so as to accurately simulate memory influences on model dynamics.

Acknowledgments

The authors would like to express their thanks to the editor and anonymous referees for their helpful comments and suggestions which further improve the paper. This research was funded by the Deanship of Scientific Research at Prince Sattam Bin Abdulaziz University within the Specialized Research Grant program and under contract number 2019/01/10899.

Author contributions

All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors declare that they have no conflict of interest.