Periodic solution of a stage-structured predator-prey model incorporating prey refuge

1.   Introduction

It is well known that the optimal tracking control (OTC) problem plays an important role in the field of optimal control and develops fast in applications^[1,2,3,4]. The goal of OTC problem is to design a controller, which can make the output of the system track the reference trajectory by minimizing the cost function. Traditional OTC problem is realized by feedback linearization ^[5] and object inversion ^[6], but this usually requires complex mathematical analysis. As for the linear quadratic tracking (LQT) problem, the traditional method of LQT problem is to solve the algebraic Riccati equation (ARE) and the noncausal difference equation. However, these methods require accurate system model^[7]. In practical situations, the system parameters are partially unknown or completely unknown, so it is impossible to be realized by traditional methods.

The key to the OTC problem is to solve Hamilton-Jacobi-Bellman (HJB) equation. However, HJB equation involves solving difference or differential equations, so it is difficult to solve it. Although dynamic programming has always been an effective method to solve the HJB equation, it is not feasible in the calculation of large dimensions because of "the curse of dimensionality". To solve the solution of the HJB equation, adaptive dynamic programming (ADP) algorithms have been widely used and developed. In ^[8], a policy iteration (PI) scheme was adopted to approximate the optimal control for the partly unknown continuous-time systems. In ^[9], B. Kiumarsi solves the LQT problem online only by measuring the input, output, and reference trajectory data of the system. In ^[10], a Q-learning method was proposed to calculate the optimal control, only relying on system parameters and command generators.

In recent years, stochastic system control theory has become the focus of optimal control theory because of its academic difficulty and wide application, especially the model-free SLQ optimal tracking problem has attracted more and more attention^{[11,12,13,14,15]}. In ^[14], ADP algorithm based on neural networks is proposed to solve the model-free SLQ optimal tracking control problem. In addition, the Q-learning algorithm is used to solve the model-free SLQ optimal tracking control problem in ^[15]. For all we know, there seem to be many research results on the model-free SLQ optimal tracking problem based on ADP algorithm, but the SLQ optimal tracking problem with delays has received little attention. Time delay ^[16] is an important factor that cannot be ignored. It exists in many practical systems, such as industrial processes, power grids, chemical reactions, and so on ^{[17,18,19,20]}. However, in these methods^{[11,12,13,14,15]}, the influence of time delay on the system is neglected. If the time delay is ignored, it will affect the control effect and even make the system divergence. The method proposed in ^[16] takes into account the time delay but ignores the influence of stochastic disturbance disturbances on the system. As far as we know, there is no research on the optimal tracking problem of stochastic linear systems with delays. Therefore, how to use ADP algorithm to deal with the model-free SLQ optimal tracking control problem has important practical significance. This is the motivation we study in this paper.

The main contributions of this paper include:

(1) For stochastic linear system, this paper proposes Q-learning to model-free solve SLQ optimal tracking control problem with delays for the first time, which enhances the practicability of ADP algorithm in tracking problems.

(2) By introducing the delay factor, the influence of delays on the subsequent algorithm can be effectively eliminated.

(3) In this paper, the Q-learning algorithm is used to solve the model-free SLQ optimal tracking control problem with delays. Compared with other methods which need accurate system model to obtain the optimal control, this method makes full use of the online system state information to obtain the optimal control and avoids solving augmented stochastic algebraic equation (SAE).

The structure of this paper is organized as follows. In section 2, we give the problem formulation and conversion. In section 3, we derive the Q-learning algorithm and prove its convergence. In section 4, we give the implementation steps of Q-learning algorithm. In section 5, a simulation example is given to verify the effectiveness of the algorithm. In section 6, the conclusion is given.

2.   Problem formulation and transformation

2.1.   Problem formulation

Consider the following linear stochastic systems with delays

where $x_{k}\in\mathcal{R}^{n}$ is the system state vector, $u_{k}\in\mathcal{R}^{m}$ is the control input vector, $y_{k}\in\mathcal{R}^{q}$ is the system output, while $x_{k-d}, u_{k-d}$ and $y_{k-d}$ are the delay variables with delay index $d \in N$. $A\in\mathcal{R}^{n\times n}$, $B\in\mathcal{R}^{n\times m}$, $C\in\mathcal{R}^{n\times n}$, $D\in\mathcal{R}^{n\times m}$, $E\in\mathcal{R}^{q\times n}$ are given constant, $A_{d}\in\mathcal{R}^{n\times n}$, $B_{d}\in\mathcal{R}^{n\times m}$, $C_{d}\in\mathcal{R}^{n\times n}$, $D_{d}\in\mathcal{R}^{n\times m}$, $E_{d}\in\mathcal{R}^{q\times n}$ are their corresponding delay dynamics matrices. One-dimensional stochastic disturbance sequence $\omega_{k}$ is defined on the given probability space $(\Omega, \mathcal{F}, \mathcal{P}, \mathcal{F}_{k})$, and meets the following condition $E(\omega_{k}\mid\mathcal{F}_{k}) = 0$, $E(\omega_{k}^{2}\mid\mathcal{F}_{k}) = 1$. The initial state $x_{0}$ is irrelevant with $\omega_{k}$.

Assume the reference trajectory of SLQ optimal tracking control is generated by a command generator

where $r_{k}\in\mathcal{R}^{q}$ represents the reference system trajectory, and $F$ is the constant matrix.

The tracking error can be expressed as

where $r_{k}$ is the reference trajectory.

The goal of the SLQ optimal tracking problem with delays is to design an optimal controller, which can not only ensure that the output of the target system track the reference trajectory stably, but also minimize the cost function. The cost function is denoted as

where $U_{i}(x_{i}, x_{i-d}, u_{i}) = (y_{i}-r_{i})^{T}O(y_{i}-r_{i})+u_{i}^{T}\mathcal{R}u_{i}+u_{i-d}^{T}\mathcal{R}_{d} u_{i-d}$ is the utility function. $O = O^{T}\in\mathcal{R}^{q\times q} \ge0$, $R = R^{T}\in\mathcal{R}^{m\times m} \ge0$, $R_{d} = R_{d}^{T}\in\mathcal{R}^{m\times m} \ge0$ are the constant matrices.

Only when $F$ is Hurwitz can the cost function (2.4) be used, that is, the reference trajectory system is required to be asymptotically stable. If the reference trajectory does not tend to zero with time delay, then the cost function (2.4) will be unbounded. In practice, this condition is difficult to achieve. Therefore, a discount factor $\gamma$ is introduced into the cost function (2.4) to relax this restriction. Based on (2.4), the cost function with discount factor is redefined as

where $0 < \gamma\leq1$ is the discount factor.

Definition 1 (^[21]). $u_{k}$ is called mean-square stabilizing at $e_{0}$ if there exists a linear feedback form of $u_{k}$ for every initial state $e_{0}$ satisfies $\mathop {\lim }\limits_{k \to \infty } E(e_k^T{e_k}) = 0$. The system (2.3) with a mean-square stabilizing control $u_{k}$ is called mean-square stabilizable.

Definition 2 (^[21]). $u_{k}$ is said to be admissible if $u_{k}$ satisfies the following: (1) $u_{k}$ is a $F_{k}$ adapted and measurable stochastic process; (2) $u_{k}$ is mean-square stabilizing; (3) It enables the cost function to reach the minimum value.

The goal of this paper is to seek an admissible control, which not only minimizes the cost function (2.5) but also stabilizes the system (2.3) for each initial state $e_{0}$. We denote the optimal cost function as follows

In order to achieve the above goal, this paper establishes an augmented system composed of system (2.1) and the reference trajectory system (2.2), and then transforms the optimal tracking problem into an optimal regulation problem.

The system (2.1) can be rewritten as the following equivalent form:

According to ^[16,22,23], we define the delay operator $\nabla_{d}$ satisfies $\nabla_{d}x_{k} = x_{k-d}$ and $(\nabla_{d}x_{k})^{T} = x_{k-d}^{T}$. Then, the system (2.7) can be expressed as

where $A_{\nabla} = A+A_{d}\nabla_{d}$, $B_{\nabla} = B+B_{d}\nabla_{d}$, $C_{\nabla} = C+C_{d}\nabla_{d}$, $D_{\nabla} = D+D_{d}\nabla_{d}$, $E_{\nabla} = E+E_{d}\nabla_{d}$.

Based on the system (2.1) and the reference trajectory system (2.2), the augmented system can be defined as

where $G_{k} = \left[\begin{array}{c} x_{k} \\r_{k}\end{array}\right]\in\mathcal{R}^{n+q}$, $T\in\mathcal{R}^{(n+q)\times(n+q)}$, $B_{0}\in\mathcal{R}^{(n+q)\times m}$.

Based on the augmented system (2.9), the cost function (2.5) can be expressed as

where $O_{1} = \left[\begin{array}{c c} E & -I\end{array}\right]^{T}O\left[\begin{array}{c c} E & -I\end{array}\right]\in\mathcal{R}^{(n+q)\times(n+q)}$, $R_{\nabla} = R+R_{d}\nabla_{d}$.

The state feedback linear controller is defined as

where $K$ represents the control gain matrix of the system.

Substituting (2.11) into (2.10), the cost function (2.10) can be transformed into

Therefore, the target of SQL optimal tracking problem with delays can be further expressed as

Definition 3. The SLQ optimal control problem is well posed if

Before solving the SLQ control problem, we need to know whether it is well-posed. Therefore, we give the following lemma first.

Lemma 1. If there exists an admissible control $u_{k} = KG_{k}$, then the SLQ optimal tracking control is well-posed, and the cost function can be expressed as

where the matrix $P\in\mathcal{R}^{(n+q)\times(n+q)}$ satisfies the following augmented SAE

where $A_{1} = \left[\begin{array}{c c} A_{\nabla} & 0\\0&F\end{array}\right] \in\mathcal{R}^{(n+q)\times(n+q)}$, $B_{1} = \left[\begin{array}{c } B_{\nabla} \\0\end{array}\right] \in\mathcal{R}^{(n+q)\times m}$, $C_{1} = \left[\begin{array}{c c} C_{\nabla} & 0\\0 & 0\end{array}\right] \in\mathcal{R}^{(n+q)\times(n+q)}$, $D_{1} = \left[\begin{array}{c } D_{\nabla} \\0\end{array}\right] \in\mathcal{R}^{(n+q)\times m}$.

Proof. Assuming that the control $u_{k}$ is admissible and the matrix $P$ satisfies (2.15), then

Based on (2.12) and (2.15), we have

Since the feedback control $u_{k}$ is admissible, we can obtain $J({G_k}, K){\rm{ = E(}}{G_k}^TP{G_k}{\rm{)}}$, which satisfies the well-posedness of SLQ optimal tracking control problem.

To make sure the mean-square stable control, we make the following assumption.

Assumption 1. The system (2.9) is mean-square stabilizable.

2.2.   Problem transformation

At present, ADP algorithm has achieved great success in the optimal tracking control of deterministic systems ^[24,25,26], which inspires us to transform stochastic problems into deterministic problems through system transformation.

Let $M_{k} = E(G_{k}G_{k}^{T})$, then the system (2.9) can be converted to

where $M_{k}\in\mathcal{R}^{(n+q)\times(n+q)}$ is the state of a deterministic system and $M_{0}$ is the initial state.

Therefore, the cost function (2.10) can be rewritten as

Remark 1. After system transformation, the stochastic system is transformed into deterministic system. The system (2.17) completely gets rid of stochastic disturbance $\omega_{k}$ and will only be dependent on the initial state $M_{0}$ and control gain matrix $K$, which makes preparation for the derivation and application of Q-learning algorithm.

3.   The Q-learning algorithm and convergence proof

In this paper, Q-learning method is used to solve the SLQ optimal tracking problem, which avoids the need for accurate system model. Thus we first give the formula of the optimal control and the corresponding augmented SAE.

Lemma 2. Given the admissible control $u_{k}$, we can get the following optimal control

and the optimal cost function

where the matrix $P$ satisfies the following augmented SAE

Proof. Suppose $u_{k}$ is an admissible control. According to Lemma 1 and (2.17), the cost function can be written as

According to Bellman optimality principle, the optimal cost function satisfies

The optimal control gain matrix can be obtained as follow

Considering the first-order necessary condition

we can obtain

where the matrix $P$ satisfies augmented SAE (2.15).

Supposing $R_{\nabla}+\gamma B^{T}_{1}PB_{1} + \gamma D^{T}_{1}PD^{T} > 0$, we have

When taking (3.9) into the (2.15), we can obtain

From Lemma 2, the SQL optimal tracking problem can be dealt with by the solution of augmented SAE (3.3). However, solving augmented SAE (3.3) requires accurate system model, so this method is not feasible when the dynamics are unknown.

3.1.   Derivation of Q-learning algorithm

To solve model-free SQL optimal tracking problem with delays, we give the definition of the Q function and the corresponding matrix $H$.

Based on (2.10) and Bellman optimality principle, we know that the optimal cost function satisfies Hamilton Jacobi Bellman (HJB) equation

The Q-function is defined as

According to Lemma 1, $V{\rm{(}}{G_{k + 1}}{\rm{)}}$ can be written as

Substitute (3.13) into (3.12), we can get

where $H = H^{T}\in\mathcal{R}^{(n+q+m)\times(n+q+m)}$,

Let $\frac{\partial Q(G_{k}, u_{k})}{\partial u_{k}} = 0$, then the optimal control can be obtained as follow

From Lemma 1 and (3.15), we can know the relationship between matrix $P$ and matrix $H$.

As can be seen from (3.16), the optimal control only depends on the matrix $H$, which is completely get rid of the constraints of the system parameters. Next, we will present the Q-learning iterative algorithm for estimating the matrix $H$.

In this section, we propose Q-learning iterative algorithm based on the Ⅵ. This method starts with the initial value $Q_{0}(G_{k}, u_{k}) = 0$ and the initial admissible control $u_{0}(G_{k})$, $Q_{1}(G_{k}, u_{k})$ will be updated by the initial value and the initial control as follows

The control is updated as follows

for $i \ge 1$, Q-learning algorithm iterates between

and

where $i$ is the iteration index and $k$ is time index.

According to (3.14), the Q function can be rewritten as

and we can obtain the optimal controller

According to (3.17), we can get

3.2.   The convergence of Q-learning algorithm

Before proving the convergence of Q-learning algorithm, we first give the following two lemmas.

Lemma 3. Q-learning algorithm (3.22) and (3.23) is equivalent to

Proof. According to (2.11), the last term of (3.22) can be written as

Substitute (3.26) into (3.22), according to (3.24), we can get

Based on (3.24), we have

Substitute (3.27) into (3.28), we can get

where ${R_\nabla } + \gamma B_1^{^T}P{B_1} + D_1^{^T}P{D_1} > 0$.

Lemma 4 (^[27]). The value iteration algorithm iterates between

and

is the convergence, then

where the matrix ${P }$ satisfies the augmented SAE (3.3).

Theorem 3.1. Assuming that system (2.9) is mean-square stabilizable, the matrix sequence ${\rm{\{ }}{H_i}{\rm{\} }}$ calculated by Q-learning algorithm (3.22) converges to matrix $H$ and the matrix sequence ${\rm{\{ }}{P_i}{\rm{\} }}$ calculated by (3.24) converges to the solution $P$ of augmented SAE (3.3).

Proof. According to Lemma 4, (3.30) can be rewritten as

We can update the control gain matrix by (3.31) as follows

Substituting (3.33) into (3.32), we can get

According to Lemmas 3 and 4, we can conclude $\mathop {\lim }\limits_{i \to \infty } {P_i} = {P}$. when $i \to \infty$, the matrix $P$ satisfies

Based on (3.27), we can know $H$ satisfies $\mathop {\lim }\limits_{i \to \infty } {H_i} = H$, where

So the Q-learning algorithm converges.

4.   Implementation of the Q-learning algorithm

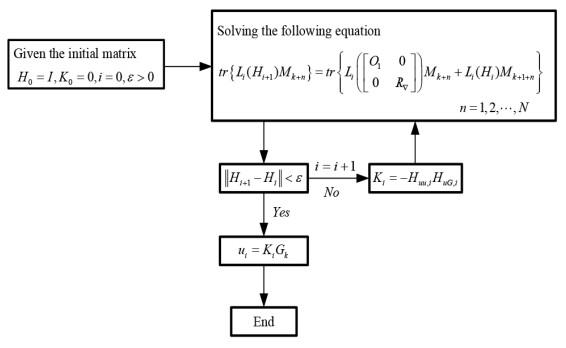
Due to the existence of stochastic disturbance, the output trajectory of the system is uncertain, and the cost function has expectations, the online algorithm cannot achieve the function. Therefore, it is necessary to transform the stochastic Q-learning algorithm into a deterministic Q-learning algorithm. In this section, we will give the implementation steps of deterministic Q-learning algorithm. The flow chart of Q learning algorithm is shown in Figure 1.

According to Eq (2.11), the left side of (3.22) can be simplified to

The right side of (3.22) can be simplified as

For simplicity, let

Then (3.22) can be simplified as

The Q-learning iterative algorithm consisting of (4.4) and (3.23) only relies on determining the state $M_{k}$ of the system (2.16) and iteratively controlling the gain matrix $K_{i}$, avoiding the constraints of system parameters and stochastic disturbance.

Remark 2. The Q-learning algorithm based on Ⅵ is performed online and solves (4.4) using least squares (LS) without knowing augmented system. In fact, (4.4) is a scalar equation and $H$ is a symmetric $(n + q + m) \times (n + q + m)$ matrix with $(n + q + m) \times (n + q + m + 1)/2$ independent elements. Therefore, at least $(n + q + m + 1) \times (n + q + m + 1)/2$ data tuples are required before (4.4) can be solved using LS.

Remark 3. Q-learning algorithm based on Ⅵ requires a persistent excitation (PE) condition ^[28] to ensure the sufficient exploration of the state space.

5.   Simulation

In this section, a simulation example is given to illustrate the effectiveness of Q-learning algorithm. Consider the following stochastic linear system with delays

in which $A = \left({\begin{array}{*{20}{c}} {0.2} & { - 0.8}\\ {0.5} & { - 0.7} \end{array}} \right)$, ${A_d} = \left({\begin{array}{*{20}{c}} {0.2} & { - 0.2}\\ {0.1} & {0.15} \end{array}} \right)$, $B = \left({\begin{array}{*{20}{c}} {0.03}\\ { - 0.5} \end{array}} \right)$, ${B_d} = \left({\begin{array}{*{20}{c}} {0.3}\\ { - 0.2} \end{array}} \right)$, $C = \left({\begin{array}{*{20}{c}} { - 0.04} & {0.4}\\ { - 0.3} & {0.13} \end{array}} \right)$, ${C_d} = \left({\begin{array}{*{20}{c}} {0.2} & { - 0.1}\\ {0.2} & {0.11} \end{array}} \right)$, $D = \left({\begin{array}{*{20}{c}} {0.05}\\ { - 0.3} \end{array}} \right)$, ${D_d} = \left({\begin{array}{*{20}{c}} {0.1}\\ {0.1} \end{array}} \right)$, $E = \left({\begin{array}{*{20}{c}} 3 & 3 \end{array}} \right)$, ${E_d} = \left({\begin{array}{*{20}{c}} {0.1} & {0.12} \end{array}} \right)$.

Suppose the reference trajectory is as follows

where ${r_0} = 1$.

The cost function is considered as (2.5) with $R = 1$, $R_{d} = 1$, $O = 10$ and delay index $d = 1$. The initial state for augmented system (2.9) is chosen as ${G_0} = {\left[ {\begin{array}{*{20}{c}}{10} & {{\rm{ - }}10} & 1\end{array}} \right]^T}$. The initial control gain matrix is selected as $K = \left[ {\begin{array}{*{20}{c}}0 & 0 & 0\end{array}} \right]$. In each iteration of the algorithm, 21 samples are collected to update the control gain matrix $K$.

In order to verify the effectiveness of the iterative Q-learning algorithm, we compared $K$ with optimal solution $K^{\ast}$ solved by SAE (3.1). Figure 2 shows the control gain matrix $K$ converges to the optimal control gain matrix $K^{\ast}$ as the number of iterations increases. Figure 3 shows the convergence process of $H$ to its optimal values $H^{\ast}$, which can be calculated by (3.15). The goal of the optimal tracking problem is to trace the reference signal trajectory. In Figure 4, the expectation of system output $E(y)$ can track the reference trajectory $r_{k}$. This further proves the effectiveness of the proposed Q-learning algorithm.

6.   Conclusions

For the model-free SLQ optimal tracking problem with delays, Q-learning algorithm based on Ⅵ is proposed in this paper. This method makes full use of the system information to approximate the optimal control online, and never needs the system parameter information. In the iterative process of the algorithm, the $H$ matrix sequence and the control gain matrix $K$ sequence are guaranteed to approximate the optimal value. Finally, the simulation results show that the system output can track the reference trajectory effectively.

Conflict of interest

The authors declare that they have no conflicts of interest.