Citation: Yangyang Li, Fengxue Zhang, Xianglai Zhuo. Flip bifurcation of a discrete predator-prey model with modified Leslie-Gower and Holling-type III schemes[J]. Mathematical Biosciences and Engineering, 2020, 17(3): 2003-2015. doi: 10.3934/mbe.2020106
| [1] | Ceyu Lei, Xiaoling Han, Weiming Wang . Bifurcation analysis and chaos control of a discrete-time prey-predator model with fear factor. Mathematical Biosciences and Engineering, 2022, 19(7): 6659-6679. doi: 10.3934/mbe.2022313 |
| [2] | Yajie Sun, Ming Zhao, Yunfei Du . Multiple bifurcations of a discrete modified Leslie-Gower predator-prey model. Mathematical Biosciences and Engineering, 2023, 20(12): 20437-20467. doi: 10.3934/mbe.2023904 |
| [3] | Xiaoling Han, Xiongxiong Du . Dynamics study of nonlinear discrete predator-prey system with Michaelis-Menten type harvesting. Mathematical Biosciences and Engineering, 2023, 20(9): 16939-16961. doi: 10.3934/mbe.2023755 |
| [4] | Shuo Yao, Jingen Yang, Sanling Yuan . Bifurcation analysis in a modified Leslie-Gower predator-prey model with fear effect and multiple delays. Mathematical Biosciences and Engineering, 2024, 21(4): 5658-5685. doi: 10.3934/mbe.2024249 |
| [5] | Mengyun Xing, Mengxin He, Zhong Li . Dynamics of a modified Leslie-Gower predator-prey model with double Allee effects. Mathematical Biosciences and Engineering, 2024, 21(1): 792-831. doi: 10.3934/mbe.2024034 |
| [6] | Xiaoyuan Chang, Junjie Wei . Stability and Hopf bifurcation in a diffusivepredator-prey system incorporating a prey refuge. Mathematical Biosciences and Engineering, 2013, 10(4): 979-996. doi: 10.3934/mbe.2013.10.979 |
| [7] | Saheb Pal, Nikhil Pal, Sudip Samanta, Joydev Chattopadhyay . Fear effect in prey and hunting cooperation among predators in a Leslie-Gower model. Mathematical Biosciences and Engineering, 2019, 16(5): 5146-5179. doi: 10.3934/mbe.2019258 |
| [8] | Hongqiuxue Wu, Zhong Li, Mengxin He . Dynamic analysis of a Leslie-Gower predator-prey model with the fear effect and nonlinear harvesting. Mathematical Biosciences and Engineering, 2023, 20(10): 18592-18629. doi: 10.3934/mbe.2023825 |
| [9] | Christian Cortés García . Bifurcations in a discontinuous Leslie-Gower model with harvesting and alternative food for predators and constant prey refuge at low density. Mathematical Biosciences and Engineering, 2022, 19(12): 14029-14055. doi: 10.3934/mbe.2022653 |
| [10] | A. Q. Khan, I. Ahmad, H. S. Alayachi, M. S. M. Noorani, A. Khaliq . Discrete-time predator-prey model with flip bifurcation and chaos control. Mathematical Biosciences and Engineering, 2020, 17(5): 5944-5960. doi: 10.3934/mbe.2020317 |
In biological systems, the continuous predator-prey model has been successfully investigated and many interesting results have been obtained (cf. [1,2,3,4,5,6,7,8,9] and the references therein). Moreover, based on the continuous predator-prey model, many human factors, such as time delay [10,11,12], impulsive effect [13,14,15,16,17,18,19,20], Markov Switching [21], are considered. The existing researches mainly focus on stability, periodic solution, persistence, extinction and boundedness [22,23,24,25,26,27,28].
In 2011, the authors [28] considered the system incorporating a modified version of Leslie-Gower functional response as well as that of the Holling-type Ⅲ:
| {˙x(t)=x(a1−bx−c1y2x2+k1),˙y(t)=y(a2−c2yx+k2). | (1) |
With the diffusion of the species being also taken into account, the authors [28] studied a reaction-diffusion predator-prey model, and gave the stability of this model.
In model (1) x represents a prey population, y represents a predator with population, a1 and a2 represent the growth rate of prey x and predator y respectively, constant b represents the strength of competition among individuals of prey x, c1 measures the maximum value of the per capita reduction rate of prey x due to predator y, k1 and k2 represent the extent to which environment provides protection to x and to y respectively, c2 admits a same meaning as c1. All the constants a1,a2,b,c1,c2,k1,k2 are positive parameters.
However, provided with experimental and numerical researches, it has been obtained that bifurcation is a widespread phenomenon in biological systems, from simple enzyme reactions to complex ecosystems. In general, the bifurcation may put a population at a risk of extinction and thus hinder reproduction, so the bifurcation has always been regarded as a unfavorable phenomenon in biology [29]. This bifurcation phenomenon has attracted the attention of many mathematicians, so the research on bifurcation problem is more and more abundant [30,31,32,33,34,35,36,37,38,39,40].
Although the continuous predator-prey model has been successfully applied in many ways, its disadvantages are also obvious. It requires that the species studied should have continuous and overlapping generations. In fact, we have noticed that many species do not have these characteristics, such as salmon, which have an annual spawning season and are born at the same time each year. For the population with non-overlapping generation characteristics, the discrete time model is more practical than the continuous model [38], and discrete models can generate richer and more complex dynamic properties than continuous time models [39]. In addition, since many continuous models cannot be solved by symbolic calculation, people usually use difference equations for approximation and then use numerical methods to solve the continuous model.
In view of the above discussion, the study of discrete system is paid more and more attention by mathematicians. Many latest research works have focused on flip bifurcation for different models, such as, discrete predator-prey model [41,42]; discrete reduced Lorenz system [43]; coupled thermoacoustic systems [44]; mathematical cardiac system [45]; chemostat model [46], etc.
For the above reasons, we will study from different perspectives in this paper, focusing on the discrete scheme of Eq (1).
In order to get a discrete form of Eq (1), we first let
| u=ba1x,v=c1a1y,τ=a1t, |
and rewrite u,v,τ as x,y,t, then (1) changes into:
| {˙x(t)=x(1−x−β1y2x2+h1),˙y(t)=αy(1−β2yx+h2), | (2) |
where β1=b2c1a1,h1=b2k1a21,α=a2c1,β2=c2bc1a2,h2=bk2a1.
Next, we use Euler approximation method, i.e., let
| dxdt≈xn+1−xn△t,dydt≈yn+1−yn△t, |
where △t denotes a time step, xn,yn and xn+1,yn+1 represent consecutive points. Provided with Euler approximation method with the time step △t=1, (2) changes into a two-dimensional discrete dynamical system:
| {xn+1=xn+xn(1−xn−β1y2nx2n+h1),yn+1=yn+αyn(1−β2ynxn+h2). | (3) |
For the sake of analysis, we rewrite (3) in the following map form:
| (xy)↦(x+x(1−x−β1y2x2+h1)y+αy(1−β2yx+h2)). | (4) |
In this paper, we will consider the effect of the coefficients of map (4) on the dynamic behavior of the map (4). Our goal is to show how a flipped bifurcation of map (4) can appear under some certain conditions.
The remainder of the present paper is organized as follows. In section 2, we discuss the fixed points of map (4) including existence and stability. In section 3, we investigate the flip bifurcation at equilibria E2 and E∗. It has been proved that map (4) can undergo the flip bifurcation provided with that some values of parameters be given certain. In section 4, we give an example to support the theoretical results of the present paper. As the conclusion, we make a brief discussion in section 5.
Obviously, E1(1,0) and E2(0,h2β2) are fixed points of map (4). Given the biological significance of the system, we focus on the existence of an interior fixed point E∗(x∗,y∗), where x∗>0,y∗>0 and satisfy
| 1−x∗=β1(y∗)2(x∗)2+h1,x∗+h2=β2y∗, |
i.e., x∗ is the positive root of the following cubic equation:
| β22x3+(β1−β22)x2+(β22h1+2β1h2)x+β1h22−β22h1=0. | (5) |
Based on the relationship between the roots and the coefficients of Eq (5), we have
Lemma 2.1 Assume that β1h22−β22h1<0, then Eq (5) has least one positive root, and in particular
(ⅰ) a unique positive root, if β1≥β22;
(ⅱ) three positive roots, if β1<β22.
The proof of Lemma 2.1 is easy, and so it is omitted.
In order to study the stability of equilibria, we first give the Jacobian matrix J(E) of map (4) at any a fixed point E(x,y), which can be written as
| J(E)=(2−2x−β1y2(h1−x2)(x2+h1)2−2β1xyx2+h1αβ2y2(x+h2)21+α−2αβ2yx+h2). |
For equilibria E1, we have
| J(E1)=(0001+α). |
The eigenvalues of J(E1) are λ1=0,λ2=1+α with λ2>1 due to the constant α>0, so E1(1,0) is a saddle.
For equilibria E2, note that
| J(E2)=(2−β1h22β22h10αβ21−α), |
then the eigenvalues of J(E2) are λ1=2−β1h22β22h1,λ2=1−α, and so we get
Lemma 2.2 The fixed point E2(0,h2β2) is
(ⅰ) a sink if 1<β1h22β22h1<3 and 0<α<2;
(ⅱ) a source if β1h22β22h1<1 or β1h22β22h1>3 and α>2;
(ⅲ) a a saddle if 1<β1h22β22h1<3 and α>2, or, β1h22β22h1<1 or β1h22β22h1>3 and 0<α<2;
(ⅳ) non-hyperbolic if β1h22β22h1=1 or β1h22β22h1=3 or α=2.
In this section, we will use the relevant results of literature [38,39,40] to study the flip bifurcation at equilibria E2 and E∗.
Based on (ⅲ) in Lemma 2.2, it is known that if α=2, the eigenvalues of J(E2) are: λ1=2−β1h22β22h1,λ2=−1. Define
| Fl={(β1,β2,h1,h2,α):α=2,β1,β2,h1,h2>0}. |
We conclude that a flip bifurcation at E2(0,h2β2) of map (4) can appear if the parameters vary in a small neighborhood of the set Fl.
To study the flip bifurcation, we take constant α as the bifurcation parameter, and transform E2(0,h2β2) into the origin. Let e=2−β1h22β22h1,α1=α−2, and
| u(n)=x(n),v(n)=y(n)−h2β2, |
then map (4) can be turned into
| (uv)↦(eu−u2−2β1h2β2h1uv+O((|u|+|v|+|α1|)3)2β2u−v−2β2h2u2−2β2h2v2+4h2uv+α1β2u−α1v−α1β2h2u2−α1β2h2v2+2α1h2uv+O((|u|+|v|+|α1|)3)). | (6) |
Let
| T1=(1+e02β21), |
then by the following invertible transformation:
| (uv)=T1(sw), |
map (6) turns into
| (sw)↦(es−(1+e)s2−2β1h2β2h1s(2sβ2+w)+O(|s|+|w|+|α1|)3−w+F2(s,w,α1)), | (7) |
where
| F2=2β2[(1+e)s2+2β1h2β2h1s(2sβ2+w)]−2β2h2(1+e)2s2−2β2h2(2sβ2+w)2+4(1+e)h2s(2sβ2+w) |
| +(1+e)α1β2s−α1(2sβ2+w)−(1+e)2α1β2h2s2−α1β2h2(2sβ2+w)2 |
| +2(1+e)α1h2s(2sβ2+w)+O(|s|+|w|+|α1|)3. |
Provided with the center manifold theorem (Theorem 7 in [40]), it can be obtained that there will exist a center manifold Wc(0,0) for map (7), and the center manifold Wc(0,0) can be approximated as:
| Wc(0,0)={(w,s,α1)∈R3:s=aw2+bwα1+c(α1)2+O(|w|+|α1|)3}. |
As the center manifold satisfies:
| s=a(−w+F2)2+b(−w+F2)α1+c(α1)2=e(aw2+bwα1+c(α1)2)−(1+e)(aw2+bwα1+c(α1)2)2−2β1h2β2h1(aw2+bwα1+c(α1)2)(2β2(aw2+bwα1+c(α1)2)+w)+O(|s|+|w|+|α1|)3, |
it can be obtained by comparing the coefficients of the above equality that a=0,b=0,c=0, so the center manifold of map (7) at E2(0,h2β2) is s=0. Then map (7) restricted to the center manifold turns into
| w(n+1)=−w(n)−α1w(n)−2β2h2w2(n)−α1β2h2w2(n)+O(|w(n)|+|α1|)3 |
| ≜f(w,α1). |
Obviously,
| fw(0,0)=−1,fww(0,0)=−4β2h2, |
so
| (fww(0,0))22+fwww(0,0)3≠0,fwα1(0,0)=−1≠0. |
Therefore, Theorem 4.3 in [38] guarantees that map (3) undergoes a flip bifurcation at E2(0,h2β2).
Note that
| J(E∗)=(2−2x∗−β1(y∗)2(h1−(x∗)2)((x∗)2+h1)2−2β1x∗y∗(x∗)2+h1αβ21−α), |
then the characteristic equation of Jacobian matrix J(E∗) of map (3) at E∗(x∗,y∗) is:
| λ2−(1+α0−α)λ+(1−α)α0−ηα=0, | (8) |
where
| α0=2−2x∗−β1(y∗)2(h1−(x∗)2)((x∗)2+h1)2,η=−2β1x∗y∗β2((x∗)2+h1). |
Firstly, we discuss the stability of the fixed point E∗(x∗,y∗). The stability results can be described as the the following Lemma, which can be easily proved by the relations between roots and coefficients of the characteristic Eq (8), so the proof has been omitted.
Lemma 3.1 The fixed point E∗(x∗,y∗) is
(ⅰ) a sink if one of the following conditions holds.
(ⅰ.1) 0<α0+η<1, and α0−1α0+η<α<2(1+α0)1+α0+η;
(ⅰ.2) −1<α0+η<0, and α<min
(ⅰ.3) \alpha_{0}+\eta < -1, and \frac{\alpha_{0}-1}{\alpha_{0}+\eta} > \alpha > \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};
(ⅱ) a source if one of the following conditions holds.
(ⅱ.1) 0 < \alpha_{0}+\eta < 1, and \alpha < \min \{\frac{\alpha_{0}-1}{\alpha_{0}+\eta}, \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta} \};
(ⅱ.2) -1 < \alpha_{0}+\eta < 0, and \frac{\alpha_{0}-1}{\alpha_{0}+\eta} < \alpha < \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};
(ⅱ.3) \alpha_{0}+\eta < -1, and \alpha > \max \{\frac{\alpha_{0}-1}{\alpha_{0}+\eta}, \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta} \};
(ⅲ) a saddle if one of the following conditions holds.
(ⅲ.1) -1 < \alpha_{0}+\eta < 1, and \alpha > \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};
(ⅲ.2) \alpha_{0}+\eta < -1, and \alpha < \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};
(ⅳ) non-hyperbolic if one of the following conditions holds.
(ⅳ.1) \alpha_{0}+\eta = 1;
(ⅳ.2) \alpha_{0}+\eta\neq -1; and \alpha = \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};
(ⅳ.3) \alpha_{0}+\eta\neq 0, \alpha = \frac{\alpha_{0}-1}{\alpha_{0}+\eta} and (1+\alpha_{0}-\alpha)^{2} < 4((1-\alpha)\alpha_{0}-\eta\alpha).
Then based on (ⅳ.2) of Lemma 3.1 and \alpha\neq 1+\alpha_{0}, 3+\alpha_{0}, we get that one of the eigenvalues at E^{\ast}(x^{\ast}, y^{\ast}) is -1 and the other satisfies |\lambda|\neq 1. For \alpha, \beta_{1}, \beta_{2}, h_{1}, h_{2} > 0, let us define a set:
| Fl = \{(\beta_{1}, \beta_{2}, h_{1}, h_{2}, \alpha):\alpha = \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta}, \alpha_{0}+\eta\neq -1, \alpha\neq 1+\alpha_{0}, 3+\alpha_{0} \}. |
We assert that a flip bifurcation at E^{\ast}(x^{\ast}, y^{\ast}) of map (3) can appear if the parameters vary in a small neighborhood of the set Fl.
To discuss flip bifurcation at E^{\ast}(x^{\ast}, y^{\ast}) of map (3), we choose constant \alpha as the bifurcation parameter and adopt the central manifold and bifurcation theory [38,39,40].
Let parameters (\alpha_{1}, \beta_{1}, \beta_{2}, h_{1}, h_{2})\in Fl, and consider map (3) with (\alpha_{1}, \beta_{1}, \beta_{2}, h_{1}, h_{2}), then map (3) can be described as
| \begin{align} \begin{cases} x_{n+1} = x_{n}+x_{n}(1-x_{n}-\frac{\beta_{1}y_{n}^{2}}{x_{n}^{2}+h_{1}} ), \\ y_{n+1} = y_{n}+\alpha_{1} y_{n}(1-\frac{\beta_{2}y_{n}}{x_{n}+h_{2}} ). \end{cases} \end{align} | (9) |
Obviously, map (9) has only a unique positive fixed point E^{\ast}(x^{\ast}, y^{\ast}), and the eigenvalues are \lambda_{1} = \; -\; 1, \lambda_{2} = 2+\alpha_{0}-\alpha, where |\lambda_{2}|\neq1.
Note that (\alpha_{1}, \beta_{1}, \beta_{2}, h_{1}, h_{2})\in Fl, then \alpha_{1} = \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta}. Let |\alpha^{\ast}| small enough, and consider the following perturbation of map (9) described by
| \begin{align} \begin{cases} x_{n+1} = x_{n}+x_{n}(1-x_{n}-\frac{\beta_{1}y_{n}^{2}}{x_{n}^{2}+h_{1}} ), \\ y_{n+1} = y_{n}+(\alpha_{1}+\alpha^{\ast}) y_{n}(1-\frac{\beta_{2}y_{n}}{x_{n}+h_{2}} ), \end{cases} \end{align} | (10) |
with \alpha^{\ast} be a perturbation parameter.
To transform E^{\ast}(x^{\ast}, y^{\ast}) into the origin, we let u = x-x^{\ast}, v = y- y^{\ast}, then map (10) changes into
| \begin{align} \left( \begin{array}{cc} {u}\\ {v} \end{array} \right) \mapsto \left( \begin{array}{cc} {a_{1}u+a_{2}v+ a_{3}u^{2}+a_{4}uv+ a_{5}v^{2}+ a_{6}u^{3}+ a_{7}u^{2}v \; \; \; \; \; \; \; \; \; \; \; \; \; } \\ { + a_{8}uv^{2} + a_{9}v^{3} +O((|u|+|v|)^{4} )\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; } \\ {b_{1}u+b_{2}v+ b_{3}u^{2}+b_{4}uv+ b_{5}v^{2}+c_{1}u\alpha^{\ast}+c_{2}v\alpha^{\ast}+c_{3}u^{2}\alpha^{\ast} }\\ {+c_{4}uv\alpha^{\ast}+c_{5}v^{2}\alpha^{\ast}+ b_{6}u^{3}+ b_{7}u^{2}v+ b_{8}uv^{2} + b_{9}v^{3}\; } \\ { +O((|u|+|v|+|\alpha^{\ast}|)^{4} )\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; } \end{array} \right), \end{align} | (11) |
where
a_{1} = 2-2x^{\ast}-\beta_{1}(y^{\ast})^{2}f(0)-\beta_{1}x^{\ast}(y^{\ast})^{2}f'(0); a_{2} = -2\beta_{1}x^{\ast}y^{\ast}f(0);
a_{3} = -1-\beta_{1}(y^{\ast})^{2}f'(0)-\frac{1}{2}\beta_{1}x^{\ast}(y^{\ast})^{2}f''(0); a_{4} = -2\beta_{1}y^{\ast}f(0)-2\beta_{1}x^{\ast}y^{\ast}f'(0);
a_{5} = -\beta_{1}x^{\ast}f(0); a_{6} = -\frac{1}{2}\beta_{1}(y^{\ast})^{2}f''(0)-\frac{1}{6}\beta_{1}x^{\ast}(y^{\ast})^{2}f'''(0);
a_{7} = -\beta_{1}x^{\ast}y^{\ast}f''(0)-2\beta_{1}y^{\ast}f'(0); a_{8} = -\beta_{1}f(0)-\beta_{1}x^{\ast}f'(0), \; \; \; a_{9} = 0;
f(0) = \frac{1}{(x^{\ast})^{2}+h_{1}}, f'(0) = \frac{-2x^{\ast}}{[(x^{\ast})^{2}+h_{1}]^{2}}, f''(0) = \frac{6(x^{\ast})^{2}-2h_{1}}{[(x^{\ast})^{2}+h_{1}]^{3}}, f'''(0) = \frac{ 24x^{\ast} (h_{1}-(x^{\ast})^{2})}{[(x^{\ast})^{2}+h_{1}]^{4}}.
b_{1} = \frac{\alpha_{1}\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{2} }; b_{2} = 1+\alpha_{1}-\frac{\alpha_{1}\beta_{2}y^{\ast} }{x^{\ast}+h_{2}}; b_{3} = -\frac{\alpha_{1}\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{3} }; b_{4} = \frac{2\alpha_{1}\beta_{2}y^{\ast} }{ (x^{\ast}+h_{2})^{2} };
b_{5} = -\frac{\alpha_{1}\beta_{2} }{x^{\ast}+h_{2}}; c_{1} = \frac{\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{2} }; c_{2} = 1-\frac{\beta_{2}y^{\ast} }{x^{\ast}+h_{2}}; c_{3} = -\frac{\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{3} };
c_{4} = \frac{2\beta_{2}y^{\ast} }{(x^{\ast}+h_{2})^{2} }; c_{5} = -\frac{\beta_{2} }{x^{\ast}+h_{2} }; b_{6} = \frac{\alpha_{1}\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{4} }; b_{7} = -\frac{2\alpha_{1}\beta_{2}y^{\ast} }{ (x^{\ast}+h_{2})^{3} };
| b_{8} = \frac{\alpha_{1}\beta_{2} }{(x^{\ast}+h_{2})^{2} }; \; \; \; \; b_{9} = 0.\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; |
Now let's construct an matrix
| \begin{gather*} T_{2} = \begin{pmatrix}a_{2} & a_{2} \\-1-a_{1} & \lambda_{2}-a_{1} \end{pmatrix}. \end{gather*} |
It's obvious that the matrix T_{2} is invertible due to \lambda_{2}\neq -1, and then we use the following invertible translation
| \left( \begin{array}{cc} {u}\\ {v} \end{array} \right) = T_{2} \left( \begin{array}{cc} {s } \\ {w } \end{array} \right), |
map (11) can be described by
| \begin{align} \left( \begin{array}{cc} {s}\\ {w} \end{array} \right) \mapsto \left( \begin{array}{cc} {-s +f_{1}(s, w, \alpha^{\ast}) } \\ {\lambda_{2}w +f_{2}(s, w, \alpha^{\ast}) } \end{array} \right), \end{align} | (12) |
where
| f_{1}(s, w, \alpha^{\ast}) = \frac{(\lambda_{2}-a_{1})a_{3}-a_{2} b_{3}}{ a_{2}(\lambda_{2}+1) }u^{2} + \frac{(\lambda_{2}-a_{1})a_{4}-a_{2} b_{4}}{ a_{2}(\lambda_{2}+1) }uv +\frac{(\lambda_{2}-a_{1})a_{5}-a_{2} b_{5}}{ a_{2}(\lambda_{2}+1) }v^{2} +\frac{(\lambda_{2}-a_{1})a_{6}-a_{2} b_{6}}{ a_{2}(\lambda_{2}+1) }u^{3} \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; +\frac{(\lambda_{2}-a_{1})a_{7}-a_{2} b_{7}}{ a_{2}(\lambda_{2}+1) }u^{2}v +\frac{(\lambda_{2}-1)a_{8}-a_{2} b_{8}}{ a_{2}(\lambda_{2}+1) }uv^{2} +\frac{(\lambda_{2}-a_{1})a_{9}-a_{2} b_{9}}{ a_{2}(\lambda_{2}+1) }v^{3}- \frac{a_{2}c_{1}}{a_{2}(\lambda_{2}+1)}u\alpha^{\ast} \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; - \frac{a_{2}c_{2}}{a_{2}(\lambda_{2}+1)}v\alpha^{\ast}- \frac{a_{2}c_{3}}{a_{2}(\lambda_{2}+1)}u^{2}\alpha^{\ast} - \frac{a_{2}c_{4}}{a_{2}(\lambda_{2}+1)}uv\alpha^{\ast} - \frac{a_{2}c_{5}}{a_{2}(\lambda_{2}+1)}v^{2}\alpha^{\ast} \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; +O((|s|+ |w|+|\alpha^{\ast}| )^{4}), \\ f_{2}(s, w, \alpha^{\ast}) = \frac{(a_{1}+1)a_{3}+a_{2} b_{3}}{ a_{2}(\lambda_{2}+1) }u^{2} + \frac{(a_{1}+1)a_{4}+a_{2} b_{4}}{ a_{2}(\lambda_{2}+1) }uv +\frac{(a_{1}+1)a_{5}+a_{2} b_{5}}{ a_{2}(\lambda_{2}+1) }v^{2} +\frac{(a_{1}+1)a_{6}+a_{2} b_{6}}{ a_{2}(\lambda_{2}+1) }u^{3} \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; +\frac{(a_{1}+1)a_{7}+a_{2} b_{7}}{ a_{2}(\lambda_{2}+1) }u^{2}v +\frac{(a_{1}+1)a_{8}+a_{2} b_{8}}{ a_{2}(\lambda_{2}+1) }uv^{2}+\frac{(a_{1}+1)a_{9}+a_{2} b_{9}}{ a_{2}(\lambda_{2}+1) }v^{3}+ \frac{a_{2}c_{1}}{a_{2}(\lambda_{2}+1)}u\alpha^{\ast}\\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; + \frac{a_{2}c_{2}}{a_{2}(\lambda_{2}+1)}v\alpha^{\ast}+ \frac{a_{2}c_{3}}{a_{2}(\lambda_{2}+1)}u^{2}\alpha^{\ast}+ \frac{a_{2}c_{4}}{a_{2}(\lambda_{2}+1)}uv\alpha^{\ast} + \frac{a_{2}c_{5}}{a_{2}(\lambda_{2}+1)}v^{2}\alpha^{\ast}\\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; +O((|s|+ |w|+|\alpha^{\ast}| )^{4}), |
with
u = a_{2}(s+w), v = (\lambda_{2}-a_{1})w-(a_{1}+1)s;
u^{2} = (a_{2}(s+w))^{2};
uv = (a_{2}(s+w))((\lambda_{2}-a_{1})w-(a_{1}+1)s);
v^{2} = ((\lambda_{2}-a_{1})w-(a_{1}+1)s)^{2};
u^{3} = (a_{2}(s+w))^{3};
u^{2}v = (a_{2}(s+w))^{2}((\lambda_{2}-a_{1})w-(a_{1}+1)s);
uv^{2} = (a_{2}(s+w))((\lambda_{2}-a_{1})w-(a_{1}+1)s)^{2};
v^{3} = ((\lambda_{2}-a_{1})w-(a_{1}+1)s)^{3}.
In the following, we will study the center manifold of map (12) at fixed point (0, 0) in a small neighborhood of \alpha^{\ast} = 0. The well-known center manifold theorem guarantee that a center manifold W^{c}(0, 0) can exist, and it can be approximated as follows
| W^{c}(0, 0) = \{(s, w, \alpha^{\ast})\in R^{3}:w = d_{1}s^{2}+d_{2}s\alpha^{\ast}+d_{3}(\alpha^{\ast})^{2}+ O(( |s|+ |\alpha^{\ast}|)^{3}) \}, |
which satisfies
| w = d_{1}(-s+f_{1}(s, w, \alpha^{\ast}))^{2}+d_{2}(-s+f_{1}(s, w, \alpha^{\ast}))\alpha^{\ast}+d_{3}(\alpha^{\ast})^{2} |
| = \lambda_{2}( d_{1}s^{2}+d_{2}s\alpha^{\ast}+d_{3}(\alpha^{\ast})^{2} )+f_{2}(s, w, \alpha^{\ast}).\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; |
By comparing the coefficients of the above equation, we have
| d_{1} = \frac{a_{2}((a_{1}+1)a_{3}+a_{2}b_{3})}{1-\lambda_{2}^{2}}-\frac{(a_{1}+1)((a_{1}+1)a_{4}+a_{2}b_{4})}{1-\lambda_{2}^{2}}+ \frac{(a_{1}+1)^{2}((a_{1}+1)a_{5}+a_{2}b_{5})}{1-\lambda_{2}^{2}}, \\ d_{2} = \frac{c_{2}(a_{1}+1) -a_{2}c_{1} }{(1+\lambda_{2})^{2}}, \; \; \; \; \; \; d_{3} = 0.\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; |
So, restricted to the center manifold W^{c}(0, 0), map (12) turns into
| \begin{align} s \mapsto -s+e_{1}s^{2}+e_{2}s\alpha^{\ast}+e_{3}s^{2}\alpha^{\ast}+e_{4}s(\alpha^{\ast})^{2}+e_{5}s^{3}+O(( |s|+ |\alpha^{\ast}|)^{4}) \\ \triangleq F_{2}(s, \alpha^{\ast}), \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \end{align} | (13) |
where
e_{1} = A_{1}a_{2}^{2}-A_{2}a_{2}(a_{1}+1)+ A_{3}(a_{1}+1)^{2};
e_{2} = -A_{8}a_{2}+ A_{9}(a_{1}+1);
e_{3} = 2A_{1}d_{2}a_{2}^{2}+ A_{2}a_{2}d_{2}(\lambda_{2}-2a_{1}-1)-2A_{3}d_{2}(\lambda_{2}-a_{1})(a_{1}+1)-A_{8}a_{2}d_{1}
-A_{9}(\lambda_{2}-a_{1})d_{1}-A_{10}a_{2}^{2}+A_{11}a_{2}(a_{1}+1)-A_{12}(a_{1}+1)^{2};
e_{4} = -A_{8}a_{2}d_{2}-A_{9}(\lambda_{2}-a_{1})d_{2};
e_{5} = 2A_{1}a_{2}^{2}d_{1}+A_{2}a_{2}d_{1}(\lambda_{2}-2a_{1}-1)-2A_{3}d_{1}(\lambda_{2}-a_{1})(a_{1}+1)+A_{4}a_{2}^{3}
-A_{5}a_{2}^{2}(a_{1}+1)+A_{6}a_{2}(a_{1}+1)^{2}-A_{7}(a_{1}+1)^{3};
with
A_{1} = \frac{(\lambda_{2}-a_{1})a_{3}-a_{2} b_{3}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{2} = \frac{(\lambda_{2}-a_{1})a_{4}-a_{2} b_{4}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{3} = \frac{(\lambda_{2}-a_{1})a_{5}-a_{2} b_{5}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{4} = \frac{(\lambda_{2}-a_{1})a_{6}-a_{2} b_{6}}{ a_{2}(\lambda_{2}+1) };
A_{5} = \frac{(\lambda_{2}-a_{1})a_{7}-a_{2} b_{7}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{6} = \frac{(\lambda_{2}-1)a_{8}-a_{2} b_{8}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{7} = \frac{(\lambda_{2}-a_{1})a_{9}-a_{2} b_{9}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{8} = \frac{a_{2}c_{1}}{a_{2}(\lambda_{2}+1)};
A_{9} = \frac{a_{2}c_{2}}{a_{2}(\lambda_{2}+1)}; \; \; \; \; \; \; \; \; A_{10} = \frac{a_{2}c_{3}}{a_{2}(\lambda_{2}+1)}; \; \; \; \; \; \; \; \; A_{11} = \frac{a_{2}c_{4}}{a_{2}(\lambda_{2}+1)}; \; \; \; \; \; \; \; \; A_{12} = \frac{a_{2}c_{5}}{a_{2}(\lambda_{2}+1)}.
To study the flip bifurcation of map (13), we define the following two discriminatory quantities
| \mu_{1} = \left( \frac{\partial^{2}F_{2}}{\partial s\partial\alpha^{\ast}}+\frac{1}{2}\frac{\partial F_{2}}{\partial\alpha^{\ast}} \frac{\partial^{2}F_{2}}{\partial s^{2}} \right )|_{(0, 0)}, |
and
| \mu_{2} = \left(\frac{1}{6} \frac{\partial^{3}F_{2}}{\partial s^{3}}+\left(\frac{1}{2} \frac{\partial^{2}F_{2}}{\partial s^{2}}\right)^{2} \right )|_{(0, 0)} |
which can be showed in [38]. Then provided with Theorem 3.1 in [38], the following result can be given as
Theorem 3.1. Assume that \mu_{1} and \mu_{2} are not zero, then a flip bifurcation can occur at E^{\ast}(x^{\ast}, y^{\ast}) of map (3) if the parameter \alpha^{\ast} varies in a small neighborhood of origin. And that when \mu_{2} > 0 (<0), the period-2 orbit bifurcated from E^{\ast}(x^{\ast}, y^{\ast}) of map (3) is stable (unstable).
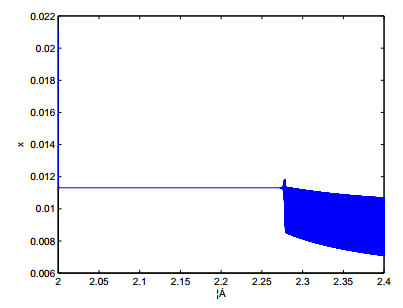
As application, we now give an example to support the theoretical results of this paper by using MATLAB. Let \beta_{1} = 1, \beta_{2} = 0.5, h_{1} = 0.05, h_{2} = 0.1, then we get from (5) that map (3) has only one positive point E^{\ast}(0.0113, 0.2226). And we further have \mu_{1} = e_{2} = 0.1134 \neq 0, \mu_{2} = e_{5}+e_{1}^{2} = -4.4869 \neq 0, which implies that all conditions of Theorem 3.1 hold, a flip bifurcation comes from E^{\ast} at the bifurcation parameter \alpha = 2.2238 , so the flip bifurcation is supercritical, i.e., the period-2 orbit is unstable.
According to Figures 1 and 2, the positive point E^{\ast}(0.0113, 0.2226) is stable for 2\leq \alpha \leq 2.4 and loses its stability at the bifurcation parameter value \alpha = 2.2238. Which implies that map (3) has complex dynamical properties.
In this paper, a predator-prey model with modified Leslie-Gower and Holling-type Ⅲ schemes is considered from another aspect. The complex behavior of the corresponding discrete time dynamic system is investigated. we have obtained that the fixed point E_{1} of map (4) is a saddle, and the fixed points E_{2} and E^{\ast} of map (4) can undergo flip bifurcation. Moreover, Theorem 3.1 tell us that the period-2 orbit bifurcated from E^{\ast}(x^{\ast}, y^{\ast}) of map (3) is stable under some sufficient conditions, which means that the predator and prey can coexist on the stable period-2 orbit. So, compared with previous studies [28] on the continuous predator-prey model, our discrete model shows more irregular and complex dynamic characteristics. The present research can be regarded as the continuation and development of the former studies in [28].
This work is supported by the National Natural Science Foundation of China (60672085), Natural Foundation of Shandong Province (ZR2016EEB07) and the Reform of Undergraduate Education in Shandong Province Research Projects (2015M139).
The authors would like to thank the referee for his/her valuable suggestions and comments which led to improvement of the manuscript.
The authors declare that they have no competing interests.
YYL carried out the proofs of main results in the manuscript. FXZ and XLZ participated in the design of the study and drafted the manuscripts. All the authors read and approved the final manuscripts.
| [1] | N. Wang, M. Han, Relaxation oscillations in predator-prey model with distributed delay, Comput. Appl. Math., 37 (2018), 475-484. |
| [2] | T. Zhang, X. Meng, T. Zhang, Global analysis for a delayed SIV model with direct and environmental transmissions, J. Appl. Anal. Comput., 6 (2016), 479-491. |
| [3] | B. S. Chen, X. Lin, W. Zhang, T. Zhou, On the system entropy and energy dissipativity of stochastic systems and their application in biological systems, Complexity, 2018 (2018), 1628472. |
| [4] | T. Zhang, N. Gao, T. Wang, H. Liu, Z. Jiang, Global dynamics of a model for treating microorganisms in sewage by periodically adding microbial flocculants, Math. Bio. Eng., 17 (2020), 179-201. |
| [5] | M. Han, X. Hou, L. Sheng, C. Wang, Theory of rotated equations and applications to a population model, Discrete Contin. Dyn. Syst. A, 38 (2018), 2171-2185. |
| [6] | M. Chi, W. Zhao, Dynamical analysis of multi-nutrient and single microorganism chemostat model in a polluted environment, Adv. Differ. Eq., 2018 (2018), 8719067. |
| [7] | N. Gao, Y. Song, X. Wang, J. Liu, Dynamics of a stochastic SIS epidemic model with nonlinear incidence rates, Adv. Differ. Eq., 2019 (2019). |
| [8] | X. Dong, Z. Bai, S. Zhang, Positive solutions to boundary value problems of p-Laplacian with fractional derivative, Boundary Value Probl., 2017 (2017). |
| [9] | X. Meng, S. Zhao, W. Zhang, Adaptive dynamics analysis of a predator-prey model with selective disturbance, Appl. Math. Comput., 266 (2015), 946-958. |
| [10] | T. Ma, X. Meng, Z. Chang, Dynamics and optimal harvesting control for a stochastic one-predatortwo-prey time delay system with jumps, Complexity, 2019 (2019), 5342031. |
| [11] | X. Meng, F. Li, S. Gao, Global analysis and numerical simulations of a novel stochastic ecoepidemiological model with time delay, Appl. Math. Comput., 339 (2018), 701-726. |
| [12] | X. Liang, R. Wang, Global well-posedness and dynamical behavior of delayed reaction-diffusion BAM neural networks driven by Wiener processes, IEEE Access, 6 (2018), 69265-69278. |
| [13] | T. Zhang, T. Xu, J. Wang, Y. Song, Z. Jiang, Geometrical analysis of a pest management model in food-limited environments with nonlinear impulsive state feedback control, J. Appl. Anal. Comput., 9 (2019), 2261-2277. |
| [14] | S. Gao, L. Luo, S. Yan, X. Meng, Dynamical behavior of a novel impulsive switching model for HLB with seasonal fluctuations, Complexity, 2018 (2018), 2953623. |
| [15] | J. Wang, H. Cheng, Y. Li, X. Zhang, The geometrical analysis of a predator-prey model with multi-state dependent impulses, J. Appl. Anal. Comput., 8 (2018), 427-442. |
| [16] | X.Lv, X. Meng, X. Wang, Extinction and stationary distribution of an impulsive stochastic chemostat model with nonlinear perturbation, Chaos, Solitons Fractals, 110 (2018), 273-279. |
| [17] | F. Bian, W. Zhao, Y. Song, R. Yue, Dynamical analysis of a class of prey-predator model with beddington-deangelis functional response, stochastic perturbation, and impulsive toxicant input, Complexity, 2017 (2017), 3742197. |
| [18] | J. Wang, H. Cheng, X. Meng, B. G. S. A. Pradeep, Geometrical analysis and control optimization of a predator-prey model with multi state-dependent impulse, Adv. Differ. Eq., 2017 (2017), 252. |
| [19] | Z. Jiang, X. Bi, T. Zhang, B.G. S. A. Pradeep, Global Hopf bifurcation of a delayed phytoplanktonzooplankton system considering toxin producing effect and delay dependent coefficient, Math. Biosci. Eng., 16 (2019), 3807-3829. |
| [20] | Y. Li, H. Cheng, Y. Wang, A Lycaon pictus impulsive state feedback control model with Allee effect and continuous time delay, Adv. Diff. Eq., 2018 (2018), 367. |
| [21] | G. Liu, Z. Chang, X. Meng, Asymptotic analysis of impulsive dispersal predator-prey systems with Markov switching on finite-state space, J. Funct. Spaces, 2019 (2019), 1-18. |
| [22] | X. Zhuo, Global attractability and permanence for a new stage-structured delay impulsive ecosystem, J. Appl. Anal. Comput., 8 (2018), 457-470. |
| [23] | X. Feng, Y. Song, J. Liu, G. Wang, Permanence, stability, and coexistence of a diffusive predatorprey model with modified Leslie-Gower and B-D functional response, Adv. Differ. Eq., 2018 (2018), 314. |
| [24] | X. Zhuo, F. Zhang, Stability for a new discrete ratio-dependent predator-prey system, Qual. Theory Dyn. Syst., 17 (2018), 189-202. |
| [25] | Z. Bai, Z. Shuo, S. Sun, C. Yin, Monotone iterative method for fractional differential equations, Elect. J. Differ. Eq., 2016 (2016), 06. |
| [26] | T. Zhang, W. Ma, X. Meng, T. Zhang, Periodic solution of a prey-predator model with nonlinear state feedback control, Appl. Math. Comput., 266 (2015), 95-107. |
| [27] | Y. Li, X. Zhuo, F. Zhang, Multiperiodicity to a certain delayed predator-prey model, Qual. Theory Dyn. Syst., 18 (2019), 793-811. |
| [28] | K. Liu, T. Zhang, L. Chen, State-dependent pulse vaccination and therapeutic strategy in an SI epidemic model with nonlinear incidence rate, Comput. Math. Methods Med., 2019 (2019), 3859815. |
| [29] | X. Zhang, Q. Zhang, V. Sreeram, Bifurcation analysis and control of a discrete harvested preypredator system with Beddington-DeAngelis functional response, J. Franklin Inst., 347 (2010), 1076-1096. |
| [30] | M. Han, V. G. Romanovski, X. Zhang, Equivalence of the Melnikov function method and the averaging method, Qual. Theory Dyn. Sys., 15 (2016), 471-479. |
| [31] | M. Han, L. Sheng, Bifurcation of limit cycles in piecewise smooth systems via Melnikov function, J. Appl. Anal. Comput., 5 (2015), 809-815. |
| [32] | M. Han, L. Sheng, X. Zhang, Bifurcation theory for finitely smooth planar autonomous differential systems, J. Differ. Eq., 264 (2018), 3596-3618. |
| [33] | Q. Song, R. Yang, C. Zhang, L. Tang, Bifurcation analysis in a diffusive predator-prey system with michaelis-menten-type predator harvesting, Adv. Differ. Eq., 2018 (2018), 329. |
| [34] | X. Liang, X. Zhuo, R. Wang, Global attractor of reaction-diffusion gene regulatory networks with S-Type delay, Neural Process. Lett., 2019 (2019), 1-21. |
| [35] | F. Liu, R. Yang, L. Tang, Hopf bifurcation in a diffusive predator-prey model with competitive interference, Chaos, Solitons Fractals, 120 (2019), 250-258. |
| [36] | Z. Li, M. Han, F. Chen, Almost periodic solutions of a discrete almost periodic logistic equation with delay, Appl. Math. Comput., 232 (2014), 743-751. |
| [37] | J. Zhao, Y. Yan, Stability and bifurcation analysis of a discrete predator-prey system with modified Holling-Tanner functional response, Adv. Differ. Eq., 2018 (2018), 402. |
| [38] | Y. A. Kuznetsov, Elements of Applied Bifurcation Throry, 2nd edition, Springer-Verlag, New York, 1998. |
| [39] | J. Guckenheimer, P. Holmes, Nonlinear Oscillations, Dynamical System and Bifurcation of Vector Fields, Springer-Verlag, New York, 2002. |
| [40] | J. Carr, Application of Center Manifold Theory, Springer-Verlag, New York, 1981. |
| [41] | S. Huang, S. Ruan, D. Xiao, Bifurcations in a discrete predator-prey model with nonmonotonic functional response, J. Math. Anal. Appl., 464 (2018), 201-230. |
| [42] | L. Meng, Y. Han, Z. Lu, G. Zhang, Bifurcation, chaos, and pattern formation for the discrete predator-prey reaction-diffusion model, Discrete Dyn. Nat. Soc., 2019 (2019), 9592878. |
| [43] | E. M. Elabbasy, A. A. Elsadany, Y. Zhang, Bifurcation analysis and chaos in a discrete reduced Lorenz system, Appl. Math. Comput., 228 (2014), 184-194. |
| [44] | S. Dange, K. Manoj, S. Banerjee1, S. A. Pawar, S. Mondal, R. I. Sujith, Oscillation quenching and phase-flip bifurcation in coupled thermoacoustic systems, Chaos: Interdiscip. J. Nonlinear Sci., 29 (2019), 093135. |
| [45] | H. Kitajima, T. Yazawa, Flip-flip bifurcation in a mathematical cardiac system, Int. J. Bifurcation Chaos, 29 (2019), 1950045. |
| [46] | M. Chi, W. Zhao, Dynamical analysis of two-microorganism and single nutrient stochastic chemostat model with monod-haldane response function, Complexity, 2019 (2019), 8719067. |
| 1. | 桂珍 王, A Class of Mathematical Model Concerning Impulsive Pest Control Strategies, 2021, 10, 2324-7991, 548, 10.12677/AAM.2021.102060 | |
| 2. | Liyan Zhong, Jianhe Shen, Degenerate Transcritical Bifurcation Point can be an Attractor: A Case Study in a Slow–Fast Modified Leslie–Gower Model, 2022, 21, 1575-5460, 10.1007/s12346-022-00608-8 | |
| 3. | Naqi Abbas, Rizwan Ahmed, Stability and bifurcation analysis of a discrete Leslie predator-prey model with fear effect, 2024, 12, 2309-0022, 16, 10.21015/vtm.v12i1.1686 | |
| 4. | Fethi Souna, Salih Djilali, Sultan Alyobi, Anwar Zeb, Nadia Gul, Suliman Alsaeed, Kottakkaran Sooppy Nisar, Spatiotemporal dynamics of a diffusive predator-prey system incorporating social behavior, 2023, 8, 2473-6988, 15723, 10.3934/math.2023803 | |
| 5. | Parvaiz Ahmad Naik, Muhammad Amer, Rizwan Ahmed, Sania Qureshi, Zhengxin Huang, Stability and bifurcation analysis of a discrete predator-prey system of Ricker type with refuge effect, 2024, 21, 1551-0018, 4554, 10.3934/mbe.2024201 | |
| 6. | Neriman Kartal, Multiple Bifurcations and Chaos Control in a Coupled Network of Discrete Fractional Order Predator–Prey System, 2024, 2731-8095, 10.1007/s40995-024-01665-1 | |
| 7. | Parvaiz Ahmad Naik, Rizwan Ahmed, Aniqa Faizan, Theoretical and Numerical Bifurcation Analysis of a Discrete Predator–Prey System of Ricker Type with Weak Allee Effect, 2024, 23, 1575-5460, 10.1007/s12346-024-01124-7 | |
| 8. | Saud Fahad Aldosary, Rizwan Ahmed, Stability and bifurcation analysis of a discrete Leslie predator-prey system via piecewise constant argument method, 2024, 9, 2473-6988, 4684, 10.3934/math.2024226 | |
| 9. | Parvaiz Ahmad Naik, Yashra Javaid, Rizwan Ahmed, Zohreh Eskandari, Abdul Hamid Ganie, Stability and bifurcation analysis of a population dynamic model with Allee effect via piecewise constant argument method, 2024, 70, 1598-5865, 4189, 10.1007/s12190-024-02119-y |