Time-delayed model of autoimmune dynamics

1.   Introduction

The main role of the immune system is to effectively protect its host against {pathogens by} identifying and destroying pathogen-infected cells. In most cases, this is achieved by T cells that upon encountering a foreign antigen presented on antigen-presenting cells (APCs) undergo clonal expansion and then eliminate cells presenting this antigen ^[1,2]. In order for this immune response to be successful, it is essential for T cells to be able to discriminate between cells presenting self- and foreign antigens, so that T cells would exhibit tolerance towards self-antigens, which is known as self-tolerance. The breakdown of self-tolerance, i.e. a failure of self/non-self discrimination, results in a pathological immune response known as autoimmune disease, whereby T cells are attacking host's own healthy cells. Regulatory T cells (Tregs) play a major role in mitigating this process by limiting such immune response ^[3,4,5].

In order to facilitate effective diagnosis and treatment of autoimmune disease, it is crucial to identify possible causes of its onset and development. Autoimmunity is a very complex phenomenon, and a large number of different internal and external contributing factors have been identified that are involved in facilitating autoimmune response, including age and genetic predisposition, as well as various environmental triggers, such as previous immune challenge and exposure to pathogens. While intrinsic factors may determine the degree to which an individual patient may be prone to developing an autoimmune response, it is usually the external factors, most often, infections that are necessary to actually trigger the onset of autoimmunity ^[6,7,8]. Over the years, a number of pathogens have been identified that appear to be very strongly associated with specific autoimmune diseases, such as Epstein-Barr virus associated with rheumatoid arthritis, multiple sclerosis (MS), autoimmune thyroid disease, and systemic lupus erythematosus (SLE) ^[9,10], the Coxsackie viruses associated with type-1 diabetes ^[11,12], and HSV-1 virus associated with autoimmune stromal keratitis ^[13,14]. Similarly, gut microbiota is known to play an important role in gut and systemic autoimmune diseases, and it has been very recently shown that translocation of a gut bacterium E. gallinarium into liver and other tissues in mice and humans results in triggering autoimmune response ^[15]. A number of different mechanisms have been identified that explain the dynamics of onset of pathogen-induced autoimmune disease ^[16,17], including bystander activation ^[18], epitope spreading, cryptic antigen, and molecular mimicry ^[17,19,20], with the latter being most relevant for autoimmune diseases caused by viral infections ^[17,18,21].

Despite the complexity of the immune system, over the years a number of mathematical models have been proposed that studied various aspects of immune dynamics and autoimmunity. Compartmental models have proved very successful at capturing various aspects of immune dynamics, including "burstiness" of the viral process (mostly, new virus particles are released through lysis of virus-infected cells), as well as the effects of treatment ^{[22,23,24,25]}. In fact, a number of such models have been very effective at modelling the dynamics of specific viral infections, such as influenza A ^[26,27,28], HIV ^[29,30], hepatitis B ^[31], hepatitis C ^[32,33,34], and they have been very accurately parameterised using available clinical data. In the context of autoimmunity, some of the early models analysed interactions between effector and regulatory T cells, focusing on T cell vaccination but without explicitly identifying origins of autoimmune response ^[35]. In another version of that model, it was shown that autoimmunity can actually arise as a result of interaction between regulatory and autoreactive T cells, with the autoimmunity being defined as a dynamical state of above-threshold oscillations in the number of autoreactive cells ^[36,37]. Iwami et al. ^[38,39] analysed a mathematical model for autoimmune diseases, which explicitly includes virus population and its interactions with the immune system. Interestingly, they have shown that a functional form (linear or density-dependent) for the term representing the growth of target cells has an effect on the type of immune dynamics exhibited by the model. Although that model was able to produce sustained periodic oscillations that can be interpreted as a manifestation of autoimmune response, it was not able to also capture a regime of normal clearance of a viral infection. León et al. ^[40,41,42] and Carneiro et al. ^[43] have analysed more advanced models of immune dynamics that included different types of T cells, focusing on the suppressive role of regulatory T cells in controlling autoimmune response. Wodarz and Jansen ^[44] have analysed autoimmunity in the context of viral cancer by including viral infections indirectly through an increased rate of uptake of self-antigen by APCs. An overview of various recent mathematical models of immune dynamics, with particular emphasis on modelling the onset and development of autoimmune disease, can be found in a special issue on "Theories and modeling of autoimmunity" ^[45].

Due to a very significant role being played by the regulatory T cells in maintaining self-tolerance and controlling autoimmune response ^[46,47,48], a number of papers have looked at modelling the dynamics of regulatory T cells in the specific context of autoimmunity. Alexander and Wahl ^[49] have studied interactions between regulatory T cells with professional APCs and effector cells for the purpose of controlling immune response. Both this model, and the models analysed by Burroughs et al. ^[50,51], have represented Tregs as a separate compartment in the model to investigate how Tregs are activated by autoantigens, and how they in their turn suppress the activity of autoreactive T cells. Another interesting modelling approach stems from the idea that the same T cells can perform a number of distinct immune functions by virtue of having different or tunable activation thresholds, which allows them to adjust their response to stimulation by autoantigens. This modelling framework was originally proposed in theoretical studies of peripheral and central T cell activation ^[52,53,54], and it was later shown how the need for tunable activation thresholds in T cells can be derived directly from the first principles of signal detection theory ^[55]. Subsequent murine and human experiments have validated the feasibility of this methodology by demonstrating that activation thresholds of T cells do change dynamically during T cell circulation ^{[56,57,58,59,60]}. Altan-Bonnet and Germain ^[61] have analysed differences in activation and response thresholds that are dependent on the activation state of the T cells, while van den Berg and Rand ^[62] and Scherer et al. ^[63] have investigated stochastic tuning of activation thresholds. Carneiro et al. ^[43] have compared alternative origins of self-tolerance as mediated by tuning of activation thresholds, as well as the control of proliferation of autoreactive T lymphocytes by the regulatory T cells.

A particularly important role in the immune dynamics, and more specifically, in the performance of T cells, is played by cytokines. Activated T cells produce growth cytokines (primarily, interleukin-2, IL-2), and expression of IL-2 receptor by these T cells triggers cytokine-driven proliferation ^[64,65], characterised by a certain quorum threshold ^[66,67]. Importantly, whereas IL-2 appears to be essential for proliferation of regulatory T cells ^[68], these T cells do not actually produce IL-2 even upon activation ^[68,69]. It has been suggested that regulatory T cells may control these thresholds by inhibiting IL-2 secretion ^[70]. Burroughs et al. ^[50,51,66] have considered the case where pathogen-induced autoimmunity arises through the mechanism of bystander activation, and the model they developed analyses interactions between T cells and IL-2. In a very recent paper, Oliveira et al. ^[71] have shown how a competition between T cells for IL-2 in response to a pathogenic infection can result in the depletion of the pool of autoreactive T cells, thus suppressing autoimmune response.

One of the fundamental features of the immune dynamics is the fact that various processes associated with the development of infection, as well as with mounting the appropriate immune response, are characterised by time delays, which can be non-negligible, and thus have to be properly accounted for in mathematical models ^{[72,73,74,75]}. In the specific context of viral infections, earlier mathematical models of influenza, HIV and HCV have highlighted the importance of including viral lag phase in the analysis of interactions between viruses and the immune system ^{[24,25,27,28]}. This lag phase of the virus life cycle includes an eclipse phase consisting of virus attachment, cell penetration and uncoating, and a latent phase, which includes virus assembly, maturation and release of new virions. Precise measurements of different stages of virus life cycle have been performed for several viruses that have been associated with triggering or exacerbating autoimmune disease ^{[9,10,11,12,13,14]}. All of these processes result in a delayed production and release of virions, as well as in the delay between a cell becoming infectious and the time it becomes recognised as an infected cell by the cytotoxic T lymphocytes (CTLs) ^[76]. Hence, it is essential to correctly account for this in models of pathogen-induced autoimmunity. Other time delays involved include a delay between infection and developing immune response ^{[74,77,78,79,80]}, as well as the delay associated with the process of stimulation of T cells by the IL-2 cytokine and their subsequent proliferation. Kim et al. ^[70] have developed and analysed a very detailed model of immune regulation that includes various time delays associated with proliferation and stimulation of different types of T cells.

Focusing on molecular mimicry as the primary mechanism of virus-induced autoimmune response, Blyuss and Nicholson ^[81,82] have developed a mathematical model that explicitly includes both a viral population, and two types of T cells with different activation thresholds. This model allows for a possibility of viral infection and autoimmune response occurring in different organs of the host. Besides normal clearance of a viral infection, and a state of chronic infection, the model also exhibits an autoimmune state characterised by stable endogenous oscillations of cell populations, which are reminiscent of relapses and remissions that are observed in clinical manifestations of uveitis, autoimmune thyroid disease, and MS ^[83,84,85]. One limitation of that model is that oscillations can only be observed in the presence of non-zero viral population and infected cells, while clinical observations suggest that autoimmunity is more often observed after the clearance of the initial viral infection. Fatehi et al. ^[86] have shown that this limitation can be overcome by including in the model IL-2 and regulatory T cells, which provides a more realistic representation of immune dynamics. Importantly, this modified model also exhibits multi-stability, where for the same values of parameters, the initial state of the immune system and the level of infection determine which of the dynamic scenarios will be realised, i.e. whether the infection will just be cleared without any lasting consequences, or the resulting breakdown of immune tolerance will lead to autoimmunity. Under a simplifying assumption of fast release of virions, which eliminates the need for a separate compartment representing free virus, Fatehi et al. ^[87] have analysed the effects of time delays in the model, and also investigated the role of regulatory T cells in suppressing the expression of IL-2. Fatehi et al. ^[88] have looked at the same simplified model from the perspective of stochastic dynamics. Their results provide a characterisation of basins of attraction of different dynamical states under the influence of stochasticity, as well as the dependence of the variance of stochastic oscillations around deterministically stable steady states on system parameters. This latter result is particularly relevant for analysis and interpretation of experimental observations, which show that there are noticeable differences in the progress of autoimmune disease even in apparently identical situations, such as two eyes of the same mouse, or a population of genetically identical mice ^[89,90].

In this paper we study the effects of the above-mentioned viral lag phase, as well as time delays associated with different aspects of the immune response, on the onset and development of autoimmunity, using the framework of T cells with tunable activation thresholds. In the next section, we derive the model and identify its steady states. Analytical conditions for stability and bifurcations of different steady states are derived in Section 3. Section 4 contains the results of numerical stability analysis, including identifying basins of attraction of various dynamical states, as well as numerical simulations of the model, which illustrate its behaviour in different dynamical regimes. The paper concludes in Section 5 with a discussion of results and open problems.

2.   Model derivation

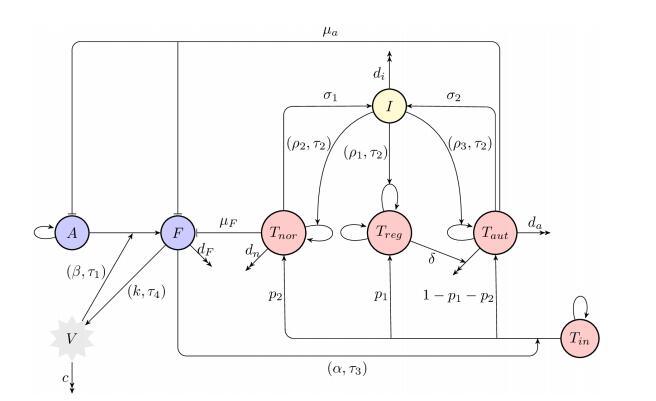
To analyse the dynamics of immune response to a viral infection and subsequent breakdown of immune tolerance, we consider a full model presented earlier in Fatehi et al. ^[86], as illustrated in Figure 1, in which we now also include time delays. In this model it is assumed that in the absence of infection, healthy host cells, whose number is denoted by $A(t)$, grow logistically with the linear growth rate $r$ and the carrying capacity $N$. Upon encountering free virus particles, whose population is denoted by $V(t)$, after some time delay $\tau_1$ they become infected cells $F(t)$ at rate $\beta$. From a biological point of view, the time delay $\tau_1$ models the eclipse phase, i.e. it represents the cumulative duration of the processes of viral attachment and entry into host cell, as well as subsequent uncoating inside the cell.

After this time $\tau_1$, the cell containing virus can be identified by CTL cells ^[76]. Even after a cell has been infected, it takes some time before it is able to produce new virus particles ^[91], hence, we include a time delay $\tau_4$ to represent the latent phase, associated with the processes of virus assembly, maturation and release of new virions. Together, the time delays $\tau_1$ and $\tau_4$ represent the above-mentioned lag phase of the viral life cycle.

In terms of immune dynamics, in light of the fact that autoimmune response can develop in the absence of B cells ^[92], and experimental evidence suggesting that antibodies play a secondary role in autoimmune dynamics compared to T cells ^[93], in our model we focus primarily on the T cell dynamics. We assume that in the absence of infection, there is some number of naïve (inactivated) T cells $T_{in}(t)$, which is maintained in a homeostasis, which is represented by a constant production at rate $\lambda_{in}$ and constant degradation at rate $d_{in}$. It is worth noting that the functional form representing homeostasis can also play an important role in controlling immune dynamics ^[38,39]. Similarly, the population of regulatory T cells $T_{reg}(t)$, which are responsible for suppression of autoreactive T cells at rate $\delta$, is also maintained at a homeostasis ^[94]. Upon receiving stimulation from mature antigen-presenting cells, which is represented in the model indirectly through interactions between naïve T cells and infected cells happening at rate $\alpha$, the naïve T cells expand, and, after some time delay $\tau_3$, a proportion $p_1$ of them differentiate into further regulatory T cells, a proportion $p_2$ become normal activated T cells $T_{nor}(t)$, and the remaining proportion $(1-p_1-p_2)$ become autoreactive T cells $T_{aut}(t)$. While normal activated T cells are responsible for eliminating infected T cells at rate $\mu_F$, autoreactive T cells are assumed to have a lower activation threshold, which results in them destroying not only infected cells, but also healthy host cells at rate $\mu_a$. This happens due to a cross-reactivity between some of the epitopes in foreign and self-antigens.

Dynamics of immune response, and, in particular, proliferation and activity of T cells are known to be affected by a number of different cytokines, with a particularly important role being played by IL-2, represented in the model by the variable $I(t)$. While IL-2 enhances the proliferation of all types of T cells, it is only secreted by the activated T cells, but not by the regulatory T cells ^[1,4]. Hence, in the model we consider that proliferation of T cells $T_{reg}$, $T_{nor}$ and $T_{aut}$ is enhanced by IL-2 $I(t)$ at rates $\rho_1$, $\rho_2$ and $\rho_3$, respectively, and this process is characterised by a time delay $\tau_2$, while IL-2 is produced by $T_{nor}$ and $T_{aut}$ at rates $\sigma_1$ and $\sigma_2$. Although regulatory T cells are suppressing the expression of IL-2 by other T cells ^[3,66], we have recently shown that this does not have a major effect on the dynamics compared to other contributions, such as the suppressive effect of regulatory T cells on autoreactive T cells ^[87].

With the above assumptions, the complete model for immune response takes the form

where $0\leq p_1+p_2\leq 1$. Introducing non-dimensional variables

this model is modified into

where

and, to simplify the notation, the hats have been dropped in all variables and parameters. This model has been found to have at most eight biologically feasible steady states ^[86], of which four are always unstable, and the other four can be stable or unstable depending on the values of parameters. The first of these is the disease-free steady state that exists for any parameter values, and is given by

Next, we have two steady states with $T_{nor} = 0$ and $T_{aut}\neq 0$,

and

where $T^{\ast}_{reg}$ satisfies the following quadratic equation:

The steady state $S^{\ast}_{2}$ has $A = 0$, which implies the death of host cells, whereas the steady state $S^{\ast}_{3}$ corresponds to an autoimmune regime. Finally, the system (2.2) can have a chronic steady state $S^{\ast}_4$, characterised by all of its components being positive, but it does not prove possible to find a closed form expression for this state.

3.   Stability analysis of the steady states

Linearising the system (2.2) near the disease-free steady state $S^{\ast}_1$ shows that this steady state is stable if all roots $\lambda$ of the following equation have negative real part

where $\overline{\tau} = \tau_1+\tau_4$. If $cd_F < k\beta$, the above equation always has a real positive root for any value of $\overline{\tau}\geq 0$, implying that the disease-free steady state is always unstable for any value of the time delays. If, however, the condition $cd_F > k\beta$ holds, the disease-free steady state is stable for $\overline{\tau} = 0$. To find out whether it can lose stability for $\overline{\tau} > 0$, we look for solutions of equation (3.1) in the form $\lambda = i\omega$. Separating real and imaginary parts yields

Squaring and adding these two equations gives the following equation for potential Hopf frequency $\omega$

Since $cd_F > k\beta$, this equation does not have positive roots for $z$, suggesting that there can be no roots of the form $\lambda = i\omega$ of the equation (3.1). This implies that in the case $cd_F > k\beta$ the disease-free steady state $S^{\ast}_1$ is stable for all values of the time delay $\overline{\tau}\geq 0$.

The steady state $S^{\ast}_2$ is stable if

and all roots of the following equation have negative real part

where

For $\tau_2 = 0$, this steady state is stable if $T^{\ast}_{reg}$ satisfies (3.2), and the following conditions hold

To investigate whether stability can be lost for $\tau_2 > 0$, we use an iterative procedure described in ^[95,96] to determine a function $F(\omega)$, whose roots give the Hopf frequency associated with purely imaginary roots of equation (3.3). Substituting $\lambda = i\omega$ into equation (3.3), we define $\Delta^{(1)}(\tau_2, \lambda)$ as

where

If we define

then $\Delta(\tau_2, i\omega) = 0$, whenever $\omega$ is a root of $F(\omega) = 0$. The function $F(\omega)$ has the explicit form

with

and

Introducing $s = \omega^2$, the equation $F(\omega) = 0$ can be equivalently rewritten as follows,

Without loss of generality, suppose that equation (3.5) has six distinct positive roots denoted by $s_1$, $s_2$, ..., $s_6$, which means that the equation $F(\omega) = 0$ has six positive roots

Substituting $\lambda_k = i\omega_k$ into equation (3.3) gives

where

This allows us to find

as the first time delay for which the roots of the characteristic equation (3.3) cross the imaginary axis. To determine whether the steady state $S^{\ast}_2$ actually undergoes a Hopf bifurcation at $\tau_2 = \tau^{\ast}$, we have to compute the sign of $d\mbox{Re}[\lambda(\tau^{\ast})]/d\tau_2$. For $\tau_2 = \tau^{\ast}$, $\lambda(\tau^{\ast}) = i\omega_0$, and we also define $s_0 = \omega_0^2$.

Lemma 3.1. Suppose $h^{\prime}(s_0)\neq 0$ and $p_0^{(1)}(i\omega_0)\neq 0$. Then the following transversality condition holds

Proof. Considering $p_j(i\omega_0) = x_j(\omega_0)+iy_j(\omega_0)$ for $j = 0, 1, 2$, we have

where all $x_j$ and $y_j$ are expressed in terms of system parameters and steady state values of the variables. Substituting these expressions into $\Delta(\tau_2, i\omega_0) = 0$ and $\Delta^{(1)}(\tau_2, i\omega_0) = 0$, and then separating real and imaginary parts gives

Solving this system of equations provides the values of $\sin(\omega_0\tau^{\ast})$, $\cos(\omega_0\tau^{\ast})$, $\sin(2\omega_0\tau^{\ast})$, and $\cos(2\omega_0\tau^{\ast})$. Taking the derivative of equation (3.3) with respect to $\tau_2$, one finds

Hence,

where

Substituting the values of $\sin(\omega_0\tau^{\ast})$, $\cos(\omega_0\tau^{\ast})$, $\sin(2\omega_0\tau^{\ast})$, and $\cos(2\omega_0\tau^{\ast})$ found earlier gives

Therefore,

which completes the proof.

We can now formulate the main result concerning stability of the steady state $S^{\ast}_2$.

Theorem 3.2. Suppose the value of $T_{reg}^{\ast}$ for $S^{\ast}_2$ satisfies conditions (3.2) and (3.4). If equation (3.5) has at least one positive root $s_0$ with $h^{\prime}(s_0)\neq 0$, and $p_0^{(1)}(i\omega_0)\neq 0$, then the steady state $S_2^{\ast}$ is stable for $0\leq \tau_2 < \tau^{\ast}$, unstable for $\tau_2 > \tau^{\ast}$, and undergoes a Hopf bifurcation at $\tau_2 = \tau^{\ast}$.

Stability analysis for the steady state $S^{\ast}_3$ is very similar, and it shows that this steady state is stable if

and all the roots of equation (3.3) have a negative real part. The analysis then proceeds in exactly the same way, and since the value of $T^{\ast}_{reg}$ is the same for $S^{\ast}_2$ and $S^{\ast}_3$, hence, the conclusion of Theorem 3.2 also holds for $S^{\ast}_3$.

4.   Numerical stability analysis and simulations

To explore how various parameters affect stability of different steady states, as well as the overall dynamics of the model, we perform numerical stability analysis and simulations using baseline values of model parameters, as given in Table 1. It is clear that for this choice of parameters, the condition $cd_F-k\beta > 0$ holds, implying that the disease-free steady state $S^{\ast}_1$ is stable, the steady states $S^{\ast}_2$ and $S^{\ast}_3$ can be either stable or unstable, while the chronic steady state $S^{\ast}_4$ is not biologically feasible. Later, we will also investigate what happens in the case when $cd_F-k\beta < 0$, for which the disease-free steady state $S^{\ast}_1$ is unstable.

Since the model can potentially exhibit multi-stability, an important role is played by the initial conditions. We have chosen the following initial condition

which biologically represents a situation at the start of viral infection, where there are still no infected cells, and no activated T cells.

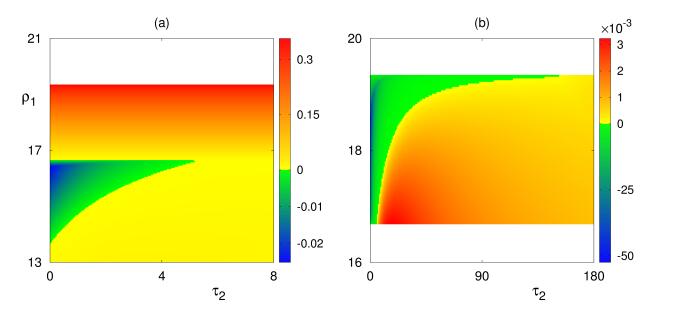
Earlier analysis of the model without time delays ^[86] has indicated that increasing the rate $\rho_1$, at which IL-2 enhances proliferation of regulatory T cells, can affect stability of the steady states $S^{\ast}_2$ and $S^{\ast}_3$. Figure 2 shows that increasing the time delay $\tau_2$, associated with this process of enhancement of proliferation, results in the smaller stability region of the steady state $S^{\ast}_2$, associated with the death of host cells. In contrast, stability of $S^{\ast}_3$ for small $\tau_2$ is unaffected by $\rho_1$, but once $\tau_2$ exceeds some threshold value, $S^{\ast}_3$ is stable for smaller values of $\tau_2$ and unstable for higher values of $\tau_2$, with a Hopf bifurcation of $S^{\ast}_3$ occurring at some critical value of $\tau_2$, which increases with $\rho_1$, as described in Theorem 3.2. This Figure also suggests that if $\tau_2$ is sufficiently large, both steady states $S^{\ast}_2$ and $S^{\ast}_3$ are unstable. Importantly, one should note that if $\rho_1$ is sufficiently high, neither of these steady states are feasible, and the system only has a single stable disease-free steady state $S^{\ast}_1$. Interestingly, the autoimmune state $S^{\ast}_3$ can only exist if $\rho_1$ exceeds some minimum value, suggesting a rather counter-intuitive result that within our model the onset of autoimmune dynamics relies, at least partially, on the immune system functioning more effectively in terms of enhancing the proliferation of regulatory T cells.

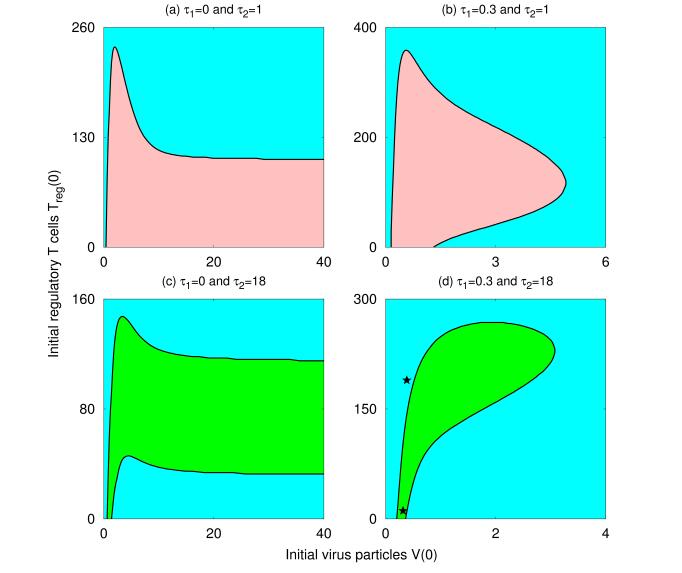
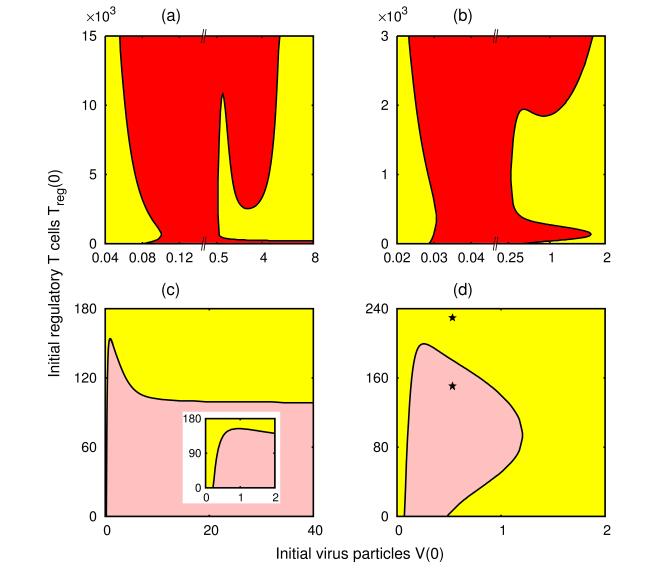
To explore the role played by the strength of infection and the state of the immune system prior to infection in determining disease outcome, Figure 3 illustrates basins of attraction of different steady states and periodic solutions of the model depending on the initial viral load $V(0)$, and the initial number of regulatory T cells $T_{reg}(0)$. This Figure was computed by numerically solving the system (2.2) with the initial condition (4.1) for every combination of initial values of $V(0)$ and $T_{reg}(0)$ until $t = 10000$, and then identifying from the solution, which dynamical state the system had reached by that point. Whereas time delay $\tau_1$, which represents the time it takes for infected cell to become identifiable as such to CTLs, does not have an effect on feasibility or stability of the steady states $S^{\ast}_1$ and $S^{\ast}_3$, changing this time delay affects the shape of basins of attraction of these states.

On the other hand, $\tau_3$ and $\tau_4$ do not have significant effect on the shape of basins of attraction. We can see that for negligibly small values of $\tau_1$, the system can converge to a stable steady state $S^{\ast}_3$ or a periodic orbit around this steady state for an arbitrarily large initial viral load. As the delay $\tau_1$ is increased, this results in making the basin of attraction of $S^{\ast}_3$, or periodic solution around it, bounded, and for sufficiently high values of $V(0)$ or $T_{reg}(0)$, the system approaches a stable disease-free steady state $S^{\ast}_1$. One also observes that in this case the system converges to $S^{\ast}_3$ or a periodic orbit around it for some intermediate values of $T_{reg}(0)$, while for very small or very large $T_{reg}(0)$ it converges instead to $S^{\ast}_1$. We have earlier shown ^[86] that for every $\lambda_r$ smaller that some threshold value, which ensures the existence of steady states $S^{\ast}_2/S^{\ast}_3$, there is some critical value of $\mu_a$, so that for larger values of $\mu_a$ there is a stable steady state $S^{\ast}_3$ or a stable periodic orbit around it, whereas for smaller values of $\mu_a$ there is a stable steady state $S^{\ast}_2$ or a stable periodic orbit around it. At the same time, the shape of the basins of attraction remains exactly the same as the one shown in Figure 3, with $S^{\ast}_2$ replacing $S^{\ast}_3$ if the value of $\mu_a$ is reduced. Comparison of plots 3(a) and (c) indicates that increasing the rate $\rho_1$ at which IL-2 enhances the proliferation of Tregs results in a modification of basins of attraction, namely, for higher $\rho_1$, it is possible to have a stable disease-free steady state for arbitrarily small initial numbers of regulatory T cells, while for smaller $\rho_1$ this can only occur, provided $T_{reg}(0)$ exceeds some minimum value. Figure 3(d) illustrates the fact that {in our model}, decreasing the level of infection, as quantified by $V(0)$, can actually result in the onset and/or exacerbation of autoimmune disease. Experimentally, this result has been demonstrated in earlier studies of diabetes in NOD mice ^[1].

In Figure 4 we demonstrate the regime of bi-stability indicated in Figure 3(d), where for the same values of parameters, depending on the initial condition, the system either converges to a stable disease-free steady state $S^{\ast}_1$, or approaches a periodic orbit around $S^{\ast}_3$. From a biological perspective, this periodic solution represents an autoimmune state, where the initial infection has been successfully cleared, but subsequently the immune system exhibits sustained endogenous oscillations in the population of autoreactive T cells that can cause damage to the host cells. In clinical practice, this oscillatory behaviour is associated with relapses/remissions that are characteristic for many autoimmune diseases, such as autoimmune thyroid disease, uveitis, and MS ^[83,84,85]. This bi-stability is very important from a practical point of view, as it highlights the fact that it is not only the kinetic parameters of the immune response, but also the strength of the infection (as represented by the initial viral load), and the initial state of the immune system that determine which dynamical state the system will evolve to. From a clinical perspective, this amount to distinguishing between a particular patient being able to clear an infection without any lasting consequences, or proceeding to develop autoimmune disease.

If all the parameters are kept constant, increasing the time delay $\tau_2$ associated wth IL-2-induced proliferation of regulatory T cells can result in suppression of oscillations, so that the system would settle on a stable steady state $S^{\ast}_3$.

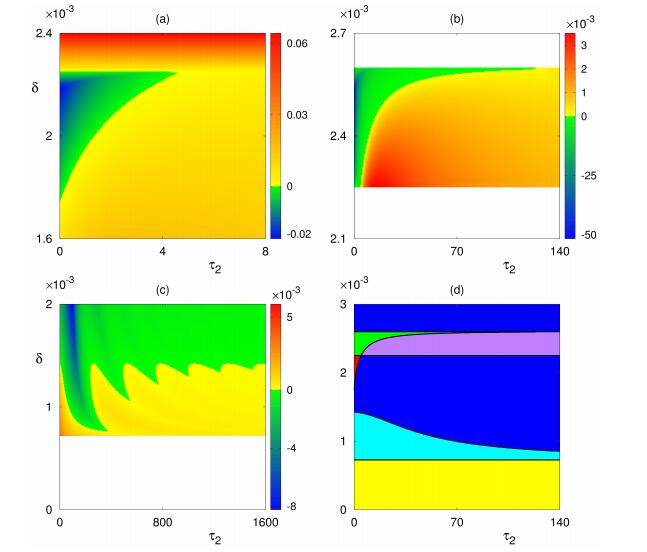
Next, consider the case when $cd_F < k\beta$, which means that the disease-free steady state $S^{\ast}_1$ is unstable, and the chronic steady state $S^{\ast}_4$ is feasible, and in this case, the steady states $S^{\ast}_2$ and $S^{\ast}_3$ can also be stable. Figure 5 illustrates how the feasibility and stability of $S^{\ast}_2$, $S^{\ast}_3$, and $S^{\ast}_4$ depends on the time delay $\tau_2$, and also on the parameter $\delta$ that characterises how strongly regulatory T cells suppress autoreactive T cells. Regions of feasibility and stability $S^{\ast}_2$ and $S^{\ast}_3$, presented in Figures 5(a) and (b) are qualitatively similar to regions of feasibility and stability of these steady states for the case where the disease-free steady states is stable, as was shown earlier in Figures 2(a) and (b).

For the chronic steady state $S^{\ast}_4$, one observes that if the rate $\delta$ is sufficiently high, this steady state is stable for any value of the time delay $\tau_2$. For smaller $\delta$, the steady state $S^{\ast}_4$ undergoes a finite number of stability switches as the time delay $\tau_2$ increases, and eventually it becomes unstable, as shown in Figure 5(c). Figure 5(d) illustrates various regimes of multii-stability between different steady states that can be observed in the model for $cd_F < k\beta$, i.e. when the disease-free steady state $S^{\ast}_1$ is unstable. One observes that for a very small time delay $\tau_2$, there are two ranges of values of $\delta$, for which either both $S^{\ast}_2$ and $S^{\ast}_4$ are stable, or both $S^{\ast}_3$ and $S^{\ast}_4$ are stable. As $\tau_2$ increases, these ranges, where bi-stability is observed, become narrower and eventually disappear, with only the chronic steady state $S^{\ast}_4$ remaining as the single stable steady state. For lower values of $\delta$, the steady state $S^{\ast}_4$ is unstable through a Hopf bifurcation, and for sufficiently small $\delta$ it is infeasible.

Figure 6 shows basins of attraction for different steady states that correspond to various stability regions illustrated in Figure 5(d). In the case of sufficiently small rate $\delta$ of suppression of autoreactive T cells by regulatory T cells, for intermediate initial viral loads the system converges to a steady state $S^{\ast}_2$, corresponding to the death of host cells for any initial numbers of regulatory T cells, while for smaller and higher viral loads, it would settle on a chronic steady state $S^{\ast}_4$.

For higher values of $\delta$, the behaviour is very similar to that observed earlier in Figure 3(a) and (b), i.e. for a negligibly small delay $\tau_1$, starting from some initial viral load, the system approaches a stable chronic steady state $S^{\ast}_4$ for higher initial number of Tregs, and approaches an autoreactive steady state $S^{\ast}_3$ for smaller initial number of Tregs, irrespective of the initial viral load. In this case, increasing the delay $\tau_1$ results in making the basin of attraction of the steady state $S^{\ast}_3$ bounded, so that for sufficiently small and sufficiently large initial viral loads, and for sufficiently high initial number of regulatory T cells, the system approaches a stable chronic state $S^{\ast}_4$. Figure 8 illustrates the regime of bi-stability shown in Figure 6(d), where for the same values of parameters and the same initial viral load, the system either approaches the autoimmune steady state $S^{\ast}_3$ for smaller $T_{reg}(0)$, or tends to the chronic steady state $S^{\ast}_4$ for higher $T_{reg}(0)$.

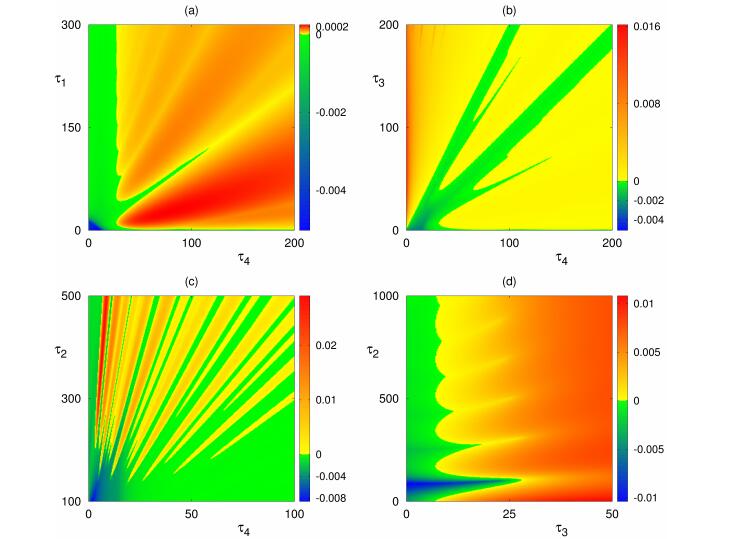
Since the stability of the steady states $S^{\ast}_2$ and $S^{\ast}_3$ is independent of the time delays $\tau_1$, $\tau_3$, and $\tau_4$, we now illustrate in Figure 7 how these time delays, as well as $\tau_2$, affect stability of the chronic steady state $S^{\ast}_4$, with the steady state being stable for sufficiently small values of all time delays. Figure 7(a) shows what happens when the time delays $\tau_2$ and $\tau_3$ that are associated, respectively, with cytokine-mediated enhancement of T cell proliferation, and T cell expansion in response to foreign antigen, are fixed. One observes that if new virus particles are produced by the infected cells sufficiently fast, i.e. the time delay $\tau_4$ is small, the chronic steady state $S^{\ast}_4$ is stable for any value of the time delay $\tau_1$ associated with the process of infection, provided other parameters ensure the feasibility of $S^{\ast}_4$. For higher values of $\tau_4$, this steady state undergoes a finite number of stability switches as $\tau_1$ is increased, before becoming unstable. Similar behaviour can be observed in Figure 7(d), which corresponds to a situation where $\tau_1$ and $\tau_4$ are fixed, while $\tau_2$ and $\tau_3$ are allowed to vary.

Figure 7(b) shows that for fixed $\tau_1$ and $\tau_2$, increasing just one of the time delays $\tau_3$ or $\tau_4$ results in a destabilisation of the chronic state $S^{\ast}_4$, while for each $\tau_1$ there is a range of values of $\tau_4$ (roughly centred around $\tau_4\approx\tau_1$), for which $S^{\ast}_4$ is stable. Finally, in the case where $\tau_1$ and $\tau_3$ are fixed, as shown in Figure 7(c), $S^{\ast}_4$ is stable for any value of $\tau_4$ for sufficiently small $\tau_2$, and then it is stable for small $\tau_4$ and very large $\tau_4$, with a finite number of stability switches between those values.

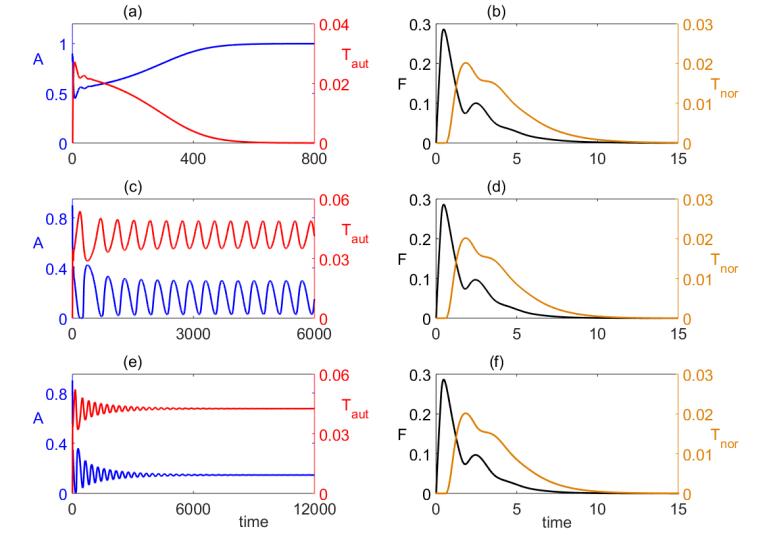
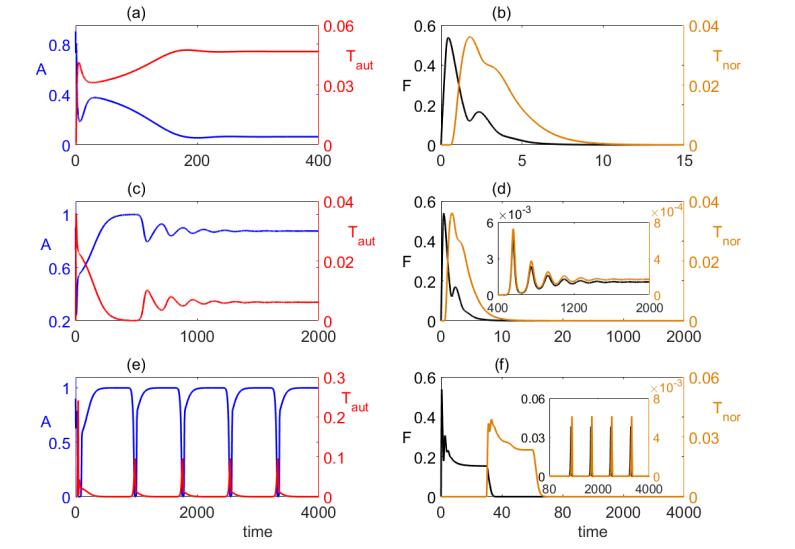
Figure 8 demonstrates different dynamical regimes in the model based on Figure 6(d) and Figure 7(b). Figures 8(a)–(b) show how the system approaches the autoimmune steady state $S_3^*$ for initial conditions indicated by a star in the pink region in Figure 6(d). For the same parameter values but a higher initial number of regulatory T cells, which corresponds to a star in the yellow region in Figure 6(d), the system instead tends to a stable chronic steady state $S_4^*$, as shown in Figures 8(c)–(d). In agreement with Figure 7(b), for the same values of parameters and initial conditions, increasing the time delay $\tau_3$ leads to a destabilisation of the steady state $S_4^*$ and the emergence of stable periodic oscillations around this steady state, as shown in Figures 8(e)–(f). This suggests that when the system is experiencing a chronic infection, a time delay associated with the differentiation of T cells into regulatory or activated T cells controls whether this chronic infection is characterised by some steady levels of cell populations, or oscillations around these steady levels.

5.   Discussion

In this paper we have analysed a model of immune response to a viral infection, which includes T cells with different activation thresholds, regulatory T cells and IL-2 cytokine. Since other types of T cells are not included in the model, we consider a situation where that IL-2 is only produced by CTLs, but it regulates the proliferation of both CTLs, and regulatory T cells. A particular emphasis has been made on the role of time delays associated with the following four aspects of immune dynamics: a lag between the time a cell becomes infected and the time it becomes recognised as infected by CTLs, the time it takes for IL-2 to stimulate the proliferation of T cells, the time it takes for naïve T cells to differentiate into regulatory T cells or CTLs, and the time that is required for infected cells to start releasing mature new virions.

Depending on the values of parameters, the model can have up to four biologically feasible steady states that represent the disease-free state $S^{\ast}_1$, the steady state characterised by the death of host cells $S^{\ast}_2$, the autoimmune steady state $S^{\ast}_3$, and the steady state of chronic infection $S^{\ast}_4$. Stability of the disease-free steady state is completely determined by the difference between the product of the rate of clearance of free virus with the death rate of infected cells, and the product of infection rate with the rate of production of new virus particles, but is independent of any other parameters and any of the time delays. In contrast, stability of the steady states $S^{\ast}_2$ and $S^{\ast}_3$ depends on the time delay $\tau_2$, and we have found analytical conditions for stability of these steady states in terms of $\tau_2$ and other parameters, but importantly, other time delays have no effect on stability. When stability of the steady state $S^{\ast}_3$ is lost through a Hopf bifurcation, this results in the emergence of sustained periodic oscillations around this steady state, which can be interpreted as a proper autoimmune state, where after the clearance of the primary infection, due to the breakdown of immune tolerance the immune system attacks host's own healthy cells, and the oscillations can be associated with periods of relapses and remission that are characteristic for many autoimmune diseases. The analysis suggests that one possible reason for the emergence of autoimmune state is an insufficiently strong effect of IL-2 on promoting the proliferation of regulatory T cells, resulting in a destabilisation of the steady state $S^{\ast}_3$.

Of particular interest is the regime of bi-stability between different steady states and/or periodic orbits, which indicates that even for the same values of parameters characterising the immune system and the infection, the ultimate dynamical state is also determined by the initial conditions, which include the initial viral load and the state of the immune system, such as the initial number of regulatory T cells. This is a very important result for clinical observations, since effectively it suggests that whether or not a given patient will successfully clear the infection, or will proceed to develop an autoimmune disease, is determined not only by how effective their immune system is, but also by the state of their immune system at the time of infection. To better understand the dynamics of the model in the bi-stable regime, we have explored how the shape of basins of attraction of different dynamical states changes with parameters. Extensive numerical simulations show that although the time delay $\tau_1$ between the time a cell becomes infected, and the time it becomes recognised as such by the immune system, does not have an effect on stability of the autoimmune steady state, it does, however, affect the shape of basins of attraction. Furthermore, numerical computations of the basins of attractions have shown another interesting result which suggests that reducing the initial viral load for the same level of regulatory T cells can result in someone developing autoimmunity, where previously they would just clear the infection without any further consequences. This result agrees with experimental observations of the onset and progression of diabetes in NOD mice ^[1].

There are several directions in which the work presented in this paper could be developed further. To account for the fact that immune response is a very complex multi-factor process, we have recently investigated the effects of stochasticity on the dynamics of immune response ^[87]. Those results show that while, on average, cell populations may exhibit decaying oscillations, stochastic amplification can yield sustained stochastic oscillations in individual realisations, which has major implications for analysis of clinical observations of immune response. It would be very insightful and practically important to investigate how those results are affected by the time delays, such as those analysed in this paper using deterministic models. From a mathematical perspective, this would require the development and analysis of a stochastic delayed model of immune responses, which, to our knowledge, has not yet been done. Another important question within the framework of T cells with tunable activation thresholds concerns an observation that during the process of immune response, activation thresholds themselves can also change ^[53,61,62], which can have a major effect on the progress of immune dynamics. Embedding activation thresholds as additional variables in a model similar to the one studied in this paper would provide a more comprehensive and accurate representation of T cell dynamics during immune response. Further realism can be added to the model by considering the effects of T cells on IL-2 secretion ^[66,87], as well as including other aspects of immune system, such as memory T cells ^[97,98].

Acknowledgments

F.F. acknowledges the support from Chancellor's Studentship from the University of Sussex.

Conflict of interest

All authors declare no conflicts of interest in this paper.