Adaptive dynamics of hematopoietic stem cells and their supporting stroma: a model and mathematical analysis

1.   Introduction

Hematopoietic stem cells (HSCs), developing in the bone marrow, are immature cells that are (the earliest in development) precursors of all lineages of blood cells: red blood cells, white blood cells and megacaryocytes (whose fragmentation gives rise to platelets). Blood cell formation, also called hematopoiesis, is a complex phenomenon basing on the self-renewal, differentiation and maturation of HSCs. It produces about $10^{11}$ blood cells per day in humans and is one of the most stable biological processes in vertebrate organisms. A dysfunction in the hematopoietic process may induce blood cancer diseases (usually named malignant hemopathies) such as leukaemia where blockade of maturation and of differentiation occurs in the hematopoietic tree. As a consequence, malignant cells, resulting from an accumulation of irregular genetic events, appear and proliferate abnormally.

Many mathematical models have been proposed to understand blood cell development and blood diseases. Mackey ^[1], inspired by Burns and Tannock ^[2] and Lajtha ^[3], have introduced a first mathematical model of the form of a system of delay differential equations for the dynamics of HSCs where the populations are divided into two groups (proliferating cells and quiescent cells) and the time delay corresponds to the proliferating phase duration. Further improvements both in modelling and mathematical analysis are investigated by many authors; see, for example, ^[5,6,7,8]—models in the form of ODEs or age-structured transport equations with applications to chronic myelogenous leukaemia, ^[9]—a diffusion model including spatial competition between cells–, reviews ^[4,10,11] and the references therein.

Despite extensive studies on the dynamics of HSCs and diseases of the hematopoietic system, none of the above-mentioned models takes into account the interactions between HSCs and the hematopoietic niche which is a specific microenvironment ensuring the maintenance and regulation of HCSs locally. It is worth noting that the interactions between HSCs and their niche, of which mesenchymal stem cells (MSCs) are the most important component, play a crucial role in the formation of mature blood cells. Also, alterations in the bidirectional exchanges between HSCs and MSCs may give rise among HSCs to blood cancer stem cells, i.e., leukemic stem cells, LSCs.

Note that healthy HSCs need the close presence of stromal cells for their development but stromal cells can proliferate without HSCs. Similar to HSCs, cancer cells in the early stages need stromal cells for their development whereas in the later stages they can proliferate without support cells. In other words, the more malignant a cell is, the more independent of stromal cells it is. Here, cancer cells in earlier stages are cells with few mutation events and cancer cells in later stages stand for the ones with more mutation events. We refer to, for example, ^[12,13,14] for reviews of the interaction between HSCs and stromal cells, ^[15] for acute myeloid leukemic cells.

In the present paper, we introduce a mathematical model for the interaction between HSCs and stromal cells with the aim to better understand the nature of the dialogue between them as well as their dynamics. We also perform a mathematical analysis for the long-time behaviour of the hepatopoietic and stromal cells in the framework of adaptive dynamics. Our mathematical model and some notions in the framework of adaptive dynamics, in particular, evolutionary stable distributions (ESDs) are given in the remaining part of this section.

1.1.   A mathematical model

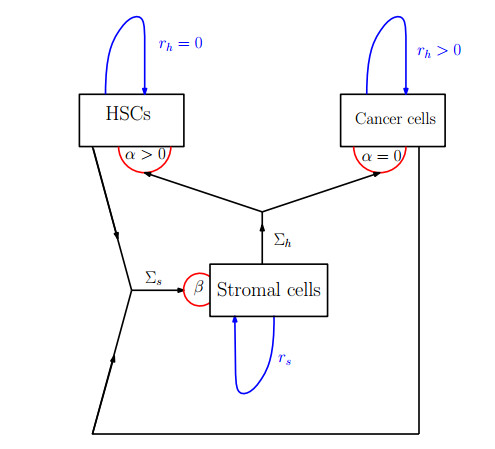
Let $n_h(t, x)$ be the population density of hematopoietic stem cells (HSCs) and cancer cells at time $t$ with phenotype $x$, continuous structure variable assumed to characterise the population heterogeneity in a way relevant to the question at stake. Here $x$ will represent a malignancy potential of HSCs, from its minimal (representing a totally healthy state) to its maximal value (representing maximum malignancy), considered independently of their stromal support. From a biological point of view, $x$ might represent a pathological combination of both high plasticity (i.e., ability to change phenotype; stem cells are plastic, but physiologically, they not proliferate much) and fecundity (i.e., ability to proliferate; differentiated cells are able to proliferate, but physiologically, they show little plasticity). Let $n_s(t, y)$ be their corresponding stromal cell population density - that we will sometimes call support cells - at time $t$ and with phenotype $y$ (here the continuous phenotype variable $y$ will denote the supporting capacity of MSCs to HSCs). Assume for simplicity that $x$ and $y$ are real variables with $x \in (a, b), y \in (c, d)$, where $0 < a < b$ and $0 < c < d$. Totally healthy HSCs will thus have a phenotype $x$ close to $a$, while agammaessive leukemic HSCs (i.e., LSCs) will have a phenotype $x$ close to $b$. We consider a mathematical model of the form

This system is completed with initial data

Here our assumptions and notations are

● $\rho_h(t): = \int_a^b n_h(t, x)\, dx, \rho_s(t): = \int_c^d n_s(t, y)\, dy$ are the total populations of HSCs and their support cells, respectively.

● The terms $\Sigma_h(t): = \int_a^b \psi_h (x) n_h(t, x)\, dx, \Sigma_s(t): = \int_c^d \psi_s (y) n_s(t, y)\, dy$ denote an assumed chemical signal ($\Sigma_h$) from the hematopoietic immature stem cells (HSCs) to their supporting stroma (MSCs), i.e., ``call for support'' and conversely, a trophic message ($\Sigma_s$) from MSCs to HSCs. The cytokine stem cell factor (SCF) and the C-X-C motif chemokine ligand 12 (CXCL12) are typical examples for such supporting messages ^[13,14]. The nonnegative functions $\psi_h, \psi_s$ defined on $(a, b)$ and $(c, d)$ measure the contribution of each phenotype in the interactive messages. Assume that $\psi'_s \ge 0$ (the higher the support phenotype in MSCs, the stronger the trophic message to HSCs); in the same way, unless otherwise specified, we shall assume that $\psi'_h \ge 0$.

● The term $r_h \ge 0$ represents the intrinsic (i.e., without contribution from trophic messages from MSCs, nor limitation by the non local logistic terms $\rho_h$ and $\rho_s$, that represent competition for space and nutrients within the whole population of cells) proliferation rate of HSCs. Assume that $r_h$ is non-decreasing (the more malignant, the more proliferative), $r_h(a) = 0$ and $r_h(b) > 0$.

● The term $\alpha \ge 0$, satisfying $\alpha' \le 0$ and $\alpha(b) = 0$, is the sensitivity of HSCs to the trophic messages from support cells

● For the term $r_s \ge 0$, we assume that $r'_s(y) \le 0$ (there is a cost in proliferation for support cells to increase their support capacity). The term $\beta(y) \ge 0$ with $\beta'(y) \ge 0$ represents the sensitivity of the stromal cells MSCs to the (call for support) message coming from HSCs.

System (1.1) falls within the broader class of models for interacting populations where competitive, prey-predator and cooperative types are typical examples of such interaction; see, for example, [27,Chapter 3]. Apart from the cases mentioned in [27,Chapter 3], in the context of adaptive dynamics, the populations are often structured by phenotypical traits to take into account the heterogeneity in the population (e.g. ^[16]). We refer to ^[17] a related competitive system with healthy and cancer cells structured by a phenotypic variable related with their resistance to chemotherapy, to ^[18] an integro-differential Lotka-Volterra system for the interaction of $N$ populations $(N \ge 2)$. In our model, besides the competition terms between cells, we introduce new terms $\Sigma_h, \Sigma_s, \alpha, \beta$ to represent the interacting messages between HSCs and stromal cells. The presence of these terms makes the problem difficult to study since the nature of (1.1) is unknown and may vary in time. It could be competitive, co-operative or other types depending on the sign of the terms $-\rho_s(t)+\alpha(x)\Sigma_s(t)$ and $-\rho_h(t)+\beta(y)\Sigma_h(t)$. Note that if $\Sigma_h = \Sigma_s = 0$, our model reduces to the cases studied in ^[16,17]. Also when $\psi_h = \psi_s = 1$, our problem becomes a particular case of ^[18].

Let us briefly sum up the meaning of our assumptions. From a biological point of view, the healthy HSCs cannot proliferate without support cells while cancer cells persist even without support cells. In our model $n_h(t, a)$ corresponds to healthy HSCs and $n_h(t, b)$ are leukemic cells since the intrinsic proliferation rate $r_h$ satisfies $r_h(a) = 0, r_h(b) > 0$. The monotonicity of $r_h$ implies that the higher $x$ is, the more agammaessive is a HSC (in fact, a LSC, since it is then cancerous). Also the monotonicity of $\alpha$ (this function stands for the sensitivity of HSCs to the trophic messages coming from MSCs) indicates that the more agammaessive $x$ is, the less sensitivity has a HSC to the trophic message sent by MSCs (i.e., the more independent it is from the surrounding stroma). Moreover, the condition $\alpha(b) = 0$ shows that $n(t, b)$ (i.e., cancer cells in the latter stages) proliferate independently of the supporting stroma. Furthermore, the monotonicity of $r_s, \beta$ shows that the more supporting stromal capacity MSCs have, the less they proliferate and the more sensitive to messages from HSCs they are.

As a simple case, the parameters $r_h, \alpha, r_h, r_h, \psi_h, \psi_s$ can be chosen as linear or quadratic functions. For example, $r_h$, $\alpha$ are given by $r_h = r_h^*(x-a)$ or $r_h = r_h^*(x-a)^2$, $\alpha(x) = \alpha^*(b-x)$ with positive constants $r_h^*, \alpha^*$, $\psi_h(x) = x$, $\psi_s(y) = y$.

A more general model which includes the possibility of mutations has the form:

Here the diffusion terms represent mutation with rates $\mu_h, \mu_s$ and $c_{11}, c_{12}, c_{22}, c_{22}$ measure the strength of competition between cells. Problem (1.3) reduces to (1.1) by setting $\mu_h = \mu_s = 0$ and $c_{11}(x) = c_{12}(x) = 1, c_{21}(y) = c_{22}(y) = 1$. Thus (1.1) can be considered as a good approximation of (1.3) in the regime $\mu_h, \mu_s < < 1$ which is realistic since mutations occur rarely in physiology (to fix ideas, let us say between once every $10^6$ and $10^9$ cell divisions; of course, in evolved cancers, such low rates may increase).

1.2.   Some notions in the theory of adaptive dynamics

Hereafter, we will use the notation $\int$ to denote the integrals over $[a, b]$ and $[c, d]$, as long as there is no risk of confusion. Let $\hat n_h, \hat n_s$ be measures defined on $[a, b], [c, d]$, respectively. We set

Definition 1.1. The pair $(\hat n_h, \hat n_s)$ is a steady state of (1.1) if

Furthermore, $\hat n_h$ (resp. $\hat n_s$) is said

(ⅰ) to be monomorphic if ${\rm{supp}}\ \hat n_h$ (resp. ${\rm{supp}}\ \hat n_s$) is a singleton,

(ⅱ) to be dimorphic if ${\rm{supp}}\ \hat n_h$ (resp. ${\rm{supp}}\ \hat n_s$) is a set of two points.

Definition 1.2. We say that $(\hat n_h, \hat n_s)$ is an evolutionary stable distribution (ESD) of problem (1.1) if it is a steady state and the condition below is fulfilled

Remark 1.3. It follows from Definition 1.2 that any $x \in I$ (resp. $y \in J$) is a maximum point of $G_h$ (resp. $G_s$).

As our equation arises from biological cell population dynamics, we only consider non-negative steady states and ESDs in this paper.

In the context of adaptive dynamics, when (1.5) holds, we say that the phenotypes $x \in I, y \in J$ are living in the stationary environment given by $(\hat \rho_h, \hat \rho_s, \hat \Sigma_h, \hat \Sigma_s)$. The functions $G_h, G_s$ are fitness functions associated with this environment. The quantities $G_h(x), G_s(y)$ are growth rates of phenotypes $x, y$ and they tell us whether $(x, y)$ can invade this environment: If $G_h(x) > 0, G_s(y) > 0$, $(x, y)$ can grow and the system will reach a new equilibrium. We refer to ^[20,25] for more details about the framework of adaptive dynamics.

1.3.   Summary of main results and organization of the remaining part of the paper

We first present mathematical results to verify biological properties concerning the independence of stromal cells on HSCs and its vital support to HSCs in Section 2.1. A uniform bound in time and a well-posedness result are given in Section 2.2.

As generally only a finite number of traits is represented in the equilibrium, we study, for simplicity, in Section 3, equilibria with only one trait, i.e., those of the form of single Dirac mass. The linear stability result of single Dirac mass steady states (Theorem 3.2) exhibits the mechanisms by which another trait can or cannot invade the stationary state produced by a given trait.

ESDs—equilibria corresponding to optimal states of the evolution—are studied in Section 4. We study the impact of the parameters on the form of ESDs. Two cases are investigated: monomorphic situation (i.e., only one trait is represented in ESDs) and dimorphic one (two traits are represented in ESDs). More precisely, we provide sufficient conditions to guarantee that all ESDs are monomorphic or dimorphic (Proposition 4.1). Also in Theorem 4.2 we obtain a result on the uniqueness of ESDs and we show that this unique ESD is monomorphic. Another result on the uniqueness of ESD (Theorem 4.5) hold for rather than general functions $r_h, r_s$ and under some homogeneity assumptions of stromal cells. This theorem is concerned with more general ESDs which are not necessary to be monomorphic or dimorphic.

Section 5 is concerned with dominant traits which are the best adapted ones to the environment and favored at high population densities. These traits are represented by maximum points of the population densities and change in time because of the variation of environment. We study the movement of these traits in a long time scale, hence make the change of variable, $\tau = \varepsilon t$, with small $\varepsilon > 0$. We represent the dynamics of dominant traits (Theorems 5.1 and 5.2) in the regime as $\varepsilon \to 0$ (asymptotic analysis). Also we obtain the equation for dominant traits Eq (5.11).

In Section 6, we provide numerical simulations to illustrate our results and finally, some discussions are given in Section 7.

2.   Preliminary results

2.1.   Hematopoietic stem cells or stromal cells without mutual interaction

In the absence of stromal cells, the system (1.1) reduces to the equation

Similarly, the behaviour of stromal cells without HSCs is given by

In view of [28,Theorem 2.1,Page 29], we have the following selection principle:

Lemma 2.1. Suppose that $r_h$ is bounded and strictly increasing. Suppose furthermore that $r_s$ is bounded and strictly decreasing. Assume that $n_{h0}, n_{s0} \in L^1$ are positive on $[a, b]$ and $[c, d]$, respectively.

(ⅰ) For (2.1), we have $n_h(t, x) \rightarrow r_h(b) \delta_{\{x = b\}}$ weakly in the sense of measures as $t \to \infty$.

(ⅱ) For (2.2), we have $n_h(t, y) \rightarrow r_s(c) \delta_{\{y = c\}}$ weakly in the sense of measures as $t \to \infty$.

These results confirm biological properties mentioned in Section 1 about the bi-directional interaction between HSCs and stromal cells. More precisely, in the absence of stromal cells for HSCs or of HSCs for stromal cells, the phenotypes of $n_h$ and $n_s$, respectively, behave as monomorphic. Moreover, Lemma 2.1(ⅰ) implies that healthy hematopoietic cells eventually go extinct while cancer cells (with the phenotype $y = b$) are selected and persist. Furthermore, stromal cells persist without HSCs and stromal cells with the lowest capacity of support will be selected (cf. Lemma 2.1(ⅱ)).

2.2.   A well-posedness result

For a function $f$ defined on an interval $I$, we set

In the results below, we only need the boundedness of $r_h, r_s, \alpha, \beta, \psi_h, \psi_s$. We do not need the monotonicity assumption of these functions.

Proposition 2.2. Assume that $r_h, r_s, \alpha, \beta, \psi_h, \psi_s$ are non-negative and bounded. Suppose furthermore that

Set

Then the solution of (1.1)- (1.2) is non-negative and satisfies

Proof. First note that the solution of (1.1) can be written in the form

where

Thus $n_h(t, x) \ge 0, n_s(t, y) \ge 0$ since $n_{h0}(x) \ge 0, n_{s0}(y) \ge 0$. This yields the first inequality of (2.4).

Integrating the two equations in (1.1) yields

Summing up these two identities and using the non-negativity of $n_h, n_s$, we obtain

Hence the second inequality of (2.4) follows.

Proposition (2.2) and a standard argument imply the following result.

Theorem 2.3. Let $(n_{h0}, n_{s0}) \in L^1(a, b) \times L^1(c, d)$ be non-negative. Then (1.1) possesses a unique solution $(n_h, n_s) \in C^1([0, \infty); L^1(a, b) \times L^1(c, d))$.

3.   Steady states and linear stability

Hereafter, for simplicity, we assume that $\psi_h(x) = x, \psi_s(y) = y$. Then Problem (1.1) becomes

3.1.   Single Dirac mass steady states

Let $\hat x \in [a, b], \hat y \in [c, d]$. Consider a particular case where hematopoietic and support cells evolve as single Dirac masses concentrated at $\hat x, \hat y$. In other words, we focus on the behaviour of the size of the populations. In this case, $n_h, n_s$ have the form

where $\rho_h(t), \rho_s(t)$ satisfy

We can obtain an explicit form of single Dirac mass steady states.

Lemma 3.1. Let $\hat x \in [a, b], \hat y \in [c, d]$ and assume that $1-(1-\alpha(\hat x) \hat y)(1-\beta(\hat y)\hat x)\! \neq\! 0$. Set

Then $(\hat n_h = \hat \rho_h \delta_{\{x = \hat x\}}, \hat n_s = \hat \rho_s \delta_{\{y = \hat y\}})$ is a steady state of problem (3.1). If the three conditions below hold

then $\hat \rho_h > 0, \hat \rho_s > 0$ and $(\hat \rho_h, \hat \rho_s)$ is a linearly stable steady state of (3.2).

Proof. Single Dirac mass steady state solution yields

An elementary calculation shows that $(\hat \rho_h, \hat \rho_s)$ is a steady state of (3.2) and the corresponding Jacobian matrix is given by

In view of (3.4), ${\rm{tr}}(\mathcal J) < 0, \det(\mathcal J) > 0$ so that the two eigenvalues of $\mathcal J$ are negative. Thus the linear stability of $(\hat \rho_h, \hat \rho_s)$ follows.

3.2.   Linear stability of single Dirac mass steady states

The results below are concerned with the linear stability of single Dirac mass steady states among perturbations of particular forms.

Theorem 3.2 (Stability of monomorphic steady states). Let $(\hat n_h = \hat \rho_h \delta_{\{x = \hat x\}}, \hat n_s = \hat \rho_s \delta_{\{y = \hat y\}})$ be a steady state of (3.1) as in Lemma 3.1. Assume that (3.4) holds. Let $x^*, y^*$ satisfy $x^* \neq \hat x, y^* \neq \hat y$ and

Then $(\hat n_h, \hat n_s)$ is linearly stable among perturbations starting by

Proof. We linearize the system at $(\hat n_h, \hat n_s)$. For $g_h(t, x): = n_h(t, x)-\hat n_h(x), g_s(t, y): = n_s(t, y)-\hat n_s(y)$ we obtain

Note that $g_h, g_s$ have the form

Therefore, we obtain

The corresponding matrix is given by

The eigenvalues of the above matrix are

and the two eigenvalues of the matrix $\mathcal J$ in (3.6). All are negative due to (3.7) and Lemma 3.1. Thus the stability of $(\hat n_h, \hat n_s)$ follows.

Interpretations of Theorem 3.2: With the notation (1.4), in view of (3.5), we have $G_h(\hat x) = 0, G_s(\hat y) = 0$. Also the conditions $G_h(x^*) < 0, G_s(y^*) < 0$ show that the phenotypes $x^*, y^*$ cannot invade the stable equilibrium $(\hat n_h, \hat n_s)$. As a consequence, no new equilibrium can be reached but a mutant invading the resident population $(\hat x, \hat y)$.

4.   Evolutionary stable distributions (ESDs)

4.1.   Sufficient conditions for monomophic and dimorphic ESDs

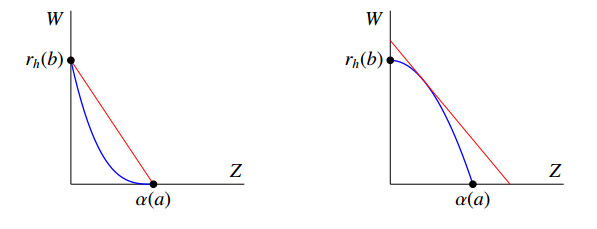
Recall that from the defintion 1.2, an ESD $(\hat n_h, \hat n_s)$ is characterised by the conditions (1.5)– (1.6). Graphically, we plot the curve $x\in [a, b] \mapsto (Z = \alpha(x), W = r_h(x))$ by the blue curve and the red straight line $Z \hat \Sigma_s + W = \hat \rho_h + \hat \rho_s$; see Figure 2. Then the conditions (1.5)– (1.6) for $\hat n_h$ mean that the blue curve must be below the red line and that the pair $(\alpha(x), r_h(x))$ for all $x \in I: = {\rm{supp}}\ \hat n_h$ are the coordinates of the intersection points between the blue curve and the red line. Similarly, we have the same illustration for $\hat n_s$.

If $\alpha$ (resp. $r_h$) is strictly monotone and if $r_h(\alpha^{-1})$ (resp. $\alpha(r_h^{-1})$) is concave on $[0, \alpha(a)]$ (resp. $[0, r_h(b)]$). Then there is at most one intersection point satisfying the conditions (1.5)– (1.6) for $\hat n_h$. Thus, the strict monotonicity of $\alpha$ implies that $I$ is a singleton, hence $\hat n_h$ is monomorphic. In the case where $r_h(\alpha^{-1}(z))$ (resp. $\alpha(r_h^{-1})$) is convex, $I$ contains at most two points, thus $\hat n_h$ is at most dimorphic.

Note that by Remark 1.3, we can also check if an ESD is monomorphic or dimorphic by studying the set of maximum points of the corresponding fitness functions. We state the above results in the following proposition.

Proposition 4.1 (Conditions for monomorphism or dimorphism). Assume that $(\hat n_h, \hat n_s)$ is an ESD arbitrarily that does not vanish. Then $\hat n_h$ is monomorphic if one of the following hypotheses is fulfilled:

(ⅰ) either $\alpha$ is strictly monotone and $r_h(\alpha^{-1})$ is concave on $[0,\alpha (a)]$,

(ⅱ) or $r_h$ is strictly monotone and $\alpha(r_h^{-1})$) is concave on $[0, r_h(b)]$,

(ⅲ) or $r_h, \alpha$ are strictly concave.

Also $\hat n_h$ is at most dimorphic if one of the following hypotheses is fulfilled:

(ⅰ) either $\alpha$ is strictly monotone and $r_h(\alpha^{-1})$ is convex on $[0, \alpha(a)]$,

(ⅱ) or $r_h$ is strictly monotone and $\alpha(r_h^{-1})$) is convex on $[0, r_h(b)]$,

(ⅲ) or $r_h, \alpha$ are strictly convex.

Furthermore, the same conclusions as above hold for $\hat n_s$ provided that similar assumptions on $r_s, \beta$ are supposed.

The next result is concerned with the existence and uniqueness of ESDs. We also show that the unique ESD is monomorphic and that the concentration points are endpoints of the intervals $(a, b), (c, d)$. For simplicity, set $(a, b): = (1, 2), (c, d): = (3, 4)$. Here we employ the two distinct sets $(1, 2)$ and $(3, 4)$ to insist on that fact that the two phenotypes of HSCs and of stromal cells are not the same. We will suppose two of the following assumptions:

${\bf (H_1)} \ r_h'(x)+ 3 \alpha'(x) \bar r_s < 0$ for all $x \in (1, 2)$ and $\beta(y)\ge 1$ for all $y \in (3, 4)$,

${\bf (H_2)} \ r_h'(x)+ 4 \alpha'(x) \bar r_s > 0$ for all $x \in (1, 2)$ and $\beta(y) \le 1/2$ for all $y \in (3, 4)$,

${\bf (H_3)} \ \beta = \beta^* > 0$ is constant and $r_s$ is strictly decreasing,

${\bf (H_4)} \ \beta$ is strictly increasing and $r_s = r_s^* > 0$ is constant.

Theorem 4.2 (Existence and uniqueness of ESDs). Set $(a, b): = (1, 2), (c, d): = (3, 4)$. Suppose that $r_h, \alpha \in C([1, 2]) \cap C^1((1, 2)), r_s, \beta \in C([3, 4]) \cap C^1((3, 4))$. Suppose furthermore that the pair $(\hat n_h, \hat n_s)$ below is non-negative and that the assumptions (depending on situations) mentioned below hold. Then there exists a unique (non-negative) ESD and it is monomorphic or vanishes.

(ⅰ) Under the assumptions $\bf (H_1)$ and $\bf (H_3)$, the unique ESD is given by

(ⅱ) Under the assumptions $\bf (H_2)$ and $\bf (H_3)$, the unique ESD is given by

(ⅲ) Under the assumptions $\bf (H_1)$ and $\bf (H_4)$, the unique ESD is given by

(ⅳ) Under the assumptions $\bf (H_2)$ and $\bf (H_4)$, the unique ESD is given by

Proof. We only prove (ⅰ). The other cases can be proved in the same way. First note that under the assumptions $\bf (H_1)$ and $\bf (H_3)$, $\beta = \beta^* \ge 1$. We have $G_s(y) = r_s(y)-\hat \rho_h-\hat \rho_s + \beta^* \hat \Sigma_h$ is strictly decreasing (by $\bf (H_3)$) so that it attains its global maximum only at $y = 3$. This, in view of Remark 1.3, yields that ${\rm{supp}}\ \hat n_s = \{3\}$. As a consequence, $G_s(3) = 0$ so that

Therefore,

This together with the property that $\alpha' \le 0$ implies that

where we used the hypothesis $\bf (H_1)$ in the last inequality. Consequently, $G_h$ is strictly decreasing on ^[1,2] so that it has only one maximum point $x = 1$. Hence ${\rm{supp}}\ \hat n_h = \{1\}$. The expression of $(\hat n_h, \hat n_s)$ follows from (3.3) with $(\hat x, \hat y): = (1, 3)$.

Below, we compute all ESDs explicitly. We also see that the dimorphic situation may occurs. For simplicity, we only consider the dimorphic distribution for hematopoietic stem cells.

Proposition 4.3 (Explicit formulas of all ESDs). Set $(a, b): = (1, 2), (c, d): = (3, 4)$. Assume that $r_h$ is strictly convex and that $\alpha$ is convex. Suppose furthermore that $(\bf H_3)$ is satisfied (i.e., $\beta = \beta^*$ is a positive constant and $r_s$ is strictly decreasing). Then all ESDs are given by

(ⅰ) $(\hat n_h = \hat \rho_h \delta_{\{x = 1\}}, \hat n_s = \hat \rho_s \delta_{\{y = 3\}})$ with

provided that $\hat \rho_h \ge 0, \hat \rho_s \ge 0$ and

(ⅱ) $(\hat n_h = \hat \rho_h \delta_{\{x = 2\}}, \hat n_s = \hat \rho_s \delta_{\{y = 3\}})$ with

provided that $\hat \rho_h\ge 0, \hat \rho_s \ge 0$ and

(ⅲ) $(\hat n_h = \hat \rho_{h1} \delta_{\{x = 1\}}+\hat \rho_{h2} \delta_{\{x = 2\}}, \hat n_s = \hat \rho_s \delta_{\{y = 3\}})$ with

provided that $\hat \rho_{h1}\ge 0, \hat \rho_{h2}\ge 0, \hat \rho_s\ge 0$.

Remark 4.4. We can also prove similar results as in Proposition 4.3 when we suppose the hypothesis $\bf (H_4)$ instead of $\bf (H_3)$.

Proof. First note that $G_h(x)$ is strictly convex. Thus $G_h$ attains its global maximum only at endpoints of the interval ^[1,2]. Note also that $G_s(y) = r_s(y)-\hat \rho_h -\hat \rho_s +\beta^*\hat \Sigma_h$ is strictly decreasing so that ${y = 3}$ is its unique maximum point. The above observations and Remark 1.3 imply that ${\rm{supp}}\ \hat n_s = {3}$ and $\text{either } {\rm{supp}}\ \hat n_h = \{1\} \text{ or } {\rm{supp}}\ \hat n_h = \{2\} \text{ or } {\rm{supp}}\ \hat n_h = \{1, 2\}.$

(ⅰ) The case ${\rm{supp}}\ \hat n_h = \{1\}, {\rm{supp}}\ \hat n_s = \{3\}$. The expressions of $\hat \rho_h, \hat \rho_s$ follows from (3.3) with $\hat x = 1, \hat y = 3$. Because of the convexity of $G_h$ and the decreasing monotonicity of $G_s$, the condition (1.6) is equivalent to $G_h(1) \ge G_h(2)$ which implies (4.1). Similarly, Item (ⅱ) — the case ${\rm{supp}}\ \hat n_h = \{2\}, {\rm{supp}}\ \hat n_s = \{3\}$ — can be treated in the same way.

(ⅲ) The case ${\rm{supp}}\ \hat n_h = \{1, 2\}, {\rm{supp}}\ \hat n_s = \{3\}$. The pair $(\hat n_h, \hat n_s)$ have the form

Thus we have

The conditions in the definition 1.2 are equivalent to

that is

Solving this system yields the expressions of $\hat \rho_{h1}, \hat \rho_{h2}, \hat \rho_{s}$.

Let us consider two concrete examples below.

Example 1: Suppose that $r_h, \alpha, r_s, \beta$ are given by

According to Proposition 4.3, there are only two positive ESDs which are

● Monomorphic distribution:

● Dimorphic distribution:

Example 2: Suppose that $r_h, \alpha, r_s, \beta$ are given by

Then, there is only one positive ESD. This ESD is dimorphic and has the form

4.2.   Partial uniqueness of ESDs under homogeneity assumptions on stromal cells

We suppose that all stromal cells have some similar properties. More precisely, we consider the case where the contribution of each phenotype $y$ in the message from stromal cells to HSCs and the sensitivity of stromal cells to the message from HSCs are the same. Mathematically, assume that the weight function $\psi_s(y) = 1$, and that $\beta > 0$ is constant. Suppose furthermore that $\alpha(x) = b-x, \psi_h(x) = x$. Problem (1.1) becomes

Below we state a result about the partial uniqueness of ESDs.

Theorem 4.5 (Partial uniqueness results of ESDs). Assume that $(\hat n_h, \hat n_s)$ and $(\tilde n_h, \tilde n_s)$ are two (non-negative) ESDs of the system (4.2). Assume further that $\beta$ is a positive constant satisfying

Then

Moreover,

(ⅰ) If $r_s$ is strictly decreasing, then $\hat n_s = \tilde n_s$ either is monomorphic concentrated at $y = c$ or vanishes. Also we have

(ⅱ) In addition to (i), if $\hat n_s$ does not vanish, then

Proof. The definition of ESD and the non-negativity of $\hat n_h$ yield that

Similarly, it follows from the inequality

that

Summing up (4.9) and (4.10), we obtain

Similarly, we deduce from the inequality

that

This together with (4.11) yields

Equivalently,

Therefore, the hypothesis (4.3) yields that the equality in (4.13) (also in all above inequalities) holds. Thus each term in (4.13) vanishes so that (4.4) follows. The identities (4.5), (4.6) follow from the fact that

respectively.

(ⅰ) If $r_s$ is strictly decreasing on $[c, d]$, the fitness function $G_s$ attains its global maximum at $y = c$. Thus $\hat n_s$ and $\hat n_s$ either vanish or are the Dirac mass concentrated at $y = c$. As a consequence we have $\hat n_s = \tilde n_s = S \delta_{\{y = c\}}$ with $S \ge 0$. Using the formula for $\hat n_s$, (4.5) and (4.6), we obtain (4.7)

(ⅱ) The case $\hat n_s = \tilde n_s = S \delta_{\{y = c\}}$ with $S > 0$. Identity (4.8) follows from (4.6).

In the case $\alpha \Sigma_h = \beta \Sigma_s = 0$, an entropy functional has been found by Jabin and Raoul ^[16] and used to prove the convergence of the solution to the unique ESD. In the general form of the system (1.1), we do not expect to find an entropy functional due to the complexity of the terms $\alpha \Sigma_h, \beta \Sigma_s$. However, we obtain an entropy functional similar to that of Jabin and Raoul for the system (4.2) corresponding to particular choices of $\alpha \Sigma_h$ and $\beta \Sigma_s$. We obtain below a partial information about the dynamics of the solution of (4.2) as $t \to \infty$: the entropy functional decreases monotonically on orbits. The question of the convergence of the solution to the unique ESD remains open but this functional could be an essential ingredient to solve this issue.

Proposition 4.6 (Entropy functional). Let $(\hat n_h, \hat n_s)$ be an (non-negative) ESD of problem (4.2). Set

Then E is an entropy functional for (4.2), i.e., $\dfrac{d}{dt}E(t) \le 0$ provide that $\beta$ is a positive constant satisfying

Proof. Set

We have

In the above inequality, we have used the definition of ESDs and the non-negativity of $n_h$ (cf. Proposition 2.2). Similarly, for $E_2: = \int n_s - \int \hat n_s \ln (n_s),$ we have

Therefore, as $E = \beta E_1 +E_2$, we have

where the last inequality follows from the negativity of the discriminant of this polynomial:

5.   Dynamics of the fittest traits: an asymptotic point of view

We are interested in the dynamics of HSCs and stromal cells with initial data close to a monomorphic state and, in particular, in tracking the movements of concentration point towards an ESD. We follows the analysis in ^[23] and perform the time change variable $\tau = t \varepsilon$ to accelerate time and observe the dynamics. The parameter $\varepsilon$ is also used to measure how close is the distribution from the Dirac distribution.

The change of variable $t \mapsto \tau$ converts the system (3.1) to

This system is completed with the initial data

Rather than working on $n_h^ \varepsilon, n_s^ \varepsilon$ directly, we define as usual ^[19,21,23] the functions $u^ \varepsilon, v^ \varepsilon$ given by

The functions $u^ \varepsilon, v^ \varepsilon$ satisfy

Our purpose is to study the behaviour of $u^ \varepsilon, v^ \varepsilon$ as $\varepsilon \to 0$ (at least with subsequences). In order to guarantee the existence of a global solution, suppose that (2.3) is fulfilled. Thus, under the assumption that $\rho_{h0}^ \varepsilon+\rho_{s0}^ \varepsilon$ is uniformly bounded, Proposition 2.2 yields that there exists $(\hat n_h, \hat n_s)$ such that as $\varepsilon \to 0$ (after extracting subsequences),

Theorem 5.1. Assume that $r_h, \alpha \in C^1([a, b]), r_s, \beta \in C^1([c, d])$ and that

Then

(ⅰ) The function $u^ \varepsilon$ (resp. $v^ \varepsilon$) is uniformly Lipschitz continuous on $[0, T] \times [a, b]$ (resp. $[0, T] \times [c, d]$) for all $T > 0$.

(ⅱ) As $\varepsilon \to 0$ (after extractions of subsequences), the functions $u^ \varepsilon$ and $v^ \varepsilon$ converge locally uniformly to Lipschitz continuous functions $u$ and $v$. Moreover, $u, v$ satisfy

Furthermore we have for a.e. $\tau$,

Proof. (ⅰ) First note that by Proposition 2.2, there is a constant $K_1 > 0$ such that

Differentiating the equation for $u^ \varepsilon$ with respect to $x$ yields

Thus, using (5.6), we obtain $|\partial_\tau u_x^ \varepsilon(\tau, x)| \le |\overline{r'}_h| +\overline{|\alpha'|} d K_1$ so that

On the other hand, in view of (5.1), we have

Hence $u^ \varepsilon$ is uniformly Lipschitz continuous on $[0, T] \times [a, b]$. Similarly, the same property holds for $v^ \varepsilon$.

(ⅱ) Using the point (ⅰ) and the Arzelà–Ascoli Theorem, we may extract subsequences $(u^ \varepsilon, v^ \varepsilon)$ which converge as indicated in the statement. The equations for $u$ and $v$ are obtained by passing to the limit in (5.1). Moreover, $u, v$ cannot take positive values. Otherwise $(\rho^ \varepsilon_h, \rho^ \varepsilon_s)$ blows up in the limit as $\varepsilon$ vanishes and this is in contradiction with (5.6).

5.1.   Monomorphic states

We provide sufficient conditions so that $(\hat n_h, \hat n_s)$ defined in (5.2), (5.3) is a monomorphic state.

Theorem 5.2. Let all hypotheses as in Theorem 5.1 hold. Suppose furthermore that

Then, in the distributional sense

Thus for all $\tau$, the functions $u(\tau, \cdot), v(\tau, \cdot)$ are concave so that they have a unique maximum point. As a consequence, $\hat n_h, \hat n_s$ have the form

Moreover,

Proof. Differentiating twice the equation of $u^ \varepsilon$, we obtain

Thus $u_{xx}^ \varepsilon(\tau, x) \le u_{xx}^ \varepsilon(\tau = 0, x) \le -K^*$. Therefore $u_{xx} \le -K^*$. Similarly, $v_{yy} \le -K^*$. Hence the theorem follows.

5.2.   Equations for concentration points

In this section we derive the equations for the concentration point $\hat x(\tau), \hat y(\tau)$. Our equations are valid until the time $T^*$ where $\hat \rho_h(\tau) > 0, \hat \rho_s(\tau) > 0$ and that $\hat x(\tau), \hat y(\tau)$ do not touch the boundary and that $\dot{\hat x}, \dot{\hat y}$ are smooth enough (see Remark 5.3 below for the regularity of $\hat x, \hat y$). For all $\tau \in (0, T^*)$ we have $\hat x(\tau) \in (a, b)$ is the maximum point of $u(\tau, \cdot)$ on $[a, b]$. It follows that $u_x(\tau, \hat x(\tau)) = 0$ so that

This implies

Similarly, we have

The equations (5.9) and (5.10) describe the dynamics of $\hat x(\tau), \hat y(\tau)$. We also can obtain a more explicit form of (5.9) and (5.10) by representing $\hat \rho_h, \hat \rho_s$ in terms of $\hat x, \hat y$. To that purpose, we first notice that $u (\tau, \hat x(\tau)) = 0$ for $\tau \in [0, T^*)$ so that

Similarly,

Therefore, under the assumption that $1-(1-\alpha(\hat x(\tau)) \hat y(\tau))(1-\beta(\hat y(\tau))\hat x(\tau)) \neq 0$, we have

Substituting these expressions of $\hat \rho_h(\tau), \hat \rho_s(\tau)$ in (5.9) and (5.10) we obtain

Canonical equations

Remark 5.3. In view of the two first equations in (5.5), if $u_0, v_0, r_h, \alpha, r_s, \beta$ are smooth enough (e.g., $C^2$ functions), then $u_{xx}$ is continuous. Thus the right-hand-sides of (5.11) are continuous as functions of $\hat x, \hat y, \tau$. Therefore, the standard ordinary differential equation theory implies that the solution of (5.11) $(\hat x, \hat y)$ is a $C^1$ function of time. We refer to ^[26], for a results about the regularity of $u, v$ in the case of Hamilton–Jacobi equations.

6.   Numerical illustrations

Let us illustrate numerically the convergence of the solution of (3.1) towards an ESD as well as the movement of concentration points. We employ the two distinct sets $(a, b): = (1, 2)$ and $(c, d): = (3, 4)$ to insist on that fact that the two phenotypes of HSCs and of stromal cells are not the same. The space and time steps are given by

Define for $0 \le k \le 200$ and $p = 0, 1, 2, ...$,

Our numerical simulations are performed in MATLAB and based on the implicit-explicit scheme below:

Here $(\rho_h)^p, (\rho_s)^p, (\Sigma_h)^p, (\Sigma_s)^p$ are the approximation of $\rho_h, \rho_s, \Sigma_h, \Sigma_s$ at the time $p$. We use the initial conditions

for Figures 3, 4, 5 and 6. For the last figures, we choose

The parameters are chosen as in the table below.

Remark 6.1. The parameters in the three cases satisfy the assumptions of Theorem 4.2(ⅲ), (ⅱ) and Proposition 4.3(ⅲ), respectively. Also they are chosen small enough such that the condition (2.3) for the global existence of the solution holds. In the first case (Figures 3 and 4), we use the homogeneous proliferation rate and the inhomogeneous sensitivity of stromal cells. Conversely, in the last two cases, the parameters correspond to the inhomogeous proliferation rate and the homogeneous sensitivity of stromal cells. Note also that in the monomorphic situatations, the corresponding fitness functions are monotone while in the dimorphic situation, the fitness function (for HSCs) is strictly convex.

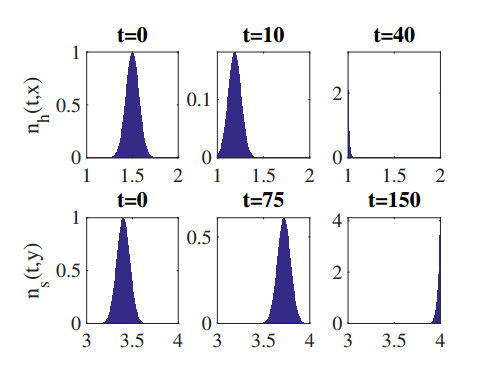
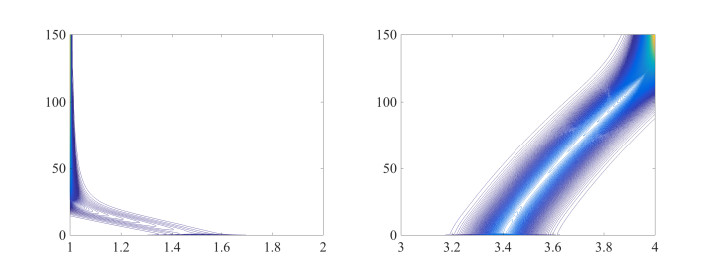
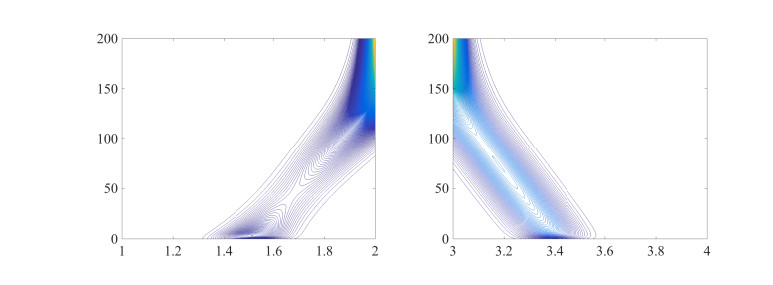
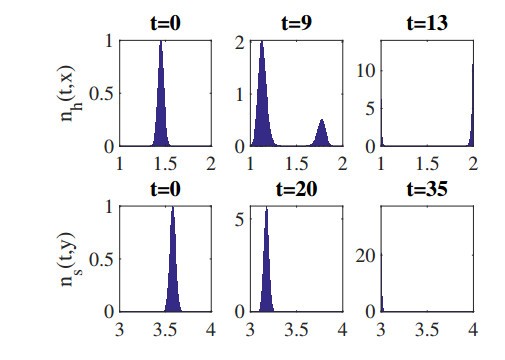
Figures 3 and 4 display the behavior of $n_h$ and $n_s$ in the time scale $t: = 10^{-2}t$. In Figure 3, the population densities for HSCs and their support cells $n_h, n_s$ are monomorphic and behave as Dirac masses. The concentration point of $n_h$ moves towards $x = 1$ and the one of $n_s$ moves towards the point $y = 4$. In this situation, the phenotype $(x, y) = (1, 4)$ is selected. This represents a good scenario: healthy HSCs and stromal cells with the best support capacity are selected. The evolution of the corresponding dominant phenotypes are given in Figure 4. Figures 5 and 6 below show another monomorphic situation where stromal cells with lowest support capacity are selected. Healthy HSCs cannot survive and cancer cells are selected.

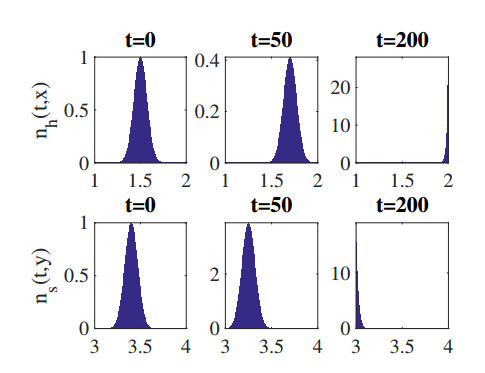
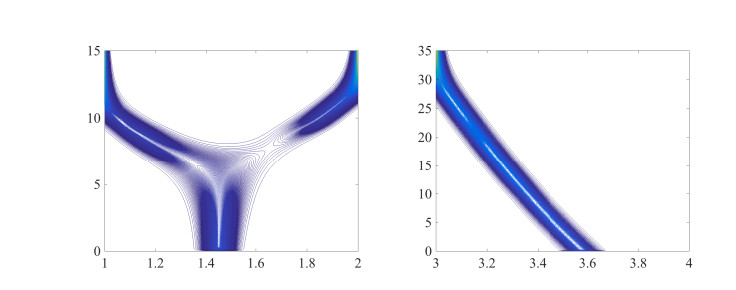
Figures 7 and 8 represent the dimorphic situation for HSCs in the time scale $t: = 10^{-2}t$. This situation corresponds to Proposition 4.3(ⅲ). Starting from an initial distribution with one peak at $x = 1.45$, a branching process appears. There are two dominant phenotypes of HSCs. The first one moves to the left (only healthy cells selected about the time until $t = 10$) and the second one move towards $x = 2$ (and selected in a little bit later). In other words, cancerous cells invade the population of HSCs, however without occupying it in totality: healthy HSCs and cancerous cells (LSCs) coexist.

7.   Conclusion and perspectives

In this paper, we have introduced a mathematical model for the interaction between hematopoietic stem cells and their support cells. Leukemic stem cells are also taken into account in the model and the phenotype $x$, characterising the population heterogeneity in a way relevant to the question at stake, represents for both the intrinsic proliferation rate of HSCs and the malignancy potential of cancer cells (i.e., as mentioned in the introduction, a proposed pathological combination of both plasticity and fecundity, likely related to how many mutations are involved in cancer cells). Note also that the monotonicity assumption on $r_h$ means that we assumed that the malignant cells proliferate more than healthy HSCs.

We performed a study concerning the adaptive dynamics of HSCs and support cells, in particular, investigating Dirac masses (or sums of Dirac masses) that arose in the solutions of particular cases of the system. Linear stability results for single Dirac mass steady states, suggesting that another phenotype will invade the stationary environment corresponding to the steady state if the corresponding fitness function computed at that phenotype is positive. We also provided sufficient conditions to ensure that ESDs are dimorphic or monomorphic. These conditions are related to the convexity, concavity, monotonicity assumptions of the function parameters. In many cases, we could show the existence and uniqueness of ESDs as well as compute explicitly all ESDs in the case of non-uniqueness.

Applying an asymptotic approach, we showed that without extinction, the population density of HSCs and of their support cells behave as Dirac masses:

Here the points of concentration $\hat x(\tau), \hat y(\tau)$ represent well adapted phenotypes at the time $\tau$. Also these points are maximum points of the phase functions $u(\cdot, \tau)$ and $v(\cdot, \tau)$. The system (5.11) gives us the dynamics of $\hat x(\tau), \hat y(\tau)$, in other words, the adaptive process for HSCs and its support cells during their evolution. Our numerical illustrations provide the case of the existence of HSCs, or LCSs (only). Also, we illustrate the case of invasion of LCSs as well as the coexistence of HSCs and LSCs. This latter situation does not seem to be usually seen in the clinic of acute leukemias, which may be due to the fact that in reality, the competition for space and nutrients turns to the advantage of leukemic cells (The biological fact is that stromal cells change to adapt to healthy cells or malignant cells. Thus LSCs and HSCs have different hematopoietic niches so that the competitive strength of HSCs and LSCs for space and nutrients will be different). In our model, the advantage of leukemic cells in competition could be represented by a diversified non local logistic term in the equation for HSCs such as $- k_1\int\!(b-x)n_h(t, x)dx - k_2\int\!(x-a)n_h(t, x)dx$, with $k_2 > k_1$, instead of the neutral term $- \rho_h$, thus attributing more importance in the competition to cells close to the malignant phenotype $x = b$. Or else, could it be that actual biological coexistence between HSCs and LSCs could come from the fact that leukemic cells may have been reduced to a state of dormancy? Note that this perspective of dormancy has recently been investigated in a rather different modelling setting (no adaptive dynamics, no interaction with stromal cells) in ^[22].

Our analytic results, except in Section 4.2, hold for more general choices of the weight functions $\psi_h, \psi_s$. However, we present our results here mainly for the case $\psi_h = x, \psi_s = y$ to clarify the ideas and avoid complex computations. The mathematical question related to the convergence of the solution of (1.1) to its limit (which is an ESD) remains open. The BV-method (see, for example, ^[24,28]) seems not amenable be applied due to the complexity of function parameters. However, we could find an entropy functional for a simplified system (4.2). This functional decreases to $-\infty$, however it could be an essential ingredient to solve this issue.

The present model and its mathematical analysis represent to the best of our knowledge a first attempt to study the interactions between HSCs and their supporting stromal cells in the framework of adaptive dynamics. One could certainly complicate it to introduce multidimensional phenotypes related to refined cell functionalities such as fecundity, viability, plasticity, in the two cell populations, but even simple as it is, it relies on many unknown functions that should first be experimentally evaluated to go further in this modelling work, which we actually plan to do in the future.

Acknowledgments

B.P. has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No 740623). The authors acknowledge funding by Plan Cancer HTE programm EcoAML.

Conflict of interest

The authors declare there is no conflict of interest.