Epidemics and underlying factors of multiple-peak pattern on hand, foot and mouth disease inWenzhou, China

1.   Introduction

Fundus image diagnosis in the clinic can assist in screening various diseases, such as hypertension and diabetes. Ophthalmologists can make an initial diagnosis of the disease by observing the morphology of retinal blood vessels. However, the accuracy of automatic fundus vessel segmentation is still unsatisfactory, due to the complex morphology of the vessels and the observer dependence. Therefore, accurate retinal vessel segmentation technologies are extremely valuable in clinical environments.

Currently, the automatic segmentation methods of fundus blood vessels can be mainly divided into two categories: machine learning and deep learning. Furthermore, according to different strategies, machine learning-based approaches can be divided into unsupervised and supervised approaches.

For unsupervised machining methods, Chaudhuri et al. ^[1] introduced a Gaussian function in the segmentation task for the problem of low local contrast, and successfully designed a two-dimensional matched filter to detect blood vessel segments in images. Li et al. ^[2] constructed a simple and efficient multi-scale filtering method based on the response relationship of matched filters at three scales. After that, Sreejini et al. ^[3] introduced the particle swarm optimization algorithm in the multi-scale matched filter method, and discussed the process more comprehensively. The matched filter method is easy to implement, and the amount of calculation is relatively small. However, this method is highly restricted by factors, such as image contrast and noise, and its ability to distinguish vessel pixels from background ones is relatively poor.

In addition, Aibinu et al. ^[4] proposed a method for segmentation at the crossing and branching of vessels, which uses a hybrid crossing point method to identify the crossing and branching points of vessels, realize vessel tracking and extraction. Finally, Vlachos et al. ^[5] proposed a linear multi-scale tracking method, which tracks the gray-scale characteristics of blood vessel pixels from the initial seed node to form a gridded extraction of blood vessels. The blood vessel tracking method can obtain very accurate blood vessel width. However, the segmentation effect largely depends on the selection of the initial seed node. In addition, it is susceptible to noise interference, and the problem of segmenting blood vessel breakage occurs.

Moreover, Zana et al. ^[6] first determined the Gaussian-like contours of blood vessels, and then combined morphological processing with cross-curvature evaluation for segmentation. Fraz et al. ^[7] further obtained the blood vessel's skeleton based on detecting the centerline of the blood vessel. It received the direction map with the help of morphological plane slices, and generated the shape of the blood vessel at the same time. The vessel neutral line image is reconstructed through the orientation map and vessel shape, and, finally, the segmented vessel choroid map is obtained. Yang et al. ^[8] proposed a hybrid method to extract blood vessels based on mathematical morphology and fuzzy clustering. However, these traditional unsupervised-based image processing methods are less robust. Besides, they suffer from poor generalization ability due to customizing artificial features and expert annotations for specified datasets based on prior knowledge.

For supervised machine learning-based methods, its segmentation accuracy is higher than that of unsupervised ones, but with a possibility of overfitting. It has been widely used in retinal vessel segmentation. Staal et al. ^[9] used the K-nearest neighbor (KNN) algorithm to intercept the first k data to compare further and determine its pixel category, which is essentially a binary classification of each pixel. Soares et al. ^[10] used a two-dimensional Gabor filter to extract the overall features of retinal images, and then used a naive Bayesian classifier to classify retinal vessels and backgrounds. Osareh et al. ^[11] first computed feature vectors on a per-pixel basis, and then used a Gaussian mixture model combined with a support vector machine to classify the feature vectors. Khowaja et al. ^[12] proposed a framework based on a hybrid feature set and hierarchical classification approach. They first employed random forests for classification and evaluating the performance of each feature class for feature selection, and then combined the selected feature set with a hierarchical classification approach for vessel segmentation. Conventional machine learning methods is more suitable for scenarios with a small amount of data. However, deep learning performance will be more prominent if the amount of data increases rapidly.

Deep learning-based methods can automatically learn vessel features from the retinal image and avoid manual participation. Therefore, it has stronger robustness, higher frontal segmentation accuracy and more vital generalization ability. In recent years, deep learning has shown excellent performance in the field of medical image segmentation, and many researchers have conducted research in retinal blood vessel segmentation. Specifically, the proposal of U-Net ^[13] makes the U shape network a popular framework, and many improved models are proposed for retinal vessel segmentation. For example, Wu et al. ^[14] proposed a multi-scale network followed network (MS-NFN) to solve the small vessel segmentation problem. Zhuang et al. ^[15] introduced multiple encoding and decoding structures in their LadderNet, and increased the information flow path via skip connections. Alom et al. ^[16] proposed a recursive residual convolutional neural network (R2U-net) based on the U-shaped network model, which better retains feature information and achieves the effect of feature reuse. Finally, Li et al. ^[17] proposed a small U-Net segmentation method IterNet with multiple iterations, which expands the model's depth while considering the segmentation details. Gu et al. ^[18] proposed CE-Net, which introduces a cascaded upper and lower feature extraction module in the middle layer of the codec. It can ensure the acquisition of complete feature information, and extract deeper feature information. Lin et al. ^[19] proposed a multi-path high-resolution retinal vessel segmentation method combined with HR-Net. The feature map maintained high resolution in the feature extraction process, and enabled the information interaction between high and low-resolution branches, thus resulting in more accurate probability maps.

Although the models mentioned above achieved good results in retinal blood vessel segmentation, there are still some limitations:

➢    The codec structure transmits and receives information features in a single layer through skip connections, which aggravates the problem of information loss.

➢    The connecting layer of codec cannot thoroughly combine context information, and continuous pooling and convolution further cause a decrease in the recognition rate of the vessel ends.

To alleviate the above problems, this paper proposes a multi-scale integrated context network to improve blood vessel segmentation accuracy further. Aiming at the issues that existing algorithms have an insufficient feature extraction ability, serious feature information loss and low segmentation accuracy for color fundus retinal vascular images, an aggregated multi-scale integrated context model is proposed to further improve the accuracy of vascular segmentation. Its main new feature is that it has a multi-layer feature fusion mechanism, which can fully use the information in different scales. The main contributions of the network are as follows:

➢    A multi-layer feature fusion mechanism is proposed, combining the low-level details of feature maps at different scales with high-level semantic information through full-scale skip connections from the encoding path to the decoding path.

➢    In the encoder, a hybrid stride sampling (HSS) block is constructed to extract deeper semantic information while reducing the dimensionality of features.

➢    A Dense Hybrid Dilated Convolution (DHDC) block is designed between the encoder and the decoder to improve the accurate recovery of blood vessel details by obtaining richer contextual information.

➢    The Squeeze-and-Excitation module with residual connections is introduced into the decoder, and the weight of each scale feature is adaptively adjusted to strengthen the effective channel while suppressing redundant information.

The rest of this paper is organized as follows: Section Ⅱ introduces the proposed method in detail. Section Ⅲ describes the experimental implementation and illustrates the experimental results. Section Ⅳ gives the conclusions of this paper.

2.   Proposed method

2.1.   Pre-processing

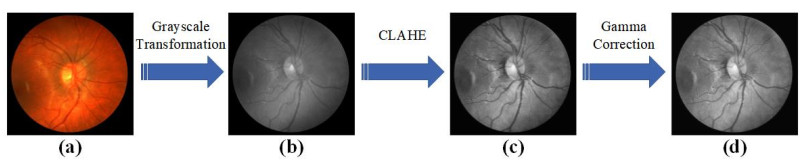
The retinal images in the fundus dataset have many samples with poor contrast and high noise. Therefore, proper preprocessing is critical for later training. This paper uses four preprocessing methods, including gray-scale transformation, data standardization, contrast limited adaptive histogram equalization (CLAHE) and gamma correction ^{[18,20,21,22]}, to process each original retinal blood vessel image.

Figure 1 provides a schematic diagram of the staged processing results of the original color retinal image after gray-scale transformation, contrast-limited adaptive histogram equalization and gamma correction. It can be seen from the figure that the image texture after preprocessing is clear, the edge is prominent, and the detailed information is enhanced.

Figure 1.  The flowchart of data preprocessing.

DownLoad: Full-Size Img PowerPoint

We use a patch extraction strategy to augment the experimental data and avoid the overfitting problem. There are three patch extraction ways: sequential crop, overlap crop and random crop.

This paper selects random cropping for data augmentation in the training phase. In addition, to maintain the consistency of the training data, we performed the same augmentation processing for the ground truth images manually segmented by experts.

Different from the cropping approach in the training phase, in the testing phase, each image block needs to be re-spliced into a complete image and then binarized to obtain the segmentation result map. All patches must be spliced to restore their separation ratios to the level of the original fundus image. However, if random cropping is used, the time and space complexity of splicing according to the index is extremely high. To avoid this problem, the overlap crop is chosen in the testing phase. We set the stride to 12 based on the trade-off of workstation performance.

As shown in Figure 2, each test image is divided into several patches by the overlapping cropping strategy, and Eq (1) calculates the number of patches for each image:

Figure 2.  The overlapping cropping strategy.

DownLoad: Full-Size Img PowerPoint

where img_h and img_w represent the height and width of the test image, patch_h and patch_w represent the height and width of the image block, and stride_h and stride_w represent the step size of horizontal and vertical sliding, respectively. After obtaining the prediction results of overlapping patches, a reconstruction algorithm continuously reconstructs the final average segmentation results (final_avg) by Eq (2).

where full_pro and full_sum represent the sum of each pixel's prediction probability and extraction frequency in each patch, respectively.

2.2.   Framework of proposed MIC-Net

Figure 3 presents the overall framework of the MIC-Net proposed in this paper (the source code is publicly available at https://github.com/Mamdanni/MIC-Net). The network preserves the two-layer end-to-end basic structure of U-Net. First,a hybrid stride sampling (HSS) block is designed in the encoder,which uses full-scale skip connections to replace the single one of U-Net. Second,the interconnection between encoding and decoding paths is redesigned as the dense hybrid dilated convolution (DHDC) block. Finally,the decoder utilized the Squeeze-and-Excitation module with residual connections. Each part is described in detail below.

Figure 3.  The structure of proposed MIC-Net.

DownLoad: Full-Size Img PowerPoint

2.2.1.   Hybrid stride sampling block

The max pooling downsampling is mainly used to reduce the image's resolution. However, valuable information is lost while extracting features. To minimize the data loss caused by the downsampling, we designed an HSS block in the encoding process. It performs the downsampling process before two successive convolutions, which can reduce the feature dimension. Meanwhile, it alleviates the loss of helpful information as much as possible and thus extracts deeper semantic information.

As shown in Figure 4, the HSS module is implemented by paralleling a convolution operation with a convolution kernel size of 2 × 2 or 4 × 4, a stride of 2 or 4, and a pooling kernel size of 2 × 2 or 4 × 4. It is executed by max pooling downsampling with stride 2 or 4.

Figure 4.  The structure of the Hybrid Stride Sampling Block.

DownLoad: Full-Size Img PowerPoint

Compared with downsampling by a single max-pooling or a fixed stride convolution, the proposed sampling module could reduce the information loss caused by dimension reduction. Besides, it is worth noting that we also conducted the HSS block before the full-scale skip connection. On the other hand, upsampling uses transposed convolution to achieve the fusion of different scale features.

2.2.2.   Full-scale skip connections

Skip connections can fuse the high-resolution information from the encoder with the decoder upsampled feature maps, thereby helping to refine the tiny features of the segmentation map. However, though the single skip connection is intuitive and straightforward, the single-layer transmission and reception information features lead to the inability to utilize the full-scale information fully.

However, the feature maps of different scales often contain extra information. Therefore, this paper introduces the full-scale skip connections mechanism, as shown in Figure 5. First, the feature map is re-sampled to a uniform size before downsampling at each layer. Then, we implement full-scale skip connections from the encoding path to the decoding path, thereby achieving a fusion of feature maps at different scales, that is, a complete fusion of low-level details and high-level semantic information.

Figure 5.  Illustration of full-scale skip connections.

DownLoad: Full-Size Img PowerPoint

2.2.3.   Dense hybrid dilated convolution block

To improve the receptive field without losing information and cascade convolutional convolutions with different dilation ratios to obtain multi-scale information gain, we developed the DHDC block (shown in Figure 6) between the encoder and the decoder inspired by DenseASPP ^[23]. A set of atrous convolutions are connected in the form of dense connections, and atrous convolutional layers share information through residual connections. Among them, d represents the expansion rate of the hole convolution. The convolution layers with different expansion rates are interdependent. The feedforward process will not only form a denser feature pyramid, but also increase the receptive field of the convolution kernel to perceive richer contextual information.

Figure 6.  Construction of Dense Hybrid Dilated Convolution Block.

DownLoad: Full-Size Img PowerPoint

2.2.4.   Squeeze-and-Excitation with residual connections

During the decoding process, we use twice transposed convolution with a kernel size of 3 × 3 to upsample the feature map. Besides, we introduce squeeze-and-excitation with residual connections (SERC) in the decoder (as shown in Figure 7).

Figure 7.  The structure of the squeeze-and-excitation with residual connections.

DownLoad: Full-Size Img PowerPoint

We first fused the feature maps obtained by sampling with that of different scales, and then input the residual SERC block. As a result, the weight of each scale feature is adaptively adjusted. It, thus, strengthens the effective channel and suppresses redundant information. Finally, the channels are adjusted using a 1 × 1 convolution kernel.

2.3.   Evaluation metrics

Eight standard evaluation metrics for retinal vessel segmentation tasks include Accuracy (Acc), Specificity (Spe), Sensitivity (Sen), Precision (Pre), and F1_Score, Intersection over Union (IoU), Floating point operations (FLOPs) and Parameters (Params) ^{[17,20,22,39]}.

In addition, we depicted the receiver operating characteristic curve (ROC), which was generated with TP as the ordinate and FP as the abscissa. We also provided the Area under the ROC curve (AUC), which considers the Sen and Spe under different thresholds, and is suitable for measuring retinal vessel segmentation.

3.   Experiments and results

3.1.   Datasets

We evaluated our proposed method on three public datasets of fundus images, including DRIVE, STARE and CHASE. Figure 8 shows some typical cases from the three datasets.

Figure 8.  Fundus images from three different datasets. (a) Original fundus image, (b) ground truth, (c) mask.

DownLoad: Full-Size Img PowerPoint

The DRIVE dataset (https://drive.grand-challenge.org/) contains 40 fundus retinal color images, seven of which are from patients with early diabetic retinopathy, with a resolution of 565 × 584 and stored in JPEG format. The original dataset uses 20 images for training and 20 for testing with masks, and two experts manually annotated the dataset. In this paper, we divide the dataset into a training set, a validation set, and a test set according to the ratio of 18:2:20, and choose the first expert's result as the ground truth. Specifically, 110,000 image patches were obtained based on the original dataset for the later training.

The STARE dataset (http://cecas.clemson.edu/~ahoover/stare/) provides 20 fundus color images with a resolution of 700 × 605. We use 15 of these images for training and five for testing. The original dataset is not divided into a validation set like the DRIVE dataset. Thus, we choose 10% of the training data for validation. The STARE dataset also provides annotated images of two experts, and we chose the first ones as the ground truth. Finally, a total of 130,000 image patches were obtained.

The CHASE dataset (https://blogs.kingston.ac.uk/retinal/chasedb1/) contains 28 color retinal images with a resolution of 996 × 960. It was taken from the left and right eyes of 14 children. We used 20 of these images for training and eight for testing, and a total of 230,000 patches were extracted for training.

3.2.   Implementation details

All experiments were run on a GPU server with Intel Xeon Silver 4110 CPU, NVIDIA GeForce RTX 2080Ti GPU and 64GB RAM. The development environment is based on CUDA11.2 + cuDNN8.1 + TensorFlow2.6.0 + keras2.6.0, Python 3.7.13 and the Ubuntu 18.04 operating system.

In the training process, we set the maximum number of training epochs to 30, batch_size to 4, and initial learning rate to 0.0001. A binary cross-entropy loss (BCE) was used as the objective function to supervise the model's training process. The DRIVE, STARE and CHASE datasets followed the same data augmentation strategy: randomly extract image patches with a resolution of 48 × 48 from the preprocessed images.

Unlike the training phase, we performed overlap cropping in the original image with a fixed step size. Since these patches had overlapping areas (i.e., each pixel appears multiple times in different patches), we averaged the probability value of each pixel belonging to retinal blood vessels and set the threshold to obtain a binarized prediction map. In addition, we used an early stopping mechanism to prevent the occurrence of overfitting,

3.3.   Loss of function

The proposed MIC-Net needed to convert the vessel segmentation task into pixel-level classification. Therefore, we chose the BCE loss function to complete the classification task in this paper. Its equation is defined as follows:

In the above formula, g represents the label value. There are only two possible values of 0 and 1, and p represents the predicted value of the pixel. When g is 0, the first half of the formula equals 0. If you want the loss value to be smaller, p should be as close to 0 as possible; conversely, when g is 1, the second half of the formula is 0. For a minor loss, p should be as close to 1 as possible. Furthermore, the sigmoid activation function is necessary to ensure that the model output is in the range of (0, 1).

3.4.   Ablations

We conducted ablation experiments on the DRIVE dataset to verify each module's contribution to the entire model's performance. As can be seen from Table 1, the AUC, Acc, Spe and Sen of MIC-Net reached 98.62, 97.02, 98.80 and 80.02%, respectively. Compared with the baseline model in the DRIVE dataset, the performance of the final model is improved by 0.2, 0.22, 0.23 and 0.31%, respectively.

Table 1.  Ablation experiments on the DRIVE dataset.

Methods	AUC (%)	Acc (%)	Spe (%)	Sen (%)
Baseline	98.42	96.80	98.57	78.50
No FSC	98.48	96.89	98.85	76.40
No DHDC	98.54	96.96	98.58	78.81
No SERC	98.58	96.99	98.69	79.23
MIC-Net	98.62	97.02	98.80	80.02
*Note: For each metric, the bold value indicates that column's best result.

---

 | Show Table

DownLoad: CSV

Figure 9 shows the segmentation results of the MIC-Net model for different combinations of ablation models. It can be observed from the figure that the segmentation results of the complete MIC-Net model proposed by us have more minor errors than other combinations, and are closer to the standard segmentation images, thus verifying the rationality of the model combination.

Figure 9.  Illustration of ablation results. (a) Original fundus image, (b) Baseline, (c) No_FSC, (d) No_DHDC, (e) No_SERC, (f) Proposed MIC-Net, (g) Ground truth.

DownLoad: Full-Size Img PowerPoint

3.5.   Model parameters and FLOPs

Generally, the number of parameters of a model is directly proportional to its computational complexity, while fewer model parameters often degrade the performance of the network. Table 2 lists the number of parameters, FLOPs and AUC (on DRIVE dataset) of different methods. Compared with other existing models, the parameters and FLOPs of our proposed MIC-Net are comparable to those of Att-Unet, MultiResUNet, and FCN = 8s (all less than 10M). Besides, the segmentation performance of our proposed method is slightly higher than other models. Therefore, the proposed MIC-Net achieves high segmentation performance with lower computational complexity.

Table 2.  Comparisons of different methods on Parameters, FLOPs and AUC.

Methods	Parameters (M)	FLOPs (M)	AUC
SegNet	29.46	58.91	0.9294
FCN_8s	9.01	18.01	0.9410
MultiResUNet	7.26	14.55	0.9451
LinkNet	11.55	23.62	0.9492
DeepLabV3+	41.06	82.23	0.9575
Att-UNet	8.91	17.82	0.9793
R2U-Net	17.65	51.03	0.9804
MIC-Net	9.13	18.23	0.9862
*Note: For each metric, the bold value indicates that column's best result.

---

 | Show Table

DownLoad: CSV

3.6.   Generalization in cross-training experiments

To verify the model's generalization performance, we trained on the DRIVE dataset, and applied the saved weights to testing on the STARE dataset. Figure 10 shows our segmentation results. The generalization visualization experiment shows that the detection of vessels is relatively complete, and the ends and bifurcations can also be completely segmented, which verifies the consistency of the proposed method in different data distributions, and its generalization ability is strong.

Figure 10.  Comparison of generalization in cross-experiments. (a) cases from the STARE dataset, (b) ground truth and (c) test results.

DownLoad: Full-Size Img PowerPoint

In addition, Table 3 lists the generalization performance comparison between the proposed method and other methods. Among them, the method proposed in this paper has obtained the optimal value in the two indicators of AUC and Sen, thus verifying that the proposed method has a good consistency and generalization ability.

Table 3.  Comparison of generalization performance indicators.

Methods	AUC (%)	Acc (%)	Spe (%)	Sen (%)
Yan et al. [41]	97.08	95.69	98.40	72.11
Jin et al. [42]	94.45	96.90	97.59	70.00
Wu et al. [22]	96.35	95.44	97.85	73.78
Proposed method	97.70	96.44	97.51	76.02

---

 | Show Table

DownLoad: CSV

3.7.   Results on three datasets

Figure 11 and Table 4 present our proposed method's partial segmentation results on three datasets. As can be seen from the table and figure, the segmentation result of our proposed MIC-Net is very close to the ground truth, which cannot only extract the main vessel from the background, but also correctly segment the vessel edge.

Figure 11.  Segmentation results of the proposed method on three datasets. (a) original image, (b) preprocessed, (c) ground truth and (d) our results.

DownLoad: Full-Size Img PowerPoint

Table 4.  Performance of our method tested on three datasets.

Dataset	AUC (%)	Acc (%)	Spe (%)	Sen (%)	Pre (%)	F1-score (%)	IoU (%)
DRIVE	98.62	97.02	98.80	80.02	86.32	82.20	68.32
STARE	98.60	97.76	98.61	87.72	93.70	85.99	69.51
CHASE	98.73	97.38	98.44	81.60	77.95	79.73	64.07

---

 | Show Table

DownLoad: CSV

In addition, we also give the ROC curves of the three datasets in Figure 12. It can be seen from the figure that the value of AUC is relatively close to 1, which proves the superior performance of our proposed method on retinal vessel segmentation.

Figure 12.  ROC curves of the proposed MIC-Net tested on three datasets.

DownLoad: Full-Size Img PowerPoint

Although the proposed MIC-Net can successfully segment blood vessels, some intractable abnormalities still occur. For example, as shown in Figure 13, in the segmentation results of the DRIVE dataset and the CHASE dataset, we found two cases where the optic disc boundary was identified as a blood vessel, which indicates that the specificity of the proposed method needs to be improved.

Figure 13.  Cases of abnormalities.

DownLoad: Full-Size Img PowerPoint

*Note: For each metric, bold values are the best result in that column.

3.8.   Comparisons with SOTA methods

We further compare the proposed method with existing state-of-the-art (SOTA) methods to verify the effectiveness of the proposed method. Table 5 presents our quantitative experimental results on the DRIVE, STARE and CHASE datasets. All compared methods refer to open-source codes on GitHub. The experiment's environment configuration and the specific parameter settings, including batch size, epoch, learning rate, etc., are consistent with the settings of our proposed method in this paper during training and testing.

Table 5.  Performance of methods on three datasets.

Methods	Year	DRIVE(%)					STARE(%)					CHASE(%)
		AUC	Acc	Spe	Sen		AUC	Acc	Spe	Sen		AUC	Acc	Spe	Sen
Azzopardi [24]	2015	96.14	94.42	97.04	76.55		95.63	94.97	97.01	77.16		94.87	93.87	95.87	75.85
Li et al. [25]	2015	97.38	95.27	98.16	75.69		98.79	96.28	98.44	77.26		97.16	95.81	97.93	75.07
Liskowski [26]	2016	97.20	94.95	97.68	77.63		97.85	95.66	97.54	78.67		-	-	-	-
Fu et al. [27]	2016	-	95.23	-	76.03		-	95.85	-	74.12		-	94.89	-	71.30
Dasgupta [28]	2016	97.44	95.33	98.01	76.91		-	-	-	-		-	-	-	-
Chen et al. [29]	2017	95.16	94.53	97.35	74.26		95.57	94.49	96.96	72.95		-	-	-	-
Yan et al. [30]	2018	97.52	95.42	98.18	76.53		98.01	96.12	98.46	75.81		97.81	96.10	98.09	76.33
Wu et al. [14]	2018	98.07	95.67	98.19	78.44		-	-	-	-		98.25	96.37	98.47	75.38
Yan et al. [31]	2019	97.50	95.38	98.20	76.31		98.33	96.38	98.57	77.35		97.76	96.07	98.06	76.41
Jin et al. [20]	2019	98.02	95.66	98.00	79.63		98.32	96.41	98.78	75.95		98.04	96.10	97.52	81.55
Wang et al. [32]	2020	98.23	95.81	98.13	79.91		98.81	96.73	98.44	81.86		-	-	-	-
Li et al. [17]	2020	98.16	95.73	98.38	77.35		98.81	97.01	98.86	77.15		98.51	96.55	98.23	79.70
Shi et al. [33]	2021	-	96.76	98.26	80.65		-	97.32	98.66	82.90		-	97.31	98.89	75.04
Guo et al. [34]	2021	98.53	96.67	98.17	82.21		98.97	97.24	98.59	82.10		98.69	96.97	98.45	81.89
Xu et al. [35]	2015	96.70	96.30	98.23	87.45		-	-	-	-		96.77	96.94	97.94	89.16
Zhang et al. [36]	2022	88.95	97.01	97.99	77.19		83.91	96.91	99.11	69.12		91.42	98.11	99.81	85.06
Deng et al. [37]	2022	97.93	95.39	97.12	83.68		98.55	96.43	97.79	84.35		98.06	95.87	96.93	85.43
Our MIC-Net	2022	98.62	97.02	98.80	80.02		98.60	97.76	98.61	87.72		98.73	97.38	98.44	81.60

---

 | Show Table

DownLoad: CSV

In the comparative experiment, the statistical method of t-test is also used to verify whether the proposed method is significantly different from other methods on the accuracy. All statistical hypothesis tests are based on the representative metrics of Acc.

It can be seen that the overall performance of our proposed method achieves significant improvements on all performance metrics, outperforming existing SOTA methods on the three datasets. Besides, regarding AUC metrics, our AUC is 0.46% higher than the second on the DRIVE dataset, 0.52% higher than the second on the STARE dataset and 0.41% higher than the second on the CHASE dataset.

However, compared with the experiments of existing methods, the proposed module has improved the performance of retinal vessel detection. Still, Spe and Sen performances on the three datasets are not outstanding, which indicates that, although the performance improvement of our proposed method is achieved to a certain extent, there is still a significant error on FP and FN.

Figure 13 compares the visualization results of several SOTA methods on three datasets. Our method achieves satisfactory segmentation results from the locally zoom-in images. Compared with other improved approaches, such as scSEU-Net ^[38] and R2U-Net ^[16], our proposed MIC-Net can detect retinal vessels more correctly and reduce misclassified retinal vessel pixels. In addition, better recognition is achieved for tiny vessels and edge regions.

Figure 13.  Comparative results of the SOTA methods and our proposed MIC-Net on three datasets, where the second, fourth, and sixth rows give the local zoomed-in results of the vessel ends.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

This paper proposes an end-to-end fundus retinal vessel segmentation network called MIC-Net. This multi-layer feature fusion mechanism can fully utilize the information on different scales to improve information flow. First, the HSS block we designed on the encoder side can minimize the loss of helpful information caused by the downsampling operation. Second, the DHDC block between the encoder and decoder can perceive richer contextual information without sacrificing feature resolution. Third, the SERC module at the decoder can strengthen the effective channel, while suppressing redundant information.

The experimental results show that the performance of our proposed method on the DRIVE, STARE and CHASE datasets could achieve comparable segmentation results to existing SOTA methods on retinal vessel segmentation. Thus, it has significant application prospects in the early screening of diabetic retinopathy. Nevertheless, the proposed MIC-Net still has some limitations for segmenting tiny blood vessels that cannot be effectively distinguished by direct observation of the human eye. Therefore, our future work will focus on the cascaded semantic segmentation framework for segmenting small blood vessels.

Acknowledgments

This work was supported by the National Nature Science Foundation (No. 61741106, 61701178).

Competing Interests

We declare that there are no conflicts of interest.