Citation: Suxia Zhang, Hongbin Guo, Robert Smith?. Dynamical analysis for a hepatitis B transmission model with immigration and infection age[J]. Mathematical Biosciences and Engineering, 2018, 15(6): 1291-1313. doi: 10.3934/mbe.2018060
| [1] | Yicang Zhou, Zhien Ma . Global stability of a class of discrete age-structured SIS models with immigration. Mathematical Biosciences and Engineering, 2009, 6(2): 409-425. doi: 10.3934/mbe.2009.6.409 |
| [2] | Dong-Me Li, Bing Chai, Qi Wang . A model of hepatitis B virus with random interference infection rate. Mathematical Biosciences and Engineering, 2021, 18(6): 8257-8297. doi: 10.3934/mbe.2021410 |
| [3] | Xichao Duan, Sanling Yuan, Kaifa Wang . Dynamics of a diffusive age-structured HBV model with saturating incidence. Mathematical Biosciences and Engineering, 2016, 13(5): 935-968. doi: 10.3934/mbe.2016024 |
| [4] | Tingting Xue, Long Zhang, Xiaolin Fan . Dynamic modeling and analysis of Hepatitis B epidemic with general incidence. Mathematical Biosciences and Engineering, 2023, 20(6): 10883-10908. doi: 10.3934/mbe.2023483 |
| [5] | Bao-Zhu Guo, Li-Ming Cai . A note for the global stability of a delay differential equation of hepatitis B virus infection. Mathematical Biosciences and Engineering, 2011, 8(3): 689-694. doi: 10.3934/mbe.2011.8.689 |
| [6] | Maysaa Al Qurashi, Saima Rashid, Fahd Jarad . A computational study of a stochastic fractal-fractional hepatitis B virus infection incorporating delayed immune reactions via the exponential decay. Mathematical Biosciences and Engineering, 2022, 19(12): 12950-12980. doi: 10.3934/mbe.2022605 |
| [7] | Tahir Khan, Fathalla A. Rihan, Muhammad Ibrahim, Shuo Li, Atif M. Alamri, Salman A. AlQahtani . Modeling different infectious phases of hepatitis B with generalized saturated incidence: An analysis and control. Mathematical Biosciences and Engineering, 2024, 21(4): 5207-5226. doi: 10.3934/mbe.2024230 |
| [8] | Jiying Ma, Shasha Ma . Dynamics of a stochastic hepatitis B virus transmission model with media coverage and a case study of China. Mathematical Biosciences and Engineering, 2023, 20(2): 3070-3098. doi: 10.3934/mbe.2023145 |
| [9] | C. Connell McCluskey . Global stability for an $SEI$ model of infectious disease with age structure and immigration of infecteds. Mathematical Biosciences and Engineering, 2016, 13(2): 381-400. doi: 10.3934/mbe.2015008 |
| [10] | Tailei Zhang, Hui Li, Na Xie, Wenhui Fu, Kai Wang, Xiongjie Ding . Mathematical analysis and simulation of a Hepatitis B model with time delay: A case study for Xinjiang, China. Mathematical Biosciences and Engineering, 2020, 17(2): 1757-1775. doi: 10.3934/mbe.2020092 |
Hepatitis B virus infection is a major public-health concern, both in developing countries and immigrant communities in developed countries. An estimated two billion people worldwide are infected with the virus, with about 378 million chronic carriers worldwide and approximately 620, 000 deaths each year [8]. Each year, about 4.5 million new infections occur, of which a quarter progress to liver disease [8]. Approximately 45% of the world's population live in areas with high prevalence of chronic HBV infection [16]. Prevalence ranges between 2% in low-endemic countries and 8% in high-endemic countries [8]. In high-endemic countries, the lifetime risk for HBV infection is greater than 60% [16].
HBV infection exhibits an acute infection stage and a chronic liver infection, characterized by persistent serum level of HBV surface antigen (HBsAg), IgG anti-core antigen (anti-HBc) and HBV DNA [4]. Acute disease usually occurs when the immune response is well preserved, while patients with an immunodeficiency are more likely to develop a chronic disease, in turn becoming a source for new infections [8]. Chronic infection may later develop into serious disease such as cirrhosis or liver cancer, causing major morbidity and mortality [14].
Safe and effective HBV vaccines have been commercially available since 1962 [16], being also the first vaccine to protect against cancer [14]. More than 150 countries have HBV vaccine immunization programs, with routine infant vaccination designated a high priority in all countries [16]. However, coverage in developing countries with high endemicity is limited due to high cost and social hurdles [8]. This is despite the cost-effectiveness of the vaccine in both high- and low-endemic countries [14]. In the developed world, the hepatitis B vaccine is one that was targeted by anti-vaccine campaigners, due to the presence of mercury-based thimerosal; however, by March 2001, thimerosal had been removed from all childhood vaccines [10]. An investigation of the literature established that no credible studies demonstrated a link between hepatitis B vaccination and autism [21]. Nevertheless, vaccination in adults in the United States decreased by 2.1% between 2012 and 2013, with 25% of adults
The probability of becoming chronically infected is positively correlated to the age of the infected host [14,6,19,9], while progression of acute-stage and chronic-stage HBV is related to the time since infection. Furthermore, the infectivity of patients varies at different ages during the infectious period. Thus, mathematical models that can examine infection-age structure can be useful in investigating the consequences of infection age on HBV transmission dynamics and disease progression. Continuous age-structured models usually lead to partial differential equation (PDE) formulation. Population migration occurs at regional, national and global scales due to various factors, such as economic development. Labour workers transition from rural regions to large cities in both developing and industrialized countries, while immigrants and refugees migrate from developing countries to immigrant-receiving countries [20].
Although dynamical analysis of epidemic models with age structures is particularly challenging, there has been recent progress in global analysis [13,22,2,7,15,17,18]. Age-structured models have also been developed to study the epidemiology of HBV infection [6,19,27,29,26]. Medley et al. observed a feedback mechanism that determines the prevalence of HBV infection, using an ODE model to relate the rate of transmission, average age at infection and age-related probability of developing carriage following infection [19]. Based on sero-survey data in China, Zhao et al. [27] constructed an age-structured HBV model to evaluate the long-term effectiveness of vaccination programmes. Zou et al. in [29] proposed a full PDE model that incorporated multiple age structures to study the transmission dynamics of HBV and analyzed the existence and stability of the disease-free and endemic equilibria. In [26], age of infection and nontrivial vertical transmission were incorporated into the model to study the possible effects of variable infectivity on HBV dynamics.
Brauer and van den Driessche [3] studied an SIS model with a constant flow of infective immigrants into the infectious compartment. Such immigration models do not contain an infection-free equilibrium and consequently have no reproduction number. Guo and Li [11] generalized the immigration model to a high-dimensional SEIR model with constant immigration into each compartment, and the global stability of unique endemic equilibrium was shown by a global Lyapunov function. McCluskey [17,18] proved the global stability of the unique endemic equilibrium by a Lyapunov functional for an SEIR model with age structure consisting of a latent compartment, an infectious compartment and variable-age immigration terms. Guo and Li [12] demonstrated that the immigration inflow is vital to the dynamical behaviour: small variations in the immigration term into infectious compartment and/or latent compartment can profoundly change the resultant dynamics.
Based on the characteristics of HBV transmission and progression, we divide the population into five classes: susceptible, exposed, acute infection, chronic carriers and immunized. Let
Vertical transmission from mother to child is also incorporated into our model. For simplicity, we assume all newborns are vaccinated with the same efficacy and that all the neonates who acquire HBV infection perinatally become chronic carriers, due to the high risk (up to 90%) of becoming chronic for this group. The model flow diagram is shown in Figure 1. Based on the natural history of HBV transmission and the assumptions of infection age, we have the following system of combined ordinary and partial differential equations:
| S′(t)=ΛS−bω∫∞a1v(a)c(a,t)da−(μS+p)S(t)−∫a10β(a)i(a,t)S(t)da−∫∞a1αβ(a)c(a,t)S(t)da,E′(t)=ΛE+∫a10β(a)i(a,t)S(t)da | (1) |
| +∫∞a1αβ(a)c(a,t)S(t)da−(μE+σ)E(t),∂i(a,t)∂a+∂i(a,t)∂t=Λi(a)−(μi(a)+γ1(a))i(a,t),0<a≤a1∂c(a,t)∂a+∂c(a,t)∂t=Λc(a)−(μc(a)+γ2(a)+θ(a))c(a,t),a1<a<∞R′(t)=ΛR+b(1−ω)+∫a10(1−q(a))γ1(a)i(a,t)da+∫∞a1γ2(a)c(a,t)da−μRR(t)+pS(t), |
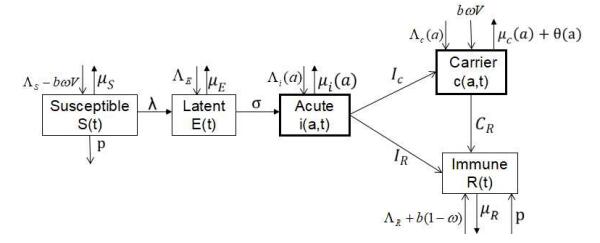 Figure 1. Flow diagram of the age-structured HBV transmission model (1).
Figure 1. Flow diagram of the age-structured HBV transmission model (1).with the boundary conditions
| i(0,t)=σE(t),c(a1,t)=∫a10q(a)γ1(a)i(a,t)da+bω∫∞a1v(a)c(a,t)da |
and initial conditions
| S(0)=S0,E(0)=E0,i(a,0)=i0(a),c(a,0)=c0(a),R(0)=R0. |
The age-dependent function
| V=∫∞a1ν(a)c(a,t)da. |
The movement from acute individuals to carriers is given by
| Ic=∫a10q(a)γ1(a)i(a,t)da. |
The recovery rate is
| IR=∫a10(1−q(a))γ1(a)i(a,t)da. |
The definitions of the other parameters in system (1) are listed in the Table 1. See also Zhang and Xu [26]. Note that unsuccessfully immunized birth is included in
| Symbol | Definition |
| rate of recruitment into the susceptible compartment, | |
| including unsuccessfully immunized birth and immigration | |
| immigration rate into class |
|
| age-dependent immigration rate into class |
|
| per capital death rate for class |
|
| age-dependent death rate for class |
|
| birth rate | |
| proportion of newborns who are unsuccessfully immunized | |
| transfer rate from exposed to acute infection | |
| vaccination rate | |
| degree of infectiousness of carriers relative to acute infections ( |
|
| age-dependent transmission coefficient | |
| age-dependent rate of children born to carrier mothers | |
| who become HBV carriers | |
| age-dependent transfer rate from acute to immunized or carrier class | |
| age-dependent transfer rate from carrier to immunized class | |
| age-dependent progression from acute infection to carrier class | |
| age-dependent HBV-induced death rate |
In order to simplify the analysis, we made the following assumptions.
(H1)
Let
(H2)
(H3)
(H4) The constant parameters
(H5) The initial conditions satisfy
(H6) The supports of
(H7) essential infimum (support(
essential infimum (support(
for
To simplify expressions, we introduce the following notations
| π1(a)=e−∫a0(μi(s)+γ1(s))dsa∈[0,a1],π2(a)=e−∫aa1(μc(s)+γ2(s)+θ(s))dsa∈[a1,∞), |
where
| i(a,t)={i(0,t−a)π1(a)+∫a0Λi(s)π1(a)π1(s)ds,t>a, a∈[0,a1],i0(a−t)π1(a)π1(a−t)+∫aa−tΛi(s)π1(a)π1(s)ds,t≤a, a∈[0,a1], | (2) |
and
| {c(a1,a1+t−a)π2(a)+∫aa1Λc(s)π2(a)π2(s)ds,t+a1>a,a∈[a1,∞),c0(a−t−a1)π2(a)π2(a−t−a1)+∫aa−t−a1Λc(s)π2(a)π2(s)ds,t+a1≤a,a∈[a1,∞). | (3) |
By classical existence and uniqueness results for functional differential equations, there exists a unique solution for the integro-differential system (1) in which
For (2) and (3), it is easy to see that
| Y=R2≥0×L1(R≥0,R≥0)×L1(R≥0,R≥0)×R≥0 |
be the state space of system (1). Then
| Φt:Y→Y. |
Denote
| ‖u‖=S+E+∫a10i(a,t)da+∫∞a1c(a,t)da+R. |
Notice that the variable
Let
| N(t)=S(t)+E(t)+∫a10i(a,t)da+∫∞a1c(a,t)da+R(t)=‖u‖. |
In the following, we establish that
From (2), we can obtain
| ∫a10i(a,t)da=∫t0i(a,t)da+∫a1ti(a,t)da=∫t0i(0,t−a)π1(a)da+∫t0∫a0Λi(τ)π1(a)π1(τ)dτda+∫a1ti0(a−t)π1(a)π1(a−t)da+∫a1t∫aa−tΛi(τ)π1(a)π1(τ)dτda. |
Changing the order of integration for two double integrals in the above, we have
| ∫t0∫a0Λi(τ)π1(a)π1(τ)dτda=∫t0∫tτΛi(τ)π1(a)π1(τ)dadτ,∫a1t∫aa−tΛi(τ)π1(a)π1(τ)dτda=∫t0∫τ+ttΛi(τ)π1(a)π1(τ)dadτ+∫a1t∫τ+tτΛi(τ)π1(a)π1(τ)dadτ−∫a1a1−t∫τ+ta1Λi(τ)π1(a)π1(τ)dadτ. |
Making substitutions
| ∫a10i(a,t)da=∫t0i(0,τ)π1(t−τ)dτ+∫a1−t0i0(τ)π1(τ+t)π1(τ)dτ+∫a10∫τ+tτΛi(τ)π1(a)π1(τ)dadτ−∫a1a1−t∫τ+ta1Λi(τ)π1(a)π1(τ)dτda. |
Thus differentiating
| ddt∫a10i(a,t)da=i(0,t)−i0(a1−t)π1(a1)π1(a1−t)+∫t0i(0,τ)π′1(t−τ)dτ+∫a1−t0i0(τ)π′1(τ+t)π1(τ)dτ+∫a10Λi(τ)π1(τ+t)π1(τ)dτ−ddt∫a1a1−t∫τ+ta1Λi(τ)π1(a)π1(τ)dadτ. |
We have
| ∫a1−t0i0(τ)π′1(τ+t)π1(τ)dτ=∫a1ti0(a−t)π′1(a)π1(a−t)da |
and
| ∫t0∫a0Λi(τ)π′1(a)π1(τ)dτda+∫a1t∫aa−tΛi(τ)π′1(a)π1(τ)dτda+∫a1a1−t∫τ+ta1Λi(τ)π′1(a)π1(τ)dadτ=∫a10∫τ+tτΛi(τ)π′1(a)π1(τ)dadτ=∫a10Λi(τ)π1(τ+t)−π1(τ)π1(τ)dτ=∫a10Λi(τ)π1(τ+t)π1(τ)dτ−∫a10Λi(τ)dτ. |
Noticing that
| ddt∫a10i(a,t)da=i(0,t)−i0(a1−t)π1(a1)π1(a1−t)+∫t0i(0,τ)π′1(t−τ)dτ+∫a1ti0(a−t)π′1(a)π1(a−t)da+∫t0∫a0Λi(τ)π′1(a)π1(τ)dτda+∫a1t∫aa−tΛi(τ)π′1(a)π1(τ)dτda+∫a10Λi(τ)dτ−∫a1a1−tΛi(τ)π1(τ+t)π1(τ)dτ=i(0,t)−i0(a1−t)π1(a1)π1(a1−t)+˜Λi−∫a1a1−tΛi(τ)π1(τ+t)π1(τ)dτ−∫a10(μi(a)+γ1(a))i(a,t)da. | (4) |
A similar calculation for (3) yields
| ∫∞a1c(a,t)da=∫a1+ta1c(a,t)da+∫∞a1+tc(a,t)da=∫t0c(a1,τ)π2(a1+t−τ)dτ+∫∞0c0(τ)π2(t+a1+τ)π2(τ)dτ+∫∞a1∫τ+tτΛc(τ)π2(a)π2(τ)dadτ, |
and hence
| ddt∫∞a1c(a,t)da=c(a1,t)+∫a1+ta1c(a1,a1+t−a)π′2(a)da+∫∞a1+tc0(a−t−a1)π′2(a)π2(a−t−a1)da+∫a1+ta1∫aa1Λc(τ)π′2(a)π2(τ)dτda+∫∞a1+t∫aa−t−a1Λc(τ)π′2(a)π2(τ)dτda+∫∞a1Λc(τ)dτ=c(a1,t)−∫∞a1(μc(a)+γ2(a)+θ(a))c(a,t)da+˜Λc. | (5) |
Combining the equations gives
| N′(t)=ΛS+ΛE+˜Λi+˜Λc+ΛR+b(1−ω)−i0(a1−t)π1(a1)π1(a1−t)−∫a1a1−tΛi(τ)π1(τ+t)π1(τ)dτ−μSS(t)−μEE(t)−μRR(t)−∫a10μi(a)i(a,t)da−∫∞a1(μc(a)+θ(a))c(a,t)da≤Λ∗−μ∗N(t), |
where
| \displaystyle{\limsup\limits_{t\to\infty}} N(t)\leq N^* |
which implies that all solutions of system (1) are ultimately bounded. Moreover, when
| \Omega = \left\{u(t) = (S(t), E(t), i(., t), c(., t), R(t))\in\mathcal{Y}:\| u\| \leq \max\left\{N^*, N(0)\right\}\right\} |
is positively invariant and absorbing under the semiflow
Lemma 3.1. The unique solution semiflow
Lemma 3.2. There exists
Proof. First, since
| \begin{align*} S'(t)\geq{}&\Lambda_S-b\omega\int_{a_1}^{\infty}v(a)c(a, t)da-\bar{\beta}S(t)\left(\int_0^{a_1}i(a, t)da+\alpha\int_{a_1}^{\infty}c(a, t)da\right)\\ &-(\mu_S+p)S(t)\\ \geq{}&\Lambda_S-b\omega\int_{a_1}^{\infty}v(a)c(a, t)da-S(t)\left[\bar{\beta}(N^*+\epsilon)(1+\alpha)+(\mu_S+p)\right], \end{align*} |
from which it follows that
| \liminf\limits_{t\to\infty} S(t)\geq\dfrac{\Lambda_S-b\omega\int_{a_1}^{\infty}v(a)c(a, t)da}{\bar{\beta}(N^*+\epsilon)(1+\alpha)+\mu_S+p}\equiv M_S. |
Next we have
| \begin{align*} E'(t)&\geq\Lambda_E+\underline \beta S(t)(\int_0^{a_1}i(a, t)da+\alpha\int_{a_1}^{\infty}c(a, t)da)-(\mu_E+\sigma)E(t)\\ &\geq\Lambda_E+\underline \beta M_S(\int_0^{a_1}i(a, t)da+\alpha\int_{a_1}^{\infty}c(a, t)da)-(\mu_E+\sigma)E(t), \end{align*} |
which implies
| \liminf\limits_{t\to\infty} E(t)\geq\frac{\Lambda_E+\underline \beta M_S(\int_0^{a_1}i(a, t)da+\alpha\int_{a_1}^{\infty}c(a, t)da)}{\mu_E+\sigma}\equiv M_E. |
Therefore there exists
| \label{e} i(0, t) = \sigma E(t)\geq\frac{\sigma M_E}{2} | (6) |
for all
| \begin{align*} \int_0^t\int_0^aq(a)\gamma_1(a)\Lambda_i(\tau)\frac{\pi_1(a)}{\pi_1(\tau)}d\tau da\geq\delta \end{align*} |
for all
| \label{f} \begin{split} c(a_1, t)&\geq\int_0^{a_1}q(a)\gamma_1(a)i(a, t)da\\ &\geq\int_0^t\int_0^aq(a)\gamma_1(a)\Lambda_i(\tau)\frac{\pi_1(a)}{\pi_1(\tau)}d\tau da\\ &\geq\delta. \end{split} | (7) |
Then, when
Lemma 4.1. The semi-flow
| \Phi(t, u) = \Theta(t, u)+\Psi(t, u) |
and, for any bounded closed set
This is a special case of Theorem 2.46 in [23]. Note that
| \begin{align*} \tilde{i}(a, t)& = \begin{cases} i(0, t-a)\pi_1(a), &t>a, \;\;a\in[0, a_1], \\ 0, &t\leq a, \;\;a\in[0, a_1], \end{cases}\\ \tilde{c}(a, t)& = \begin{cases} c(a_1, a_1+t-a)\pi_2(a), &t+a_1>a, a\in[a_1, \infty), \\ 0, &t+a_1\leq a, a\in[a_1, \infty), \end{cases}\\ \tilde{i}_0(a, t)& = \begin{cases} \int_0^a \Lambda_i(s)\frac{\pi_1(a)}{\pi_1(s)}ds, &t>a, \;\;a\in[0, a_1], \\ i_0(a-t)\frac{\pi_1(a)}{\pi_1(a-t)}+\int_{a-t}^a \Lambda_i(s)\frac{\pi_1(a)}{\pi_1(s)}ds, &t\leq a, \;\;a\in[0, a_1], \end{cases}\\ \tilde{c}_0(a, t)& = \begin{cases} \int_{a_1}^a \Lambda_c(s)\frac{\pi_2(a)}{\pi_2(s)}ds, &t+a_1>a, \\ c_0(a-t-a_1)\frac{\pi_2(a)}{\pi_2(a-t-a_1)}+\int_{a-t-a_1}^a \Lambda_c(s)\frac{\pi_2(a)}{\pi_2(s)}ds, &t+a_1\leq a, \end{cases} \end{align*} |
for
| \Phi(t, u_0^j) = (S^j(t), E^j(t), i^j(., t), c^j(., t), R^j(t)). |
In the following, we evaluate the distance between
Noting that
| \tilde{i}_0^1(a, t)-\tilde{i}_0^2(a, t) = \begin{cases} 0, &t>a, a\in[0, a_1], \\ (i_0^1(a-t)-i_0^2(a-t))\frac{\pi_1(a)}{\pi_1(a-t)}&t\leq a,\;\; a\in[0, a_1], \end{cases} |
then
| \begin{align*} \|\tilde{i}_0^1(a, t)-\tilde{i}_0^2(a, t)\|_1& = \int_t^{a_1}\left|i_0^1(a-t)-i_0^2(a-t)\right|\frac{\pi_1(a)}{\pi_1(a-t)}da\\ & = \int_0^{a_1-t}\left|i_0^1(\tau)-i_0^2(\tau)\right|\frac{\pi_1(\tau+t)}{\pi_1(\tau)}d\tau\\ & = \int_0^{a_1-t}\left|i_0^1(\tau)-i_0^2(\tau)\right|e^{-\int_{\tau}^{\tau+t}(\mu_i(s)+\gamma_1(s))ds}d\tau\\ &\leq e^{-{\underline \mu _i}t}\int_0^{a_1}\left|i_0^1(\tau)-i_0^2(\tau)\right|d\tau\\ &\leq e^{-{\underline \mu _i}t}(\| i_0^1\|_1+\|i_0^2\|_1)\\ &\leq 2Ke^{-{\underline \mu _i}t}, \end{align*} |
which approaches zero as
Similarly,
| \|\Theta(t, u_0^1)-\Theta(t, u_0^2)\|\leq2K(e^{-{\underline \mu _i}t}+e^{-{\underline \mu _c}t}) |
for all
| \text{diam}\, \Theta(t, C)\leq2K(e^{-{\underline \mu _i}t}+e^{-{\underline \mu _c}t}) |
so condition (a) in Lemma 4.1 is satisfied.
In the following, we verify condition (b) in Lemma 4.1, which can be alternatively proved by verifying four conditions in Lemma 4.2 below. This shows that
Lemma 4.2.
1.
2.
3.
4.
Conditions 1, 2 and 4 are easy to show, since
| 0\leq\tilde{i}(a, t) = \left\{ \begin{aligned} &i(0, t-a)\pi_1(a), &t>a, \;\;a\in[0, a_1]\\ &0, &t\leq a,\;\; a\in[0, a_1] \end{aligned} \right\} \leq\sigma Ke^{-{\underline \mu _i}a} |
and
| \left\{ \begin{aligned} &c(a_1, a_1+t-a)\pi_2(a)&t+a_1>a, a\in[a_1, \infty)\\& 0, &t+a_1\leq a, a\in[a_1, \infty) \end{aligned} \right\}\leq (\bar{q}\bar{\gamma}_1+b\omega \bar{v}) Ke^{-{\underline \mu _c}a}. |
Next we show that Condition 3 is also satisfied. As
| \label{g} \begin{split} \int_0^{a_1}\left|\tilde{i}(a+h, t)-\tilde{i}(a, t)\right|da = {}&\int_0^{t-h}\left|i(0, t-a-h)\pi_1(a+h)-i(0, t-a)\pi_1(a)\right|da\\ ~&+\int_{t-h}^{t}\left|0-i(0, t-a)\pi_1(a)\right|da\\ ~\leq{}&\int_0^{t-h}\left|i(0, t-a-h)\pi_1(a+h)-i(0, t-a)\pi_1(a)\right|da\\&+\sigma Kh\\ ~\leq{}&\sigma Kh+\int_0^{t-h}i(0, t-a-h)\left|\pi_1(a+h)-\pi_1(a)\right|da\\ ~&+\int_0^{t-h}\left|i(0, t-a-h)-i(0, t-a)\right|\pi_1(a)da\\ ~\leq{}&\sigma Kh+\sigma K\int_0^{t-h}\left|\pi_1(a+h)-\pi_1(a)\right|da\\ ~&+\int_0^{t-h}\left|i(0, t-a-h)-i(0, t-a)\right|\pi_1(a)da. \end{split} | (8) |
Noting that
| \left|i(0, t-a-h)-i(0, t-a)\right|\pi_1(a) = \sigma\left|E(t-a-h)-E(t-a)\right|\pi_1(a), |
which leads to
| \label{h} \int_0^{t-h}\left|i(0, t-a-h)-i(0, t-a)\right|\pi_1(a)da\leq \sigma L_E\frac{h}{{\underline \mu _i}}. | (9) |
Note that
| \begin{split} \int_0^{t-h}\left|\pi_1(a+h)-\pi_1(a)\right| & = \int_0^{t-h}\pi_1(a)da-\int_0^{t-h}\pi_1(a+h)da\\ & = \int_0^{t-h}\pi_1(a)da-\int_h^{t}\pi_1(a)da\\ & = \int_0^{t-h}\pi_1(a)da+\int_0^{h}\pi_1(a)da-\int_0^t\pi_1(a)da\\ & = \int_0^{h}\pi_1(a)da-\int_{t-h}^{t}\pi_1(a)da\\ &<\int_0^{h}\pi_1(a)da\\ &\leq h. \end{split} | (10) |
Substituting (9) and (10) into (8), we have
| \label{j} \int_0^{a_1}\left|\tilde{i}(a+h, t)-\tilde{i}(a, t)\right|da\leq 2\sigma Kh+\sigma L_Eh/{\underline \mu _i}. | (11) |
The constant in (11) is dependent on
Lemma 4.3. Both
Proof. The result for
| \begin{split} &\int_{a_1}^{\infty}\left|\tilde{c}(a+h, t)-\tilde{c}(a, t)\right|da\\ = &\int_{a_1}^{a_1+t-h}\left|c(a_1, a_1+t-a-h)\pi_2(a+h)-c(a_1, a_1+t-a)\pi_2(a)\right|da\\ &+\int_{a_1+t-h}^{a_1+t}\left|0-c(a_1, a_1+t-a)\pi_2(a)\right|da\\ = &\int_{a_1}^{a_1+t-h}c(a_1, a_1+t-a-h)\left|\pi_2(a+h)-\pi_2(a)\right|da\\ &+\int_{a_1}^{a_1+t-h}\left|c(a_1, a_1+t-a-h)-c(a_1, a_1+t-a)\right|\pi_2(a)da\\ &+\int_{a_1+t-h}^{a_1+t}\left|0-c(a_1, a_1+t-a)\pi_2(a)\right|da. \end{split} | (12) |
Recalling the boundary conditions on
| \label{l} \left|0-c(a_1, a_1+t-a)\pi_2(a)\right|\leq(\bar{q}\bar{\gamma}_1+b\omega \bar{v})K. | (13) |
Similar to (10), we have
| \label{m} \int_{a_1}^{a_1+t-h}c(a_1, a_1+t-a-h)\left|\pi_2(a+h)-\pi_2(a)\right|da\leq(\bar{q}\bar{\gamma}_1+b\omega \bar{v})Kh. | (14) |
For the second integral in (12), we have
| \begin{align*} \big|c(a_1, a_1+t-a&-h)-c(a_1, a_1+t-a)\big|\\ \leq{}&\int_0^{a_1}\left|q(a)\gamma_1(a)i(a, a_1+t-a-h)-q(a)\gamma_1(a)i(a, a_1+t-a)\right|da\\ &+b\omega\int_{a_1}^{\infty}\left|v(a)c(a, a_1+t-a-h)-v(a)c(a, a_1+t-a)\right|da, \end{align*} |
since
| \begin{split} \int_0^{a_1}q(a)&\gamma_1(a)i(a, t+h)da-\int_0^{a_1}q(a)\gamma_1(a)i(a, t)da\\ = {}&\int_0^hq(a)\gamma_1(a)i(a, t+h)da+\int_h^{a_1}q(a)\gamma_1(a)i(a, t+h)da\\ &-\int_0^{a_1}q(a)\gamma_1(a)i(a, t)da\\ = {}&\int_0^hq(a)\gamma_1(a)i(0, t+h-a)\pi_1(a)da+\int_0^hq(a)\gamma_1(a)\int_0^a\Lambda_i(\tau)\frac{\pi_1(a)}{\pi_1(\tau)}d\tau da\\ &+\int_h^{a_1}q(a)\gamma_1(a)i(a, t+h)da-\int_0^{a_1}q(a)\gamma_1(a)i(a, t)da\\ \leq{}& \bar{q}\bar{\gamma}_1\sigma Kh+\bar{q}\bar{\gamma}_1\tilde{\Lambda}_i h+\int_0^{a_1-h}q(\tau+h)\gamma_1(\tau+h)i(\tau+h, t+h)d\tau\\ &-\int_0^{a_1}q(a)\gamma_1(a)i(a, t)da\\ = {}&\bar{q}\bar{\gamma}_1(\sigma K+\tilde{\Lambda}_i)h+\int_0^{a_1-h}q(\tau+h)\gamma_1(\tau+h)i(\tau, t)\frac{\pi_1(\tau+h)}{\pi_1(\tau)}d\tau\\ & +\int_0^{a_1-h}q(\tau+h)\gamma_1(\tau+h)\int_{\tau}^{\tau+h}\Lambda_i(s)\frac{\pi_1(\tau+h)}{\pi_1(s)}dsd\tau\\ & -\int_0^{a_1}q(a)\gamma_1(a)i(a, t)da. \end{split} | (15) |
Observing the fact that
| \begin{align*} i(\tau+h, t+h) = i(\tau, t)\frac{\pi_1(\tau+h)}{\pi_1(\tau)}+\int_{\tau}^{\tau+h}\Lambda_i(s)\frac{\pi_1(\tau+h)}{\pi_1(s)}ds \end{align*} |
and
| \begin{split} \int_0^{a_1-h}q(\tau+h)\gamma_1(\tau+h)&\int_{\tau}^{\tau+h}\Lambda_i(s)\frac{\pi_1(\tau+h)}{\pi_1(s)}dsd\tau\\ & \leq \bar{q}\bar{\gamma}_1\int_0^{a_1-h}\int_{\tau}^{\tau+h}\Lambda_i(s)dsd\tau\\ & = \bar{q}\bar{\gamma}_1\left(\int_0^h\int_0^s\Lambda_i(s)d\tau ds+\int_0^h\int_h^{a_1}\int_{s-h}^{s}\Lambda_i(s)d\tau ds\right)\\ & = \bar{q}\bar{\gamma}_1\left(\int_0^hs\Lambda_i(s)ds+\int_h^{a_1}h\Lambda_i(s)ds\right) \end{split} |
| \begin{split}& \leq\bar{q}\bar{\gamma}_1h\int_0^{a_1}\Lambda_i(s)ds\\ & = \bar{q}\bar{\gamma}_1\tilde{\Lambda}_ih, \end{split} | (16) |
and
| 1-\bar{\mu}_ih\leq e^{-\bar{\mu}_ih}\leq e^{-\int_a^{a+h}\mu_i(s)ds}\leq 1 |
for
| \begin{split} \int_0^{a_1}&\left|q(a)\gamma_1(a)i(a, t+h)-q(a)\gamma_1(a)i(a, t)\right|da\\ \leq{}&\bar{q}\bar{\gamma}_1(\sigma K+2\tilde{\Lambda}_i)h+\int_0^{a_1-h}\left|q(a+h)\gamma_1(a+h)\frac{\pi_1(a+h)}{\pi_1(a)}-q(a)\gamma_1(a)\right|i(a, t)da\\ \leq{}&\bar{q}\bar{\gamma}_1(\sigma K+2\tilde{\Lambda}_i)h+\int_0^{a_1-h}q(a+h)\gamma_1(a+h)\left|e^{-\int_a^{a+h}\mu_i(s)ds}-1\right|i(a, t)da\\ ~~ &+\int_0^{a_1-h}\left|q(a+h)\gamma_1(a+h)-q(a)\gamma_1(a)\right|i(a, t)da\\ \leq{}&\bar{q}\bar{\gamma}_1(\sigma K+2\tilde{\Lambda}_i+\bar{\mu}_iK)h+L_{\gamma_1}^{q}Kh. \end{split} | (17) |
Here
| \label{o} \int_{a_1}^{\infty}\left|v(a)c(a, t+h)-v(a)c(a, t)\right|da \leq\bar{v}(K+2\tilde{\Lambda}_c+\bar{\mu}_cK)h+L_vKh. | (18) |
Substituting (13)-(18) into (12) gives
| \int_{a_1}^{\infty}|\tilde{c}(a+h, t)-\tilde{c}(a, t)|da\leq Lh, |
where
Consequently,
Theorem 4.4. The solution semiflow
This result is implied by Lemma 3.1, Theorem 4.4 and Theorem 1.1.3 in [28].
In this section, we will investigate the existence of the endemic equilibrium and its global stability, in the special case of
| \begin{split} S'(t)& = \Lambda_S-\int_0^{a_1}\beta(a)i(a, t)S(t)da-\int_{a_1}^\infty \alpha\beta(a)c(a, t)S(t)da-(\mu_S+p) S, \nonumber \end{split} |
| \label{reducedmodel} \begin{split} E'(t)& = \Lambda_E+\int_0^{a_1}\beta(a)i(a, t)S(t)da+\int_{a_1}^\infty \alpha\beta(a)c(a, t)S(t)da-(\mu_E+\sigma)E, \\ \frac{\partial i(a, t)}{\partial a}&+ \frac{\partial i(a, t)}{\partial t} = \Lambda_i(a)-(\mu_i(a)+\gamma_1(a))i(a, t), 0 <a\leq a_1 \\ \frac{\partial c(a, t)}{\partial a}&+ \frac{\partial c(a, t)}{\partial t} = \Lambda_c(a)-(\mu_c(a)+\gamma_2(a)+\theta(a))c(a, t), a_1 <a <\infty \end{split} | (19) |
with boundary conditions
| \begin{align*} i(0, t)& = \sigma E(t) \\ c(a_1, t)& = \int_0^{a_1}q(a)\gamma_1(a)i(a, t)da \end{align*} |
and initial conditions
| S\left( 0 \right){\rm{ }} = {S_0}, \;\;\;E\left( 0 \right){\rm{ }} = {E_0}, \;\;\;i(a, 0){\rm{ }} = {i_0}(a), \;\;\;c(a, 0){\rm{ }} = {c_0}(a). |
For convenience, denote
| \begin{align*} W_1& = \int_0^{a_1}\beta(a)\pi_1(a)da, \\ W_2& = \int_0^{a_1}q(a)\gamma_1(a)\pi_1(a)da, \\ W_3& = \int_{a_1}^\infty \beta(a)\pi_2(a)da, \\ W_4& = \int_{a_1}^\infty v(a)\pi_2(a)da, \\ W_5& = \int_0^{a_1}q(a)\gamma_1(a)\int_0^{a}\Lambda_i(\tau)\frac{\pi_1(a)}{\pi_1(\tau)}d\tau da, \\ W_6& = \int_{a_1}^\infty v(a)\int_{a_1}^{a}\Lambda_c(\tau)\frac{\pi_2(a)}{\pi_2(\tau)}d\tau da, \\ W_7& = \int_0^{a_1}\beta(a)\int_0^{a}\Lambda_i(\tau)\frac{\pi_1(a)}{\pi_1(\tau)}d\tau da, \\ W_8& = \int_{a_1}^{\infty}\beta(a)\int_{a_1}^{a}\Lambda_c(\tau)\frac{\pi_2(a)}{\pi_2(\tau)}d\tau da, \\ W_9(a)& = \int_0^{a}\frac{\Lambda_i(\tau)}{\pi_1(\tau)}d\tau, \\ W_{10}(a)& = \int_{a_1}^a\frac{\Lambda_c(\tau)}{\pi_2(\tau)}d\tau \end{align*} |
and
| V_1 = \frac{\Lambda_S+\Lambda_E}{\mu_S+p}, \;\;\;\;V_2 = \frac{\mu_E+\sigma}{\mu_S+p}, \;\;\;\;V_3 = \frac{b\omega(c^*(a_1)W_4+W_6)}{\mu_S+p}. |
Let
| \begin{align*} i^*(a)& = \sigma E^*\pi_1(a)+W_9\pi_1(a), \\ c^*(a)& = c^*(a_1)\pi_2(a)+W_{10}\pi_2(a). \end{align*} |
Substituting
| \begin{align*} c^*(a_1) = {}&\sigma E^*W_2+\int_0^{a_1}q(a)\gamma_1(a)W_9(a)\pi_1(a)da\\ &+b\omega\int_{a_1}^\infty v(a)(c^*(a_1)\pi_2(a)+W_{10}(a)\pi_2(a))da. \end{align*} |
It follows that
| c^*(a_1) = \dfrac{\sigma E^*W_2+W_5+b\omega W_6}{1-b\omega W_4} |
Solving the first two equations of system (1) in terms of
| \begin{align*} S^* = \frac{1}{\mu_S+p}\left[(\Lambda_S+\Lambda_E)-(\mu_E+\sigma)E^*-b\omega(c^*(a_1)W_4+W_6)\right] = V_1-V_2E^*-V_3. \end{align*} |
Noting that
Since
| \begin{align*} ~~\, \int_0^{a_1}\beta(a)i^*(a)da+&\alpha\int_{a_1}^\infty\beta(a)c^*(a)da\\ = {}&\int_0^{a_1}\beta(a)\sigma E^*\pi_1(a)da+\int_0^{a_1}\beta(a)W_9(a)\pi_1(a)da\\ ~~ &+\alpha\int_{a_1}^\infty\beta(a)c^*(a_1)\pi_2(a)da+\alpha\int_{a_1}^\infty\beta(a)W_{10}(a)\pi_2(a)da\\ = {}&\sigma E^*W_1+W_7+\alpha c^*(a_1)W_3+\alpha W_8, \end{align*} |
we have
| (\sigma E^*W_1+W_7+\alpha c^*(a_1)W_3+\alpha W_8)(V_1-V_2E^*-V_3) = (\mu_E+\sigma)E^*-\Lambda_E. |
Let
| f(E^*) = A_0(E^*)^2+A_1E^*+A_2. |
Then
| \begin{align*} A_0& = -V_2(\sigma W_1+\frac{\alpha\sigma W_2W_3}{1-b\omega W_4})\\ A_1& = (V_1-V_3)\left(\sigma W_1+\frac{\alpha\sigma W_2W_3}{1-b\omega W_4}\right)\\ &-V_2\left(\frac{\alpha W_3(W_5+W_6)}{1-b\omega W_4}+W_7+\alpha W_8\right)-(\mu_E+\sigma)\\ A_2& = \Lambda_E+(V_1-V_3)(W_7+\alpha W_8). \end{align*} |
Noting that
In the following, based on the techniques used in [26,18], a Lyapunov functional is constructed to prove the global stability of the unique positive equilibrium
Theorem 5.1. When
Proof. For
| G(x, x^*) = x-x^*-x^*\ln\frac{x}{x^*} ~~~~\hbox{and}~~~~ g(x) = x-1-\ln x. |
It is obvious that
| \begin{align*} L_1(t)& = G(S(t), S^*), \\ L_2(t)& = G(E(t), E^*), \\ L_3(t)& = \int_0^{a_1}\varphi(a)G(i(a, t), i^*(a))da, \\ L_4(t)& = \int_{a_1}^\infty\psi(a)G(c(a, t), c^*(a))da, \end{align*} |
where
| \begin{align*} \varphi(a)& = \int_a^{a_1}\left[\beta(s)S^*+\psi(a_1)q(s)\gamma_1(s)\right]\frac{\pi_1(s)}{\pi_1(a)}ds, \\ ~~~ \psi(a)& = \alpha\int_a^\infty\beta(s)S^*\frac{\pi_2(s)}{\pi_2(a)}ds. \end{align*} |
Noting that
| \begin{align*} ~~~ \varphi(0)& = \int_0^{a_1}[\beta(s)S^*+\psi(a_1)q(s)\gamma_1(s)]\pi_1(s)ds, \\ ~~~ \psi(a_1)& = \alpha\int_{a_1}^\infty \beta(s)S^*\pi_2(s)ds = \alpha S^*W_3, \\ ~~~ \varphi'(a)& = -(\beta(a)S^*+\psi(a_1)q(a)\gamma_1(a))+(\mu_i(a)+\gamma_1(a))\varphi(a), \\ ~~~ \psi'(a)& = -\alpha\beta(a)S^*+(\mu_c(a)+\gamma_2(a)+\theta(a))\psi(a), \end{align*} |
and
| \begin{align*} \dfrac{di^*(a)}{da}& = \Lambda_i(a)-(\mu_i(a)+\gamma_1(a))i^*(a), \\ \dfrac{i(a, t)}{i^*(a)}& = \dfrac{i(0, t-a)+W_9(a)}{i^*(0)+W_9(a)}, \end{align*} |
we have
| \begin{split} &\int_{t-a_1}^{t}\varphi(t-\tau)i^*(t-\tau)\frac{d}{dt}g\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)d\tau \\ & = \int_{t-a_1}^{t}\varphi(t-\tau)i^*(t-\tau)g'\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)\frac{d}{dt}\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)d\tau\\ & = \int_{t-a_1}^{t}\varphi(t-\tau)i^*(t-\tau)g'\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)\\ & \times\frac{W'_9(t-\tau)(i^*(0)+W_9(t-\tau))-(i(0, \tau)+W_9(t-\tau))W'_9(t-\tau)}{(i^*(0)+W_9(t-\tau))^2}d\tau\\ & = \int_0^{a_1}\varphi(a)i^*(a)g'\left(\frac{i(a, t)}{i^*(a)}\right)\frac{W'_9(a)(i^*(0)+W_9(a))-(i(0, t-a)+W_9(a))W'_9(a)}{(i^*(0)+W_9(a))^2}da \end{split} |
| \label{1} \begin{split}& = \int_0^{a_1}\varphi(a)i^*(a)g'\left(\frac{i(a, t)}{i^*(a)}\right)\frac{W'_9(a)}{i^*(0)+W_9(a)}\left(1-\frac{i(a, t)}{i^*(a)}\right)da\\ & = \int_0^{a_1}\varphi(a)\Lambda_i(a)\left(1-\frac{i^*(a)}{i(a, t)}\right)\left(1-\frac{i(a, t)}{i^*(a)}\right)da\\ & = \int_0^{a_1}\varphi(a)\Lambda_i(a)\left(2-\frac{i^*(a)}{i(a, t)}-\frac{i(a, t)}{i^*(a)}\right)da, \end{split} | (20) |
and
| \begin{split} ~~~ &\int_{t-a_1}^{t}\varphi(t-\tau)\frac{di^*(t-\tau)}{dt}g\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)d\tau\\ & = \int_{t-a_1}^{t}\varphi(t-\tau)\left[\Lambda_i(t-\tau)-(\mu_i(t-\tau)+\gamma_1(t-\tau))i^*(t-\tau)\right]g\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)d\tau\\ & = \int_0^{a_1}\varphi(a)\Lambda_i(a)g\left(\frac{i(a, t)}{i^*(a)}\right)da -\int_0^{a_1}\varphi(a)(\mu_i(a)+\gamma_1(a))i^*(a)g\left(\frac{i(a, t)}{i^*(a)}\right)da. \end{split} | (21) |
Combining (20) with (21), we get
| \label{3} \begin{split} ~~\int_{t-a_1}^{t}&\varphi(t-\tau)\left[i^*(t-\tau)\frac{d}{dt}g\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right) +\frac{d}{dt}(i^*(t-\tau))g\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)\right]d\tau\\ = {}&\int_0^{a_1}\varphi(a)\Lambda_i(a)\left[2-\frac{i^*(a)}{i(a, t)}-\frac{i(a, t)}{i^*(a)}+g\left(\frac{i(a, t)}{i^*(a)}\right)\right]da\\ &-\int_0^{a_1}\varphi(a)(\mu_i(a)+\gamma_1(a))i^*(a)g\left(\frac{i(a, t)}{i^*(a)}\right)da\\ = {}&\int_0^{a_1}\varphi(a)\Lambda_i(a)\left(1-\frac{i^*(a)}{i(a, t)}+\ln\frac{i^*(a)}{i(a, t)}\right)da\\ &-\int_0^{a_1}\varphi(a)(\mu_i(a)+\gamma_1(a))i^*(a)g\left(\frac{i(a, t)}{i^*(a)}\right)da\\ = {}&-\int_0^{a_1}\varphi(a)\Lambda_i(a)g\left(\frac{i^*(a)}{i(a, t)}\right)da -\int_0^{a_1}\varphi(a)(\mu_i(a)+\gamma_1(a))i^*(a)g\left(\frac{i(a, t)}{i^*(a)}\right)da\\ \equiv{}& I_i\leq 0, \end{split} | (22) |
since
| \label{4} \begin{split} ~~ \int_{-\infty}^{t-a_1}&\psi(t-\tau)\left [c^*(t-\tau)\frac{d}{dt}g\left(\frac{c(t-\tau, t)}{c^*(t-\tau)}\right)+\frac{d}{dt}(c^*(t-\tau))g\left(\frac{c(t-\tau, t)}{c^*(t-\tau)}\right)\right] d\tau\\ = {}&\int_{a_1}^{\infty}\psi(a)\Lambda_c(a)\left(1-\frac{c^*(a)}{c(a, t)}+\ln\frac{c^*(a)}{c(a, t)}\right)da\\ ~~&-\int_{a_1}^{\infty}\psi(a)(\mu_c(a)+\gamma_2(a)+\theta(a))c^*(a)g\left(\frac{c(a, t)}{c^*(a)}\right)da\\ = {}&-\int_{a_1}^{\infty}\psi(a)\Lambda_c(a)g\left(\frac{c^*(a)}{c(a, t)}\right)da\\ &-\int_{a_1}^{\infty}\psi(a)(\mu_c(a)+\gamma_2(a)+\theta(a))c^*(a)g\left(\frac{c(a, t)}{c^*(a)}\right)da\\ \equiv{}& I_c\leq 0. \end{split} | (23) |
The terms (22) and (23) are a result of incorporating immigration; compare with the model in [26].
The time derivatives of functions
| \begin{align*} L_1'(t) = {}&-\frac{\mu_S+p}{S}(S-S^*)^2+S^*\left(\int_0^{a_1}\beta(a)i^*(a)da+\alpha\int_{a_1}^{\infty}\beta(a)c^*(a)da\right)\\ ~~~~~~~~~~ &+S^*\left(\int_0^{a_1}\beta(a)i(a, t)da+\alpha\int_{a_1}^{\infty}\beta(a)c(a, t)da\right)\\ ~~~~~~~~~~ &-S\left(\int_0^{a_1}\beta(a)i(a, t)da+\alpha\int_{a_1}^{\infty}\beta(a)c(a, t)da\right)\\ ~~~~~~~~~~ &-\frac{(S^*)^2}{S}\left(\int_0^{a_1}\beta(a)i^*(a)da+\alpha\int_{a_1}^{\infty}\beta(a)c^*(a)da\right), \\ L_2'(t) = {}&S\left(\int_0^{a_1}\beta(a)i(a, t)da+\alpha\int_{a_1}^{\infty}\beta(a)c(a, t)da\right)\\ ~~~~~~~~~~ &-\frac{E^*}{E}S\left(\int_0^{a_1}\beta(a)i(a, t)da+\alpha\int_{a_1}^{\infty}\beta(a)c(a, t)da\right)\\ ~~~~~~~~~~ &-(\sigma+\mu_E)(E-E^*)+\Lambda_E\left(1-\frac{E^*}{E}\right), \\ L_3'(t) = {}&\frac{d}{dt}\int_0^{a_1}\varphi(a)i^*(a)g\left(\frac{i(a, t)}{i^*(a)}\right)da\\ ~~~~~~~ = {}&\frac{d}{dt}\int_{t-a_1}^{t}\varphi(t-\tau)i^*(t-\tau)g\left(\frac{i(t-\tau, t)}{i^*(t-\tau)}\right)d\tau\\ ~~~~~~~ = {}&\varphi(0)G(i(0, t), i^*(0))+\int_0^{a_1}\varphi'(a)G(i(a, t), i^*(a))da+I_i, \end{align*} |
and
| \begin{align*} L_4'(t)& = \dfrac{d}{dt}\int_{a_1}^{\infty}\psi(a)c^*(a)g\left(\frac{c(a, t)}{c^*(a)}\right)da\\ ~~~~~~~ & = \dfrac{d}{dt}\int_{-\infty}^{t-a_1}\psi(t-\tau)c^*(t-\tau)g\left(\frac{c(t-\tau, t)}{c^*(t-\tau)}\right)d\tau\\ ~~~~~~~ & = \psi(a_1)G(c(0, t), c^*(0))+\int_{a_1}^{\infty}\psi'(a)G(c(a, t), c^*(a))da+I_c. \end{align*} |
We construct the following Lyapunov functional:
| L(t) = L_1(t)+L_2(t)+L_3(t)+L_4(t). |
We need to show that the time derivative along the solutions of (1) satisfies
| \frac{d}{dt}L(t) = L'_1(t)+L'_2(t)+L'_3(t)+L'_4(t)\leq 0. |
Note that
| \begin{align*} i(0, t)-i^*(0)& = \sigma(E-E^*), \\ c(a_1, t)-c^*(a_1)& = \int_0^{a_1}q(a)\gamma_1(a)[i(a, t)-i^*(a)]da, \\ (\sigma+\mu_E)E^*-\Lambda_E& = \int_0^{a_1}\beta(a)S^*i^*(a)da+\alpha\int_{a_1}^\infty\beta(a)S^*c^*(a)da. \end{align*} |
We have
| \begin{align*} (\sigma+\mu_E)E^*-\Lambda_E = {}&\int_0^{a_1}\beta(a)S^*i^*(0)\pi_1(a)da+\int_0^{a_1}\beta(a)S^*W_9(a)\pi_1(a)da\\ ~~&+\alpha\int_{a_1}^\infty\beta(a)S^*\pi_2(a)(c^*(a_1)+W_{10}(a))da\\ = {}&\int_0^{a_1}\beta(a)S^*i^*(0)\pi_1(a)da+\int_0^{a_1}\beta(a)S^*W_9(a)\pi_1(a)da\\ ~~&+\alpha\int_{a_1}^\infty\beta(s)S^*\pi_2(s)\int_0^{a_1}q(a)\gamma_1(a)(i^*(0)+W_9(a))\pi_1(a)dads\\ ~~&+\alpha\int_{a_1}^\infty\beta(s)S^*\pi_2(s)W_{10}(s)ds. \end{align*} |
Then
| \varphi(0)i^*(0)\ln\frac{i(0, t)}{i^*(0)} = ((\sigma+\mu_E)E^*-\Lambda_E)\ln\frac{i(0, t)}{i^*(0)}-W\ln\frac{i(0, t)}{i^*(0)} |
and
| \varphi(0)(i(0, t)-i^*(0)) = (\sigma+\mu_E)(E-E^*)-\Lambda_E\left(\frac{E}{E^*}-1\right)-W\left(\frac{E}{E^*}-1\right), |
where
| \begin{align*} W = {}&\int_0^{a_1}\beta(a)S^*W_9(a)\pi_1(a)da\\ &+\alpha\int_{a_1}^\infty\beta(s)S^*\pi_2(s)\int_0^{a_1}q(a)\gamma_1(a)W_9(a)\pi_1(a)dads\\ &+\alpha\int_{a_1}^\infty\beta(s)S^*\pi_2(s)W_{10}(s)ds. \end{align*} |
We also have
| \begin{align*} ~~\int_0^{a_1}q(a)&\gamma_1(a)i^*(a)\left[1-\frac{i(a, t)c^*(a_1)}{i^*(a)c(a_1, t)}\right]da \\ & = \int_0^{a_1}q(a)\gamma_1(a)i^*(a)da-\frac{c^*(a_1)}{c(a_1, t)}\int_0^{a_1}q(a)\gamma_1(a)i(a, t)da \\ & = c^*(a_1)-\frac{c^*(a_1)}{c(a_1, t)}c(a_1, t)\\ & = 0 \end{align*} |
and
| \begin{align*} ~~\frac{E^*}{E}S\bigg(\int_0^{a_1}\beta(a)&i(a, t)da+\alpha\int_{a_1}^\infty\beta(a)c(a, t)da\bigg)\\ & = \frac{i^*(0)}{i(0, t)}S\left(\int_0^{a_1}\beta(a)i(a, t)da+\alpha\int_{a_1}^\infty\beta(a)c(a, t)da\right)\\ & = \int_0^{a_1}\beta(a)S^*i^*(a)\frac{Si^*(0)i(a, t)}{S^*i(0, t)i^*(a)}da+\\ &\alpha\int_{a_1}^\infty\beta(a)S^*c^*(a)\frac{Si^*(0)c(a, t)}{S^*i(0, t)c^*(a)}da. \end{align*} |
Combining all these time derivatives of
| \begin{align*} &L'(t) = -\frac{\mu_S+p}{S}(S-S^*)^2\\ ~~~~~~~~~ &+\int_0^{a_1}\beta(a)S^*i^*(a)\left[1-\frac{S^*}{S}+\ln\frac{S^*}{S}+1-\frac{i(a, t)Si^*(0)}{i^*(a)S^*i(0, t)}+\ln\frac{Si^*(0)i(a, t)}{S^*i^*(a)i(0, t)}\right]da \\ ~~~~~~~~~ &+\alpha\int_{a_1}^\infty\beta(a)S^*c^*(a)\left[1-\frac{S^*}{S}+\ln\frac{S^*}{S}+1-\frac{Sc(a, t)i^*(0)}{S^*c^*(a)i(0, t)}+\ln\frac{Sc(a, t)i^*(0)}{S^*c^*(a)i(0, t)}\right]da \\ ~~~~~~~~~ &+\alpha S^* W_3\int_0^{a_1}q(a)\gamma_1(a)i^*(a)\left[1-\frac{i(a, t)c^*(a_1)}{i^*(a)c(a_1, t)}+\ln\frac{i(a, t)c^*(a_1)}{i^*(a)c(a_1, t)}\right]da\\ ~~~~~~~~~ &+\Lambda_E\left(2-\frac{E^*}{E}-\frac{E}{E^*}\right)+W\left(1-\frac{E}{E^*}+\ln\frac{i(0, t)}{i^*(0)}\right)+I_i+I_c. \end{align*} |
Noting that
| \frac{i(a, t)}{i^*(a)} = \frac{i(0, t)}{i^*(0)} = \frac{c(a, t)}{c^*(a)} = \frac{c(a_1, t)}{c^*(a_1)}. |
It can be verified that the largest invariant set where
Many epidemiological models assume that all infected individuals are equally infectious during their infectivity period, which is reasonable for some diseases, such as influenza. However, the infection of HBV is a dynamic process characterized by replicative and non-replicative phases based on virus-host interaction so that the infectivity of HBV individuals varies at different age of infection. It follows that age structure of the host population is an important factor for the dynamics of HBV transmission. In general, there are two different age structures in disease models: biological age and infection age. In this paper, according to the characteristics of HBV, we formulated a PDE model incorporating infection-age structure, as well as immigration age, into all compartments, in order to describe the possible effects of variable infectivity and immigration on the transmission dynamics.
The model studied in this paper is a refined version of the one investigated in [26], with age-dependent immigration into both acute and chronic infection stages. Immigration models do not have infection-free equilibria and hence have no reproduction number [17,18,11,3]. When immigration is introduced into the infectious compartment, the model has a unique globally asymptotically stable equilibrium. Age structure is only applicable to two infectious classes in this paper: the acute and chronic stages. In a more general setting, it can be added to any compartment [29].
In the case that the perinatal-related parameter
Relevant simulations in [12] suggest that immigration inflow is vital to the amplitude of the endemic equilibrium: small variations of the rate of immigration to the infectious and/or latent compartments can cause abrupt changes of quantity of endemicity. The feasible epidemiological solution is to screen immigrants with high risk of disease as a first step to control infection from the source. Finally, the scale of the problem and the availability of a safe and effective vaccine means that many more people should be protected from HBV than currently are. Outmoded and ignorant attitudes towards vaccines are costing a great deal of lives that could be saved with the application of evidence-based research.
For citation purposes, please note that the question mark in "Smith?" is part of his name.
| [1] | [ World Health Organization, 2008, Hepatitis B. World Health Organization Fact Sheet N°204, Available from http://www.who.int/mediacentre/factsheets/fs204/en/index.html |
| [2] |
[ F. Brauer, Z. Shuai and P. van den Driessche, Dynamics of an age-of-infection cholera model, Math. Biosci. Eng., 10 (2013), 1335-1349. doi: 10.3934/mbe.2013.10.1335

|
| [3] |
[ F. Brauer and P. van den Driessche, Models for transmission of disease with immigration of infectives, Math. Biosci., 171 (2001), 143-154. doi: 10.1016/S0025-5564(01)00057-8

|
| [4] | [ D. Candotti, O. Opare-Sem and H. Rezvan, Molecular and serological characterization of hepatitis B virus in deferred Ghanaian blood donors with and without elevated alanine aminotransferase, J. Viral. Hepat., 13 (2006), 715-724. |
| [5] | [ P. Dény and F. Zoulim, Hepatitis B virus: from diagnosis to treatment, Pathol Biol., 58 (2010), 245-253. |
| [6] |
[ W. Edmunds, G. Medley and D. Nokes, The influence of age on the development of the hepatitis B carrier state, Proc. R. Soc. Lond. B., 253 (1993), 197-201. doi: 10.1098/rspb.1993.0102

|
| [7] |
[ A. Franceschetti and A. Pugliese, Threshold behaviour of a SIR epidemic model with age structure and immigration, J. Math. Biol., 57 (2008), 1-27. doi: 10.1007/s00285-007-0143-1

|
| [8] | [ E. Franco, B. Bagnato and M. G. Marino, Hepatitis B: Epidemiology and prevention in developing countries, World J. Hepatol., 4 (2012), 74-80. |
| [9] |
[ D. Ganem and A. M. Prince, Hepatitis B virus infection-natural history and clinical consequences, N. Engl. J. Med., 350 (2004), 1118-1129. doi: 10.1056/NEJMra031087

|
| [10] |
[ L. Gross, A Broken Trust: Lessons from the Vaccine-Autism Wars, PLoS Biol., 7 (2009), e1000114. doi: 10.1371/journal.pbio.1000114

|
| [11] |
[ H. Guo and M. Y. Li, Impacts of migration and immigration on disease transmission dynamics in heterogenous populations, Discrete Contin. Dyn. Syst. Ser B, 17 (2012), 2413-2430. doi: 10.3934/dcdsb.2012.17.2413

|
| [12] | [ H. Guo and M. Y. Li, Global stability of the endemic equilibrium of a tuberculosis model with immigration and treatment, Canad. Appl. Math. Quart., 19 (2012), 1-17. |
| [13] |
[ G. Huang, X. Liu and Y. Takeuchi, Lyapunov functions and global stability for age-structured HIV infection model, SIAM J. Appl. Math., 72 (2012), 25-38. doi: 10.1137/110826588

|
| [14] | [ M. Kane, Global programme for control of hepatitis B infection, Vaccine, 13 (1995), S47-S49. |
| [15] |
[ P. Magal, C. McCluskey and G. Webb, Lyapunov functional and global asymptotic stability for an infection-age model, Applicable Analysis, 89 (2010), 1109-1140. doi: 10.1080/00036810903208122

|
| [16] | [ E. E. Mast, J. W. Ward and H. B Vaccine, Vaccines (S. Plotkin, W. Orenstein & P. Offit), 5th edition, WB Saunders Company, (2008), 205–242. |
| [17] |
[ C. McCluskey, Global stability for an SEI epidemiological model with continuous age-structure in the exposed and infectious classes, Math. Biosci. Eng., 9 (2012), 819-841. doi: 10.3934/mbe.2012.9.819

|
| [18] |
[ C. McCluskey, Global stability for an SEI model of infectious disease with age structure and immigration of infecteds, Math. Biosci. Eng., 13 (2016), 381-400. doi: 10.3934/mbe.2015008

|
| [19] |
[ G. Medley, N. Lindop, W. Edmunds and D. Nokes, Hepatitis-B virus endemicity: Heterogeneity, catastrophic dynamics and control, Nature Medicine, 7 (2001), 619-624. doi: 10.1038/87953

|
| [20] | [ Y. Mekonnen, R. Jegou and R. A. Coutinho, Demographic impact of AIDS in a low-fertility urban African setting: Projection for Addis Ababa, Ethiopia, J. Health Popul. Nutr., 20 (2002), 120-129. |
| [21] |
[ S. K. Parker, B. Schwartz, J. Todd and L. K. Pickering, Thimerosal-Containing Vaccines and Autistic Spectrum Disorder: A Critical Review of Published Original Data, Pediatrics, 114 (2004), 793-804. doi: 10.1137/060663945

|
| [22] | [ L. Rong, Z. Feng and A. Perelson, Mathematical analysis of age-structured HIV-1 dynamics with combination antiretroviral therapy, SIAM J. Appl. Math., 67 (2007), 731-756. |
| [23] | [ H. Smith and H. Thieme, Dynamical Systems and Population Persistence, American Mathematical Society, Providence, 2011. |
| [24] | [ G. F. Webb, Theory of Nonlinear Age-dependent Population Dynamics, Marcel Dekker, New York, 1985. |
| [25] | [ W. W. Williams, P.-J. Lu and A. O'Halloran, Vaccination Coverage Among Adults, Excluding Influenza Vaccination -- United States, 2013, Morbidity and Mortality Weekly Report, 64 (2015), 95-102. |
| [26] |
[ S. Zhang and X. Xu, A mathematical model for hepatitis B with infection-age structure, Discrete Contin. Dyn. Syst. Ser. B, 21 (2016), 1329-1346. doi: 10.3934/dcdsb.2016.21.1329

|
| [27] |
[ S. Zhao, Z. Xu and Y. Lu, A mathematical model of hepatitis B virus transmission and its application for vaccination strategy in China, Int. J. Epidemiol., 29 (1994), 744-752. doi: 10.1093/ije/29.4.744

|
| [28] |
[ X. Zhao, Dynamical Systems in Population Biology, Springer-Verlag, New York, 2003. doi: 10.1007/978-0-387-21761-1

|
| [29] |
[ L. Zou, S. Ruan and W. Zhang, An age-structured model for the transmission dynamics of hepatitis B, SIAM J. Appl. Math., 70 (2010), 3121-3139. doi: 10.1137/090777645

|
| 1. | Jean Pierre II Kouenkam, Joseph Mbang, Yves Emvudu, Global dynamics of a model of hepatitis B virus infection in a sub-Saharan African rural area, 2020, 13, 1793-5245, 2050054, 10.1142/S1793524520500540 | |
| 2. | Getachew Teshome Tilahun, Woldegebriel Assefa Woldegerima, Nesredin Mohammed, A fractional order model for the transmission dynamics of hepatitis B virus with two-age structure in the presence of vaccination, 2021, 28, 2576-5299, 87, 10.1080/25765299.2021.1896423 | |
| 3. | Chao Liu, Peng Chen, Qiyu Jia, Lora Cheung, Effects of Media Coverage on Global Stability Analysis and Optimal Control of an Age-Structured Epidemic Model with Multi-Staged Progression, 2022, 10, 2227-7390, 2712, 10.3390/math10152712 | |
| 4. | Jianquan Li, Yuming Chen, Peijun Zhang, Dian Zhang, Global Stability of a Viral Infection Model with Defectively Infected Cells and Latent Age, 2024, 45, 0252-9599, 555, 10.1007/s11401-024-0028-2 | |
| 5. | Salah Boulaaras, Aasim Ullah Jan, Tahir Hassan, Taha Radwan, Mathematical modeling and computational analysis of hepatitis B virus transmission using the higher-order Galerkin scheme, 2024, 13, 2192-8029, 10.1515/nleng-2024-0048 |
| Symbol | Definition |
| rate of recruitment into the susceptible compartment, | |
| including unsuccessfully immunized birth and immigration | |
| immigration rate into class |
|
| age-dependent immigration rate into class |
|
| per capital death rate for class |
|
| age-dependent death rate for class |
|
| birth rate | |
| proportion of newborns who are unsuccessfully immunized | |
| transfer rate from exposed to acute infection | |
| vaccination rate | |
| degree of infectiousness of carriers relative to acute infections ( |
|
| age-dependent transmission coefficient | |
| age-dependent rate of children born to carrier mothers | |
| who become HBV carriers | |
| age-dependent transfer rate from acute to immunized or carrier class | |
| age-dependent transfer rate from carrier to immunized class | |
| age-dependent progression from acute infection to carrier class | |
| age-dependent HBV-induced death rate |
| Symbol | Definition |
| rate of recruitment into the susceptible compartment, | |
| including unsuccessfully immunized birth and immigration | |
| immigration rate into class |
|
| age-dependent immigration rate into class |
|
| per capital death rate for class |
|
| age-dependent death rate for class |
|
| birth rate | |
| proportion of newborns who are unsuccessfully immunized | |
| transfer rate from exposed to acute infection | |
| vaccination rate | |
| degree of infectiousness of carriers relative to acute infections ( |
|
| age-dependent transmission coefficient | |
| age-dependent rate of children born to carrier mothers | |
| who become HBV carriers | |
| age-dependent transfer rate from acute to immunized or carrier class | |
| age-dependent transfer rate from carrier to immunized class | |
| age-dependent progression from acute infection to carrier class | |
| age-dependent HBV-induced death rate |