1. Introduction

We consider the spread of a disease carried by a biological species and transmitted through contaminated environment. We assume the diseased individuals move randomly in a spatial domain $\Omega$ (a smooth open bounded set in a finite dimensional space) following the standard diffusion, and subject to the Dirichlet condition on the boundary $\partial \Omega$ as the boundary is not suitable for the diseased individuals to survive (due to disease prevention and control, or due to the natural environmental constraints). We model the situation where the growth of the infection in the biological population is proportional to the number of diseased individuals as the amount of pathogen loads released to the environment is proportional to this number of diseased cases. We further consider the case where a certain amount of resources is available to clean the environment, a portion of the sources can be used to respond to the contamination relatively faster (with a delay given by $\tau_1$) and the rest can be used for slower response characterized by another average delay $\tau_2>\tau_1$. This yields the following model

$\dfrac{\partial u}{\partial t}=d\Delta u+ru[1-a_1\int_\Omega P_1(x, y)u(y, t-\tau_1)dy-a_2\int_\Omega P_2(x, y)u(y, t-\tau_2)dy],$

(1)

where $u(t, x)$ is the population density of infected individuals at time $t$ and location $x$, $(t, x)\in(0, \infty)\times \Omega$, $d$ is the diffusion rate, $r$ is the reproduction ratio of the diseased populations. The total environment available for the pathogen contamination is normalized to 1. In the first nonlocal delayed integration, $u(y, t-\tau _1)$ is the pathogen loads released by the infected individuals at time $t-\tau _1$ and spatial location $y$ and $P_1(x, y)$ is the probability of the pathogen moved from the spatial location $y$ to current location $x$. A certain biosafety intervention measure is implemented, in proportion to the pathogen loads $\int _{\Omega }P_1(x, y)u(y, t-\tau _1)dy$, but with a time lag $\tau _1$. Similar interpretations apply to the second integration, but with a longer delay $\tau _2$. The constants $a_1$ and $a_2$ satisfy $a_1+a_2=1$, where $a_1 \in [0, 1]$ represents the allocation of resources to be allocated to implement the intervention measure for either rapid or slow response to protect the environment from being used to be contaminated to spread the disease back to the biological species under consideration. The kernel function are relevant to the mobility of the virus and this can be derived in a similar fashion as in [14].

Note that we assume the time for the biosafety intervention is much slower than the virus spread in the environment, and hence the delay in the spread process is ignored. $\Delta$ stands for the Laplacian operator, with following Dirichlet boundary condition

$u(x, t)=0, x\in \partial\Omega \;\; \text{and} \;\; t\in(0, +\infty)$

which implies that the exterior environment is hostile and the species cannot move across the boundary of environment, and initial condition satisfies

$u(x, s)=\eta(x, s)\geq 0, x\in \Omega \;\; \text{and} \;\; t\in[-\tau, 0],$

where $\Omega\subset \mathbb{R}^n(n\geq 1)$ is a bounded domain with smooth boundary $\partial \Omega$, $\tau=\max(\tau_1, \tau_2)$, $\eta\in \mathcal{C}:=C([-\tau, 0], Y)$ and $Y=L^2(\Omega)$.

This study is motivated by the spread of avian influenza, an infectious disease of birds that is caused by influenza virus type A strains. The involvement of different bird species and their interactions with environments together lead to complex transmission pathways which include birds to birds, birds to mammals, birds to human, birds to insects, human to human, and environment to birds/mammals/human and vice-versa [9]. How to model the interplay of different transmission pathways and its impact on the spread of avian influenza imposes significant challenge [1][11][16]. In the study of Wang et al.[17], a system of reaction diffusion equations on unbounded domains was proposed to establish the existence and nonexistence of traveling wave solutions of a reaction-convection epidemic model for the spatial spread of avian influenza involving a wide range of bird species and environmental contamination. In the earlier studies of Gourley et al.[6], the role of migrating birds were examined using partial differential equations and their reduction to delay differential systems. Here we focus on the spread of avian influenza among the wild birds, where the virus is shredded into the environment, through which the virus further spreads and infects other wild birds coming to contact with contaminated environment. The parameter $r$ represents the intrinsic susceptibility and transmissibility of the environment, which can be reduced through biosafety intervention so the nonlinearity in the kinetic equation for the infected individuals resembles the classical delayed non-local logistic equations. Note that a large portion of the environment for the virus spread and contamination involves water, the kernel functions $P_1$ and $P_2$ for the virus spread in the environment can involve both diffusion and convercation.

Our goal in this paper is to 1). Determine whether there is a critical value of $r$ above which the disease will persist in the population in the form of a nonnegative non-trivial equilibrium (note this is necessarily spatially varying due to the Dirichlet condition); 2). Identify critical value of the rapid response delay where the nontrivial equilibrium remains locally stable when all resources are committed for the rapid biosafety intervention; 3). Identify critical value of the slow response delay where the nontrivial equilibrium loses its locally stability even when all resources are committed for the slow biosafety intervention; 4). Identify the critical resource allocation parameter $\alpha$ when a Hopf bifurcation takes place from the nontrivial equilibrium, in this case we examine the patterns of bifurcated periodic solutions to examine impact of parameters on the peak and frequency of the spatiotemporally varying stable patterns.

We use $r_*$ to denote the principal eigenvalue of the following one-dimensional eigenvalue problem

$\begin{cases} -d\Delta u(x)=ru(x), x\in\Omega, \\ u(x)=0, x\in \partial \Omega, \\ \end{cases}$

and $\phi$ is the corresponding eigenfunction of $r_*$ with $\phi (x)>0$ for $x\in \Omega$. The following notations are needed. Let $L^p(\Omega)$ $(p\geq 1)$ be the space consisting of measurable functions on $\Omega$ that are $p$-integrable, and $H^k(\Omega)$ $(k\geq 0)$ be the space consisting of functions whose $k$-th order weak derivatives belong to $L^2(\Omega)$. Denote the spaces $X=H^2(\Omega)\cap H_0^1(\Omega)$ and $Y=L^2(\Omega)$, where $H_0^1(\Omega)=\{u\in H^1(\Omega)|u(x)=0 \;\;\text{ for all }\;\; x\in \partial \Omega\}$. For any real-valued vector space $Z$, we also denote the complexification of $Z$ to be $Z_\mathbb{C}:=Z\oplus iZ=\{x_1+ix_2|x_1, x_2\in Z\}$. For a linear operator $L: Z_1\rightarrow Z_2$, we denote the domain of $L$ by $\mathscr{D}(L)$, the null space by $\mathscr{N}(L)$ and the range of $L$ by $\mathscr{R}(L)$. For the complex-valued Hilbert space $Y_\mathbb{C}$, the standard inner product is $<u, v>=\int_\Omega \bar{u}(x)v(x)dx$. In what follows, we assume the comparability condition between the kernel functions $P_i(x, y),$ $i=1, 2$ and the eigenfunction $\phi$. Namely, we assume $\int_\Omega\int_\Omega (P_1(x, y)+P_2(x, y))\phi(y)\phi(x)dydx\neq 0$. This is because one of the kernel functions can be zero.

---

2. Existence of steady state solution

The positive steady state solutions of (1) satisfy the following equation:

$\begin{cases} d\Delta u+ru[1-\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_\Omega P_i(x, y)u(y)dy]=0, x\in\Omega, \\ u(x)=0, x\in \partial \Omega.\\ \end{cases}$

(2)

Let $\mathscr{N}(d\Delta+r_*)$ and $\mathscr{R}(d\Delta+r_*)$ be the null space and the range of the operator $d\Delta+r_*$, then

$\begin{aligned}\mathscr{N}(d\Delta+r_*)&=span\{\phi\}, \\ \mathscr{R}(d\Delta+r_*)&=\{y\in L^2(\Omega)|<\phi, y>=0\}. \end{aligned}$

Then we have the following decompositions:

$\begin{aligned}X&=\mathscr{N}(d\Delta+r_*)\oplus \hat X, \\ Y&=\mathscr{N}(d\Delta+r_*)\oplus \mathscr{R}(d\Delta+r_*), \end{aligned}$

where

$\hat X=\{y\in X|<\phi, y>=0\}.$

Then we have the following result on positive steady state solution of model (1).

Theorem 2.1. There exist $r^*>r_*$ and a continuously differential mapping $r\mapsto (\xi_r, \alpha_r)$ from $[r_*, r^*]$ to $\hat X\times \mathbb{R}^+$ such that the model (1) has a positive steady state solution as follows

$u_r(x)=\alpha_r(r-r_*)[\phi(x)+(r-r_*)\xi_r(x)], r\in[r_*, r^*].$

Moreover,

$\alpha_{r_*}=\dfrac{\int_\Omega \phi^2(x)dx}{r_*\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_\Omega\int_\Omega P_i(x, y)\phi^2(x)\phi(y)dxdy\end{pmatrix}}$

and $\xi_{r_*}\in X_1$ is the unique solution of the following equation

$(d\Delta+r_*)\xi+\phi[1-r_*\alpha_{r_*}\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_{\Omega}P_i(x, y)\phi(y)dy\end{pmatrix}]=0.$

The proof is standard. Namely, we let $f: \hat X\times \mathbb{R}\times \mathbb{R}\rightarrow Y$ be defined by

$\begin{aligned}f(\xi_r, \alpha_r, r)=&(d\Delta+r_*)\xi_r+\phi(x)+(r-r_*)\xi_r-r\alpha_r\begin{pmatrix}\phi(x)+(r-r_*)\xi_r\end{pmatrix}\\&\cdot\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_{\Omega}P_i(x, y)\begin{pmatrix}\phi(y)+(r-r_*)\xi(y)\end{pmatrix}dy\end{pmatrix}, \end{aligned}$

then $f(\xi_{r_*}, \alpha_{r_*}, r_*)=0$. The partial derivative of $f$ at $(\xi_{r_*}, \alpha_{r_*}, r_*)$ is given by

$D_{(\xi_r, \alpha_r)}f(\xi_{r_*}, \alpha_{r_*}, r_*)(\eta, \epsilon)=(d\Delta+r_*)\eta-r\phi(x)\epsilon\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^2}a_i\int_{\Omega}P_i(x, y)\phi(y)dy\end{pmatrix}.$

Under the comparability condition, we have $\phi(x)\int_{\Omega}(P_1(x, y)+P_2(x, y))\phi(y)dy\notin \mathscr{R}(d\Delta+r_*)$. Then $D_{(\xi_r, \alpha_r)}f(\xi_{r_*}, \alpha_{r_*}, r_*)$ is bijective from $\hat X\times \mathbb{R}$ to $Y$. From the implicit function theorem, there exist $r^*>r_*$ and a unique continuously differential mapping $r\mapsto (\xi_r, \alpha_r)$ from $[r_*, r^*]$ to $\hat X\times \mathbb{R}^+$ such that

$f(\xi_r, \alpha_r, r)=0, r\in[r_*, r^*].$

Therefore, $u_r(x)=\alpha_r(r-r_*)[\phi(x)+(r-r_*)\xi_r(x)]$ solves the boundary value problem (2).

In what follows, we always assume that $r\in (r_*, r^*]$ and $r^*-r_*\ll 1$.

---

3. Eigenvalue analysis

It is easy to see that the linearized equation of the model (1) at the steady state solution $u_r$ can be written as

$\left\{ \begin{aligned} \dfrac{\partial v(x, t)}{\partial t}=&d\Delta v(x, t)+rv(x, t)[1-\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_\Omega P_i(x, y)u_r(y)dy\end{pmatrix}] -ru_r(x)\\&\cdot\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_\Omega P_i(x, y)v(y, t-\tau_i)dy\end{pmatrix}, x\in\Omega, t>0, \\ v(x, t)=&0, x\in \partial \Omega, \ t>0, \\ v(x, t)=&\eta(x, t), (x, t)\in \Omega\times [-\tau, 0], \end{aligned}\right.$

(3)

where $\eta\in \mathcal{C}$.

Define a operator $A_r: \mathscr{D}(A_r)\rightarrow Y$ with domain $\mathscr{D}(A_r)=X$ by

$A_r=d\Delta+r[1-\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_{\Omega}P_i(x, y)u_r(y)dy\end{pmatrix}].$

From [13], $A_r$ is an infinitesimal generator of a strong continuous semigroup and $A_r$ is also self-adjoint. Then the study of the stability of $u_r$ is transferred to the analysis of the following eigenvalue problem

$\Lambda(r, \lambda, \tau_1, \tau_2)\psi=A_r\psi-ru_r\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_ie^{-\lambda\tau_i}\int_\Omega P_i(x, y)\psi(y)dy\end{pmatrix}-\lambda\psi=0,$

(4)

where $\psi\in X_{\mathbb{C}}\backslash \{0\}$, i.e., the study of the following spectral set

$\sigma(A_{\tau_1\tau_2, r})=\{\lambda\in \mathbb{C}: \Lambda(r, \lambda, \tau_1, \tau_2)\psi=0, \;\;\text{for}\;\; \psi\in X_{\mathbb{C}}\backslash \{0\}\},$

where $A_{\tau_1\tau_2, r}$ is the infinitesimal generator of the semigroup induced by the solutions of equation (3) with

$A_{\tau_1\tau_2, r}\psi=\dot{\psi},$

and

$\begin{aligned}&\mathscr{D}(A_{\tau_1\tau_2, r})\\=&\{\psi\in C_{\mathbb{C}}\cap C_{\mathbb{C}}^1: \psi(0)\in X_{\mathbb{C}}, \dot{\psi}(0) =A_r\psi(0)-ru_r\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_i\int_{\Omega}P_i(x, y)\psi(y, -\tau_i)dy\end{pmatrix}\}, \end{aligned}$

where $C_{\mathbb{C}}^1=C^1([-\tau, 0], Y_{\mathbb{C}})$.

Then $A_{\tau_1\tau_2, r}$ has a purely imaginary roots $\lambda=i\omega\;(\omega\neq 0)$ for $\tau_1, \ \tau_2\geq 0$ if and only if

$A_r\psi-ru_r\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_ie^{-i\omega\tau_i}\int_{\Omega}P_i(x, y)\psi(y)dy\end{pmatrix}-i\omega\psi=0$

is solvable for some $\omega>0$ and $\psi\in X_{\mathbb{C}}\backslash\{0\}$.

Next, we discuss the effects of two nonlocal delays on the stability at the positive steady state solution $u_r$ in four different cases.

Case 1. $\tau_1=0$ and $\tau_2>0$.

In this case, the equation (4) can be reduced into

$\begin{aligned} &\Lambda(r, \lambda, 0, \tau_2)\psi\\=&A_r\psi-ru_r[a_1\int_\Omega P_1(x, y)\psi(y)dy+a_2e^{-\lambda \tau_2}\int_\Omega P_2(x, y)\psi(y)dy]-\lambda\psi=0. \end{aligned}$

(5)

If there exit $i\omega_{\tau_2} (\omega_{\tau_2}>0)$ and $\psi_{\tau_2}\in X_{\mathbb{C}}\backslash \{0\}$ satisfying (5), then

$\left\langle A_r\psi_{\tau_2}-ru_r\int_\Omega \begin{pmatrix}a_1P_1(x, y)+a_2e^{-i\omega_{\tau_2}\tau_2}P_2(x, y)\end{pmatrix}\psi_{\tau_2}(y)dy-i\omega_{\tau_2}\psi_{\tau_2}, \psi_{\tau_2} \right\rangle=0.$

(6)

Separating the real and imaginary parts, we obtain

$\begin{aligned}&\left\langle \omega_{\tau_2}\psi_{\tau_2}, \psi_{\tau_2} \right\rangle\\ =&\text{Im}\left\langle-ru_r\int_{\Omega}(a_1P_1(x, y)+a_2e^{-i\omega_{\tau_2}\tau_2}P_2(x, y))\psi_{\tau_2}(y)dy, \psi_{\tau_2}\right\rangle\\ \leq &\displaystyle{\sum\limits_{i=1}^2}\left|\left\langle ru_r\int_{\Omega}a_iP_i(x, y)\psi_{\tau_2}(y)dy, \psi_{\tau_2}\right\rangle\right|. \end{aligned}$

Thus,

$\dfrac{\omega_{\tau_2}}{r-r_*}\leq (a_1+a_2)r\alpha_r(\| \phi\|_\infty+(r-r_*)\|\xi_r\|_\infty)\max\limits_{\bar{\Omega}\times \bar{\Omega}}P_i(x, y)|\Omega|.$

(7)

It implies that $\frac{\omega_{\tau_2}}{r-r_*}$ is uniformly bounded for $r\in(r_*, r^*]$.

Ignoring a scalar factor, we know that $\psi_{\tau_2}$ can be expressed as

$\begin{aligned}\psi_{\tau_2}=\beta_{\tau_2}\phi+(r-r_*)z_{\tau_2}, \langle \phi, z_{\tau_2} \rangle=0, \beta_{\tau_2}\geq 0, \\ \|\psi_{\tau_2}\|_{Y_{\mathbb{C}}}^2=\beta_{\tau_2}^2\|\phi\|_{Y_{\mathbb{C}}}^2+(r-r_*)^2\|z_{\tau_2}\|_{Y_\mathbb{C}}^2=\|\phi\|_{Y_\mathbb{C}}^2. \end{aligned}$

(8)

Substituting (8) and $\omega_{\tau_2}=(r-r_*)k_{\tau_2}$ into (5), we have the following equivalent equation to (5)

$\begin{aligned}g_1(z_{\tau_2}, \beta_{\tau_2}, k_{\tau_2}, r)=&(d\Delta+r_*)z_{\tau_2}+[1-ik_{\tau_2}-\displaystyle{\sum\limits_{i=1}^{2}}\int_{\Omega}a_ir\alpha_rP_i(x, y)(\phi(y)+(r-r_*)\\&\cdot\xi_r(y))dy] (\beta_{\tau_2}\phi+(r-r_*)z_{\tau_2})-r\alpha_r(\phi(x)+(r-r_*)\xi_r(x))\\ &\cdot\int_{\Omega}(a_1P_1(x, y)+a_2e^{-i\omega_{\tau_2}\tau_2}P_2(x, y))(\beta_{\tau_2}\phi+(r-r_*)z_{\tau_2})dy\\=&0, \\ g_2(z_{\tau_2}, \beta_{\tau_2}, k_{\tau_2}, r)=&(\beta_{\tau_2}^2-1)\|\phi\|_{Y_{\mathbb{C}}}^2+(r-r_*)^2\|z_{\tau_2}\|_{Y_\mathbb{C}}^2=0. \end{aligned}$

Define $G_{\tau_2}: \hat{X}_\mathbb{C}\times \mathbb{R}^3\mapsto Y_{\mathbb{C}}\times \mathbb{R}$ by $G_{\tau_2}=(g_1, g_2)$. It is clear that

$G_{\tau_2}(z_{\tau_2, r_*}, \beta_{\tau_2, r_*}, k_{\tau_2, r_*}, r_*)=0.$

Denote

$\tilde a_i=a_i\int_{\Omega}\int_{\Omega}P_i(x, y)\phi^2(x)\phi(y)dxdy, \;\;\text{for}\;\; i=1, 2.$

Separating the real and imaginary parts of $g_1(z_{\tau_2, r_*}, \beta_{\tau_2, r_*}, k_{\tau_2, r_*}, r_*)=0$, we have

$\left\{\begin{aligned} (d\Delta+r_*)z_{\tau_2, r_*}^1+&[1-\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^{2}}a_ir_*\alpha_{r_*}\int_{\Omega}P_i(x, y)\phi(y)dy\end{pmatrix}] \phi-r_*\alpha_{r_*}\phi(x)\\&\cdot\int_{\Omega}(a_1P_1(x, y)+a_2P_2(x, y)\cos(\omega_{\tau_2, r_*}\tau_2))\phi(y)dy=0, \\ (d\Delta+r_*)z_{\tau_2, r_*}^2-&k_{\tau_2, r_*}\phi+a_2r_*\alpha_{r_*}\phi(x)\int_{\Omega}P_2(x, y)\phi(y)dy\sin(\omega_{\tau_2, r_*}\tau_2)=0, \end{aligned}\right.$

(9)

where $z_{\tau_2, r_*}=z_{\tau_2, r_*}^1+iz_{\tau_2, r_*}^2$.

From Theorem (2.1), it can be seen that Eq. (9) is solvable if and only if

$\begin{aligned}z_{\tau_2, r_*}&=(1-ik_{\tau_2, r_*})\xi_{r_*}, k_{\tau_2, r_*}=\dfrac{\sqrt{\tilde{a}_2^2-\tilde{a}_1^2}}{\tilde{a}_1+\tilde{a}_2}, (\tilde{a}_2>\tilde{a}_1)\\\beta_{\tau_2, r_*}&=1, \omega_{\tau_2, r_*}\tau_2=\arccos(-\dfrac{\tilde a_1}{\tilde a_2})+2n\pi, n=0, 1, 2, \cdots.\end{aligned}$

Case 2. $\tau_1>0$ and $\tau_2=0$.

Assume that $\tilde a_1\geq \tilde a_2$. Using a similar analysis as in the Case 1, we can obtain the following result:

If there exit $i\omega_{\tau_1} (\omega_{\tau_1}>0)$ and $\psi_{\tau_1}\in X_{\mathbb{C}}\backslash \{0\}$ satisfying

$A_r\psi_{\tau_1}-ru_r\int_\Omega \begin{pmatrix}a_1e^{-i\omega_{\tau_1}\tau_1}P_1(x, y)+a_2P_2(x, y)\end{pmatrix} \psi_{\tau_1}(y)dy-i\omega_{\tau_1}\psi_{\tau_1}=0,$

then $\frac{\omega_{\tau_1}}{r-r_*}$ is uniformly bounded for $r\in(r_*, r^*]$. The equivalent equation to (5) is $G_{\tau_1}=(g_1(z_{\tau_1}, \beta_{\tau_1}, k_{\tau_1}, r), g_2(z_{\tau_1}, \beta_{\tau_1}, k_{\tau_1}, r))$, where

$\begin{aligned}g_1(z_{\tau_1}, \beta_{\tau_1}, k_{\tau_1}, r)&=(d\Delta+r_*)z_{\tau_1}+[1-ik_{\tau_1}-\displaystyle{\sum\limits_{i=1}^{2}}\int_{\Omega}a_ir\alpha_rP_i(x, y)(\phi(y)+(r-r_*)\\&\cdot\xi_r(y))dy] (\beta_{\tau_1}\phi+(r-r_*)z_{\tau_1})-r\alpha_r(\phi(x)+(r-r_*)\xi_r(x))\\ &\cdot\int_{\Omega}(a_1e^{-i\omega_{\tau_1}\tau_1}P_1(x, y)+a_2P_2(x, y))(\beta_{\tau_1}\phi+(r-r_*)z_{\tau_1})dy=0, \\ g_2(z_{\tau_1}, \beta_{\tau_1}, k_{\tau_1}, r)&=(\beta_{\tau_1}^2-1)\|\phi\|_{Y_{\mathbb{C}}}^2+(r-r_*)^2\|z_{\tau_1}\|_{Y_\mathbb{C}}^2=0. \end{aligned}$

Moreover, it is easy to see that $G_{\tau_1}(z_{\tau_1, r_*}, \beta_{\tau_1, r_*}, k_{\tau_1, r_*}, r_*)=0$, where

$\begin{aligned}&z_{\tau_1, r_*}=(1-ik_{\tau_1, r_*})\xi_{r_*}, k_{\tau_1, r_*}=\dfrac{\sqrt{\tilde a_1^2-\tilde a_2^2}}{\tilde a_1+\tilde a_2}, (\tilde a_1>\tilde a_2)\\ &\beta_{\tau_1, r_*}=1, \omega_{\tau_1, r_*}\tau_1=\arccos(-\dfrac{\tilde a_2}{\tilde a_1})+2n\pi, n=0, 1, 2, \cdots.\end{aligned}$

Case 3. $\tau_1\in(0, \tau_{10})$ and $\tau_2>0$.

In this case, we consider $\tau_2$ as a parameter and $\tau_1$ being in the stable interval $(0, \tau_{10})$. Assume that, for some $\tau_2>0$, $i\omega_{\tau_1\tau_2}\ (\omega_{\tau_1\tau_2}>0)$ and $\psi_{\tau_1\tau_2}\in X_{\mathbb{C}}\backslash \{0\}$ are a solution of the equation (4). If we substitute this solution into the inner product $\left\langle \Delta(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)\psi_{\tau_1\tau_2}, \psi_{\tau_1\tau_2}\right\rangle$ and separate the imaginary part, then we obtain the following equation:

$\begin{aligned}&\left\langle \omega_{\tau_1\tau_2}\psi_{\tau_1\tau_2}, \psi_{\tau_1\tau_2} \right\rangle\\ =&\text{Im}\left\langle-ru_r\int_{\Omega}\begin{pmatrix}a_1e^{-i\omega_{\tau_1\tau_2}\tau_1}P_1(x, y)+a_2e^{-i\omega_{\tau_1\tau_2}\tau_2}P_2(x, y)\end{pmatrix}\psi_{\tau_1\tau_2}(y)dy, \psi_{\tau_1\tau_2}\right\rangle. \end{aligned}$

Therefore, $\frac{\omega_{\tau_1\tau_2}}{r-r_*}$ has the same boundary as shown in (7), i.e., $\frac{\omega_{\tau_1\tau_2}}{r-r_*}$ is uniformly bounded for $r\in(r_*, r^*]$. Then we can rewrite $\psi_{\tau_1\tau_2}$ as

$\begin{aligned}\psi_{\tau_1\tau_2}=\beta_{\tau_1\tau_2}\phi+(r-r_*)z_{\tau_1\tau_2}, \langle \phi, z_{\tau_1\tau_2} \rangle=0, \beta_{\tau_1\tau_2}\geq 0, \\ \|\psi_{\tau_1\tau_2}\|_{Y_{\mathbb{C}}}^2=\beta_{\tau_1\tau_2}^2\|\phi\|_{Y_{\mathbb{C}}}^2+(r-r_*)^2\|z_{\tau_1\tau_2}\|_{Y_\mathbb{C}}^2=\|\phi\|_{Y_\mathbb{C}}^2. \end{aligned}$

(10)

Based on (10) and $\omega_{\tau_1\tau_2}=(r-r_*)k_{\tau_1\tau_2}$, we obtain the equivalent equation to (5) as follows:

$\begin{aligned}g_1(z_{\tau_1\tau_2}, \beta_{\tau_1\tau_2}, k_{\tau_1\tau_2}, r)=&(d\Delta+r_*)z_{\tau_1\tau_2}+[1-ik_{\tau_1\tau_2}-\displaystyle{\sum\limits_{i=1}^{2}}\int_{\Omega}a_ir\alpha_rP_i(x, y)(\phi(y)\\&+(r-r_*)\xi_r(y))dy] (\beta_{\tau_1\tau_2}\phi+(r-r_*)z_{\tau_1\tau_2})-r\alpha_r(\phi(x)\\&+(r-r_*)\xi_r(x)) \displaystyle{\sum\limits_{i=1}^2}\int_{\Omega}a_ie^{-i\omega_{\tau_1\tau_2}\tau_i}P_i(x, y)(\beta_{\tau_1\tau_2}\phi\\&+(r-r_*)z_{\tau_1\tau_2})dy=0, \\ g_2(z_{\tau_1\tau_2}, \beta_{\tau_1\tau_2}, k_{\tau_1\tau_2}, r)=&(\beta_{\tau_1\tau_2}^2-1)\|\phi\|_{Y_{\mathbb{C}}}^2+(r-r_*)^2\|z_{\tau_1\tau_2}\|_{Y_\mathbb{C}}^2=0. \end{aligned}$

Define $G_{\tau_1\tau_2}: \hat{X}_\mathbb{C}\times \mathbb{R}^3\mapsto Y_{\mathbb{C}}\times \mathbb{R}$ by $G_{\tau_1\tau_2}=(g_1, g_2)$. By separating the real and imaginary parts of $g_1(z_{\tau_1\tau_2, r_*}, \beta_{\tau_1\tau_2, r_*}, k_{\tau_1\tau_2, r_*}, r_*)=0$ similar to Case 1, it is easy to see that $G_{\tau_1\tau_2}=0$ at $r=r_*$ when the following equations are satisfied

$\begin{aligned}&z_{\tau_1\tau_2, r_*}=(1-ik_{\tau_1\tau_2, r_*})\xi_{r_*}, k_{\tau_1\tau_2, r_*}=\dfrac{\sqrt{\tilde{a}_2^2-\tilde{a}_1^2}}{\tilde{a}_1+\tilde{a}_2}, (\tilde{a}_2>\tilde{a}_1) \\&\beta_{\tau_1\tau_2, r_*}=1, \omega_{\tau_1\tau_2, r_*}\tau_2=\arccos(-\dfrac{\tilde a_1}{\tilde a_2})+2n\pi, n=0, 1, 2, \cdots.\end{aligned}$

Case 4. $\tau_1>0$ and $\tau_2\in(0, \tau_{20})$.

Assume that there exit $i\omega_{\tau_2\tau_1} (\omega_{\tau_2\tau_1}>0)$ and $\psi_{\tau_2\tau_1}\in X_{\mathbb{C}}\backslash \{0\}$ such that

$A_r\psi_{\tau_2\tau_1}-ru_r\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^2}a_ie^{-i\omega_{\tau_2\tau_1}\tau_i}\int_\Omega P_i(x, y)\psi_{\tau_2\tau_1}(y)dy\end{pmatrix}-i\omega_{\tau_2\tau_1}\psi_{\tau_2\tau_1}=0.$

By the similar analysis as in the Case 3, the following result can be obtained:

$\frac{\omega_{\tau_2\tau_1}}{r-r_*}$ is uniformly bounded for $r\in(r_*, r^*]$. The equivalent equation to (5) is $G_{\tau_2\tau_1}=(g_1(z_{\tau_2\tau_1}, \beta_{\tau_2\tau_1}, k_{\tau_2\tau_1}, r), g_2(z_{\tau_2\tau_1}, \beta_{\tau_2\tau_1}, k_{\tau_2\tau_1}, r))=0$, which has the same form as $G_{\tau_1\tau_2}$. Moreover, $G_{\tau_2\tau_1}=0$ at $r=r_*$ if the following equations are satisfied

$\begin{aligned}&z_{\tau_2\tau_1, r_*}=(1-ik_{\tau_2\tau_1, r_*})\xi_{r_*}, k_{\tau_2\tau_1, r_*}=\dfrac{\sqrt{\tilde{a}_1^2-\tilde{a}_2^2}}{\tilde{a}_1+\tilde{a}_2}, (\tilde{a}_1>\tilde{a}_2) \\&\beta_{\tau_2\tau_1, r_*}=1, \omega_{\tau_2\tau_1, r_*}\tau_1=\arccos(-\dfrac{\tilde a_2}{\tilde a_1})+2n\pi, n=0, 1, 2, \cdots.\end{aligned}$

Since stability analysis is similar for the above four cases, we will only discuss Case 3. For other cases, we omit them in this paper.

Theorem 3.1. There exists a continuously differentiable mapping

$r\mapsto (z_{\tau_1\tau_2, r}, \beta_{\tau_1\tau_2, r}, k_{\tau_1\tau_2, r})$

from $[r_*, r^*]$ to $X_{\mathbb{C}}\times \mathbb{R}^3$ such that $G_{\tau_1\tau_2}(z_{\tau_1\tau_2, r}, \beta_{\tau_1\tau_2, r}, k_{\tau_1\tau_2, r}, r)=0$. Furthermore, the solution of $G_{\tau_1\tau_2}=0$ is unique for $r\in(r_*, r^*]$.

Proof. Define $\theta_{\tau_1\tau_2}=\omega_{\tau_1\tau_2}\tau_2$. Let $T=(T_1, T_2): X_\mathbb{C}\times \mathbb{R}^3\mapsto Y_{\mathbb{C}}\times \mathbb{R}$ be defined by the Fréchet derivative of $G$ at $r=r_*$ as follows

$\begin{aligned}T_1(z, \beta, k, \theta)=&(d\Delta+r_*)z+[1-r_*\alpha_{r_*}(a_1e^{-i\omega_{\tau_1\tau_2, r_*}\tau_1}\int_{\Omega}P_1(x, y)\phi(y)dy \\&+(a_2-i\sqrt{a_2^2-a_1^2})\int_{\Omega}P_2(x, y)\phi(y)dy)-\dfrac{\sqrt{a_2^2-a_1^2}}{a_1+a_2}i] \phi\beta-i\phi k\\&-r\alpha_r(a_1i-\sqrt{a_2^2-a_1^2})\phi(x)\theta\int_{\Omega}P_2(x, y)\phi(y)dy, \\ T_2(z, \beta, k, \theta)=&2\|\phi\|_{Y_{\mathbb{C}}}^2\beta.\end{aligned}$

Then $T$ is one-to-one from $X_\mathbb{C}\times R^3$ to $\mapsto Y_{\mathbb{C}}\times R$. Hence, from the implicit function theorem, the proof of the existence is completed. Since the proof of the uniqueness is similar to Theorem 2.4 in [15], we omit it here.

Now, from the analysis above, we can obtain the following conclusion:

Remark 1. For $r\in(r_*, r^*]$, the eigenvalue problem

$\Delta(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)\psi_{\tau_1\tau_2}=0, \omega_{\tau_1\tau_2}>0, \tau_2>0, \psi\in X_{\mathbb{C}}\backslash\{0\}$

has a solution $\psi_{\tau_1\tau_2}=\beta_{\tau_1\tau_2}\phi+(r-r_*)z_{\tau_1\tau_2}$ if and only if

$\omega_{\tau_1\tau_2}=(r-r_*)k_{\tau_1\tau_2},$

where $z_{\tau_1\tau_2}, \beta_{\tau_1\tau_2}, k_{\tau_1\tau_2}$ are defined in Case 3.

---

4. Hopf bifurcation

Theorem 4.1. When $\tau_1=\tau_2=0$, all eigenvalues of $A_{\tau_1\tau_2, r}$ have negative real parts for any $r\in(r_*, r^*]$, i.e., $u_r$ is locally asymptotically stable for $\tau_1=\tau_2=0$.

The proof is essentially same as Proposition 2.9 in [3], hence is omitted.

Next, we introduce the adjoint operator of $A_{\tau_1\tau_2, r}$ and $\Delta(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)$, denoted by $A_{\tau_1\tau_2, r}^*$ and $\Delta^*(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)$, respectively. $\Delta^*(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)$ is defined as follows

$\Delta^*(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)\psi^*=A_r\psi^*+i\omega_{\tau_1\tau_2}\psi^*-r\displaystyle{\sum\limits_{i=1}^2}\int_{\Omega}a_ie^{i\omega_{\tau_1\tau_2}\tau_i}P_i(x, y)u_r(y)\psi^*(y)dy.$

Similar to the analysis of (4), we conclude that the following adjoint equation

$A_r\psi^*-r\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^2}a_ie^{i\omega_{\tau_1\tau_2}\tau_i}\int_{\Omega}P_i(x, y)u_r(y)\psi^*(y)dy\end{pmatrix}+i\omega^*_{\tau_1\tau_2}\psi^*=0$

(11)

is solvable and the solution is denoted by $\omega^*_{\tau_1\tau_2}>0$ and $\psi^*\in X_{\mathbb{C}}\backslash \{0\}$. It is well-known that the spectrum set satisfies

$\sigma(\Delta(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2))=\sigma(\Delta^*(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)).$

Define the following function

$\begin{aligned}S_n(r):=&\int_{\Omega}\bar{\psi^*}(x)\psi(x)dx-ra_1\tau_1\int_{\Omega}\int_{\Omega}P_1(x, y)u_r(x)\bar{\psi^*}(x)\psi(y)dxdye^{-i\omega\tau_1}\\ &-ra_2\tau_{2n}\int_{\Omega}\int_{\Omega}P_2(x, y)u_r(x)\bar{\psi^*}(x)\psi(y)dxdye^{-i\omega\tau_{2n}}.\end{aligned}$

It is easy to see that

$\begin{aligned}S_n(r)\rightarrow &[\dfrac{(a_1+a_2)\int_{\Omega}\int_{\Omega}P_2(x, y)\phi^2(x)\phi(y)dxdy}{\displaystyle{\sum\limits_{i=1}^2}a_i\int_{\Omega}\int_{\Omega}P_i(x, y)\phi^2(x)\phi(y)dxdy} (\arccos(-\dfrac{a_1}{a_2}\cos{(\omega_{\tau_1\tau_2, r_*}\tau_1)})+2n\pi)\\&\cdot\dfrac{a_1\sin(\omega_{\tau_1\tau_2, r_*}\tau_1)-\sqrt{a_2^2-a_1^2\cos^2(\omega_{\tau_1\tau_2, r_*}\tau_1)}}{a_1-a_2} (i\sqrt{a_2^2-a_1^2\cos^2(\omega_{\tau_1\tau_2, r_*}\tau_1)}\\&+a_1\cos(\omega_{\tau_1\tau_2, r_*}\tau_1))+1]\int_{\Omega}\phi^2(x)dx, \;\;\text{as} \;\;r\rightarrow r_*, \end{aligned}$

which leads to $S_n(r)\neq 0$ for any $r\in(r_*, r^*]$.

Theorem 4.2. For $r\in(r_*, r^*]$, $i\omega_{\tau_1\tau_2}$ is a simple eigenvalue of $A_{\tau_1\tau_{2n}, r}$, $n=0, 1, 2\cdots$.

Proof. Notice that $\mathscr{N}[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}]=\text{Span}\{e^{i\omega_{\tau_1\tau_2}\cdot}\psi_{\tau_1\tau_2}\}$. If $\xi\in\mathscr{D}(A_{\tau_1\tau_{2n}, r})\cap\mathscr{D}([A_{\tau_1\tau_{2n}, r}]^2)$, then we can obtain

$[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}]^2\xi=0,$

which leads to

$[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}]\xi\in\mathscr{N}[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}]=\text{Span}\{e^{i\omega_{\tau_1\tau_2}\cdot}\psi_{\tau_1\tau_2}\}.$

Thus, there exists a constant $l$ such that

$[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}]\xi=le^{i\omega_{\tau_1\tau_2}\cdot}\psi_{\tau_1\tau_2},$

i.e.,

$\begin{aligned} \dot{\xi}(\theta)&=i\omega_{\tau_1\tau_2}\xi(\theta)+le^{i\omega_{\tau_1\tau_2}\theta}\psi_{\tau_1\tau_2} \theta\in[-\tau_{2n}, 0]\\ \dot\xi(0)&=A_r\xi(0)-a_1ru_r\int_{\Omega}P_1(x, y)\xi(-\tau_1)(y)dy-a_2ru_r\int_{\Omega}P_2(x, y)\xi(-\tau_{2n})(y)dy. \end{aligned}$

(12)

The first equation of (12) leads to

$\begin{aligned} \xi(\theta)&=\xi(0)e^{i\omega_{\tau_1\tau_2}\theta}+l\theta e^{i\omega_{\tau_1\tau_2}\theta}\psi_{\tau_1\tau_2} \\ \dot\xi(0)&=i\omega_{\tau_1\tau_2}\xi(0)+l\psi_{\tau_1\tau_2}. \end{aligned}$

Thus, we have

$\begin{aligned}&\Delta(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_{2n})\xi(0)\\=&l[\psi_{\tau_1\tau_2}-ru_r(a_1\tau_1e^{-i\omega\tau_1}\int_{\Omega}P_1(x, y)\psi(y)dy+a_2\tau_{2n}e^{-i\omega\tau_{2n}}\int_{\Omega}P_2(x, y)\psi(y)dy)].\end{aligned}$

Moreover,

$\begin{aligned}0=&\langle \Delta^*(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_{2n})\psi^*_{\tau_1\tau_2}, \xi(0) \rangle\\=&\langle \psi^*_{\tau_1\tau_2}, \Delta(r, i\omega_{\tau_1\tau_2}, \tau_1, \tau_{2n})\xi(0) \rangle\\=&l[\int_{\Omega}\bar{\psi^*}(x)\psi(x)dx-r\int_{\Omega}\int_{\Omega}\bar{\psi^*}(x)u_r(x)(a_1\tau_1e^{-i\omega_{\tau_1\tau_2}\tau_1}P_1(x, y)\\&+a_2\tau_{2n}e^{-i\omega_{\tau_1\tau_2}\tau_2}P_2(x, y))\psi(y)dxdy] \\=&lS_n(r).\end{aligned}$

Due to $S_n(r)\neq 0$, the coefficient $l=0$ and this leads to $\xi\in\mathscr{N}[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}].$ Hence, we have

$\xi\in\mathscr{N}[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}]^j=\mathscr{N}[A_{\tau_1\tau_{2n}, r}-i\omega_{\tau_1\tau_2}], j=1, 2, 3\cdots, n=0, 1, 2\cdots,$

and this shows that $\lambda=i\omega_{\tau_1\tau_2}$ is a simple eigenvalue of $A_{\tau_1\tau_{2n}, r}$ for $n=0, 1, 2\cdots$. This completes the proof.

From the implicit function theorem, we can obtain that there is a neighborhood $O_n\times D_n\times H_n\subset \mathbb{R}\times\mathbb{C}\times X_{\mathbb{C}}$ of $(\tau_{2n}, i\omega, \psi)$ and a continuously differential function $(\lambda, \psi): O_n\rightarrow D_n\times H_n$ such that for each $\tau_2\in O_n$, the only eigenvalue of $A_{\tau_1\tau_2, r}$ in $D_n$ is $\mu(r)$ and

$\begin{aligned} \lambda(\tau_{2n})&=i\omega_{\tau_1\tau_2, r}, \psi(\tau_{2n})=\psi_{\tau_1\tau_2, r}, \\ \Delta(r, \mu, \tau_1, \tau_2)\psi&=(A_r-\mu(\tau_2))\psi-ru_r\displaystyle{\sum\limits_{i=1}^2}\int_{\Omega}a_ie^{-\mu(\tau_2)\tau_i}P_i(x, y)\psi(\tau_2)(y)dy=0. \end{aligned}$

(13)

Then, the following result describes the transversality condition of Hopf bifurcation:

Theorem 4.3. For any $r\in(r_*, r^*]$, $\text{Re}\dfrac{d\lambda(\tau_{2n})}{\tau_2}>0$, $n=0, 1, 2\cdots.$

Proof. Differentiating (13) with respect to $\tau_2$ at $\tau_2=\tau_{2n}$, we obtain that

$\begin{aligned}\dfrac{d\lambda(\tau_2)}{d\tau_2}=&\dfrac{a_2ri\omega\int_{\Omega}\int_{\Omega}\bar{\psi^*}(x)u_r(x)P_2(x, y)\psi(\tau_2)(y)dxdye^{-i\theta}}{\int_{\Omega}\bar{\psi^*}(x)\psi(x)dx-r\int_{\Omega}\int_{\Omega}\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^2}a_i\tau_ie^{-i\omega\tau_i}P_i(x, y)\end{pmatrix}\bar{\psi^*}(x)u_r(x)\psi(y)dxdy}\\ =&\dfrac{1}{|S_n(r)|^2}\{a_2ri\omega e^{-i\theta}\int_{\Omega}\psi^*(x)\bar{\psi}(x)dx\int_{\Omega}\int_{\Omega}P_2(x, y)u_r(x)\bar{\psi^*}(x)\psi(y)dxdy\\&-a_1a_2r^2i\omega\tau_1e^{i(\omega\tau_1-\theta)}\int_{\Omega}\int_{\Omega}P_1(x, y)u_r(x)\psi^*(x)\bar{\psi}(y)dxdy\\&\cdot\int_{\Omega}\int_{\Omega}P_2(x, y)u_r(x)\bar{\psi^*}(x)\psi(\tau_2)(y)dxdy-a_2^2r^2\tau_2 i\omega\int_{\Omega}\int_{\Omega}P_2(x, y)u_r(x)\\&\cdot\psi^*(x)\bar{\psi}(y)dxdy\int_{\Omega}\int_{\Omega}P_2(x, y)u_r(x)\bar{\psi^*}(x)\psi(\tau_2)(y)dxdy\}. \end{aligned}$

Therefore,

$\begin{aligned}&\lim\limits_{r\rightarrow r_*}\text{Re}(\dfrac{d\lambda(\tau_2)}{d\tau_2})\\=&\dfrac{1}{|S_n(r)|^2}\sqrt{a_2^2-a_1^2\cos^2(\omega_{\tau_1\tau_2}\tau_1)}\arccos(-\dfrac{a_1}{a_2}\cos(\omega_{\tau_1\tau_2}\tau_1))r_*\alpha_{r_*}\int_{\Omega}\phi^2(x)dx\\&\cdot\int_{\Omega}\int_{\Omega}P_2(x, y)\phi^2(x)\phi(y)dxdy>0.\end{aligned}$

Then we conclude

Theorem 4.4. For $r\in(r_*, r^*]$, the positive steady state solution $u_r$ of model (1) is locally asymptotically stable for $\tau_2\in[0, \tau_{20})$ and there undergoes Hopf bifurcation at $\tau_2=\tau_{20}$.

---

5. Stability of bifurcated periodic solutions

This section contains lengthy and technical discussions about the direction of Hopf bifurcation, stability and period of the periodic solution bifurcating from the positive steady solution $u_r$. Following the ideas of Wu [19], we derive the explicit formulae for determining the properties of Hopf bifurcation at the critical value $\tau_{20}$ for fixed $\tau_1\in(0, \tau_{10})$ by employing the normal form method and center manifold theorem. Without loss of generality, this section assumes that $\tau_1<\tau_{20}$. Let $U(t)=u(\cdot, t)-u_r$ and $\tau_2=\tau_{20}+\nu$. Then $\nu=0$ is the Hopf bifurcation value of model (1). Re-scaling the time by $t\rightarrow \frac{t}{\tau_2}$ to normalize the delay, model (1) is transformed into the following form

$\dfrac{dU(t)}{dt}=\tau_{20}d\Delta U(t)+\tau_{20}L_0(U_t)+F(U_t, \nu),$

(14)

and $L_0: C\rightarrow C$, $F: C\times \mathbb{R}\rightarrow C$ are given respectively by

$\begin{aligned}L_0(\psi)=&r[1-\begin{pmatrix}\displaystyle{\sum\limits_{i=1}^2}a_i\int_{\Omega}P_i(x, y)u_r(y)dy\end{pmatrix}]\psi(0)-ru_r[a_1\int_{\Omega}P_1(x, y)\psi(-\dfrac{\tau_1}{\tau_{20}})dy\\&+a_2\int_{\Omega}P_2(x, y)\psi(-1)dy], \\ F(\psi, \nu)=&\nu d\Delta\psi(0)+\nu L_0(\psi)-r(\nu+\tau_{20})(a_1\int_{\Omega}P_1(x, y)\psi(-\dfrac{\tau_1}{\tau_{20}})dy\\&+a_2\int_{\Omega}P_2(x, y)\psi(-1)dy)\psi(0), \end{aligned}$

where $\psi\in C([-1, 0], Y)$.

There exists a function $\eta(\theta, x, \psi(\theta))$ of bounded variation for $\theta\in[-1, 0]$ such that

$L_0\psi=\int_{-1}^{0}d\eta (\theta, x, \psi(\theta)),$

where

$\begin{aligned} \eta(\theta,x,\psi(\theta))=&r[1-\begin{pmatrix}\displaystyle{\sum_{i=1}^2}a_i\int_{\Omega}P_i(x,y)u_r(y)dy\end{pmatrix}]\delta(\theta)\psi(\theta)-a_1ru_r\int_{\Omega}P_1(x,y)\\&\cdot\delta(\theta+\dfrac{\tau_1}{\tau_{20}})\psi(\theta)(y)dy -a_2ru_r\int_{\Omega}P_2(x,y)\delta(\theta+1)\psi(\theta)(y)dy. \end{aligned}$

For $\psi\in C([-1, 0], Y)$, define

$A_{\tau_2}\psi=\begin{cases} \dfrac{d\psi(\theta)}{d\theta}\quad \theta\in[-1, 0), \\ \tau_2d\Delta\psi(0)+\tau_2\int_{-1}^0d\eta(\theta, x, \psi(\theta)) \theta=0, \end{cases}$

and

$R(\psi, \nu)=\begin{cases}0 \quad \theta\in[-1, 0)\\F(\psi, \nu) \quad \theta=0\end{cases}$

Then system (14) is equivalent to

$\dfrac{dU_t}{dt}=A_{\tau_2}U_t+R(U_t, \nu),$

(15)

where $U_t(\theta)=U(t+\theta)$ for $\theta\in[-1, 0].$

For $\psi\in C([0, 1], Y)$, define

$A^*_{\tau_2}\tilde\psi(s)=\begin{cases} -\dfrac{d\tilde\psi(s)}{ds}\quad s\in(0, 1], \\ \tau_2d\Delta\tilde\psi(0)+\tau_2\int_{-1}^0d\eta(s, x, \tilde\psi(-s))\quad s=0, \end{cases}$

and the formal duality

$\ll \tilde\psi, \psi\gg=\langle \tilde\psi(0), \psi(0)\rangle-\int_{-1}^0\int_{\xi=0}^\theta \langle \tilde\psi(\xi-\theta), d\eta(\theta, y, \psi(\xi)) \rangle d\xi.$

From the previous definition, we have

$\begin{aligned}&\ll A_{\tau_2}^*\tilde\psi, \psi\gg\\=&\langle A_{\tau_2}^*\tilde\psi(0), \psi(0) \rangle-a_1r\tau_{20}\int_{-\dfrac{\tau_1}{\tau_{2}}}^{0}\langle A_{\tau_2}^*\tilde\psi(s+\dfrac{\tau_1}{\tau_{2}}), u_r(x)\int_{\Omega}P_1(x, y)\psi(s)(y)dy\rangle ds\\ &-a_2r\tau_{20}\int_{-1}^{0}\langle A_{\tau_2}^*\tilde\psi(s+1), u_r(x)\int_{\Omega}P_2(x, y)\psi(s)(y)dy\rangle ds\\ =&\langle \tau_2d\Delta\tilde\psi(0)+\tau_2r\begin{pmatrix}1-\displaystyle{\sum\limits_{i=1}^{2}}\int_{\Omega}a_iP_i(x, y)u_r(y)dy\end{pmatrix}\tilde\psi(0) -ra_1\tau_2u_r(x)\\ &\cdot\int_{\Omega}P_1(x, y)\psi(\dfrac{\tau_1}{\tau_2})(y)dy-ra_2\tau_2u_r(x)\int_{\Omega}P_2(x, y)\psi(1)(y)dy, \psi(0)\rangle \\ &-a_1r\tau_{20}\int_{-\dfrac{\tau_1}{\tau_2}}^{0}\langle -\dot{\tilde\psi}(s+\dfrac{\tau_1}{\tau_2}), u_r(x)\int_{\Omega}P_1(x, y)\psi(s)(y)dy\rangle ds\\ &-a_2r\tau_{2}\int_{-1}^{0}\langle -\dot{\tilde\psi}(s+1), u_r(x)\int_{\Omega}P_2(x, y)\psi(s)(y)dy\rangle ds\\ =& \langle \tilde\psi(0), \tau_2d\Delta\psi(0)+\tau_2r\begin{pmatrix}1-\displaystyle{\sum\limits_{i=1}^{2}}\int_{\Omega}a_iP_i(x, y)u_r(y)dy\end{pmatrix}\psi(0)\rangle -ra_1\tau_2\langle \tilde\psi(\dfrac{\tau_1}{\tau_2}), \\&u_r(x)\int_{\Omega}P_1(x, y)\psi(0)(y)dy\rangle-ra_2\tau_2\langle \tilde\psi(1), u_r(x)\int_{\Omega}P_2(x, y)\psi(0)(y)dy\rangle \\&+a_1r\tau_{20}\int_{-\dfrac{\tau_1}{\tau_2}}^{0}\langle \dot{\tilde\psi}(s+\dfrac{\tau_1}{\tau_2}), u_r(x)\int_{\Omega}P_1(x, y)\psi(s)(y)dy\rangle ds+a_2r\tau_{2}\int_{-1}^{0}\langle \dot{\tilde\psi}(s+1), \\& u_r(x)\int_{\Omega}P_2(x, y)\psi(s)(y)dy\rangle ds\\ =&\langle \tilde\psi(0), A_{\tau_2}\psi(0) \rangle-a_1r\tau_2\int_{-\dfrac{\tau_1}{\tau_2}}^{0} \langle \tilde\psi(s+\dfrac{\tau_1}{\tau_2}), u_r(x)\int_{\Omega}P_1(x, y)\dot\psi(s)(y)dy\rangle ds\\&-a_2r\tau_{20}\int_{-1}^{0} \langle \tilde\psi(s+1), u_r(x)\int_{\Omega}P_2(x, y)\dot{\psi}(s)(y)dy\rangle ds\\ =&\ll \tilde\psi, A_{\tau_2}\psi \gg. \end{aligned}$

Since $\pm i\omega_{\tau_1\tau_2}\tau_{20}$ are eigenvalues of $A_{\tau_2}$, they are also eigenvalues of $A^*_{\tau_2}$. Based on the previous eigenvalue analysis, $\psi_{\tau_1\tau_2}e^{i\omega_{\tau_1\tau_2}\tau_{20}\theta}$ and $\bar\psi_{\tau_1\tau_2}e^{-i\omega_{\tau_1\tau_2}\tau_{20}\theta}$ are the eigenfunctions of $A_{\tau_2}$ corresponding to $i\omega_{\tau_1\tau_2}\tau_{20}$ and $-i\omega_{\tau_1\tau_2}\tau_{20}$, respectively. Let $\Phi=(q(\theta), \bar{q}(\theta))=(\psi_{\tau_1\tau_2}e^{i\omega\tau_2\theta}, \bar\psi_{\tau_1\tau_2}e^{-i\omega\tau_2\theta})$, $\theta\in[-1, 0]$, then $P=\text{Span}\{\Phi\}$ is the generalized eigenspace of $A_{\tau_2}$ with respect to eigenvalues set $\{i\omega_{\tau_1\tau_2}\tau_{20}, -i\omega_{\tau_1\tau_2}\tau_{20}\}$. Similarly $P^*=\text{Span}\{q^*(s), \bar{q^*}(s)\}$ is generalized eigenspace of the adjoint operator $A^*_{\tau_2}$, where $q^*(s)=\psi^*_{\tau_1\tau_2}e^{i\omega\tau_2s}$ is the eigenfunction with respect to $-i\omega\tau_2$. Then the phase space $C_{\mathbb{C}}$ can be decomposed as $C_{\mathbb{C}}=P\oplus Q$, where

$Q=\{\psi\in C_{\mathbb{C}}: \ll \psi, \phi \gg=0, \;\;\text{for all} \;\; \psi\in P^*\}.$

Denote

$\Psi=\begin{pmatrix}\dfrac{1}{\bar{S}_n(r)}q^*(s)\\ \dfrac{1}{S_n(r)}\bar{q^*}(s)\end{pmatrix},$

then $\ll \Psi, \Phi \gg=I_{2\times 2}$.

Let $U_t$ be the solution of (15) when $\nu=0$. Define

$z(t)=\ll \dfrac{1}{\bar S_n(r)}q^*(s), U_t\gg, W(t, \theta)=U_t-\Phi(\theta)\cdot (z(t), \bar{z}(t))^T.$

(16)

Then we obtain the following center manifold

$W(t, \theta)=W(z(t), \bar{z}(t), \theta)=W_{20}(\theta)\dfrac{z^2}{2}+W_{11}(\theta)z\bar{z}+W_{02}(\theta)\dfrac{\bar{z}^2}{2}+\cdots$

(17)

with the range in $Q$. From the definition of (16), we have

$\begin{aligned} \dot{z}(t)&=\dfrac{d}{dt}\ll \dfrac{1}{\bar{S}_n(r)}q^*(s), U_t\gg\\&=\ll \dfrac{1}{\bar{S}_n(r)}q^*(s), A_{\tau_2}U_t\gg+\ll \dfrac{1}{\bar{S}_n(r)}q^*(s), R(U_t, 0)\gg\\ &=\ll \dfrac{1}{\bar{S}_n(r)}A^*_{\tau_2}q(s), U_t\gg+\dfrac{1}{S_n(r)}\langle q^*(0), F(U_t, 0)\rangle\\&=i\omega\tau_{20}z(t)+\dfrac{1}{S_n(r)}\langle q^*(0), F(W(z(t), \bar{z}(t), 0)+2Re\{z(t)q(\theta)\}, 0) \rangle. \end{aligned}$

We rewrite this equation as

$\dot{z}(t)=i\omega\tau_{20}z(t)+g(z, \bar{z}),$

where

$\begin{aligned}g(z, \bar{z})&=\dfrac{1}{S_n(r)}\langle q^*(0), F(W(z(t), \bar{z}(t), 0)+2Re\{z(t)q(\theta)\}, 0)\rangle\\ &=g_{20}\dfrac{z^2}{2}+g_{11}z\bar{z}+g_{02}\dfrac{\bar{z}^2}{2}+g_{21}\dfrac{z^2\bar{z}}{2}+\cdots.\end{aligned}$

(18)

Computing the coefficients of (18), we have

$\begin{aligned}g_{20}=&-\dfrac{2\tau_{20}r}{S_n}\int_{\Omega}\int_{\Omega}(a_1e^{-i\omega\tau_1}P_1(x, y)+a_2e^{-i\omega\tau_{20}}P_2(x, y))\bar{\psi}^*_{\tau_1\tau_2}(x)\psi_{\tau_1\tau_2}(x)\\&\cdot\psi_{\tau_1\tau_2}(y)dxdy, \end{aligned}$

$\begin{aligned}g_{11}=&-\dfrac{\tau_{20}r}{S_n}[\int_{\Omega}\int_{\Omega}(a_1e^{-i\omega\tau_1}P_1(x, y)+a_2e^{-i\omega\tau_{20}}P_2(x, y))\bar{\psi}^*_{\tau_1\tau_2}(x)\bar\psi_{\tau_1\tau_2}(x)\\&\cdot\psi_{\tau_1\tau_2}(y)dxdy+\int_{\Omega}\int_{\Omega}(a_1e^{i\omega\tau_1}P_1(x, y)+a_2e^{i\omega\tau_{20}}P_2(x, y))\bar{\psi}^*_{\tau_1\tau_2}(x)\\&\cdot\psi_{\tau_1\tau_2}(x)\bar\psi_{\tau_1\tau_2}(y)dxdy], \end{aligned}$

$\begin{aligned}g_{02}=&-\dfrac{2\tau_{20}r}{S_n}\int_{\Omega}\int_{\Omega}(a_1e^{i\omega\tau_1}P_1(x, y)+a_2e^{i\omega\tau_{20}}P_2(x, y))\bar{\psi}^*_{\tau_1\tau_2}(x)\bar\psi_{\tau_1\tau_2}(x)\\&\cdot\bar\psi_{\tau_1\tau_2}(y)dxdy, \end{aligned}$

$\begin{aligned}g_{21}=&-\dfrac{2\tau_{20}r}{S_n}\int_{\Omega}\int_{\Omega}(a_1e^{-i\omega\tau_1}P_1(x, y)+a_2e^{-i\omega\tau_{20}}P_2(x, y))\bar{\psi}^*_{\tau_1\tau_2}(x)\psi_{\tau_1\tau_2}(y)\\&\cdot W_{11}(0)(x)dxdy-\dfrac{\tau_{20}r}{S_n}\int_{\Omega}\int_{\Omega}(a_1e^{i\omega\tau_1}P_1(x, y)+a_2e^{i\omega\tau_{20}}P_2(x, y))\bar{\psi}^*_{\tau_1\tau_2}(x)\\&\bar\psi_{\tau_1\tau_2}(y)W_{20}(0)(x)dxdy -\dfrac{\tau_{20}r}{S_n}\int_{\Omega}\int_{\Omega}\bar{\psi}^*_{\tau_1\tau_2}(x)\bar\psi_{\tau_1\tau_2}(x)(a_1P_1(x, y)\\&W_{20}(-\dfrac{\tau_1}{\tau_2})(y)+a_2P_2(x, y)W_{20}(-1)(y))dxdy -\dfrac{2\tau_{20}r}{S_n}\int_{\Omega}\int_{\Omega}\bar{\psi}^*_{\tau_1\tau_2}(x)\psi_{\tau_1\tau_2}(x)\\&\cdot(a_1P_1(x, y)W_{11}(-\dfrac{\tau_1}{\tau_2})(y)+a_2P_2(x, y)W_{11}(-1)(y))dxdy. \end{aligned}$

From the expression of $g_{21}$, we need to compute $W_{20}(\theta)$ and $W_{11}(\theta)$. From (15) and (16), we have

$\begin{aligned}\dot W&=\left\{\begin{aligned}A_{\tau_2}W-\Phi(\theta)\langle \Psi(0), F(W(z, \bar{z})+\Phi(z, \bar{z})^T, 0) \rangle,\quad -1\leq\theta< 0, &\\ A_{\tau_2}W-\Phi(\theta)\langle \Psi(0), F(W(z, \bar{z})+\Phi(z, \bar{z})^T, 0) \rangle+F(W(z, \bar{z})+\Phi&(z, \bar{z})^T, 0) \\ & \theta=0, \end{aligned} \right.\\&=A_{\tau_2}W+H(z, \bar{z}, \theta), \end{aligned}$

(19)

where

$H(z, \bar{z}, \theta)=H_{20}(\theta)\dfrac{z^2}{2}+H_{11}(\theta)z\bar{z}+H_{02}(\theta)\dfrac{\bar{z}^2}{2}+\cdots.$

(20)

Due to the chain rule

$\dot W=W_z\dot{z}+W_{\bar{z}}\dot{\bar{z}},$

we have

$(-2i\omega_{\tau_1\tau_2}\tau_{20}+A_{\tau_2})W_{20}(\theta)=-H_{20}(\theta), A_{\tau_2}W_{11}(\theta)=-H_{11}(\theta).$

(21)

From (19), we know that for $\theta\in[-1, 0)$

$H(z, \bar{z}, \theta)=-\Phi(\theta)\langle \Psi(0), F(W(z, \bar{z}, \theta)+\Phi(z, \bar{z})^T, 0) \rangle=-gq(\theta)-\bar{g}\bar{q}(\theta).$

Comparing the coefficients with (20), we obtain

$H_{20}(\theta)=-g_{20}q(\theta)-\bar{g}_{02}\bar{q}(\theta), H_{11}(\theta)=-g_{11}q(\theta)-\bar g_{11}\bar{q}(\theta).$

(22)

From (21) and (22) and the definition of $A_{\tau_2}$, it follows that

$\dot{W}_{20}(\theta)=2i\omega_{\tau_1\tau_2}\tau_{20}W_{20}(\theta)+g_{20}q(\theta)+\bar{g}_{02}\bar{q}(\theta).$

(23)

Hence,

$W_{20}(\theta)=\dfrac{ig_{20}}{\omega_{\tau_1\tau_2}\tau_{20}}q(\theta)+\dfrac{i\bar{g}_{02}}{3\omega_{\tau_1\tau_2}\tau_{20}}\bar{q}(\theta)+M_1e^{2i\omega_{\tau_1\tau_2}\tau_{20}\theta}.$

(24)

Similarly, we can obtain

$W_{11}(\theta)=-\dfrac{ig_{11}}{\omega_{\tau_1\tau_2}\tau_{20}}q(\theta)+\dfrac{i\bar{g}_{11}}{\omega_{\tau_1\tau_2}\tau_{20}}\bar{q}(\theta)+M_2.$

(25)

In the following we shall find out $M_1$ and $M_2$. From (19) and (20), we have

$\begin{aligned}H_{20}(0)=&-g_{20}q(0)-\bar{g}_{02}\bar{q}(0)-2r\tau_{20}\psi_{\tau_1\tau_2}(x)\int_{\Omega}(a_1e^{-i\omega_{\tau_1\tau_2}\tau_1}P_1(x, y)\\&+a_2e^{-i\omega_{\tau_1\tau_2}\tau_{20}}P_2(x, y))\psi_{\tau_1\tau_2}(y)dy, \\ H_{11}(0)=&-g_{11}q(0)-\bar{g}_{11}\bar{q}(0)-r\tau_{20}[\psi_{\tau_1\tau_2}(x)(a_1\int_{\Omega}P_1(x, y)\bar{\psi}_{\tau_1\tau_2}(y)e^{i\omega_{\tau_1\tau_2}\tau_1}dy\\&+a_2\int_{\Omega}P_2(x, y)\bar{\psi}_{\tau_1\tau_2}(y)e^{i\omega_{\tau_1\tau_2}\tau_{20}}dy) +\bar\psi_{\tau_1\tau_2}(x)(a_1\int_{\Omega}P_1(x, y)\psi_{\tau_1\tau_2}(y)\\&\cdot e^{-i\omega_{\tau_1\tau_2}\tau_1}dy+a_2\int_{\Omega}P_2(x, y)\psi_{\tau_1\tau_2}(y)e^{-i\omega_{\tau_1\tau_2}\tau_{20}}dy)]. \end{aligned}$

Thus, we can compute $M_1$ and $M_2$ satisfying

$\begin{aligned}M_1=&2r\Delta^{-1}(r, 2i\omega_{\tau_1\tau_2}, \tau_1, \tau_2)\psi_{\tau_1\tau_2}(x)\int_{\Omega}(a_1e^{-i\omega_{\tau_1\tau_2}\tau_{1}}P_1(x, y)\\&+a_2e^{-i\omega_{\tau_1\tau_2}\tau_{20}}P_2(x, y))\cdot\psi_{\tau_1\tau_2}(y)dy, \\ M_2=&r\Delta^{-1}(r, 0, \tau_1, \tau_2)[\psi_{\tau_1\tau_2}(x)\int_{\Omega}(a_1e^{i\omega_{\tau_1\tau_2}\tau_1}P_1(x, y)\\&+a_2e^{i\omega_{\tau_1\tau_2}\tau_{20}}P_2(x, y))\bar{\psi}_{\tau_1\tau_2}(y)dy\\ &+\bar\psi_{\tau_1\tau_2}(x)\int_{\Omega}(a_1P_1(x, y)e^{-i\omega_{\tau_1\tau_2}\tau_1}+a_2P_2(x, y)e^{-i\omega_{\tau_1\tau_2}\tau_{20}})\psi_{\tau_1\tau_2}(y)dy] \end{aligned}$

Now, we can determine $W_{20}(\theta)$ and $W_{11}(\theta)$ from (24) and (25). Furthermore, $g_{21}$ can be expressed. Hence, we can compute the following values

$\begin{aligned}c_1(0)&=\dfrac{i}{2\omega_{\tau_1\tau_2}\tau_{20}}(g_{20}g_{11}-2|g_{11}|^2-\dfrac{|g_{02}|^2}{3})+\dfrac{g_{21}}{2}, \\ \mu_2&=-\dfrac{Re \{c_1(0)\}}{Re \{\lambda'(\tau_{20})\}}, \\ \beta_2&=2Re\{c_1(0)\}, \\ T_2&=-\dfrac{Im\{c_1(0)\}+\mu_2Im\{\lambda'(\tau_{20})\}}{\omega_{\tau_1\tau_2}\tau_{20}}.\end{aligned}$

From the conclusion of [19], [8], we have the following results.

Theorem 5.1. $\mu_2$ determines the direction of the Hopf bifurcation: if $\mu_2>0$ $(\mu_2<0)$, the Hopf bifurcation is supercritical (subcritical); $\beta_2$ determines the stability of the bifurcating periodic solution: the bifurcating periodic solution is stable (unstable) if $\beta_2<0$ $(\beta_2>0)$ and $T_2$ determines the period of the bifurcating periodic solution: the period increases (decrease) if $T_2>0$ $(T_2<0)$.

---

6. Numerical simulation

In this section, we present some numerical simulations to demonstrate our analytical results.

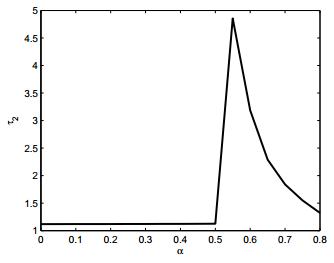
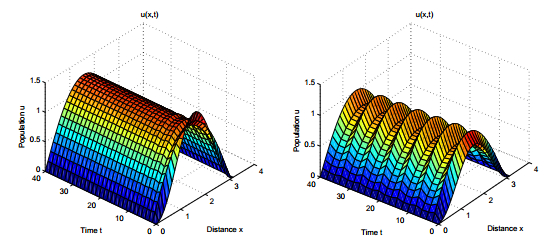
We choose the parameters $d=1$, $r=2.5$ and the initial condition $u(x, t)=0.9\sin^2 x$ for all $-\tau<t\leq 0$. And $a_1=0.6$, $a_2=0.4$ satisfying $a_1+a_2=1$. Without loss the generality, let $a_1=\alpha$ and then $a_2=1-\alpha$. Kernel function takes the form $P_i(x, y)=\frac{1}{\sqrt{4\pi\alpha_i}}e^{-\frac{(x-y)^2}{4\alpha_i}}$, $i=1, 2$. For the simplicity, $\alpha_1=\alpha_2=1$. For $\tau_2=0$, we can get $\tau_{10}=3.4294$. Now, let the delay $\tau_1=1\in [0, \tau_{10})$ be fixed. Based on theoretical analysis above, we can figure out $\omega_{\tau_1\tau_2}=1.4933$, $\lambda'(\tau_{20})=0.1810-0.0225i$, $c_1(0)=-0.0941-0.1298i$, $\mu_2=0.52$, $\beta_2=-0.1882$, $T_2=0.0838$ and delay critical value $\tau_{20}=1.1299$. Then we know that the positive steady state solution $u_r$ is locally asymptotically stable when $\tau_2<\tau_{20}$. This is numerically illustrated in left panel of Fig. 1. According to Theorem 5.1, model (1) undergoes a supercritical Hopf bifurcation at the positive state solution $u_r(x)$ and bifurcating periodic solution exists for $\tau_{2}$ slightly larger than $\tau_{20}$ and the bifurcated periodic solution is stable, as depicted in right panel of Fig. 1. Moreover, Fig. 2 plots a critical curve $\tau_2=f(\alpha)$ w.r.t. two parameters $\tau_2$ and $\alpha$ for the fixed delay $\tau_1=1$. We shall explore the significance of the change of monotonicity of this curve in the next section.

---

7. Discussion

Here we interpreted the classical logistic model with two non-local delayed terms in the framework of avian influenza spread between wild birds and the environment---the environment is contaminated by infected birds and the contaminated environment then pass on the pathogen to other susceptible birds. Due to the random movement of the infected birds and pathogens, the disease spreads in the geographical domain and pathogen loads in any given spatial location are not just the consequence of local contamination. Here we consider the case where resources are available for cleaning the environment. These resources can be used to launch either rapid or slow environment cleaning interventions, but the resources are limited so optimal allocations will be needed. Our study shows that disease outbreak in the form of a nontrivial equilibrium is possible assuming the intrinsic reproduction number is sufficiently large, and nonlinear oscillations around this nontrivial equilibrium can take place. Our analysis and simulations show that to prevent this oscillation, the resources should be distributed for both rapid and slow responses, focusing on either rapid or slow response will require the slow response to be also very rapid. For example, in Figure 3, if we normalized the delay so that the rapid response takes place with $\tau _1=1$, then the critical value for nonlinear oscillation ($\tau _{20}$) to take place can be large, and close to 5 when $\alpha$ is close to 0.5.

In recent years, reaction-diffusion equations with time delay have been investigated extensively. Su et al.[15] studied a diffusive logistic equation with mixed delayed and instantaneous density dependence, with some interesting results on global continuation of Hopf bifurcation branches. Hu and Yuan[10] proposed a coupled system of reaction-diffusion system with distributed delay and studied stability of the positive steady state solution and the occurrence of Hopf bifurcation. The Hopf bifurcation was also considered in Ma [12] for a coupled reaction-diffusion systems involving three interacting species. The earlier work introducing nonlocal terms into the diffusive Fisher equation included the paper of Britton[2]. Guo[7] investigated the existence, stability and multiplicity of spatially nonhomogeneous steady state solutions and periodic solutions for reaction-diffusion models with nonlocal delay effect by using the Lyapunov-Schmidt reduction. Deng and Wu[5] established a comparison principle and constructed monotone sequences to show the global stability for a nonlocal reaction-diffusion population model. Zuo and Song[22] studied the effect of three weight functions on the dynamics of a general reaction-diffusion equation with nonlocal delay and showed that the average delay for the case of strong kernel may induce the stability switches. Chen and Yu [4] considered a nonlocal delayed reaction-diffusion equation with general form of nonlocal delay. More discussions about the biological backgrounds of non-local reaction diffusion equations with delay and further results on the existence of nontrivial equilibria and Hopf bifurcations can be found in [21][20][18] and references therein. Here we link a logistic model with two non-local delay terms to the understanding of optimal strategies to prevent nonlinear oscillations in disease spread involving environment contamination and resources allocation, and we believe this line of research in modeling and analysis may generate interest for further expanding the models to reflect more biological realities and disease spread such as temporal heterogeneity and multiple routes of transmission.

---

Acknowledgments

This work was supported by the Fundamental Research Funds for the Central University of China (N140504005) and the Natural Sciences and Engineering Research Council of Canada (105588-2011-RGPIN).

---