1. Introduction

The temporal behavior of population of one species which inhabits a strip of dimensionless width and obeys the logistic growth law can be modeled by a reaction-diffusion equation

$\label{rdeintro} \dfrac{\partial w(t,X)}{\partial t}=r w(t,X)\left[1-\dfrac{w(t,X)}{K}\right]+d\dfrac{\partial ^{2}w(t,X)}{\partial X^{2}}$

(1.1)

with suitable boundary conditions (BCs), where $w(t,X)$ is the population density of a species at time $t$ and location $X$. Such a model was derived by Ludwig, Aronson and Weinberger [20] in 1979, based on a more general model whose derivation can be found in [23,26]. (1.1) is called the Fisher equation proposed by Fisher [11] to model the advance of a mutant gene in an infinite one-dimensional habitat.

It is well known that exploiting biological resources and harvesting populations often occur in fishery, forestry, and wildlife management [4,5,6,7], and overexploitation leads to extinction of species [3,17,27,29]. This leads to the introduction of harvest rates into a variety of population models. The population models with harvesting rates governed by one or two first-order ordinary differential equations have been widely studied in [4,6,7,17,27,29] and the references therein. From [17,27,29], one can see that the constant harvest rates greater than $1/4$ lead to extinction of species.

There are a few papers which study on population models with harvesting rates governed by reaction-diffusion equations [22,24,25]. One of these harvesting rates is the quasi-constant-yield harvest rate introduced by Roques and Chekroun [25] in 2007. This leads to the following population model

$\label{rdeintro2} \dfrac{\partial w(t,X)}{\partial t}=r w(t,X)\left[1-\dfrac{w(t,X)}{K}\right]+d\dfrac{\partial ^{2}w(t,X)}{\partial X^{2}}- \delta H(X)\rho_{\varepsilon_{0}}(w(t,X)),$

(1.2)

where $\rho_{\varepsilon_{0}}:\mathbb R\to \mathbb R_{+}$ is a differentiable and increasing function satisfying $\rho_{\varepsilon_{0}}(w)=0$ for $w\in (-\infty,0]$ and $\rho_{\varepsilon_{0}}(w)=1$ for $w\in (\varepsilon_{0},\infty).$ In the model, the harvest term is requested to depend on the population densities when the densities are very lower ($\le \varepsilon_{0}$) to ensure the nonnegativity of the solution $w$. However, when the population densities are greater than $\varepsilon_{0}$, the harvest rate at location $X$ is a constant $\delta H(X)$. It is mentioned in [25] that considering a constant harvest rate $\delta H(X)$ without the function $\rho_{\varepsilon_{0}}$ would result in a harvest on zero-populations, which makes the model unrealistic.

Equation (1.2) with Neumann BCs or periodic function $H$ was studied in [25] even in a more general setting, where $X\in \Omega\subset \mathbb R^{n}$ and heterogeneous environments were considered, that is, the first term on the right side of (1.2) is replaced by $w(t,X)\bigl[\mu(X)-\nu(X)w(t,X)\bigr]$. Using sub-and supersolution methods it was proved in [25] that there exists $\delta^{*}>0$ such that for $\delta\le \delta^{*}$ the positive steady-state solutions exist and for $\delta>\delta^{*}$ there are no such solutions [25,Theorem 2.6]. It is mentioned in [25,p.139] that obtaining information on the threshold value $\delta^{*}$ is precious for ecological questions such as the study of the relationship between $\delta^{*}$ and the environmental heterogeneities. There is only one result on the computable bounds for $\delta^{*}$ [25,Theorem 2.10], where Neumann BCs or periodic functions $H$ are considered.

Neubert [22] considered the population models with the proportional harvest rates, that is, the harvesting term of (1.2) is replaced by $\delta H(X)w(t,X)$, subject to the Dirichlet BCs: $w(t,0)=w(t,l)=0$, where $l$ is the habitat patch size. It is pointed out in [22,p.845] that considering the Dirichlet BCs is of ecological importance since they reflect the discontinuity between the habitat patch and its uninhabitable surroundings.

To the best of our knowledge, there are no results on model (1.2) with the Dirichlet BCs. In this paper, we investigate (1.2) with the Dirichlet BCs via its steady-state solutions. We shall study the following two essential problems to the population models (1.2) with the Dirichlet BCs.

(1) Since the population is diffusing, some members in the population may be lost through the boundary. Hence, it is of importance to find a critical patch size $l^{*}$ such that the population cannot sustain itself against boundary losses if the patch size is less than $l^{*}$, and can always maintain itself if the patch size is greater than $l^{*}$. When $H\equiv 0$, this problem was studied in [20,p.224].

(2) The effects of the quasi-constant-yield harvest rates on the population system, that is, to seek the threshold value $\delta^{*}$ for (1.2) with the Dirichlet BCs.

However, it seems difficult to find the exact critical patch size $l^{*}$ and determine the exact threshold value $\delta^{*}$ for (1.2) with the Dirichlet BCs. It turns out for us to find the ranges for the patch size $l$ and the computable expressions for the bounds of $\delta^{*}$ under which the population persists or becomes extinct. Similar to the problem studied in [25], seeking the computable bounds of $\delta^{*}$ for (1.2) with the Dirichlet BCs is precious for the population models since they can tell the exact quantity of harvest rates of the species without having the population die out.

After rescaling the variables of (1.2), the steady-state equations of (1.2) with the Dirichlet BCs is of the form

$\label{logintro3} \begin{cases} -y''(x)=\lambda \bigl[y(x)(1-y(x))-h_{\lambda}(x)\rho_{\varepsilon}(y(x))\bigr] \mbox{ for }x\in [0,1],\\ y(0)=y(1)=0, \end{cases}$

(1.3)

where $\lambda$ is related to the patch size $l$ and the norm $\|h_{\lambda}\|$ can be used to determine the value $\delta$ in (1.2). Note that the function $h_{\lambda}$ in the harvest term depends on $\lambda$, which implies that harvesting policy must be made based on the patch size $l$.

The persistence or extinction of the population corresponds to existence or nonexistence of positive solutions of (1.3), respectively. A solution $y$ of (1.3) is said to be positive if it satisfies $y(x)>0$ for $x\in (0,1)$.

Our purpose is to seek the range of $\lambda$ and the function $h_{\lambda}$ (equivalently, the function $H$) under which (1.3) has no positive solutions or has positive solutions. This is equivalent to look for the range of $\lambda$ and a function $h$ independent of $\lambda$ under which the following second order boundary value problem

$\label{logintro2} \begin{cases} -y''(x)=\lambda \Bigl\{y(x)[1-y(x)]-h(x)\rho_{\varepsilon}(y(x))\Bigr\} \mbox{ for }x\in [0,1],\\ y(0)=y(1)=0 \end{cases}$

(1.4)

has no positive solutions or has positive solutions.

We shall prove that when $\lambda\in (0,\pi^{2}]$, (1.4) has no positive solutions for any continuous function $h$, and when $\lambda>32$, (1.4) has positive solutions under suitable assumptions on the norm $\|h\|$. These assumptions provide computable explicit expressions for the upper bound of $\|h\|$. All the expressions are hyperbola functions of $\lambda$ or rational functions of $\lambda$ with the degrees of the numerator and denominator being 1 and 2, respectively, so the values of the upper bounds can be easily computed when $\lambda>32$ is given. This provides the exact quantity of harvest rates of the species without having the population die out.

When $\pi^{2}<\lambda\le 32$, we do not obtain any results on existence of positive solutions of (1.4), but we conjecture that the critical size $\lambda$ for (1.4) is $\pi^{2}$ since it is true when $h\equiv 0$, see [9,Lemma 1(ⅰ)] or [19,Lemma 1.1(ⅱ)]) and [8,Lemma 1.1].

As illustrations of our results, we consider two specific functions $h$: one is a location-independent constant function defined by $h(x)\equiv\sigma(\lambda)$, and another is the unimodal polynomial defined by $h(x)=\gamma(\lambda) x(1-x)$ for $x\in [0,1]$, which corresponds to a radial harvest rate approaching maximum only at the center of the patch. When $\lambda>32$, we provide the intervals for $\sigma(\lambda)$ or $\gamma(\lambda)$ under which the harvest activity does not result in extinction of the population.

Our method is to study the existence of positive solutions of a semi-positone Hammerstein integral equation of the form

$y(x)=\lambda \int_{0}^{1}k(x,s)f(x,y(s))\,ds \mbox{ for }x\in [0,1],$

(1.5)

where the nonlinearity $f$ satisfies the semi-positone condition:

$f(x,u)\ge -\eta(x) \mbox{ for a.e. }x\in [0,1]\; \mbox{ and all} \;u\in \mathbb R_{+},$

(1.6)

and $\eta$ is a measurable and positive real-valued function defined on $[0,1]$. Previous results considered the case when $\eta$ is a constant function (for example see [2,12,13,14,21] and the references therein).

By employing the well-known nonzero fixed point theorems for compact maps defined on cones obtained via the fixed point index [1], we prove a result on the existence of nonzero nonnegative solutions of (1.5) with $\lambda=1$ and then apply the result to obtain a new result on the eigenvalue problem (1.5). The last result is the key of dealing with the biological model (1.4). By defining a suitable nonlinearity $f$, we are able to transfer the boundary value problem (1.4) into (1.5) with the well-known Green's function.

To the best of our knowledge, this is the first paper to apply results on existence of positive solutions of semi-positone integral equations (1.5) to tackle the ecological model described by the equation (1.4). We believe that the results on existence of positive solutions of (1.5) would be also interesting to researchers working on integral equations and boundary value problems.

In section 2 of this paper, we formulate the model, rescale the variables, derive the steady-state equation of (1.2) with the Dirichlet BCs, and state the main results on positive steady-state solutions. In section 3 we provide and prove results on the existence of positive solutions of semi-positone Hammerstein integral equations (1.5) and apply them to section 4 to prove all the results mentioned in section 2. In the last section, we discuss and propose some questions about the model (1.2) with the Dirichlet BCs and its generalization.

---

2. Main results on the logistic models with quasi-constant-yield harvest rates

In this section, we derive the logistic models with quasi-constant-yield harvest rates subject to the Dirichlet BCs, derive the stead-state equations of the models and give the main results on the positive steady-state solutions.

We consider population of one species whose density varies in space and time. Following [20,22], we assume that the species inhabits a patch of favorable environment, in a one-dimensional strip of length $l$, surrounded by unsuitable habitat, and individuals that cross the boundary immediately die. Individuals in the population are assumed to disperse randomly, without regard to the positions of their neighbors, and the dispersal of the species is purely diffusive, so systematic motions are not considered. Under these assumptions, if the population obeys the logistic growth law and quasi-constant-yield harvesting is considered, then the temporal behavior of the species can be modeled by the following reaction-diffusion equation

$\label{rdapp} \dfrac{\partial w(t,X)}{\partial t}=r w(t,X)\left[1-\dfrac{w(t,X)}{K}\right]+d\dfrac{\partial ^{2}w(t,X)}{\partial X^{2}}-\delta H(X)\rho_{\varepsilon_{0}}(w(t,X)),$

(2.1)

subject to the Dirichlet boundary conditions:

$\label{dbc} w(t,0)=w(t,l)=0,$

(2.2)

where $w(t,X)$ is the population density of a species at time $t$ and location $X$.

Equation (2.1) shows that the rate of change of population density at a given location depends on population growth, movement and harvesting. The first term on the right side of (2.1) represents logistic growth rate. The parameter $r$ is the intrinsic growth rate of the species and $K$ is the environmental carrying capacity. The second term describes the movement of the population as by diffusion; the parameter $d$ is the diffusion coefficient. The last term denotes the quasi-constant-yield harvesting introduced in [25,p.136]. This corresponds for example, to a population of animals from which some of individuals are removed per year by hunting or trapping. The function $H$ is called the harvesting scalar field, the parameter $\delta$ is the amplitude of this field, and $\rho_{\varepsilon_{0}}:\mathbb R\to \mathbb R_{+}$ is a differentiable and increasing function satisfying

$\label{frho} \rho_{\varepsilon_{0}}(w)=\left\{ \begin{array}{ll} 1 & \mbox{ if }w\in (\varepsilon_{0},\infty),\\ 0& \mbox{ if }w\in (-\infty,0), \end{array} \right.$

(2.3)

where $\varepsilon_{0}\in [0,1)$ is a given small constant. With such a function $\rho_{\varepsilon_{0}}$, the yield depends on the population density when $u<\varepsilon_{0}$, but it is a constant $\delta H(X)$ when $u\ge \varepsilon_{0}$. Biologically, the number $\varepsilon_{0}$ is a threshold value below which harvesting is progressively abandoned. It was pointed out in [25,p.136] that without the threshold value, the model equation (2.1) only with constant-yield harvesting function $\delta H(X)$ is unrealistic since it would lead to a harvest on zero population.

Since it is assumed that no members of the population survive outside the strip, the population density at the habitat boundary is zero, which leads to the boundary conditions (2.2). The model is complete.

Let $x=X/l$ and $v(t,x)=w(t,X)/K.$ Then (2.1)-(2.2) is equivalent to the following boundary value problem

$\label{rdapp2} \begin{cases} \dfrac{\partial v(t,x)}{\partial t}-\dfrac{d}{l^{2}}\dfrac{\partial ^{2}v(t,x)}{\partial x^{2}}= r v(t,x)[1-v(t,x)]-\delta H(lx)\rho_{\varepsilon_{0}}(Kv(t,x)),\\ v(t,0)=v(t,1)=0. \end{cases}$

(2.4)

If a solution $v$ of (2.4) satisfies $\partial v(t,x)/\partial t\equiv 0$, then $v$ is independent of $t$, and is a function of $x$. Such solutions are called the stead-state solutions of (2.4) and are of the form

$\label{log0} \begin{cases} -\dfrac{d}{l^{2}}y''(x)=ry(x)[1-y(x)]-\delta H(lx)\rho_{\varepsilon_{0}}(Ky(x)) \mbox{ for }x\in [0,1],\\ y(0)= y(1)=0. \end{cases}$

(2.5)

Let

$\label{muh} \lambda=l^{2}r/d,\varepsilon=\varepsilon_{0}/K\mbox{ and }h_{\lambda}(x)=\delta H(lx)/r.$

(2.6)

Since the first term of (2.6) implies that $\lambda$ is related to the patch size $l$, by the last term of (2.6), we see that the harvest function $h_{\lambda}$ depends essentially on $l$. Biologically, it implies that making the harvest strategies must be based on the patch size.

By (2.6), (2.5) becomes the second order boundary value problem

$\label{loglambda} \begin{cases} -y''(x)=\lambda \Bigl\{y(x)[1-y(x)]-h_{\lambda}(x)\rho_{\varepsilon}(y(x))\Bigr\} \mbox{ for }x\in [0,1],\\ y(0)=y(1)=0. \end{cases}$

(2.7)

where $\rho_{\varepsilon}:\mathbb R\to \mathbb R_{+}$ is a differentiable and increasing function satisfying $\rho_{\varepsilon}(y)=0$ for $y\in (-\infty,0]$ and $\rho_{\varepsilon}(y)=1$ for $y\in (\varepsilon,\infty).$

We denote by $C[0,1]$ the Banach space of continuous functions defined on $[0,1]$ with the norm $\|y\|=\max\{|y(x)|: x\in [0,1]\}$ and by $P$ the positive cone, that is,

$\label{conep} P=\{y\in C[0,1]: y(x)\ge 0\mbox{ for }x\in [0,1]\}.$

(2.8)

A function $y:[0,1]\to \mathbb R$ is called a solution of (2.7) if $y\in C^{2}[0,1]$ satisfies (2.7), where $C^{2}[0,1]=\{y\in C[0,1]: y''(x)\in C[0,1]\,\,\mbox{ for }x\in [0, 1]\}.$ If $y$ is a solution of (2.7), then $v(t,x)\equiv y(x)$ is a solution of (2.4). A solution $y$ of (2.7) is called a nonnegative solution if $y\in P$, and a positive solution if $y(x)>0$ for $x\in (0,1)$.

Our purpose is to seek the range of $\lambda$ and the function $h_{\lambda}$ under which (2.7) has no positive solutions or has positive solutions. This is equivalent to look for the range of $\lambda$ and a function $h$ under which the following second order boundary value problem

$\label{log} \begin{cases} -y''(x)=\lambda \Bigl\{y(x)[1-y(x)]-h(x)\rho_{\varepsilon}(y(x))\Bigr\} \mbox{ for }x\in [0,1],\\ y(0)=y(1)=0 \end{cases}$

(2.9)

has no positive solutions or has positive solutions.

Now, we state the main results on existence and nonexistence of positive solutions of (2.9) and postpone their proofs to section 4. For simplification, throughout this paper we always assume that the following condition holds.

$(C)$: The function $h:[0,1]\to [0,\infty)$ is continuous.

We first give a result on nonexistence of nonzero nonnegative solutions of (2.9).

Theorem 2.1. For each $\lambda\in (0,\pi^{2}]$ and each function $h$ satisfying $(C)$, (2.9) has no solutions in $P\setminus\{0\}$.

Remark 2.1. Theorem 2.1 shows that if the patch size $l=\sqrt{\lambda d/r}$ is less than or equal to $\pi\sqrt{d/r}$, the species dies out everywhere on $(0,1)$. Also, Theorem 2.1 is a generalization of [9,Lemma 1(ⅰ)] or [19,Lemma 1.1(ⅱ)], where $h\equiv 0$.

From Theorem 2.1, we see that the necessary condition for the species to survive is to require that the patch size is greater than $\pi\sqrt{d/r}$, equivalently, $\lambda>\pi^{2}$.

In the following, we provide sufficient conditions on $\lambda$ and $h$ for the species to survive, that is, (2.9) has a positive solution.

Notation. Let $a,b\in (0,1)$ with $a<b$ and let

$\label{deltaabrho} \omega(a,b)=\left\{ \begin{array}{ll} a(1-b)& \mbox{ if }0\le a\le b\le \frac{1}{2},\\ \frac{1}{2}\min\{a,1-b\}& \mbox{ if }0\le a\le \frac{1}{2}\le b\le 1,\\ (1-a)(1-b)& \mbox{ if }\frac{1}{2}\le a\le b\le 1, \end{array} \right.$

(2.10)

$\label{M1} M_{1}(a,b)=\left(\min\Bigl\{\int_{a}^{x}(1-x)s\,ds+\int_{x}^{b}x(1-s)\,ds: x\in [a,b]\Bigr\}\right)^{-1},$

(2.11)

$\label{ouh} \overline{h}(a,b)=\max\{h(x): x\in [a,b]\},\,\underline{h}(a,b)=\min\{h(x): x\in [a,b]\},$

(2.12)

and

$\label{dab} h^{*}(a,b)=\overline{h}(a,b)-\underline{h}(a,b).$

(2.13)

The following result provides sufficient conditions on the patch size and the harvesting rate for the species to survive everywhere on $(0,1)$.

Theorem 2.2. Assume that there exist $a,b\in (0,1)$ with $a<b$ and $\rho\in (0, 1)$ such that the following conditions hold.

$(H_{1})$ $\lambda\in \left(\dfrac{\min\{a,1-b\} M_{1}(a,b)} {\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}},\infty\right)$.

$(H_{2})$ $h^{*}(a,b) <\rho\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}-\dfrac{\rho\min\{a,1-b\} M_{1}(a,b)}{\lambda}.$

$(H_{3})$ $\max\left\{\displaystyle\int_{0}^{1}sh(s)\,ds, \displaystyle\int_{0}^{1}(1-s)h(s)\,ds\right\} <\dfrac{\rho \min\{a,1-b\}}{\lambda}$.

Then (2.9) has a positive solution.

Remark 2.2. Under $(H_{1})$ and $(H_{3})$, $\underline{h}(0,1)=\min\{h(s): s\in [0,1]\}<1/2$.

Let

$\label{etarho} \eta_{\rho}=\left\{ \begin{array}{ll} \frac{8-\rho}{64} & \mbox{ if }0<\rho\le \frac{8}{9},\\ 1-\rho& \mbox{ if }\frac{8}{9}<\rho<1. \end{array} \right.$

(2.14)

Theorem 2.2 depends on the choices of $a$ and $b$. One of the choices is $a=\frac{1}{4}$ and $b=\frac{3}{4}$. This leads to the following result.

Corollary 2.1. Assume that there exists $\rho\in (0, 1)$ such that the following conditions hold.

$(1)$ Either $\lambda\in \left[\dfrac{9}{2\eta_{\rho}},\infty\right]$ or $\lambda\in \left(\dfrac{4}{\eta_{\rho}}, \dfrac{9}{2\eta_{\rho}}\right]$ and $h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)<\rho\eta_{\rho}-\dfrac{4\rho}{\lambda}$.

$(2)$ $\|h\|<\dfrac{\rho}{2\lambda}$.

Then (2.9) has a positive solution.

In Corollary 2.1, the intervals of $\lambda$ and $\|h\|$ depend heavily on the existence of $\rho$.

The following result gives the intervals of $\lambda$ and $\|h\|$ which do not involve the number $\rho$ explicitly, so is easily verified and applied.

Theorem 2.3. Assume that one of the following conditions holds.

$(T_{1})$ $\lambda\in (32,36]$ and one of the following conditions holds.

$(i)$ $\|h\|<\dfrac{2(\lambda-32)}{\lambda^{2}}$ and $h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)< \dfrac{(\lambda-32)^{2}}{4\lambda^{2}}$.

$(ii)$ $\dfrac{2(\lambda-32)}{\lambda^{2}}\le \|h\|<\dfrac{4(\lambda-32)}{\lambda^{2}}$ and $h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)<\dfrac{\|h\|(-\|h\|\lambda^{2}+4\lambda-128)}{16}.$

$(T_{2})$ $36<\lambda\le\dfrac{81}{2}$ and one of the following conditions holds:

$(i)$ $\|h\|<\dfrac{4(\lambda-36)}{\lambda^{2}}.$

$(ii)$ $\dfrac{4(\lambda-36)}{\lambda^{2}}\le \|h\|<\dfrac{4}{9\lambda}$ and $h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)<\dfrac{8(\lambda-36)}{81\lambda}$.

$(iii)$ $\dfrac{4}{9\lambda}\le \|h\|<\dfrac{\lambda-4}{2\lambda^{2}}$ and $h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)<2\|h\|(-2\|h\|\lambda^{2}+\lambda-4)$.

$(T_{3})$ $\dfrac{81}{2}<\lambda<\infty$ and one of the following conditions holds.

$(i)$ $\|h\|<\dfrac{2\lambda-9}{4\lambda^{2}}$.

$(ii)$ $\dfrac{2\lambda-9}{4\lambda^{2}}\le \|h\|<\dfrac{\lambda-4}{2\lambda^{2}}$ and $h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)<2\|h\|(-2\|h\|\lambda^{2}+\lambda-4)$.

Then (2.9) has a positive solution.

In Theorem 2.3, both conditions $(T_{2})$ $(i)$ and $(T_{3})$ $(i)$ do not contain the term $h^{*}\bigl(\frac{1}{4},\frac{3}{4}\bigr)$, but all others do. However, the conditions on $h^{*}$ can be removed when $h$ satisfies suitable conditions (see Examples 2.1 and 2.2 below).

As first illustration, we consider $h$ to be a location-independent constant function.

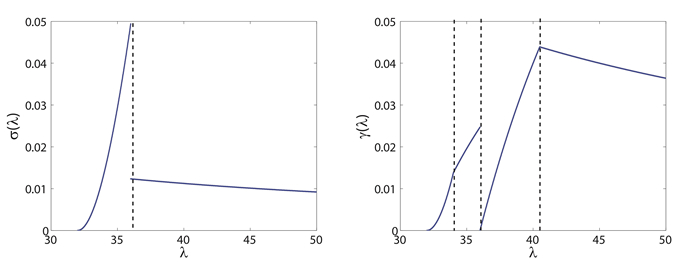
Example 2.1. Assume that $\lambda$ and $\sigma (\lambda)$ satisfy the following condition:

$\label{sigma} 0<\sigma(\lambda)<\left\{ \begin{array}{ll} \dfrac{4(\lambda-32)^{2}}{\lambda^{2}} & \mbox{ if }32<\lambda\le 36,\\ \dfrac{\lambda-4}{2\lambda^{2}}& \mbox{ if }36<\lambda<\infty. \end{array} \right.$

(2.15)

Then (2.9) with $h(x)\equiv \sigma(\lambda)$ has a positive solution.

As second illustration, we consider a unimodal polynomial $h$ defined by

$\label{hrf} h(x)=\gamma(\lambda) x(1-x)\mbox{ for }x\in [0,1].$

(2.16)

Considering (2.16) is realistic since it corresponds to a radial harvest rate reaching the maximum at the center of the patch and approaching zero at both boundaries.

Example 2.2. Assume that $\lambda$ and $\gamma(\lambda)$ satisfy the following condition:

$\label{gamma1} \gamma(\lambda)<\left\{ \begin{array}{ll} \dfrac{4(\lambda-32)^{2}}{\lambda^{2}} & \mbox{ if }32<\lambda\le 34,\\ \dfrac{8(\lambda-32)}{\lambda^{2}}& \mbox{ if }34<\lambda\le 36,\\ \dfrac{128(\lambda-36)}{81\lambda} & \mbox{ if }36<\lambda\le \frac{81}{2},\\ \dfrac{2\lambda-9}{\lambda^{2}}& \mbox{ if }\frac{81}{2}<\lambda<\infty. \end{array} \right.$

(2.17)

Then (2.9) with $h$ defined in (2.16) has a positive solution.

As shown in Figure 1, Examples 2.1 and 2.2 actually provide feasible regions of the quantity of harvest rates of the species for each patch size under which the population survives. We expect that these ranges will be useful in management of sustainable ecological systems.

---

3. Positive solutions of semi-positone Hammerstein integral equations

To prove results on the persistence of the one-dimensional diffusive logistic models with quasi-constant-yield harvest rates given in section 2, we first establish new results on the existence of positive solutions of a semi-positone Hammerstein integral equation of the form

$\label{ho1} y(x)=\int_{0}^{1}k(x,s)f(s,y(s))\,ds:\equiv Ty(x) \mbox{ for }x\in [0,1],$

(3.1)

where the nonlinearity $f$ satisfies a semi-positone condition to be given below. This allows $f$ to take negative values and to have a lower bound depending on $x$.

We denote by $\mathfrak{M}^{+}$ the set of all measurable real-valued positive functions defined on $[0,1]$. We list the following conditions.

$(C_{1})$ $k:[0,1]\times [0,1]\to \mathbb R_{+}$ satisfies the following conditions:

(ⅰ) For each $x\in [0,1]$, $k(x,\cdot)\in \mathfrak{M}^{+}$.

(ⅱ) There exist a continuous function $C:[0,1]\to [0,1]$ and a function $\Phi\in \mathfrak{M}^{+}$ such that for almost every (a.e.) $x\in [0,1]$ and all $s \in [0,1]$,

$\label{ink} C(x)\Phi(s)\le k(x,s)\le \Phi(s).$

With the function $\Phi$ given in $(C_{1})$, we let

$\mathfrak{M}_{\Phi}^{+}=\{z\in \mathfrak{M}^{+}: z\Phi\in L^{1}[0,1]\}.$

$(C_{2})$ $f:[0,1]\times \mathbb R_{+}\to \mathbb R$ satisfies Carathéodory conditions on $[0,1]\times \mathbb R_{+}$, that is, $f(\cdot,u)$ is measurable for $u\in \mathbb R_{+}$ and $f(x,\cdot)$ is continuous for a.e. $x\in [0,1]$, and for $r>0$, there exists $g_{r}\in \mathfrak{M}_{\Phi}^{+}$ satisfying the following conditions:

(ⅰ) For each $\tau\in [0,1]$, $\lim_{x\to \tau}\int_{0}^{1}|k(x,s)-k(\tau,s)|g_{r}(s)\, ds=0$.

(ⅱ) $|f(x,u)|\le g_{r}(x)$ for a.e. $x\in [0,1]$ and all $u\in [0,r].$

$(C_{3})$ (Semi-positone condition) There exists $\eta\in \mathfrak{M}_{\Phi}^{+}$ such that

$\label{semip} f(x,u)\ge -\eta(x) \mbox{ for a.e. }x\in [0,1]\; \mbox{ and all }\;u\in \mathbb R_{+}.$

$(C_{4})$ There exists $r(\eta)>0$ such that

$\int_{0}^{1}k(x,s)\eta(s)\, ds\le r(\eta)C(x)\mbox{ for }x\in [0,1].$

$(C_{5})$ There exist $a,b\in[0,1]$ with $a<b$ such that

$\underline{c}(a,b):=\min\{C(x):x\in [a,b]\}>0.$

The conditions $(C_{1})$, $(C_{2})$ and $(C_{5})$ are the standard conditions used in [12,13,14,28], and $(C_{4})$ with a constant $\eta$ was used in some of these references. $(C_{3})$ allows $f$ to take negative values and is more general than those in [2,12,13,14,21], where the lower bound function $\eta$ is a constant. $(C_{3})$ was used in [28], where $\eta$ is integrable and its main result can not be applied to treat the biological models in section 2.

Recall that a function $y\in C[0,1]$ is said to be a nonnegative solution of (3.1) if $y\in P$ and $y$ satisfies (3.1). A nonnegative solution $y$ is said to be positive if it satisfies

$\label{ps} y(x)>0\mbox{ for }x\in (0,1).$

(3.2)

To obtain positive solutions of (3.1), we need some knowledge on the fixed point index theory for compact maps defined in cones in Banach spaces [1].

Let $K$ be a cone in a Banach space $X$ and $D$ a bounded open set in $X$. We denote by $\overline{D}_K$ and $\partial D_K$ the closure and the boundary, respectively, of $D_{K}=D\cap K$ relative to $K$. Recall that a map $A: \Omega\subset X\to X$ is said to be compact if it is continuous and $\overline{A(D)}$ is compact for each bounded subset $D\subset\Omega.$ We shall use the following result (see Lemma 2.3 in [15]).

Lemma 3.1. Let $D^{1}$ be open in $X$ such that $\overline{D_{K}^{1}}\ne \emptyset$ and $\overline{D_{K}^{1}}\subset D_K$. Assume that $A: \overline{D}_{K}\to K$ is a compact map and satisfies the following conditions.

$(i)$ There exists $e\in K\setminus \{0\}$ such that

$z\ne Az+\beta e\; for \;z\in \partial D_{K}^{1}\; and \;\beta \ge 0.$

$(ii)$ $z\ne \varrho Az$ for $z\in \partial D_{K}$ and $\varrho\in [0,1]$.

Then $A$ has a fixed point in $D_{K}\setminus \overline{D_{K}^{1}}$.

The fixed point index theory for compact maps defined on $K$ requires the maps to be self-maps taking values in $K$. Since the semi-positone condition $(C_{3})$ allows $f$ to take negative values, the integral operator $T$ defined in (3.1), in general, is not a self-map on the cone $P$ in (2.8). This leads to considering the following equation

$\label{ho} z(x)= \int_{0}^{1}k(x,s)\big[f(s,z(s)-w(s))+\eta(s)\big]\,ds: \equiv Az(x)\mbox{ for }x\in [0,1],$

(3.3)

where

$\label{w} w(x)= \int_{0}^{1}k(x,s)\eta(s)\, ds\mbox{ for }x\in [0,1].$

(3.4)

By the condition $(C_{3})$, we have

$f(s,z(s)-w(s))+\eta(s)\ge 0\mbox{ for }s\in [0,1]$

and $Az(x)\ge 0$ for $x\in [0,1]$. Since $f$ is defined only on $[0,1]\times \mathbb R_{+}$ and $z(s)-w(s)$ may be negative for some $z\in P$ and $s\in [0,1]$, $Az$ is defined only for $z(s)\ge w(s)$ for $s\in [0,1]$. This implies that $A$ is not, in general, defined on the entire cone $P$. In addition, since there is difficulty to prove that the index for the operator $A$ is zero if one uses the cone $P$, the following cone $K$ smaller than $P$ is often employed:

$\label{cone} K=\{z\in C[0,1]: z(x)\ge C(x)\|z\|\mbox{ for }x\in [0,1]\}.$

(3.5)

Such a cone has been used in [12,13,14,28] to study the existence of nonnegative solutions for some Hammerstein integral equations and differential equations.

Let $r>0$ and let $K_{r}=\{x\in K: \|x\|<r\}$ and $\overline{K}_{r}=\{x\in K: \|x\|\le r\}$.

The following result shows that $A$ is well defined on $K\setminus K_{r(\eta)}$ and is compact from $K\setminus K_{r(\eta)}$ to $K$, and gives the relation between the solutions of (3.1) and (3.3).

Lemma 3.2. $(i)$ Under the hypotheses $(C_{1})$-$(C_{4})$ the map $A$ defined in (3.3) maps $K\setminus K_{r(\eta)}$ into $K$ and is compact.

$(ii)$ A function $z\in K\setminus \overline{K}_{r(\eta)}$ is a solution of (3.3) if and only if $z-w$ is a nonnegative solution of (3.1).

$(iii)$ If $C(x)>0$ for $x\in (0,1)$ and $z\in K\setminus \overline{K}_{r(\eta)}$ is a solution of (3.3), then $z-w$ is a positive solution of (3.1).

Proof. $(i)$ Let $z\in K\setminus K_{r(\eta)}$. Then $\|z\|\ge r(\eta)$ and by (3.5), we have

$\label{etain} z(x)-w(x)\ge C(x)\|z\|-r(\eta)C(x)\ge 0 \mbox{ for }x\in [0,1].$

(3.6)

This implies that $\mathcal{F}z(x):=f(x,z(x)-w(x))+\eta(x)$ is well defined for $x\in [0,1]$. By Lemmas 2.1 and 2.2 in [16], $A:K\setminus K_{r(\eta)}\to P$ is compact. By $(C_{1})$ $(ii)$, we have $\|Az\|\le \int_{0}^{1}\Phi(s)\mathcal{F}z(s)\,ds$ for $z\in K\setminus K_{r(\eta)}$ and

$Az(x)\ge C(x)\int_{0}^{1}\Phi(s)\mathcal{F}z(s)\,ds\mbox{ for }x\in [0,1].$

This implies $Az(x)\ge C(x)\|Az\|$ for $x\in [0,1]$ and $Az\in K$ for $z\in K\setminus K_{r(\eta)}$.

$(ii)$ The proof follows from (3.6) and $(C_{1})$ $(ii)$.

$(iii)$ Let $z\in K\setminus \overline{K}_{r(\eta)}$. Note that $C(x)>0$ for $x\in (0,1)$. By (3.6), we have

$y(x)=z(x)-w(x)\ge C(x)\|z\|-r(\eta)C(x)=C(x)[\|z\|-r(\eta)]>0 \mbox{ for }x\in (0,1)$

and $(iii)$ holds.

Remark 3.1. Lemma 3.2 $(i)$ and $(ii)$ are generalizations of [13,Theorem 1] and Lemma 3.2 $(iii)$ is new and will be used in section 4.

By Dugundji's theorem [10], there is a compact map $A^{*}:K\to K$ such that

$\label{aa} A^{*}z=Az\mbox{ for }z\in K\setminus K_{r(\eta)}.$

(3.7)

We need the following relatively open subset and its properties:

$\label{omega1} \Omega_{\rho}=\{z\in K: q(z)<c\rho\}=K\cap \{z\in P:c\|z\|\le q(z)<c\rho\},$

where $q(z)=\min\{z(x):x\in [a,b]\}$ and $c=\underline{c}(a,b)$ is given in $(C_{5})$.

Lemma 3.3 [12]. $\Omega_{\rho}$ defined above has the following properties.

$(1)$ $\Omega_{\rho}$ is open relative to $K$.

$(2)$ $K_{c\rho}\subset \Omega_{\rho}\subset K_\rho$.

$(3)$ $z\in \partial \Omega_\rho$ if and only if $z\in K$ and $q(z)=c\rho$, where $\partial \Omega_{\rho}$ denotes the boundary of $\Omega_\rho$ relative to $K$.

$(4)$ If $z\in \partial \Omega_\rho$, then $c\rho\le z(x)\le \rho$ for $x\in [a,b]$.

We will use the following notations: Let $\psi\in \mathfrak{M}_{\Phi}^{+}$ and let

$\label{mpsi} m_{\psi}(a,b)=\left(\max\limits_{x\in [a,b]}\int_{0}^{1}k(x,s)\psi(s)\,ds\right)^{-1}$

and

$\label{Mmpsi} M_{\psi}(a,b) = \left(\min\limits_{x\in [a,b]}\int_{a}^{b} k(x,s)\psi(s)\,ds\right)^{-1}.$

(3.8)

To obtain the fixed point index of $A$ is $1$, we need the characteristic value, denoted by $\mu_{\phi}$, of the following linear integral equation

$u(x)=\mu\int_{0}^{1} k(x,s)\phi(s) u(s)\,ds:=\mu (Lu)(x)\mbox{ for }x\in [0,1].$

(3.9)

By [14,Theorem 2.1], it is known that if the conditions $(C_{1})$ and $(C_{2})$ $(i)$ hold and

$\label{gamma} \int_{0}^{1}\Phi(s)\phi(s)C(s)\,ds>0,$

then there exists $\psi\in K\setminus\{0\}$ such that

$\psi(x)=\mu_{\phi}\int_{0}^{1} k(x,s)\phi(s) \psi(s)\,ds\mbox{ for }x\in [0,1],$

where $\mu_{\phi}=1/r(L)$ and

$r(L)=\lim\limits_{n \to \infty} \|L^n\|^{1/n}$

is the spectral radius of the compact linear operator $L$ defined in (3.9).

We now prove the following new result on the existence of nonnegative solutions of (3.3).

Theorem 3.1. Assume that the conditions $(C_{1})$-$(C_{5})$ hold and there exist $\rho, \rho_{0}\in (r(\eta)\underline{c}(a,b)^{-1},\infty)$ with $\rho<\rho_{0}$ such that the following conditions hold.

$(H_{\ge}^{0})_{\rho}$ There exists $\psi(s)\in \mathfrak{M}_{\Phi}^{+}$ with $\int_{0}^{1}\Phi(s)\psi(s)\,ds>0$ such that

$f(s,u)\ge \rho\underline{c}(a,b) M_{\psi}(a,b)\psi(s)-\eta(s) \;for\; a.e. \;s\in [a,b]\; and \;u\in [\rho_{*},\rho].$

where $\rho_{*}=\rho\underline{c}(a,b)-m_{\eta}(a,b)^{-1}$.

$(H_{\le}^{1})_{\phi_{\rho_{0}}}^{\infty}$ There exist $\phi_{\rho_{0}}\in L_{+}^{1}(0,1)$ with $\int_{0}^{1}\Phi(s)\phi_{\rho_{0}}(s)C(s)\,ds>0$ and $\varepsilon>0$ such that

$f(s,u)\le (\mu_{\phi_{\rho_{0}}}-\varepsilon)\phi_{\rho_{0}}(s)u \;for\; a.e. \;s\in [0,1]\; and \;u\in [\rho_{0},\infty).$

(3.10)

Then (3.1) has one nonnegative solution. In addition, if $C(x)>0$ for $x\in (0,1)$, then (3.1) has one positive solution.

Proof. By Lemma 3.2 $(ii)$, to obtain nonnegative solutions of (3.1), we prove that (3.3) has a solution in $K\setminus \overline{K}_{r(\eta)}$, that is, $A$ defined in (3.3) has a fixed point in $K\setminus \overline{K}_{r(\eta)}$. Without loss of generalization, we assume that $z\ne Az$ for $z\in \partial \Omega_\rho$. Let $e(x)\equiv 1$ for $x\in [0,1]$. Then $e\in K$ with $\|e\|=1$. We prove that

$\label{za} z\ne A^{*}z+\beta e\mbox{ for }z\in \partial \Omega_{\rho} \mbox{ and } \beta\ge 0.$

(3.11)

In fact, if not, there exist $z\in \partial \Omega_\rho$ and $\beta>0$ such that $z=A^{*}z+\beta e$. By Lemma 3.3 $(3)$, we have $\|z\|\ge q(z)\ge \rho\underline{c}(a,b)>r(\eta)$ and $z\in K\setminus K_{r(\eta)}$. It is easy to verify that

$\rho_{*}=\rho\underline{c}(a,b)-m_{\eta}(a,b)^{-1}\le z(s)-w(s)\le \rho\mbox{ for }s\in [a,b].$

Since $\|z\|>r(\eta)$, by (3.7), $A^{*}z=Az$. By $(H_{\ge}^{0})_{\rho}$, we have for $x\in [a,b]$,

$\begin{align*} z(x)&=A^{*}z+\beta =Az+\beta =\int_{0}^{1}k(x,s)[f(s,z(s)-w(s))+\eta(s)]\,ds+\beta\\ &\ge \int_{a}^{b}k(x,s)[f(s,z(s)-w(s))+\eta(s)]\,ds+\beta\\ &\ge \rho\underline{c}(a,b) M_{\psi}(a,b)\int_{a}^{b}k(x,s)\psi(s)\,ds+\beta \\ &\ge \rho\underline{c}(a,b) M_{\psi}(a,b)\min\limits_{x\in [a,b]}\int_{a}^{b} k(x,s)\psi(s)\,ds+\beta = \rho\underline{c}(a,b)+\beta. \end{align*}$

This implies that $q(z)\ge \rho\underline{c}(a,b)+\beta>\rho\underline{c}(a,b)$. By Lemma 3.3 $(3)$, we have

$\rho\underline{c}(a,b)=q(z)>\rho\underline{c}(a,b),$

a contradiction. It follows from (3.11) and Lemma 3.1 $(2)$ that $i_{K}(A^{*},\Omega_{\rho})=0$.

By $(C_{2})$ $(ii)$, there exists $g_{\rho_{0}}\in \mathfrak{M}_{\Phi}^{+}$ such that

$f(s,u)\le g_{\rho_{0}}(s) \mbox{ for a.e. }s\in [0,1]\; \mbox{ and } \;u\in [0,\rho_{0}].$

This, together with (3.10), implies

$\label{eqabc22} f(s,u)\le g_{\rho_{0}}(s)+(\mu_{\phi_{\rho_{0}}}-\varepsilon)\phi_{\rho_{0}}(s)u\mbox{ for a.e. }s\in [0,1]\; \mbox{ and all }\;u\in \mathbb R_{+}.$

(3.12)

Let

$Su(x) =\int_{0}^{1}k(x,s)\phi_{\rho_{0}}(s)u(s)\,ds\mbox{ for }x\in [0,1].$

Since $r((\mu_{\phi_{\rho_{0}}}-\varepsilon) S)=(\mu_{\phi_{\rho_{0}}}-\varepsilon)r(S) <1$, $\bigl(I-(\mu_{\phi_{\rho_{0}}}-\varepsilon) S\bigr)^{-1}$ exists and is a bounded linear operator satisfying $\bigl(I-(\mu_{\phi_{\rho_{0}}}-\varepsilon)S\bigr)^{-1}(K)\subset K$. Let

$u_{1}(x)=\int_{0}^{1}k(x,s)[g_{\rho_{0}}(s)+(\mu_{\phi_{\rho_{0}}}-\varepsilon)w(s)+\eta(s)]\,ds\mbox{ for }x\in [0,1]$

and

$\rho^{*}>\max\bigl\{r(\eta),\|\bigl(I-(\mu_{\phi_{\rho_{0}}}-\varepsilon) S\bigr)^{-1}(u_{1})\|\bigr\}.$

Then $\rho^{*}\in (r(\eta),\infty)$. Let $\rho>\rho^{*}$. We prove that

$\label{lsin} z\ne \varrho Az\mbox{ for }z\in \partial K_{\rho}\; \mbox{ and }\;\varrho\in [0,1].$

(3.13)

In fact, if not, there exist $z\in \partial K_{\rho}$ and $\varrho\in (0,1]$ such that $z=\varrho A z$. By (3.12), we have for $x\in [0,1]$,

$\begin{align*} z(x)&\le Az(x)=\int_{0}^{1}k(x,s)\bigl[f(s,z(s)-w(s))+\eta(s)\bigr]\,ds\\ &\le\int_{0}^{1}k(x,s)\bigl[g_{\rho_{0}}(s)+(\mu_{\phi_{\rho_{0}}}-\varepsilon)\phi_{\rho_{0}}(s)(z(s)-w(s))+\eta(s)\bigr]\,ds\\ &\le\int_{0}^{1}k(x,s)\bigl[g_{\rho_{0}}(s)+(\mu_{\phi_{\rho_{0}}}-\varepsilon)\phi_{\rho_{0}}(s)(z(s)+w(s))+\eta(s)\bigr]\,ds\\ & \le (\mu_{\phi_{\rho_{0}}}-\varepsilon)Sz(x)+u_{1}(x) \end{align*}$

and $(I-(\mu_{\phi_{\rho_{0}}}-\varepsilon)S)z\le u_{1}.$ This, together with $\bigl(I-(\mu_{\phi_{\rho_{0}}}-\varepsilon) S\bigr)^{-1}(K)\subset K$, implies

$z\le \bigl(I-(\mu_{\phi_{\rho_{0}}}-\varepsilon) S\bigr)^{-1}(u_1)$

and

$\|z\|\le \|\bigl(I-(\mu_{\phi_{\rho_{0}}}-\varepsilon) S\bigr)^{-1}(u_1)\| < \rho^{*}.$

Hence, we have $\rho=\|z\|<\rho^{*}<\rho$, a contradiction. By (3.13) and Lemma 3.1 $(1)$, $i_{K}(A^{*},K_{\rho})=1$ for $\rho>\rho_{1}$.

By Lemma 3.1, $A^{*}$ has a fixed point $z$ in $K_{\rho_{0}}\setminus \overline{K}_{\rho}$. Since

$\|z\|>\rho>r(\eta)\underline{c}(a,b)^{-1}\ge r(\eta),$

$z=A^{*}z=Az$ and $z$ is a fixed point of $A$. By Lemma 3.2 $(ii)$, $y=z-w$ is a nonnegative solution of (3.3). If $C(x)>0$ for $x\in (0,1)$, it follows from Lemma 3.2 $(iii)$ that $y$ is a positive solution of (3.3).

To study the biological model (2.9), we consider the following eigenvalue problems of semi-positone Hammerstein integral equation

$\label{hoeigen} y(x)=\lambda \int_{0}^{1}k(x,s)f(s,y(s))\,ds \mbox{ for }x\in [0,1].$

(3.14)

Equation (3.14) was studied in [14], where the nonlinearity is a product of a measurable function $g(s)$ and a continuous function $f(s,u)$, and multiple positive solutions were studied. Here we apply Theorem 3.1 to prove a new result which is different from those obtained in [14] and is suitable to tackling (2.9).

Notation. Let

$\label{delta} \delta^{*}:=\delta^{*}(a,b,\rho, \eta)=\rho \underline{c}(a,b)\left[1-\frac{1}{r(\eta)m_{\eta}(a,b)}\right],$

(3.15)

$\begin{align*} \overline{f}(u)&=\sup\limits_{x \in [0,1]} f(x,u), \;\; f^{\infty}=\limsup\limits_{u \to \infty}\overline{f}(u)/u,\;\; \underline{f}_{a,b}(u)=\inf\limits_{x \in [a,b]} f(x,u),\\ \underline{f}_{\delta}^{\rho}(a,b)&=\min\left\{\underline{f}_{a,b}(u): u\in [\delta,\rho]\right\},\;\; \underline{\eta}(a,b)=\min\{\eta(s): s\in [a,b]\}. \end{align*}$

Theorem 3.2. Assume that the hypotheses $(C_{1})$-$(C_{5})$ hold and there exist $\rho>0$ and $\delta\in (0, \delta^{*}]$ such that the following conditions hold.

$(i)$ $-\infty\le f^{\infty}<\infty$.

$(ii)$ $\underline{f}_{\delta}^{\rho}(a,b)+\underline{\eta}(a,b)>0$.

$(iii)$ $\mu_{*}(a,b,\rho, \delta)<\mu^{*}(a,b,\rho),$ where

$\label{muupper} \mu^{*}(a,b,\rho)=\left\{ \begin{array}{ll} \min\left\{\dfrac{\rho \underline{c}(a,b)}{r(\eta)},\dfrac{\mu_{1}}{f^{\infty}}\right\}, & \;if\;0<f^{\infty}<\infty,\\ \dfrac{\rho \underline{c}(a,b)}{r(\eta)},&\;if\;-\infty\le f^{\infty}\le 0, \end{array} \right.$

(3.16)

and

$\label{mulower} \mu_{*}(a,b, \rho, \delta)=\dfrac{\rho\underline{c}(a,b)M_{1}(a,b)} {\underline{f}_{\delta}^{\rho}(a,b)+\underline{\eta}(a,b)},$

(3.17)

where $M_{1}(a,b)$ is specified in (3.8) with $\psi(s)\equiv 1$.

Then for each $\lambda\in \bigl(\mu_{*}(a,b, \rho, \delta),\mu^{*}(a,b,\rho)\bigr)$, (3.14) has one nonnegative solution, and if $C(x)>0$ for $x\in (0,1)$, then (3.14) has one positive solution.

Proof. Let $\lambda\in \bigl(\mu_{*}(a,b,\rho, \delta),\mu^{*}(a,b,\rho)\bigr)$. We define $f_{\lambda}:[0,1]\times \mathbb R_{+}\to \mathbb R$ by

$f_{\lambda}(x,u)=\lambda f(x,u).$

Then $f_{\lambda}$ satisfies $(C_{2})$. Let $\eta_{\lambda}(x)=\lambda \eta(x)$ for $x\in [0,1]$. Since $f$ satisfies $(C_{3})$,

$f_{\lambda}(x,u)\ge -\lambda \eta(x)=-\eta_{\lambda}(x) \mbox{ for a.e. }x\in [0,1]\;\mbox{ and all }u\in \mathbb R_{+}$

and $f_{\lambda}$ satisfies $(C_{3})$. Let $r(\eta_{\lambda})=\lambda r(\eta)$. Since $\eta$ satisfies $(C_{4})$, we have

$\int_{0}^{1}k(x,s)\eta_{\lambda}(s)\,ds\le \lambda r(\eta)C(x)=r(\eta_{\lambda})C(x)\ \mbox{ for }x\in [0,1]$

and $\eta_{\lambda}$ satisfies $(C_{4})$. Since $\lambda<\mu^{*}(a,b,\rho)\le \dfrac{\rho \underline{c}(a,b)}{r(\eta)}$, it follows that

$\rho\in (r(\eta_{\lambda})\underline{c}(a,b)^{-1},\infty).$

Since $\lambda>\mu_{*}(a,b, \rho, \delta),$ we have $\lambda \underline{f}_{\delta}^{\rho}(a,b)\ge \rho\underline{c}(a,b) M_{1}(a,b)-\lambda \underline{\eta}(a,b)$ and

$\label{imp} \lambda f(s,u)\ge \rho\underline{c}(a,b) M_{1}(a,b)-\lambda\eta(s)\mbox{ for a.e. }s\in [a,b] \mbox{ and }u\in[\delta,\rho].$

(3.18)

Since $\lambda<\mu^{*}(a,b,\rho)\le \dfrac{\rho \underline{c}(a,b)}{r(\eta)}$, we have

$m_{\eta_{\lambda}}(a,b)^{-1}=\lambda m_{\eta}(a,b)^{-1} <\dfrac{\rho\underline{c}(a,b)}{r(\eta)m_{\eta}(a,b)}.$

Let $(\rho_{\lambda})_{*}=\rho\underline{c}(a,b)-m_{\eta_{\lambda}}(a,b)^{-1}.$ Then

$(\rho_{\lambda})_{*} > \rho\underline{c}(a,b)-\dfrac{\rho\underline{c}(a,b)}{r(\eta)m_{\eta}(a,b)} =\delta^{*}(a,b,\rho, \eta)$

and

$\bigl[(\rho_{\lambda})_{*},\rho\bigr]\subset [\delta^{*}(a,b,\rho, \eta), \rho] \subset[\delta,\rho].$

This, together with (3.18), implies

$f_{\lambda}(s,u) \ge \rho\underline{c}(a,b) M_{1}(a,b)-\eta_{\lambda}(s)\mbox{ for a.e. }s\in [a,b]\mbox{ and }u\in \bigl[(\rho_{\lambda})_{*},\rho\bigr]$

and $f_{\lambda}$ satisfies Theorem 3.1 $(H_{\ge}^{0})_{\rho}$ with $\psi\equiv 1$.

If $0<f^{\infty}<\infty$, then since $\lambda<\mu^{*}(a,b,\rho)$, it follows from (3.16) that

$\label{lambdafmu} \lambda f^{\infty}<\mu_{1}.$

(3.19)

Let $\varepsilon\in (0, \mu_{1}-\lambda f^{\infty})$. Then by (3.19), there exists $\rho_{0}>\rho$ such that

$\lambda \overline{f}(u)\le (\mu_{1}-\varepsilon)u\mbox{ for }u\in [\rho_{0},\infty).$

This implies

$f_{\lambda}(s,u)=\lambda f(s,u)\le (\mu_{1}-\varepsilon)u\mbox{ for a.e. }s\in [0,1]\mbox{ and }u\in [\rho_{0},\infty)$

and $f_{\lambda}$ satisfies (3.10) with $\phi_{\rho_{0}}\equiv 1$.

If $-\infty\le f^{\infty}\le 0$, then there exist $\rho_{0}>\rho$ and $\varepsilon\in (0,\mu_{1})$ such that

$f_{\lambda}(s,u)=\lambda f(s,u)\le (\mu_{1}-\varepsilon)u\mbox{ for a.e. }s\in [0,1]\mbox{ and }u\in [\rho_{0},\infty)$

and $f_{\lambda}$ satisfies (3.10) with $\phi_{\rho_{0}}\equiv 1$. Hence, $f_{\lambda}$ satisfies Theorem 3.1 $(H_{\le}^{1})_{\phi_{\rho_{0}}}^{\infty}$ with $\phi_{\rho_{0}}\equiv 1$. The result of Theorem 3.2 follows from Theorem 3.1.

---

4. Proofs of results in section 2

In this section, we provide all the proofs of results mentioned in section 2. Recall that the function $h:[0,1]\to [0,\infty)$ satisfies the condition $(C)$ if $h$ is continuous on $[0,1]$.

Proof of Theorem 2.1. The proof is by contradiction. Assume that there exist $\lambda\in (0,\pi^{2}]$ and $y\in P\setminus\{0\}$ satisfying (2.9). Let $\phi_{1}(x)=\sin (\pi x)$ for $x\in [0,1]$. Multiplying (2.9) by $\phi_{1}$ and integrating the resulting equation implies

$(\lambda-\pi^{2})\int_{0}^{1}y(x)\phi_{1}(x)\,dx =\lambda\int_{0}^{1}y^{2}(x)\phi_{1}(x)\,dx+\lambda\int_{0}^{1}h(x)\rho_{\varepsilon}(y(x))\phi_{1}(x)\,dx.$

Since $\lambda\in (0,\pi^{2}]$ and $h(x)\rho_{\varepsilon}(y(x))\ge 0$ for $x\in [0,1]$, $\int_{0}^{1}y^{2}(x)\phi_{1}(x)\,{\rm d}x=0.$ Noting that $\phi_{1}(x)>0$ for $x\in (0,1)$, we have $y(x)=0$ for $x\in [0,1]$ and $y=0$, which contradicts the fact $y\in P\setminus\{0\}$.

To prove Theorem 2.2, we first prove an equivalent result on the boundary value problem (2.9). We define a function $f:[0,1]\times \mathbb R_{+}\to \mathbb R$ by

$f(x,u)=\left\{ \begin{array}{ll} u(1-u)-h(x)\rho_{\varepsilon}(u) & \mbox{ if }x\in [0,1]\mbox{ and }u\in [0,1],\\ -h(x)& \mbox{ if }x\in [0,1]\mbox{ and }u\in (1,\infty). \end{array} \right.$

(4.1)

Since $h$ and $\rho_{\varepsilon}$ are continuous and $\rho_{\varepsilon}(u)=1$ for $u>1$, $f$ is continuous on $[0,1]\times \mathbb R_{+}$.

The following result shows that (2.9) is equivalent to the following boundary value problem.

$\label{log1} \begin{cases} -y''(x)=\lambda f(x,y(x)) \mbox{ for }x\in [0,1],\\ y(0)=y(1)=0. \end{cases}$

(4.2)

Theorem 4.1. Assume that $h$ satisfies the condition $(C)$ and let $\lambda>0$. Then the following assertions hold.

$(1)$ If $y\in P$ is a solution of (2.9), then $\|y\|\le 1$.

$(2)$ If $y\in P$ is a solution of (4.2), then $\|y\|\le 1$.

$(3)$ $y\in P$ is a solution of (2.9) if and only if $y\in P$ is a solution of (4.2).

Proof. $(1)$ Suppose $y\in P$ is a solution of (2.9). If $\|y\|>1$, then there exists $x_{0}\in [0,1]$ such that $y(x_{0})=\|y\|>1$. By $y(0)=y(1)=0$, $x_{0}\in (0,1)$. Since $y\in C^{2}[0,1]$, $y'(x_{0})=0$ and $y''(x_{0})\le 0$, and since $1-y(x_{0})<0$, by (2.9) we have

$0\le -y''(x_{0})=\lambda \bigl[y(x_{0})(1-y(x_{0}))-h(x_{0})\rho_{\varepsilon}(y(x_{0}))\bigr]<0,$

a contradiction. This shows that the solution $y$ satisfies $\|y\|\le 1.$

$(2)$ Assume that $y\in P$ is a solution of (4.2). If $\|y\|>1$, then there exists $x_{0}\in (0,1)$ such that $y(x_{0})=\|y\|>1$. Then $y'(x_{0})=0$ and there exists $\delta_{0}\in (0, \min\{x_{0}, 1-x_{0}\})$ such that $y(x)>1$ for $x\in (x_{0}-\delta_{0}, x_{0}+\delta_{0})$. Let

$\label{x1} x_{1}=\inf\{x\in [0,1]: y(s)>1 \mbox{ for }s\in [x,x_{0}]\}$

and

$\label{x2} x_{2}=\sup\{x\in [0,1]: y(s)>1\mbox{ for }s\in [x_{0},x]\}.$

Noting that $y(0)=y(1)=0$, we have $(i)$ $0<x_{1}<x_{0}< x_{2}<1$, $(ii)$ $y(x)>1$ for $x\in (x_{1},x_{2})$ and $(iii)$ $y(x_{1})=1$ and $y(x_{2})=1$. Since

$f(x,u)=-h(x)\rho_{\varepsilon}(u)=-h(x)\mbox{ for }x\in [0,1]\; \mbox{ and }\;u\ge 1,$

it follows from (4.2) that

$-y''(x)=\lambda f(x,y(x))=-\lambda h(x)\mbox{ for }x\in (x_{1},x_{2}).$

Integrating the above equation from $x_{0}$ to $x$ implies

$\label{inty} y'(x)=y'(x)-y'(x_{0})=\int_{x_{0}}^{x}y''(s)\,ds=\lambda \int_{x_{0}}^{x}h(s)\,ds\mbox{ for }x\in [x_{1},x_{2}].$

(4.3)

Since $h(s)\ge 0$ for $s\in [0,1]$, by (4.3) we have $y'(x)\le 0$ for $x\in [x_{1},x_{0}]$ and $y'(x)\ge 0$ for $x\in [x_{0},x_{2}]$. Hence, $y$ is decreasing on $[x_{1},x_{0}]$ and increasing on $[x_{0},x_{2}]$. Hence, $y(x)\ge y(x_{0})$ for $x\in [x_{1},x_{2}]$ and

$y(x)=y(x_{0})=\|y\|>1\mbox{ for }x\in [x_{1},x_{2}].$

It follows that $y(x_{1})>1$, which contradicts the fact $y(x_{1})=1$ given in the above property $(iii)$. Hence, the solution $y$ of (4.2) satisfies $\|y\|\le 1$.

$(3)$ Assume that $y\in P$ is a solution of (2.9). By the assertion $(1)$, $\|y\|\le 1$ and $0\le y(x)\le 1$ for $x\in [0,1]$. By (4.1), we obtain

$\label{inq2} f(x,y(x))=y(x)[1-y(x)]-h(x)\rho_{\varepsilon}(y(x))\mbox{ for }x\in [0,1].$

(4.4)

By (2.9), $y$ satisfies (4.2). Conversely, assume that $y\in P$ is a solution of (4.2). By the assertion $(2)$, $\|y\|\le 1$. By (4.1) and (4.4), $y$ satisfies (2.9).

Theorem 4.1 $(1)$ shows that if $y\in P$ is a solution of (2.9), then $y(x)\le 1$ for $x\in (0,1)$. Hence, the size of the population must be below the carrying capacity $1$ everywhere on $[0,1]$. When $h\equiv 0$, the result was proved in [20,p.222].

It is well known that the boundary value problem (4.2) is equivalent to the following eigenvalue problem

$\label{hamapp} y(x)=\lambda \int_{0}^{1}k(x,s)f(s,y(s))\,ds\mbox{ for }x\in [0,1],$

(4.5)

where $k:[0,1]\times [0,1]\to \mathbb R_{+}$ is the Green's function defined by

$\label{kernel} k(x,s)=\left\{ \begin{array}{ll} (1-x)s& \mbox{ if }0\le s\le x\le 1,\\ x(1-s)& \mbox{ if }0\le x<s\le 1. \end{array} \right.$

(4.6)

Proof of Theorem 2.2. We prove that the Green's function defined in (4.6) and the function $f$ defined in (4.1) satisfy all the conditions of Theorem 3.2.

Let $\Phi(s)=s(1-s)$ for $s\in [0,1]$ and

$\label{c} C(x)=\min\{x, 1-x\}\mbox{ for }x\in [0,1].$

By [12,Lemma 2.1], $(C_{1})$ holds. For $r\in \mathbb R_{+}$, we define a function $g_{r}:[0,1]\to \mathbb R_{+}$ by

$\label{gr} g_{r}(x)=\frac{1}{4}+h(x).$

By (4.1), if $r\in [0,1]$, then

$|f(x,u)|\le u(1-u)+h(x)\le \frac{1}{4}+h(x)=g_{r}(x)\mbox{ for }x\in [0,1]\;\mbox{ and }\;u\in [0,r]$

and if $r>1$, then

$|f(x,u)|\le g_{r}(x)\mbox{ for }x\in [0,1]\mbox{ and }u\in [0,1]$

and

$|f(x,u)|=h(x)\rho_{\varepsilon}(u)= h(x) \le g_{r}(x)\mbox{ for }x\in [0,1]\mbox{ and }u\in (1,r].$

Hence, $f$ satisfies $(C_{2})$ $(ii)$. Since $k$ and $g_{r}$ are continuous, it follows from [12,Lemma 2.1] that $(C_{2})$ $(i)$ holds. We define a function $\eta:[0,1]\to \mathbb R_{+}$ by

$\eta(x)=h(x).$

(4.7)

By (4.1), we see that

$f(x,u)\ge -h(x)\rho_{\varepsilon}(u)\ge-h(x)\mbox{ for }x\in [0,1]\mbox{ and }u\in \mathbb R_{+}$

and $(C_{3})$ with $\eta=h$ holds. By [13,Proposition 1], we have

$\label{khc} \int_{0}^{1}k(x,s)h(s)\,ds\le r(h)C(x)\mbox{ for }x\in [0,1],$

(4.8)

where

$r(h)=\max\Bigl\{\int_{0}^{1}sh(s)\,ds, \int_{0}^{1}(1-s)h(s)\,ds\Bigr\}$

and $(C_{4})$ with $\eta=h$ holds. Since $a,b\in (0,1)$ with $a<b$, we have

$\underline{c}(a,b)=\min\{C(x):x\in [a,b]\}=\min\{a,1-b\}>0$

(4.9)

and $(C_{5})$ holds. By (4.1), we have

$\overline{f}(u)=\sup\limits_{0\le x\le 1}f(x,u)=\left\{ \begin{array}{ll} u(1-u)-\underline{h}(0,1)\rho_{\varepsilon}(u)& \mbox{ if }0\le u\le 1,\\ -\underline{h}(0,1)& \mbox{ if }1<u<\infty. \end{array} \right.$

Hence,

$\label{finfty} f^{\infty}=\lim\limits_{u\to \infty}\dfrac{\overline{f}(u)}{u}=\lim\limits_{u\to \infty}\dfrac{-\underline{h}(0,1)}{u}=0$

(4.10)

and Theorem 3.2 $(i)$ holds. By (4.8), we have

$\begin{align*} m_{h}(a,b)&=\left(\max\limits_{a\le x\le b}\int_{0}^{1}k(x,s)h(s)\,ds\right)^{-1}\ge r(h)^{-1}(\max\{C(x): a\le x\le b\})^{-1}\\ &=r(h)^{-1}\overline{c}(a,b)^{-1}. \end{align*}$

This implies

$\dfrac{1}{r(h)m_{h}(a,b)}\le \overline{c}(a,b) \mbox{ and } 1-\dfrac{1}{r(h)m_{h}(a,b)}\ge 1-\overline{c}(a,b)>0.$

By (4.9), we see

$\label{cablower} \underline{c}(a,b)=\left\{ \begin{array}{ll} a& \mbox{ if }0\le a\le b\le \frac{1}{2},\\ \min\{a,1-b\}& \mbox{ if }0\le a\le \frac{1}{2}\le b\le 1,\\ 1-b& \mbox{ if }\frac{1}{2}\le a\le b\le 1 \end{array} \right.$

and

$\label{cabupper} \overline{c}(a,b)=\left\{ \begin{array}{ll} b& \mbox{ if }0\le a\le b\le \frac{1}{2},\\ \dfrac{1}{2}& \mbox{ if }0\le a\le \frac{1}{2}\le b\le 1,\\ 1-a& \mbox{ if }\frac{1}{2}\le a\le b\le 1. \end{array} \right.$

Hence, by (2.10), we have

$\omega(a,b)=\underline{c}(a,b)[1-\overline{c}(a,b)].$

Let $\delta=\rho \omega(a,b)$. Then

$\label{omegaabrho} \rho\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\} = \min\{\delta(1-\delta), \rho(1-\rho)\}.$

(4.11)

By (4.7), (4.9) and (3.15), we have

$\begin{align*} \delta^{*}=\delta^{*}(a,b,\rho,\eta)&=\rho \underline{c}(a,b)\bigl(1-\frac{1}{r(\eta)m_{\eta}(a,b)}\bigr)= \rho \underline{c}(a,b)\Bigl(1-\dfrac{1}{r(h)m_{h}(a,b)}\Bigr)\\ &\ge \rho \underline{c}(a,b)[1-\overline{c}(a,b)]=\delta \end{align*}$

and $\delta\in (0,\delta^{*}]$. Noting that

$f(x,u)=u(1-u)-h(x)\rho_{\varepsilon}(u)\mbox{ for }x\in [0,1]\mbox{ and }u\in [0,1],$

we have for $u\in [0,1]$,

$\underline{f}_{a,b}(u)=\min\{f(x,u): x\in [a,b]\}=u(1-u)-\overline{h}(a,b)\rho_{\varepsilon}(u).$

Hence,

$\begin{align*} \underline{f}_{\delta}^{\rho}&=\min\{\underline{f}_{a,b}(u): u\in [\delta,\rho]\}=\min\{u(1-u)-\overline{h}(a,b)\rho_{\varepsilon}(u): u\in [\delta,\rho]\}\\ &\ge \min\{u(1-u)-\overline{h}(a,b): u\in [\delta,\rho]\}\\ &=\min\{\delta(1-\delta)-\overline{h}(a,b), \rho(1-\rho)-\overline{h}(a,b)\}\\ &= \min\{\delta(1-\delta), \rho(1-\rho)\}-\overline{h}(a,b). \end{align*}$

This, together with (4.11) and $(H_{2})$ implies

$\begin{align*} \underline{f}_{\delta}^{\rho}+\underline{\eta}(a,b)&= \underline{f}_{\delta}^{\rho}+\underline{h}(a,b)\ge\min\{\delta(1-\delta), \rho(1-\rho)\}-(\overline{h}(a,b)-\underline{h}(a,b))\\ &\ge \dfrac{\rho\min\{a,1-b\} M_{1}(a,b)}{\lambda}>0 \end{align*}$

and Theorem 3.2 $(ii)$ holds. By (3.17) and (4.11),

$\begin{align*} \mu_{*}(a,b, \rho, \delta)&=\dfrac{\rho\underline{c}(a,b) M_{1}(a,b)}{\underline{f}_{\delta}^{\rho}(a,b)+\underline{\eta}(a,b)}\le \dfrac{\rho \min\{a,1-b\}M_{1}(a,b)}{\min\{\delta(1-\delta), \rho(1-\rho)\}-(\overline{h}(a,b)-\underline{h}(a,b))}\\ &=\dfrac{\rho \min\{a,1-b\}M_{1}(a,b)}{\rho\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}-(\overline{h}(a,b)-\underline{h}(a,b))}. \end{align*}$

This, together with $(H_{2})$, implies

$\lambda>\dfrac{\rho \min\{a,1-b\}M_{1}(a,b)}{\rho\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}-(\overline{h}(a,b)-\underline{h}(a,b))}\ge\mu_{*}(a,b, \rho, \delta).$

By (4.10) and (3.16), $\mu^{*}(a,b,\rho)=\rho \underline{c}(a,b)r(h)^{-1}$ and by $(H_{3})$, $\lambda<\mu^{*}(a,b,\rho)$. Hence,

$\label{muabrho1} \mu_{*}(a,b, \rho, \delta)<\lambda<\mu^{*}(a,b,\rho)$

(4.12)

and $\mu_{*}(a,b, \rho, \delta)<\mu^{*}(a,b,\rho)$. This shows that Theorem 3.2 $(iii)$ holds. Since $\lambda\in \bigl(\mu_{*}(a,b, \rho),\mu^{*}(a,b,\rho)\bigr)$, it follows from (4.12) and Theorem 3.2 that (4.5) has one solution $z$ in $P$. By the equivalence of solutions of (4.5) and (4.2), $z$ is nonnegative solution of (4.2). By Lemma 4.1, $z$ is a nonnegative solution of (2.9). Since $C(x)>0$ for $x\in (0,1)$, it follows from Lemma 3.2 $(iii)$ that $y(x)>0$ for $x\in (0,1)$.

Proof of Remark 2.2. By $(H_{1})$, we have

$\lambda>\dfrac{\min\{a,1-b\} M_{1}(a,b)} {\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}}.$

It follows that

$\begin{align*} \dfrac{\rho \min\{a,1-b\}}{\lambda}& < \dfrac{ \min\{\rho\omega(a,b)(1-\rho\omega(a,b)), \rho(1-\rho)\}}{M_{1}(a,b)}\\ &\le \dfrac{1}{4M_{1}(a,b)}=\dfrac{1}{4}\min\limits_{a\le x\le b}\int_{a}^{b}k(x,s)\,ds\le \dfrac{1}{4}. \end{align*}$

By $(H_{3})$, we see that

$\underline{h}(0,1)/2\le \max\left\{\int_{0}^{1}sh(s)\,ds, \int_{0}^{1}(1-s)h(s)\,ds\right\}<\dfrac{\rho \min\{a,1-b\}}{\lambda}<\dfrac{1}{4}.$

It follows that $\underline{h}(0,1)<1/2$.

Proof of Corollary 2.1. We prove that Theorem 2.2 with $a=\frac{1}{4}$ and $b=\frac{3}{4}$ holds. Let $a=\frac{1}{4}$ and $b=\frac{3}{4}$. By [18,Corollary 3.2 and its proof] or [12,Example 2.1], $M_{1}(\frac{1}{4},\frac{3}{4})=16$ and $\underline{c}(\frac{1}{4},\frac{3}{4})=\frac{1}{4}$. By computations, we have $\min\{a,1-b\}=\frac{1}{4}$, $\overline{c}(\frac{1}{4},\frac{3}{4})=\|C\|=\frac{1}{2}$, $\omega(\frac{1}{4},\frac{3}{4})= \dfrac{1}{8}$ and

$\dfrac{\min\{a,1-b\} M_{1}(a,b)} {\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}}=\dfrac{\frac{1}{4} (16)} {\min\left\{\dfrac{1}{8}\left(1-\dfrac{\rho}{8}\right), 1-\rho\right\}}=\dfrac{4}{\eta_{\rho}}.$

Hence, the condition $(1)$ implies that Theorem 2.2 $(H_{1})$ with $a=\frac{1}{4}$ and $b=\frac{3}{4}$ holds. If $a=\frac{1}{4}$ and $b=\frac{3}{4}$, then

$\rho\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}= \rho \min\left\{\dfrac{1}{8}\left(1-\dfrac{\rho}{8}\right), 1-\rho\right\}=\rho \eta_{\rho}$

and

$\dfrac{\rho\min\{a,1-b\} M_{1}(a,b)}{\lambda}=\dfrac{4\rho}{\lambda}.$

Hence, if $a=\frac{1}{4}$ and $b=\frac{3}{4}$, then

$\label{eqanb} \rho \eta_{\rho}-\dfrac{4\rho}{\lambda}= \rho\min\{\omega(a,b)(1-\rho\omega(a,b)), 1-\rho\}-\dfrac{\rho\min\{a,1-b\} M_{1}(a,b)}{\lambda}.$

(4.13)

When $\lambda\in \left[\dfrac{9}{2\eta_{\rho}},\infty\right)$, it is easy to verify that $\dfrac{\rho}{2\lambda}\le \rho\eta_{\rho}-\dfrac{4\rho}{\lambda}.$ This, together with the condition $(2)$ implies

$\label{hh8} h^{*}\left(\frac{1}{4},\frac{3}{4}\right)\le \|h\|<\dfrac{\rho}{2\lambda}\le \rho\eta_{\rho}-\dfrac{4\rho}{\lambda}.$

This, together with the second part of the condition $(1)$, implies that

$\label{hh9} h^{*}\left(\frac{1}{4},\frac{3}{4}\right)< \rho\eta_{\rho}-\dfrac{4\rho}{\lambda}\mbox{for each }\lambda\in \left(\dfrac{4}{\eta_{\rho}}, \infty\right).$

By (4.13), we see that Theorem 2.2 $(H_{2})$ with $a=\frac{1}{4}$ and $b=\frac{3}{4}$ holds.

By the condition $(2)$ and $a=\frac{1}{4}$ and $b=\frac{3}{4}$, we have

$\begin{align*} r(h)&=\max\left\{\int_{0}^{1}sh(s)\,ds, \int_{0}^{1}(1-s)h(s)\,ds\right\} \le \|h\|\max\left\{\int_{0}^{1}s\,ds, \int_{0}^{1}(1-s)\,ds\right\}\\ &=\frac{\|h\|}{2}< \dfrac{\rho}{4\lambda}= \dfrac{\rho \min\{a,1-b\}}{\lambda}. \end{align*}$

Hence, Theorem 2.2 $(H_{3})$ with $a=\frac{1}{4}$ and $b=\frac{3}{4}$ holds. The result follows from Theorem 2.2.

Proof of Theorem 2.3. It is sufficient to show that for each case, Corollary 2.1 $(1)$ and $(2)$ hold.

$(T_{1})$ If $32<\lambda\le 36$, then it is easy to verify

$\dfrac{8(\lambda-36)}{\lambda}\le 0< \frac{8(\lambda-32)}{\lambda}\le \frac{8}{9}$

and

$\label{inqeta1} \frac{4}{\eta_{\rho}}< \lambda<\frac{9}{2\eta_{\rho}}\mbox{ for }\rho\in \left(0,\dfrac{8(\lambda-32)}{\lambda}\right)\subset \left(\dfrac{8(\lambda-36)}{\lambda}, \dfrac{8(\lambda-32)}{\lambda}\right),$

(4.14)

where $\eta_{\rho}=\dfrac{8-\rho}{64}$. We define a function $D_{\lambda}:(0,\frac{8}{9})\to \mathbb R$ by

$\label{H**} D_{\lambda}(\rho)=\rho\eta_{\rho}-\dfrac{4\rho}{\lambda}.$

Then $D_{\lambda}(\rho)=\dfrac{\rho(8-\rho)}{64}-\dfrac{4\rho}{\lambda}$ and

$(D_{\lambda})'(\rho)=-\frac{1}{32}\left[\rho-\frac{4(\lambda-32)}{\lambda}\right]\mbox{ for }\rho\in (0,\frac{8}{9}).$

Since $32<\lambda\le 36$, we have $0<\frac{4(\lambda-32)}{\lambda}\le \frac{4}{9}.$ Hence, $D_{\lambda}$ is strictly increasing on $\Bigl(0,\frac{4(\lambda-32)}{\lambda}\Bigr)$, strictly decreasing on $\Bigl(\frac{4(\lambda-32)}{\lambda}, \frac{8}{9}\Bigr)$ and

$\label{max1} D_{\lambda}\left(\frac{4(\lambda-32)}{\lambda}\right)=\frac{(\lambda-32)^{2}}{4\lambda^{2}}.$

(4.15)

$(i)$ By the first inequality of the condition $(i)$, we have

$\label{inqhlambda} 2\lambda\|h\|<\frac{4(\lambda-32)}{\lambda}.$

(4.16)

By the second inequality of the condition $(i)$, (4.15), (4.16) and the continuity of $D_{\lambda}$, there exists $\rho\in \bigl(2\lambda\|h\|,\frac{4(\lambda-32)}{\lambda}\bigr)$ such that

$\label{hh} h^{*}\left(\frac{1}{4},\frac{3}{4}\right)<D_{\lambda}(\rho)=\rho\eta_{\rho}-\dfrac{4\rho}{\lambda}.$

(4.17)

Since $\|h\|<\frac{\rho}{2\lambda}$, we see from (4.14) and (4.17) that Corollary 2.1 $(1)$ and $(2)$ hold.

$(ii)$ By the first part of the condition $(ii)$, we have

$\frac{4(\lambda-32)}{\lambda}\le 2\lambda\|h\|<\frac{8(\lambda-32)}{\lambda}\le \frac{8}{9}.$

By computation, we have

$D_{\lambda}(2\lambda\|h\|)=\dfrac{\|h\|(-\|h\|\lambda^{2}+4\lambda-128)}{16}.$

This, together with the second part of the condition $(ii)$ and the continuity of $D_{\lambda}$, implies that there exists $\rho\in \left(2\lambda\|h\|,\frac{8(\lambda-32)}{\lambda}\right)$ such that

$\label{last1} h^{*}\left(\frac{1}{4},\frac{3}{4}\right)<D_{\lambda}(\rho)=\rho\eta_{\rho}-\dfrac{4\rho}{\lambda}.$

From this and (4.14) we see that Corollary 2.1 $(1)$ and $(2)$ hold.

$(T_{2})$ $(i)$ By $36<\lambda\le \frac{81}{2}$ and the inequality of the condition $(i)$, we have

$2\lambda \|h\|<\frac{8(\lambda-36)}{\lambda}\le \frac{8}{9}.$

Let $\rho\in \Bigl(2\lambda \|h\|, \frac{8(\lambda-36)}{\lambda}\Bigr]$ and $\eta_{\rho}=\dfrac{8-\rho}{64}$. Then $\|h\|<\dfrac{\rho}{2\lambda}$ and it is easy to verify that $\lambda\ge \frac{9}{2\eta_{\rho}}.$ Hence, Corollary 2.1 $(1)$ and $(2)$ hold.

$(ii)$ Since $36<\lambda\le \frac{81}{2}$, we have $1-\frac{9}{2\lambda}\le \frac{8}{9}<\frac{\lambda-4}{\lambda}$ and

$\label{ininq} \frac{4}{\eta_{\rho}}<\lambda<\frac{9}{2\eta_{\rho}}\mbox{ for }\rho\in \Bigl[\frac{8}{9}, \frac{\lambda-4}{\lambda}\Bigr).$

where $\eta_{\rho}=1-\rho$. We define a function $D^{*}_{\lambda}:\Bigl[\frac{8}{9}, \frac{\lambda-4}{\lambda}\Bigr)\to \mathbb R$ by

$D^{*}_{\lambda}(\rho)=\rho\eta_{\rho}-\dfrac{4\rho}{\lambda}.$

Then $D^{*}_{\lambda}(\rho)=\rho(1-\rho)-\dfrac{4\rho}{\lambda}$ and

$(D^{*}_{\lambda})'(\rho)=-2\Bigl(\rho-\frac{\lambda-4}{2\lambda}\Bigr) \mbox{ for }\rho\in \Bigl[\frac{8}{9}, \frac{\lambda-4}{\lambda}\Bigr).$

Since $\frac{\lambda-4}{2\lambda}<\frac{8}{9}$, $(D^{*}_{\lambda})'(\rho)<0$ for $\rho\in \Bigl[\frac{8}{9}, \frac{\lambda-4}{\lambda}\Bigr)$ and $D^{*}_{\lambda}$ is strictly decreasing on $\Bigl[\frac{8}{9}, \frac{\lambda-4}{\lambda}\Bigr)$. By computation, $D^{*}_{\lambda}(\frac{8}{9})=\frac{8(\lambda-36)}{81\lambda}$. This, together with the second part of the condition $(ii)$, and the continuity of $D^{*}_{\lambda}$, implies that there exists $\rho\in \Bigl(\frac{8}{9}, \frac{\lambda-4}{\lambda}\Bigr)$ such that $h^{*}(\frac{1}{4},\frac{3}{4})<D^{*}_{\lambda}(\rho)$. Since $\|h\|<\frac{4}{9\lambda}$, we have $2\lambda\|h\|<\frac{8}{9}\le \rho$ and $\|h\|<\frac{\rho}{2\lambda}.$ Hence, Corollary 2.1 $(1)$ and $(2)$ hold.

$(iii)$ By the first part of the condition $(iii)$, we have

$\frac{8}{9}\le 2\lambda\|h\|<\frac{\lambda-4}{\lambda}.$

By computation,

$\label{haha1} D^{*}_{\lambda}(2\lambda\|h\|)=2\|h\|(-2\|h\|\lambda^{2}+\lambda-4).$

(4.18)

This, together with the second part of the condition $(iii)$ and the continuity of $D^{*}_{\lambda}$, implies that there exists $\rho\in (2\lambda\|h\|,\frac{\lambda-4}{\lambda})$ such that $h^{*}(\frac{1}{4},\frac{3}{4})<D^{*}_{\lambda}(\rho)$. Hence, Corollary 2.1 $(1)$ and $(2)$ hold.

$(T_{3})$ $(i)$ Since $\lambda>\frac{81}{2}$, we have

$2\lambda\|h\|<\frac{2\lambda-9}{2\lambda}\mbox{ and }\dfrac{8}{9}<\dfrac{2\lambda-9}{2\lambda}.$

Let $\rho\in \Bigl(\max\bigl\{\frac{8}{9}, 2\lambda\|h\|\bigr\}, \frac{2\lambda-9}{2\lambda}\Bigr)$ and $\eta_{\rho}=1-\rho$. Then

$\label{r2} \frac{9}{2\eta_{\rho}}=\frac{9}{2(1-\rho)}<\lambda\mbox{ and }\|h\|<\dfrac{\rho}{2\lambda}$

and Corollary 2.1 $(1)$ and $(2)$ hold.

$(ii)$ By $\lambda>\frac{81}{2}$ and the first part of the condition $(ii)$, we have

$\label{com} \frac{8}{9}< 1-\frac{9}{2\lambda}\le 2\lambda\|h\|<\frac{\lambda-4}{\lambda}.$

By (4.18), the second part of the condition $(ii)$ and the continuity of $D^{*}_{\lambda}$, there exists $\rho\in \bigl(2\lambda\|h\|,\frac{\lambda-4}{\lambda}\bigr)$ such that $h^{*}(\frac{1}{4},\frac{3}{4})<D^{*}_{\lambda}(\rho)$ and Corollary 2.1 $(1)$ and $(2)$ hold.

Proof of Example 2.1. Since $h(x)\equiv\sigma(\lambda)$ for $x\in [0,1]$, $h^{*}\bigl(\frac{1}{4},\frac{3}{4}\bigr)=0$. When $32<\lambda\le 36$, combining $(T_{1})$ $(i)$ and $(ii)$ of Theorem 2.3 with $h^{*}\bigl(\frac{1}{4},\frac{3}{4}\bigr)=0$ implies $\|h\|<\frac{4(\lambda-32)^{2}}{\lambda^{2}}$. When $36<\lambda<\infty,$ combining $(T_{2})$ and $(T_{3})$ with $h^{*}\bigl(\frac{1}{4},\frac{3}{4}\bigr)=0$ implies $\|h\|<\frac{\lambda-4}{2\lambda^{2}}$. The result follows from (2.15) and Theorem 2.3.

Proof of Example 2.2. Let $h$ be the same as in (2.16). By (2.12), (2.13) and (2.16), we have

$\|h\|=\overline{h}\left(\frac{1}{4},\frac{3}{4}\right)=\frac{\gamma(\lambda)}{4} \mbox{ and }\underline{h}\left(\dfrac{1}{4},\dfrac{3}{4}\right)=\dfrac{3\gamma(\lambda)}{16}.$

$(i)$ We consider three cases: $(1)$ If $\lambda\in (32,36]$, then

$h^{*}\left(\frac{1}{4},\frac{3}{4}\right)=\overline{h}\left(\frac{1}{4},\frac{3}{4}\right)-\underline{h}\left(\frac{1}{4},\frac{3}{4}\right) =\frac{\gamma(\lambda)}{16}.$

It is easy to verify that

$\min\left\{\dfrac{4(\lambda-32)^{2}}{\lambda^{2}},\dfrac{8(\lambda-32)}{\lambda^{2}}\right\}=\left\{ \begin{array}{ll} \dfrac{4(\lambda-32)^{2}}{\lambda^{2}} & \mbox{ if }32<\lambda\le 34,\\ \dfrac{8(\lambda-32)}{\lambda^{2}}& \mbox{ if }34<\lambda\le 36. \end{array} \right.$

Hence, we obtain

$\|h\|<\dfrac{2(\lambda-32)}{\lambda^{2}}\mbox{ and }h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)< \dfrac{(\lambda-32)^{2}}{4\lambda^{2}}.$

The result follows from Theorem 2.3 $(T_{1})$ $(i)$.

$(2)$ If $\lambda\in (36, \frac{81}{2}]$ and $\gamma(\lambda)<\dfrac{16(\lambda-36)}{\lambda^{2}}$, then

$\|h\|=\dfrac{\gamma(\lambda)}{4}< \dfrac{4(\lambda-36)}{\lambda^{2}}.$

The result follows from Theorem 2.3 $(T_{2})$ $(i)$.

If $\lambda\in (36, \frac{81}{2}]$ and $\frac{16(\lambda-36)}{\lambda^{2}}\le \gamma(\lambda)<\frac{128(\lambda-36)}{81\lambda},$ then $\frac{128(\lambda-36)}{81\lambda} \le \frac{16}{9\lambda}.$ Hence,

$\dfrac{4(\lambda-36)}{\lambda^{2}}\le \|h\|<\dfrac{4}{9\lambda}\mbox{ and }h^{*}\left(\dfrac{1}{4},\dfrac{3}{4}\right)<\dfrac{8(\lambda-36)}{81\lambda}.$

The result follows from Theorem 2.3 $(T_{2})$ $(ii)$.

$(3)$ If $\lambda\in (\frac{81}{2}, \infty)$, then by the last inequality of (2.17),

$\|h\|=\dfrac{\gamma(\lambda)}{4}< \frac{2\lambda-9}{4\lambda^{2}}.$

The result follows from Theorem 2.3 $(T_{3})$ $(i)$.

---

5. Discussion

We have studied a one dimensional logistic population model of one species with quasi-constant-yield harvest rates governed by a reaction-diffusion equation subject to the Dirichlet BCs, an important BCs for population model of one species as pointed out in [22]. The emphasis is placed in seeking the intervals for $\lambda$ related to the patch size $l$ and the explicit expressions for the upper bounds of the norm of $\|h\|$ related to the amplitude $\delta$ under which the population becomes extinct or can survive. Two types of results on positive steady-state solutions are obtained for $0<\lambda<\pi^{2}$ (nonexistence results) or $\lambda>32$ (existence results). It remains open whether positive steady-state solutions exist for $\pi^{2}<\lambda\le 32$. For $\lambda>32$, the existence results are obtained for suitable function $h$ whose norm is below a piecewise rational function of $\lambda$. As illustrations, two realistic cases with $h$ being a location-independent constant or a unimodal polynomial have been used to exhibit the methods of how to get the upper bound of $h$. These results provide accurate quantities of harvest rates for the species without having the population die out.

Novel results on existence of positive solutions of a semi-positone Hammerstein integral equation are obtained, where the semi-positone condition allows the lower bound of the nonlinearity $f$ to be a function of $x$. It is the first paper to tackle the ecological model equation via semi-positone Hammerstein integral equations and the fixed point index theory. All of these would be interesting to mathematicians or ecologists who work on integral equations and boundary value problems with applications to real problems of ecological significance.

There are several interesting subjects for future work. The first one is to generalize the results obtained in this paper from one-dimensional models to higher-dimensional ones, that is, (1.1) with $X\in \Omega\subset \mathbb R^{n}$ subject to the Dirichlet BCs: $w(t,X)=0$ for $X\in \partial \Omega$. The approach involving semi-positone integral equation seems unsuitable to treating the positive steady-state solutions for higher-dimensional models due to lack of Green's functions. It would motivate the establishment of new theories to tackle the higher-dimensional ones. The second one is to drop the semi-positone condition on $f$, which may lead to solve the open question mentioned above. The last one is to seek the optimal values of $a$ and $b$ in Theorems 2.2 for the larger intervals of $\lambda$ or $h^{*}(a,b)$. This will improve Corollary 2.1 and Theorems 2.3-2.2, where $a=1/4$ and $b=3/4$ may not be the optimal choice.

---