Exothermic thermosolutal convection in a nanofluid-filled square cavity with a rotating Z-Fin: ISPH and AI integration

1.   Introduction

Convection heat transfer in ventilated cavities has numerous applications in industrial systems for building ventilation, thermal control of electronic devices, and removal of contaminated particles ^[1,2]. In addition, exothermic chemical reactions play an important role in chemical fractionation, combustion, explosions, oil recovery, and moisture transfer in grain storage. Nanofluids are a combination of a host fluid and nano-sized metal particles ^[3]. Nanofluids are widely used in the cooling process of heat exchangers and electronic devices ^[4]. In particular, the analysis of heat transfer and chemical reactions of nanofluids is expected to receive more attention in the near future because of its practical applications in petroleum extraction, nuclear reactors, evaporation, chemistry, and refrigeration industries ^{[5,6,7,8,9,10,11,12,13,14,15]}. Nanofluids—suspensions of nano-sized particles in base fluids—are drawing wide interest for their superior heat transfer capabilities. Early experiments revealed discrepancies between predicted and measured heat transfer coefficients (Yang et al. ^[5]). Nonetheless, subsequent findings underscore their broad potential. Putra et al. ^[6] show that adding nanofluids and thermoelectric cooling "significantly enhances heat removal". Mahian et al. ^[7] report that nanofluids "boost solar collector efficiency", while Rashidi et al. ^[8] highlight their impact on condensation and evaporation processes. In porous media, Khanafer and Vafai ^[9] call nanofluids "an effective means" to enhance convective heat transfer. Alhuyi Nazari et al. ^[10] confirm their ability to lower thermal resistance in heat pipes. Sajid and Ali ^[11], however, emphasize "key challenges", including high pumping power. Wahab et al. ^[12] demonstrate "notable performance gains" in solar energy systems, given proper stability management. Saidina et al. ^[13] confirm strong cooling effects for electronics, stressing the need for property optimization. Li et al. ^[14] propose neural networks for "accurate modeling" of nanofluid thermal behavior. Finally, Sheremet et al. ^[15] observes "substantial progress", while urging further research on stability and standardization. Mathematically, the chemical reaction is characterized by Arrhenius kinetics ^[16,17]. Rahman et al. ^[18] explored how exothermic reactions, modeled by Arrhenius kinetics, influence natural convection in a porous square cavity with nanofluids, utilizing the Galerkin finite element method (GFEM). Raees-ul-Haq ^[19] simulated the effects of exothermic reactions on free convection within a magnetized nanofluid-filled triangular porous cavity. Similarly, Hasan et al. ^[20] applied GFEM to examine magnetohydrodynamics (MHD) driven convective flows in a cavity influenced by such chemical reactions. Magnetic field and nanofluid flow interactions within cavities are valuable in engineering applications, such as refrigeration and cooling systems ^[21,22,23]. Aly et al. ^[24] used the incompressible smoothed particle hydrodynamics (ISPH) approach to examine how varying magnetic fields and helical structures affect convection within a ferrofluid cavity. Aly ^[25] also leveraged ISPH to simulate the thermosolutal convection in a nanofluid cavity, highlighting magnetic and thermal diffusion effects. Introduced by Gingold and Monaghan ^[26] and Lucy ^[27], the meshless Lagrangian nature of the SPH method has led to its widespread use in handling complex fluid dynamics scenarios, such as multi-phase flows, free surfaces, strong nonlinearities, and turbulent behaviors like jet impingement and nozzles ^{[28,29,30,31,32]}. Violeau and Issa ^[28] provided an extensive overview of the SPH method's capabilities in modeling turbulent, complex free-surface flows, highlighting its potential for simulating challenging fluid dynamics scenarios. Qiang et al. ^[29] utilized the SPH approach to study two-dimensional droplet collisions, effectively addressing the complexities of multi-phase flows with large density variations. Aly et al. ^[30] applied the ISPH method to investigate mixed convection in an inclined cavity with sinusoidal heated walls, advancing the understanding of convective flows in confined spaces. Garoosi and Shakibaeinia ^[31] proposed a refined high-order ISPH approach for simulating free-surface flows and heat transfer, enhancing accuracy in complex fluid–thermal interactions. More recently, Shimizu et al. ^[32] examined the applicability of a higher-order consistent ISPH method, assessing its performance in detailed simulations for ocean and polar engineering applications. To enhance heat and mass transfer in closed systems, heat exchangers and solar cells frequently utilize fins or textured surfaces. Saeid ^[33] investigated the influence of fin geometry on heating within a square cavity. Aly and El-Sapa ^[34] employed ISPH to analyze MHD thermosolutal convection in a nanofluid cavity featuring a rotating cylinder and a cross-shaped fin. Meanwhile, El Moutaouakil et al. ^[35] studied the impact of vertical fins on natural convection within cavities. Recent studies have explored the application of artificial neural networks (ANNs) to heat and mass transfer in cavities, demonstrating the potential of these models to accurately predict complex thermal and solutal behaviors under various boundaries and initial conditions. ANNs are a powerful computational tool in various fields due to their ability to represent complex nonlinear interactions and rapidly process large datasets. They are particularly useful for complex boundary conditions or multi-physics phenomena. ANNs can accurately forecast system behavior, improve performance, and provide real-time solutions. They have been used to predict thermal conductivity, examine fluid flow properties, and analyze convection in heat exchangers. Their generalization capability makes them an ideal complement to conventional numerical techniques like ISPH. This study shows that combining ANNs with ISPH improves accuracy and computing efficiency in addressing exothermic thermosolutal convection in a nanofluid-filled square cavity. ANN models have become instrumental in handling nonlinear interactions and diverse parameters like temperature, concentration, velocity, and Nusselt and Sherwood numbers (^[36,37,38]). Lagaris et al. ^[39] utilized an ANN model to solve ordinary and partial differential equations, showing its effectiveness for complex equations. Díaz et al. ^[40] applied ANNs to simulate heat exchanger performance, improving predictive accuracy. Varol et al. ^[41] predicted natural convection flow and temperature in a triangular enclosure using ANN and ANFIS models. Motahar ^[42] used ANN to estimate non-Newtonian nanofluid behavior with phase change materials. Alhejaili et al. ^[43] combined ANN with ISPH to study heat and mass transfer in nano-encapsulated materials within complex cavities. Elshehabey et al. ^[44] integrated ANN and ISPH for modeling thermal radiation in porous, finned cavities. Lastly, Abdelsalam et al. ^[45] applied AI-powered ANN for bioconvection analysis involving nano-encapsulation and oxytactic microorganisms. This research explores the effects of exothermic reactions, magnetic fields, and Cattaneo–Christov heat flux on thermosolutal convection by applying the ISPH method within a nanofluid-filled cavity containing a rotating Z-shaped fin. The ANN model is also employed to precisely estimate average Nusselt and Sherwood numbers, providing deeper insights into the heat and mass transfer processes in this setup.

2.   Mathematical analysis

2.1.   Physical model and governing equations

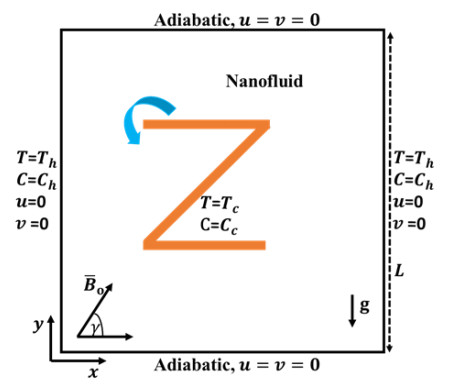
The initial setup of the rotating Z-shaped fin for thermosolutal convection analysis is depicted in Figure 1. The fin rotates with a circular velocity, represented by $\mathbf{V} = \omega \left(\mathbf{r}-{\mathbf{r}}_{0}\right)$, and is maintained at a specified low temperature (${T}_{c}$) and concentration (${C}_{c}$). The cavity's vertical walls are maintained at elevated temperature (${T}_{h}$) and concentration (${C}_{h}$), while the horizontal walls are adiabatic. The flow is modeled under the following assumptions:

● The flow is incompressible, laminar, and time dependent.

● The Boussinesq approximation is applied, accounting for buoyancy effects due to temperature and concentration variations.

● The fluid is Newtonian, and the nanofluid properties are assumed to be constant, except for density in the buoyancy term.

● Heat and mass transfer are driven by both thermal and solutal gradients.

● The governing equations are formulated in a Cartesian coordinate system ($x, y$) to represent the geometry of the square cavity.

● The rotating Z-shaped fin is modeled as a rigid body with no deformation.

The dimensional form of the governing equations, as outlined in references ^[46,47,48], is:

The subsequent dimensionless variables ^[46,47,48] are substituted into Eqs (1)−(5) as:

The dimensionless equations ^[46,47,48] are obtained as:

where $Sr = \frac{{D}_{2}}{{\alpha }_{f}}\left(\frac{\left({T}_{h}-{T}_{c}\right)}{\left({C}_{h}-{C}_{c}\right)}\right)$ is the Soret number, $Du = \frac{{D}_{1}}{{\alpha }_{f}}\left(\frac{\left({C}_{h}-{C}_{c}\right)}{\left({T}_{h}-{T}_{c}\right)}\right)$ is the Dufour number, ${\delta }_{C} = \frac{{\nu }_{f}{\delta }_{1}}{{L}^{2}}$ is a parameter of Cattaneo–Christov heat flux, $Ha = \sqrt{\frac{{\sigma }_{\mathrm{f}}}{{\mu }_{\mathrm{f}}}}{B}_{0}L$ is the Hartmann number, $Ra = \frac{\mathrm{g}{\beta }_{T}\left({T}_{h}-{T}_{c}\right){L}^{3}}{{\nu }_{f}{\alpha }_{\mathrm{f}}}$ is Rayleigh's number, $Pr = \frac{{\nu }_{f}}{{\alpha }_{f}}$ is the Prandtl number, $Le = \frac{{\alpha }_{f}}{{D}_{m}}$ is the Lewis number, and $N = \frac{{\beta }_{C}\left({C}_{h}-{C}_{c}\right)}{{\beta }_{T}\left({T}_{h}-{T}_{c}\right)}$ is a buoyancy ratio.

2.2.   Dimensionless boundary conditions

The boundary conditions for the model are defined as follows:

Vertical walls: Temperature ($\theta$) and concentration (${\Phi }$) are set to 1, with no-slip velocity conditions ($U = 0$, $V = 0$). (12)

Horizontal walls: Adiabatic and impermeable conditions are applied, ensuring no heat or mass flux ($\frac{\partial \theta }{\partial Y} = 0$, $\frac{\partial {\Phi }}{\partial Y} = 0$) and no-slip velocity ($U = 0$, $V = 0$).

Inner Z-shaped fin: The fin rotates, imposing velocity conditions ($U = {U}_{\mathrm{r}\mathrm{o}\mathrm{t}}$, $V = {V}_{\mathrm{r}\mathrm{o}\mathrm{t}}$) and maintaining lower temperature and concentration levels ($\theta = 0$, ${\Phi } = 0$).

The mean values for Nusselt and Sherwood numbers are:

2.3.   Nanofluid properties

The nanofluid properties are determined using the following equations ^[49,50,51]:

3.   The SPH formulation

The core concept of the SPH approximation is:

Here, $W$ is a quintic smoothing function:

where $\kappa = \frac{3}{16\pi {h}^{2}}$, and $q = {\boldsymbol{r}}_{ij}/h$ with $h$ as a smoothing length.

The renormalization factor ${\xi }_{i}$ is defined as ^[47,52]:

The first derivative is:

Figure 2 shows the initial schematic description of the SPH discretization of a target geometry and kernel (smoothing) function. The initial geometry is discretized into uniform nodes (particles). Any hydrodynamic function is calculated according to the SPH approximation.

4.   The ISPH method

The ISPH algorithm ^{[46,47,53,54]} is summarized in the following steps:

Step 1: Predict velocities.

Step 2: Solve the pressure Poisson equation.

Step 3: Correct velocities.

Step 4: Update thermal and solutal equations.

Step 5: Update the position of particles.

The shifting technique ^[55,56] is as follows:

Boundary treatment

This study employs the boundary particle renormalization method to handle boundary conditions within the ISPH framework. Figure 3 illustrates the setup, including the dummy boundary particles, renormalization boundary particles, and the computation of the kernel renormalization factor (${\gamma }_{a}$).

● Dummy boundary particles: These consist of a layer of boundary particles supplemented by two fictitious particles. The fictitious particles exert repulsive forces to minimize truncation errors in the smoothing function near the wall boundary. However, the use of dummy particles can lead to increased computational complexity in three-dimensional simulations due to the requirement for multiple particle layers.

● Renormalization boundary particles: This approach requires only a single boundary layer, significantly enhancing computational efficiency. The method calculates the kernel renormalization factor ($\gamma_a$) and its gradient ($\nabla \gamma_a$) at the boundary to implement the boundary conditions ^[47,52]. The Dirichlet conditions (e.g., fixed temperature and concentration) are straightforward to apply, while Neumann conditions (e.g., zero flux) are more challenging in complex geometries.

By adopting the renormalization approach, the study ensures accurate and computationally efficient boundary condition handling, suitable for the complex geometries involved in the cavity.

5.   Validation tests

The validation section highlights the effectiveness and accuracy of the ISPH method by comparing its results with benchmark FEM simulations ^[57] and Davis's numerical data ^[58] across various Rayleigh numbers ($Ra$), demonstrating its robustness for natural convection scenarios. Figure 4 presents a comparative analysis between the current ISPH model and previously validated finite element method (FEM) results ^[57] for natural convection in a square cavity at various Rayleigh numbers ($Ra = {10}^{3}, {10}^{4}, {10}^{5}, {10}^{6}$). Figures 4(a)–4(c) depict vertical velocity at $X = 0.5$, horizontal velocity at $Y = 0.5$, and temperature profiles at $Y = 0.5$, respectively. The results indicate strong agreement between the ISPH and FEM models, with deviations primarily at higher Rayleigh numbers due to the increasing nonlinearity of natural convection. The velocity and temperature profiles show consistent trends across all $Ra$ values, demonstrating the accuracy and reliability of the ISPH approach for capturing flow and thermal behaviors. These validations establish the robustness of the ISPH method in simulating natural convection and provide confidence in its application to complex configurations. Table 1 compares the average Nusselt numbers ($\overline{\mathrm{N}\mathrm{u}}$) obtained using the present ISPH model, the FEM method ^[57], and benchmark results from Davis ^[58] for natural convection in a square cavity across Rayleigh numbers ($Ra$) ranging from ${10}^{3}$ to ${10}^{6}$. The results show that the ISPH model closely aligns with both the FEM ^[57] and Davis benchmarks ^[58], with deviations becoming slightly more noticeable at higher $Ra$. These differences are attributed to the inherent approximations in numerical methods and the increased complexity of convection phenomena at higher $Ra$. The comparison demonstrates that the ISPH method provides reliable and accurate predictions, validating its effectiveness in modeling natural convection scenarios. Figure 5 illustrates the comparison of isotherm contour maps generated by the present ISPH method and the FEM ^[57] results at different Rayleigh numbers ($Ra$). Figures 5(a)–5(d) correspond to $Ra = {10}^{3}$, $Ra = {10}^{4}$, $Ra = {10}^{5}$, and $Ra = {10}^{6}$, respectively. The contours represent temperature distributions within the cavity, with values ranging from 0 to 1.0 at intervals of 0.1. The isotherms exhibit progressively steeper gradients and more pronounced curvature as $Ra$ increases, indicating intensified convection. At lower Rayleigh numbers, the conduction-dominated regime produces smoother contours, while at higher $Ra$, convection becomes dominant, leading to more complex isotherm patterns. The close agreement between the ISPH and FEM results across all cases demonstrates the reliability and accuracy of the ISPH method for modeling thermal behavior in natural convection scenarios.

6.   ANN modeling

An ANN model was developed to estimate $\overline{Nu}$ and $\overline{Sh}$ using an artificial intelligence-based approach. The model follows a multilayer perceptron (MLP) structure, a versatile neural network model known for its strong learning capabilities ^[59]. MLP networks consist of interconnected layers, with each layer directly connected to the next layer. There are basically three types of layers in an MLP network: input, hidden, and output layers. Within this MLP framework, time ($\tau$) and the Frank-Kamenetskii number (Fk) are used as input features, while the output layer generates the values of $\overline{Nu}$ and $\overline{Sh}$. The ANN architecture was based on an MLP with a single hidden layer. Determining the optimal number of neurons in the hidden layer posed a significant challenge, as no universally applicable method exists for this task ^[60]. To address this, an iterative approach was employed. Various configurations with different neuron counts were systematically tested, and their performance was evaluated based on metrics. Among these configurations, the model with 13 neurons in the hidden layer demonstrated the best overall performance, achieving a balance between accuracy and computational efficiency. Figure 6 displays the structure of the ANN model. The training process required careful organization of the dataset to ensure robust model generalization. A total of 56 data points were curated, following established methodologies in the literature ^[61]. These data points were divided into three subsets: 40 data points were allocated for training the model, 8 data points for validation, and 8 data points for testing. The training subset was used to optimize the model's weights and biases through backpropagation, while the validation subset served to monitor the model's performance during training and to prevent overfitting. Finally, the testing subset provided an independent evaluation of the model's predictive capability. The training process employed the Levenberg–Marquardt algorithm, a widely used optimization method in ANN applications due to its efficiency in handling nonlinear optimization problems. The activation function used in the hidden layer was the hyperbolic tangent sigmoid (tansig) function, which facilitates learning complex nonlinear relationships, while the output layer utilized a linear activation function to accommodate the continuous output variables. The equations for these transfer functions are:

The training process was terminated when the validation error failed to improve for a predetermined number of epochs (early stopping criterion), thereby minimizing the risk of overfitting. This detailed procedure ensured that the ANN model was appropriately configured, trained, and validated to achieve an accurate solution to the governing equations while maintaining computational efficiency. To assess the model's performance, several standard metrics were used, including mean squared error (MSE), coefficient of determination (R), and margin of deviation (MoD). The formulas for these metrics, essential in evaluating model accuracy, are provided below ^[60]:

The ANN model's training performance was evaluated for its robustness and reliability. The dataset was designed to capture a wide range of parametric variations in a problem. The model's predictive accuracy and generalization ability were assessed using a comparison between predicted and target values. The results showed high prediction accuracy, minimal residual errors, and strong correlation between predicted and target values. The consistency of the model's performance across validation and testing subsets confirmed its security and diversity, demonstrating the model's representativeness and dependability.

7.   Results and discussion

This study performed numerical simulations to analyze the impact of exothermic chemical reactions, magnetic fields, and the Cattaneo–Christov heat flux on double diffusion within a nanofluid-filled cavity with a rotating Z-shaped fin. The following ranges for the controlling parameters were considered: Frank-Kamenetskii number ($Fk$): $0\le Fk\le 6$; Cattaneo–Christov heat flux coefficient (${\delta }_{c}$): $0\le {\delta }_{c}\le 0.001$; Hartmann number ($Ha$): $0\le Ha\le 50$; Soret number ($Sr$): $0\le Sr\le 2$; Dufour number ($Du$): $0\le Du\le 2$; nanoparticle volume fraction ($\phi$): $0\le \phi \le 0.15$; and Z-shaped fin height from 0.5 to 0.6 $m$, width from 0.4 to 0.7 $m$, and length from 0.3 to 0.8 $m$. Fixed parameters included ${\delta }_{c} = 0.0001$, Rayleigh number ($Ra = {10}^{4}$), ${S}_{r} = 1.2$, $Du = 0.6$, $\phi = 0.05$, fin orientation angle ($\gamma = {45}^{\circ }$), ${F}_{k} = 2$, $N = 2$, and ${H}_{a} = 10$. Figures 7–9 depict temperature contours $\left(\theta \right)$, concentration contours $\left({\Phi }\right)$, and the velocity field $\left(V\right)$ under varying ${F}_{k}$ values across time intervals $\tau = 0.01$, $0.1$, and $0.3$. When ${F}_{k}$ increases, heat transfer intensifies, expanding thermal contours over time $\left(\tau \right)$. At $\tau = 0.01$, the cooling region covers much of the cavity, with hot areas along the vertical walls. As time progresses, the isotherms spread upward. Figure 8 shows that concentration $\left({\Phi }\right)$ shifts slightly as ${F}_{k}$ increases, while rotation of the Z-shaped fin at $\tau = 0.3$ causes ${\Phi }$ to spread from top to bottom. In Figure 9, higher ${F}_{k}$ values enhance the maximum velocity field. Figure 10 illustrates how varying the Hartmann number $\left(Ha\right)$ affects $\theta$, $\Phi$, and $V$, with Lorentz forces from a larger $Ha$ value slowing fluid velocity. When $Ha$ rises from 0 to 50, maximum velocity drops by 61.99%. Higher $Ha$ values also narrow the temperature and concentration distributions. Figure 11 shows the variations in the average Nusselt number ($\overline{Nu}$) and average Sherwood number ($\overline{Sh}$) over dimensionless time ($\tau$) under different Hartmann numbers ($Ha$), demonstrating the influence of magnetic fields on heat and mass transfer. At $Ha = 0$, where no magnetic field is present, $\overline{Nu}$ and $\overline{Sh}$ are highest due to enhanced convection. As $Ha$ increases to 20 and 50, the Lorentz force suppresses fluid motion, leading to reduced convective heat and mass transfer, as reflected in the decreasing $\overline{Nu}$ and $\overline{Sh}$ values. These results highlight the magnetic field's ability to regulate convection, which has significant applications in industries such as magnetic cooling, MHD pumps, and thermal management systems. The ability to control $Ha$ offers practical solutions for optimizing processes that require precise heat and mass transfer control, such as preventing overheating or improving chemical reactor efficiency. The observed suppression of convection with increasing Hartmann number ($Ha$) demonstrates its applicability in magnetic cooling systems and MHD pumps, where precise thermal regulation is critical. Figure 12 assesses Dufour number $\left(Du\right)$ effects on $\theta$, ${\Phi }$, and $V$. Results suggest that $Du$, which relates mass gradients to energy flux, has minimal impact on temperature, concentration, and velocity fields, likely due to the cooling fin's presence. $\overline{Nu}$ and $\overline{Sh}$ remained largely unaffected by $Du$ variations. Figure 13 examines how temperature, concentration, and velocity fields respond to increases in nanoparticle volume fraction $\left(\phi \right)$, representing the percentage of solid particles within the nanofluid mixture. Higher $\phi$ values extend the cooling region and raise fluid viscosity, reducing velocity. When $\phi$ increases from 0 to 0.15, maximum velocity decreases by 19.71% due to increased viscosity. Figure 14 indicates that as $\phi$ grows from 0 to 0.15, $\overline{Nu}$ increases by 22.43%, and $\overline{Sh}$ increases by 116.3%. The enhancement in $\overline{Nu}$ and $\overline{Sh}$ with increasing nanoparticle volume fraction ($\phi$) highlights its potential for optimizing heat exchangers and nanofluid-based solar collectors. Figures 15 and 16 analyze the Cattaneo–Christov heat flux $\left({\delta }_{c}\right)$ effects on $\theta$ and $V$ across times $\tau = 0.01$, $0.1$, and $0.3$, showing mild changes in temperature fields and a slight velocity rise with increasing ${\delta }_{c}$. Figures 17 and 18 explore the influence of Soret number $\left(Sr\right)$ on $\theta$, ${\Phi }$, and $V$, and on $\overline{Nu}$ and $\overline{Sh}$. As $Sr$ increases, thermal gradients cause lighter particles to move toward warmer areas and heavier particles toward cooler zones. Figure 17 shows that higher $Sr$ slightly modifies the isotherms and significantly enhances concentration. With $Sr$ increasing from 0 to 2, maximum velocity accelerates by 130.27%. Figures 19 and 20 explore how altering Z-shaped fin length affects $\theta$, ${\Phi }$, $V$, and $\overline{Nu}$ and $\overline{Sh}$. Reducing the fin's length strengthens temperature and concentration distributions within the cavity, raising maximum velocity by 16.99%. The Z-shaped fin's presence, despite slow rotation, acts as a flow barrier, highlighting the importance of optimal fin sizing for industrial cooling. Figure 20 shows that reducing fin size results in decreases in $\overline{Nu}$ and $\overline{Sh}$, underscoring the fin's role in regulating heat and mass transfer and fluid velocity within the cavity.

The training process of the ANN model was thoroughly evaluated using performance metrics and visual aids for better understanding and clarity. Figure 21 illustrates the training performance graph, which tracks the variation of the MSE over successive training epochs. The graph clearly demonstrates a consistent decline in MSE values, starting from an initially high value and converging toward minimal error levels as the training progressed. The convergence indicates effective learning and optimization of the ANN model. For clarity, annotations in Figure 21 highlight key stages in the training process, such as the initialization phase with high errors, the rapid error reduction phase, and the stabilization of error levels as the model approaches optimal performance. These annotations provide insight into the dynamics of the training process, aiding readers in interpreting the graph more effectively. Figure 22 provides additional validation of the model's training through an error histogram, which visualizes the distribution of prediction errors across the dataset. The error values are concentrated near zero, confirming that the model achieves a high degree of accuracy and minimal residuals. Following training verification, Figure 23 compares ANN-predicted and target $\overline{Nu}$ and $\overline{Sh}$ values, with close alignment seen. Figure 24 presents MoD values, which largely remain near zero, signifying minimal prediction error. Mean deviation rates for $\overline{Nu}$ and $\overline{Sh}$ are 0.01% and 0.06%, respectively. In Figure 25, differences between target and ANN values further support model precision. Figure 26 plots target values (x-axis) against ANN predictions (y-axis), showing alignment along the zero-error line for both outputs. The ANN model's MSE was $4.21\times {10}^{-6}$ and $R$ value was 0.99994, confirming high prediction accuracy for $\overline{Nu}$ and $\overline{Sh}$.

8.   Conclusions

This study employed numerical simulations to investigate the effects of exothermic chemical reactions, magnetic fields, and Cattaneo–Christov heat flux on thermal and solutal transport within a nanofluid-filled square cavity containing a rotating Z-shaped fin. The ISPH approach facilitated the analysis of fluid-structure interactions between the rotating fin and nanofluid, providing insights applicable to cooling, energy, and heat exchange systems. The study revealed that increasing the Frank-Kamenetskii number significantly enhances convection, improving thermal and concentration transfer and velocity. Magnetic field–induced Lorentz forces were shown to suppress fluid motion, reducing velocity by 61.99% and leading to decreases in average Nusselt and Sherwood numbers by 16.87% and 11.81%, respectively. Increasing the nanoparticle volume fraction to 15% raised the average Nusselt number by 22.43% and the Sherwood number by 116.3%, despite slowing fluid velocity by 19.71% due to increased viscosity. The Soret effect significantly improved concentration and velocity fields, while fin geometry was found to play a critical role in optimizing heat and mass transfer. The integration of an ANN model demonstrated high accuracy in predicting average Nusselt and Sherwood numbers, making it an effective tool for evaluating nanofluid performance. This work advances the understanding of heat exchange in nanofluids by providing a detailed analysis of the combined effects of magnetic fields, exothermic reactions, and nanoparticle concentration. The novelty lies in the integrated ISPH-ANN framework, which efficiently models complex thermal and solutal interactions, enabling accurate predictions for practical applications such as thermal management systems, energy storage devices, and industrial cooling processes. These findings offer valuable guidance for designing and optimizing advanced heat exchange technologies in various industrial settings. Future work could explore extending the model to three-dimensional systems, considering non-Newtonian nanofluids, or incorporating transient effects of dynamic fin motion. Additionally, experimental validation and application of the ISPH-ANN framework to practical systems, such as solar collectors, desalination units, and heat exchangers, would provide deeper insights and further generalize the findings.

Limitations of the study

This study assumes incompressible, laminar, and two-dimensional flow using the Boussinesq approximation and constant nanofluid properties, which may not fully capture real-world complexities such as three-dimensional effects or variable properties. The boundary conditions, including adiabatic and impermeable walls, simplify practical scenarios. The results are specific to the chosen geometry and parameter ranges, limiting generalizability to other configurations. Additionally, the Z-shaped fin is modeled as a rigid body with fixed rotational speed, excluding potential effects of deformation or variable speeds. Finally, computational constraints, such as resolution and the efficiency of the ISPH method, may restrict the precision of the simulations. These limitations highlight areas for future research to enhance the model's applicability and accuracy.

Author contributions

Kuiyu Cheng and Abdelraheem M. Aly conceptualized the study, while Abdelraheem M. Aly, Nghia Nguyen Ho, and Andaç Batur Çolak handled methodology and software. Validation and formal analysis were conducted by Sang-Wook Lee and Weaam Alhejaili. Kuiyu Cheng, Nghia Nguyen Ho, and Andaç Batur Çolak managed data curation, with all authors contributing to writing, review, and editing. Abdelraheem M. Aly and Sang-Wook Lee supervised the work, and project administration and funding were managed by Sang-Wook Lee and Weaam Alhejaili. All authors approved the final manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The first author (A.M. Aly) extends his appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number (RGP. 2/613/45). This research was funded by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R229), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by Regional Innovation Cluster Development (R & D) by the Ministry of Trade, Industry and Energy (MOTIE, Korea) [Project Name: Open Innovation Project for Convergence Industry of Battery/Fuel Cell for Mobility Electrification and Energy Production/Storage (P0025406).

Conflict of interest

The authors declare that they have no conflict of interest.